Percolation on Fractal Networks: A Survey
Abstract
:1. Introduction
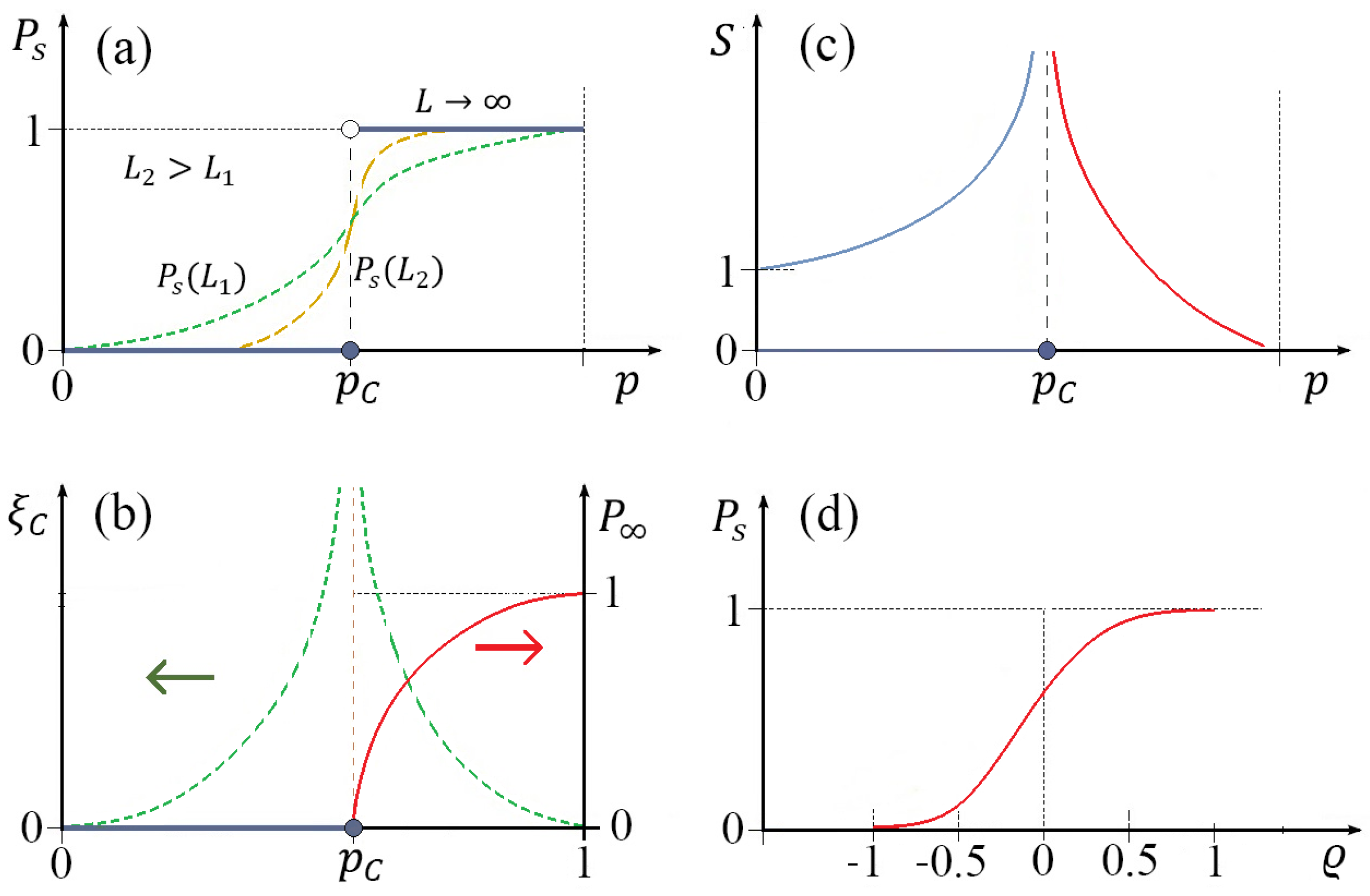
2. Main Features of Percolation
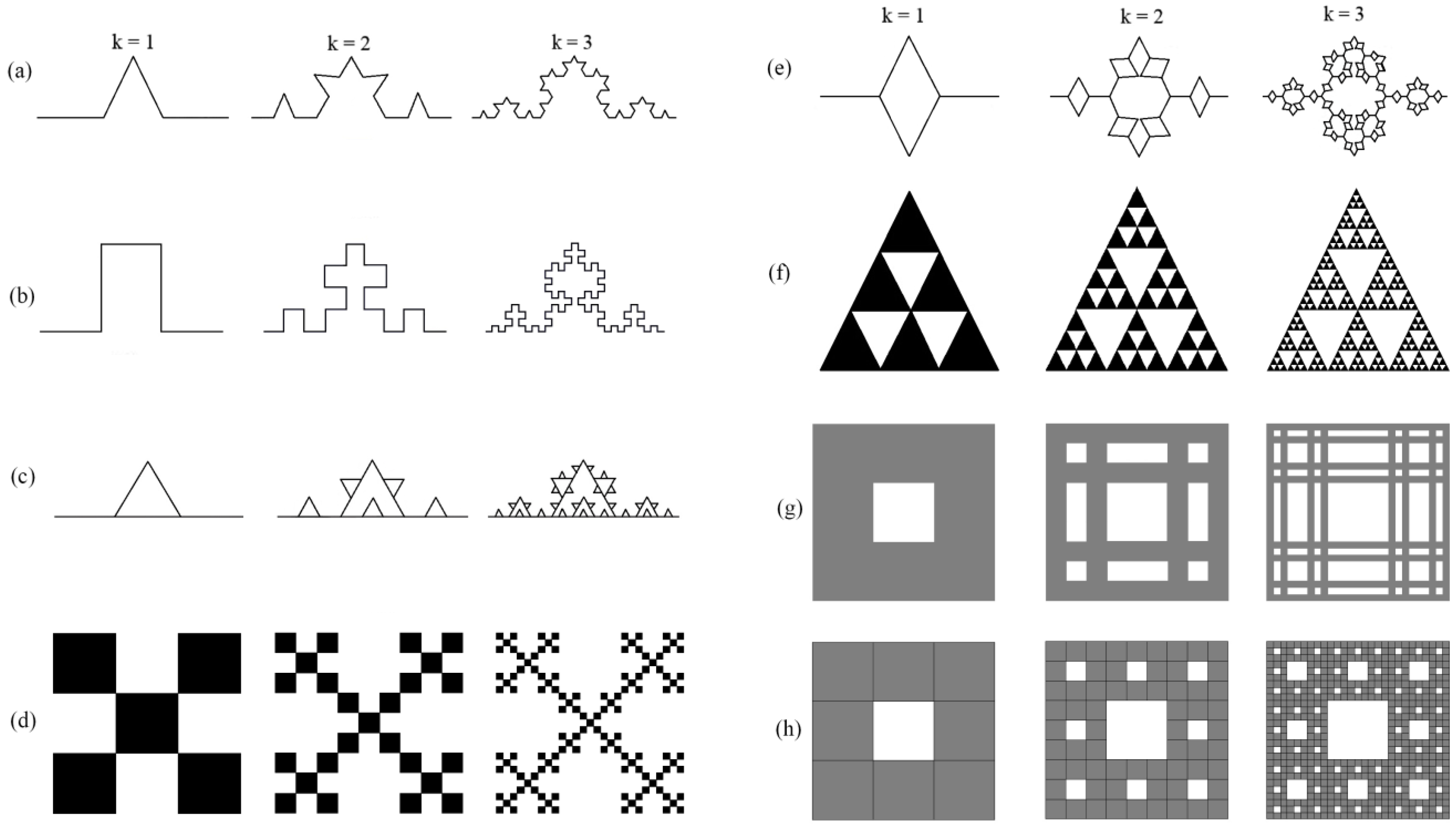
3. Key Attributes of Fractal Networks
3.1. Fractal Features of Infinitely Ramified Sierpinski Carpets
3.2. Cantor Tartans
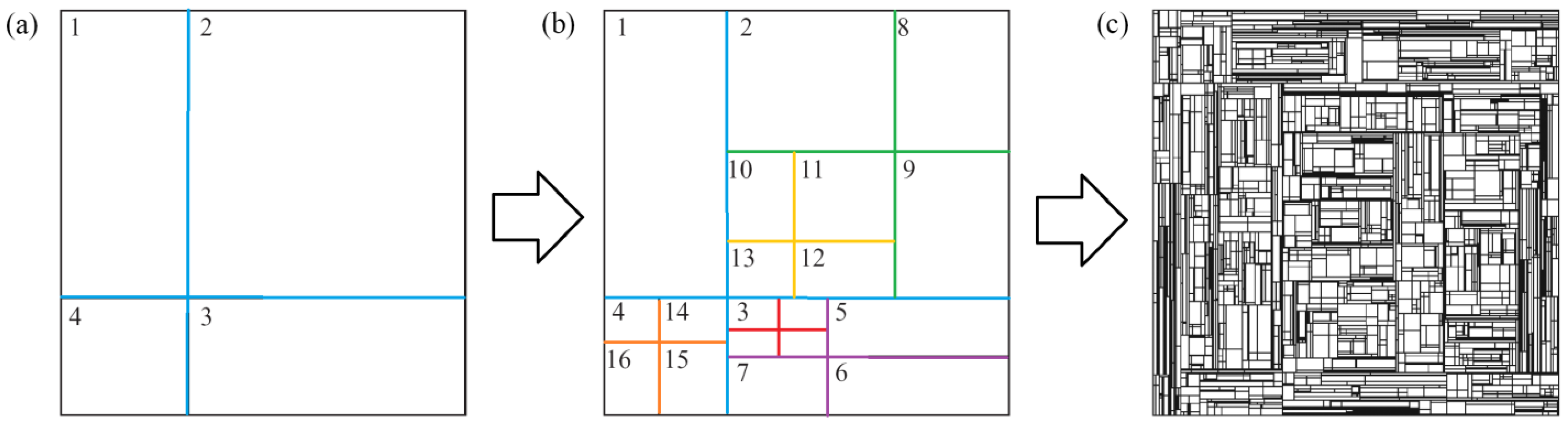
3.3. Multifractal Weighted Planar Stochastic Lattice
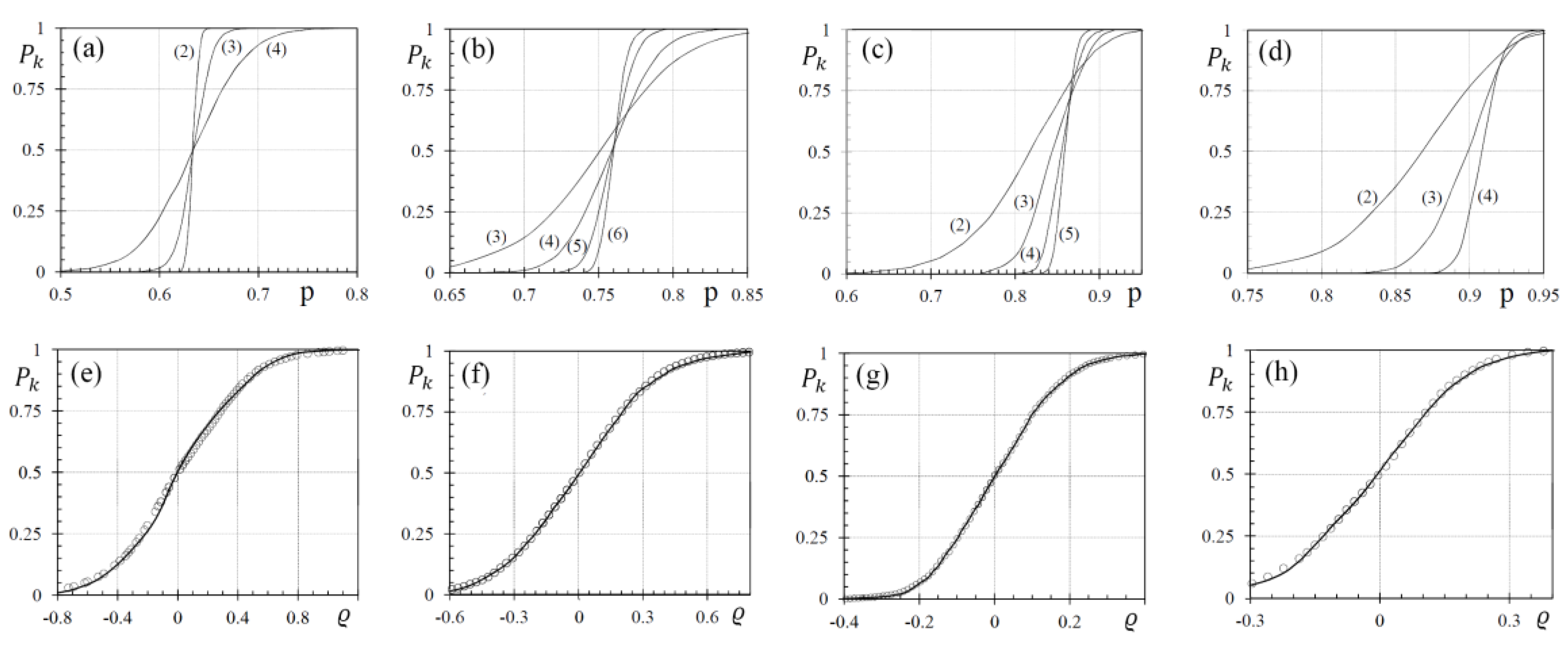
4. Percolation on Finitely Ramified Fractal Networks
5. Percolation on Infinitely Ramified Fractal Networks
5.1. Percolation on Sierpinski Carpets
5.2. Percolation on Cantor Tartans
5.3. Percolation on Critical Percolation Clusters and on WPSL
5.4. Effects of Network Connectivity and Ramification on Site Percolation Threshold
5.5. About Universality Classes of Site Percolation on Fractal Networks
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kirkpatrick, S. Percolation and Conduction. Rev. Mod. Phys. 1973, 45, 574–588. [Google Scholar] [CrossRef]
- Stauffer, D.; Coniglio, A.; Adam, M. Gelation and critical phenomena. Polym. Netw. Adv. Polym. Sci. 1982, 44, 103–158. [Google Scholar] [CrossRef]
- Li, M.; Liu, R.R.; Lü, L.; Hua, M.B.; Xu, S.; Zhang, Y.C. Percolation on complex networks: Theory and application. Phys. Rep. 2021, 907, 1–68. [Google Scholar] [CrossRef]
- Broadbent, S.R.; Hammersley, J.M. Percolation processes. I. Crystals and mazes. Proc. Camb. Philos. Soc. 1957, 53, 629–641. [Google Scholar] [CrossRef]
- Sahimi, M. Applications of Percolation Theory; Taylor and Francis: London, UK, 1994. [Google Scholar]
- Araujo, N.; Grassberger, P.; Kahng, B.; Schrenk, K.J.; Ziff, R.M. Recent advances and open challenges in percolation. Eur. Phys. J. Spec. Top. 2014, 223, 2307–2321. [Google Scholar] [CrossRef]
- Saberi, A.A. Recent advances in percolation theory and its applications. Phys. Rep. 2015, 578, 1–32. [Google Scholar] [CrossRef]
- Stauffer, D.; Aharony, A. Introduction to Percolation Theory, 2nd ed.; Taylor and Francis: London, UK, 1994. [Google Scholar] [CrossRef]
- Dorogovtsev, S.N.; Goltsev, A.V.; Mendes, J.F.F. Critical phenomena in complex networks. Rev. Mod. Phys. 2008, 80, 1275–1335. [Google Scholar] [CrossRef]
- Stauffer, D. Scaling theory of percolation clusters. Phys. Rep. 1979, 54, 1–74. [Google Scholar] [CrossRef]
- Essam, J.W. Percolation theory. Rep. Prog. Phys. 1980, 43, 833–912. [Google Scholar] [CrossRef]
- Sokolov, I.M. Dimensionalities and other geometric critical exponents in percolation theory. Sov. Phys. Usp. 1986, 29, 924–945. [Google Scholar] [CrossRef]
- Isichenko, M.B. Percolation, statistical topography, and transport in random media. Rev. Mod. Phys. 1992, 64, 961–1043. [Google Scholar] [CrossRef]
- Wu, F.Y. The Potts model. Rev. Mod. Phys. 1982, 54, 235–268. [Google Scholar] [CrossRef]
- Ódor, G. Universality classes in nonequilibrium lattice systems. Rev. Mod. Phys. 2004, 76, 663–724. [Google Scholar] [CrossRef]
- Fortuin, C.M.; Kasteleyn, P.W. On the random-cluster model: I. Introduction and relation to other models. Physica 1972, 57, 536–564. [Google Scholar] [CrossRef]
- Gefen, Y.; Mandelbrot, B.B.; Aharony, A. Critical Phenomena on Fractal Lattices. Phys. Rev. Lett. 1980, 45, 855–858. [Google Scholar] [CrossRef]
- Suzuki, M. Phase Transition and Fractals. Prog. Theor. Phys. 1983, 69, 65–75. [Google Scholar] [CrossRef]
- Gefen, Y.; Aharony, A.; Mandelbrot, B.B. Phase transitions on fractals. I. Quasi-linear lattices. Phys. A Math. Gen. 1983, 16, 1267–1278. [Google Scholar] [CrossRef]
- Gefen, Y.; Aharony, A.; Shapir, Y.; Mandelbrot, B.B. Phase transitions on fractals. II. Sierpinski gaskets. Phys. A Math. Gen. 1984, 17, 435–444. [Google Scholar] [CrossRef]
- Gefen, Y.; Aharony, A.; Mandelbrot, B.B. Phase transitions on fractals. III. Infinitely ramified lattices. Phys. A Math. Gen. 1984, 17, 1277–1289. [Google Scholar] [CrossRef]
- Bo-Ming, Y.; Kai-Lun, Y. Numerical evidence of the critical percolation probability Pc = 1 for site problems on Sierpinski gaskets. J. Phys. A Math. Gen. 1988, 21, 3269–3274. [Google Scholar] [CrossRef]
- Taitelbaum, H.; Havlini, S.; Grassberger, P.; Moenig, U. Percolation thresholds on finitely ramified fractals. J. Phys. A Math. Gen. 1990, 23, 371–373. [Google Scholar] [CrossRef]
- Wu, S.; Yang, Z.R. Bond percolation on branching Koch curves. J. Phys. A Mat. Gen. 1995, 28, 2729–2735. [Google Scholar] [CrossRef]
- Trugman, S.A.; Weinrib, A. Percolation with a threshold at zero: A new universality class. Phys. Rev. B 1985, 31, 2974–2980. [Google Scholar] [CrossRef] [PubMed]
- Weinrib, A. Percolation threshold of a two-dimensional continuum system. Phys. Rev. B 1982, 26, 1352–1361. [Google Scholar] [CrossRef]
- Serrano, M.A.; Krioukov, D.; Boguna, M. Percolation in Self-Similar Networks. Phys. Rev. Lett. 2011, 106, 048701. [Google Scholar] [CrossRef]
- Rozenfeld, H.D.; ben-Avraham, D. Percolation in hierarchical scale-free nets. Phys. Rev. E 2007, 75, 056115. [Google Scholar] [CrossRef] [PubMed]
- Havlin, S.; Ben-Avraham, D.; Movshovitz, D. Percolation on Fractal Lattices. Phys. Rev. Lett. 1983, 51, 2347–2350. [Google Scholar] [CrossRef]
- Ben-Avraham, D.; Havlin, S.; Movshovitz, D. Infinitely ramified fractal lattices and percolation. Phil. Mad. B 1984, 50, 297–306. [Google Scholar] [CrossRef]
- Havlin, S.; Ben-Avraham, D.; Movshovitz, D. Percolation on Infinitely Ramified Fractals. J. Stat. Phys. 1984, 36, 831–841. [Google Scholar] [CrossRef]
- Bo-Ming, Y.; Kai-Lun, Y. Critical Percolation Probabilities for Site Problems on Sierpinski Carpets. Z. Phys. B-Condens. Matter 1988, 70, 209–212. [Google Scholar] [CrossRef]
- Lin, Z.Q.; Yang, Z.R. Thresholds and Universality of the Site Percolation on the Sierpinski Carpets. Commun. Theor. Phys. 1997, 27, 145–152. [Google Scholar] [CrossRef]
- Zhen-quan, L.; Zhan-ru, Y.; Yong, Q. Renormalization group approach to the bond percolation on Sierpinski carpets. Acta Phys. Sin. 1997, 6, 257–265. [Google Scholar] [CrossRef]
- Perreau, M.; Peiro, J.; Berthier, S. Percolation in random-Sierpinski carpets: A real space renormalization group approach. Phys. Rev. E 1996, 54, 4590–4595. [Google Scholar] [CrossRef] [PubMed]
- Hovi, J.-P.; Aharony, A. Renormalization group calculation of distribution functions: Structural properties for percolation clusters. Phys. Rev. E 1997, 56, 172–184. [Google Scholar] [CrossRef]
- Sukop, M.C.; Van Dijk, G.J.; Perfect, E.; Van Loon, W.K.P. Percolation Thresholds in 2-Dimensional Prefractal Models of Porous Media. Transp. Porous Med. 2002, 48, 187–208. [Google Scholar] [CrossRef]
- Corso, G.; Freitas, J.E.; Lucena, L.S.; Soares, R.F. Percolation on a multifractal. Phys. Rev. E 2004, 69, 066135. [Google Scholar] [CrossRef]
- Hassan, M.K.; Rahman, M.M. Percolation on a multifractal scale-free planar stochastic lattice and its universality class. Phys. Rev. E 2015, 92, 040101. [Google Scholar] [CrossRef]
- Hassan, M.K.; Rahman, M.M. Universality class of site and bond percolation on multifractal scale-free planar stochastic lattice. Phys. Rev. E 2016, 94, 042109. [Google Scholar] [CrossRef] [PubMed]
- Rahman, M.M.; Hassan, M.K. Explosive percolation on a scale-free multifractal weighted planar stochastic lattice. Phys. Rev. E 2017, 95, 042133. [Google Scholar] [CrossRef] [PubMed]
- Herega, A.N.; Drik, N.G.; Ugol’nikov, A.P. Hybrid ramified Sierpinski carpet: Percolation transition, critical exponents, and force field. Physics-Uspekhi 2012, 55, 519–521. [Google Scholar] [CrossRef]
- Wu, X.Y. Uniqueness of the Infinite Open Cluster for High-density Percolation on Lattice Sierpinski Carpet. Acta Math. Sin. 2001, 17, 141–146. [Google Scholar] [CrossRef]
- Machlus, S.; Zhang, S.; Mao, X. Correlated rigidity percolation in fractal lattices. Phys. Rev. E 2011, 103, 012104. [Google Scholar] [CrossRef]
- Liu, X.W.; Deng, Y.; Jacobsen, J.L. Recursive percolation. Phys. Rev. E 2015, 92, 010103. [Google Scholar] [CrossRef] [PubMed]
- Shinoda, M. Existence of phase transition of percolation on Sierpinski carpet lattices. J. Appl. Prob. 2002, 39, 1–10. [Google Scholar] [CrossRef]
- Monceau, P.; Yi Hsiao, P.Y. Percolation transition in fractal dimensions. Phys. Lett. A 2004, 332, 310–319. [Google Scholar] [CrossRef]
- Higuchi, Y.; Wu, X.Y. Uniqueness of the critical probability for percolation in the two-dimensional Sierpinski carpet lattice. Kobe J. Math. 2008, 25, 1–24. [Google Scholar]
- Balankin, A.S.; Martínez-Cruz, M.A.; Susarrey-Huerta, O.; Damian-Adame, L. Percolation on infinitely ramified fractal networks. Phys. Lett. A 2018, 382, 12–19. [Google Scholar] [CrossRef]
- Balankin, A.S.; Martínez-Cruz, M.A.; Álvarez-Jasso, M.D.; Patiño-Ortiz, M.; Patiño-Ortiz, J. Effects of ramification and connectivity degree on site percolation threshold on regular lattices and fractal networks. Phys. Lett. A 2019, 383, 957–966. [Google Scholar] [CrossRef]
- Halberstam, N.; Hutchcroft, T. What are the limits of universality? Proc. Royal Soc. A 2022, 478, 2259. [Google Scholar] [CrossRef]
- Christensen, K. Percolation Theory; Imperial College London: London, UK, 2002. [Google Scholar]
- Scullard, C.R. Exact site percolation thresholds using a site-to-bond transformation and the star-triangle transformation. Phys. Rev. E 2006, 73, 016107. [Google Scholar] [CrossRef]
- Ziff, R.M.; Scullard, C.R. Exact bond percolation thresholds in two dimensions. J. Phys. A Math. Gen. 2006, 39, 15083–15090. [Google Scholar] [CrossRef]
- Kownacki, J.-P. Site percolation on planar Φ3 random graphs. Phys. Rev. E 2008, 77, 021121. [Google Scholar] [CrossRef] [PubMed]
- Sykes, M.F.; Essam, J.W. Exact Critical Percolation Probabilities for Site and Bond Problems in Two Dimensions. J. Math. Phys. 1964, 5, 1117–1127. [Google Scholar] [CrossRef]
- Becker, A.M.; Ziff, R.M. Percolation thresholds on two-dimensional Voronoi networks and Delaunay triangulations. Phys. Rev. E 2009, 80, 041101. [Google Scholar] [CrossRef] [PubMed]
- Ziff, R.M.; Suding, P.N. Determination of the bond percolation threshold for the Kagomé lattice. J. Phys. A Math. Gen. 1997, 30, 5351–5359. [Google Scholar] [CrossRef]
- Suding, P.N.; Ziff, R.M. Site percolation thresholds for Archimedean lattices. Phys. Rev. E 1999, 60, 275–283. [Google Scholar] [CrossRef]
- Lorenz, C.D.; Ziff, R.M. Precise determination of the bond percolation thresholds and finite-size scaling corrections for the sc, fcc, and bcc lattices. Phys. Rev. E 1998, 57, 230–236. [Google Scholar] [CrossRef]
- Van der Marck, S.C. Calculation of percolation thresholds in high dimensions for fcc, bcc and diamond lattices. Int. J. Mod. Phys. C 1998, 9, 529–540. [Google Scholar] [CrossRef]
- Wang, J.; Zhou, Z.; Zhang, W.; Garoni, T.M.; Deng, Y. Bond and site percolation in three dimensions. Phys. Rev. E 2013, 87, 052107. [Google Scholar] [CrossRef]
- Mertens, S.; Moore, C. Percolation thresholds and Fisher exponents in hypercubic lattices. Phys. Rev. B 2018, 98, 022120. [Google Scholar] [CrossRef]
- Stauffer, D.; Jayaprakash, C. Critical exponents for one-dimensional percolation clusters. Phys. Lett. A 1978, 64, 433–434. [Google Scholar] [CrossRef]
- Smirnov, S.; Werner, W. Critical exponents for two-dimensional percolation. Math. Res. Lett. 2001, 8, 729–744. [Google Scholar] [CrossRef]
- Gracey, J.A. Four loop renormalization of ϕ3 theory in six dimensions. Phys. Rev. D 2015, 92, 025012. [Google Scholar] [CrossRef]
- Duminil-Copin, H.; Manolescu, I. Planar random-cluster model: Scaling relations. Forum Math. Pi 2022, 10, 1–83. [Google Scholar] [CrossRef]
- Gwak, S.-H.; Goh, K.-I. No-exclaves percolation. J. Korean Phys. Soc. 2022, 81, 680–687. [Google Scholar] [CrossRef] [PubMed]
- Stanley, N.E. Application of fractal concepts to polymer statistics and to anomalous transport in randomly porous media. J. Stat. Phys. 1984, 36, 843–860. [Google Scholar] [CrossRef]
- Stella, A.L.; Vanderzande, C. Scaling and fractal dimension of Ising clusters at the d-2 critical point. Phys. Rev. Lett. 1989, 962, 1067–1070. [Google Scholar] [CrossRef] [PubMed]
- Higuchi, Y.; Takei, M.; Zhang, Y. Scaling relations for two-dimensional Ising percolation. J. Stat. Phys. 2012, 148, 777–799. [Google Scholar] [CrossRef]
- Balankin, A.S.; Martínez-Cruz, M.A.; Gayosso-Martínez, F.; Mena, B.; Tobon, A.; Patiño-Ortiz, J.; Patiño-Ortiz, M.; Samayoa, D. Ising percolation in a three-state majority vote model. Phys. Lett. A 2017, 381, 440–445. [Google Scholar] [CrossRef]
- Kutlu, B. Critical exponents of the two-dimensional Ising model with next-nearest-neighbor and four-spin interactions on the Creutz cellular automaton. Phys. A 1997, 243, 199–212. [Google Scholar] [CrossRef]
- Pelissetto, A.; Vicari, E. Critical phenomena and renormalization-group theory. Phys. Rep. 2002, 368, 549–727. [Google Scholar] [CrossRef]
- Wipf, A. Classical Spin Models: An Introduction. In Statistical Approach to Quantum Field Theory, Lecture Notes in Physics; Springer: Cham, Switzerland, 2021; Volume 992. [Google Scholar] [CrossRef]
- Fytas, N.G.; Martín-Mayor, V.; Picco, M.; Sourlas, N. Restoration of dimensional reduction in the random-field Ising model at five dimensions. Phys. Rev. E 2017, 95, 042117. [Google Scholar] [CrossRef] [PubMed]
- Kumar, M.; Banerjee, V.; Puri, S.; Weigel, M. Critical behavior of the three-state random-field Potts model in three dimensions. arXiv 2022, arXiv:2205.13047. [Google Scholar] [CrossRef]
- Holm, C.; Janke, W. Critical exponents of the classical three-dimensional Heisenberg model: A single-cluster Monte Carlo study. Phys. Rev. B 1993, 48, 936–950. [Google Scholar] [CrossRef]
- Campostrini, M.; Hasenbusch, M.; Pelissetto, A.; Rossi, P.; Vicari, E. Critical behavior of the three-dimensional XY universality class. Phys. Rev. B 2001, 63, 214503. [Google Scholar] [CrossRef]
- Goldenfeld, N. Lectures on Phase Transitions and the Renormalization Group; CRC Press: Boca Raton, FL, USA, 1992. [Google Scholar] [CrossRef]
- Qing, Y.; You, W.L.; Liu, M. Critical exponents and the universality class of a minesweeper percolation model. Int. J. Mod. Phys. C 2020, 31, 2050129. [Google Scholar] [CrossRef]
- Balankin, A.S. A continuum framework for mechanics of fractal materials I: From fractional space to continuum with fractal metric. Eur. Phys. J. B 2015, 88, 90. [Google Scholar] [CrossRef]
- Balankin, A.S. Fractional space approach to studies of physical phenomena on fractals and in confined low-dimensional systems. Chaos Solitons Fractals 2020, 132, 109572. [Google Scholar] [CrossRef]
- Balankin, A.S.; Patiño-Ortiz, J.; Patiño-Ortiz, M. Inherent features of fractal sets and key attributes of fractal models. Fractals 2022, 30, 2250082. [Google Scholar] [CrossRef]
- Balankin, A.S. The topological Hausdorff dimension and transport properties of Sierpinski carpets. Phys. Lett. A 2017, 381, 2801–2808. [Google Scholar] [CrossRef]
- Balankin, A.S.; Mena, B.; Martinez-Cruz, M.A. Topological Hausdorff dimension and geodesic metric of critical percolation cluster in two dimensions. Phys. Lett. A 2017, 381, 2665–2672. [Google Scholar] [CrossRef]
- Balankin, A.S. Effective degrees of freedom of a random walk on a fractal. Phys. Rev. E 2015, 92, 062146. [Google Scholar] [CrossRef]
- Havlin, S.; Ben-Avraham, D. Diffusion in disordered media. Adv. Phys. 2002, 51, 187–292. [Google Scholar] [CrossRef]
- Burioni, R.; Cassi, D. Random walks on graphs: Ideas, techniques and results. J. Phys. A Math. Gen. 2005, 38, R45–R78. [Google Scholar] [CrossRef]
- Balankin, A.S.; Golmankhaneh, A.K.; Patiño-Ortiz, J.; Patiño-Ortiz, M. Noteworthy fractal features and transport properties of Cantor tartans. Phys. Lett. A 2018, 382, 1534–1539. [Google Scholar] [CrossRef]
- Durhuus, B. Hausdorff and spectral dimension of infinite random graphs. Acta Phys. Pol. B 2009, 40, 3509–3532. Available online: https://s3.cern.ch/inspire-prod-files-a/a84919e9e7db6236283e133b0dc0314a (accessed on 7 January 2023).
- Balankin, A.S.; Ramírez-Joachin, J.; Gonzalez-Lopez, G.; Gutíerrez-Hernandez, S. Formation factors for a class of deterministic models of pre-fractal pore-fracture networks. Chaos Solitons Fractals 2022, 162, 112452. [Google Scholar] [CrossRef]
- March, N.H. Toward a final theory of critical exponents in terms of dimensionality d plus universality class n. Phys. Lett. A 2015, 379, 820–822. [Google Scholar] [CrossRef]
- Bonnier, B.; Leroyer, Y.; Meyers, C. Critical exponents for Ising-like systems on Sierpinski carpets. J. Phys. 1987, 48, 553–558. [Google Scholar] [CrossRef]
- Le Guillou, J.C.; Zinn-Justin, J. Accurate critical exponents for Ising like systems in non-integer dimensions. J. Phys. 1987, 48, 19–24. [Google Scholar] [CrossRef]
- Holovatch, Y.; Shpot, M. Critical Exponents of Random Ising-Like Systems in General Dimensions. J. Stat. Phys. 1992, 66, 867–883. [Google Scholar] [CrossRef]
- Monceau, P.; Perreau, M. Critical behavior of the Ising model on fractal structures in dimensions between one and two: Finite-size scaling effects. Phys. Rev. B 2001, 63, 184420. [Google Scholar] [CrossRef]
- Bab, M.A.; Fabricius, G.; Albano, E.V. Critical behavior of an Ising system on the Sierpinski carpet: A short-time dynamics study. Phys. Rev. E 2005, 71, 036139. [Google Scholar] [CrossRef]
- Bab, M.A.; Fabricius, G.; Albano, E.V. Critical exponents of the Ising model on low-dimensional fractal media. Phys. A 2009, 388, 370–378. [Google Scholar] [CrossRef]
- Kazmin, S.; Janke, W. Critical exponents of the Ising model in three dimensions with long-range power-law correlated site disorder: A Monte Carlo study. Phys. Rev. B 2022, 105, 214111. [Google Scholar] [CrossRef]
- Newman, M.E.J.; Ziff, R.M. Efficient Monte Carlo algorithm and high-precision results for percolation. Phys. Rev. Lett. 2000, 85, 4104–4107. [Google Scholar] [CrossRef]
- Sahimi, M.; Rassamdana, H. On position-space renormalization group approach to percolation. J. Stat. Phys. 1995, 78, 1157–1164. [Google Scholar] [CrossRef]
- Wierman, J.C.; Naor, D.P. Criteria for evaluation of universal formulas for per-colation thresholds. Phys. Rev. E 2005, 71, 036143. [Google Scholar] [CrossRef] [PubMed]
- Wierman, J.C. Accuracy of universal formulas for percolation thresholds based on dimension and coordination number. Phys. Rev. E 2002, 66, 027105. [Google Scholar] [CrossRef]
- Fisher, M.E. Critical probabilities for cluster size and percolation problems. J. Math. Phys. 1961, 2, 620–627. [Google Scholar] [CrossRef]
- van den Berg, J. Percolation theory on pairs of matching lattices. J. Math. Phys. 1981, 22, 152–157. [Google Scholar] [CrossRef]
- Kesten, H. Percolation Theory for Mathematicians; Birkhäuser: Boston, MA, USA, 1982. [Google Scholar]
- Ohzeki, M.; Fujii, K. Duality analysis on random planar lattices. Phys. Rev. E 2012, 86, 051121. [Google Scholar] [CrossRef] [PubMed]
- Wierman, J.C. Bond percolation critical probability bounds derived by edge con-traction. J. Phys. A 1988, 21, 1487–1492. [Google Scholar] [CrossRef]
- Riordan, O.; Walters, M. Rigorous confidence intervals for critical probabilities. Phys. Rev. E 2007, 76, 011110. [Google Scholar] [CrossRef]
- Scullard, C.R.; Ziff, R.M. Critical surfaces for general bond percolation problems. Phys. Rev. Lett. 2008, 100, 185701. [Google Scholar] [CrossRef]
- Ball, N. Rigorous confidence intervals on critical thresholds in 3 dimensions. J. Stat. Phys. 2014, 156, 574–585. [Google Scholar] [CrossRef]
- Teixeira, A. Percolation and local isoperimetric inequalities. Probab. Theory Relat. Fields 2016, 165, 963–984. [Google Scholar] [CrossRef]
- Wierman, J.C. On bond percolation threshold bounds for Archimedean lattices with degree three. J. Phys. A Math. Theor. 2017, 50, 295001. [Google Scholar] [CrossRef]
- Torquato, S.; Jiao, Y. Effect of dimensionality on the percolation thresholds of various d-dimensional lattices. Phys. Rev. E 2013, 87, 032149. [Google Scholar] [CrossRef]


| Network | Percolation Threshold | |||
|---|---|---|---|---|
| Site Percolation | Bond Percolation | |||
| 1 | Chain [52] | 2 | 1 | 1 |
| 2 | WPSL [39,40] | 5.333 | 0.5265 | 0.3457 |
| Martini lattice [53,54] | 3 | 0.764826… | ||
| Planar random graphs [55] | 3 | 0.7360… | - | |
| Voronoi network [56] | 3 | 0.71410… | 0.666931 | |
| Delaunay network [56] | 6 | 1/2 | 0.333069… | |
| Honeycomb [57] | 3 | 0.697043… | ||
| Square [57] | 4 | 0.592746… | 1/2 | |
| Triangular [57] | 6 | 1/2 | ||
| Kagomé [58] | 4 | 0.5244053… | ||
| Bowtie [59] | 5 | 0.5474… | - | |
| 3 [60,61,62] | Diamond | 4 | 0.4301… | 0.3893… |
| Simple cubic | 6 | 0.3116077… | 0.24881182… | |
| Body-centred cubic | 8 | 0.2459615… | 0.1802875… | |
| Face-centred cubic | 12 | 0.1992365… | 0.1201635… | |
| Hexagonal close packed | 12 | 0.1992555… | 0.1201640… | |
| 4 | Hypercubic lattices [63] | 8 | 0.19688561… | 0.16013122… |
| 5 | 10 | 0.14079633… | 0.11817145… | |
| 6 | 12 | 0.109016661… | 0.09420165… | |
| 7 | 14 | 0.08895112… | 0.078675230… | |
| Bethe lattices [56] | ||||
| Erdős-Rényi networks [3] | z | |||
| Property | Critical Exponent | Scaling Relation |
|---|---|---|
| The finite cluster-size distribution | Fisher exponent | |
| Moments of the cluster size distribution , where | , | |
| The total number of finite clusters | ||
| Percolation strength (probability that an occupied site or bond belongs to the spanning cluster) | ||
| Percolation susceptibility (mean size of finite clusters) | ||
| Cluster moments ratio for | ||
| Correlation length (spanning cluster size near the percolation threshold) | ||
| The size of the largest cluster | ||
| Electrical resistivity | Resistivity exponent | |
| Pair-connectedness (the probability that two sites separated by a distance belong to the same cluster) | Connectivity exponent | |
| Probability | Volume exponent | |
| Mass (number of occupied sites or bonds) of the spanning clusters | Fractal dimension |
| Model | |||||||
|---|---|---|---|---|---|---|---|
| Bernoulli percolation (BP) on regular lattices | [64] | 1 | 0 | 1 | 1 | 2 | 1 |
| [65] | −2/3 | 5/36 0.1389 | 4/3 | 36/91 0.3956 | 187/91 2.0549 | 48/91 | |
| [66] | −0.616 | 0.405 | 0.872 | 0.452 | 2.190 | 2.52293 | |
| [66] | −0.712 | 0.639 | 0.678 | 0.482 | 2.313 | 3.0446 | |
| [66] | −0.855 | 0.845 | 0.571 | 0.497 | 2.412 | 3.5260 | |
| [7] | −1 | 1 | 1/2 | 1/2 | 5/2 | 4 | |
| BP on planar random graphs [55] | −2 | 1/2 | 1 | 2/7 0.2857 | 15/7 2.1428 | 3/2 | |
| BP on WPSL [40] | −1.272 | 0.222 | 1.635 | 0.328 | 2.0728 | 1.8642 | |
| Explosive percolation on WPSL [41] | −0.272 | 0.0679 | 1.136 | 0.454 | 2.03 | 1.941 | |
| Fortuin-Kasteleyn percolation [67] | −2/3 | 5/36 | 4/3 | 36/91 | 187/91 | 91/48 | |
| 0 | 1/8 | 1 | 8/15 | 31/15 | 15/8 | ||
| 1/3 | 1/9 | 5/6 | 9/14 | 29/14 | 28/15 | ||
| 2/3 | 1/12 0.0833 | 2/3 | 4/5 | 31/15 2.0667 | 15/8 | ||
| No-exclaves percolation | [68] | −2/3 | 0 | 4/3 | 3/8 | 2 | 2 |
| Minesweeper percolation [69] | −0.5 | 0.259 | 1.25 | 0.505 | 2.261 | 1.7928 | |
| 0.42 | 0.702 | 0.79 | 5.651 | 9.928 | 2.1114 | ||
| Ising percolation [70,71,72] | 0 | 5/96 0.05208 | 1 | 96/187 0.5134 | 379/187 2.0267 | 187/96 .9479 | |
| Ising model | [73] | 0 | 1/8 | 1 | 8/15 | 31/15 | 15/8 |
| [74] | 0.1102 | 0.32630 | 0.629912 | 0.63962 | 2.2087 | 1.482 | |
| [75] | 0 | 1/2 | 1/2 | 2/3 | 7/3 | 3 | |
| Random-field Ising [76] | −0.16 | 0.019 | 1.38 | 0.243 | 2.005 | 2.9862 | |
| Random-field Potts () [77] | −0.088 | 0.0440 | 1.376 | 0.245 | 2.011 | 2.968 | |
| Heisenberg model [78] | −0.14 | 0.362 | 0.704 | 0.571 | 2.207 | 2.486 | |
| XY model [79] | −0.015 | 0.3485 | 0.67155 | 0.6002 | 2.2092 | 2.48105 | |
| Landau theory [80] | 0 | 1/2 | 1/2 | 2/3 | 7/3 | - | |
| Gaussian exponents [80] | 1/2 | ||||||
| Dimension Number | Symbol | Definition |
|---|---|---|
| Spatial dimension | The maximum number of mutually orthogonal vectors in the embedding Euclidean space . | |
| Topological dimension | ||
| Hausdorff dimension | , where is the Hausdorff measure with respect to the Euclidean metric in is a non-negative number and the infimum is taken over all countable d-dimensional balls with diameters . | |
| Topological Hausdorff dimension | ||
| Connectivity dimension | where is the number of fractal points connected with an arbitrary point inside of the -ball of diameter . | |
| Topological connectivity dimension | such that and , where is the Hausdorff dimension of the subset with respect to the geodesic metric on the network . | |
| Fractal dimension of the minimum path | Fractal dimension of the minimum path is defined via the scaling relation , where denotes the ensemble average, while and is the Euclidean distance between these points. | |
| Random walk dimensions | , | The random walk dimensions are defined via the scaling relation of the mean squared displacement of the random walker on the network and respectively, where . |
| Spectral dimension | The number of effective dynamical degrees of freedom of random walker in the network, which is equal to the number of propagating modes. Accordingly, , where is the propagator and is the diffusion time. | |
| Number of effective spatial degrees of freedom | The number of independent directions in the network in which a random walker can move without violating any constraint imposed on it by the network topology. In numerical simulations can be determined from the probability to find the walker at the distance from its origin after a fixed number of steps. |
| Network | |||||||
|---|---|---|---|---|---|---|---|
| Koch curve (Figure 2a) | 1 | ln4/ln3 ≈ 1.262 | ln4/ln3 | 1 | 1 | 1 | 0 |
| Koch curve (Figure 2b) | 1 | ln5/ln3 ≈ 1.465 | ln5/ln3 | 1 | 1 | 1 | 0 |
| Branched Koch curve (Figure 2c) | 1 | ln5/ln3 | 1 | ln5/ln3 | 2ln5/ln(40/3) ≈ 1.243 [89] | 1.597 | 0.152 |
| Vicsek snowflake (Figure 2d) | 1 | ln5/ln3 | 1 | ln5/ln3 | ln25/ln15 ≈ 1.1886 | 1.741 | 0 |
| Branched Koch curve (Figure 2e) | 1 | ln6/ln3 ≈ 1.631 | ln4/ln3 | ln6/ln4 ≈ 1.2925 | - | - | - |
| Sierpinski gasket (Figure 2f) | 1 | ln6/ln3 | 1 | ln6/ln3 | 2ln6/(90/7) ≈ 1.403 [89] | 1.8587 | 0.1418 |
| Cantor tartan (Figure 2g) | ln6/ln3 [90] | ln6/ln3 | 1 | ln6/ln3 | ln6/ln3 [90] | ln6/ln3 | ln2/ln6 ≈ 0.387 |
| Sierpinski carpet (Figure 2h) | ln6/ln3 [85] | ln8/ln3 ≈ 1.893 | 1 | ln8/ln3 | 1.8061 [85] | 1.9795 | 0.3841 |
| WPSL (Figure 3) [40] | 2 | 2 | ≥1 | ≤2 | ≤2 | ≤2 | ≥0.5 |
| Critical percolation cluster in [86] | 7/4 | 91/48 | 1.13077 | 1.6585 | 1.3170 | 2 | 0.0555 |
| Backbone of CPC in [86] | 1 | 1.64336 | 1.13077 | 1.45331 | 1.256 | 1.65 | 0.073 |
| Critical percolation cluster in [83] | 3 | 4 | 2 | 2 | 4/3 | 8/3 | 0 |
| Planar random trees [91] | 1 | 2 | 1 | 2 | 4/3 | 8/3 | 0 |
| Carpet Parameters | Adimensional Factors | Basic Dimension Numbers | Dimension Numbers | ||||||
|---|---|---|---|---|---|---|---|---|---|
| n | m | (10b) | (11) | (3) | (9) | (8) | (12) | (13) | (14) |
| 99 | 1 | 3.9995 | 98/99 | 0.499 | 1.9977 | 1.9999 | 1.999 | 1.9999 | 1.998 |
| 7 | 1 | 3.9024 | 6/7 | 0.487 | 1.9207 | 1.9894 | 1.979 | 1.9887 | 1.933 |
| 5 | 1 | 3.7894 | 4/5 | 0.47 | 1.8613 | 1.9746 | 1.951 | 1.9723 | 1.892 |
| 6 | 2 | 3.6923 | 2/3 | 0.427 | 1.7737 | 1.9342 | 1.879 | 1.9246 | 1.86 |
| 7 | 3 | 3.6363 | 4/7 | 0.393 | 1.7124 | 1.8957 | 1.817 | 1.8767 | 1.856 |
| 3 | 1 | 3.2 | 2/3 | 0.384 | 1.6309 | 1.8927 | 1.806 | 1.8769 | 1.771 |
| 4 | 2 | 3 | 1/2 | 0.303 | 1.5 | 1.7924 | 1.659 | 1.75 | 1.792 |
| 5 | 3 | 2.9090 | 2/5 | 0.259 | 1.4306 | 1.7227 | 1.572 | 1.6584 | 1.829 |
| 6 | 4 | 2.8571 | 1/3 | 0.231 | 1.3868 | 1.6719 | 1.516 | 1.5912 | 1.860 |
| 7 | 5 | 2.8235 | 2/7 | 0.181 | 1.3562 | 1.6331 | 1.445 | 1.5401 | 1.883 |
| 99 | 97 | 2.6757 | 2/99 | 0.103 | 1.1508 | 1.2994 | 1.211 | 1.168 | 1.998 |
| 1.9746 | 1.8927 | 1.7924 | 1.7227 | 1.8613 | 1.6309 | |
| 0.634 ± 0.004 | 0.758 ± 0.002 | 0.858 ± 0.004 | 0.914 ± 0.004 | ≥0.725 | 1 ± 0.002 | |
| 1.885 | 1.829 | 1.767 | 1.718 | 1.855 | 1.631 | |
| −0.97 | −1.40 | −2.75 | −2.10 | −0.69 | - | |
| 0.134 ± 0.004 | 0.114 ± 0.004 | 0.067 ± 0.003 | 0.011 ± 0.003 | 0.010 ± 0.007 | 0 | |
| 1.50 ± 0.01 | 1.790 ± 0.007 | 2.65 ± 0.04 | 2.40 ± 0.05 | 1.45 ± 0.05 | - | |
| 2.69 | 3.16 | 4.6 | 4.1 | 2.66 | - | |
| 2.05 ± 0.05 | 2.03 ± 0.05 | 2.01 ± 0.04 | 2.00 ± 0.02 | 2.02 ± 0.05 | 2.00 ± 0.05 |
| Self-Similar Network | |||||||
|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 4/3 | 1 | - | - | |
| 1 | 1 | 2 | 4/3 | 1 | - | - | |
| 1 | 1 | 3/2 | 6/5 | 1 | - | - | |
| 1 | 1 | 3 | 3/2 | 1 | - | - | |
| 1 | 1 | 4 | 8/5 | 1 | - | - | |
| 2 | 3 | 3 | 7/3 | 0.4249 | - | 2.195 | |
| 2 | 3 | 3 | 7/3 | 0.4232 | 0.385 | 2.151 | |
| 4 | 8 | 8 | 5 | 0.11705 | 0.41 | 2.66 | |
| 4 | 8 | 8 | 5 | 0.11326 | 0.41 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cruz, M.-Á.M.; Ortiz, J.P.; Ortiz, M.P.; Balankin, A. Percolation on Fractal Networks: A Survey. Fractal Fract. 2023, 7, 231. https://doi.org/10.3390/fractalfract7030231
Cruz M-ÁM, Ortiz JP, Ortiz MP, Balankin A. Percolation on Fractal Networks: A Survey. Fractal and Fractional. 2023; 7(3):231. https://doi.org/10.3390/fractalfract7030231
Chicago/Turabian StyleCruz, Miguel-Ángel Martínez, Julián Patiño Ortiz, Miguel Patiño Ortiz, and Alexander Balankin. 2023. "Percolation on Fractal Networks: A Survey" Fractal and Fractional 7, no. 3: 231. https://doi.org/10.3390/fractalfract7030231
APA StyleCruz, M.-Á. M., Ortiz, J. P., Ortiz, M. P., & Balankin, A. (2023). Percolation on Fractal Networks: A Survey. Fractal and Fractional, 7(3), 231. https://doi.org/10.3390/fractalfract7030231







