Fractional Model of Multiple Trapping with Charge Leakage: Transient Photoconductivity and Transit–Time Dispersion
Abstract
1. Introduction
2. Anomalous Relaxation of Transient Photoconductivity
2.1. Distributed Order Relaxation
2.2. Recombination of Localized Carriers: Tempered Fractional Case
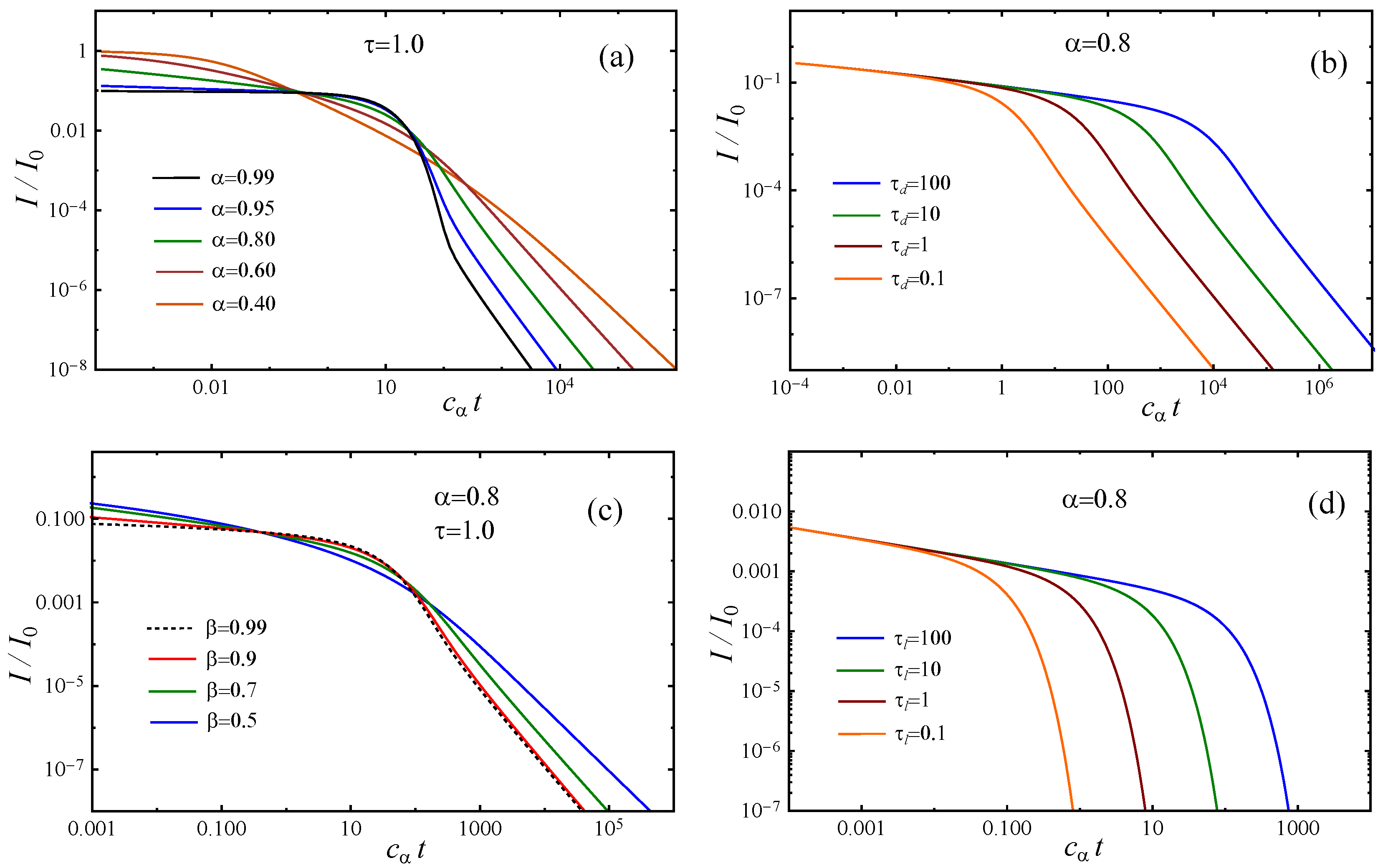
3. Transit–Time Dispersion for Fractional Drift with Leakage
- Fractional drift equation with leakage via delocalized states:
- Fractional drift equation with leakage via localized and delocalized states:
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Schmidlin, F.W. Theory of multiple trapping. Solid State Commun. 1977, 22, 451–453. [Google Scholar] [CrossRef]
- Noolandi, J. Multiple-trapping model of anomalous transit-time dispersion in a-Se. Phys. Rev. B 1977, 16, 4466. [Google Scholar] [CrossRef]
- Curtis, O., Jr.; Srour, J. The multiple-trapping model and hole transport in SiO2. J. Appl. Phys. 1977, 48, 3819–3828. [Google Scholar] [CrossRef]
- Tiedje, T.; Rose, A. A physical interpretation of dispersive transport in disordered semiconductors. Solid State Commun. 1981, 37, 49–52. [Google Scholar] [CrossRef]
- Schiff, E. Trap-controlled dispersive transport and exponential band tails in amorphous silicon. Phys. Rev. B 1981, 24, 6189. [Google Scholar] [CrossRef]
- Schiff, E.A. Transit-time measurements of charge carriers in disordered silicons: Amorphous, microcrystalline and porous. Philos. Mag. 2009, 89, 2505–2518. [Google Scholar] [CrossRef]
- Uchaikin, V.V.; Sibatov, R.T. Fractional Kinetics in Solids: Anomalous Charge Transport in Semiconductors, Dielectrics, and Nanosystems; World Scientific: Singapore, 2013. [Google Scholar]
- Noolandi, J. Equivalence of multiple-trapping model and time-dependent random walk. Phys. Rev. B 1977, 16, 4474. [Google Scholar] [CrossRef]
- Bisquert, J. Fractional diffusion in the multiple-trapping regime and revision of the equivalence with the continuous-time random walk. Phys. Rev. Lett. 2003, 91, 010602. [Google Scholar] [CrossRef]
- Scher, H.; Montroll, E. Anomalous transit-time dispersion in amorphous solids. Phys. Rev. B 1975, 12, 2455. [Google Scholar] [CrossRef]
- Pollak, M. On dispersive transport by hopping and by trapping. Philos. Mag. 1977, 36, 1157–1169. [Google Scholar] [CrossRef]
- Sibatov, R.; Uchaikin, V. Fractional differential kinetics of charge transport in unordered semiconductors. Semiconductors 2007, 41, 335–340. [Google Scholar] [CrossRef]
- Sibatov, R.T.; Uchaikin, V.V. Fractional differential approach to dispersive transport in semiconductors. Adv. Phys. Sci. 2009, 52, 1019. [Google Scholar] [CrossRef]
- Naito, H.; Ding, J.; Okuda, M. Determination of localized-state distributions in amorphous semiconductors from transient photoconductivity. Appl. Phys. Lett. 1994, 64, 1830–1832. [Google Scholar] [CrossRef]
- Sibatov, R.T.; Morozova, E.V. Multiple trapping on a comb structure as a model of electron transport in disordered nanostructured semiconductors. J. Exp. Theor. Phys. 2015, 120, 860–870. [Google Scholar] [CrossRef]
- Feller, W. An Introduction to Probability Theory and Its Applications; John Wiley & Sons: Hoboken, NJ, USA, 2008; Volume 2. [Google Scholar]
- Gorenflo, R.; Kilbas, A.A.; Mainardi, F.; Rogosin, S.V. Mittag–Leffler Functions, Related Topics and Applications; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Feldman, Y.; Puzenko, A.; Ryabov, Y. Non-Debye dielectric relaxation in complex materials. Chem. Phys. 2002, 284, 139–168. [Google Scholar] [CrossRef]
- Górska, K.; Horzela, A. The Volterra type equations related to the non-Debye relaxation. Commun. Nonlinear Sci. Numer. Simul. 2020, 85, 105246. [Google Scholar] [CrossRef]
- Calcagni, G. Towards multifractional calculus. Front. Phys. 2018, 6, 58. [Google Scholar] [CrossRef]
- Ding, W.; Patnaik, S.; Sidhardh, S.; Semperlotti, F. Applications of distributed-order fractional operators: A review. Entropy 2021, 23, 110. [Google Scholar] [CrossRef]
- Seki, K.; Wojcik, M.; Tachiya, M. Fractional reaction-diffusion equation. J. Chem. Phys. 2003, 119, 2165–2170. [Google Scholar] [CrossRef]
- Seki, K.; Murayama, K.; Tachiya, M. Dispersive photoluminescence decay by geminate recombination in amorphous semiconductors. Phys. Rev. B 2005, 71, 235212. [Google Scholar] [CrossRef]
- Serdouk, F.; Benkhedir, M.L. Density of states in pure and As doped amorphous selenium determined from transient photoconductivity using Laplace-transform method. Phys. B Condens. Matter 2015, 459, 122–128. [Google Scholar] [CrossRef]
- Serdouk, F.; Boumali, A.; Makhlouf, A.; Benkhedir, M.L. Solutions of q-deformed multiple-trapping model (MTM) for charge carrier transport from time-of-flight transient (TOF) photo-current in amorphous semiconductors. Rev. Mex. Fıs. 2020, 66, 643–655. [Google Scholar] [CrossRef]
- Shklovskii, B.I.; Efros, A.L. Electronic Properties of Doped Semiconductors; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 45. [Google Scholar]
- Andriesh, A.; Arkhipov, V.; Iovu, M.; Rudenko, A.; Shutov, S. Anomalous transient photocurrent in disordered semiconductors: Theory and experiment. Solid State Commun. 1983, 48, 1041–1043. [Google Scholar] [CrossRef]
- Baranovskii, S.; Zvyagin, I.; Cordes, H.; Yamasaki, S.; Thomas, P. Electronic transport in disordered organic and inorganic semiconductors. J. Non-Cryst. Solids 2002, 299, 416–419. [Google Scholar] [CrossRef]
- Nikitenko, V.; Tyutnev, A. Transient current in thin layers of disordered organic materials under conditions of nonequilibrium charge carrier transport. Semiconductors 2007, 41, 1118–1125. [Google Scholar] [CrossRef]
- Bogoslovskiy, N.; Tsendin, K. Physics of switching and memory effects in chalcogenide glassy semiconductors. Semiconductors 2012, 46, 559–590. [Google Scholar] [CrossRef]
- Raoux, S.; Xiong, F.; Wuttig, M.; Pop, E. Phase change materials and phase change memory. MRS Bull. 2014, 39, 703–710. [Google Scholar] [CrossRef]
- Burr, G.W.; Breitwisch, M.J.; Franceschini, M.; Garetto, D.; Gopalakrishnan, K.; Jackson, B.; Kurdi, B.; Lam, C.; Lastras, L.A.; Padilla, A.; et al. Phase change memory technology. J. Vac. Sci. Technol. B Nanotechnol. Microelectron. Mater. Process. Meas. Phenom. 2010, 28, 223–262. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Serdouk, F.; Boumali, A.; Sibatov, R.T. Fractional Model of Multiple Trapping with Charge Leakage: Transient Photoconductivity and Transit–Time Dispersion. Fractal Fract. 2023, 7, 243. https://doi.org/10.3390/fractalfract7030243
Serdouk F, Boumali A, Sibatov RT. Fractional Model of Multiple Trapping with Charge Leakage: Transient Photoconductivity and Transit–Time Dispersion. Fractal and Fractional. 2023; 7(3):243. https://doi.org/10.3390/fractalfract7030243
Chicago/Turabian StyleSerdouk, Fadila, Abdelmalek Boumali, and Renat T. Sibatov. 2023. "Fractional Model of Multiple Trapping with Charge Leakage: Transient Photoconductivity and Transit–Time Dispersion" Fractal and Fractional 7, no. 3: 243. https://doi.org/10.3390/fractalfract7030243
APA StyleSerdouk, F., Boumali, A., & Sibatov, R. T. (2023). Fractional Model of Multiple Trapping with Charge Leakage: Transient Photoconductivity and Transit–Time Dispersion. Fractal and Fractional, 7(3), 243. https://doi.org/10.3390/fractalfract7030243






