High-Order Nonlinear Functional Differential Equations: New Monotonic Properties and Their Applications
Abstract
:1. Introduction
- (H1)
- , , andwhich is called a non-canonical condition;
- (H2)
- , for , and for .
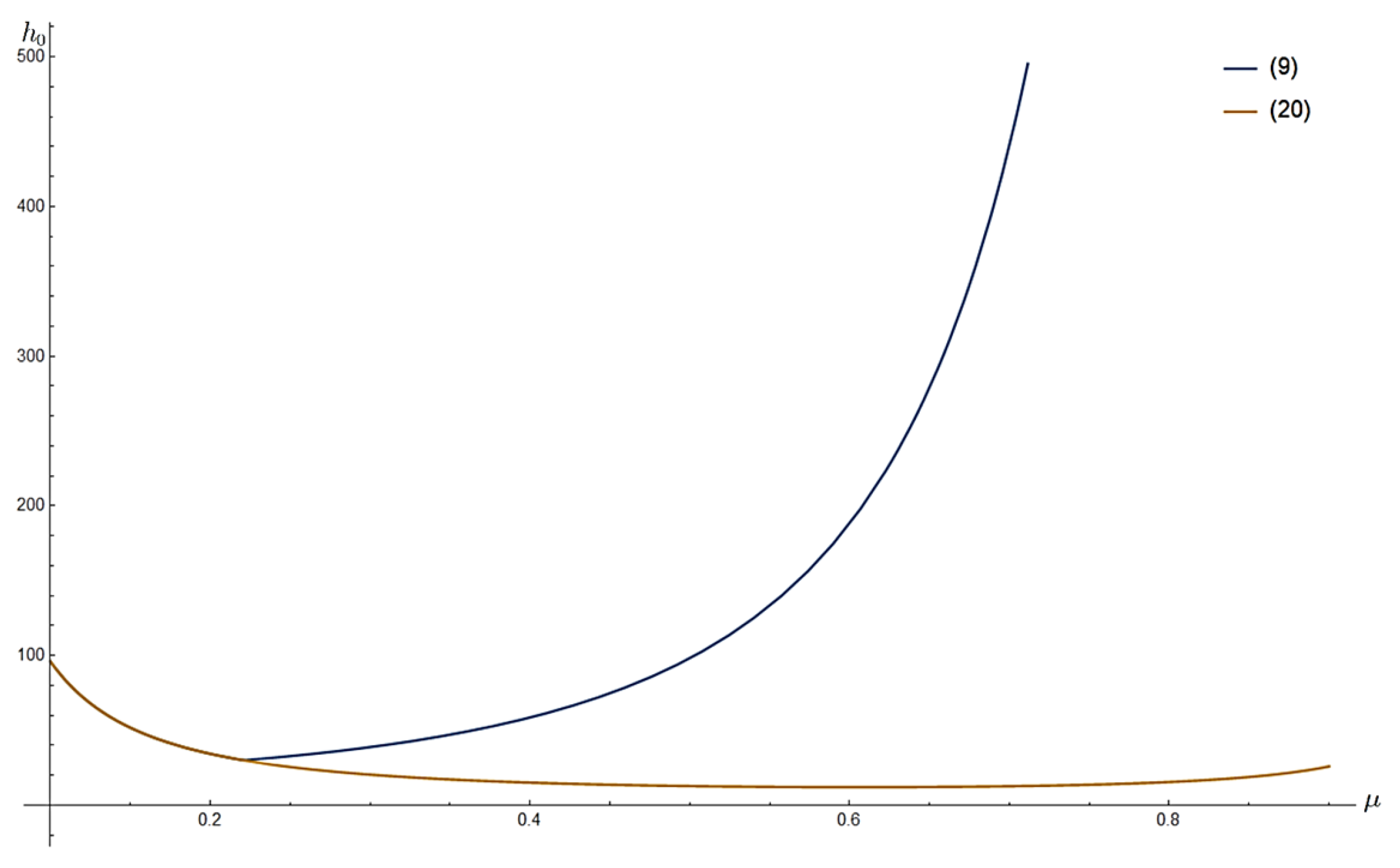
2. Preliminary Results
- (c1)
- for and
- (c2)
- for and
- (c3)
- for
3. Oscillation Theorems
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Braun, M. Qualitative theory of differential equations. In Differential Equations and Their Applications; Texts in Applied Mathematics; Springer: New York, NY, USA, 1993; Volume 11. [Google Scholar]
- Hale, J.K. Functional differential equations. In Analytic Theory of Differential Equations; Springer: Berlin/Heidelberg, Germany, 1971; pp. 9–22. [Google Scholar]
- Grace, S.R.; Tunc, E. On the oscillatory behavior of solutions of higher order nonlinear fractional differential equations. Georgian Math. J. 2018, 25, 363–369. [Google Scholar] [CrossRef]
- Grace, S.R. On the asymptotic behavior of non-oscillatory solutions of certain fractional differential equations. Mediterr. J. Math. 2018, 15, 76. [Google Scholar]
- Grace, S.R.; Graef, J.R.; Tunc, E. On the asymptotic behavior of solutions of certain forced fractional differential equations. Nonlinear Stud. 2017, 24, 329–336. [Google Scholar]
- Alzabut, J.; Agarwal, R.P.; Grace, S.R.; Jonnalagadda, J.M. Oscillation results for solutions of fractional-order differential equations. Fractal Fract. 2022, 6, 466. [Google Scholar] [CrossRef]
- Agarwal, R.P.; Grace, S.R.; O’Regan, D. Oscillation Theory for Difference and Functional Differential Equations; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2000. [Google Scholar]
- Agarwal, R.P.; Bohner, M.; Li, W.-T. Nonoscillation and oscillation: Theory for functional differential equations. In Monographs and Textbooks in Pure and Applied Mathematics; Marcel Dekker, Inc.: New York, NY, USA, 2004; Volume 267. [Google Scholar]
- Gyori, I.; Ladas, G. Oscillation Theory of Delay Differential Equations with Applications; Clarendon Press: Oxford, UK, 1991. [Google Scholar]
- Baculíková, B. Džurina, J. Graef, J.R. On the oscillation of higher-order delay differential equations. J. Math. Sci. 2012, 187, 387–400. [Google Scholar]
- Ladde, G.; Lakshmikantham, S.V.; Zhang, B.G. Oscillation Theory of Differential Equations with Deviating Arguments; Marcel Dekker: New York, NY, USA, 1987. [Google Scholar]
- Zhang, C.; Li, T.; Suna, B.; Thandapani, E. On the oscillation of higher-order half-linear delay differential equations. Appl. Math. Lett. 2011, 24, 1618–1621. [Google Scholar]
- Zhang, C.; Agarwal, R.P.; Bohner, M.; Li, T. New results for oscillatory behavior of even-order half-linear delay differential equations. Appl. Math. Lett. 2013, 26, 179–183. [Google Scholar]
- Zhang, C.; Li, T.; Saker, S.H. Oscillation of fourth-order delay differential equations. J. Math. Sci. 2014, 201, 322–335. [Google Scholar] [CrossRef]
- Moaaz, O.; Muhib, A. New oscillation criteria for nonlinear delay differential equations of fourth-order. Appl. Math. Comput. 2020, 377, 125192. [Google Scholar] [CrossRef]
- Moaaz, O.; Dassios, I.; Bin Jebreen, H.; Muhib, A. Criteria for the nonexistence of Kneser solutions of DDEs and their applications in Oscillation Theory. Appl. Sci. 2021, 11, 425. [Google Scholar]
- Moaaz, O.; Muhib, A.; Zakarya, M.; Abdel-Aty, A.-H. Delay differential equation of fourth-order: Asymptotic analysis and oscillatory behavior. Alexandria Eng. J. 2022, 61, 2919–2924. [Google Scholar] [CrossRef]
- Chatzarakis, G.E.; Grace, S.R.; Jadlovska, I. Oscillation criteria for third-order delay differential equations. Adv. Differ. Equ. 2017, 2017, 330. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Feng, R.; Jadlovská, I.; Liu, Q. Oscillation criteria for third-order nonlinear neutral dynamic equations with mixed deviating arguments on time scales. Mathematics 2021, 9, 552. [Google Scholar] [CrossRef]
- Dzurina, J.; Grace, S.R.; Jadlovska, I. On nonexistence of Kneser solutions of third-order neutral delay differential equations. Appl. Math. Lett. 2019, 88, 193–200. [Google Scholar] [CrossRef]
- Graef, J.R.; Tunc, E.; Grace, S.R. Oscillatory and asymptotic behavior of a third-order nonlinear neutral differential equation. Opusc. Math. 2017, 37, 839–852. [Google Scholar] [CrossRef]
- Graef J., R.; Jadlovská, I.; Tunç, E. Oscillation of odd-order differential equations with a nonpositive sublinear neutral term and distributed deviating arguments. Appl. Anal. Discret. Math. 2022, 16, 350–364. [Google Scholar] [CrossRef]
- Jadlovská, I.; Chatzarakis, G.E.; Džurina, J.; Grace, S.R. On sharp oscillation criteria for general third-order delay differential equations. Mathematics 2021, 9, 1675. [Google Scholar] [CrossRef]
- Moaaz, O.; Baleanu, D.; Muhib, A. New aspects for non-existence of Kneser solutions of neutral differential equations with odd-order. Mathematics 2020, 8, 494. [Google Scholar] [CrossRef] [Green Version]
- Moaaz, O.; Chalishajar, D.; Bazighifan, O. Asymptotic behavior of solutions of the third order nonlinear mixed type neutral differential equations. Mathematics 2020, 8, 485. [Google Scholar] [CrossRef] [Green Version]
- Qiu, Y.-C.; Chiu, K.-S.; Grace, S.R.; Liu, Q.; Jadlovská, I. Oscillation of solutions to third-order nonlinear neutral dynamic equations on time scales. Mathematics 2022, 10, 86. [Google Scholar] [CrossRef]
- Philos, C.G. On the existence of nonoscillatory solutions tending to zero at ∞ for dif ferential equations with positive delays. Arch. Math. 1981, 36, 168–178. [Google Scholar] [CrossRef]
- Kitamura, Y.; Kusano, T. Oscillation of first-order nonlinear differential equations with deviating arguments. Proc. Am. Math. Soc. 1980, 78, 64–68. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alrashdi, H.S.; Moaaz, O.; AlNemer, G.; Elabbasy, E.M. High-Order Nonlinear Functional Differential Equations: New Monotonic Properties and Their Applications. Fractal Fract. 2023, 7, 271. https://doi.org/10.3390/fractalfract7030271
Alrashdi HS, Moaaz O, AlNemer G, Elabbasy EM. High-Order Nonlinear Functional Differential Equations: New Monotonic Properties and Their Applications. Fractal and Fractional. 2023; 7(3):271. https://doi.org/10.3390/fractalfract7030271
Chicago/Turabian StyleAlrashdi, Hail S., Osama Moaaz, Ghada AlNemer, and Elmetwally M. Elabbasy. 2023. "High-Order Nonlinear Functional Differential Equations: New Monotonic Properties and Their Applications" Fractal and Fractional 7, no. 3: 271. https://doi.org/10.3390/fractalfract7030271
APA StyleAlrashdi, H. S., Moaaz, O., AlNemer, G., & Elabbasy, E. M. (2023). High-Order Nonlinear Functional Differential Equations: New Monotonic Properties and Their Applications. Fractal and Fractional, 7(3), 271. https://doi.org/10.3390/fractalfract7030271