Photothermal Response for the Thermoelastic Bending Effect Considering Dissipating Effects by Means of Fractional Dual-Phase-Lag Theory

Abstract

We analyze an extension of the dual-phase lag model of thermal diffusion theory to accurately predict the contribution of thermoelastic bending (TE) to the Photoacoustic (PA) signal in a transmission configuration. To achieve this, we adopt the particular case of Jeffrey’s equation, an extension of the Generalized Cattaneo Equations (GCEs). Obtaining the temperature distribution by incorporating the effects of fractional differential operators enables us to determine the TE effects in solid samples accurately. This study contributes to understanding the mechanisms that contribute to the PA signal and highlights the importance of considering fractional differential operators in the analysis of thermoelastic bending. As a result, we can determine the PA signal’s TE component. Our findings demonstrate that the fractional differential operators lead to a wide range of behaviors, including dissipative effects related to anomalous diffusion.

1. Introduction

The thermoelastic bending (TE) effect must be considered in photothermal measurements when the temperature change in the sample, due to light absorption, creates mechanical stress that leads to a non-uniform thermal displacement [1,2]. It must be carefully considered in the design and interpretation of photothermal experiments, as it can impact the accuracy of the results if not adequately accounted for [3,4]. Thin samples with significant heat expansion and materials with anisotropic thermal expansion are particularly susceptible to the TE effect. In addition, the TE effect is also essential in the analysis of the photothermal responses when thermal characteristics of solid materials are investigated using the Photoacoustic signal [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23].

To accurately quantify the thermoelastic (TE) effect, we must determine the temperature distribution in the sample as a result of light absorption. This is obtained by solving the heat diffusion equation, which describes how heat is transferred through the material. The standard heat diffusion equation considers the thermal conductivity using the Fourier Law and the heat generation rate through the Energy Conservation Law [24,25]. For the photothermal techniques, the classical model does not consider heat loss, which can be due to convection and radiation, heat loss to edges, and non-homogeneity [2].

The thermoelastic bending effect and other dissipation effects in photothermal data can be modeled mathematically using fractional calculus [24,25,26,27,28,29,30,31]. It is worth mentioning that the fractional calculus enables the modeling of processes that are not characterized by traditional (integer order) derivatives [26,29,32,33,34,35,36,37,38,39,40,41,41] and can be suitably used to analyze anomalous diffusion and viscoelasticity in many materials [42,43]. In these scenarios, the effects of memory and dissipation in the material can significantly impact temperature distribution, and the TE effect, which can be captured by modeling the heat transfer with fractional derivatives [26,27,44] and the mechanical reaction of the sample (viscoelastic), can also be analyzed using fractional calculus. Combining these methods with the fractional calculus enables modeling the mechanical response’s time-dependent behavior in photothermal measurements, where the laser power and sample temperature are quickly changing [45,46,47].

Here, we apply an extension of dual phase lag in thermal systems to predict the PA signal’s temperature distribution and TE component for transmission configuration. The extension is a new fractional operator derived from Jeffrey’s equation, an extension of the GCE-I model with a fractional dual-phase-lag, considered to obtain the thermal piston component of the PA signal [48] and photothermal response in periodic heating [49]. We show that applying fractional calculus in photothermal measurements can offer a more detailed description of the complex and dynamic behavior of the system, resulting in a more accurate calculation of the TE effect and a more transparent comprehension of the physical processes.

2. Theory

The Fourier Law connects the heat flux, $\mathbf{q}(\mathbf{r},t)$, at a given point in space and time is proportional to the temperature gradient, $\nabla T(\mathbf{r},t)$, at that same point.

$$\mathbf{q}(\mathbf{r},t)=-k\nabla T(\mathbf{r},t)$$

(1)

where k is the thermal conductivity. It has been shown that fractional equations are a useful mathematical tool for describing the dynamics of a variety of odd physical events [50,51,52]. Compte and Metzeler [53] made phenomenological generalizations of the Cattaneo Equation [54]. In particular, we have the GCE-I generalization:

$$\left(1+{\tau }_q^{\alpha }{\partial }_t^{\alpha }\right)\mathbf{q}(\mathbf{r},t)=-k_{\alpha }{\partial }_t^{1-\alpha }\nabla T(\mathbf{r},t)$$

(2)

The Jeffreys-type equation is a generalization for the study of the Fractional Dual-Phase-Lag (FDPL) [48]:

$$\left(1+{\tau }_q^{\alpha }{\partial }_t^{\alpha }\right)\mathbf{q}(\mathbf{r},t)=-k_{\gamma }{\partial }_t^{1-\gamma }\left(1+{\tau }_T^{\beta }{\partial }_t^{\beta }\right)\nabla T(\mathbf{r},t)$$

(3)

where $0<\alpha ,\beta ,\gamma <1$, and $k\gamma =k{\tau }_q^{1-\gamma }$, and ${\partial }_t^{\alpha }$ is the Caputo fractional derivative or integral, which are, respectively

$${}_{t_0}{\partial }_t^{\gamma }f(x,t)=\left\{\begin{array}{cc}\frac{1}{\mathsf{\Gamma }(1-\gamma )}{\int }_{t_0}^t\frac{d{t}^{\prime }}{{(t-t^{\prime })}^{\gamma }}\frac{\partial }{\partial t}f(x,t^{\prime }),\hfill & \hfill \mathrm{for} 0<\gamma <1\\ \frac{1}{\mathsf{\Gamma }(-\gamma )}{\int }_{t_0}^{t}d{t}^{\prime }\frac{f(x,t^{\prime })}{{(t-t^{\prime })}^{1+\gamma }},\hfill & \hfill \mathrm{for} \gamma <0\end{array}\right..$$

(4)

A special case of Jeffreys-type equation is for $\alpha =\gamma$, in which is obtained an extension of GCE-I Compte-Metzler equation with a Dual-Phase-Lag (FDPL-GCE-I):

$$\left(1+{\tau }_q^{\alpha }{\partial }_t^{\alpha }\right)\mathbf{q}(\mathbf{r},t)=-k_{\alpha }{\partial }_t^{1-\alpha }\left(1+{\tau }_T^{\beta }{\partial }_t^{\beta }\right)\nabla T(\mathbf{r},t)$$

(5)

Furthermore, the validity interval is generalized, following Jeffrey’s equations, with $0\le \alpha ,\beta \le 1$. If $\beta =1$ and ${\tau }_T=0$ in Equation (5),

The thermal diffusion equation is obtained by combining the Fourier Law, Equation (1), with the Energy Conservation Law, which is:

$$\rho c_p{\partial }_{t}T(\mathbf{r},t)+\nabla ·\mathbf{q}(\mathbf{r},t)=F(\mathbf{r},t)$$

(6)

with $F(\mathbf{r},t)$, $\rho$, and $c_p$ the heat source, density, and specific heat, respectively. The classical thermal diffusion (CTD) equation is

$${\nabla }^{2}T(\mathbf{r},t)-\frac{1}{D}{\partial }_{t}T(\mathbf{r},t)=-\frac{1}{k}F(\mathbf{r},t),$$

(7)

where the standard thermal diffusivity is defined as $D=k/\rho c_p$.

For the general case, from the Jeffreys-type equation, Equation (3), the thermal diffusion equation is:

$$\begin{array}{ccc}\hfill {\partial }_t^{1-\gamma }\left(1+{\tau }_T^{\beta }{\partial }_t^{\beta }\right){\nabla }^{2}T(\mathbf{r},t)-\frac{1}{D_{\gamma }}\left(1+{\tau }_q^{\alpha }{\partial }_t^{\alpha }\right){\partial }_{t}T(\mathbf{r},t)& =& \hfill \\ \hfill -\frac{1}{k_{\gamma }}\left(1+{\tau }_q^{\alpha }{\partial }_t^{\alpha }\right)F(\mathbf{r},t)\end{array}$$

(8)

with the fractional thermal diffusivity defined as $D_{\gamma }=k_{\gamma }/\rho c_p$. For the FDPL-GCE-I the Thermal Diffusion Equation is obtained:

$$\begin{array}{ccc}\hfill \left(1+{\tau }_T^{\beta }{\partial }_t^{\beta }\right){\nabla }^{2}T(\mathbf{r},t)-\frac{1}{D_{\alpha }}{\partial }_t^{\alpha -1}\left(1+{\tau }_q^{\alpha }{\partial }_t^{\alpha }\right){\partial }_{t}T(\mathbf{r},t)& =& \hfill \\ \hfill -\frac{1}{k_{\alpha }}{\partial }_t^{\alpha -1}\left(1+{\tau }_q^{\alpha }{\partial }_t^{\alpha }\right)F(\mathbf{r},t)\end{array}$$

(9)

The anomalous thermal conductivity $k_{\alpha }$ has dimensions $kg·m·s^{-2-\alpha }·K^{-1}$ and the anomalous thermal diffusivity $D_{\alpha }$ has dimension $m^2·s^{-\alpha }$.

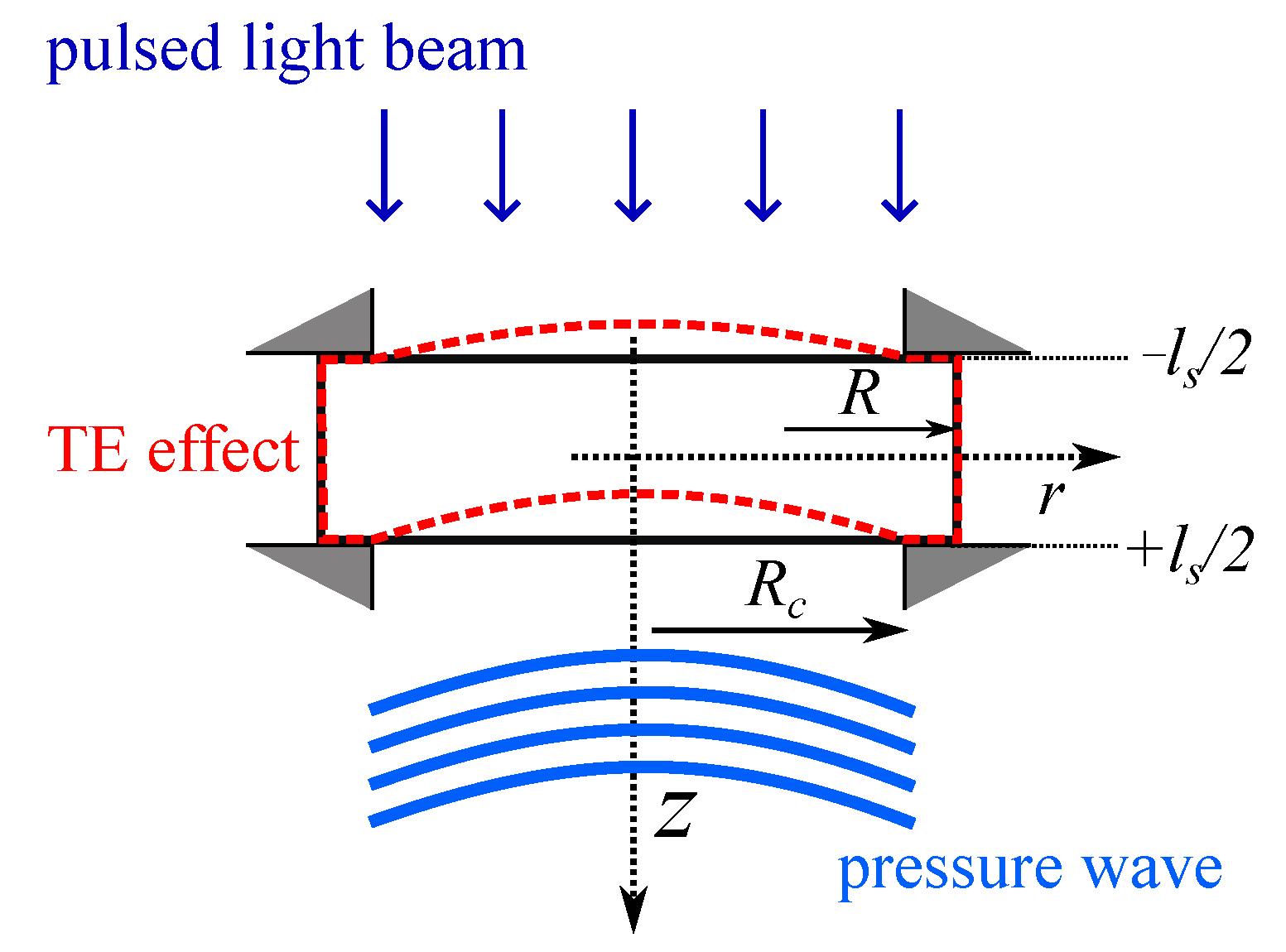
The Thermoelastic Bending Effect in Photoacoustic Signal

The Photoacoustic (PA) signal is a pressure variation recorded during PA measurements in the sample nearby gas. Figure 1 shows the geometry for the TE calculation, as in ref. [2,4]. The pressure variation $\delta P_{TE}$ due to thermoelastic effect is [1]:

$$\delta P_{TE}=\frac{\mathsf{\Gamma }{P}_0}{V_0}2\pi {\int }_0^{R}r{u}_z(z=l_s/2,r,t)dr$$

(10)

where $\mathsf{\Gamma }$ is the air-specific heat ratio, $P_0$ is the atmospheric pressure, $u_z(z=l_s/2,r,t)$ is the displacement of the sample due to the heating, R is the radius of the sample, and $V_0=\pi R_c{l}_g$ with $R_c$ the cell radius.

The displacement $u_z(r,z)$ of a thin solid-plate approach is [3,25,55]:

$$u_z\left(r,\frac{l_s}{2}\right)={\alpha }_T\frac{6(R^2-r^2)}{l_s^3}{M}_T$$

(11)

where ${\alpha }_T$ is the thermal expansion coefficient, and $M_T={\int }_{-l_s/2}^{l_s/2}z{T}_s\left(z\right)dz$ is the temperature gradient. To determine the temperature distribution, it is necessary to solve Equation (9). Therefore, it is assumed that the absorption of radiation by air is insignificant, thus the heat source is present exclusively within the sample:

$$F_s(z,t)={\eta }_s{I}_0{\lambda }_s{e}^{-{\lambda }_{s}z}{e}^{i\omega t},$$

(12)

with $\omega =2\pi f$, in which f is the frequency of light modulation, ${\lambda }_s$, $I_0$, and ${\eta }_s$ are the optical absorption coefficient, the light intensity, and the quantum coefficient of the electromagnetic energy to heat conversion of the sample, respectively (it is considered that ${\eta }_s=1$).

The photothermal signal (PA signal) is monitored with the same frequency as the heat source, requiring that the temperature variations in the three media (air-sample-air) have a similar waveform to the source. This temperature variation can be expressed as $T(z,t)=\theta \left(z\right)e^{i\omega t}$. Due to the experimental characteristics, we consider $t_0=-\infty$. Thus, ${\partial }_t^{\gamma }{e}^{i\omega t}={\left(i\omega \right)}^{\gamma }{e}^{i\omega t}$ [52]. Additionally, the photothermal analysis (PA) problem can be treated as a one-dimensional problem when the light-induced heating is uniform and covers an area larger than the sample’s radius. In such cases, the temperature profile of the sample, $T_s(z,t)$, can be obtained by solving a set of one-dimensional heat diffusion equations. This assumption simplifies the analysis and provides a more straightforward method of understanding the temperature distribution within the sample:

$$\frac{d^2}{d_z^2}{\theta }_j\left(z\right)-\frac{m_j}{D_{{\alpha }_j}}\left(i\omega \right){\theta }_j\left(z\right)=-\frac{m_j}{k_{\alpha j}}{F}_j\left(z\right)$$

(13)

with $j=b,s,g$ for backing air, sample, and air closed in PA cell, respectively, and $m_j$ is obtained from FDPL-GCE-I temporal fractional derivatives:

$$m_j=\frac{{\left(i\omega \right)}^{{\alpha }_j-1}\left(1+{\tau }_{qj}^{{\alpha }_j}{\left(i\omega \right)}^{{\alpha }_j}\right)}{\left(1+{\tau }_{Tj}^{{\beta }_j}{\left(i\omega \right)}^{{\beta }_j}\right)}$$

(14)

To solve, we considered the boundary conditions: (1) the zero temperature variation in system borders at $z=\pm \infty$, (2) continuity of temperature, and (3) continuity heat flux, both at the interfaces backing air-sample $(z=-l_s/2)$, and sample-air inner the PA cell $(z=l_s/2)$. Solving (13) and assuming that: (1) the thermal effusivity $(e={\left(k\rho c\right)}^{1/2})$ of the sample is much greater than the air [56]; (2) the fractional order derivatives for air are $\alpha =\beta =1$; and (3) the two relaxation times of air are small, ${\tau }_q\to 0$ and ${\tau }_T\to 0$, the temperature distribution is:

$$T_s(z,t)=\frac{I_{0}cosh\left({\sigma }_{m_s}\left(z-\frac{l_s}{2}\right)\right)}{k_{m_s}sinh\left({\sigma }_{m_s}{l}_s\right)}{H}_s(z,\beta )e^{i\omega t},$$

(15)

where $k_{m_s}=k_s/m_s$, ${\sigma }_{m_s}=m_s^{1/2}{\sigma }_s$, and ${\sigma }_j$ is the complex medium thermal diffusion length, with $j=g,b$ for the surrounding air and $j=s$ for the sample, given by:

$${\sigma }_j=\sqrt{\frac{i\omega }{D_j}},$$

(16)

and $H_s(z,\beta )={\mathsf{\Lambda }}_1(z,\beta )-{\mathsf{\Lambda }}_2(z,\beta )$ is the optical absorbing contribution, which tends to unit for opaque approach $({lim}_{\beta \to \infty }{H}_s(z,\beta )=1)$. The functions ${\mathsf{\Lambda }}_1$ and ${\mathsf{\Lambda }}_2$ are defined as follows:

$$\begin{array}{c}\hfill {\mathsf{\Lambda }}_1(z,\beta )=\frac{1-e^{-\beta l_s}cosh\left({\sigma }_{m_s}\left(\frac{l_s}{2}+z\right)\right)\mathrm{sech}\left({\sigma }_{m_s}\left(z-\frac{l_s}{2}\right)\right)}{1-\frac{{\sigma }_{m_s}^2}{{\beta }^2}},\\ \hfill {\mathsf{\Lambda }}_2(z,\beta )=\frac{{\sigma }_{m_s}{e}^{-\beta \left(\frac{l_s}{2}+z\right)}sinh\left(l_s{\sigma }_{m_s}\right)\mathrm{sech}\left({\sigma }_{m_s}\left(z-\frac{l_s}{2}\right)\right)}{\beta \left(1-\frac{{\sigma }_{m_s}^2}{{\beta }^2}\right)}.\end{array}$$

(17)

The GCE-I (One-Phase-Lag) presents a subdiffusive behavior for long timespans ($t<{\tau }_q$), i.e., in the high-frequency domain for photothermal techniques. It was obtained from phase velocity for the FDPL-GCE-I, which is mainly characterized by subdiffusive behavior, but the ${\tau }_T$ promotes the superdiffusive behavior mainly for high-frequency modulations [49]. The thermoelastic bending contribution $\delta P_{TE}$ of the sample to the PA signal is

$$\begin{array}{ccc}\hfill \delta P_{TE}& =& \frac{C_1{C}_2{m}_s\left(e^{-\beta l_s}+1\right)}{{\sigma }_{ms}^3\left(1-\frac{{\sigma }_{ms}^2}{{\beta }^2}\right)}\hfill \\ \hfill & & \times \left(F_{1s}-l_s{\sigma }_{ms}\left(1-\frac{{\sigma }_{ms}^2}{{\beta }^2}\right)+2tanh\left(\frac{l_s{\sigma }_{ms}}{2}\right)\right)\hfill \end{array}$$

(18)

where $F_{1s}=\frac{2{\sigma }_{\gamma s}^3\left(e^{-\beta l_s}-1\right)}{{\beta }^3\left(e^{-\beta l_s}+1\right)}$, where $C_1=\frac{\mathsf{\Gamma }{I}_0{P}_0\sqrt{{\alpha }_g}}{\sqrt{2\pi }{l}_g{T}_0{k}_s}$ is the amplitude of thermal diffusion contribution and its unit in the S.I is $\left[C_1\right]=$ Pa m${}^{-1}$s${}^{-1/2}$, and $C_2=\frac{3\sqrt{2\pi }{R}^4{T}_0{\alpha }_T}{2R_c^2\sqrt{{\alpha }_g}{l}_s^3}$ is the relative amplitude of thermoelastic contribution, and your unit in the S.I is $\left[C_2\right]$ = m${}^{-2}$s${}^{1/2}$ [45]. For the opaque approach ($\beta \to \infty$):

$$\delta P_{TE}=\frac{C_1{C}_2{m}_s\left(2tanh\left(\frac{l_s{\sigma }_{ms}}{2}\right)-l_s{\sigma }_{m_s}\right)}{l_s^3{\sigma }_{ms}^3}.$$

(19)

Considering the classical thermal diffusion ($m=1$), the PA signal tends to the equation determined by Rousset et al. [1].

3. Results and Discussion

The analytical results are obtained for an opaque sample of thickness $l_s=400$ $\mathsf{\mu }$m and thermal diffusivity ${\alpha }_s=40\times {10}^{-6}$ m${}^2/$s, as a function of fractional order derivatives $\alpha$ and $\beta$, heated by a uniform light source at $z=-l_s/2$. The temperature distribution was normalized by $\left(k_s/I_0\right)$ to show how the factor $m_s$, and hence the fractional factor $alpha$, affect temperature distribution. Furthermore, the PA signal is normalized considering $C_1{C}_2=1$. All simulations were performed until the establishment of attenuation for the subdiffusive behavior, which occurs around the $0.5<\alpha <1$ interval [49].

3.1. Temperature Distribution

Figure 2 shows the influence of the Dual-Phase-Lag in GCE-I on the absolute value of the temperature profile normalized. The temperature results are simulated as a function of position z and fractional order derivative heated by a uniform light source at $z=-l_s/2$ with frequency $f=1000$ Hz. A particular case of FDPL-GCCE-I with $\alpha =\beta$ and ${\tau }_T={\tau }_q$ is presented in Figure 2b.

The graphical representation provides the peculiar characteristics that arise during heat wave propagation through the sample for each considered model. The following remarks can be highlighted

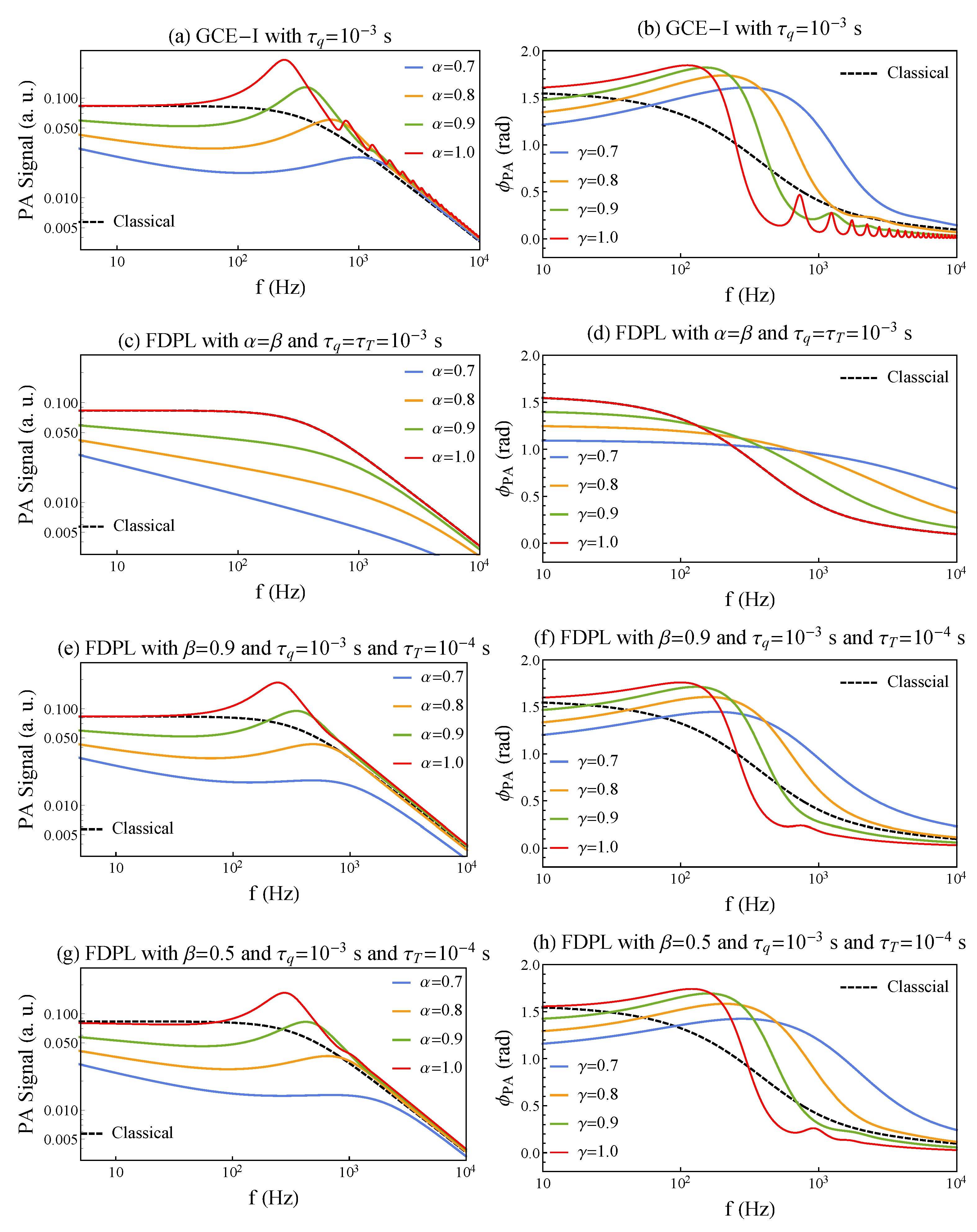
• The subdiffusive Generalized Continuous Equation of the First Kind (GCE-I) has been shown to reduce the resonant oscillations of the hyperbolic model and diminish the temperature gradient inside the sample. The attenuation of oscillations in the GCE-I model for photothermal excitations has been previously observed [23,45,57], as shown by the red curve in Figure 2a, given that the GCE-I model returns to the hyperbolic equation when $\alpha =1$. Furthermore, a decrease in the value of $\alpha$ leads to a reduction in the temperature variation, which in turn affects the amplitude of the TE effect;
• The second Phase-Lag term functions as a damping factor for the resonant oscillations in the hyperbolic model but has the consequence of increasing the temperature gradient. By setting $\gamma =\alpha$ in Jeffrey’s Equation (3), the resulting Equation (5) can be interpreted as a DPL extension of the GCE-I model. As illustrated in Figure 2c,d, the DPL parameters ${\tau }_q$ and $\beta$ lead to a reduction in the resonant oscillations while simultaneously increasing the temperature in the region of incidence radiation ($z=-l_s/2$). The degree of attenuation is determined by the fractional order $\beta$, while the relaxation time ${\tau }_q$ is responsible for the variation in a temperature gradient. This is closer to real-world scenarios, as resonant oscillations are typically absent, but the TE effect induced by the temperature gradient is present and can be measured;
• In the scenario where the fractional order, $\beta$, and relaxation time, ${\tau }_T$, are close to the values of $\alpha$ and ${\tau }_q$, respectively, the damping of resonant oscillations is maximized, which is the strongest damping situation. Additionally, the temperature gradient exhibits a weaker behavior than that predicted by the classical and GCE-I models.

3.2. Photoacoustic Signal

Figure 3 presents the influence of the FDPL-GCE-I on the PA signal. Aside from analyzing the amplitude of the PA signal $\left|\delta P\right|$, as shown in the left column graphs (Figure 3a,c,e,g), it is also possible to analyze the phase delay ${\varphi }_{PA}$ in which the signal is generated, as demonstrated in the right column graphs (Figure 3b,d,f,h). The strongest damping (particular case) with $\alpha =\beta$ and ${\tau }_q={\tau }_T$ is analyzed in Figure 3c,d.

The temperature gradient mostly strongly influences the pressure wave generated at each modulation frequency. The results of the PA signal due to the TE effect, which can be added to the discussion of temperature results, are:

• The GCE-I makes the amplitude tend the classical behavior to high frequencies increases the first resonant peak. On the other hand, the phase delay exhibits a sharp decrease around the first resonant peak, which shifts to higher frequencies as $\alpha$ decreases;
• For low $\alpha$, the PA signal is lower than the classical result, even for higher frequencies. This situation can explain the strongest dissipating phenomena;
• The influence of the fractional derivative photothermal model FDPL-GCE-I on the amplitude of the photoacoustic (PA) signal is more prominent at lower frequencies. In contrast, its impact on the phase can be detected across the entire frequency range. Specifically, the phase delay is more sensitive to anomalous effects, especially when detecting equipment works at high frequencies.

It is worth noting that when there is an inversion of the relaxation times, leaving ${\tau }_T>{\tau }_q$, a more intense attenuation occurs.

4. Conclusions

The FDPL-GCE-I equations were proposed to model the fractional heat conduction and thermal diffusion in materials by incorporating two fractional order derivatives and two relaxation times based on Jeffrey’s model. We obtained an analytical solution for the temperature profile for a periodic photothermal excitation, assuming a homogeneous sample surrounded by air, which can be either transparent or opaque, to investigate the contribution of the thermoelastic (TE) effect to the photoacoustic (PA) problem.

The model exhibiting subdiffusive behavior for a broad range of modulation frequencies typical of photothermal techniques can provide insights into anomalous effects arising from anisotropic and dissipative effects that are not accounted for in classical and hyperbolic models. This model helps explain the underlying physics of these phenomena and can enhance our understanding of the dynamics of such complex systems.