Fixed-Time Multi-Switch Combined–Combined Synchronization of Fractional-Order Chaotic Systems with Uncertainties and External Disturbances

Abstract

In this paper, the fixed-time multi-switch combination–combination synchronization (FTMSCCS) of fractional-order chaotic systems with uncertainties and external disturbances is studied. The appropriate sliding mode surface and controller are proposed based on a Lyapunov theorem, and fixed-time multi-switching combination–combination synchronizations between four fractional-order chaotic systems are realized. The Lyapunov function is designed to prove the feasibility of the controller theoretically, and the effectiveness and robustness of the synchronization mechanism are further verified by numerical simulations. The advantage of this article is that it extends fixed-time synchronization to multi-switch combination–combination synchronization, enabling synchronization for a limited time, while increasing the complexity of the synchronization mechanism and improving its confidentiality in communication applications.

1. Introduction

In the last few decades, the study of chaotic systems has received increasing attention. Chaos is a complex and fascinating natural phenomenon. It has complex, unpredictable behavior, is dependent on changes in initial conditions and parameters, and it exists in many classical systems, including the Lorenz system [1], Chen system [2], PMSM system [3], etc. Since Pecora and Carroll first considered the problem of chaos synchronization in 1990 [4], the practical application of chaos synchronization in chemical reactions, power transformation, information processing and other fields has attracted more and more attention. Currently, an increasing number of synchronization approaches are studied, for example, drive response synchronization [5], projection synchronization [6], adaptive fuzzy synchronization [7], neural network synchronization [8], feedback synchronization [9], pulse synchronization [10], and sliding mode synchronization [11].

Fractional calculus is the promotion of integer calculus, which has the same long history as integer calculus. However, due to limited computing power in the past, it was not paid attention to until recent decades with the improvement of computing power [12]. Compared with integral calculus, fractional calculus can describe chaotic and nonlinear phenomena more accurately. With the rapid development of chaos theory and application research, researchers have been widely concerned with the synchronization of fractional chaotic systems, and this field has developed rapidly over the last few years. In 2016, Wang et al. studied the synchronization of fractional-order chaotic systems with uncertain parameters [13]. Huang et al. [14] studied synchronization and anti-synchronization in a class of financial systems in 2017. In 2018, Mohammadzadeh proposed the synchronization of a time-delay fractional system [15]. In 2020, Zhang and Wu found synchronization of chaotic systems of different dimensions [16]. Haris et al. designed a new nonlinear feedback controller to realize synchronization of chaotic systems with unknown parameters [17]. In 2021, Ababneh studied synchronization and anti-synchronization between fractional-order chaotic optical systems with unknown parameters by designing an adaptive controller [18]. In 2022, Li et al. proposed a new global Mittag–Leffler synchronization criterion for fractional-order hyperchaotic financial systems by designing appropriate pulse control and state feedback controllers [19]. However, these control methods can only achieve asymptotic synchronization and stability; that is to say, they cannot achieve accurate convergence in a limited time. Moreover, we cannot estimate the convergence time of these control methods in advance. In actual situations, it is extremely important to achieve a stable and synchronous state within a specified time, especially for those applications that require precise convergence and strict settling time limitations. High-precision convergence in finite time can be realized by finite time control, but convergence time is determined by the initial conditions. However, it is difficult to obtain accurate initial condition information in practical applications; because of this, estimating the convergence time is challenging, and finite-time control’s convergence time approaches infinity, as do the initial circumstances. In order to overcome the limitation of initial conditions and obtain better response performance, Polyakov proposed a fixed-time control strategy [20]. The upper bound of stability time in this control strategy is independent of the initial conditions of the system. On the basis of the fixed-time stability theorem, more and more articles have been written about fixed-time synchronization; for example, [21,22] introduced the fixed-time synchronization of fractal-order chaotic systems. In Reference [23], an adaptive control method is added on the basis of sliding mode control to realize the synchronization of second-order chaotic systems. In this paper, fixed-time synchronization of chaotic systems with different dimensions is proposed and extended to network systems [24].

However, the above synchronization is restricted to one drive and one responsive system. In the last several years, some new synchronization schemes have appeared, among which many chaotic systems are concerned, such as combinatorial synchronization [25,26], composite synchronization [27] and dual composite synchronization [28]. In 2008, Ucar et al. proposed a multi-switch synchronization scheme [29]. It is a significant improvement over the current synchronization system. According to this plan, the various states of the driving system and the required states of the response system are synchronized. In 2011, Wang et al. realized the multi-switch synchronization of chaotic systems with unknown parameters [30]. In 2015, Vincent et al. first combined multi-switch synchronization and combined synchronization to achieve multi-switch synchronization between multiple chaotic systems [31]. Zheng et al. realized the synchronization of three different chaotic systems in 2016 by means of nonlinear control [32]. In 2017, Song et al. used Lorenz and Chen chaotic systems to achieve fractal-order multi-switch synchronization [33]. This synchronization method has been generalized to the uncertain fractional-order chaotic system in the literature [34]. In 2019, Zhang et al. realized the multi-switch combination synchronization of spatiotemporal coupled systems using the backstepping method [35]. Reference [36] proposed a new adaptive anti-synchronization control to realize multi-switch anti-synchronization between two driving systems and one system. In 2020, Muhammad et al. realized multi-switch combination synchronization between multiple chaotic systems of different orders [37]. The benefit of this is that it becomes nearly impossible for an intrusive party to ascertain which combinations are likely to be synchronized because the error system grows to such a size. These schemes provide significant resistance and anti-attack capabilities for secure communication. At present, multi-switch combination synchronization has been applied to finite time synchronization [38], but there are no related articles on fixed time. This paper combines fixed-time synchronization with multi-switch synchronization, and realizes multi-switch combination–combination synchronization with fixed time using an appropriate sliding mode surface and controller. In practical application, it is difficult to obtain a definite system; most systems have uncertainty and external interference. Therefore, this paper presents the fixed-time multi-switch combination–combination synchronization (FTMSCCS) of fractional-order chaotic systems with uncertainties and external disturbances. The main contributions of this paper are as follows:

(1)

By designing a suitable sliding mode surface and controller, the fixed-time synchronization of a fractional-order chaotic system is realized, ensuring that the system can synchronize in finite time and is not restricted by the initial value condition.

(2)

Multi-switch synchronization and fixed-time synchronization are combined for the first time to realize the fixed-time multi-switch synchronization of a fractional-order chaotic system.

(3)

Because of the multiplexing, the combinations of synchronizations become more numerous, which makes it difficult for an intruder to predict the combination of synchronizations that will occur, so this method has higher security in secure communication applications.

The advantage of this article is that it extends fixed-time synchronization to multi-switch combination–combination synchronization, enabling synchronization for a limited time, while increasing the complexity of the synchronization mechanism and improving its confidentiality in communication applications. The structure of this paper is as follows: in the first section, the basic knowledge of calculus and some necessary theorems are introduced. In the second section, the problems are expounded, and the results are given. In the third section, the results of the numerical simulation are given.

2. Preliminaries

Before we start building models, we introduce three definitions of calculus and some fundamental theorems.

Definition 1 

([39]). Let us define the fractional-order derivatives of Grünwald–Letnikov as

$${}^{GL}{D}^{\beta }f\left(\tau \right)=\underset{h\to 0}{lim}\frac{1}{h^{\beta }}\sum _{m=0}^M{(-1)}^m{C}_m^{\beta }f(\tau -mh),$$

(1)

where $\beta >0$, $M=\left[\frac{\tau }{h}\right]$, $C_m^{\beta }={(}_m^{\beta })=\frac{\beta (\beta -1)\dots (\beta -m+1)}{m!}$.

Definition 2 

([39]). Let us define the fractional-order integral of Riemann–Liouville as

$$I^{\beta }f\left(\tau \right)=\frac{1}{\Gamma \left(\beta \right)}{\int }_{{\tau }_0}^{\tau }{(\tau -\eta )}^{\beta -1}f\left(\eta \right)d\eta ,$$

(2)

and its derivatives as:

$${}^{RL}{D}_t^{\beta }f\left(\tau \right)=\frac{d^m}{d{\tau }^m}\frac{1}{\Gamma (m-\beta )}{\int }_{{\tau }_0}^{\tau }{(\tau -\eta )}^{m-\beta -1}f\left(\eta \right)d\eta ,$$

(3)

where $\Gamma (·)$ is Gamma function, $\beta >0$.

Definition 3 

([39]). Let us define the fractional-order derivatives of Caputo as

$${}^C{D}^{\beta }f\left(\tau \right)=\frac{1}{\Gamma (m-\beta )}{\int }_{{\tau }_0}^{\tau }{(\tau -\eta )}^{m-\beta -1}{f}^m\left(\eta \right)d\eta ,$$

(4)

where $\beta >0$, $m=\left[\beta \right]+1$.

Lemma 1 

([40]). There is a continuous and differentiable function $\mathit{x}\left(t\right)\in {\mathbb{R}}^n$; we come to the result:

$$\frac{1}{2}{}_{t_0}^C{D}_t^{\beta }{\mathit{x}}^2\left(t\right)-\mathit{x}\left(t\right){}_{t_0}^C{D}_t^{\beta }\mathit{x}\left(t\right)\le 0,$$

(5)

where $t>t_0$, $0<\beta <1$.

Definition 4 

([41]). If a continuous function χ: $[0,t)\to [0,\infty )$ is strictly growing and $\chi \left(0\right)=0$, then it is deemed to be of class-K.

Lemma 2 

([41]). Given the fractional-order system

$${}_{t_0}^C{D}_t^{\beta }\mathit{x}\left(t\right)=\mathit{f}(\mathit{x},t),$$

(6)

where $\mathit{x}=0$ is a fixed point, $\beta \in (0,1)$. Assuming class-K functions ${\chi }_i(i=1,2,3)$ and a Lyapunov function $v\left(\mathit{x}\right(t),t)$ exist, the following is true:

$${\chi }_1(\parallel \mathit{x}\parallel )\le v(\mathit{x}\left(t\right),t)\le {\chi }_2(\parallel \mathit{x}\parallel ),$$

(7)

$${}_{t_0}^C{D}_t^{\beta }v(\mathit{x}\left(t\right),t)\le -{\chi }_3\parallel \mathit{x}\parallel ,$$

(8)

we call system (6) asymptotically stable.

Proposition 1 

([39]). For fractional derivatives, the following equation holds:

$${}_{t_0}{D}_t^{\alpha }{(}_{t_0}{D}_t^{-\beta }f\left(t\right)){=}_{t_0}{D}_t^{\alpha -\beta }f\left(t\right),$$

(9)

where $\alpha \ge \beta \ge 0$.

The GL specification gives slightly inaccurate results at the beginning of the simulation. The RL definition cannot be used to explicitly distinguish between fractional orders; it is primarily for fractional-order integrations. The advantage of the Caputo formulation is that the initial conditions for differential equations of fractional order are the same as those for equations of integer order. As a result, the Caputo fractional definition is the one used in this essay. ${}^C{D}^{\beta }$ is conveniently replaced with $D^{\beta }$ below.

Lemma 3 

([42]). Given the fractional-order system:

$$D^{\beta }x\left(t\right)=-a{x}^{{\mu }_1}-b{x}^{{\mu }_2},x\left(0\right)=x_0,$$

(10)

where $a>0$, $b>0$ are constants, and ${\mu }_1>1$, ${\mu }_2<1$ stand for positive odd integer ratio. Then, the system (10)’s equilibrium point is fixed-time stable, and the upper bound on the settling time is:

$$T<\frac{1}{a({\mu }_1-1)}+\frac{1}{b(1-{\mu }_2)}.$$

(11)

Lemma 4. 

This inequality is true for any real variable ${\lambda }_1,{\lambda }_2,\dots ,{\lambda }_n$:

$$\sum _{i=1}^n{\lambda }_i\le \left|\sum _{i=1}^n{\lambda }_i\right|\le \sum _{i=1}^n\left|{\lambda }_i\right|.$$

(12)

3. System and Problem Description

This section presents the drive system and response system, the controller and sliding mode surface that realize their synchronization. Likewise, the drive system is described as

$$D_t^{\beta }\mathit{x}\left(t\right)=\mathit{f}(\mathit{x},t)+\Delta \mathit{f}(\mathit{x},t)+{\mathit{d}}^f\left(t\right),$$

(13)

$$D_t^{\beta }\mathit{y}\left(t\right)=\mathit{g}(\mathit{y},t)+\Delta \mathit{g}(\mathit{y},t)+{\mathit{d}}^g\left(t\right),$$

(14)

where $\mathit{x}\left(t\right)\in {\mathbb{R}}^n$, $\mathit{y}\left(t\right)\in {\mathbb{R}}^n$ are the state vectors, ${\mathit{d}}^f\left(t\right)\in {\mathbb{R}}^n$, ${\mathit{d}}^g\left(t\right)\in {\mathbb{R}}^n$ are the external disturbances, $\mathit{f}(\mathit{x},t)\in {\mathbb{R}}^n$ and $\mathit{g}(\mathit{y},t)\in {\mathbb{R}}^n$ represent the nonlinear functions, $\Delta \mathit{f}(\mathit{x},t)=[\Delta f_1(x_1,t),\Delta f_2(x_2,t),\dots ,\Delta f_n(x_n,t)]\in {\mathbb{R}}^n$ and $\Delta \mathit{g}(\mathit{y},t)=[\Delta g_1(y_1,t),\Delta g_2(y_2,t),\dots ,\Delta g_n(y_n,t)]\in {\mathbb{R}}^n$ are the nonlinear uncertainties.

Assumption 1. 

There are positive constants $k_i^{\Delta f}$, $k_i^{\Delta g}$ and $k_i^{df}$, $k_i^{dg}$, such that $|\Delta f_i(\mathit{x},t)|\le k_i^{\Delta f}$, $|\Delta g_i(\mathit{y},t)|\le k_i^{\Delta g}$ and $|d_i^f\left(t\right)|\le k_i^{df}$, $|d_i^g\left(t\right)|\le k_i^{dg}$, where the uncertainties $\Delta f_i(\mathit{x},t)$, $\Delta g_i(\mathit{y},t)$ and external disturbances $d_i^f\left(t\right)$, $d_i^g\left(t\right)$ are bounded.

The response systems are given as

$$D_t^{\beta }\mathit{w}\left(t\right)=\mathit{h}(\mathit{w},t)+\Delta \mathit{h}(\mathit{w},t)+{\mathit{d}}^h\left(t\right)+\mathit{\xi }\left(t\right),$$

(15)

$$D_t^{\beta }\mathit{z}\left(t\right)=\mathit{r}(\mathit{z},t)+\Delta \mathit{r}(\mathit{z},t)+{\mathit{d}}^r\left(t\right)+{\mathit{\xi }}^{*}\left(t\right),$$

(16)

where $\mathit{w}\left(t\right)\in {\mathbb{R}}^n$, $\mathit{z}\left(t\right)\in {\mathbb{R}}^n$ are the state vectors, ${\mathit{d}}^h\left(t\right)\in {\mathbb{R}}^n$, ${\mathit{d}}^r\left(t\right)\in {\mathbb{R}}^n$ are the external disturbances, $\mathit{h}(\mathit{w},t)\in {\mathbb{R}}^n$ and $\mathit{r}(\mathit{z},t)\in {\mathbb{R}}^n$ represent the nonlinear functions, $\Delta \mathit{h}(\mathit{w},t)=[\Delta h_1(w_1,t),\Delta h_2(w_2,t),\dots ,\Delta h_n(w_n,t)]\in {\mathbb{R}}^n$ and $\Delta \mathit{r}(\mathit{z},t)=[\Delta r_1(z_1,t),\Delta r_2(z_2,t),\dots ,\Delta r_n(z_n,t)]\in {\mathbb{R}}^n$ are the nonlinear uncertainties, $\mathit{\xi }\left(t\right)={[{\xi }_1\left(t\right),{\xi }_2\left(t\right),\dots ,{\xi }_n\left(t\right)]}^T\in {\mathbb{R}}^n$, ${\mathit{\xi }}^{*}\left(t\right)={[{\xi }_1^{*}\left(t\right),{\xi }_2^{*}\left(t\right),\dots ,{\xi }_n^{*}\left(t\right)]}^T\in {\mathbb{R}}^n$ are the control vectors, and there are nonlinear functions.

Assumption 2. 

The uncertainties $\Delta h_i(\mathit{w},t)$, $\Delta r_i(\mathit{z},t)$ and external disturbances $d_i^h\left(t\right)$, $d_i^r\left(t\right)$ are bounded; there are positive constants $k_i^{\Delta h}$, $k_i^{\Delta r}$ and $k_i^{dh}$, $k_i^{dr}$, such that $|\Delta h_i(\mathit{w},t)|\le k_i^{\Delta h}$, $|\Delta r_i(\mathit{z},t)|\le k_i^{\Delta r}$ and $|d_i^h\left(t\right)|\le k_i^{dh}$, $|d_i^r\left(t\right)|\le k_i^{dr}$.

Definition 5. 

There are four constant matrices N, P, R and $Q\in {\mathbb{R}}^{n\times n}$, $R\ne 0$, $Q\ne 0$, and the error vector $\mathit{e}\left(t\right)$ satisfies:

$$\underset{t\to \infty }{lim}\parallel \mathit{e}\left(t\right)\parallel =\underset{t\to \infty }{lim}\parallel N\mathit{x}\left(t\right)+P\mathit{y}\left(t\right)-R\mathit{w}\left(t\right)-Q\mathit{z}\left(t\right)\parallel =0,$$

(17)

then the driving systems (13) and (14) and the response systems (15) and (16) are said to be multi-switching combination–combination synchronization (MSCCS), where $\Vert ·\Vert$ represents the symbolization of the matrix norm.

Remark 1. 

Scaling matrices are the names given to the constant matrices N, P, R, and Q. We can suppose that the functional matrices for the star variables x, y, w, and z are these scaling matrices.

Remark 2. 

The above synchronization issue becomes combination synchronization if $R=0$ and $Q=0$.

Remark 3. 

Let I be the $n\times n$ identity matrix. The above synchronization issue is diminished to the projective synchronization if $N=0$, $R=I$, $Q=0$ or $N=R=0$, $Q=I$ or $P=0$, $R=I$, $Q=0$ or $P=R=0$, $Q=I$.

Remark 4. 

Let I be the $n\times n$ identity matrix. The above synchronization problem is converted to the projective anti-synchronization if $N=0$, $R=-I$, $Q=0$ or $P=0$, $R=-I$, $Q=0$ or $P=0$, $R=-I$, $Q=0$ or $P=R=0$, $Q=-I$.

Remark 5. 

Combination–combination synchronization will become chaos synchronization if the scaling matrices $N=P=R=0$ or $N=P=Q=0$.

Remark 6. 

For convenience, let us assume $N=diag({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n)$, $P=diag({\beta }_1,{\beta }_2,\dots ,{\beta }_n)$, $R=diag({\gamma }_1,{\gamma }_2,\dots ,{\gamma }_n)$ and $Q=diag({\delta }_1,{\delta }_2,\dots ,{\delta }_n)$, then the error vector $\mathit{e}$ can be written as:

$$e_{hpls}={\alpha }_h{x}_h+{\beta }_p{y}_p-{\gamma }_l{w}_l-{\delta }_s{z}_s.$$

(18)

According to this formula, we give a new definition of Definition 5.

Definition 6. 

When $h=p=l\ne s$ or $h=p=s\ne l$ or $h=l=s\ne p$ or $p=l=s\ne h$ or $h=p\ne l=s$ or $h=l\ne p=s$ or $h=s\ne p=l$ or $h=p\ne l\ne s$ or $h=l\ne p\ne s$ or $h=s\ne p\ne s$ or $h\ne p=l\ne s$ or $h\ne p\ne l=s$ or $h\ne l\ne p=s$ or $h\ne p\ne l\ne s$ and

$$\underset{t\to \infty }{lim}\parallel {\mathit{e}}_{hpls}\parallel =\underset{t\to \infty }{lim}\parallel {\alpha }_h{x}_h+{\beta }_p{y}_p-{\gamma }_l{w}_l-{\delta }_s{z}_s\parallel =0,$$

(19)

then the driving system (13) and (14) and the response system (15) and (16) are said to be multi-switching combination–combination synchronization (MSCCS), where $\Vert ·\Vert$ represents the symbolization of the matrix norm, and $e_{hpls}\left(t\right)$ is the error synchronization vector.

From Equations (13)–(16), the error dynamical system is obtained as

$$\begin{array}{cc}\hfill D^{\beta }\left(\mathit{e}\left(t\right)\right)=& N[\mathit{f}(\mathit{x},t)+\Delta \mathit{f}(\mathit{x},t)+{\mathit{d}}^f\left(t\right)]\hfill \\ \hfill & +P[\mathit{g}(\mathit{y},t)+\Delta \mathit{g}(\mathit{y},t)+{\mathit{d}}^g\left(t\right)]\hfill \\ \hfill & -R[\mathit{h}(\mathit{w},t)+\Delta \mathit{h}\left(\mathit{w}\left(t\right)\right)+{\mathit{d}}^h\left(t\right)]\hfill \\ \hfill & -Q[\mathit{r}(\mathit{z},t)+\Delta \mathit{r}\left(\mathit{z}\left(t\right)\right)+{\mathit{d}}^r\left(t\right)]-\mathit{U}(x,y,w,z),\hfill \end{array}$$

(20)

and

$$\mathit{U}(x,y,w,z)=R\mathit{\xi }\left(t\right)+Q{\mathit{\xi }}^{*}\left(t\right).$$

(21)

We consider the sliding surface as:

$$\mathit{s}=\mathit{e}+D^{-\beta }({\sigma }_1{\left|\mathit{e}\right|}^{{\mu }_1}+{\sigma }_2{\left|\mathit{e}\right|}^{{\mu }_2})sign\left(\mathit{e}\right),$$

(22)

where $sign(·)$ is a sign function and ${\sigma }_1>0$, ${\sigma }_2>0$, ${\mu }_1>1$, ${\mu }_2<1$ stands for positive odd integer ratio.

The control function is given as follows:

$$\begin{array}{cc}\hfill U=& N\mathit{f}(\mathit{x},t)+P\mathit{g}(\mathit{y},t)-R\mathit{h}(\mathit{w},t)-Q\mathit{r}(\mathit{z},t)\hfill \\ \hfill & +({\sigma }_1{\left|\mathit{e}\right|}^{{\mu }_1}+{\sigma }_2{\left|\mathit{e}\right|}^{{\mu }_2})sign\left(\mathit{e}\right)+(N{\mathit{k}}^{\Delta f}+N{\mathit{k}}^{df}\hfill \\ \hfill & +P{\mathit{k}}^{\Delta g}+P{\mathit{k}}^{dg}+R{\mathit{k}}^{\Delta h}+R{\mathit{k}}^{dh}+Q{\mathit{k}}^{\Delta r}+Q{\mathit{k}}^{dr}\hfill \\ \hfill & +{\eta }_1{\left|\mathit{s}\right|}^{{\mu }_3}+{\eta }_2{\left|\mathit{s}\right|}^{{\mu }_4})sign\left(\mathit{s}\right).\hfill \end{array}$$

(23)

Theorem 1. 

Consider the error dynamics (20) to make uncertainties and external disturbances to meet Assumptions 1 and 2. The system’s state trajectory converges to the sliding surface after a finite amount of time if the control input (23) is applied, and its upper bound is:

$$t_1<\frac{1}{{\eta }_1({\mu }_3-1)}+\frac{1}{{\eta }_2(1-{\mu }_4)}.$$

(24)

Proof. 

The definition of the sign function is:

$$sign\left(\phi \right)=\left\{\begin{array}{c}1,\phi >0,\hfill \\ -1,\phi <0,\hfill \\ 0,\phi =0.\hfill \end{array}\right.$$

(25)

We choose the Lyapunov function as:

$$V=\left|\mathit{s}\right|.$$

(26)

We take the derivative of Equation (26) and we find:

$$\begin{array}{cc}\hfill D^{\beta }V& =D^{\beta }\mathit{s}sign\left(\mathit{s}\right)\hfill \\ \hfill & =[D^{\beta }\mathit{e}+({\sigma }_1{\left|\mathit{e}\right|}^{{\mu }_1}+{\sigma }_2{\left|\mathit{e}\right|}^{{\mu }_2}\left)sign\left(\mathit{e}\right)\right]sign\left(\mathit{s}\right).\hfill \end{array}$$

(27)

When we substitute Equations (20)–(23) into (27), we find:

$$\begin{array}{cc}\hfill D^{\beta }V=& \{N[\mathit{f}(\mathit{x},t)+\Delta \mathit{f}(\mathit{x},t)+{\mathit{d}}^f\left(t\right)]+P[\mathit{g}(\mathit{y},t)+\Delta \mathit{g}(\mathit{y},t)+{\mathit{d}}^g\left(t\right)]\hfill \\ \hfill & -R[\mathit{h}(\mathit{w},t)+\Delta \mathit{h}\left(\mathit{w}\left(t\right)\right)+{\mathit{d}}^h\left(t\right)]-Q[\mathit{r}(\mathit{z},t)+\Delta \mathit{r}\left(\mathit{z}\left(t\right)\right)+{\mathit{d}}^r\left(t\right)]\hfill \\ \hfill & -[N\mathit{f}(\mathit{x},t)+P\mathit{g}(\mathit{y},t)-R\mathit{h}(\mathit{w},t)-Q\mathit{r}(\mathit{z},t)+({\sigma }_1{\left|\mathit{e}\right|}^{{\mu }_1}+{\sigma }_2{\left|\mathit{e}\right|}^{{\mu }_2})sign\left(\mathit{e}\right)\hfill \\ \hfill & +(N{\mathit{k}}^{\Delta f}+N{\mathit{k}}^{df}+P{\mathit{k}}^{\Delta g}+P{\mathit{k}}^{dg}+R{\mathit{k}}^{\Delta h}+R{\mathit{k}}^{dh}+Q{\mathit{k}}^{\Delta r}+Q{\mathit{k}}^{dr}\hfill \\ \hfill & +{\eta }_1{\left|\mathit{s}\right|}^{{\mu }_3}+{\eta }_2{\left|\mathit{s}\right|}^{{\mu }_4}\left)sign\left(\mathit{s}\right)\right]+({\sigma }_1{\left|\mathit{e}\right|}^{{\mu }_1}+{\sigma }_2{\left|\mathit{e}\right|}^{{\mu }_2}\left)sign\left(\mathit{e}\right)\right\}sign\left(\mathit{s}\right).\hfill \end{array}$$

(28)

By simplifying the above formula, we can find:

$$\begin{array}{cc}\hfill D^{\beta }V=& (N\Delta \mathit{f}(\mathit{x},t)+N{\mathit{d}}^f\left(t\right)+P\Delta \mathit{g}(\mathit{y},t)+P{\mathit{d}}^g\left(t\right)-R\Delta \mathit{h}\left(\mathit{w}\left(t\right)\right)\hfill \\ \hfill & -R{\mathit{d}}^h\left(t\right)-Q\Delta \mathit{r}\left(\mathit{z}\left(t\right)\right)-Q{\mathit{d}}^r\left(t\right))sign\left(\mathit{s}\right)\hfill \\ \hfill & -(N{\mathit{k}}^{\Delta f}+N{\mathit{k}}^{df}+P{\mathit{k}}^{\Delta g}+P{\mathit{k}}^{dg}+R{\mathit{k}}^{\Delta h}+R{\mathit{k}}^{dh}+Q{\mathit{k}}^{\Delta r}+Q{\mathit{k}}^{dr})\hfill \\ \hfill & -\left({\eta }_1\right|\mathit{s}{|}^{{\mu }_3}-{\eta }_2|\mathit{s}{|}^{{\mu }_4}.\hfill \end{array}$$

(29)

According to Lemma 4, we find

$$\begin{array}{cc}\hfill D^{\beta }V& \le |N\Delta \mathit{f}(\mathit{x},t)|+|N{\mathit{d}}^f\left(t\right)|+|P\Delta \mathit{g}(\mathit{y},t)|+|P{\mathit{d}}^g\left(t\right)|-|R\Delta \mathit{h}\left(\mathit{w}\left(t\right)\right)|-|R{\mathit{d}}^h\left(t\right)|\hfill \\ \hfill & -|Q\Delta \mathit{r}\left(\mathit{z}\left(t\right)\right)|-|Q{\mathit{d}}^r\left(t\right)|-N{\mathit{k}}^{\Delta f}-N{\mathit{k}}^{df}-P{\mathit{k}}^{\Delta g}P{\mathit{k}}^{dg}-R{\mathit{k}}^{\Delta h}\hfill \\ \hfill & -R{\mathit{k}}^{dh}-Q{\mathit{k}}^{\Delta r}-Q{\mathit{k}}^{dr}-{\eta }_1{\left|\mathit{s}\right|}^{{\mu }_3}-{\eta }_2{\left|\mathit{s}\right|}^{{\mu }_4}\hfill \\ \hfill & \le -{\eta }_1{\left|\mathit{s}\right|}^{{\mu }_3}-{\eta }_2{\left|\mathit{s}\right|}^{{\mu }_4}\hfill \\ \hfill & \le -{\eta }_1{V}^{{\mu }_3}-{\eta }_2{V}^{{\mu }_4}.\hfill \end{array}$$

(30)

According to Lemma 3, the fixed-time convergence with the upper bound of convergence time (24) is proved, thus completing the proof. □

If the error state reaches the sliding surface, then we give its dynamics as follows $(\mathit{s}=0)$:

$$\mathit{e}=-D^{-\beta }({\sigma }_1{\left|\mathit{e}\right|}^{{\mu }_1}+{\sigma }_2{\left|\mathit{e}\right|}^{{\mu }_2})sign\left(\mathit{e}\right).$$

(31)

Theorem 2. 

Considering sliding mode dynamics (31), the error state variable converges to the origin within the upper limit of finite time:

$$t_2<\frac{1}{{\sigma }_1({\mu }_1-1)}+\frac{1}{{\sigma }_2(1-{\mu }_2)}.$$

(32)

Proof. 

We choose the Lyapunov function as:

$$V=\left|\mathit{e}\right|.$$

(33)

The fractional derivative of it is:

$$\begin{array}{cc}\hfill D^{\beta }V& =D^{\beta }\mathit{e}sign\left(\mathit{e}\right)=(D^{\beta }(-D^{-\beta }({\sigma }_1{\left|\mathit{e}\right|}^{{\mu }_1}+{\sigma }_2{\left|\mathit{e}\right|}^{{\mu }_2}\left)sign\left(\mathit{e}\right)\right)sign\left(\mathit{e}\right)\hfill \\ \hfill & =-\left({\sigma }_1\right|\mathit{e}{|}^{{\mu }_1}+{\sigma }_2\left|\mathit{e}{|}^{{\mu }_2}\right)\hfill \\ \hfill & \le -{\sigma }_1{V}^{{\mu }_1}+{\sigma }_2{V}^{{\mu }_2}.\hfill \end{array}$$

(34)

According to Lemma 3, the fixed-time convergence with the upper bound of convergence time (32) is proved, thus completing the proof. □

Theorem 3. 

Considering the error dynamics (20), the uncertainties and external disturbances of the error dynamics satisfy Assumptions 1 and 2. The system’s state trajectory converges to the sliding surface after a finite amount of time if the control input (23) is applied, and its upper bound is:

$$t_3<\frac{1}{{\eta }_1({\mu }_3-1)}+\frac{1}{{\eta }_2(1-{\mu }_4)}+\frac{1}{{\sigma }_1({\mu }_1-1)}+\frac{1}{{\sigma }_2(1-{\mu }_2)}.$$

(35)

Proof. 

Fixed-time stabilization along the sliding surface and fixed-time convergence to the sliding surface are both parts of the proof procedure. Fixed-time before arrival is demonstrated in Theorem 1, while fixed-time after reaching the sliding surface is demonstrated in Theorem 2. The evidence for Theorem 3 is thus complete based on Theorems 1 and 2. □

Regardless of the initial conditions, we use $T\triangleq$ max $t_3$ to the upper bound of stable time for all synchronization.

Remark 7. 

The plan can complete accurate time synchronization and/or stability in a fixed time. Only the design parameters affect the upper bound of the time, which is constant and does not depend on the initial circumstances.

4. Numerical Simulation

Some numerical simulation results are provided in this part in order to demonstrate the viability of the suggested approach. All experiments were conducted in Matlab 2016b on a personal computer with 8 GB RAM and an Intel(R) Core(TM) i5-5250U CPU processor, and we solve fractional differential equations using Adams–Bashforth–Moulton.

The FTMSCCS method can be used for many identical or different chaotic (hyperchaotic) systems. This part shows the FTMSCCS of four chaotic systems, including Chen, Lorenz, Liu and Lü chaotic systems, with external disturbances and uncertainties. We use the Lorenz and Chen systems as the drive systems:

$$\left\{\begin{array}{c}{}_0{D}_t^{\beta }{x}_1\left(t\right)=a_1(x_2-x_1)+\Delta f_1(x_1,t)+d_1^f\left(t\right),\hfill \\ {}_0{D}_t^{\beta }{x}_2\left(t\right)=x_1(b_1-x_3)-x_2+\Delta f_2(x_2,t)+d_2^f\left(t\right),\hfill \\ {}_0{D}_t^{\beta }{x}_3\left(t\right)=x_1{x}_2-c_1{x}_3+\Delta f_3(x_3,t)+d_3^f\left(t\right),\hfill \end{array}\right.$$

(36)

$$\left\{\begin{array}{c}{}_0{D}_t^{\beta }{y}_1\left(t\right)=a_2(y_2-y_1)+\Delta g_1(y_1,t)+d_1^g\left(t\right),\hfill \\ {}_0{D}_t^{\beta }{y}_2\left(t\right)=(b_2-a_2)y_1-y_1{y}_3+b_2{y}_2+\Delta g_2(y_2,t)+d_2^g\left(t\right),\hfill \\ {}_0{D}_t^{\beta }{y}_3\left(t\right)=y_1{y}_2-c_3{y}_3+\Delta g_3(y_3,t)+d_3^g\left(t\right),\hfill \end{array}\right.$$

(37)

where $a_1=10$, $c_1=28$, $b_1=8/3$, $a_2=35$, $b_2=28$, $c_2=3$ are system parameters, and ${\mathit{x}}_i\left(t\right),{\mathit{y}}_i\left(t\right)(i=1,\dots ,3)$ represent the state vectors. We assume that the uncertainties and the external disturbances are:

$$\left\{\begin{array}{c}\Delta f_1(x_1,t)=0.1x_{1}sin\left(t\right),d_1^f\left(t\right)=0.1sin\left(2t\right),\hfill \\ \Delta f_2(x_2,t)=0.1x_{2}sin\left(5t\right),d_2^f\left(t\right)=0.1sin\left(t\right),\hfill \\ \Delta f_3(x_3,t)=0.1x_{3}sin\left(4t\right),d_3^f\left(t\right)=0.1sin(2/3t),\hfill \\ \Delta g_1(y_1,t)=0.1y_{1}sin\left(2t\right),d_1^g\left(t\right)=0.1sin(4/5t),\hfill \\ \Delta g_2(y_2,t)=0.1y_{2}sin3\left(t\right),d_2^g\left(t\right)=0.1sin(3/2t),\hfill \\ \Delta g_3(y_3,t)=0.1y_{3}sin\left(4t\right),d_3^g\left(t\right)=0.1sin(1/2t).\hfill \end{array}\right.$$

(38)

The Lü and Liu systems are viewed as response systems:

$$\left\{\begin{array}{c}{}_0{D}_t^{\beta }{w}_1\left(t\right)=a_3(w_2-w_1)+\Delta h_1(w_1,t)+d_1^h\left(t\right)+{\xi }_1\left(t\right),\hfill \\ {}_0{D}_t^{\beta }{w}_2\left(t\right)=-w_1{w}_3+b_3{w}_2+\Delta h_2(w_2,t)+d_2^h\left(t\right)+{\xi }_2\left(t\right),\hfill \\ {}_0{D}_t^{\beta }{w}_3\left(t\right)=w_1{w}_2-c_3{w}_3+\Delta h_3(w_3,t)+d_3^h\left(t\right)+{\xi }_3\left(t\right),\hfill \end{array}\right.$$

(39)

$$\left\{\begin{array}{c}{}_0{D}_t^{\beta }{z}_1\left(t\right)=-(z_3+z_2)+\Delta r_1(z_1,t)+d_1^r\left(t\right)+{\xi }_1^{*}\left(t\right),\hfill \\ {}_0{D}_t^{\beta }{z}_2\left(t\right)=z_1+a_4{z}_2+\Delta r_2(z_2,t)+d_2^r\left(t\right)+{\xi }_2^{*}\left(t\right),\hfill \\ {}_0{D}_t^{\beta }{z}_3\left(t\right)=b_4+z_3(z_1-c_4)+\Delta r_3(z_3,t)+d_3^r\left(t\right)+{\xi }_3^{*}\left(t\right),\hfill \end{array}\right.$$

(40)

where $a_3=36$, $c_3=3$, $b_3=20$, $a_4=0.2$, $b_4=0.2$, $c_4=5.7$ are system parameters, ${\mathit{w}}_i\left(t\right),{\mathit{z}}_i\left(t\right)(i=1,\dots ,3)$ are the state vectors, and $\mathit{\xi }={[{\xi }_1,{\xi }_2,{\xi }_3]}^T$, ${\mathit{\xi }}^{*}=[{\xi }_1^{*},{\xi }_2^{*},{\xi }_3^{*}]$ are the controllers to be designed. We assume that the uncertainties and the external disturbances are

$$\left\{\begin{array}{c}\Delta h_1(w_1,t)=0.1w_{1}sin\left(5t\right),d_1^h\left(t\right)=0.1sin\left(t\right),\hfill \\ \Delta h_2(w_2,t)=0.1w_{2}sin\left(2t\right),d_2^h\left(t\right)=0.1sin(1/3t),\hfill \\ \Delta h_3(w_3,t)=0.1w_{3}sin(2/5t),d_3^h\left(t\right)=0.1sin(2/3t),\hfill \\ \Delta r_1(z_1,t)=0.1z_{1}sin\left(2t\right),d_1^r\left(t\right)=0.1sin(1/5t),\hfill \\ \Delta r_2(z_2,t)=0.1z_{2}sin\left(t\right),d_2^r\left(t\right)=0.1sin(1/2t),\hfill \\ \Delta r_3(z_3,t)=0.1z_{3}sin(1/4t),d_3^r\left(t\right)=0.1sin\left(2t\right).\hfill \end{array}\right.$$

(41)

By the appropriate conditions of the indicators $h,p,l,s=1,2,3$, as described in Definition 6, there can be multiple possible switch combinations to define the error state of the master–slave system (36)–(40). These combinations are as follows:

$$\begin{array}{c}Combination1:h=p=l\ne s:\{e_{1112},e_{1113},e_{2221},e_{2223},e_{3331},e_{3332}\}\hfill \\ Combination2:h=p=s\ne l:\{e_{1121},e_{1131},e_{2212},e_{2232},e_{3313},e_{3323}\}\hfill \\ Combination3:h=l=s\ne p:\{e_{1211},e_{1311},e_{2122},e_{2322},e_{3133},e_{3233}\}\hfill \\ Combination4:p=l=s\ne h:\{e_{1222},e_{1333},e_{2111},e_{2333},e_{3111},e_{3222}\}\hfill \\ Combination5:h=p\ne l=s:\{e_{1122},e_{1133},e_{2211},e_{2233},e_{3311},e_{3322}\}\hfill \\ Combination6:h=l\ne p=s:\{e_{1212},e_{1313},e_{2121},e_{2323},e_{3131},e_{3232}\}\hfill \\ Combination7:h=s\ne p=l:\{e_{1221},e_{1331},e_{2111},e_{2331},e_{3113},e_{3223}\}\hfill \\ Combination8:h=p\ne l\ne s:\{e_{1123},e_{1132},e_{2213},e_{2231},e_{3312},e_{3321}\}\hfill \\ Combination9:h=l\ne p\ne s:\{e_{1213},e_{1312},e_{2123},e_{2321},e_{3132},e_{3231}\}\hfill \\ Combination10:h=s\ne l\ne p:\{e_{1231},e_{1321},e_{2132},e_{2312},e_{3123},e_{3213}\}\hfill \\ Combination11:h\ne p=l\ne s:\{e_{1223},e_{1332},e_{2113},e_{2331},e_{3112},e_{3221}\}\hfill \\ Combination12:h\ne p\ne l=s:\{e_{1233},e_{1322},e_{2133},e_{2311},e_{3122},e_{3211}\}\hfill \end{array}$$

Based on different switching possibilities, the results of two randomly selected error state vector combinations are established in this paper. Three arbitrary error states are selected to form our Switch 1 and Switch 2, respectively:

$$\mathrm{switch}1\left\{\begin{array}{c}{e}_{1231}={\partial }_1{x}_1+{\beta }_2{y}_2-r_3{w}_3-{\delta }_1{z}_1;\hfill \\ e_{3123}={\partial }_3{x}_3+{\beta }_1{y}_1-r_2{w}_2-{\delta }_3{z}_3;\hfill \\ e_{2312}={\partial }_2{x}_2+{\beta }_3{y}_3-r_1{w}_1-{\delta }_2{z}_2;\hfill \end{array}\right.$$

(42)

$$\mathrm{switch}2\left\{\begin{array}{c}{e}_{2121}={\partial }_2{x}_2+{\beta }_1{y}_1-{\gamma }_2{w}_2-{\delta }_1{z}_1,\hfill \\ e_{1232}={\partial }_1{x}_1+{\beta }_2{y}_3-{\gamma }_3{w}_3-{\delta }_2{z}_2,\hfill \\ e_{3313}={\partial }_3{x}_3+{\beta }_3{y}_3-r_1{w}_1-{\delta }_3{z}_3;\hfill \end{array}\right.$$

(43)

we select $N=diag({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n)$, $P=diag({\beta }_1,{\beta }_2,\dots ,{\beta }_n)$, $R=diag({\gamma }_1,{\gamma }_2,\dots ,{\gamma }_n)$ and $Q=diag({\delta }_1,{\delta }_2,\dots ,{\delta }_n)$. The ${\alpha }_k$, ${\beta }_l$, ${\gamma }_m$, ${\delta }_n(k,l,m,n=1,2,3)$ represent scale factors, which can in fact take any value.

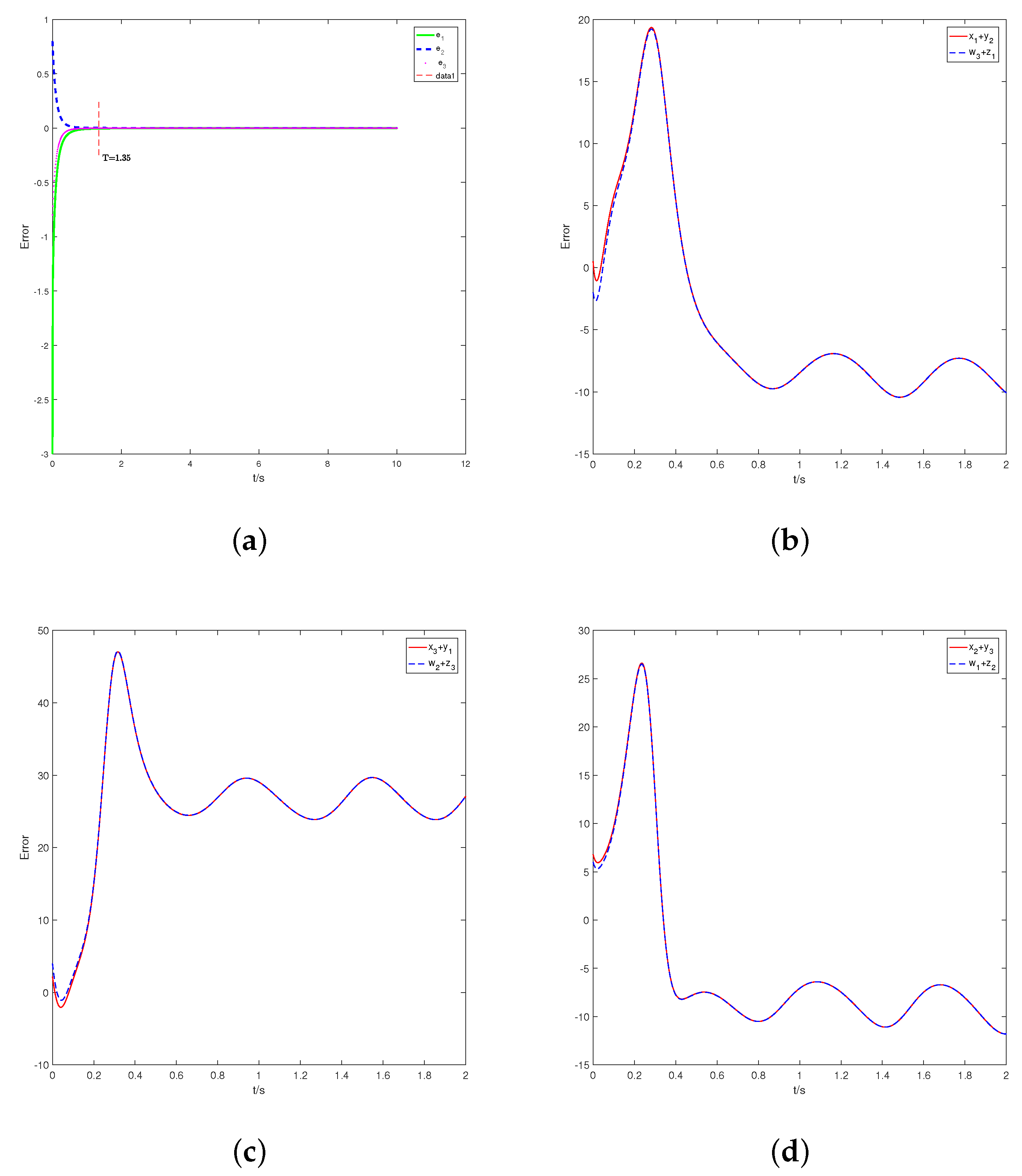
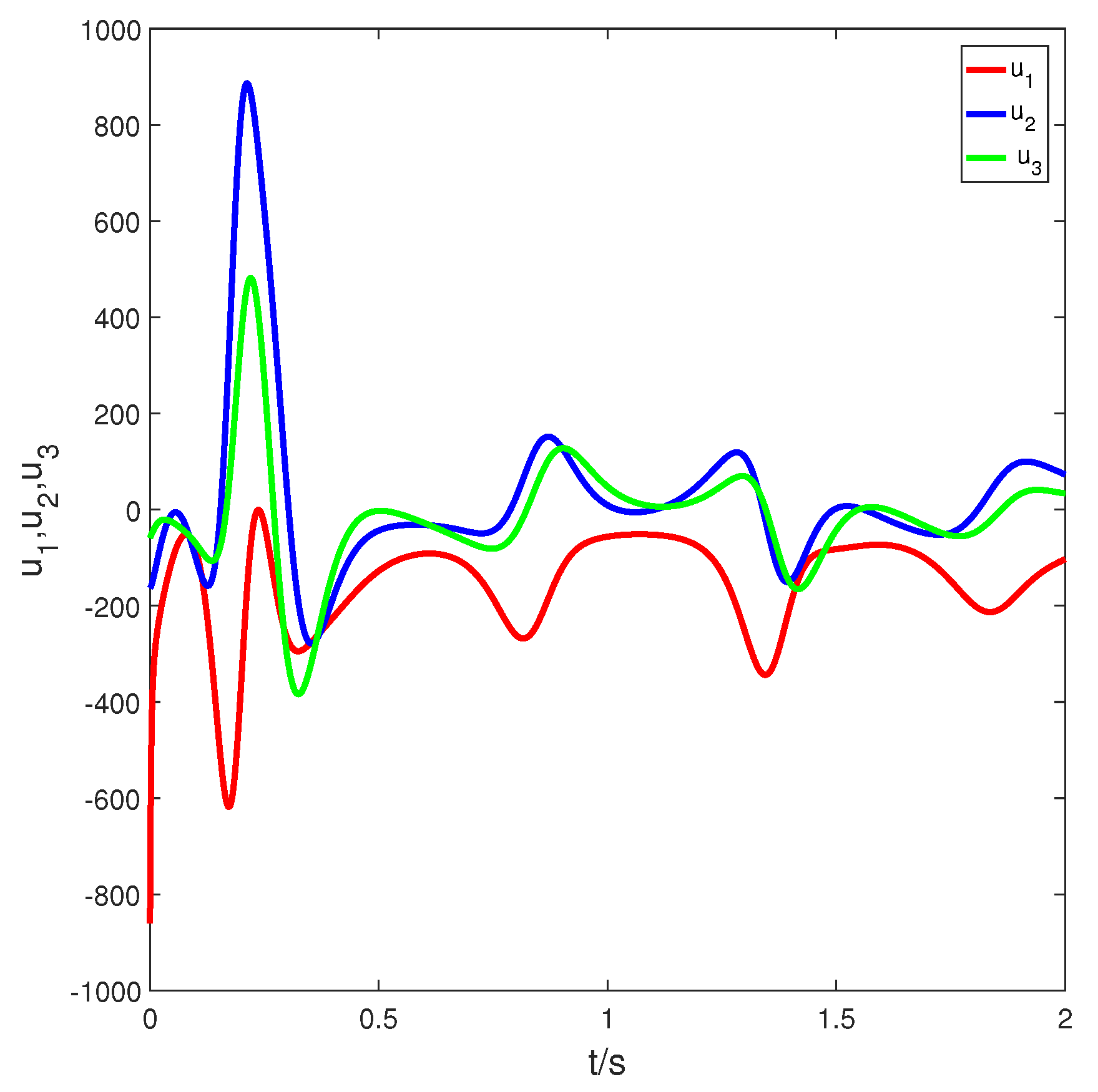
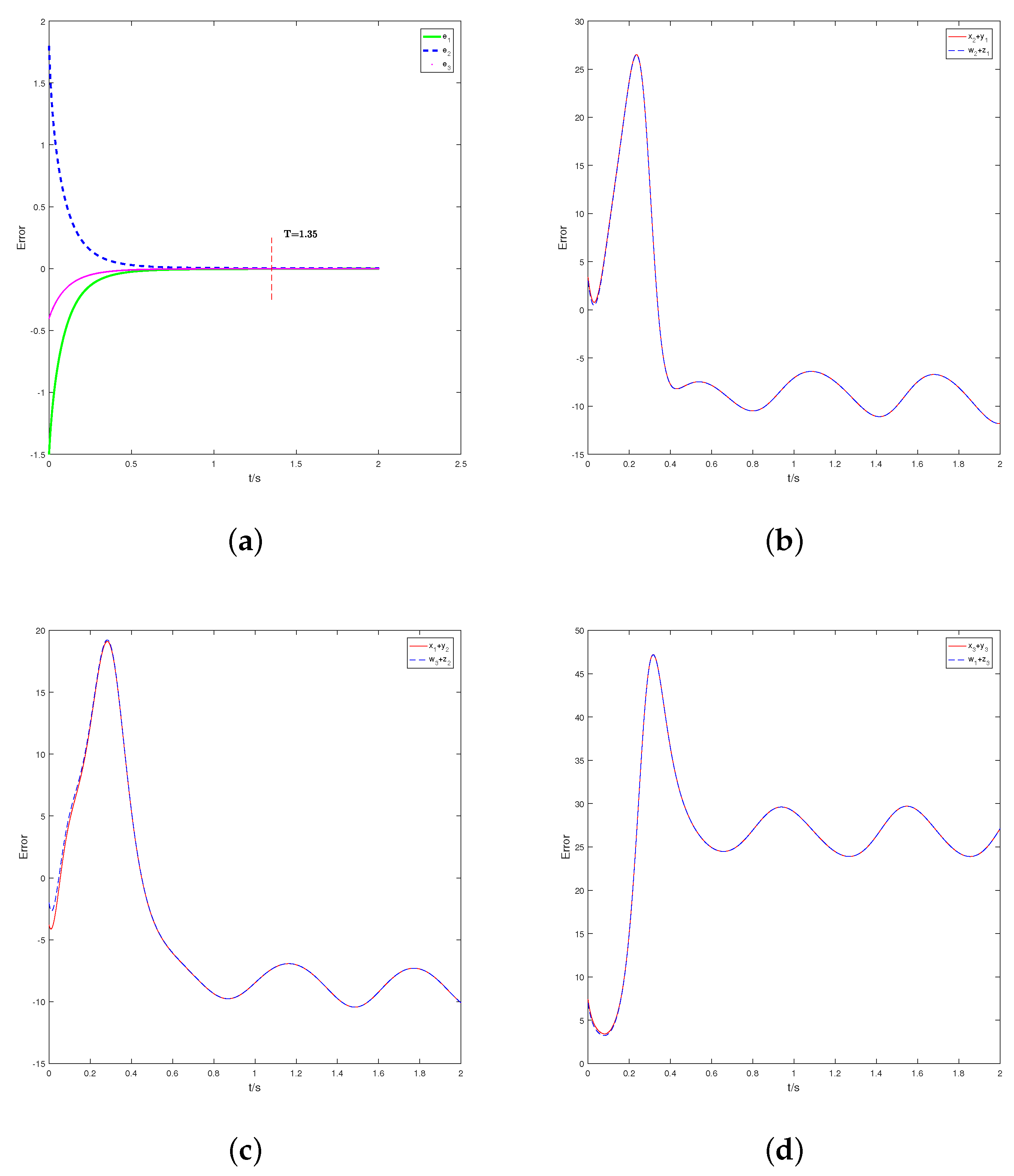
4.1. Switch 1

Switch 1: The error dynamics of Switch 1 are represented by:

$$\left\{\begin{array}{c}{D}^{\beta }{e}_{1231}={\partial }_1{D}^{\beta }{x}_1+{\beta }_2{D}^{\beta }{y}_2-r_3{D}^{\beta }{w}_3-{\delta }_1{D}^{\beta }{z}_1;\hfill \\ D^{\beta }{e}_{3123}={\partial }_3{D}^{\beta }{x}_3+{\beta }_1{D}^{\beta }{y}_1-r_2{D}^{\beta }{w}_2-{\delta }_3{D}^{\beta }{z}_3;\hfill \\ D^{\beta }{e}_{2312}={\partial }_2{D}^{\beta }{x}_2+{\beta }_3{D}^{\beta }{y}_3-r_1{D}^{\beta }{w}_1-{\delta }_2{D}^{\beta }{z}_2;\hfill \end{array}\right.$$

(44)

using Equations (36)–(41), Equations (44) is changed into:

$$\left\{\begin{array}{c}\begin{array}{cc}\hfill D^{\beta }{e}_{1231}=& {\partial }_1[a_1(x_2-x_1)+\Delta f_1(x_1,t)+d_1^f\left(t\right)]\hfill \\ \hfill & +{\beta }_2[(b_2-a_2)y_1-y_1{y}_3+b_2{y}_2+\Delta g_2(y_2,t)+d_2^g\left(t\right)]\hfill \\ \hfill & -{\gamma }_3[w_1{w}_2-c_3{w}_3+\Delta h_3(w_3,t)+d_3^h\left(t\right)+{\xi }_3\left(t\right)]\hfill \\ \hfill & -{\delta }_1[-(z_3+z_2)+\Delta r_1(z_1,t)+d_1^r\left(t\right)+{\xi }_1^{*}\left(t\right)];\hfill \\ \hfill \\ \hfill D^{\beta }{e}_{3123}=& {\partial }_3[x_1{x}_2-c_1{x}_3+\Delta f_3(x_3,t)+d_3^f\left(t\right)]\hfill \\ \hfill & +{\beta }_1[a_2(y_2-y_1)+\Delta g_1(y_1,t)+d_1^g\left(t\right)]\hfill \\ \hfill & -{\gamma }_2[-w_1{w}_2+b_3{w}_2+\Delta h_2(w_2,t)+d_2^h\left(t\right)+{\xi }_2\left(t\right)]\hfill \\ \hfill & -{\delta }_3[b_4+z_3(z_1-\left(c_4\right)+\Delta r_3(z_3,t)+d_3^r\left(t\right)+{\xi }_3^{*}\left(t\right)];\hfill \\ \hfill \\ \hfill D^{\beta }{e}_{2312}=& {\delta }_2[x_1(b_1-x_3)-x_2+\Delta f_2(x_2,t)+d_2^f\left(t\right)]\hfill \\ \hfill & +{\beta }_3[y_1{y}_2-c_3{y}_3+\Delta g_3(y_3,t)+d_3^g\left(t\right)]\hfill \\ \hfill & -r_1[a_3(w_2-w_1)+\Delta h_1(w_1,t)+d_1^h\left(t\right)+{\xi }_1\left(t\right)]\hfill \\ \hfill & -{\delta }_2[z_1+a_4{z}_2+\Delta r_2(z_2,t)+d_2^r\left(t\right)+{\xi }_2^{*}\left(t\right)].\hfill \end{array}\hfill \end{array}\right.$$

(45)

The controllers of the error system are given as:

$$\left\{\begin{array}{c}{u}_1={\gamma }_3{\xi }_3\left(t\right)+{\delta }_1{\xi }_1^{*}\left(t\right),\hfill \\ u_2={\gamma }_2{\xi }_2\left(t\right)+{\delta }_3{\xi }_3^{*}\left(t\right),\hfill \\ u_3={\gamma }_1{\xi }_1\left(t\right)+{\delta }_2{\xi }_2^{*}\left(t\right).\hfill \end{array}\right.$$

(46)

According to (22), we take the sliding mode surface as:

$$\left\{\begin{array}{c}\hfill s_{1231}=e_{1231}+D^{-\beta }({\sigma }_1|e_{1231}{|}^{{\mu }_1}+{\sigma }_2|e_{1231}{|}^{{\mu }_2})sign\left(e_{1231}\right);\\ \hfill s_{3123}=e_{3123}+D^{-\beta }({\sigma }_1|e_{3123}{|}^{{\mu }_1}+{\sigma }_2|e_{3123}{|}^{{\mu }_2})sign\left(e_{3123}\right);\\ \hfill s_{2312}=e_{2312}+D^{-\beta }({\sigma }_1|e_{2312}{|}^{{\mu }_1}+{\sigma }_2|e_{2312}{|}^{{\mu }_2})sign\left(e_{2312}\right).\end{array}\right.$$

(47)

Based on (23), we take the controller to be:

$$\left\{\begin{array}{cc}\hfill u_1=& {\partial }_1{a}_1(x_2-x_1)+{\beta }_2(b_2-a_2)y_1-{\beta }_2{y}_1{y}_3+{\beta }_2{b}_2{y}_2-r_3{w}_1{w}_2\hfill \\ \hfill & -r_3{c}_3{w}_3+{\delta }_1(z_3+z_2)+({\sigma }_1|e_{1231}{|}^{u_1}+{\sigma }_2|e_{10}{|}^{u_2})sign\left(e_{1231}\right)\hfill \\ \hfill & +({\partial }_1{k}_1^{\Delta f_1}+{\partial }_1{k}_1^{df}+{\beta }_2{k}_2^{\Delta g_2}+{\beta }_2{k}_2^{dg}+{\gamma }_3·k_3^{\Delta h}+{\gamma }_3·k_3^{dh}\hfill \\ \hfill & +{\delta }_1{k}_1^{\Delta r}+{\delta }_1{k}_1^{dr}+{\eta }_1|s_{1231}{|}^{u_3}+{\eta }_2|s_{1231}{|}^{u_4})·sign\left(s_{1231}\right);\hfill \\ \hfill \\ \hfill u_2=& {\partial }_3{x}_1{x}_2-{\partial }_3·c_1{x}_3+{\beta }_1{a}_2\left(y_2-y_1\right)+r_2{w}_1{w}_2-r_2·b_3{w}_2\hfill \\ \hfill & -{\delta }_3{b}_4-{\delta }_3{z}_3\left(z_1-c_4\right)+\left({\sigma }_1{\left|e_{3123}\right|}_1^{u_1}+{\sigma }_2{\left|e_{3123}\right|}^{u_2}\right)sign\left(e_{3123}\right)\hfill \\ \hfill & +({\partial }_3{k}_3^{\Delta f}+{\partial }_3{k}_3^{df}+{\beta }_1{k}_1^{\Delta g}+{\beta }_1{k}_1^{dg}+{\gamma }_2·k_2^{\Delta h}+{\gamma }_2·k_2^{dh}\hfill \\ \hfill & +{\delta }_3·k_3^{\Delta r}+{\delta }_3{k}_3^{dr}+{\eta }_1|s_{3123}{|}^{u_3}+{\eta }_2|s_{3123}{|}^{u_4})sign\left(s_{3123}\right);\hfill \\ \hfill \\ \hfill u_3=& {\partial }_2{x}_1\left(b_1-x_3\right)-{\partial }_2{x}_2+{\beta }_3{y}_1{y}_2-{\beta }_3{c}_3{y}_3-r_1{a}_3\left(w_2-w_1\right)\hfill \\ \hfill & -{\delta }_2{z}_1+{\delta }_2{a}_4·z_2+\left({\sigma }_1\left|e_{2312}\right|u_1+{\sigma }_2\left|e_{2312}\right|u_2\right)·sign\left(l_{2312}\right)\hfill \\ \hfill & +({\partial }_2{k}_2^{\Delta t}+{\partial }_2{k}_2^{dt}+{\beta }_3{k}_3^{\Delta g}+{\beta }_3{k}_3^{dg}+{\gamma }_1·k_1^{\Delta h}+{\gamma }_1·k_1^{dh}\hfill \\ \hfill & +delt{a}_2{k}_2^{\Delta r}+{\delta }_2{k}_2^{dr}+{\eta }_1{\left|s_{2312}\right|}^{u_3}+{\eta }_2|s_{2312}{|}^{u_4})·sign\left(s_{2312}\right).\hfill \end{array}\right.$$

(48)

According to Theorem 6, if the sliding mode surface (47) and control function (48) are selected, then the drive system (36) and (37) will implement FTMSCCS with the response system (39) and (40).

4.2. Switch 2

Switch 2: The error dynamics of Switch 2 are represented by:

$$\left\{\begin{array}{c}{D}^{\beta }{e}_{2121}={\partial }_2{D}^{\beta }{x}_2+{\beta }_1{D}^{\beta }{y}_1-r_2{D}^{\beta }{w}_2-{\delta }_1{D}^{\beta }{z}_1;\hfill \\ D^{\beta }{e}_{1232}={\partial }_1{D}^{\beta }{x}_1+{\beta }_2{D}^{\beta }{y}_2-r_3{D}^{\beta }{w}_3-{\delta }_2{D}^{\beta }{z}_2;\hfill \\ D^{\beta }{e}_{3313}={\partial }_2{D}^{\beta }{x}_3++{\beta }_3{D}^{\beta }{y}_3-r_1{D}^{\beta }{w}_1-{\delta }_3{D}^{\beta }{z}_3;\hfill \end{array}\right.$$

(49)

using Equations (36)–(41), Equations (49) is changed into:

$$\left\{\begin{array}{c}\begin{array}{cc}\hfill D^{\beta }{e}_{2121}=& {\partial }_2[x_1(b_1-x_3)-x_2+\Delta f_2(x_2,t)+d_2^f\left(t\right)]\hfill \\ \hfill & +{\beta }_1\left[a_2\left(y_2-y_1\right)+\Delta g_1\left(y_1,t\right)+d_1^g\left(t\right)\right]\hfill \\ \hfill & -{\gamma }_2\left[-w_1{w}_3+b_3{w}_2+\Delta h_2\left(w_2,t\right)+d_2^h\left(t\right)+{\xi }_2\left(t\right)\right]\hfill \\ \hfill & -{\delta }_1\left[-\left(z_3+z_2\right)+\Delta r_1\left(z_1,t\right)+d_1^r\left(t\right)+{\xi }_1^{*}\left(t\right)\right];\hfill \\ \hfill \\ \hfill D^{\beta }{e}_{1232}=& {\partial }_1\left[a_1\left(x_2-x_1\right)+\Delta f_1\left(x_1,t\right)+d_1^f\left(t\right)\right]\hfill \\ \hfill & +{\beta }_2\left[\left(b_2-a_2\right)y_1-y_1{y}_3+b_2{y}_2+\Delta g_2\left(y_2,t\right)+d_2^g\left(t\right)\right]\hfill \\ \hfill & -{\gamma }_3\left[w_1{w}_2-c_3{w}_3+\Delta h_3\left(w_3,t\right)+d_3^h\left(t\right)+{\xi }_3\left(t\right)\right]\hfill \\ \hfill & -{\delta }_2\left[z_1+a_4{z}_2+\Delta r_2\left(z_2,t\right)+d_2^r\left(t\right)+{\xi }_2^{*}\left(t\right)\right];\hfill \\ \hfill \\ \hfill D^{\beta }{e}_{3313}=& {\partial }_3\left[x_1{x}_2-c_1{x}_3+\Delta f_3\left(x_3,t\right)+d_3^f\left(t\right)\right]\hfill \\ \hfill & +{\beta }_3\left[y_1{y}_2-c_3{y}_3+\Delta g_3\left(y_3,t\right)+d_3^g\left(t\right)\right]\hfill \\ \hfill & -{\gamma }_1\left[d_3\left(w_2-w_1\right)+\Delta h_1\left(w_1,t\right)+d_1^h\left(t\right)+{\xi }_1\left(t\right)\right]\hfill \\ \hfill & -{\delta }_3\left[b_4+z_3\left(z_1-c_4\right)+\Delta r_3\left(z_3,t\right)+d_3^r\left(t\right)+{\xi }_3^{*}\left(t\right)\right].\hfill \end{array}\hfill \end{array}\right.$$

(50)

The controllers of the error system are given as:

$$\begin{array}{c}\left\{\begin{array}{c}{U}_1={\gamma }_2{\xi }_2\left(t\right)+{\delta }_1{\xi }_1^{*}\left(t\right);\hfill \\ U_2={\gamma }_3{\xi }_3\left(t\right)+{\delta }_2{\xi }_2^{*}\left(t\right);\hfill \\ U_3={\gamma }_1{\xi }_1\left(t\right)+{\delta }_3{\xi }_3^{*}\left(t\right).\hfill \end{array}\right.\hfill \end{array}$$

(51)

According to (22), we take the sliding mode surface as:

$$\left\{\begin{array}{c}\hfill s_{2121}=e_{1231}+D^{-\beta }({\sigma }_1|e_{1231}{|}^{{\mu }_1}+{\sigma }_2|e_{1231}{|}^{{\mu }_2})sign\left(e_{1231}\right);\\ \hfill s_{1232}=e_{3123}+D^{-\beta }({\sigma }_1|e_{3123}{|}^{{\mu }_1}+{\sigma }_2|e_{3123}{|}^{{\mu }_2})sign\left(e_{3123}\right);\\ \hfill s_{3313}=e_{2312}+D^{-\beta }({\sigma }_1|e_{2312}{|}^{{\mu }_1}+{\sigma }_2|e_{2312}{|}^{{\mu }_2})sign\left(e_{2312}\right).\end{array}\right.$$

(52)

Based on (23), we take the controller to be:

$$\left\{\begin{array}{c}\begin{array}{cc}\hfill u_1=& {\partial }_2{x}_1\left(b_1-x_3\right)-{\partial }_2{x}_2+{\beta }_1{a}_2\left(y_2-y_1\right)+r_2{w}_1{w}_3\hfill \\ \hfill & -r_2{b}_3{w}_2+{\delta }_1\left(z_3+z_2\right)+({\sigma }_1|e_{2121}{|}^{{\mu }_1}+{\sigma }_2|e_{2121}{|}^{{\mu }_2})sign\left(e_{2121}\right)\hfill \\ \hfill & +({\partial }_2{k}_2^{\Delta f}+{\partial }_2{k}_2^{df}+{\beta }_1{k}_1^{\Delta g}+{\beta }_1{k}_1^{dg}+{\gamma }_2{k}_2^{\Delta h}+{\gamma }_2{k}_2^{dh}\hfill \\ \hfill & +{\delta }_1{k}_1^{\delta r}+d_1{k}_1^{dr}+{\eta }_1|s_{2121}{|}^{{\mu }_3}+{\eta }_2|s_{2121}{|}^{{\mu }_4})sign\left(s_{2121}\right);\hfill \\ \hfill \\ \hfill u_2=& {\partial }_1{a}_1\left(x_2-x_1\right)+{\beta }_2\left(b_2-a_2\right)y_1-{\beta }_2{y}_1{y}_3+{\beta }_2{b}_2{y}_2\hfill \\ \hfill & -r_3{w}_1{w}_2+r_3{c}_3{w}_3-{\delta }_2{z}_1-{\delta }_2{a}_4{z}_2+\left({\sigma }_1{\left|e_{1232}\right|}^{{\mu }_1}+{\sigma }_2{\left|e_{1232}\right|}^{{\mu }_2}\right)·\hfill \\ \hfill & sign\left(e_{1232}\right)+\left({\partial }_1{k}_1^{\Delta f}+{\partial }_1{k}_1^{df}+\right.{\beta }_2{k}_2^{\Delta g}+{\beta }_2{k}_2^{dg}+{\gamma }_3{k}_3^{\Delta h}+{\gamma }_3{k}_3^{dh}\hfill \\ \hfill & +{\delta }_2{k}_2^{\Delta r}+{\delta }_2{k}_2^{dr}\left.+{\eta }_1{\left|s_{1232}\right|}^{{\mu }_3}+{\eta }_2{\left|s_{1232}\right|}^{{\mu }_4}\right)sign\left(s_{1232}\right);\hfill \\ \hfill \\ \hfill u_3=& {\partial }_3{x}_1{x}_2-{\partial }_3{c}_1{x}_3+{\beta }_3{y}_1{y}_2-{\beta }_3{c}_3{y}_3-r_1{a}_3\left(w_2-w_1\right)\hfill \\ \hfill & -{\delta }_3{b}_4-{\delta }_3{z}_3\left(z_1-c_4\right)+\left({\sigma }_1{\left|e_{3313}\right|}^{{\mu }_1}+{\sigma }_2{\left|e_{3313}\right|}^{{\mu }_2}\right)sign\left(e_{3313}\right)\hfill \\ \hfill & +\left({\partial }_3{k}_3^{\Delta f}+{\partial }_3{k}_3^{df}+{\beta }_3{k}_3^{\Delta g}+{\beta }_3{k}_3^{dg}+{\gamma }_1{k}_1^{\Delta h}+{\gamma }_1{k}_1^{dh}+{\delta }_3{k}_3^{\Delta r}+{\delta }_3{k}_3^{d_r}\right.\hfill \\ \hfill & \left.+{\eta }_1{\left|s_{3313}\right|}^{{\mu }_3}+{\eta }_2{\left|s_{3313}\right|}^{{\mu }_4}\right)sign\left(s_{3313}\right).\hfill \end{array}\hfill \end{array}\right.$$

(53)

According to Theorem 3, if the sliding mode surface (47) and control function (48) are selected, then the drive system (36) and (37) will implement FTMSCCS with the response system (39) and (40).

Finally, we further prove our conclusion using a numerical simulation. Let $N=diag(1,1,1)$, $P=diag(1,1,1)$, $R=diag(1,1,1)$ and $Q=diag(1,1,1)$ and the fractional-order $\beta =0.9$. The initial states of the drive and response systems are arbitrarily chosen as $(x_1\left(0\right),x_2\left(0\right),x_3\left(0\right))=(3,1,2)$, $(y_1\left(0\right),y_2\left(0\right),y_3\left(0\right))=(2,-5,5)$, $(w_1\left(0\right),w_2\left(0\right),w_3\left(0\right))=(3,2,2)$, $(z_1\left(0\right),z_2\left(0\right),z_3\left(0\right))=(-1,3,6.5)$. We choose the switch surface and controller parameters as ${\mu }_1={\mu }_3=11/9$, ${\mu }_2={\mu }_4=5/9$ and ${\sigma }_1={\sigma }_2={\eta }_1={\eta }_2=10$. Additionally, $k_i={[3,3,3]}^T$, where $k_i\triangleq k_i^{\Delta f}+k_i^{\Delta g}+k_i^{\Delta r}+k_i^{\Delta h}+k_i^{df}+k_i^{dg}+k_i^{dr}+k_i^{dh}$. According to (35), we find the maximum synchronization time $T<1.35$. When there are uncertainties and external disturbances on Switch 1, the synchronization time and error vectors of the two systems are as shown in Figure 1. The control input of Switch 1 is shown in Figure 2. When there are uncertainties and external disturbances on Switch 2, the synchronization time and error vectors of the two systems are as shown in Figure 3. The control input of Switch 2 is shown in Figure 4.

5. Conclusions

This paper extends fixed time to multi-switch combination–combination synchronization. This method not only ensures that the transmitted signal has stronger anti-attack and anti-translation abilities than a signal transmitted by a single transmitter, but also ensures that the signal transmission is completed in a limited time. It can be concluded that this method is very pragmatic in practical application. Aiming at four fractional-order chaotic systems with uncertainty and external disturbance, an appropriate controller and sliding mode surface are designed to realize the fixed-time multi-switch combination–combinatorial synchronization of fractional-order chaotic systems. It is worth mentioning that the defined sliding surface not only guarantees the stability of the fixed time, but also the upper bound of the synchronization time is independent of differences in the initial conditions of the master–slave system, and depends only on the design parameters. Two switches are selected for numerical simulation, and the effectiveness and robustness of the proposed method are verified. This method can further be applied to studies considering the case of parameter uncertainty, and can also be extended to more synchronization mechanisms or complex network synchronization.