Finite-Time Synchronization for Fractional Order Fuzzy Inertial Cellular Neural Networks with Piecewise Activations and Mixed Delays
Abstract
:1. Introduction
- The Caputo fractional order fuzzy inertial cellular neural networks model is established. It can be used to describe many systems of internal coherence in the real environment. In addition, it is easy to implement in engineering applications and has important application prospects.
- A novel nonlinear controller is designed to realize the finite-time synchronization of FFICNNs with piecewise activation and mixed delay. It is of high reliability and great accuracy, and can better synchronize the position and motion of the system.
- The Lyapunov direct method is applied in the analysis of the inertial system to avoid the loss of the inertia. The numerical simulation results show that the designed method is effective. Therefore, it is of more important practical significance.
2. Preliminaries and Problem Formulation
2.1. Preliminaries
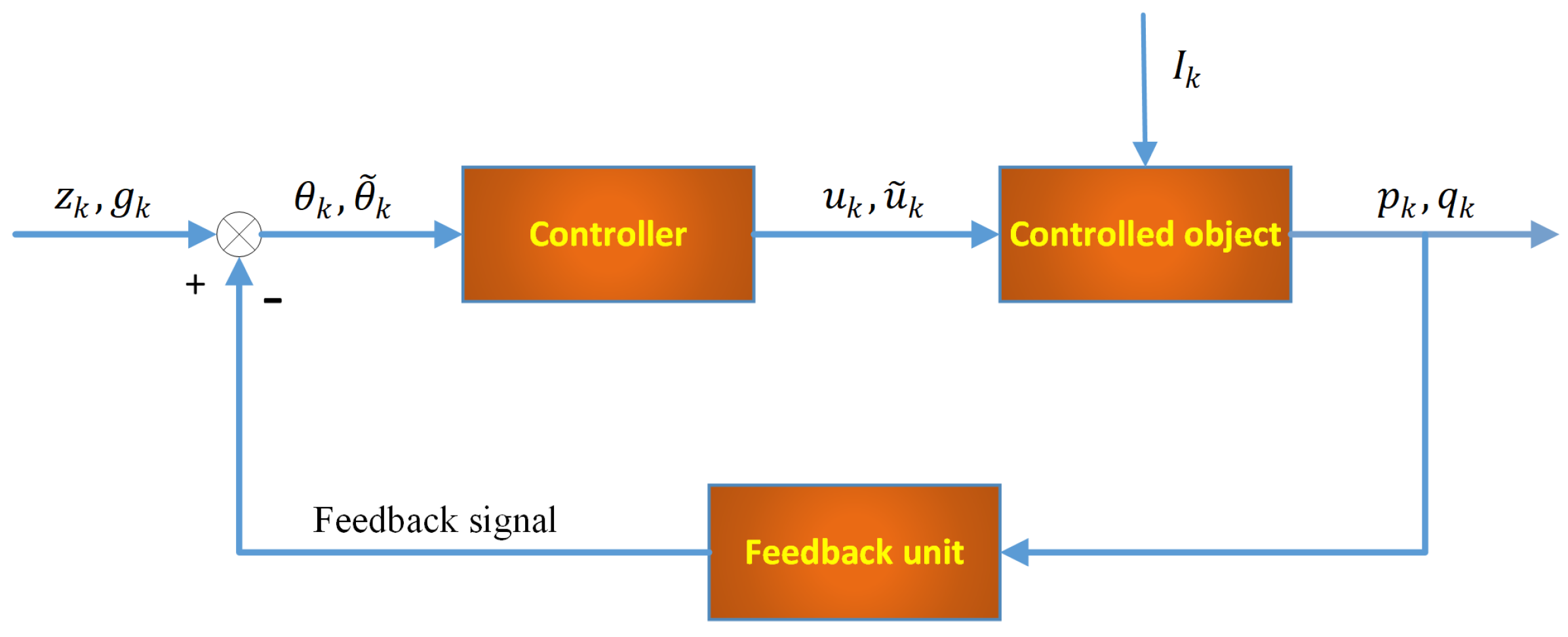
2.2. Problem Formulation
3. Finite-Time Synchronization
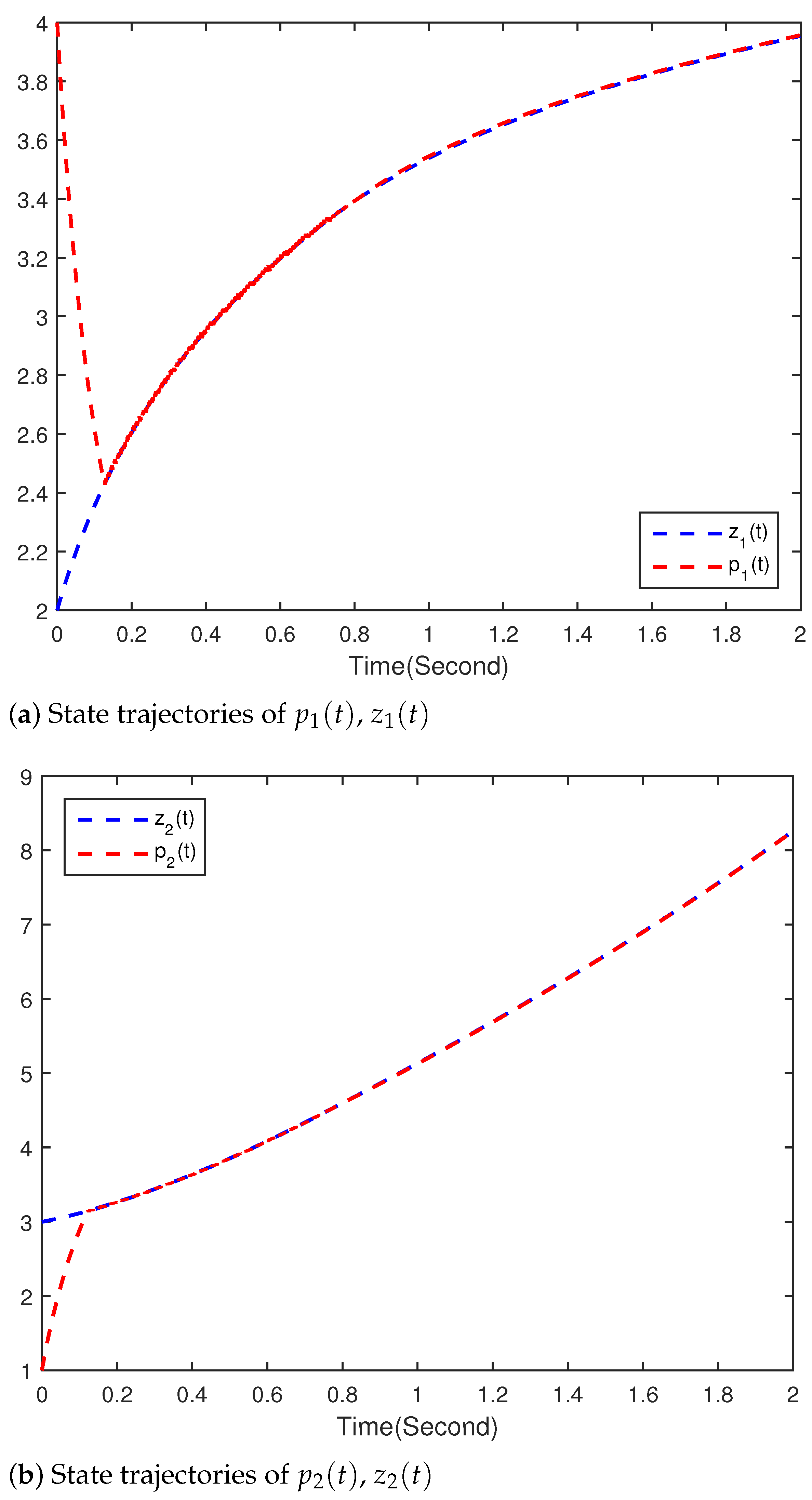
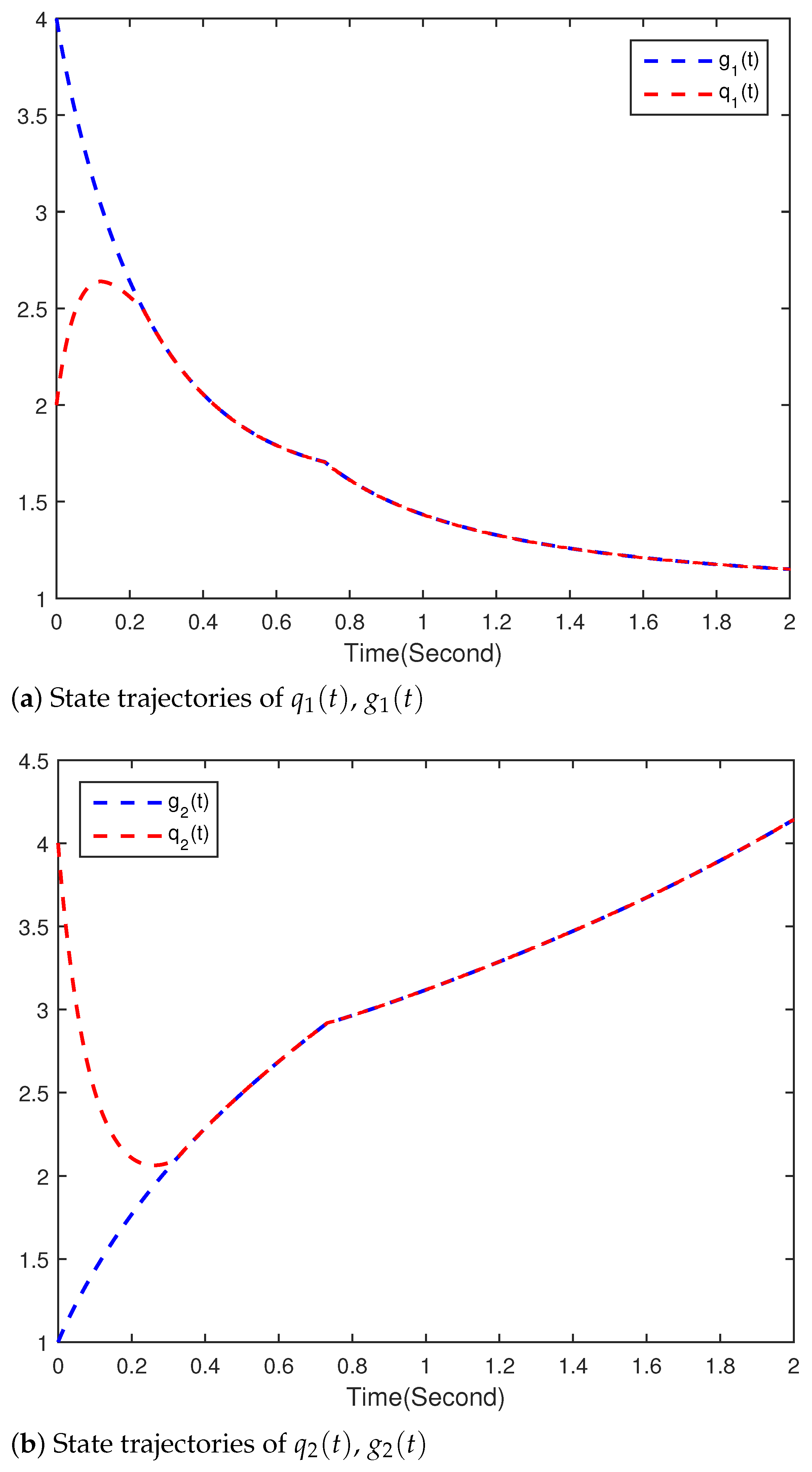
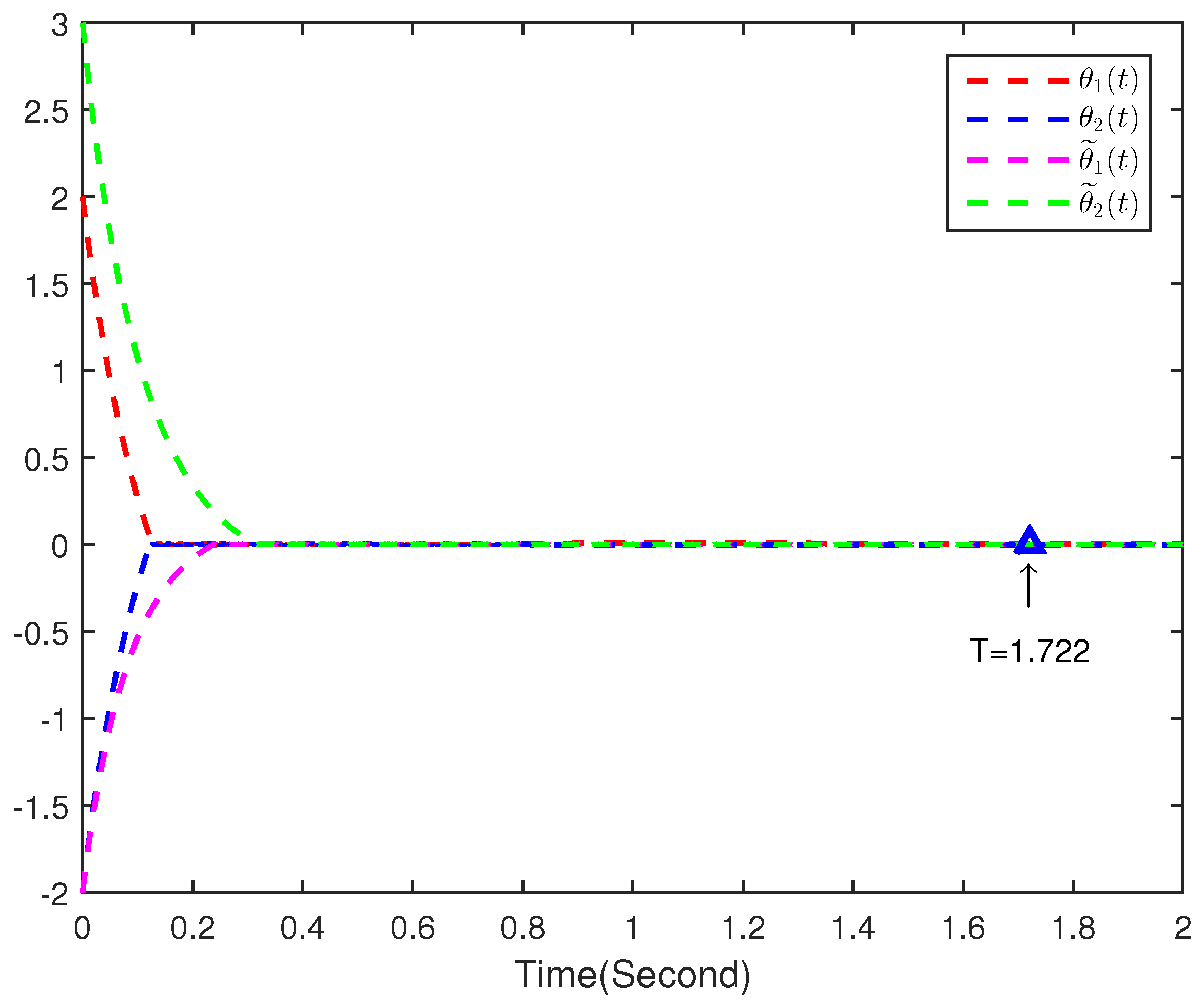
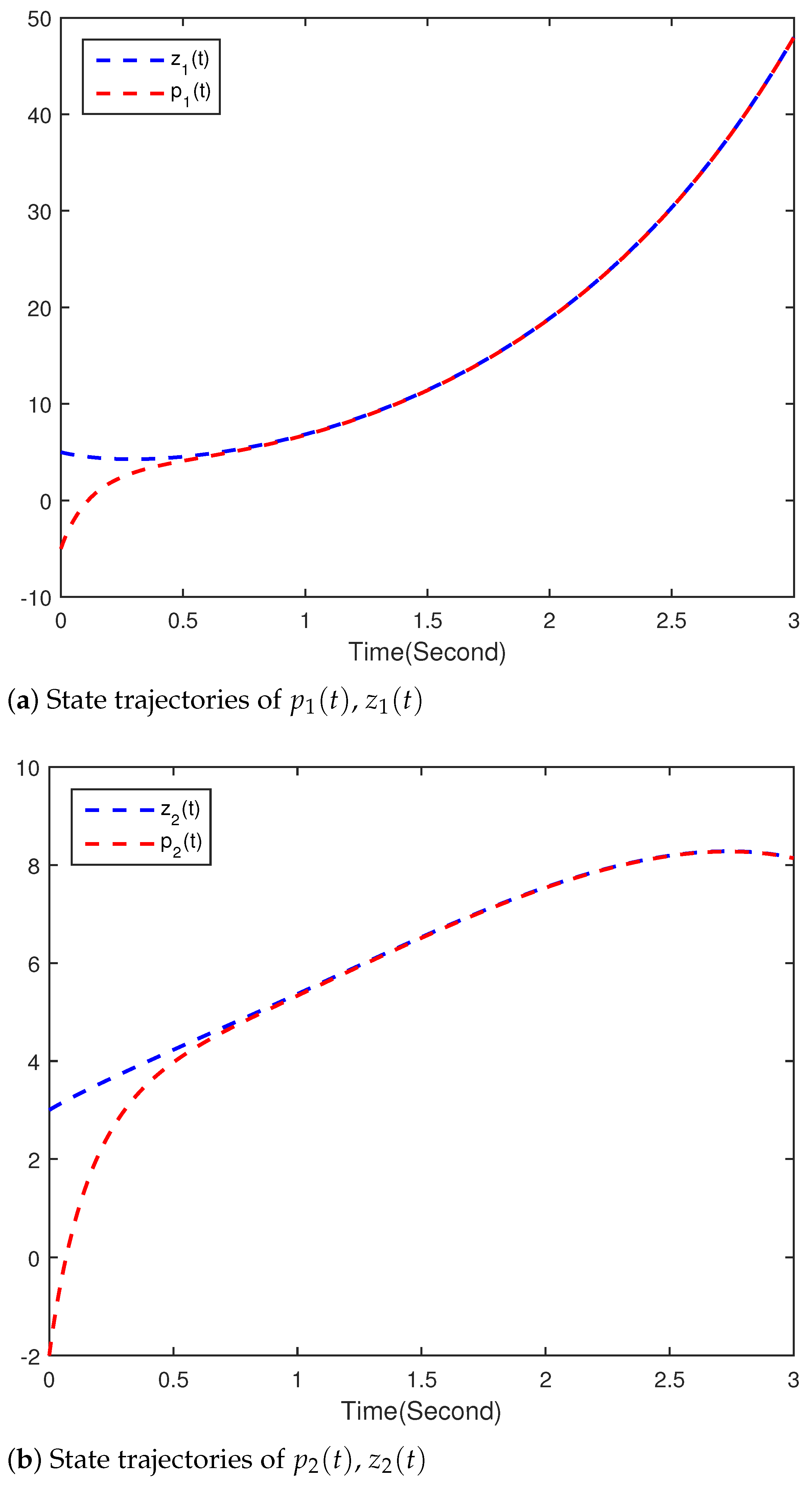
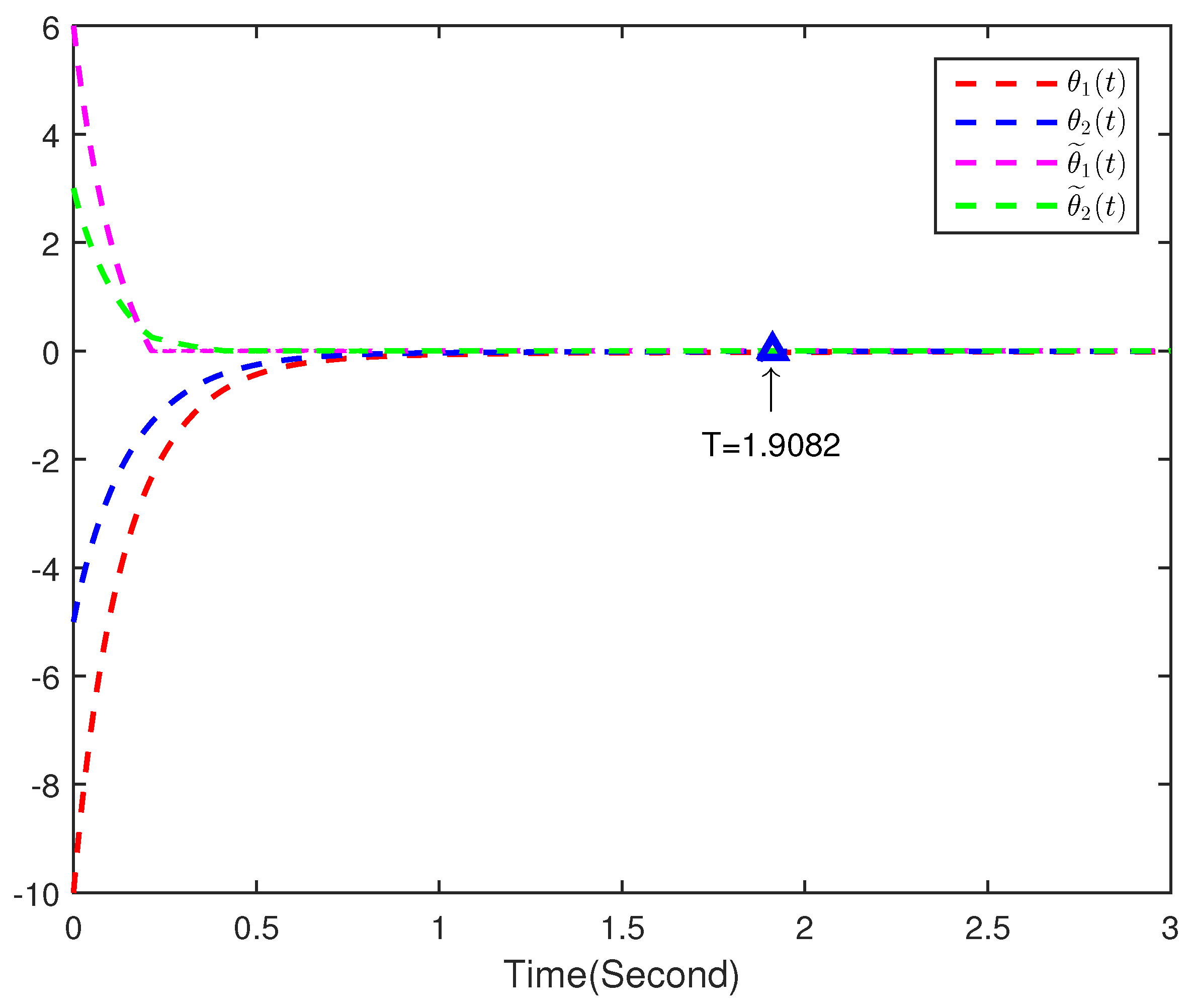
4. Numerical Simulations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, T.; Yang, L. The global stability of fuzzy cellular neural network. IEEE Trans. Circuits Syst. I 1996, 43, 880–883. [Google Scholar] [CrossRef]
- Yang, T.; Yang, L.; Wu, C.W.; Chua, L.O. Fuzzy cellular neural networks: Applications. In Proceedings of the 1996 Fourth IEEE International Workshop on Cellular Neural Networks and Their Applications Proceedings (CNNA-96), Seville, Spain, 24–26 June 1996; pp. 225–230. [Google Scholar]
- Yang, T.; Yang, L. Fuzzy cellular neural network: A new paradigm for image processing. Int. J. Circ. Theory Appl. 1997, 25, 469–481. [Google Scholar] [CrossRef]
- Shitong, W.; Min, W. A new detection algorithm (NDA) based on fuzzy cellular neural networks for white blood cell detection. IEEE Trans. Inf. Technol. Biomed. 2006, 10, 5–10. [Google Scholar] [CrossRef]
- Wang, S.; Fu, D.; Xu, M.; Hu, D. Advanced fuzzy cellular neural network: Application to CT liver images. Artif. Intell. Med. 2007, 39, 65–77. [Google Scholar] [CrossRef]
- Balasubramaniam, P.; Kalpana, M.; Rakkiyappan, R. Stationary oscillation of interval fuzzy cellular neural networks with mixed delays under impulsive perturbations. Neural Comput. Appl. 2013, 22, 1645–1654. [Google Scholar] [CrossRef]
- Ratnavelu, K.; Manikandan, M.; Balasubramaniam, P. Design of state estimator for BAM fuzzy cellular neural networks with leakage and unbounded distributed delays. Inf. Sci. 2017, 397, 91–109. [Google Scholar] [CrossRef]
- Hurtik, P.; Molek, V.; Hula, J. Data preprocessing technique for neural networks based on image represented by a fuzzy function. IEEE Trans. Fuzzy Syst. 2020, 28, 1195–1204. [Google Scholar] [CrossRef]
- Guan, C.; Wang, S.; Liew, A.W. Lip image segmentation based on a fuzzy convolutional neural network. IEEE Trans. Fuzzy Syst. 2020, 28, 1242–1251. [Google Scholar] [CrossRef]
- Chen, L.; Su, W.; Wu, M.; Pedrycz, W.; Hirota, K. A fuzzy deep neural network with sparse autoencoder for emotional intention understanding in human-robot interaction. IEEE Trans. Fuzzy Syst. 2020, 28, 1252–1264. [Google Scholar] [CrossRef]
- Babcock, K.; Westervelt, R. Stability and dynamics of simple electronic neural networks with added inertia. Phys. D Nonlinear Phenom. 1986, 23, 464–469. [Google Scholar] [CrossRef]
- Wan, P.; Jian, J. Global convergence analysis of impulsive inertial neural networks with time-varying delays. Neurocomputing 2017, 245, 68–76. [Google Scholar] [CrossRef]
- Zhang, G.; Zeng, Z.; Hu, J. New results on global exponential dissipativity analysis of memristive inertial neural networks with distributed time-varying delays. Neural Netw. 2018, 97, 183–191. [Google Scholar] [CrossRef] [PubMed]
- Aouiti, C.; Gharbia, I.B.; Cao, J.; Alsaedi, A. Dynamics of impulsive neutral-type BAM neural networks. J. Frankl. Inst. 2019, 356, 2294–2324. [Google Scholar] [CrossRef]
- Aouiti, C.; Assali, E.A. Nonlinear Lipschitz measure and adaptive control for stability and synchronization in delayed inertial Cohen-Grossberg-type neural networks. Int. J. Adapt. Control Signal Process. 2019, 33, 1457–1477. [Google Scholar] [CrossRef]
- Chaouki, A.; El Abed, A. Finite-time and fixed-time synchronization of inertial neural networks with mixed delays. J. Syst. Sci. Complex. 2021, 34, 206–235. [Google Scholar] [CrossRef]
- Lu, J.; Chen, Y. Robust stability and stabilization of fractional-order interval systems with the fractional order α: The 0 < α < 1 case. IEEE Trans. Autom. Control 2010, 55, 152–158. [Google Scholar]
- Liao, C.; Lu, C. Design of delay-dependent state estimator for discrete-time recurrent neural networks with interval discrete and infinite-distributed timevarying delays. Cognit. Neurodyn. 2011, 5, 133–143. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Sun, Y. Adaptive Fuzzy Control for Nonlinear Fractional-Order Uncertain Systems with Unknown Uncertainties and External Disturbance. Entropy 2015, 17, 5580–5592. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.; Chen, Y.; Yu, Y. A survey of fractional-order neural networks. In Proceedings of the ASME 2017 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Cleveland, OH, USA, 6–9 August 2017. [Google Scholar]
- Ma, Z.; Ma, H. Adaptive fuzzy backstepping dynamic surface control of strict-feedback fractional-order uncertain nonlinear systems. IEEE Trans. Fuzzy Syst. 2020, 28, 122–133. [Google Scholar] [CrossRef]
- Zhang, Q.; Lu, J. Bounded real lemmas for singular fractional-order systems: The 1 < α < 2 case. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 732–736. [Google Scholar]
- Yang, Z.; Zhang, Z. Global asymptotic synchronisation of fuzzy inertial neural networks with time-varying delays by applying maximum-value approach. Int. J. Syst. Sci. 2022, 53, 2281–2300. [Google Scholar] [CrossRef]
- Feng, Y.; Xiong, X.; Tang, R.; Yang, X. Exponential synchronization of inertial neural networks with mixed delays via quantized pinning control. Neurocomputing 2018, 310, 165–171. [Google Scholar] [CrossRef]
- Zhang, S.; Tang, M.; Liu, X. Synchronization of a Riemann–Liouville fractional time-delayed neural network with two inertial terms. Circuits Syst. Signal Process. 2021, 40, 5280–5308. [Google Scholar] [CrossRef]
- Tang, Q.; Jian, J. Exponential synchronization of inertial neural networks with mixed time-varying delays via periodically intermittent control. Neurocomputing 2019, 338, 181–190. [Google Scholar] [CrossRef]
- Liang, K.; Li, W. Exponential synchronization in inertial Cohen–Grossberg neural networks with time delays. J. Frankl. Inst. 2019, 356, 11285–11304. [Google Scholar] [CrossRef]
- Shi, J.; Zeng, Z. Global exponential stabilization and lag synchronization control of inertial neural networks with time delays. Neural Netw. 2020, 126, 11–20. [Google Scholar] [CrossRef]
- Zhang, Z.; Cao, J. Finite-time synchronization for fuzzy inertial neural networks by maximum value approach. IEEE Trans. Fuzzy Syst. 2021, 30, 1436–1446. [Google Scholar] [CrossRef]
- Hua, L.; Zhong, S.; Shi, K.; Zhang, X. Further results on finite-time synchronization of delayed inertial memristive neural networks via a novel analysis method. Neural Netw. 2020, 127, 47–57. [Google Scholar] [CrossRef]
- Chen, C.; Li, L.; Peng, H.; Yang, Y. Fixed-time synchronization of inertial memristor-based neural networks with discrete delay. Neural Netw. 2019, 109, 81–89. [Google Scholar] [CrossRef] [PubMed]
- Alimi, A.; Aouiti, C.; Assali, E.A. Finite-time and fixed-time synchronization of a class of inertial neural networks with multi-proportional delays and its application to secure communication. Neurocomputing 2019, 332, 29–43. [Google Scholar] [CrossRef]
- Yang, T.; Zou, R.; Liu, F. Finite/fixed-time synchronization control of fuzzy inertial cellular neural networks with mixed delays. Trans. Inst. Meas. Control 2023. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Li, C.; Deng, W. Remarks on fractional derivatives. Appl. Math. Comput. 2007, 187, 777–784. [Google Scholar] [CrossRef]
- Lakshmikantha, V.; Leela, S.; Devi, J. Theory of Fractional Dynamic Systems; Cambridge Scientific Publishers: Cambridge, UK, 2009. [Google Scholar]
- Zhang, S.; Yu, Y.; Wang, H. Mittag-Leffler stability of fractional-order Hopfield neural networks. Nonlinear Anal. Hybrid Syst. 2015, 16, 104–121. [Google Scholar] [CrossRef]
- Aguila, C.; Duarte-Mermoud, M.; Gallegos, J. Lyapunov functions for fractional order systems. Commun. Nonlinear Sci. Simul. 2014, 19, 2951–2957. [Google Scholar] [CrossRef]
- Kong, F.; Zhu, Q.; Sakthivel, R. Finite-time and fixed-time synchronization analysis of fuzzy Cohen-Grossberg neural networks with piecewise activations and parameter uncertainties. Eur. J. Control 2020, 56, 179–190. [Google Scholar] [CrossRef]
- Li, H.; Cao, J.; Jiang, H.; Alsaedi, A. Graph theory-based finite-time synchronization of fractional-order complex dynamical networks. J. Frankl. Inst. 2018, 355, 5771–5789. [Google Scholar] [CrossRef]
- Duan, L.; Jian, J.; Wang, B. Global exponential dissipativity of neutral-type BAM inertial neural networks with mixed time-varying delays. Neurocomputing 2020, 378, 399–412. [Google Scholar] [CrossRef]
- Syed Ali, M.; Narayanan, G.; Shekher, V.; Alsaedi, A.; Ahmad, B. Global Mittag-Leffler stability analysis of impulsive fractional-order complex-valued BAM neural networks with time varying delays. Commun. Nonlinear Sci. Numer. Simul. 2020, 83, 105088. [Google Scholar] [CrossRef]
- Chen, L.; Huang, T.; Machado, J.A.T.; Lopes, A.M.; Chai, Y.; Wu, R. Delay-dependent criterion for asymptotic stability of a class of fractional-order memristive neural networks with time-varying delays. Neural Netw. 2019, 118, 289–299. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Sun, Y. Finite-Time Synchronization for Fractional Order Fuzzy Inertial Cellular Neural Networks with Piecewise Activations and Mixed Delays. Fractal Fract. 2023, 7, 294. https://doi.org/10.3390/fractalfract7040294
Liu Y, Sun Y. Finite-Time Synchronization for Fractional Order Fuzzy Inertial Cellular Neural Networks with Piecewise Activations and Mixed Delays. Fractal and Fractional. 2023; 7(4):294. https://doi.org/10.3390/fractalfract7040294
Chicago/Turabian StyleLiu, Yihong, and Yeguo Sun. 2023. "Finite-Time Synchronization for Fractional Order Fuzzy Inertial Cellular Neural Networks with Piecewise Activations and Mixed Delays" Fractal and Fractional 7, no. 4: 294. https://doi.org/10.3390/fractalfract7040294
APA StyleLiu, Y., & Sun, Y. (2023). Finite-Time Synchronization for Fractional Order Fuzzy Inertial Cellular Neural Networks with Piecewise Activations and Mixed Delays. Fractal and Fractional, 7(4), 294. https://doi.org/10.3390/fractalfract7040294





