On the Solutions of a Class of Discrete PWC Systems Modeled with Caputo-Type Delta Fractional Difference Equations
Abstract
1. Introduction
2. PWC Systems Modeled with Caputo-Type Delta Fractional Difference Equations
2.1. Computational Approach
- (i)
- (ii)
- There are PWC systems with jump discontinuity, for which f is not defined at (see, e.g., [54]). In these cases, after some number of iterations, , in the internal representation, as shown above, it is possible for to enter a sufficiently small neighborhood of a, where cannot be determined, and the software considers an unpredictable value for .
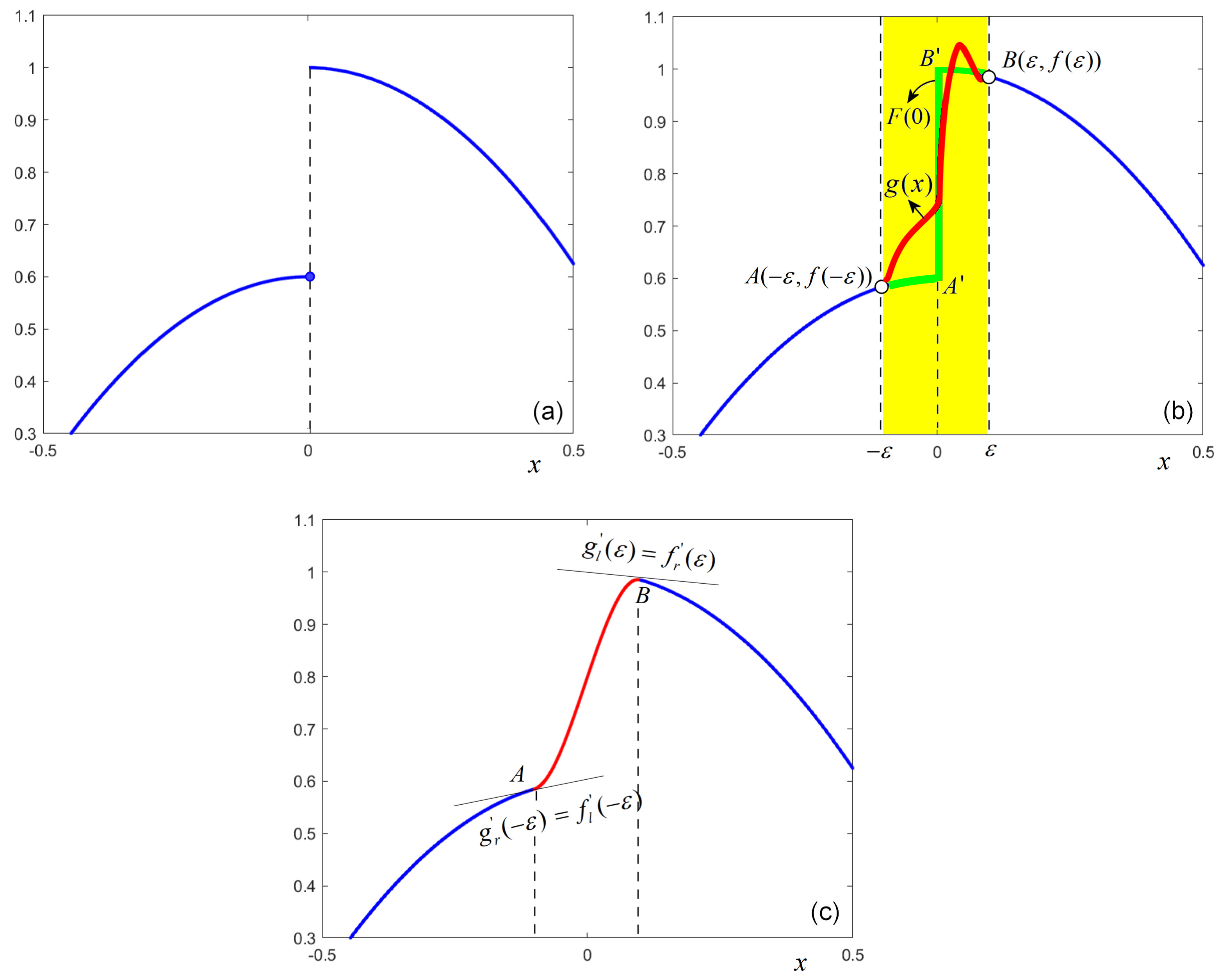
3. Continuous Approximation of Map
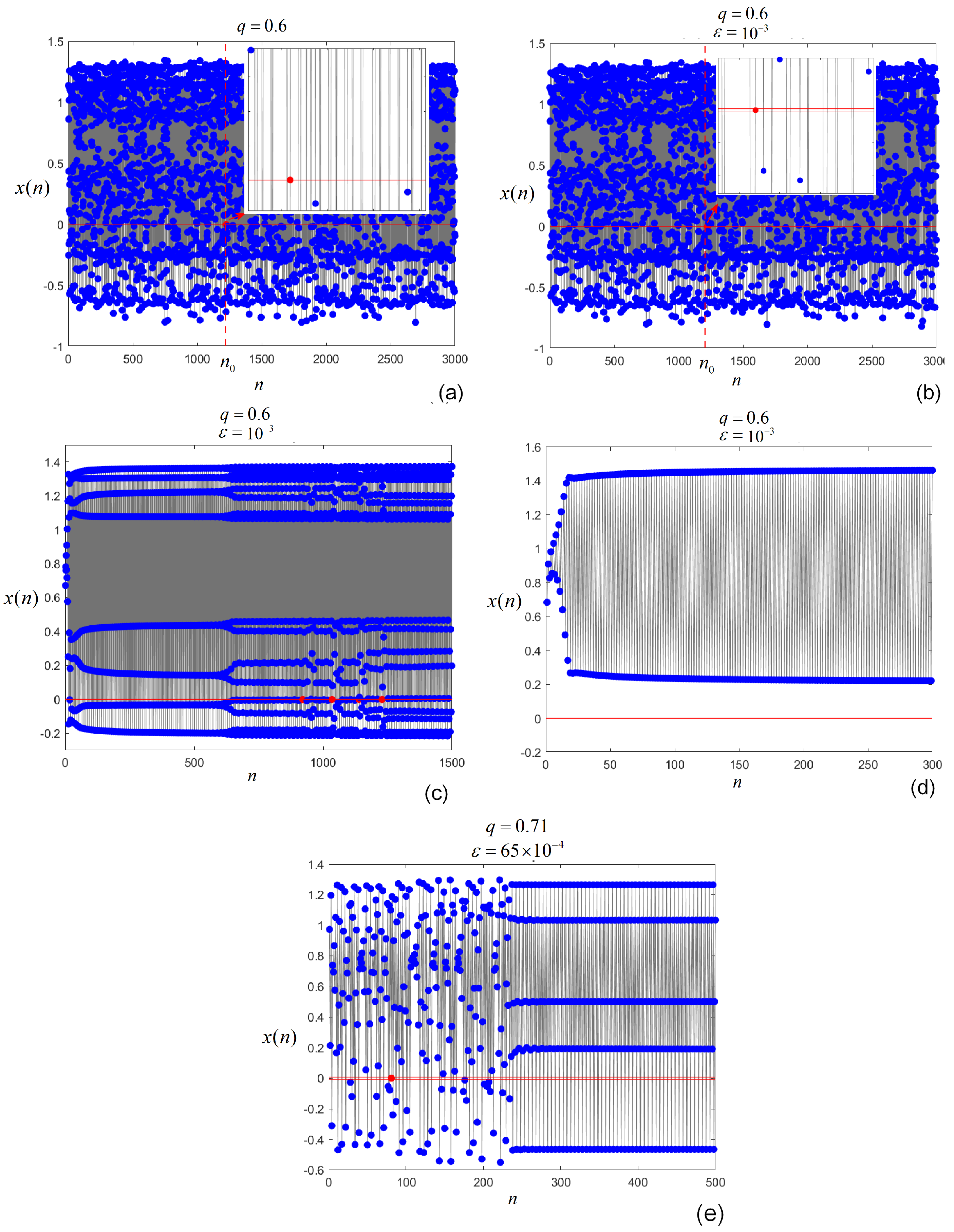
4. Dynamics of the Approximated Fractional System (11)
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Filippov, A.F. Differential Equations with Discontinuous Right-Hand Side; Kluwer Academic Publishers: Dodrecht, The Netherlands, 1988. [Google Scholar]
- Andronov, A.A.; Vitt, A.A.; Khaikin, S.E. Theory of Oscillators; Translated from the Russian by F. Immirzi; W. Fishwick Pergamon Press: Oxford, UK; New York, NY, USA; Toronto, ON, Canada, 1966. [Google Scholar]
- Chavez, J.P.; Liu, Y.; Pavlovskaia, E.; Wiercigroch, M. Path-following analysis of the dynamical response of a piecewise-linear capsule system. Commun. Nonlinear Sci. Numer. Simul. 2016, 37, 102–114. [Google Scholar] [CrossRef]
- Wiercigroch, M.; de Kraker, B. Applied Nonlinear Dynamics and Chaos of Mechanical Systems with Discontinuities; Wiercigroch, M., de Kraker, B., Eds.; World Scientific Series on Nonlinear Science Series A: Monographs and Treatises; World Scientific Publishing Co., Inc.: River Edge, NJ, USA, 2000; Volume 28. [Google Scholar]
- Popp, K.; Stelter, P. Stick-Slip Vibrations and Chaos. Philos. Trans. R. Soc. Lond. A 1990, 332, 89–105. [Google Scholar]
- di Bernardo, M.; Budd, C.J.; Champneys, A.R.; Kowalczyk, P. Piecewise-Smooth Dynamical Systems: Theory and Applications, Applied Mathematical Sciences; Springer: London, UK, 2008. [Google Scholar]
- Cortés, J. Discontinuous dynamical systems: A tutorial on solutions, nonsmooth analysis, and stability. IEEE Control Syst. Mag. 2008, 28, 36–73. [Google Scholar]
- di Bernardo, M.; Hogan, S.J. Discontinuity-induced bifurcations of piecewise smooth dynamical systems. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2010, 368, 4915–4935. [Google Scholar] [CrossRef] [PubMed]
- Páez Chávez, J.; Pavlovskaia, E.; Wiercigroch, M. Bifurcation analysis of a piecewise-linear impact oscillator with drift. Nonlinear Dynam. 2014, 77, 213–227. [Google Scholar] [CrossRef]
- Jain, P.; Banerjee, S. Soumitro Border-collision bifurcations in one-dimensional discontinuous maps. Int. J. Bifurc. Chaos 2003, 13, 3341–3351. [Google Scholar] [CrossRef]
- Danca, M.-F. Continuous approximations of a class of piece-wise continuous systems. Int. J. Bifurc. Chaos 2015, 25, 1550146. [Google Scholar] [CrossRef]
- Danca, M.-F. On a class of discontinuous dynamical systems. Math. Notes 2001, 2, 103–116. [Google Scholar] [CrossRef]
- Danca, M.-F.; Fečkan, M. On numerical integration of discontinuous dynamical systems. Int. J. Bifurc. Chaos 2017, 27, 1750218. [Google Scholar] [CrossRef]
- Danca, M.-F.; Kuznetsov, N.V.; Chen, G. Approximating hidden chaotic attractors via parameter switching. Nonlinear Dyn. 2018, 91, 2523–2540. [Google Scholar] [CrossRef]
- Lempio, F. Difference Methods for Differential Inclusions. In Modern Methods of Optimization. Lecture Notes in Economics and Mathematical Systems; Krabs, W., Zowe, J., Eds.; Springer: Berlin/Heidelberg, Germany, 1992; Volume 378, pp. 236–263. [Google Scholar]
- Dontchev, A.; Lempio, F. Difference methods for differential inclusions: A survey. SIAM Rev. 1992, 34, 263–294. [Google Scholar] [CrossRef]
- Lempio, F.; Veliov, V. Discrete approximations of differential inclusions. GAMM Mitt. Ges. Angew. Math. Mech. 1998, 21, 103–135. [Google Scholar]
- Kastner-Maresch, A.; Lempio, F. Difference methods with selection strategies for differential inclusions. Numer. Funct. Anal. Optim. 1993, 14, 555–572. [Google Scholar] [CrossRef]
- Aubin, J.-P.; Cellina, A. Differential inclusions. In Set-Valued Maps and Viability Theory; Springer: Berlin, Germany, 1984; Volume 264. [Google Scholar]
- Deimling, K. Nonlinear Functional Analysis; Springer: Berlin, Germany, 1985. [Google Scholar]
- Aubin, J.-P.; Frankowska, H. Set-valued analysis. In Systems and Control: Foundations and Applications; Birkhauser Boston, Inc.: Boston, MA, USA, 1990; Volume 2. [Google Scholar]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional integrals and derivatives. In Theory and Applications; Nikolskii, S.M., Ed.; Translated from the 1987 Russian original. Revised by the authors; Gordon and Breach Science Publishers: Yverdon, Switzerland, 1993. [Google Scholar]
- de Oliveira, E.C.; Tenreiro, M.; José, A. A review of definitions for fractional derivatives and integral. Math. Probl. Eng. 2014, 2014, 238459. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional differential equations. In An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Mathematics in Science and Engineering, Academic Press, Inc.: San Diego, CA, USA, 1999; Volume 198. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and applications of fractional differential equations. In North-Holland Mathematics Studies; Elsevier Science B.V.: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Valerio, D.; Ortigueira, M.D.; Lopes, A.M. How Many Fractional Derivatives Are There? Mathematics 2022, 10, 737. [Google Scholar] [CrossRef]
- Danca, M.-F. Approach of a Class of Discontinuous Systems of Fractional Order: Existence of Solutions. Int. J. Bifurc. Chaos 2011, 21, 3273–3276. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.J.; Freed, A.D. Predictor-corrector approach for the numerical solution of fractional differential equations. Nonlinear Dyn. 2002, 29, 3–22. [Google Scholar] [CrossRef]
- Henderson, J.; Ouahab, A. Impulsive differential inclusions with fractional order. Comput. Math. Appl. 2010, 59, 1191–1226. [Google Scholar] [CrossRef]
- Benchohra, M.; Hamani, S.; Nieto, J.J.; Slimani, B. Attou Existence of solutions to differential inclusions with fractional order and impulses. Electron. J. Differ. Eq. 2010, 2010, 1–18. [Google Scholar]
- El-Sayed, A.M.A.; Ibrahim, A.-G. Multivalued fractional differential equations. Appl. Math. Comput. 1995, 68, 15–25. [Google Scholar] [CrossRef]
- Ait Dads, E.; Benchohra, M.; Hamani, S. Impulsive fractional differential inclusions involving the Caputo fractional derivative. Fract. Calc. Appl. Anal. 2009, 12, 15–38. [Google Scholar]
- Benchohra, M.; Hamidi, N. Fractional order differential inclusions on the half-line. Surv. Math. Appl. 2010, 5, 99–111. [Google Scholar]
- Abdeljawad, T. On Riemann and Caputo fractional differences. Comput. Math. Appl. 2011, 62, 1602–1611. [Google Scholar] [CrossRef]
- Baoguo, J. The asymptotic behavior of Caputo delta fractional equations. Math. Methods Appl. Sci. 2016, 39, 5355–5364. [Google Scholar] [CrossRef]
- Ferreira, R.A. Discrete Fractional Calculus and Fractional Difference Equations; Springer: Cham, Switzerland, 2022. [Google Scholar]
- Goodrich, C.; Peterson, A.C. Discrete Fractional Calculus; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Jonnalagadda, J.M. Solutions of fractional nabla difference equations—Existence and uniqueness. Opuscula Math. 2016, 36, 215–238. [Google Scholar] [CrossRef]
- Atici, F.M.; Eloe, P.W. Discrete fractional calculus with the nabla operator. Electron. J. Qual. Theory Differ. Equ. 2009, 2009, 12. [Google Scholar] [CrossRef]
- Atici, F.M.; Wu, F. Existence of solutions for nonlinear fractional difference equations with initial conditions. Dynam. Syst. Appl. 2014, 23, 265–276. [Google Scholar]
- Chen, F.; Luo, X.; Zhou, Y. Existence results for nonlinear fractional difference equation. Adv. Differ. Equ. 2011, 2011, 713201. [Google Scholar] [CrossRef]
- Chen, C.; Bohner, M.; Jia, B. Existence and uniqueness of solutions for nonlinear Caputo fractional difference equations. Turkish J. Math. 2020, 44, 857–869. [Google Scholar] [CrossRef]
- Jonnalagadda, J. Analysis of a system of nonlinear fractional nabla difference equations. Int. J. Dyn. Syst. Differ. Equ. 2015, 5, 149–174. [Google Scholar] [CrossRef]
- Mohammed, P.O.; Baleanu, D.; Abdeljawad, T.; Sahoo, S.K.; Abualnaja, K.M. Positivity analysis for mixed order sequential fractional difference operators. AIMS Math. 2023, 8, 2673–2685. [Google Scholar] [CrossRef]
- Goodrich, C.S.; Jonnalagadda, J.M. Ananalysis of polynomial sequences and their application to discrete fractional operators. J. Differ. Equ. Appl. 2021, 27, 1081–1102. [Google Scholar] [CrossRef]
- Wu, G.-C.; Baleanu, D.; Bai, Y.-R. Discrete Fractional Masks and Their Applications to Image Enhancement; De Gruyter: Berlin, Germany, 2019. [Google Scholar]
- Selvam, G.M.; Alzabut, J.; Dhakshinamoorthy, V.; Jonnalagadda, J.M.; Abodayeh, K. Existence and stability of nonlinear discrete fractional initial value problems with application to vibrating eardrum. Math. Biosci. Eng. 2021, 18, 3907–3921. [Google Scholar] [CrossRef] [PubMed]
- Atici, F.M.; Eloe, P.W. Initial value problems in discrete fractional calculus. Proc. Am. Math. Soc. 2009, 137, 981–989. [Google Scholar] [CrossRef]
- Chia, T.T.; Tan, B.L. Results for the discontinuous logistic map. Phys. Rev. A 1992, 45, 8441. [Google Scholar] [CrossRef]
- Available online: https://floating-point-gui.de/errors/propagation/ (accessed on 8 February 2023).
- Available online: https://cs.appstate.edu/~aam/classes/1100/cn/sect1_4.html (accessed on 8 February 2023).
- Available online: https://en.wikipedia.org/wiki/Double-precision_floating-point_format (accessed on 8 February 2023).
- Available online: https://en.wikipedia.org/wiki/Pigeonhole_principle (accessed on 8 February 2023).
- Jafari, S.; Pham, V.T.; Golpayegani, S.M.R.H.; Moghtadaei, M.; Kingni, S.T. The relationship between chaotic maps and some chaotic systems with hidden attractors. Int. J. Bifurc. Chaos 2016, 26, 1650211. [Google Scholar] [CrossRef]
- Mohan, J.J.; Deekshitulu, G.V.S.R. Fractional order difference equations. Int. J. Differ. Equ. 2012, 2012, 780619. [Google Scholar] [CrossRef]
- Tavazoei, M.S.; Haeri, M. A proof for non existence of periodic solutions in time invariant fractional order systems. Autom. J. IFAC 2009, 45, 1886–1890. [Google Scholar] [CrossRef]
- Diblik, J.; Feckan, M.; Pospisil, M. Nonexistence of periodic solutions and S-asymptotically periodic solutions in fractional difference equations. Appl. Math. Comput. 2015, 257, 230–240. [Google Scholar] [CrossRef]
- Wiggins, S. Introduction to Applied Nonlinear Dynamical Systems and Chaos, 2nd ed.; Texts in Applied Mathematics; Springer: New York, NY, USA, 2003; Volume 2. [Google Scholar]
- Yazdani, M.; Salarieh, H. On the existence of periodic solutions in time-invariant fractional order systems. Autom. J. IFAC 2011, 47, 1834–1837. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Danca, M.-F.; Jonnalagadda, J.M. On the Solutions of a Class of Discrete PWC Systems Modeled with Caputo-Type Delta Fractional Difference Equations. Fractal Fract. 2023, 7, 304. https://doi.org/10.3390/fractalfract7040304
Danca M-F, Jonnalagadda JM. On the Solutions of a Class of Discrete PWC Systems Modeled with Caputo-Type Delta Fractional Difference Equations. Fractal and Fractional. 2023; 7(4):304. https://doi.org/10.3390/fractalfract7040304
Chicago/Turabian StyleDanca, Marius-F., and Jagan Mohan Jonnalagadda. 2023. "On the Solutions of a Class of Discrete PWC Systems Modeled with Caputo-Type Delta Fractional Difference Equations" Fractal and Fractional 7, no. 4: 304. https://doi.org/10.3390/fractalfract7040304
APA StyleDanca, M.-F., & Jonnalagadda, J. M. (2023). On the Solutions of a Class of Discrete PWC Systems Modeled with Caputo-Type Delta Fractional Difference Equations. Fractal and Fractional, 7(4), 304. https://doi.org/10.3390/fractalfract7040304







