A Novel Scheme of the ARA Transform for Solving Systems of Partial Fractional Differential Equations
Abstract
:1. Introduction
2. Fundamental Concepts and Properties
- The jth truncated series of the fractional expansion (5) is given by
- If has the fractional expansion (5), then can be expressed asand the jth truncated series is given by
- The ARA transform invers of order two of the fractional expansion (5) is defined as
3. Formulating Series Solutions of Fractional Neutron Diffusion Equations with One Delayed Neutrons Group
- and
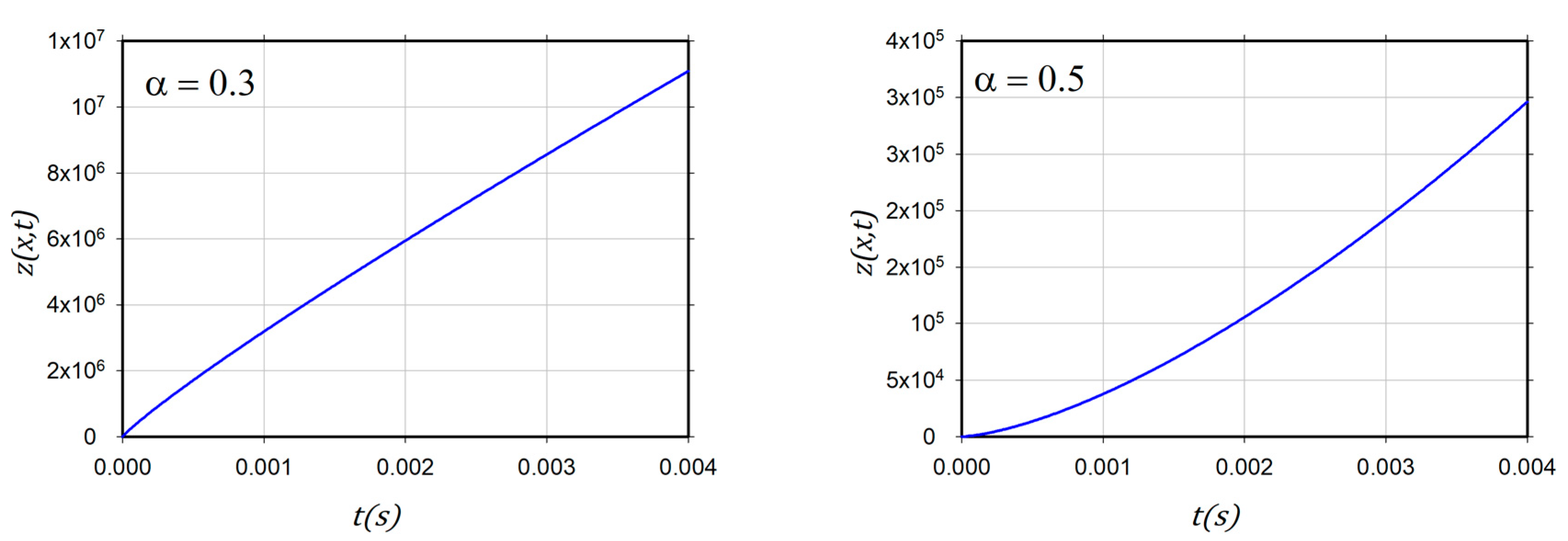
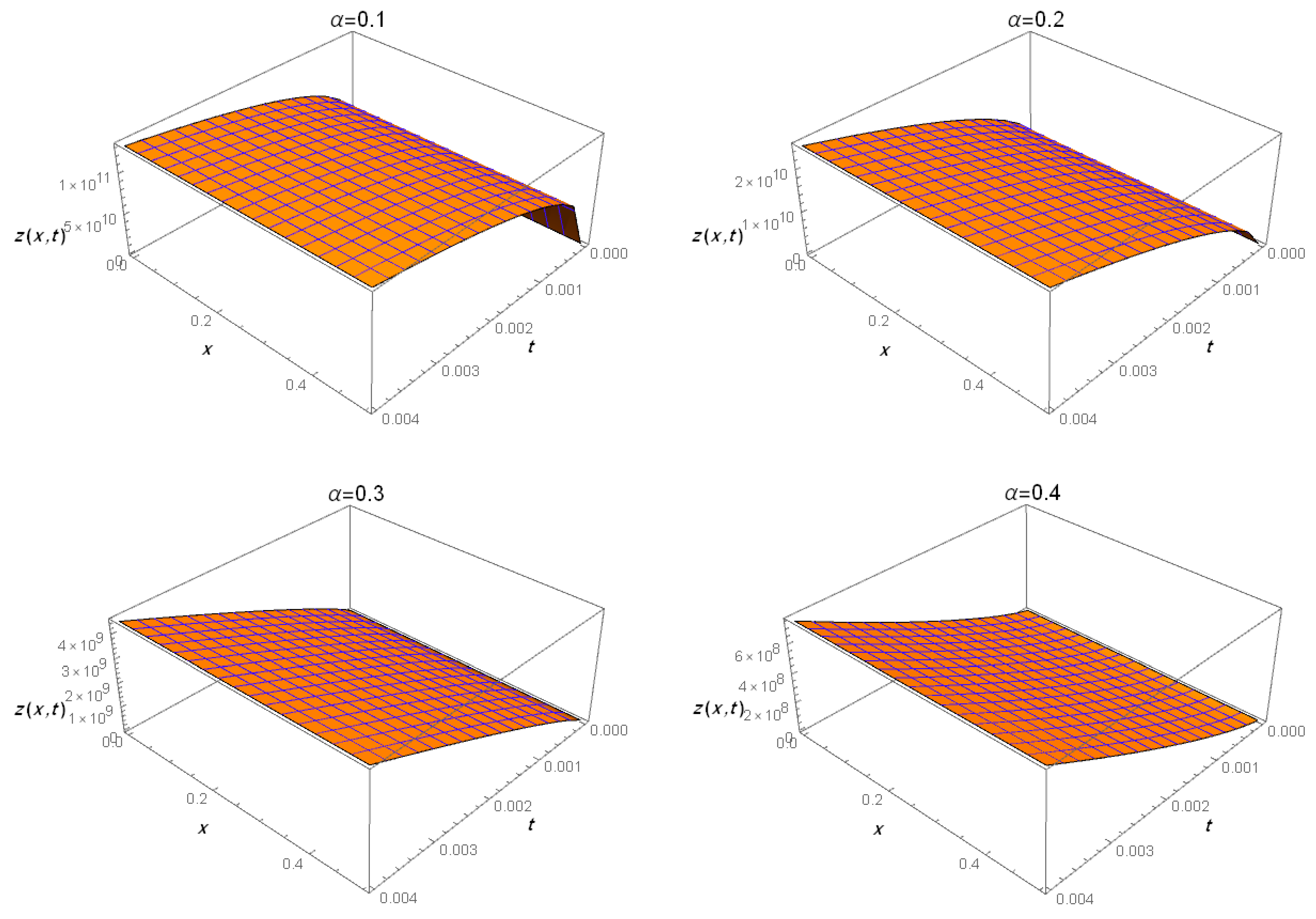
4. Numerical Results
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1998. [Google Scholar]
- Petráš, I. Fractional-Order Nonlinear Systems: Modeling, Analysis and Simulation; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Du, M.; Wang, Z.; Hu, H. Measuring memory with the order of fractional derivative. Sci. Rep. 2013, 3, 3431. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; John Wiley & Sons: New York, NY, USA, 1993. [Google Scholar]
- Cifani, S.; Jakobsen, E.R. Entropy solution theory for fractional degenerate convection–diffusion equations. Ann. De L’institut Henri Poincaré C 2011, 28, 413–441. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.; Zhang, H.Q. Fractional sub-equation method and its applications to nonlinear fractional PDEs. Phys. Lett. A 2011, 375, 1069–1073. [Google Scholar] [CrossRef]
- Caputo, M. Linear models of dissipation whose Q is almost frequency independent—II. Geophys. J. Int. 1967, 13, 529–539. [Google Scholar] [CrossRef]
- Khandaqji, M.; Burqan, A. Results on sequential conformable fractional derivatives with applications. J. Comput. Anal. Appl. 2021, 29, 1115–1125. [Google Scholar]
- Oldham, K.; Spanier, J. The Fractional Calculus Theory and Applications of Differentiation and Integration to Arbitrary Order; Elsevier: Amsterdam, The Netherlands, 1974. [Google Scholar]
- Kilbas, A.; Srivastava, H.; Trujillo, J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity; Imperial College Press: London, UK, 2010. [Google Scholar]
- Almeida, R.; Tavares, D.; Torres, D. The Variable-Order Fractional Calculus of Variations; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Khalil, R.; Horani, M.; Yousef, A.; Sababheh, M. A new definition of fractional derivative. J. Comput. Appl. Math. 2014, 264, 65–70. [Google Scholar] [CrossRef]
- El-Ajou, A. A modification to the conformable fractional calculus with some applications. Alex. Eng. J. 2020, 59, 2239–2249. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D. New fractional derivatives with non-local and non-singular kernel: Theory and application to heat transfer model. Thermal Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef] [Green Version]
- Hasan, S.; El-Ajou, A.; Hadid, S.; Al-Smadi, M.; Momani, S. Atangana-Baleanu fractional framework of reproducing kernel technique in solving fractional population dynamics system. Chaos Solitons Fractals 2020, 133, 109624. [Google Scholar] [CrossRef]
- Burqan, A.; El-Ajou, A.; Saadeh, R.; Al-Smadi, M. A new efficient technique using Laplace transforms and smooth expansions to construct a series solution to the time-fractional Navier-Stokes equations. Alex. Eng. J. 2022, 61, 1069–1077. [Google Scholar] [CrossRef]
- Jafari, H.; Seifi, S. Solving a system of nonlinear fractional partial differential equations using homotopy analysis method. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 1962–1969. [Google Scholar] [CrossRef]
- Jafari, H.; Khalique, C.M.; Nazari, M. Application of the Laplace decomposition method for solving linear and nonlinear fractional diffusion–wave equations. Appl. Math. Lett. 2011, 24, 1799–1805. [Google Scholar] [CrossRef] [Green Version]
- Wazwaz, A.M. The variational iteration method for solving linear and nonlinear systems of PDEs. Comput. Math. Appl. 2007, 54, 895–902. [Google Scholar] [CrossRef] [Green Version]
- Jafari, H.; Nazari, M.; Baleanu, D.; Khalique, C.M. A new approach for solving a system of fractional partial differential equations. Comput. Math. Appl. 2013, 66, 838–843. [Google Scholar] [CrossRef]
- El-Ajou, A.; Al-Zhour, Z.; Oqielat, M.A.; Momani, S.; Hayat, T. Series solutions of nonlinear conformable fractional KdV-Burgers equation with some applications. Eur. Phys. J. Plus 2019, 134, 402. [Google Scholar] [CrossRef]
- Moa’ath, N.O.; El-Ajou, A.; Al-Zhour, Z.; Alkhasawneh, R.; Alrabaiah, H. Series solutions for nonlinear time-fractional Schrödinger equations: Comparisons between conformable and Caputo derivatives. Alex. Eng. J. 2020, 59, 2101–2114. [Google Scholar]
- Shqair, M.; El-Ajou, A.; Nairat, M. Analytical solution for multi-energy groups of neutron diffusion equations by a residual power series method. Mathematics 2019, 7, 633. [Google Scholar] [CrossRef] [Green Version]
- El-Ajou, A.; Moa’ath, N.O.; Al-Zhour, Z.; Momani, S. A class of linear non-homogenous higher order matrix fractional differential equations: Analytical solutions and new technique. Fract. Calc. Appl. Anal. 2020, 23, 356–377. [Google Scholar] [CrossRef]
- El-Ajou, A.; Arqub, O.A.; Zhour, Z.A.; Momani, S. New results on fractional power series: Theories and applications. Entropy 2013, 15, 5305–5323. [Google Scholar] [CrossRef]
- Alquran, M. Analytical solution of time-fractional two-component evolutionary system of order 2 by residual power series method. J. Appl. Anal. Comput. 2015, 5, 589–599. [Google Scholar] [CrossRef]
- Yang, J.J.; Tian, S.F. Riemann–Hilbert problem and dynamics of soliton solutions of the fifth-order nonlinear Schrödinger equation. Appl. Math. Lett. 2022, 128, 107904. [Google Scholar] [CrossRef]
- Liu, Y.H.; Guo, R.; Li, X.L. Rogue wave solutions and modulation instability for the mixed nonlinear Schrödinger equation. Appl. Math. Lett. 2021, 121, 107450. [Google Scholar] [CrossRef]
- Dong, L.; Huang, C.; Qi, W. Nonlocal solitons in fractional dimensions. Opt. Lett. 2019, 44, 4917–4920. [Google Scholar] [CrossRef] [PubMed]
- Qazza, A.; Burqan, A.; Saadeh, R.; Khalil, R. Applications on Double ARA–Sumudu Transform in Solving Fractional Partial Differential Equations. Symmetry 2022, 14, 1817. [Google Scholar] [CrossRef]
- Burqan, A.; Saadeh, R.; Qazza, A. A novel numerical approach in solving fractional neutral pantograph equations via the ARA integral transform. Symmetry 2021, 14, 50. [Google Scholar] [CrossRef]
- Saadeh, R.; Qazza, A.; Burqan, A. A new integral transform: ARA transform and its properties and applications. Symmetry 2020, 12, 925. [Google Scholar] [CrossRef]
- Qazza, A.; Burqan, A.; Saadeh, R. A new attractive method in solving families of fractional differential equations by a new transform. Mathematics 2021, 9, 3039. [Google Scholar] [CrossRef]
- Sardar, T.; Saha Ray, S.; Bera, R.K.; Biswas, B.B.; Das, S. The solution of coupled fractional neutron diffusion equations with delayed neutrons. Int. J. Nucl. Energy Sci. Technol. 2010, 5, 105–113. [Google Scholar] [CrossRef]
- Khaled, S.M. Exact solution of the one-dimensional neutron diffusion kinetic equation with one delayed precursor concentration in Cartesian geometry. AIMS Math. 2022, 7, 12364–12373. [Google Scholar] [CrossRef]
- Almenas, K.; Lee, R.; Almenas, K.; Lee, R. Neutron Diffusion—Basic Concepts. In Nuclear Engineering: An Introduction; Springer: Berlin/Heidelberg, Germany, 1992; pp. 83–118. [Google Scholar]
- Palma, D.A.; Martinez, A.S.; Gonçalves, A.C. Analytical solution of point kinetics equations for linear reactivity variation during the start-up of a nuclear reactor. Ann. Nucl. Energy 2009, 36, 1469–1471. [Google Scholar] [CrossRef]

| ARA-RPST | ADM | ARA-RPST | ADM | ARA-RPST | ADM | |
|---|---|---|---|---|---|---|
| 0.0001 | 1302.5 | 1137.4 | ||||
| 0.00039 | 9415.6 | 8236.4 | ||||
| 0.00068 | 21,346.4 | 18,694.4 | ||||
| 0.00097 | 36,086.6 | 31,632.6 | ||||
| 0.00126 | 53,165.1 | 46,640.0 | ||||
| 0.00155 | 72,290.4 | 63,462.9 | ||||
| 0.00184 | 93,259.2 | 81,923.8 | ||||
| 0.00213 | 115,919.1 | 101,889.9 | ||||
| 0.00242 | 140,150.0 | 123,256.5 | ||||
| 0.00271 | 165,854.5 | 145,938.8 | ||||
| 0.003 | 192,951.2 | 169,865.8 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Burqan, A. A Novel Scheme of the ARA Transform for Solving Systems of Partial Fractional Differential Equations. Fractal Fract. 2023, 7, 306. https://doi.org/10.3390/fractalfract7040306
Burqan A. A Novel Scheme of the ARA Transform for Solving Systems of Partial Fractional Differential Equations. Fractal and Fractional. 2023; 7(4):306. https://doi.org/10.3390/fractalfract7040306
Chicago/Turabian StyleBurqan, Aliaa. 2023. "A Novel Scheme of the ARA Transform for Solving Systems of Partial Fractional Differential Equations" Fractal and Fractional 7, no. 4: 306. https://doi.org/10.3390/fractalfract7040306
APA StyleBurqan, A. (2023). A Novel Scheme of the ARA Transform for Solving Systems of Partial Fractional Differential Equations. Fractal and Fractional, 7(4), 306. https://doi.org/10.3390/fractalfract7040306






