Image Edge Detection Based on Fractional-Order Ant Colony Algorithm
Abstract
:1. Introduction
- (a)
- Section 2 provides an overview of fractional calculus, including its fundamental definition. Additionally, this section introduces the fundamental principles and procedures of the fractional-order ant colony algorithm.
- (b)
- In Section 3, a novel edge detection technique utilizing the fractional-order ant colony algorithm combined with fractional differential mask and coefficient of variation (FACAFCV) is presented. The heuristic function utilized in this approach is constructed by amalgamating the concepts of fractional differential mask and the coefficient of variation (CV).
- (c)
- In Section 4, a reasonable experimental strategy is designed to evaluate the results of edge detection on images with and without noise, using metrics such as recall, precision, and F-measure.
- (d)
- Section 5 performs a comprehensive analysis of our method through three distinct experiments. Firstly, the impact of the fractional differential mask and coefficient of variation on the edge detection performance is examined. Secondly, the performance of both fractional-order ant colony algorithm combined with fractional differential mask and coefficient of variation (FACAFCV) and fractional-order ant colony algorithm combined with coefficient of variation (FACACV) in the presence of multiplicative noise is studied. Finally, a standard benchmark evaluation is carried out on the widely-used dataset to assess the effectiveness of the proposed method.
- (e)
- Section 6 delves into the merits and limitations of our method, as well as future research directions. Furthermore, potential applications of our method are outlined.
2. Background
2.1. Fractional Calculus
2.2. Fractional-Order Ant Colony Algorithm (FACA)
3. Fractional-Order Ant Colony Algorithm Combined with Fractional Differential Mask and Coefficient of Variation (FACAFCV) for Image Edge Detection
4. Experiments Methodology
5. Result and Analysis
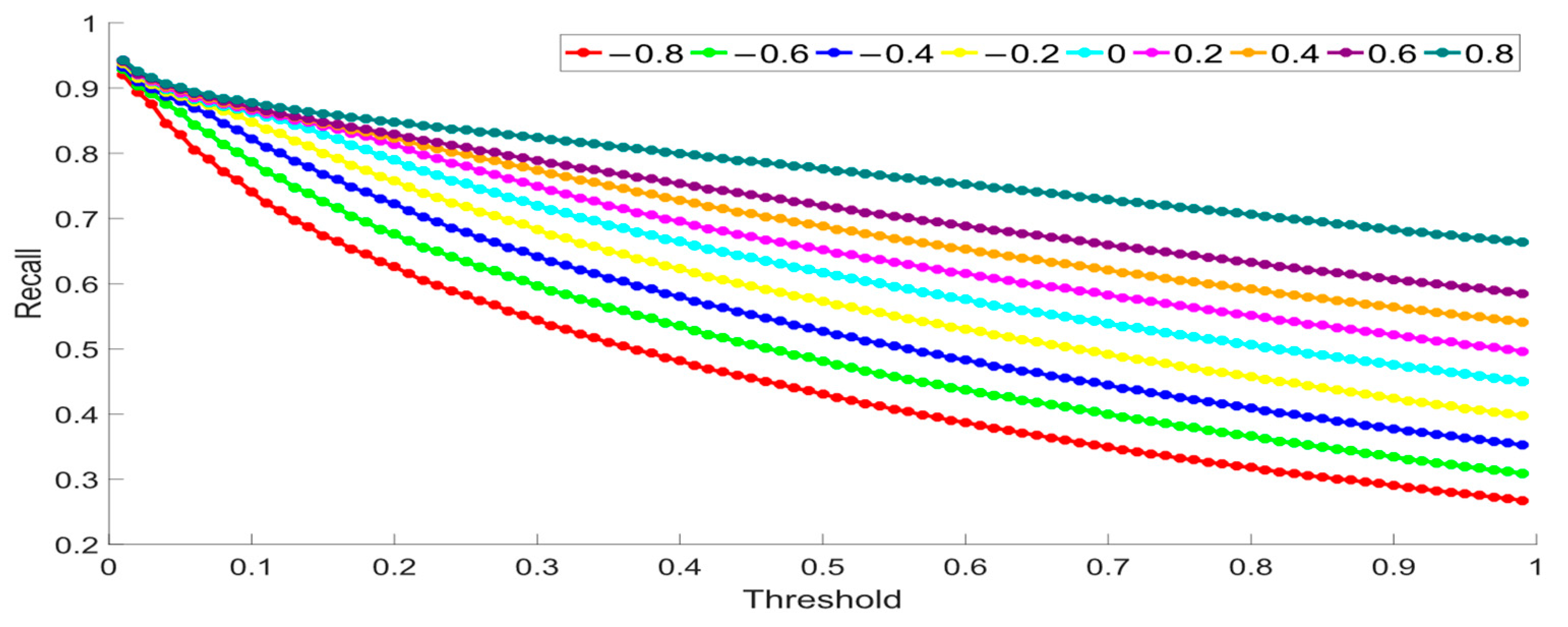
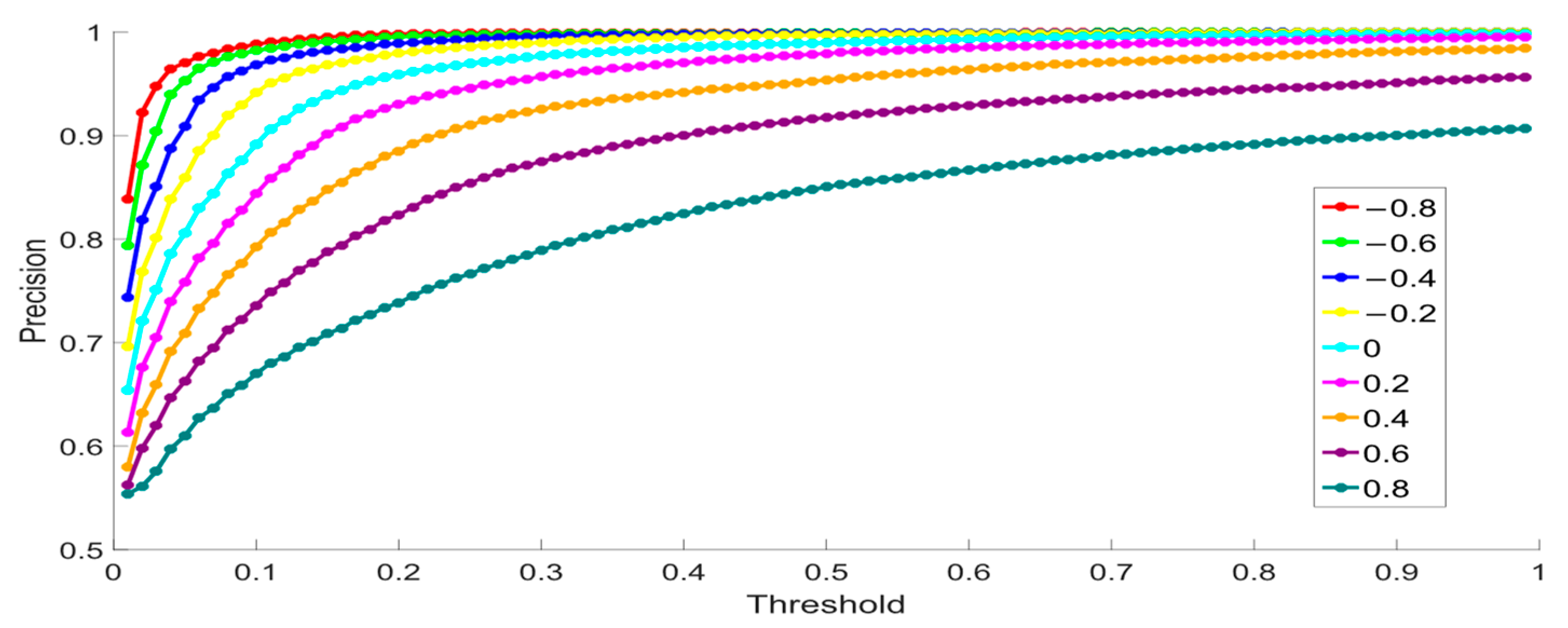
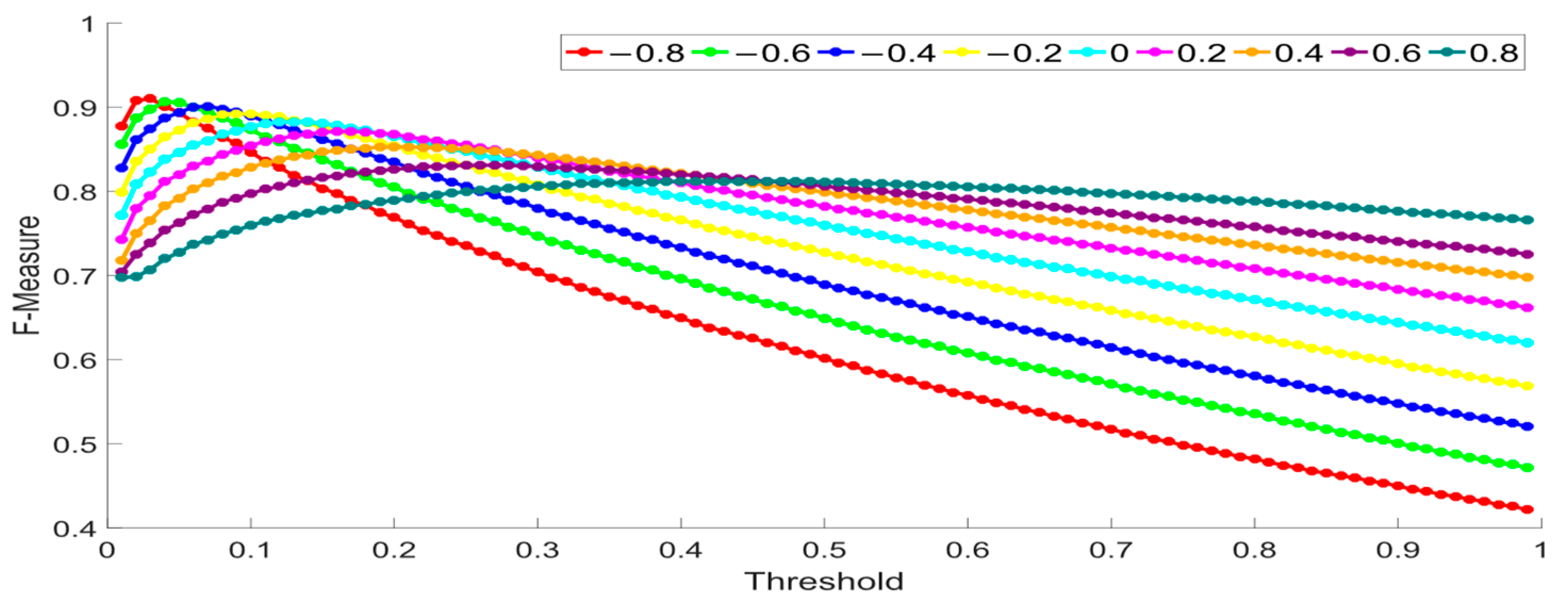
5.1. Effect of Fractional-Order Coefficients V in FACAFCV
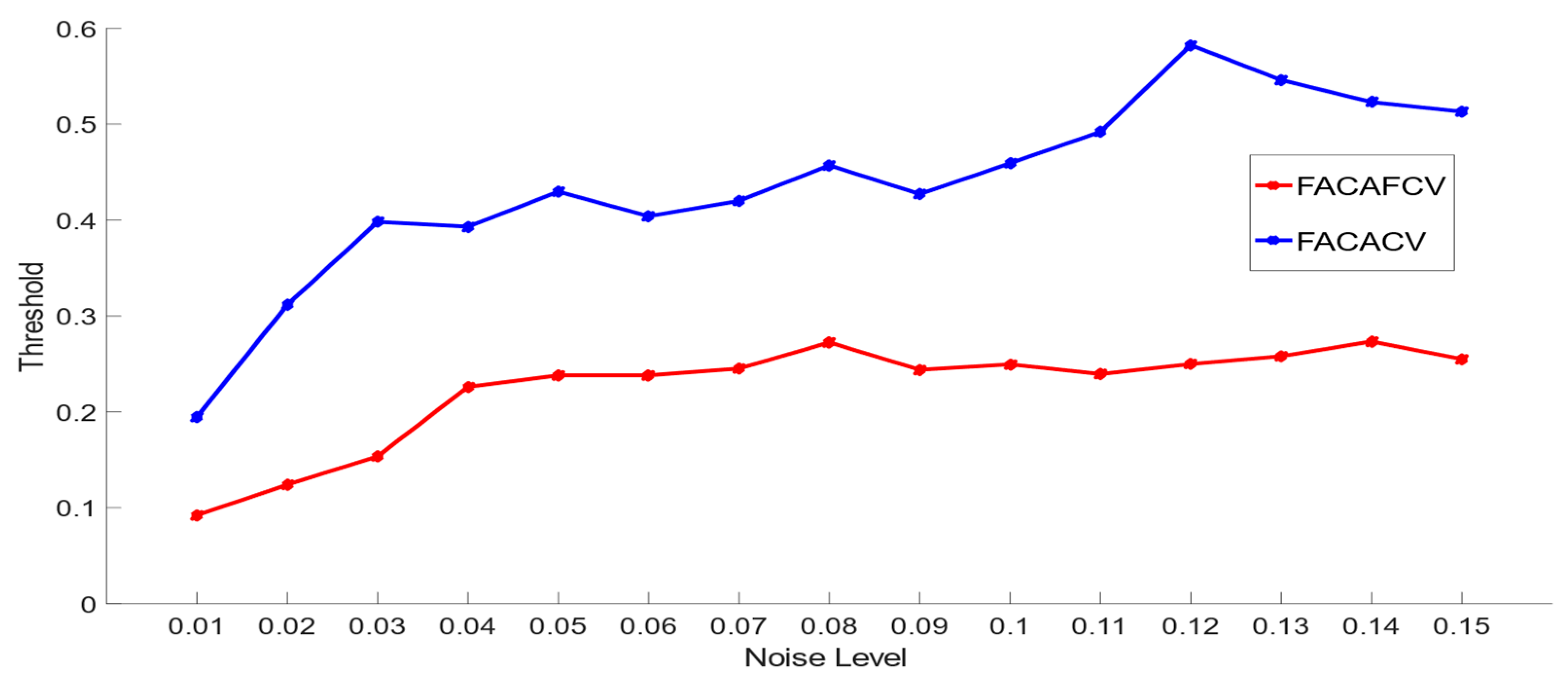
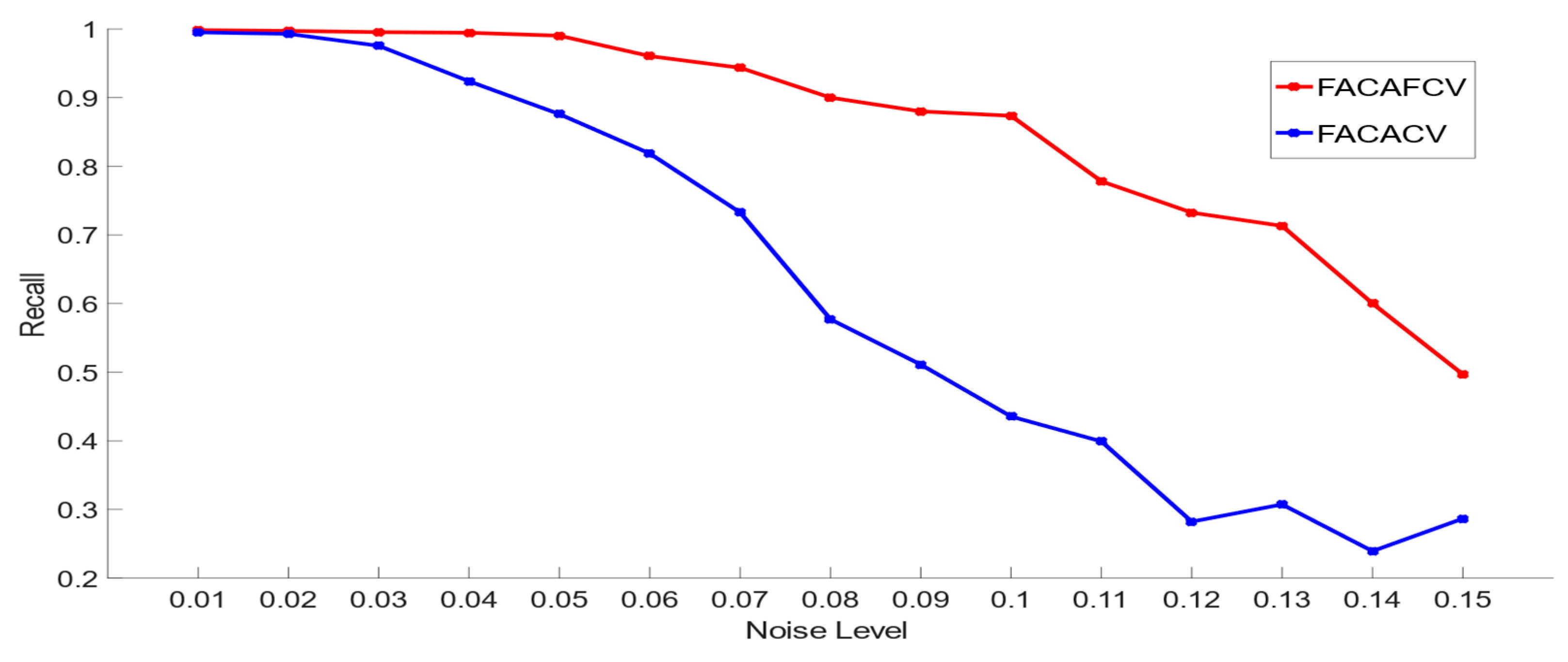
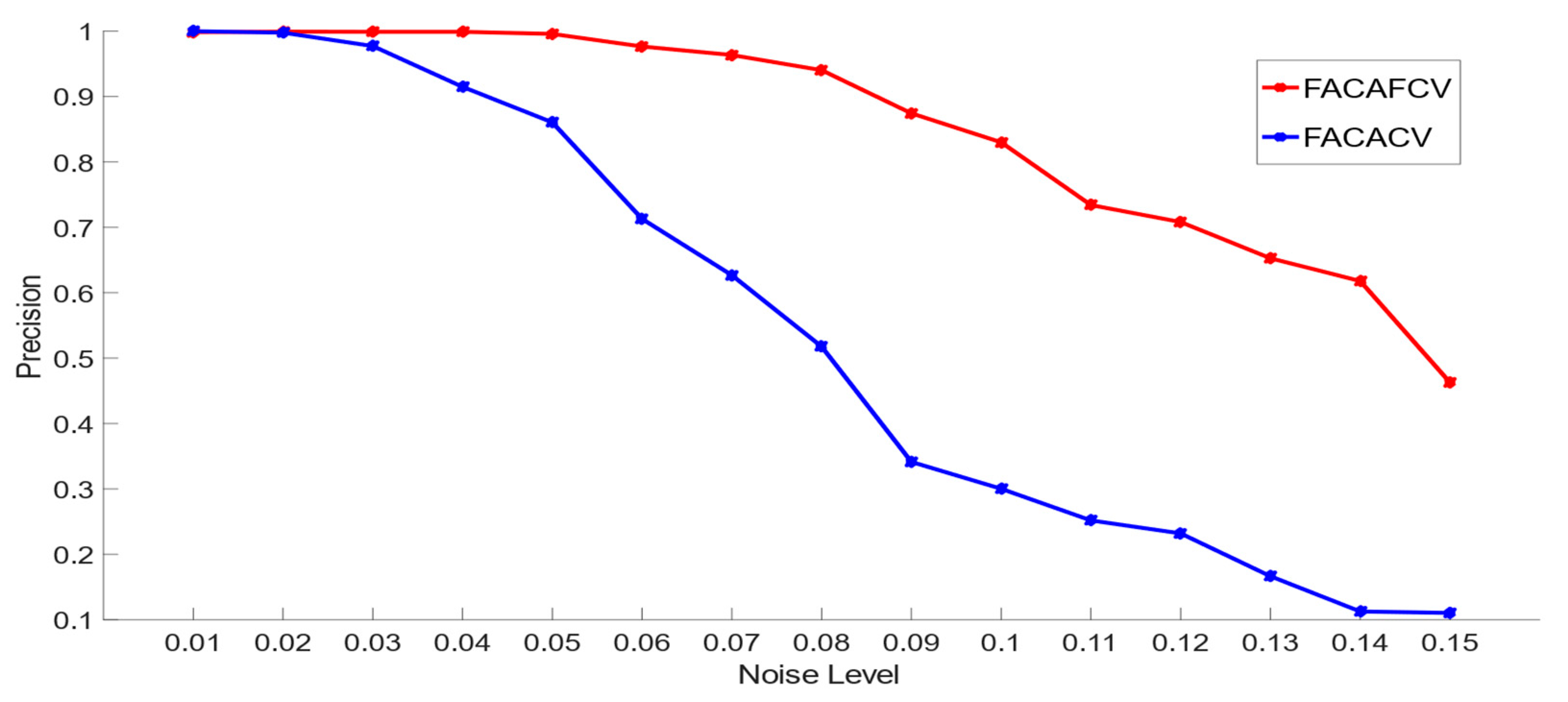
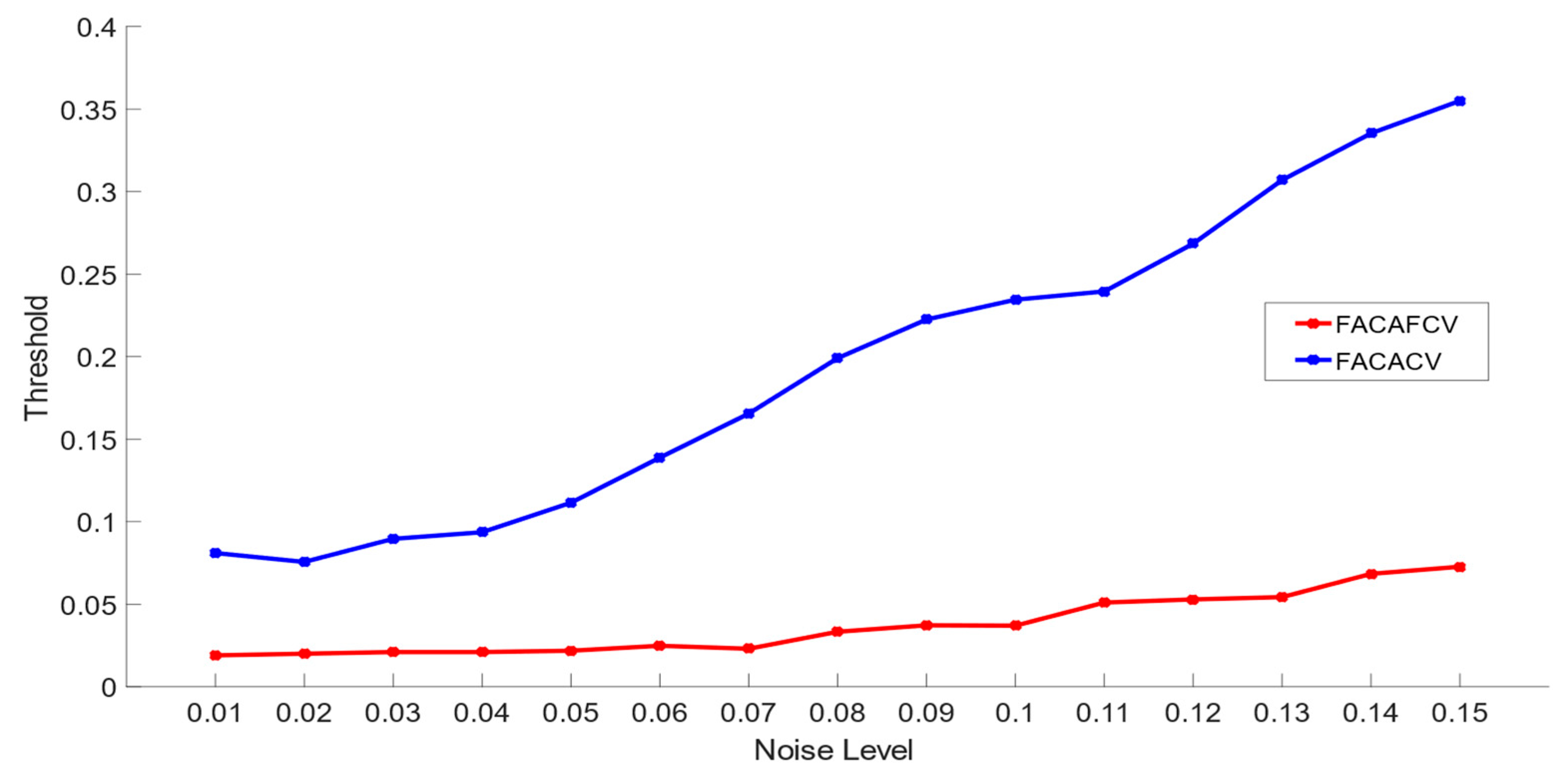
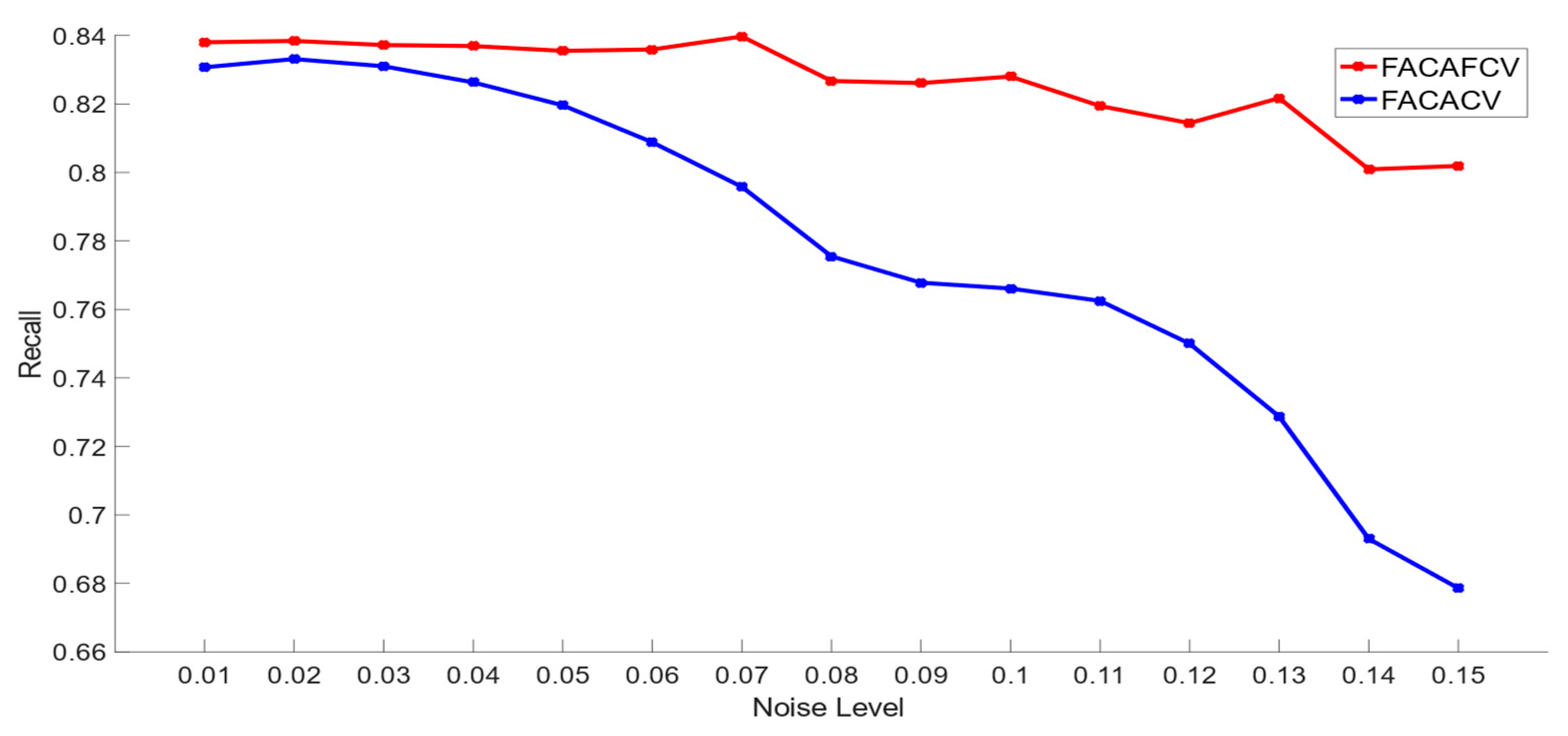
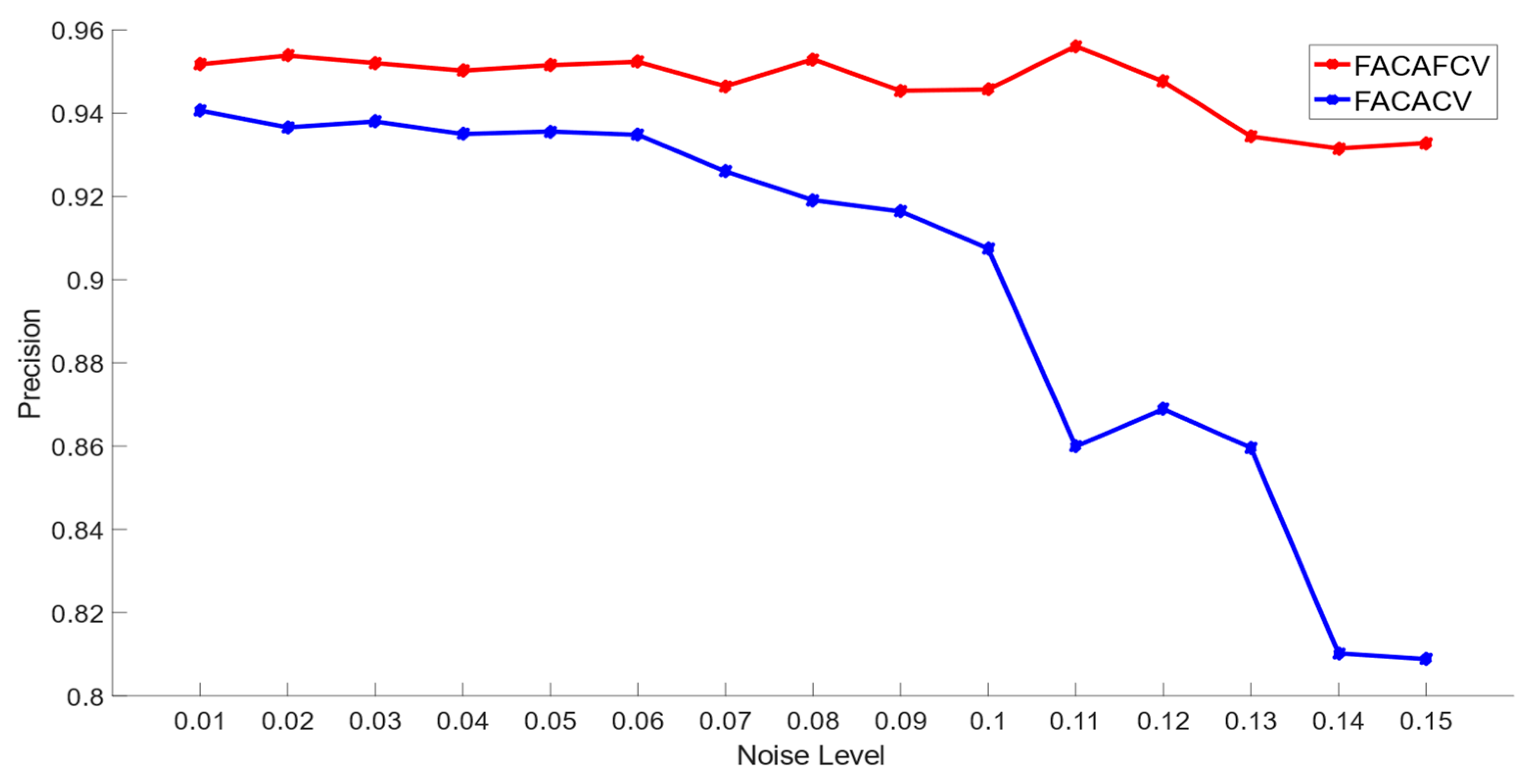
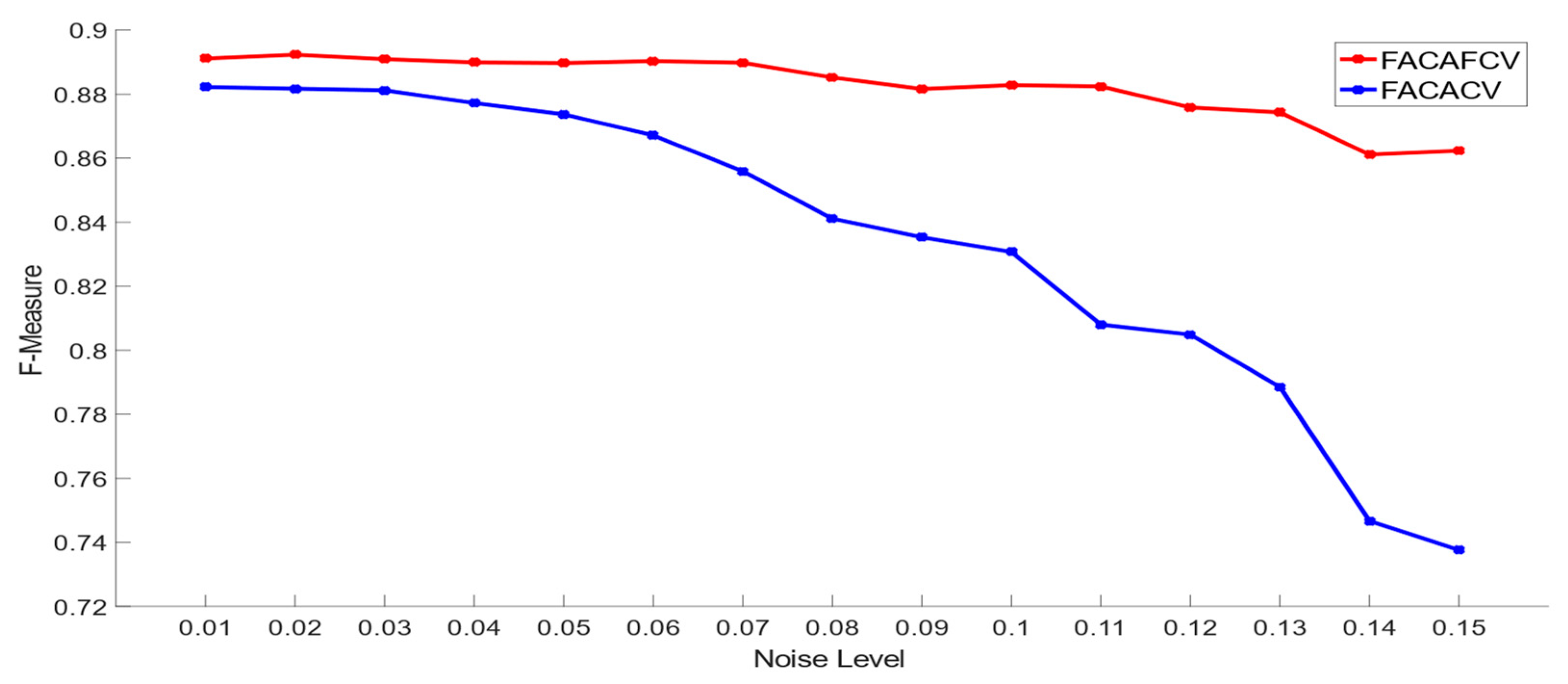
5.2. Comparison of FACAFCV and FACACV on Images with Multiplicative Noise
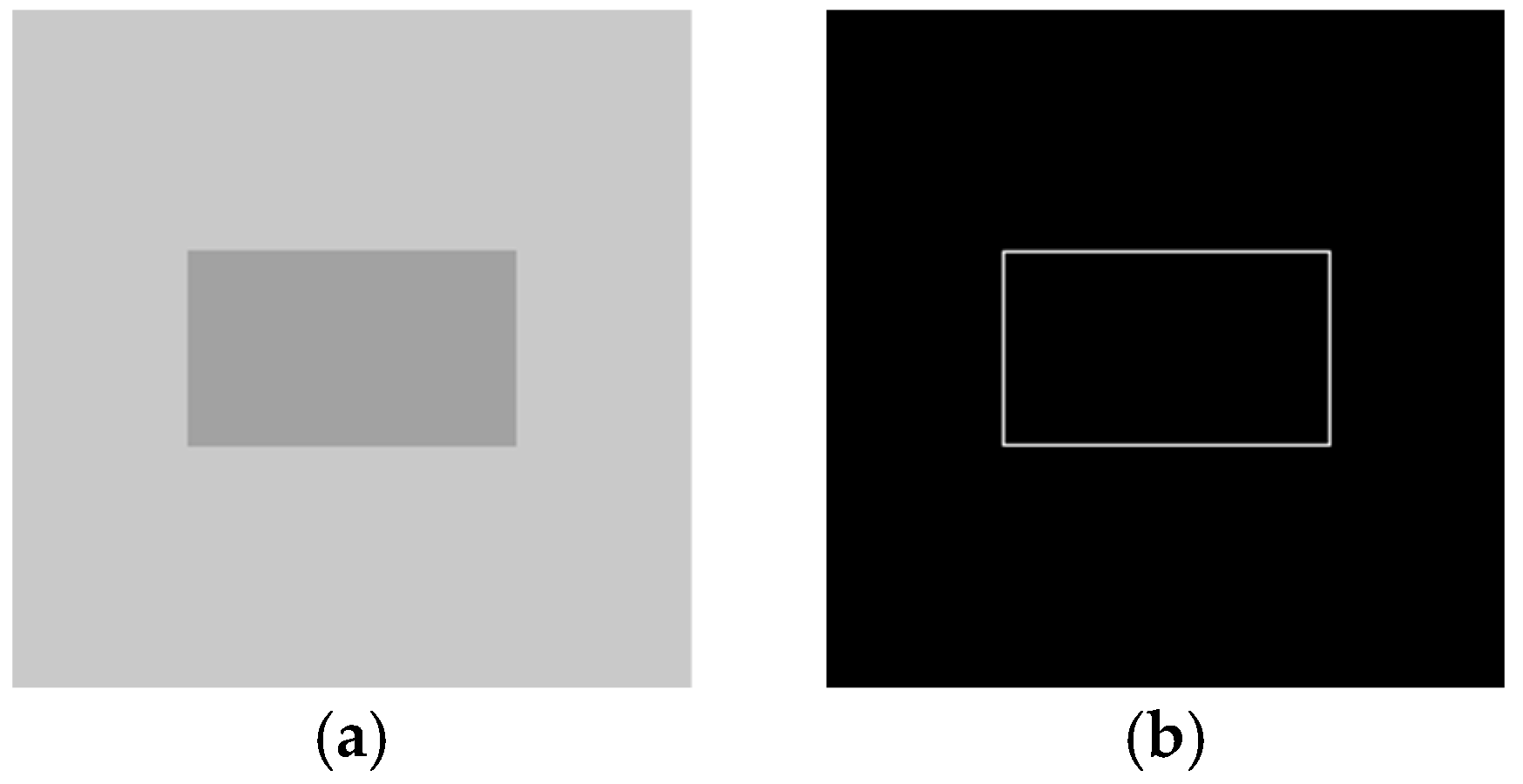
5.2.1. Synthetic Image
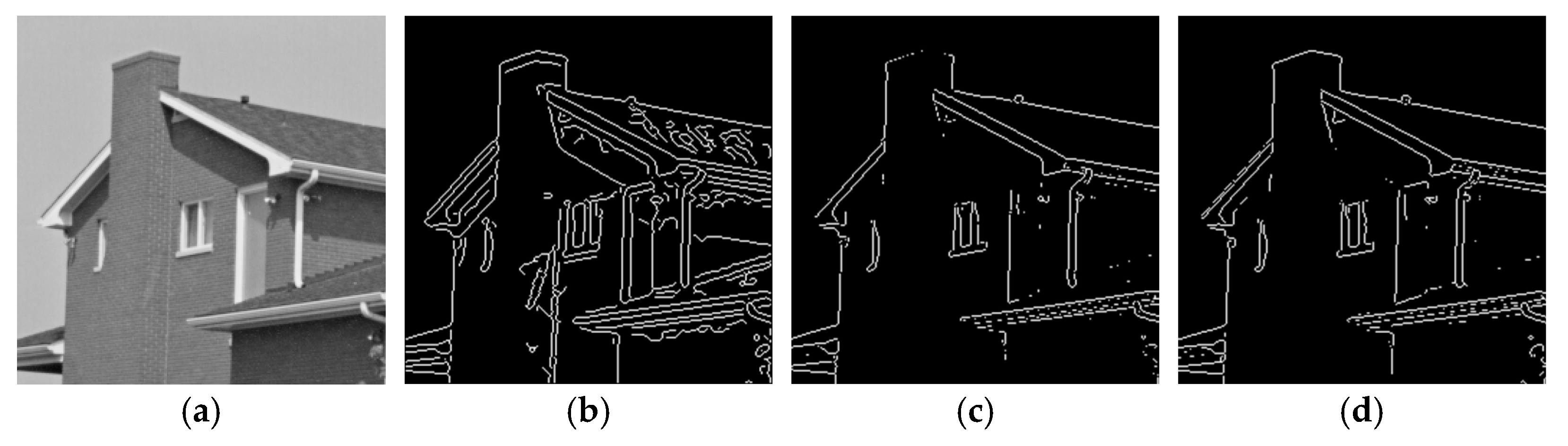
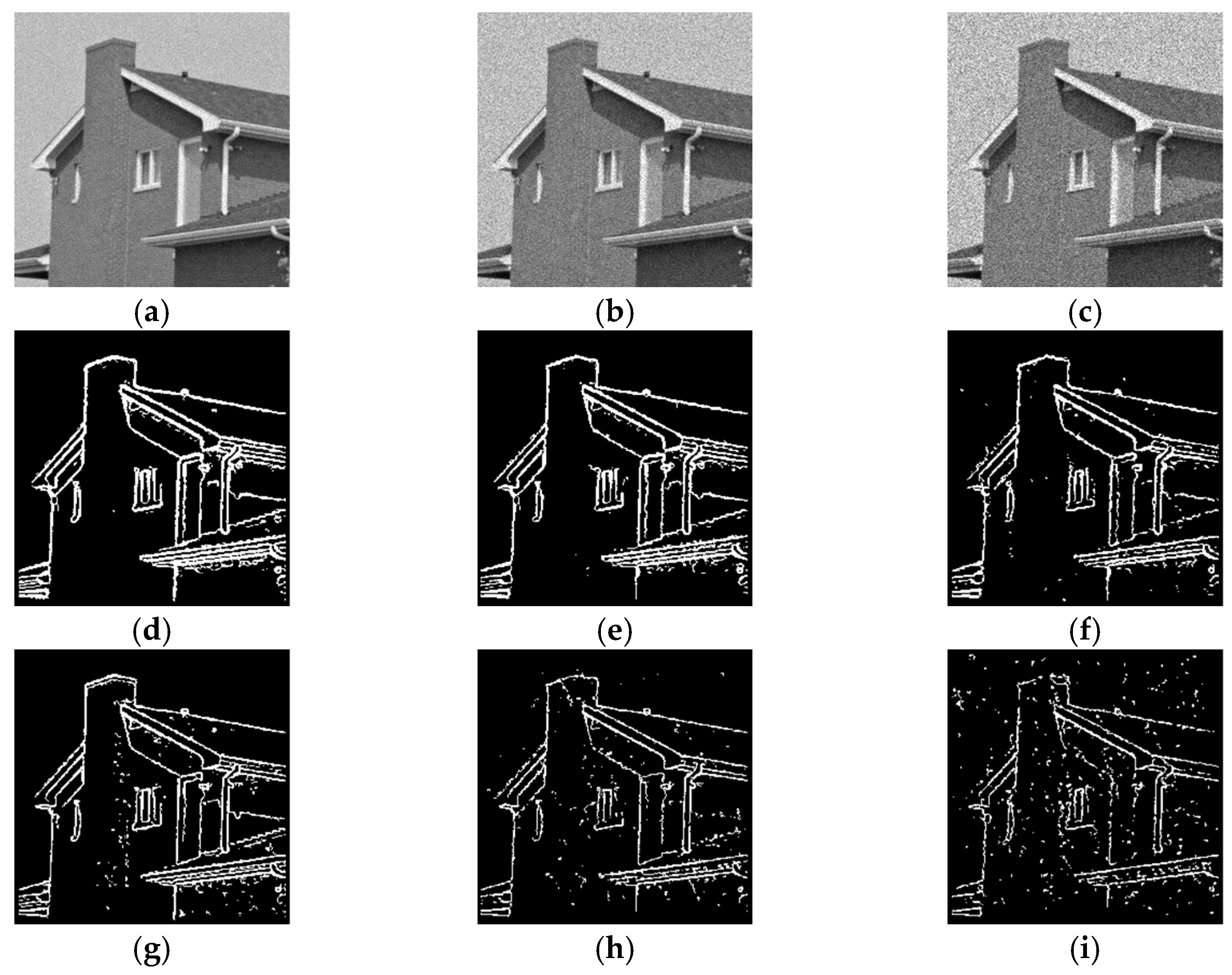
5.2.2. Real Image
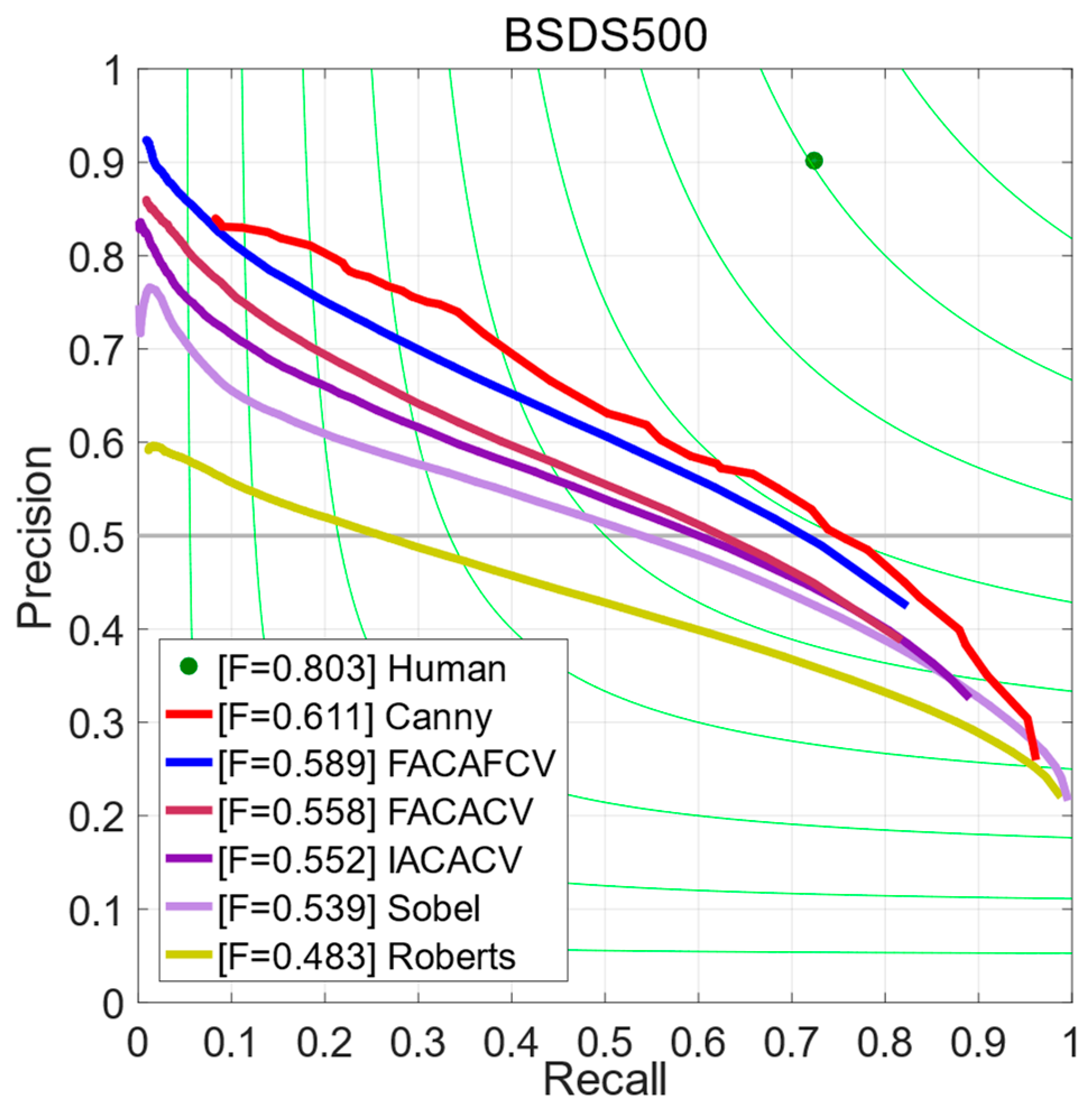
5.3. Test on BSDS500 Dataset
6. Discussion and Future Directions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, J.L.; Huang, C.H.; Du, Y.C.; Lin, C.H. Combining fractional-order edge detection and chaos synchronisation classifier for fingerprint identification. IET Image Process. 2014, 8, 354–362. [Google Scholar] [CrossRef]
- Winarno, E.; Hadikurniawati, W.; Wibisono, S.; Septiarini, A. Edge Detection and Grey Level Co-Occurrence Matrix (GLCM) Algorithms for Fingerprint Identification. In Proceedings of the 2021 2nd International Conference on Innovative and Creative Information Technology (ICITech), Salatiga, Indonesia, 23–25 September 2021; pp. 30–34. [Google Scholar]
- Anusha, K.; Siva Kumar, P. Fingerprint Image Enhancement for Crime Detection Using Deep Learning. In Proceedings of the International Conference on Cognitive and Intelligent Computing: ICCIC 2021, Hyderabad, India, 11–12 December 2021; Volume 2, pp. 257–268. [Google Scholar]
- Chen, X.; Cheng, W. Facial expression recognition based on edge detection. Int. J. Comput. Sci. Eng. Surv. 2015, 6, 1. [Google Scholar] [CrossRef]
- Zhao-Yi, P.; Yan-Hui, Z.; Yu, Z. Real-time facial expression recognition based on adaptive canny operator edge detection. In Proceedings of the 2010 Second International Conference on MultiMedia and Information Technology, Kaifeng, China, 24–25 April 2010; pp. 154–157. [Google Scholar]
- Kakran, A.; Chaudhary, H.; Kumar, P.; Sharma, A.; Singh, H. Identification and Recognition of face and number Plate for Autonomous and Secure Car Parking. In Proceedings of the 2023 International Conference on Power, Instrumentation, Energy and Control (PIECON), Aligarh, India, 10–12 February 2023; pp. 1–6. [Google Scholar]
- Al-Amri, S.S.; Kalyankar, N.; Khamitkar, S. Image segmentation by using edge detection. Int. J. Comput. Sci. Eng. 2010, 2, 804–807. [Google Scholar]
- Arbeláez, P.; Pont-Tuset, J.; Barron, J.T.; Marques, F.; Malik, J. Multiscale combinatorial grouping. In Proceedings of the Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 328–335. [Google Scholar]
- Singh, K.K.; Singh, A. A study of image segmentation algorithms for different types of images. Int. J. Comput. Sci. Issues IJCSI 2010, 7, 414. [Google Scholar]
- Tchinda, B.S.; Tchiotsop, D.; Noubom, M.; Louis-Dorr, V.; Wolf, D. Retinal blood vessels segmentation using classical edge detection filters and the neural network. Inform. Med. Unlocked 2021, 23, 100521. [Google Scholar] [CrossRef]
- Sobel, I.E. Camera Models and Machine Perception; Stanford University: Stanford, CA, USA, 1970. [Google Scholar]
- Prewitt, J.M. Object enhancement and extraction. Pict. Process. Psychopictorics 1970, 10, 15–19. [Google Scholar]
- Roberts, L.G. Machine Perception of Three-Dimensional Solids; Massachusetts Institute of Technology: Cambridge, MA, USA, 1963. [Google Scholar]
- Marr, D.; Hildreth, E. Theory of edge detection. Proc. R. Soc. Lond. Ser. B Biol. Sci. 1980, 207, 187–217. [Google Scholar]
- Canny, J. A computational approach to edge detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986, 8, 679–698. [Google Scholar] [CrossRef]
- Dorigo, M.; Birattari, M.; Stutzle, T. Ant colony optimization. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef]
- Dorigo, M.; Maniezzo, V.; Colorni, A. Ant system: Optimization by a colony of cooperating agents. IEEE Trans. Syst. Man Cybern. Part B Cybern. 1996, 26, 29–41. [Google Scholar] [CrossRef]
- Dorigo, M.; Gambardella, L.M. Ant colony system: A cooperative learning approach to the traveling salesman problem. IEEE Trans. Evol. Comput. 1997, 1, 53–66. [Google Scholar] [CrossRef]
- Stützle, T.; Hoos, H.H. MAX–MIN ant system. Future Gener. Comput. Syst. 2000, 16, 889–914. [Google Scholar] [CrossRef]
- Yi-Fei, P.; Siarry, P.; Wu-Yang, Z.; Jian, W.; Zhang, N. Fractional-order ant colony algorithm: A fractional long term memory based cooperative learning approach. Swarm Evol. Comput. 2022, 69, 101014. [Google Scholar]
- Gong, X.; Rong, Z.; Wang, J.; Zhang, K.; Yang, S. A hybrid algorithm based on state-adaptive slime mold model and fractional-order ant system for the travelling salesman problem. Complex Intell. Syst. 2022, 1–20. [Google Scholar] [CrossRef]
- Zhu, W.; Pu, Y. A Study of Fractional-Order Memristive Ant Colony Algorithm: Take Fracmemristor into Swarm Intelligent Algorithm. Fractal Fract. 2023, 7, 211. [Google Scholar] [CrossRef]
- Nezamabadi-Pour, H.; Saryazdi, S.; Rashedi, E. Edge detection using ant algorithms. Soft Comput. 2006, 10, 623–628. [Google Scholar] [CrossRef]
- Tian, J.; Yu, W.; Xie, S. An ant colony optimization algorithm for image edge detection. In Proceedings of the 2008 IEEE congress on evolutionary computation (IEEE world congress on computational intelligence), Hong Kong, China, 1–6 June 2008; pp. 751–756. [Google Scholar]
- Etemad, S.A.; White, T. An ant-inspired algorithm for detection of image edge features. Appl. Soft Comput. 2011, 11, 4883–4893. [Google Scholar] [CrossRef]
- Liu, X.; Fang, S. A convenient and robust edge detection method based on ant colony optimization. Opt. Commun. 2015, 353, 147–157. [Google Scholar] [CrossRef]
- Martínez, C.A.; Buemi, M.E. Hybrid ACO algorithm for edge detection. Evol. Syst. 2021, 12, 849–860. [Google Scholar] [CrossRef]
- Baltierra, S.; Valdebenito, J.; Mora, M. A proposal of edge detection in images with multiplicative noise using the Ant Colony System algorithm. Eng. Appl. Artif. Intell. 2022, 110, 104715. [Google Scholar] [CrossRef]
- Oldham, K.; Spanier, J. The Fractional Calculus Theory and Applications of Differentiation and Integration to Arbitrary Order; Elsevier: Amsterdam, The Netherlands, 1974. [Google Scholar]
- He, N.; Wang, J.-B.; Zhang, L.-L.; Lu, K. An improved fractional-order differentiation model for image denoising. Signal Process. 2015, 112, 180–188. [Google Scholar] [CrossRef]
- Pu, Y.-F. Fractional-order euler-Lagrange equation for fractional-order variational method: A necessary condition for fractional-order fixed boundary optimization problems in signal processing and image processing. IEEE Access 2016, 4, 10110–10135. [Google Scholar] [CrossRef]
- Li, C.; He, C. Fractional-order diffusion coupled with integer-order diffusion for multiplicative noise removal. Comput. Math. Appl. 2023, 136, 34–43. [Google Scholar] [CrossRef]
- Kommula, B.N.; Kota, V.R. Design of MFA-PSO based fractional order PID controller for effective torque controlled BLDC motor. Sustain. Energy Technol. Assess. 2022, 49, 101644. [Google Scholar]
- Padula, F.; Visioli, A. Tuning rules for optimal PID and fractional-order PID controllers. J. Process Control 2011, 21, 69–81. [Google Scholar] [CrossRef]
- Li, X.; Mou, J.; Banerjee, S.; Wang, Z.; Cao, Y. Design and DSP implementation of a fractional-order detuned laser hyperchaotic circuit with applications in image encryption. Chaos Solitons Fractals 2022, 159, 112133. [Google Scholar] [CrossRef]
- Xu, J.; Mou, J.; Liu, J.; Hao, J. The image compression–encryption algorithm based on the compression sensing and fractional-order chaotic system. Vis. Comput. 2022, 38, 1509–1526. [Google Scholar] [CrossRef]
- Pu, Y.-F.; Zhou, J.-L.; Yuan, X. Fractional differential mask: A fractional differential-based approach for multiscale texture enhancement. IEEE Trans. Image Process. 2009, 19, 491–511. [Google Scholar]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives; Gordon and Breach Science Publishers: Yverdon Yverdon-les-Bains, Switzerland, 1993; Volume 1. [Google Scholar]
- Podlubny, I. An introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications. Math. Sci. Eng 1999, 198, 340. [Google Scholar]
- Su, Z.; Liu, W.; Yu, Z.; Hu, D.; Liao, Q.; Tian, Q.; Pietikäinen, M.; Liu, L. Pixel difference networks for efficient edge detection. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 5117–5127. [Google Scholar]
- Xie, S.; Tu, Z. Holistically-nested edge detection. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1395–1403. [Google Scholar]
- Yang, J.; Price, B.; Cohen, S.; Lee, H.; Yang, M.-H. Object contour detection with a fully convolutional encoder-decoder network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 193–202. [Google Scholar]
- Lam, L.; Lee, S.-W.; Suen, C.Y. Thinning methodologies-a comprehensive survey. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 869–885. [Google Scholar] [CrossRef]
- Arbelaez, P.; Maire, M.; Fowlkes, C.; Malik, J. Contour detection and hierarchical image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 33, 898–916. [Google Scholar] [CrossRef]
- Achim, A.; Bezerianos, A.; Tsakalides, P. Novel Bayesian multiscale method for speckle removal in medical ultrasound images. IEEE Trans. Med. Imaging 2001, 20, 772–783. [Google Scholar] [CrossRef]
- Krissian, K.; Westin, C.-F.; Kikinis, R.; Vosburgh, K.G. Oriented speckle reducing anisotropic diffusion. IEEE Trans. Image Process. 2007, 16, 1412–1424. [Google Scholar] [CrossRef]
- Mora, M.; Córdova-Lepe, F.; Del-Valle, R. A non-Newtonian gradient for contour detection in images with multiplicative noise. Pattern Recognit. Lett. 2012, 33, 1245–1256. [Google Scholar] [CrossRef]





| Parameters | Value |
|---|---|
| 0.75 | |
| 1 | |
| 5 | |
| 0.2 | |
| 0.0001 | |
| 1.3 | |
| memory | |
| L |
| v | Threshold | Recall | Precision | F-Measure |
|---|---|---|---|---|
| −0.8 | 0.03 | 0.8761 | 0.9471 | 0.9102 |
| −0.6 | 0.04 | 0.8733 | 0.9426 | 0.9066 |
| −0.4 | 0.07 | 0.8612 | 0.9453 | 0.9013 |
| −0.2 | 0.10 | 0.8513 | 0.9380 | 0.8925 |
| 0 | 0.13 | 0.8418 | 0.9280 | 0.8828 |
| 0.2 | 0.17 | 0.8330 | 0.9142 | 0.8717 |
| 0.4 | 0.20 | 0.8215 | 0.8884 | 0.8536 |
| 0.6 | 0.27 | 0.8011 | 0.8644 | 0.8315 |
| 0.8 | 0.44 | 0.7916 | 0.8355 | 0.8129 |
| Low Level of Noise | Medium Level of Noise | High Level of Noise | ||||
|---|---|---|---|---|---|---|
| FACAFCV | FACACV | FACAFCV | FACACV | FACAFCV | FACACV | |
| Recall | 0.9923 | 0.8776 | 0.9286 | 0.4923 | 0.5689 | 0.2857 |
| Precision | 1.0000 | 0.8982 | 0.8771 | 0.3333 | 0.5247 | 0.1532 |
| F-Measure | 0.9962 | 0.8877 | 0.9021 | 0.3975 | 0.5459 | 0.1995 |
| Threshold | 0.25 | 0.43 | 0.25 | 0.44 | 0.26 | 0.57 |
| Low Level of Noise | Medium Level of Noise | High Level of Noise | ||||
|---|---|---|---|---|---|---|
| FACAFCV | FACACV | FACAFCV | FACACV | FACAFCV | FACACV | |
| Recall | 0.8362 | 0.8278 | 0.8236 | 0.7587 | 0.7943 | 0.6799 |
| Precision | 0.9535 | 0.9260 | 0.9551 | 0.9138 | 0.9408 | 0.7886 |
| F-Measure | 0.8910 | 0.8741 | 0.8845 | 0.8291 | 0.8614 | 0.7302 |
| Threshold | 0.02 | 0.1 | 0.04 | 0.24 | 0.08 | 0.35 |
| ODS | OIS | Average Precision | |
|---|---|---|---|
| Human | 0.803 | 0.803 | - |
| Canny | 0.611 | 0.676 | 0.520 |
| FACAFCV | 0.589 | 0.608 | 0.533 |
| FACACV | 0.558 | 0.579 | 0.487 |
| IACACV | 0.552 | 0.571 | 0.497 |
| Sobel | 0.539 | 0.575 | 0.498 |
| Roberts | 0.483 | 0.513 | 0.413 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Pu, Y.-F. Image Edge Detection Based on Fractional-Order Ant Colony Algorithm. Fractal Fract. 2023, 7, 420. https://doi.org/10.3390/fractalfract7060420
Liu X, Pu Y-F. Image Edge Detection Based on Fractional-Order Ant Colony Algorithm. Fractal and Fractional. 2023; 7(6):420. https://doi.org/10.3390/fractalfract7060420
Chicago/Turabian StyleLiu, Xinyu, and Yi-Fei Pu. 2023. "Image Edge Detection Based on Fractional-Order Ant Colony Algorithm" Fractal and Fractional 7, no. 6: 420. https://doi.org/10.3390/fractalfract7060420







