Fractional-Order Model-Free Predictive Control for Voltage Source Inverters
Abstract
:1. Introduction
- The FOPI controller and the MFPC controllers have been integrated to improve the performance of the 2L-VSI. This has been carried out by accurately estimating the unknown function of the MFPC for the voltage control of the 2L-VSI.
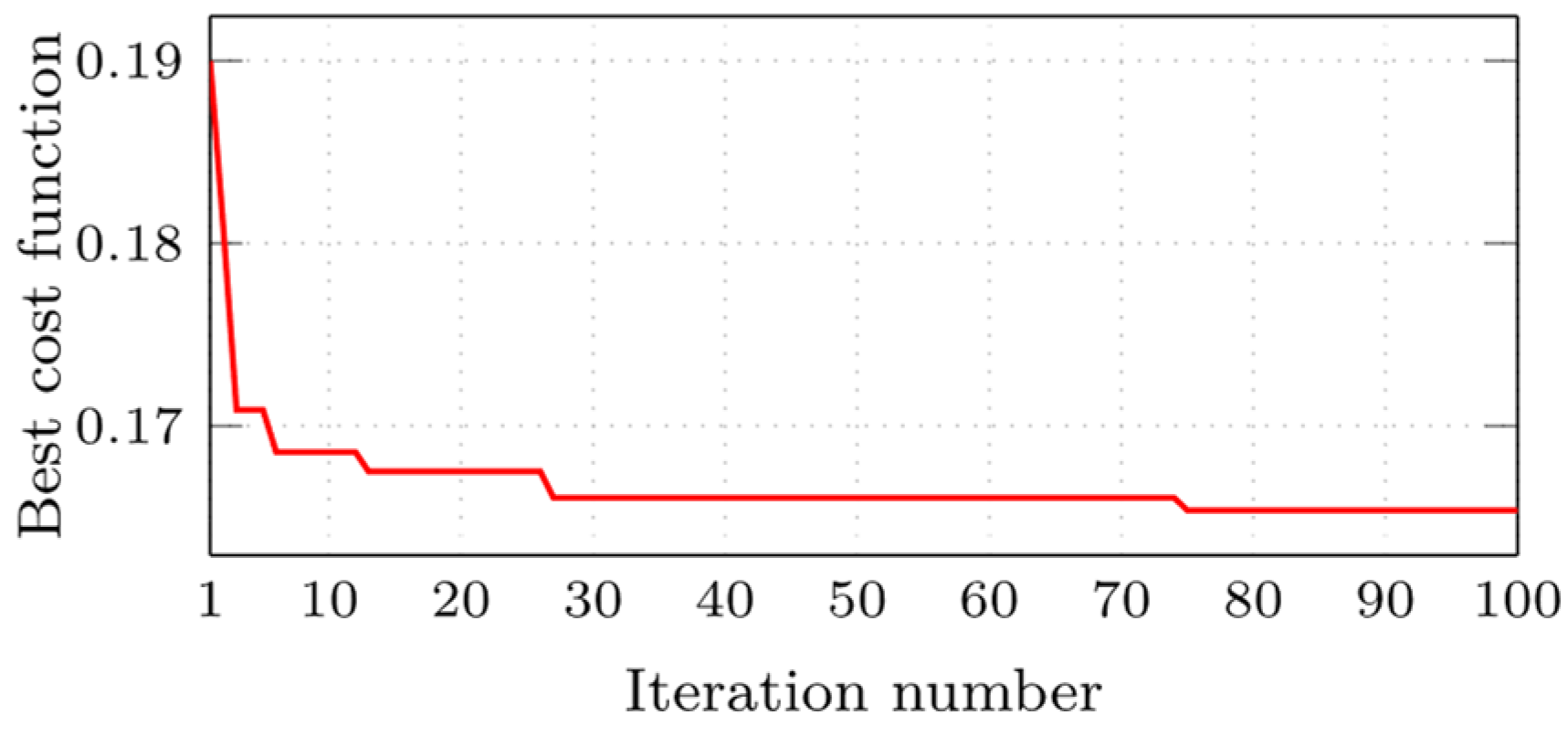
- The metaheuristic optimization approach (GWO) has been implemented to find the optimal gains of the proposed FO-MFPC controller.
- The performance of the proposed system utilizing the FO-MFPC controller and the conventional MFPC has been compared. The controller’s performance has been tested under linear and nonlinear load disturbances.
- The robustness of the proposed control system under parameter uncertainty has been discussed.
- The effect of changing the sampling period on the system performance has been studied and compared for the proposed FO-MFPC controller and the conventional MFPC.
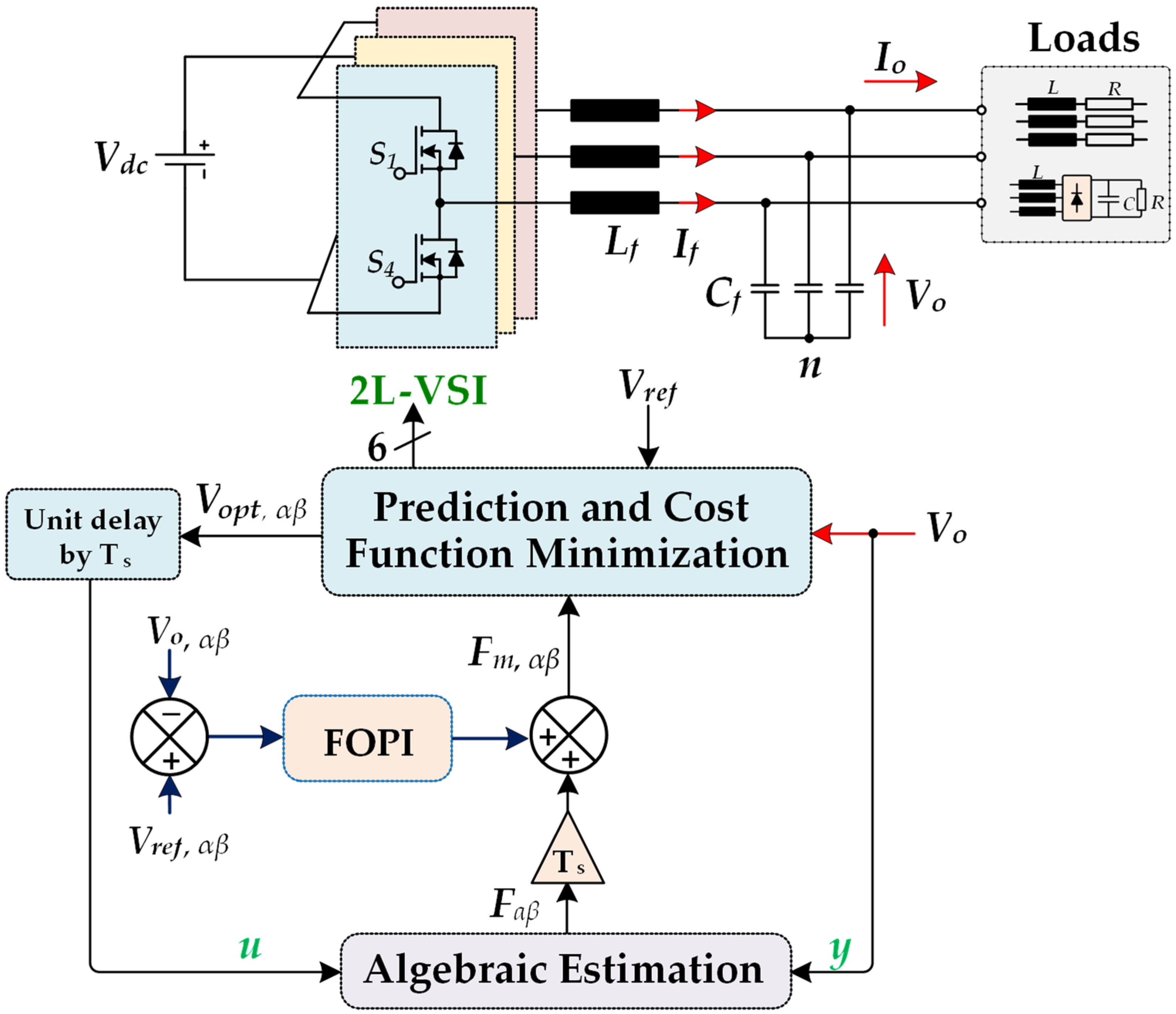
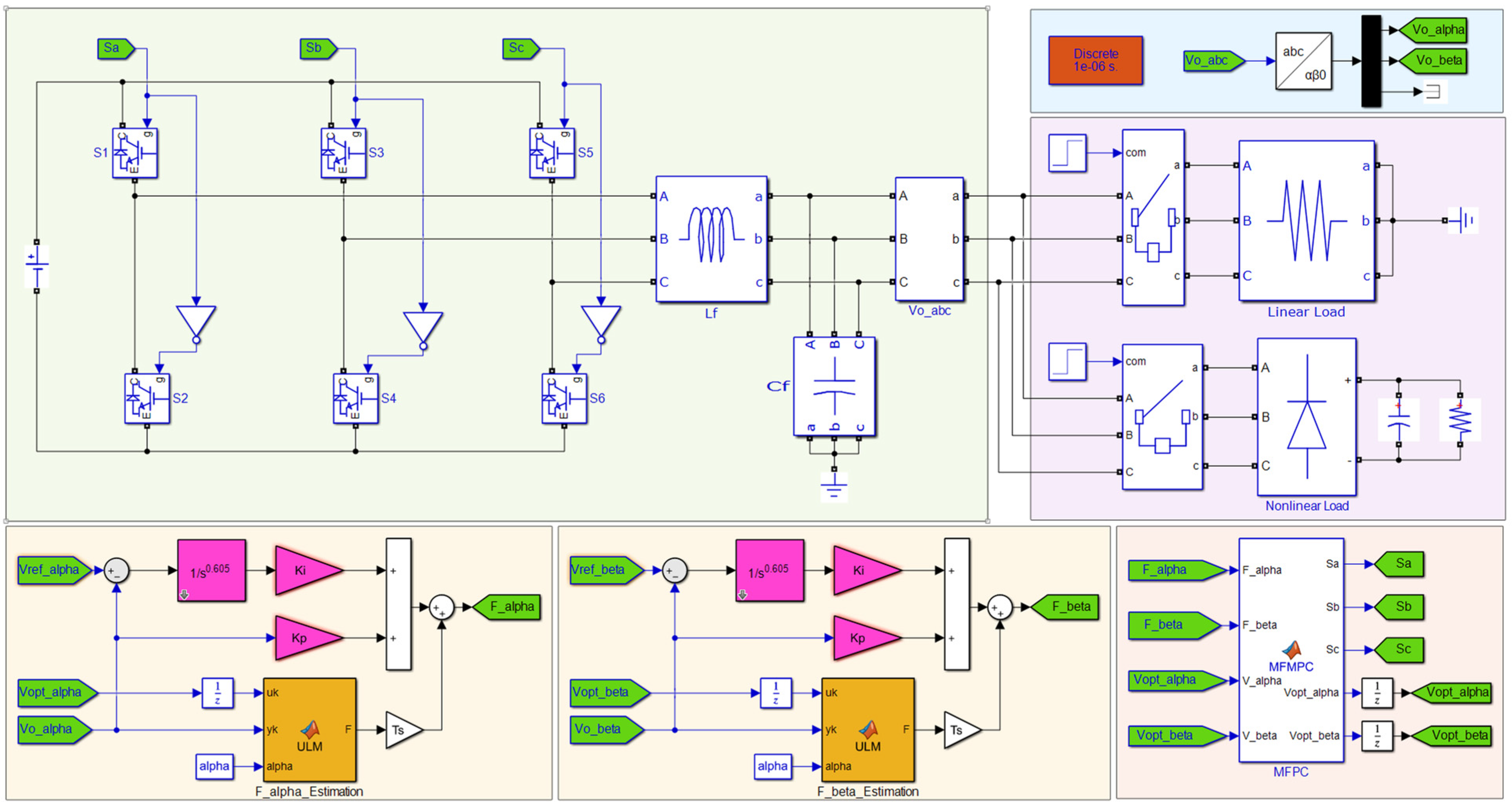
2. Conventional Model-Free Predictive Control of UPS Based on an Ultra-Local Model
3. Proposed Fractional-Order Model-Free Predictive Control
3.1. Fractional-Order Calculus
3.2. Proposed FO-MFPC for 2L-VSI in UPS Applications
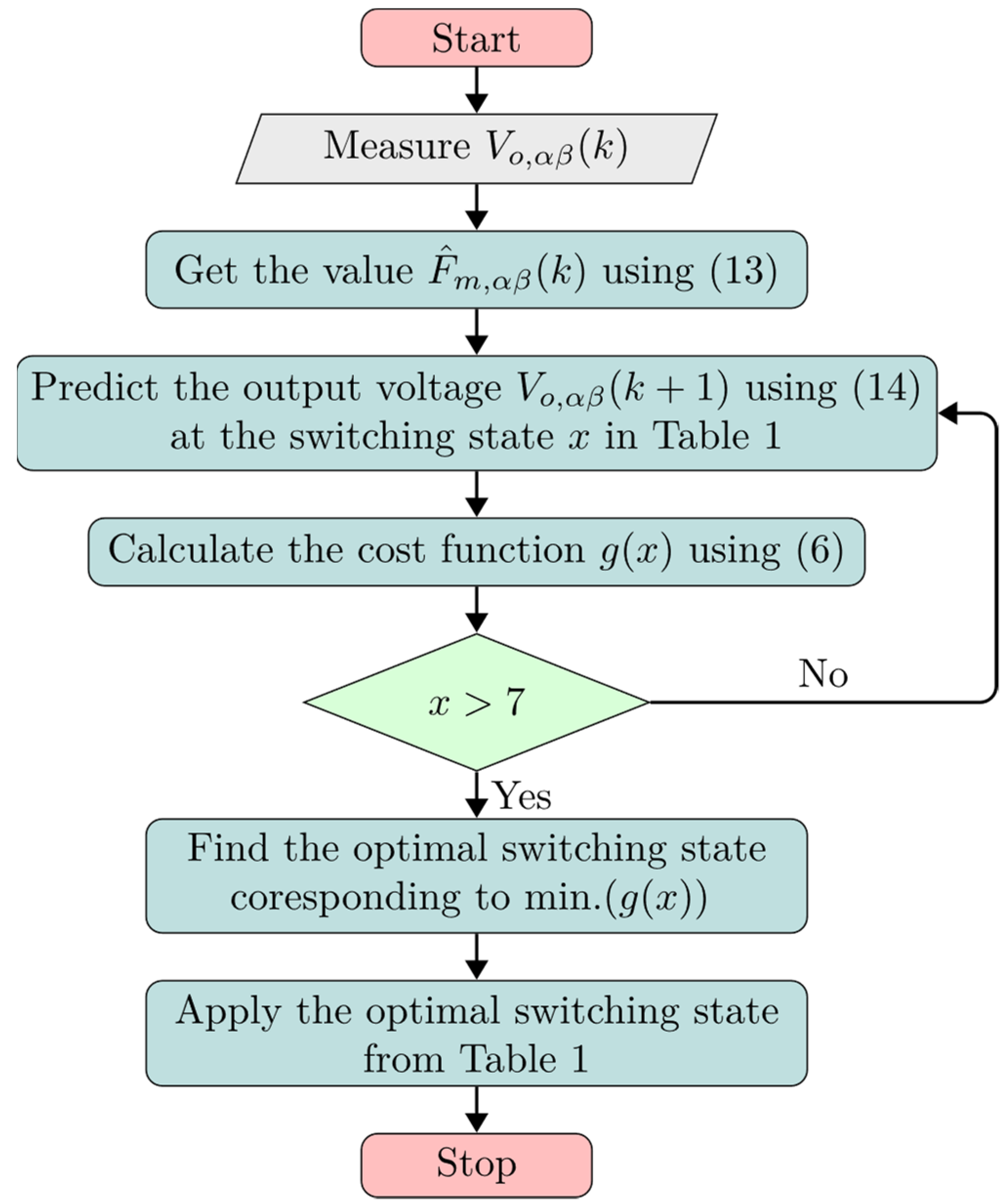
- (1)
- At sampling instant k, the controlled variables (Vo,αβ(k)) should be measured.
- (2)
- Those controlled variables are then predicted at instant k + 1 based on the discrete model of the converter given in Equation (14).
- (3)
- After defining a proper cost function g(x), as in Equation (6), it should be calculated for the current switching states (x) based on the desired value of the controlled variable.
- (4)
- As the main objective of the optimization problem is to find the optimum switching state that minimizes the cost function, the cost function of the current switching state g(x) is compared with the smallest previous value.
- (5)
- Steps (2) to (4) are repeated for all possible switching states given in Table 1.
- (6)
- Finally, the optimum switching state is applied at the next sampling instant.
4. Simulation Results
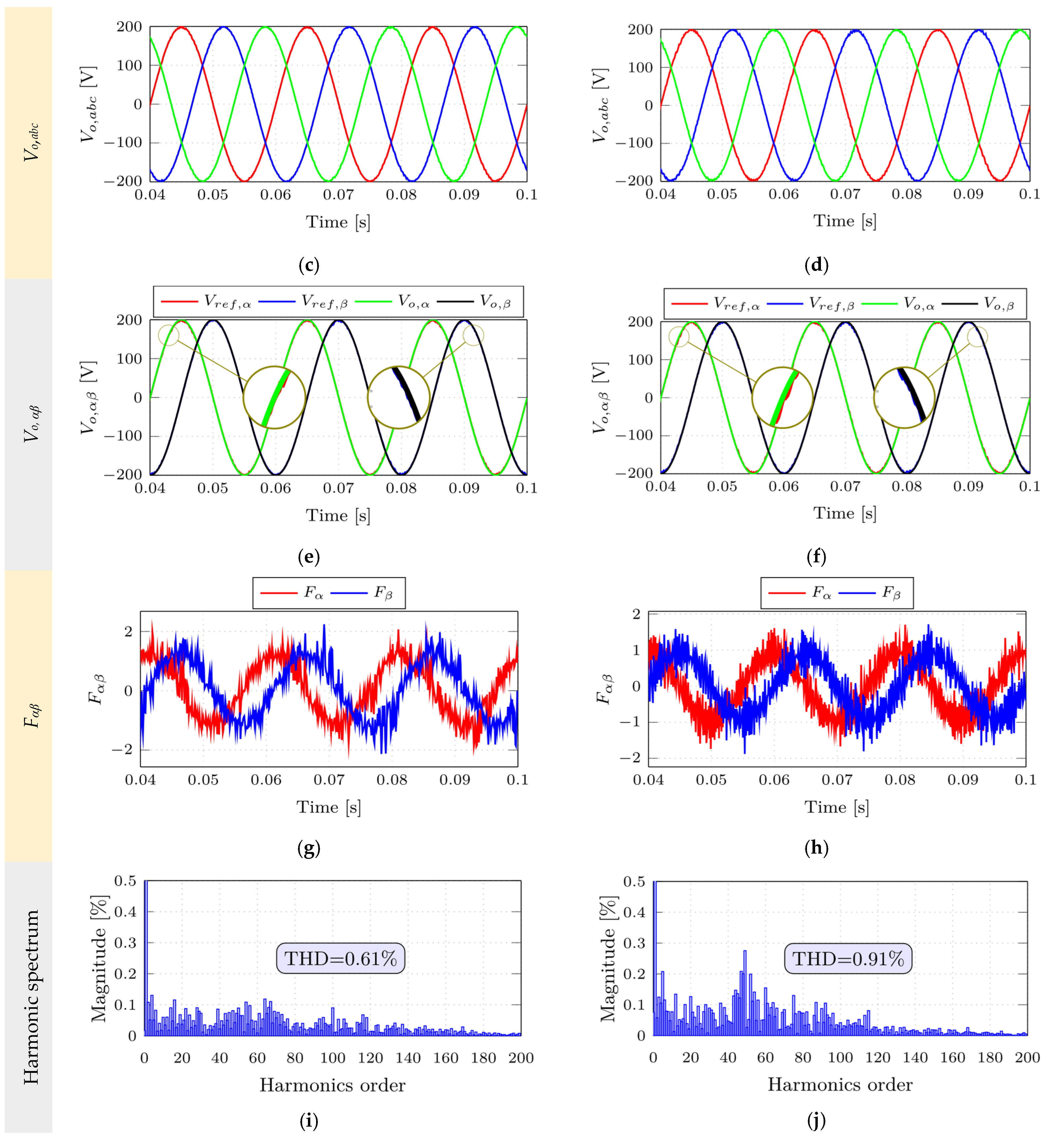
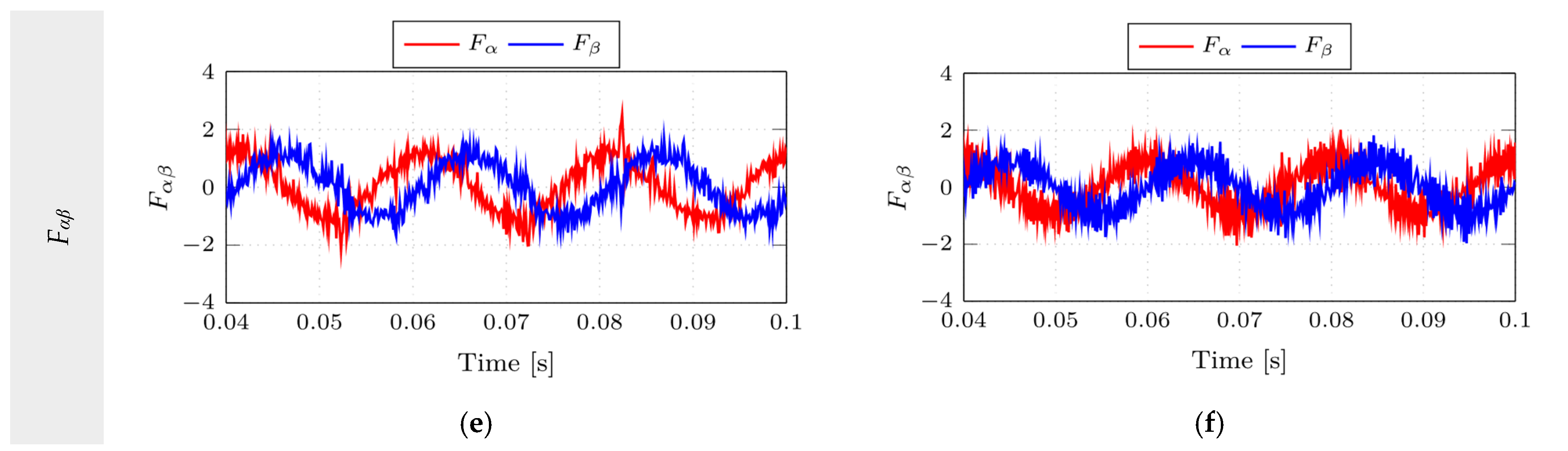
4.1. Case 1: Steady-State Response @ Linear Resistive Load
4.2. Case 2: Transient Response @ Step Resistive Load Change
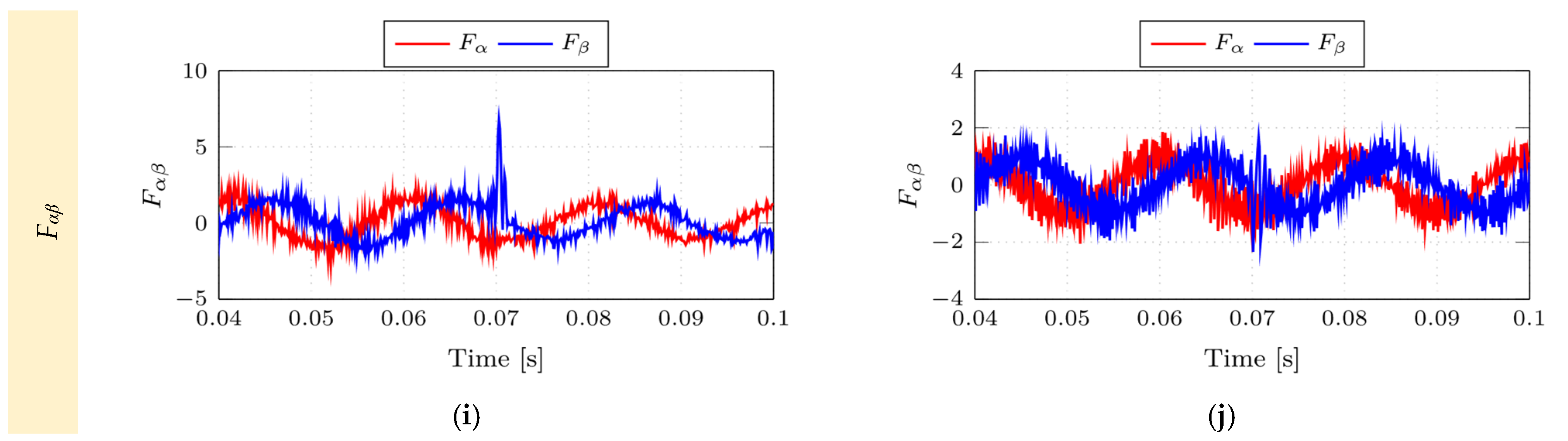
4.3. Case 3: Steady-State Response @ Nonlinear Load
4.4. Case 4: Parameter Mismatch
4.5. THD Evaluation at Different Sampling Intervals
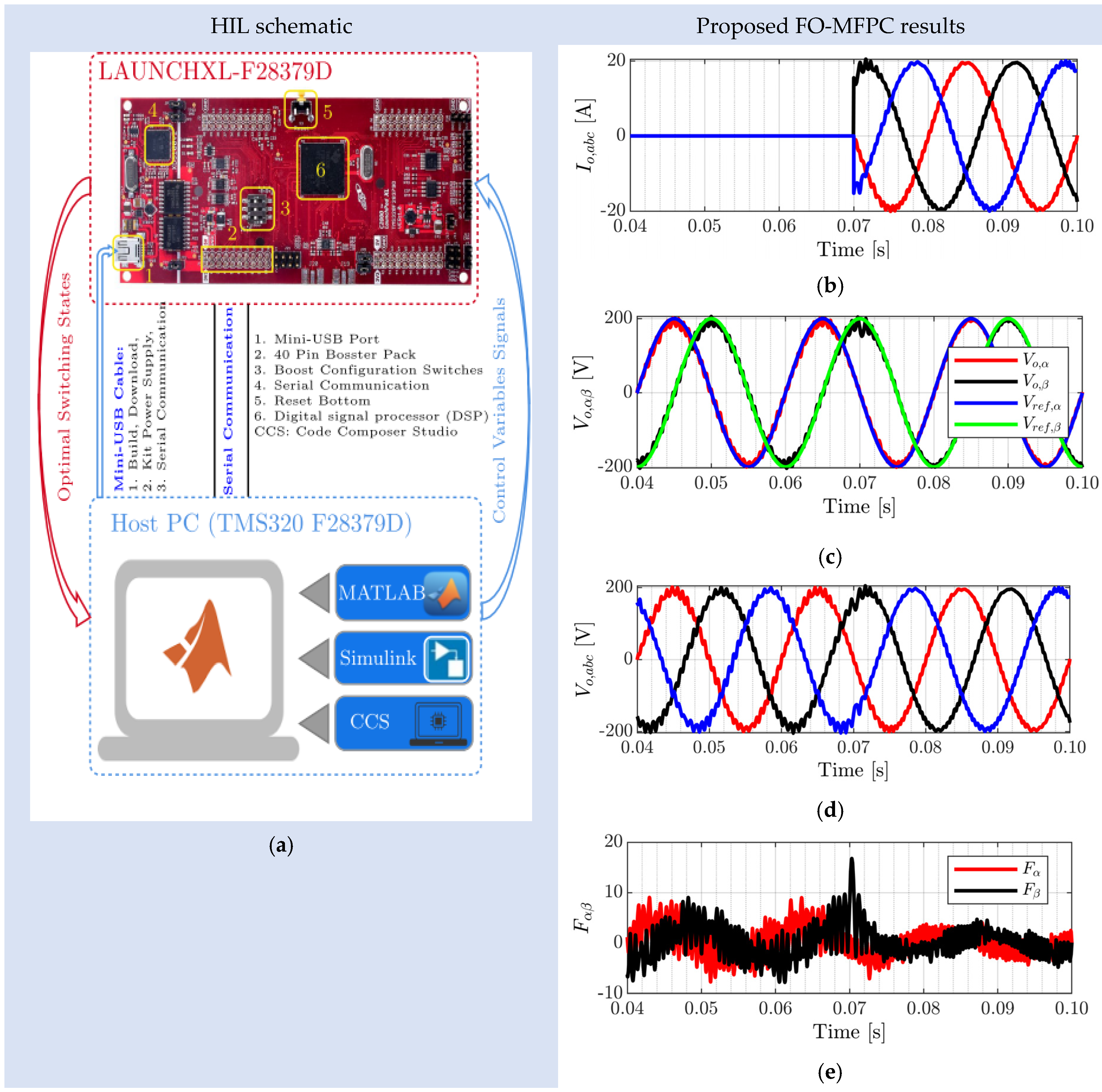
4.6. HIL Validation Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| 2L-VSI | Two-level voltage source inverter |
| FOC | Fractional-order controller |
| MFPC | Model-free predictive control |
| UPS | Uninterruptable power supply |
| ULM | Ultra-local model |
| FOPI | Fractional-order proportional-integral |
| GWO | Grey wolf optimization |
| THD | Total harmonics distortion |
| FCS-MPC | Finite control set-model predictive control |
| PWM | Pulse width modulation |
| LC | Inductor-capacitor |
| Space voltage vector | |
| F | Unknown function associated with MFPC |
| u | Plant input |
| y | Plant output |
| α | Non-physical parameter |
| Ts | Sampling time |
| Nf | Length of the window |
| Approximated value of the unknown function F | |
| Cf | Filter capacitor |
| x | Voltage vector number in Table 1 |
| FO | Fractional-order |
| q | Order of the FO calculus |
| lb | Lower band of the FO integrator |
| ub | Upper band of the FO integrator |
| R-L | Riemann–Liouville |
| Kp | Proportional gain of the FOPI |
| Ki | Integral gain of the FOPI |
| λ | Integral fractional order |
| PI | Proportional integral |
| Gc(s) | FOPI transfer function |
| s | Laplace operator |
| m,αβ | Modified value of the unknown function αβ |
| ISE | Integral square error |
References
- Yan, S.; Yang, Y.; Hui, S.Y.; Blaabjerg, F. A Review on Direct Power Control of Pulsewidth Modulation Converters. IEEE Trans. Power Electron. 2021, 36, 11984–12007. [Google Scholar] [CrossRef]
- Padmanaban, S.; Samavat, T.; Nasab, M.A.; Nasab, M.A.; Zand, M.; Nikokar, F. Electric Vehicles and IoT in Smart Cities. Artif. Intell.-Based Smart Power Syst. 2023, 273–290. [Google Scholar]
- Khalili, M.; Dashtaki, M.A.; Nasab, M.A.; Hanif, H.R.; Padmanaban, S.; Khan, B. Optimal instantaneous prediction of voltage instability due to transient faults in power networks taking into account the dynamic effect of generators. Cogent. Eng. 2022, 9, 2072568. [Google Scholar] [CrossRef]
- Zaid, S.A.; Albalawi, H.; AbdelMeguid, H.; Alhmiedat, T.A.; Bakeer, A. Performance Improvement of H8 Transformerless Grid-Tied Inverter Using Model Predictive Control Considering a Weak Grid. Processes 2022, 10, 1243. [Google Scholar] [CrossRef]
- Ahmed, A.; Biswas, S.P.; Anower, S.; Islam, R.; Mondal, S.; Muyeen, S.M. A Hybrid PWM Technique to Improve the Performance of Voltage Source Inverters. IEEE Access 2023, 11, 4717–4729. [Google Scholar] [CrossRef]
- Zaid, S.A.; Mohamed, I.S.; Bakeer, A.; Liu, L.; Albalawi, H.; Tawfiq, M.E.; Kassem, A.M. From MPC-Based to End-to-End (E2E) Learning-Based Control Policy for Grid-Tied 3L-NPC Transformerless Inverter. IEEE Access 2022, 10, 57309–57326. [Google Scholar] [CrossRef]
- Albalawi, H.; Zaid, S.A. Performance Improvement of a Grid-Tied Neutral-Point-Clamped 3-φ Transformerless Inverter Using Model Predictive Control. Processes 2019, 7, 856. [Google Scholar] [CrossRef]
- De Bén, A.A.E.; Alvarez-Diazcomas, A.; Rodriguez-Resendiz, J. Transformerless Multilevel Voltage-Source Inverter Topology Comparative Study for PV Systems. Energies 2020, 13, 3261. [Google Scholar] [CrossRef]
- Yuan, W.; Wang, T.; Diallo, D.; Delpha, C. A Fault Diagnosis Strategy Based on Multilevel Classification for a Cascaded Photovoltaic Grid-Connected Inverter. Electronics 2020, 9, 429. [Google Scholar] [CrossRef]
- Rana, R.A.; Patel, S.A.; Muthusamy, A.; Lee, C.W.; Kim, H.-J. Review of Multilevel Voltage Source Inverter Topologies and Analysis of Harmonics Distortions in FC-MLI. Electronics 2019, 8, 1329. [Google Scholar] [CrossRef]
- Anwar, M.A.; Abbas, G.; Khan, I.; Awan, A.B.; Farooq, U.; Khan, S.S. An Impedance Network-Based Three Level Quasi Neutral Point Clamped Inverter with High Voltage Gain. Energies 2020, 13, 1261. [Google Scholar] [CrossRef]
- Heredero-Peris, D.; Chillón-Antón, C.; Sánchez-Sánchez, E.; Montesinos-Miracle, D. Fractional proportional-resonant current controllers for voltage source converters. Electr. Power Syst. Res. 2018, 168, 20–45. [Google Scholar] [CrossRef]
- Carlet, P.G.; Tinazzi, F.; Bolognani, S.; Zigliotto, M. An Effective Model-Free Predictive Current Control for Synchronous Reluctance Motor Drives. IEEE Trans. Ind. Appl. 2019, 55, 3781–3790. [Google Scholar] [CrossRef]
- Mohamed, I.S.; Rovetta, S.; Do, T.D.; Dragicevi´c, T.; Diab, A.A.Z. A neural-network-based model predictive control of three-phase inverter with an output LC filter. IEEE Access 2019, 7, 124737–124749. [Google Scholar] [CrossRef]
- Mohamed-Seghir, M.; Krama, A.; Refaat, S.S.; Trabelsi, M.; Abu-Rub, H. Artificial Intelligence-BasedWeighting Factor Autotuning for Model Predictive Control of Grid-Tied Packed U-Cell Inverter. Energies 2020, 13, 3107. [Google Scholar] [CrossRef]
- Lucia, S.; Navarro, D.; Karg, B.; Sarnago, H.; Lucia, O. Deep Learning-Based Model Predictive Control for Resonant Power Converters. IEEE Trans. Ind. Inform. 2020, 17, 409–420. [Google Scholar] [CrossRef]
- Fliess, M.; Join, C. Model-free control. Int. J. Control 2013, 86, 2228–2252. [Google Scholar] [CrossRef]
- Stenman, A. Model-free predictive control. Proc. 38th IEEE Conf. Decis. Control. 1999, 4, 3712–3717. [Google Scholar]
- Rodriguez, J.; Heydari, R.; Rafiee, Z.; Young, H.A.; Flores-Bahamonde, F.; Shahparasti, M. Model-Free Predictive Current Control of a Voltage Source Inverter. IEEE Access 2020, 8, 211104–211114. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, X.; Liu, J.; Rodriguez, J.; Garcia, C. Model-Free Predictive Current Control of Power Converters Based on Ultra-Local Model. IEEE Int. Conf. Industrial Technol. (ICIT) 2020, 1089–1093. [Google Scholar] [CrossRef]
- Khalilzadeh, M.; Vaez-Zadeh, S.; Rodriguez, J.; Heydari, R. Model-Free Predictive Control of Motor Drives and Power Converters: A Review. IEEE Access 2021, 9, 105733–105747. [Google Scholar] [CrossRef]
- Wang, S.; Li, J.; Hou, Z.; Meng, Q.; Li, M. Composite Model-free Adaptive Predictive Control for Wind Power Generation Based on Full Wind Speed. CSEE J. Power Energy Syst. 2022, 8, 1659–1669. [Google Scholar] [CrossRef]
- Sabzevari, S.; Heydari, R.; Mohiti, M.; Savaghebi, M.; Rodriguez, J. Model-Free Neural Network-Based Predictive Control for Robust Operation of Power Converters. Energies 2021, 14, 2325. [Google Scholar] [CrossRef]
- Yin, Z.; Hu, C.; Luo, K.; Rui, T.; Feng, Z.; Lu, G.; Zhang, P. A Novel Model-Free Predictive Control for T-Type Three-Level Grid-Tied Inverters. Energies 2022, 15, 6557. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, J. An improved model-free predictive current control of pwm rectifiers. In Proceedings of the 20th International Conference on Electrical Machines and Systems (ICEMS), Sydney, Australia, 11–14 August 2017; pp. 1–5. [Google Scholar]
- Fliess, M.; Join, C. Model-free control and intelligent pid controllers: Towards a possible trivialization of nonlinear control? IFAC Proc. Vol. 2009, 42, 1531–1550. [Google Scholar] [CrossRef]
- Birs, I.; Muresan, C.; Nascu, I.; Ionescu, C. A Survey of Recent Advances in Fractional Order Control for Time Delay Systems. IEEE Access 2019, 7, 30951–30965. [Google Scholar] [CrossRef]
- Traver, J.E.; Nuevo-Gallardo, C.; Tejado, I.; Fernández-Portales, J.; Ortega-Morán, J.F.; Pagador, J.B.; Vinagre, B.M. Cardiovascular Circulatory System and Left Carotid Model: A Fractional Approach to Disease Modeling. Fractal Fract. 2022, 6, 64. [Google Scholar] [CrossRef]
- Shah, P.; Agashe, S. Review of fractional PID controller. Mechatronics 2016, 38, 29–41. [Google Scholar] [CrossRef]
- Nazir, R. Taylor series expansion based repetitive controllers for power converters, subject to fractional delays. Control Eng. Pract. 2017, 64, 140–147. [Google Scholar] [CrossRef]
- Pullaguram, D.; Mishra, S.; Senroy, N.; Mukherjee, M. Design and Tuning of Robust Fractional Order Controller for Autonomous Microgrid VSC System. IEEE Trans. Ind. Appl. 2017, 54, 91–101. [Google Scholar] [CrossRef]
- Bakeer, A.; Alhasheem, M.; Peyghami, S. Efficient Fixed-Switching Modulated Finite Control Set-Model Predictive Control Based on Artificial Neural Networks. Appl. Sci. 2022, 12, 3134. [Google Scholar] [CrossRef]
- Bakeer, A.; Magdy, G.; Chub, A.; Jurado, F.; Rihan, M. Optimal Ultra-Local Model Control Integrated with Load Frequency Control of Renewable Energy Sources Based Microgrids. Energies 2022, 15, 9177. [Google Scholar] [CrossRef]
- Zaid, S.A.; Bakeer, A.; Magdy, G.; Albalawi, H.; Kassem, A.M.; El-Shimy, M.E.; AbdelMeguid, H.; Manqarah, B. A New Intelligent Fractional-Order Load Frequency Control for Interconnected Modern Power Systems with Virtual Inertia Control. Fractal Fract. 2023, 7, 62. [Google Scholar] [CrossRef]
- Morsali, J.; Zare, K.; Hagh, M.T. Applying fractional order PID to design TCSC-based damping controller in coordination with automatic generation control of interconnected multi-source power system. Eng. Sci. Technol. Int. J. 2017, 20, 1–17. [Google Scholar] [CrossRef]
- Fawzy, A.; Bakeer, A.; Magdy, G.; Atawi, I.E.; Roshdy, M. Adaptive Virtual Inertia-Damping System Based on Model Predictive Control for Low-Inertia Microgrids. IEEE Access 2021, 9, 109718–109731. [Google Scholar] [CrossRef]
- Peng, Y.; Tang, S.; Huang, J.; Tang, C.; Wang, L.; Liu, Y. Fractal Analysis on Pore Structure and Modeling of Hydration of Magnesium Phosphate Cement Paste. Fractal Fract. 2022, 6, 337. [Google Scholar] [CrossRef]
- Tartaglione, V.; Farges, C.; Sabatier, J. Fractional Behaviours Modelling with Volterra Equations: Application to a Lithium-Ion Cell and Comparison with a Fractional Model. Fractal Fract. 2022, 6, 137. [Google Scholar] [CrossRef]
- ILangella, R.; Testa, A. AliiIEEE Recommended Practice and Requirements for Harmonic Control in Electric Power Systems; IEEE Std 519-2014 (Revision of IEEE Std 519-1992); IEEE: Piscataway, NJ, USA, 2014; pp. 1–29. [Google Scholar] [CrossRef]

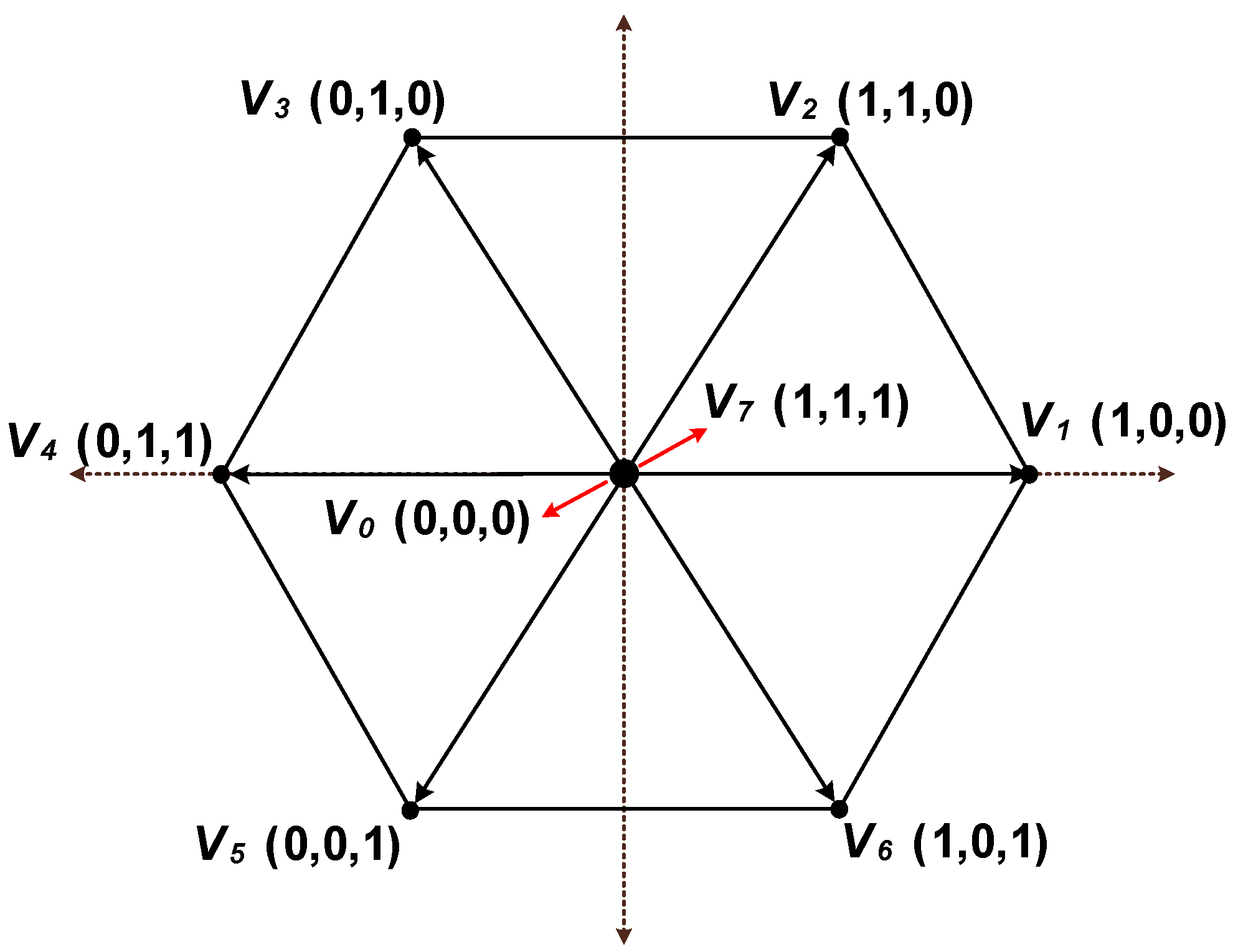








| Output Voltage Vx,αβ | ||||||||
|---|---|---|---|---|---|---|---|---|
| 0 | V0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | V1 | 1 | 0 | 0 | 0 | 1 | 1 | |
| 2 | V2 | 1 | 1 | 0 | 0 | 0 | 1 | |
| 3 | V3 | 0 | 1 | 0 | 1 | 0 | 1 | |
| 4 | V4 | 0 | 1 | 1 | 1 | 0 | 0 | |
| 5 | V5 | 0 | 0 | 1 | 1 | 1 | 0 | |
| 6 | V6 | 1 | 0 | 1 | 0 | 1 | 0 | |
| 7 | V7 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| Parameter | Value |
|---|---|
| Kp | 0.360 |
| Ki | 0.034 |
| λ | 0.605 |
| Parameter | Symbol | Value |
|---|---|---|
| Input voltage | Vdc | 500 V |
| Filter inductance | Lf | 1.5 mH |
| Filter capacitance | Cf | 150 µF |
| Nominal RMS output voltage (L-L) | Vo,ref | 200 V |
| Sampling time | Ts | 20 µs |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Albalawi, H.; Bakeer, A.; Zaid, S.A.; Aggoune, E.-H.; Ayaz, M.; Bensenouci, A.; Eisa, A. Fractional-Order Model-Free Predictive Control for Voltage Source Inverters. Fractal Fract. 2023, 7, 433. https://doi.org/10.3390/fractalfract7060433
Albalawi H, Bakeer A, Zaid SA, Aggoune E-H, Ayaz M, Bensenouci A, Eisa A. Fractional-Order Model-Free Predictive Control for Voltage Source Inverters. Fractal and Fractional. 2023; 7(6):433. https://doi.org/10.3390/fractalfract7060433
Chicago/Turabian StyleAlbalawi, Hani, Abualkasim Bakeer, Sherif A. Zaid, El-Hadi Aggoune, Muhammad Ayaz, Ahmed Bensenouci, and Amir Eisa. 2023. "Fractional-Order Model-Free Predictive Control for Voltage Source Inverters" Fractal and Fractional 7, no. 6: 433. https://doi.org/10.3390/fractalfract7060433
APA StyleAlbalawi, H., Bakeer, A., Zaid, S. A., Aggoune, E.-H., Ayaz, M., Bensenouci, A., & Eisa, A. (2023). Fractional-Order Model-Free Predictive Control for Voltage Source Inverters. Fractal and Fractional, 7(6), 433. https://doi.org/10.3390/fractalfract7060433







