Dynamical Behaviour, Control, and Boundedness of a Fractional-Order Chaotic System
Abstract
:1. Introduction
2. Fractional-Order Chaotic System
2.1. Stability Analysis of Equilibrium Points
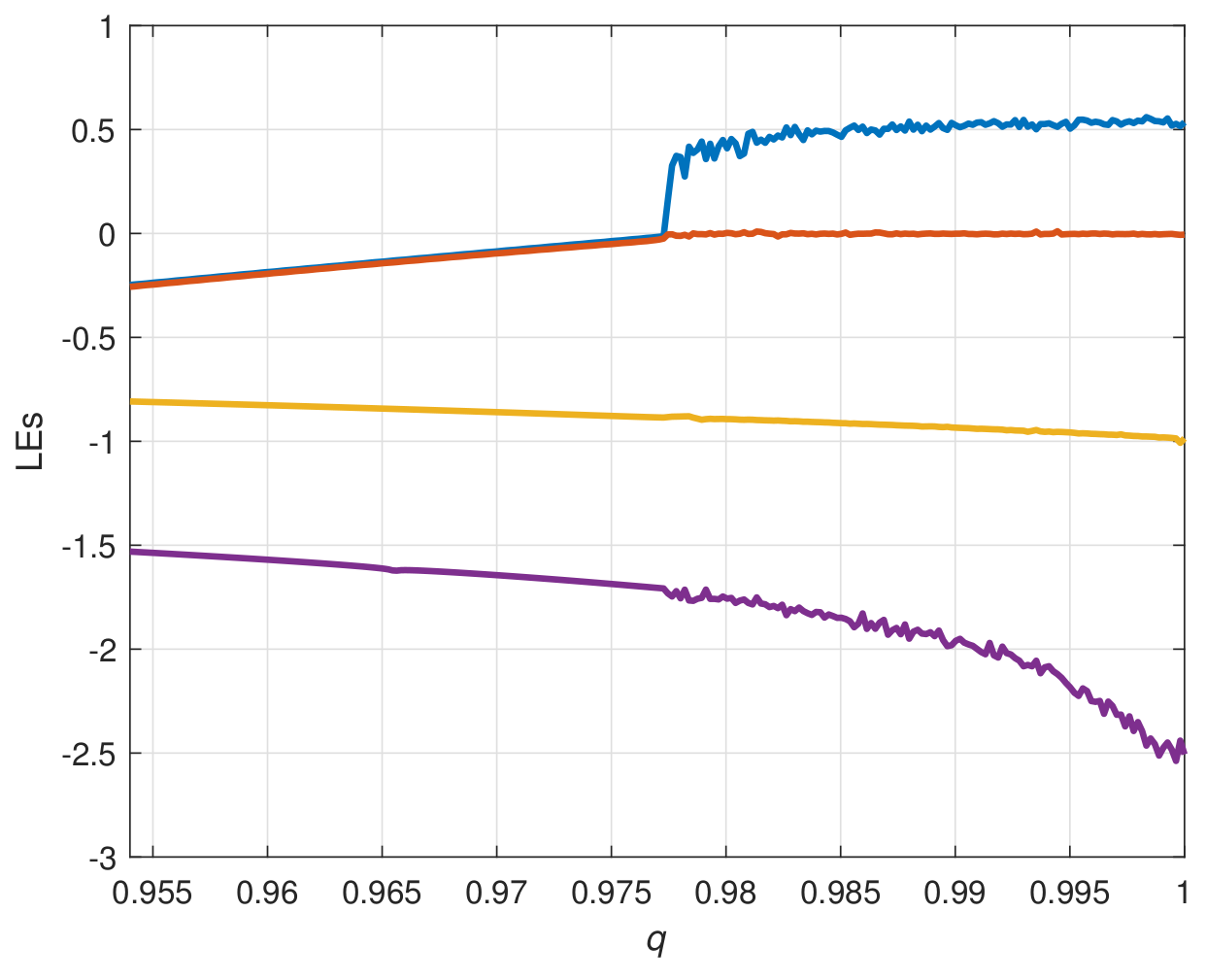
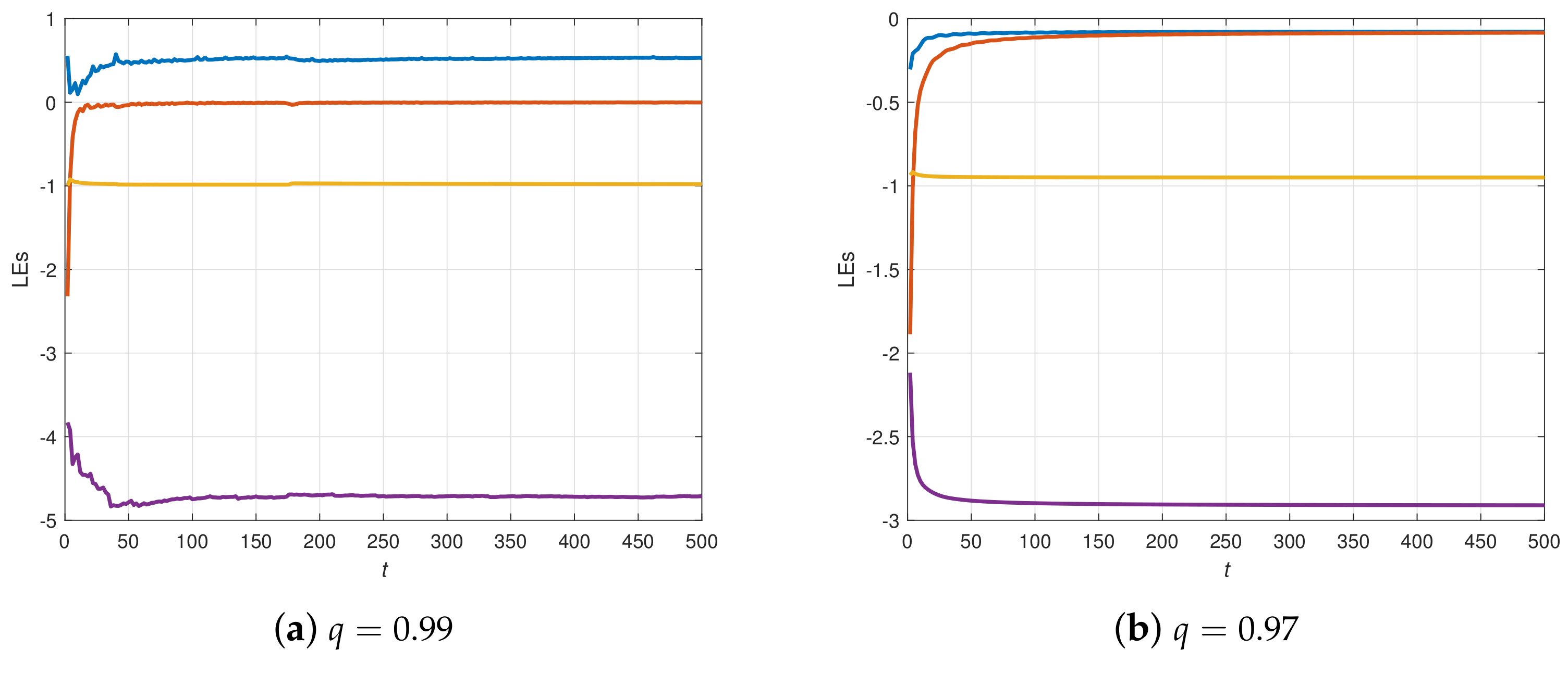
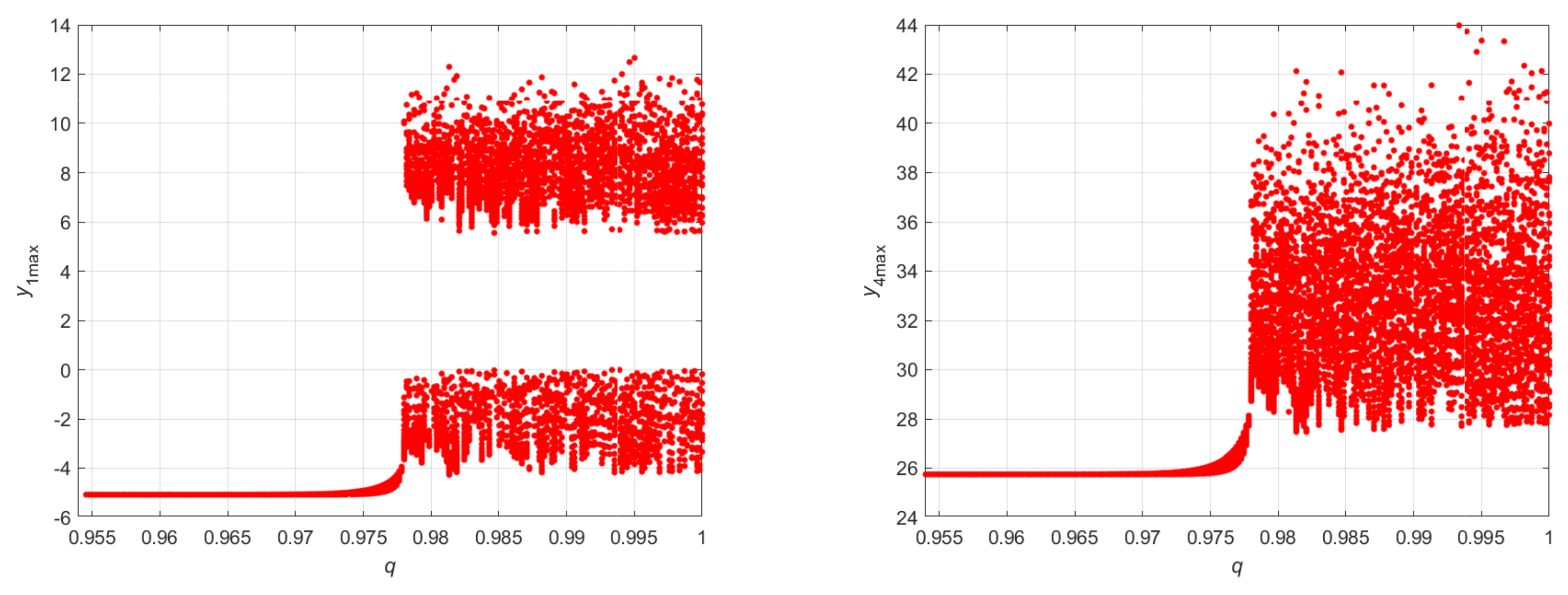
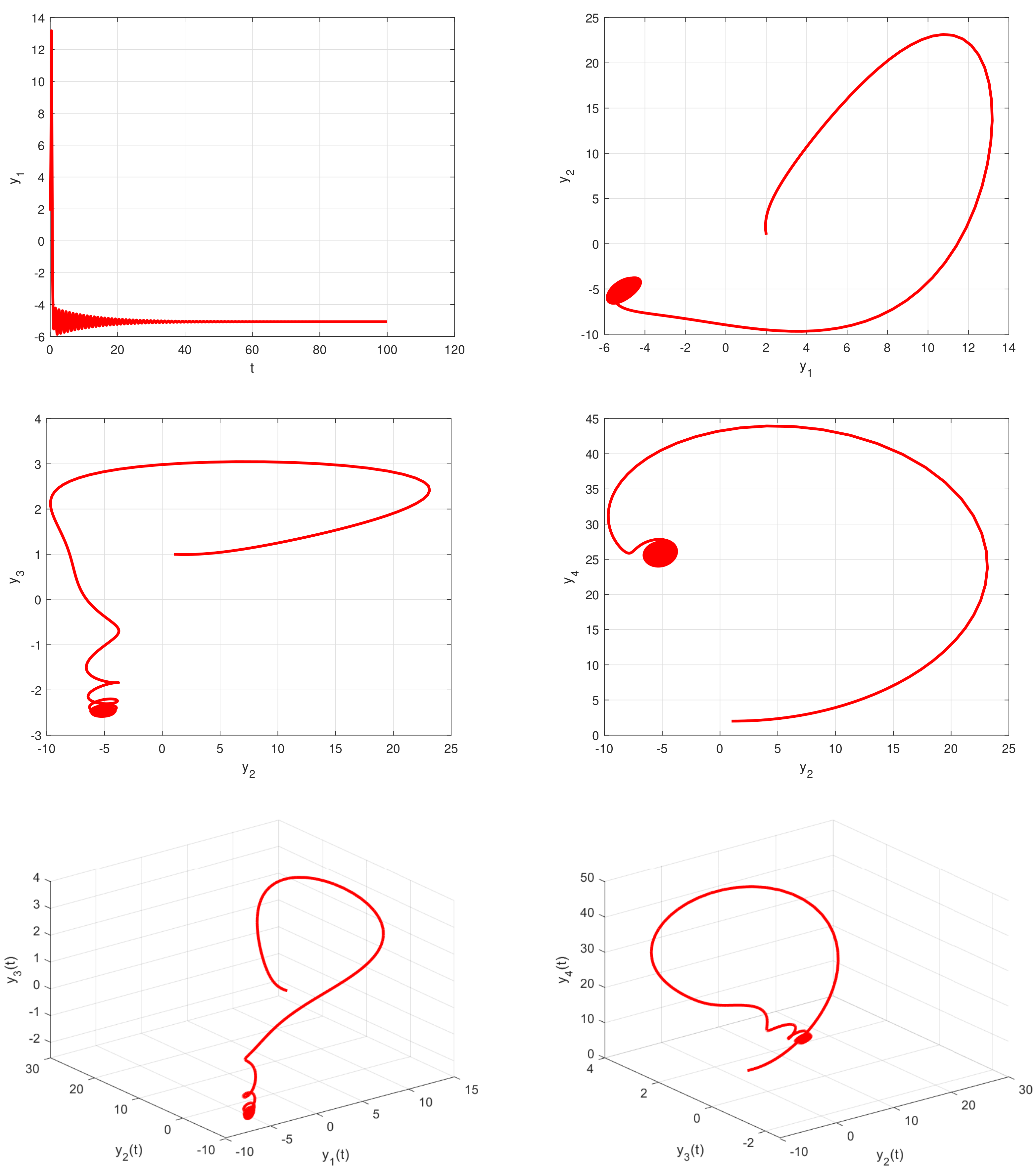
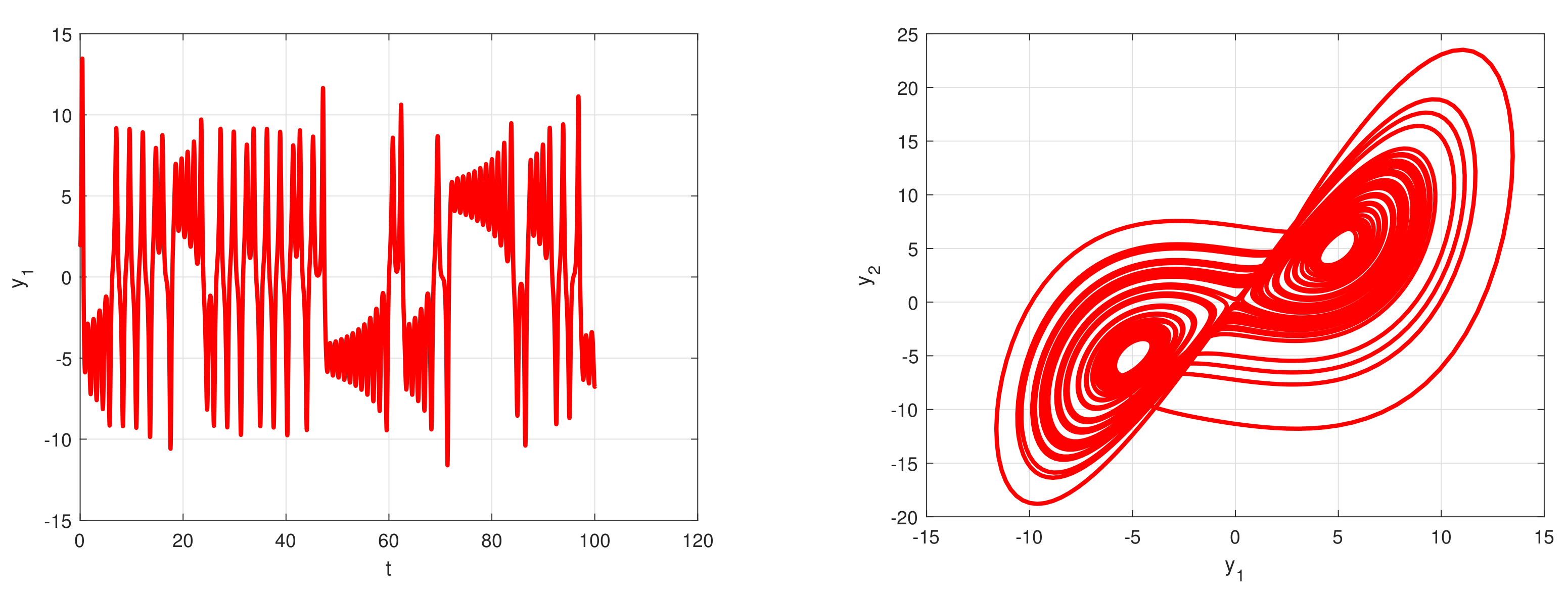
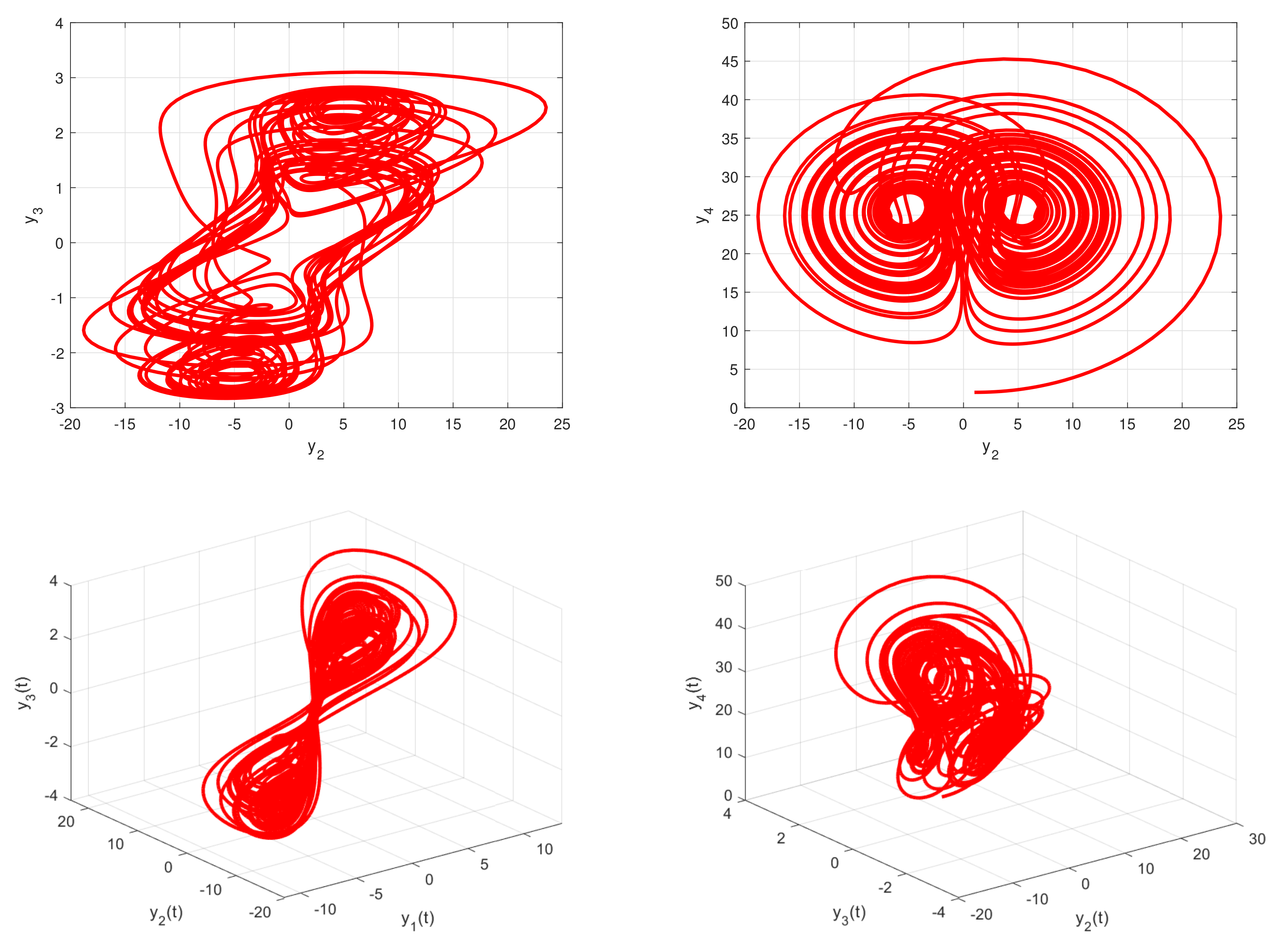
2.2. Dynamical Behaviors
3. Chaos Control
4. Global Mittag–Leffler Attractive Sets
4.1. Main Results
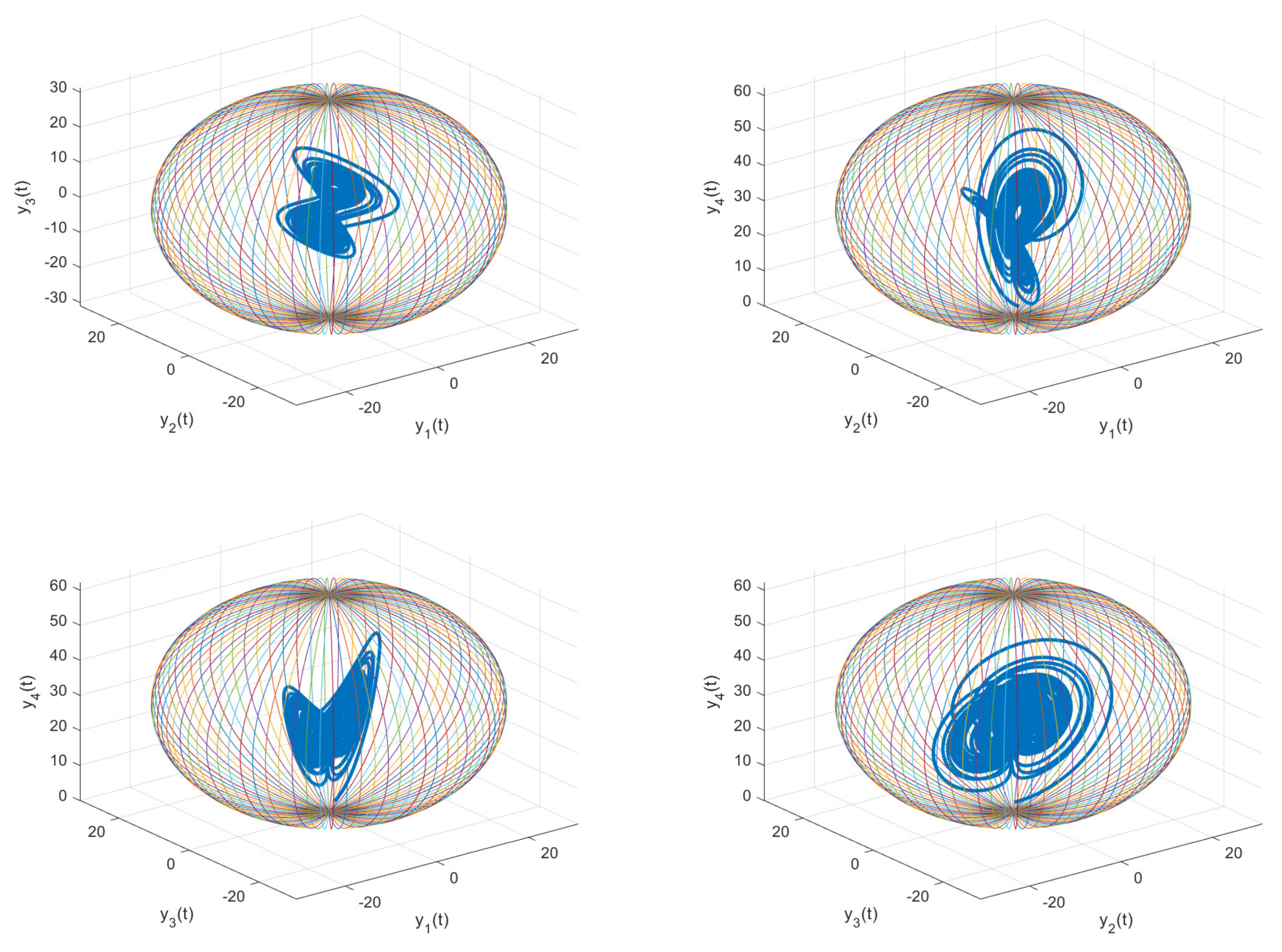
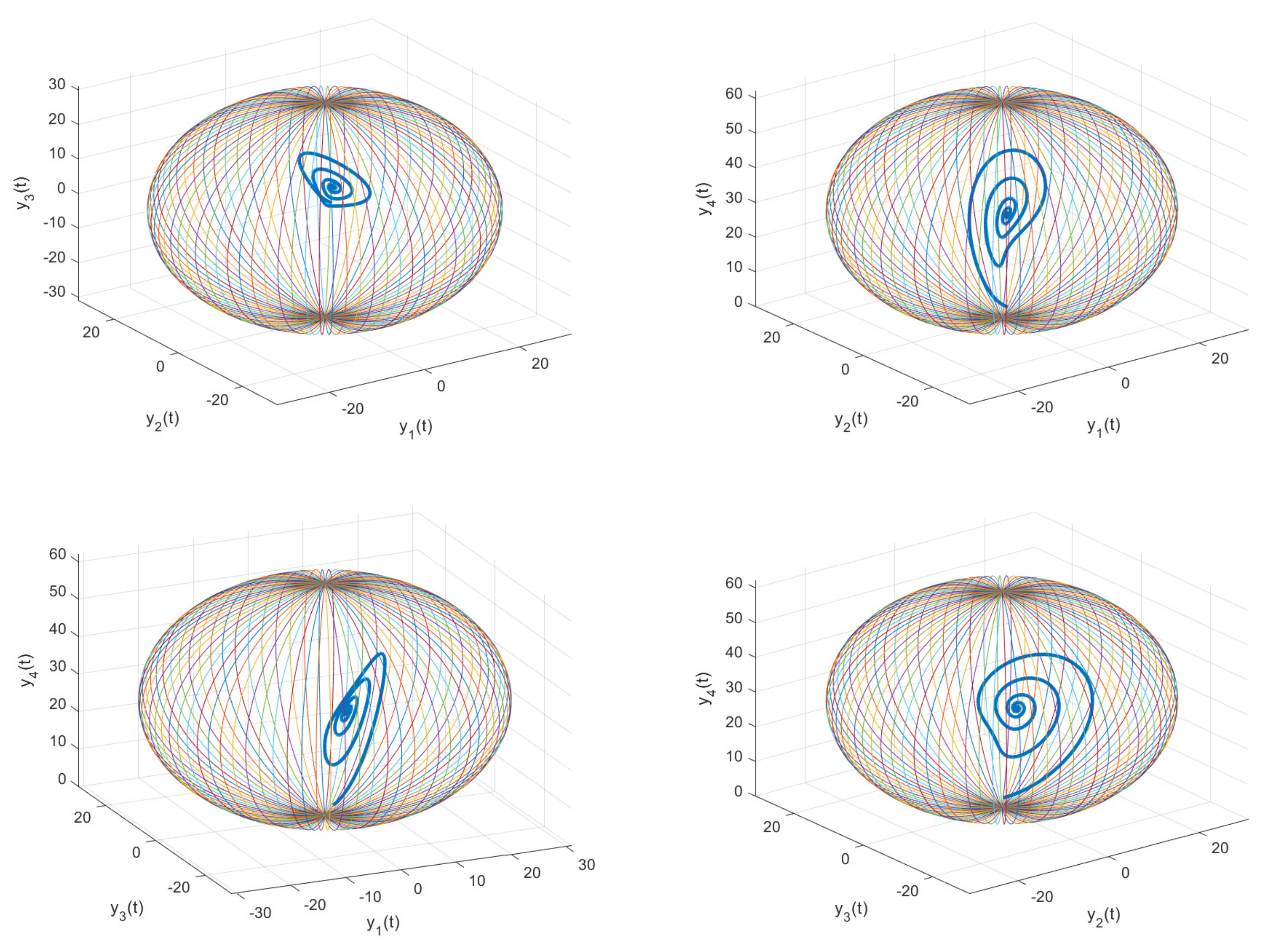
4.2. MLAS and MLPIS for the Fractional-Order System (2)
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific: Singapore, 2000. [Google Scholar]
- Tavazoei, M.S.; Haeri, M. Synchronization of chaotic fractional-order systems via active sliding mode controller. Physica A 2008, 387, 57–70. [Google Scholar] [CrossRef]
- He, Y.; Peng, J.; Zheng, S. Fractional-order financial system and fixed-time synchronization. Fractal Fract. 2022, 6, 507. [Google Scholar] [CrossRef]
- Ahmed, E.; El-Sayed, A.M.A.; El-Saka, H.A.A. On some Routh-Hurwitz conditions for fractional order differential equations and their applications in Lorenz, Rössler, Chua and Chen systems. Phys. Lett. A 2006, 358, 1–4. [Google Scholar] [CrossRef]
- He, Y.; Zheng, S.; Yuan, L. Dynamics of fractional-order digital manufacturing supply chain system and its control and synchronization. Fractal Fract. 2021, 5, 128. [Google Scholar] [CrossRef]
- Zhou, P.; Ma, J.; Tang, J. Clarify the physical process for fractional dynamical systems. Nonlinear Dyn. 2020, 100, 2353–2364. [Google Scholar] [CrossRef]
- Aghababa, M.P. Comments on “H∞ synchronization of uncertain fractional order chaotic systems: Adaptive fuzzy approach” [ISA Trans 50, 548–556 (2011)]. ISA Trans. 2012, 51, 11–12. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, B.; Chen, Y.; Wang, Y. Sliding mode control for a class of nonlinear fractional order systems with a fractional fixed-time reaching law. Fractal Fract. 2022, 6, 678. [Google Scholar] [CrossRef]
- Mahmoud, G.M.; Arafa, A.A.; Abed-Elhameed, T.M.; Mahmoud, E.E. Chaos control of integer and fractional orders of chaotic Burke–Shaw system using time delayed feedback control. Chaos Solitons Fractals 2017, 104, 680–692. [Google Scholar] [CrossRef]
- Pham, V.T.; Kingni, S.T.; Volos, C.; Jafari, S.; Kapitaniak, T. A simple three-dimensional fractional-order chaotic system without equilibrium: Dynamics, circuitry implementation, chaos control and synchronization. Int. J. Electron. Commun. 2017, 78, 220–227. [Google Scholar] [CrossRef]
- Wang, S.; He, S.; Yousefpour, A.; Jahanshahi, H.; Repnik, R.; Perc, M. Chaos and complexity in a fractional-order financial system with time delays. Chaos Solitons Fractals 2020, 131, 109521. [Google Scholar] [CrossRef]
- Sayed, W.S.; Roshdy, M.; Said, L.A.; Herencsar, N.; Radwan, A.G. CORDIC-based FPGA realization of a spatially rotating translational fractional-order multi-scroll grid chaotic system. Fractal Fract. 2022, 6, 432. [Google Scholar] [CrossRef]
- Qi, F.; Qu, J.; Chai, Y.; Chen, L.; Lopes, A.M. Synchronization of incommensurate frractional-order chaotic systems based on linear feedback control. Fractal Fract. 2022, 6, 221. [Google Scholar] [CrossRef]
- Gao, W.; Yan, L.; Saeedi, M.H.; Saberi Nik, H. Ultimate bound estimation set and chaos synchronization for a financial risk system. Math. Comput. Simul. 2018, 154, 19–33. [Google Scholar] [CrossRef]
- Lin, Z.; Wang, H. Modeling and application of fractional-order economic growth model with time delay. Fractal Fract. 2021, 5, 74. [Google Scholar] [CrossRef]
- Wen, C.; Yang, J. Complexity evolution of chaotic financial systems based on fractional calculus. Chaos Solitons Fractals 2019, 128, 242–251. [Google Scholar] [CrossRef]
- Kuznetsov, N.; Leonov, G. Hidden attractors in dynamical systems: Systems with no equilibria, multistability and coexisting attractors. IFAC Proc. 2014, 47, 5445–5454. [Google Scholar] [CrossRef] [Green Version]
- Leonov, G.; Kuznetsov, N. Hidden attractors in dynamical systems. From hidden oscillations in Hilbert-Kolmogorov, Aizerman, and Kalman problems to hidden chaotic attractor in Chua circuits. Int. J. Bifurc. Chaos 2013, 23, 1330002. [Google Scholar] [CrossRef] [Green Version]
- Ouannas, A.; Khennaoui, A.A.; Momani, S.; Pham, V.T.; El-Khazali, R. Hidden attractors in a new fractional-order discrete system: Chaos, complexity, entropy, and control. Chin. Phys. B 2022, 29, 050504. [Google Scholar] [CrossRef]
- Leonov, G.; Bunin, A.; Koksch, N. Attractor localization of the Lorenz system. Z. Angew. Math. Mech. 1987, 67, 649–656. [Google Scholar] [CrossRef]
- Liao, X.; Fu, Y.; Xie, S. On the new results of global attractive set and positive invariant set of the Lorenz chaotic system and the applications to chaos control and synchronization. Sci. China Ser. F-Inf. Sci. 2005, 48, 304–321. [Google Scholar] [CrossRef]
- Li, D.; Lu, J.A.; Wu, X.; Chen, G. Estimating the bounds for the Lorenz family of chaotic systems. Chaos Solitons Fractals 2005, 23, 529–534. [Google Scholar] [CrossRef]
- Zhao, X.; Jiang, F.; Hu, J. Globally exponentially attractive sets and positive invariant sets of three-dimensional autonomous systems with only cross-product nonlinearities. Int. J. Bifurc. Chaos 2013, 23, 1350007. [Google Scholar] [CrossRef]
- Kumar, D.; Kumar, S. Ultimate numerical bound estimation of chaotic dynamical finance model. In Modern Mathematical Methods and High Performance Computing in Science and Technology; Springer: Singapore, 2016; pp. 71–81. [Google Scholar]
- Chien, F.; Chowdhury, A.R.; Saberi-Nik, H. Competitive modes and estimation of ultimate bound sets for a chaotic dynamical financial system. Nonlinear Dyn. 2021, 106, 3601–3614. [Google Scholar] [CrossRef]
- Wang, H.; Dong, G. New dynamics coined in a 4-D quadratic autonomous hyper-chaotic system. Appl. Math. Comput. 2019, 346, 272–286. [Google Scholar] [CrossRef]
- Chien, F.; Inc, M.; Yosefzade, H.R.; Saberi Nik, H. Predicting the chaos and solution bounds in a complex dynamical system. Chaos Solitons Fractals 2021, 153, 111474. [Google Scholar] [CrossRef]
- Zhang, F.; Liao, X.; Chen, Y.A. On the dynamics of the chaotic general Lorenz system. Int. J. Bifurc. Chaos. 2017, 27, 1750075. [Google Scholar] [CrossRef]
- Wang, P.; Zhang, Y.; Tan, S.; Wan, L. Explicit ultimate bound sets of a new hyper-chaotic system and its application in estimating the Hausdorff dimension. Nonlinear Dyn. 2013, 74, 133–142. [Google Scholar] [CrossRef]
- Saberi Nik, H.; Effati, S.; Saberi-Nadjafi, J. New ultimate bound sets and exponential finite-time synchronization for the complex Lorenz system. J. Complex. 2015, 31, 715–730. [Google Scholar] [CrossRef]
- Natiq, H.; Said, M.R.M.; Al-Saidi, N.M.G.; Kilicman, A. Dynamics and complexity of a new 4D chaotic Laser system. Entropy 2019, 21, 34. [Google Scholar] [CrossRef] [Green Version]
- Jian, J.; Wu, K.; Wang, B. Global Mittag–Leffler boundedness and synchronization for fractional-order chaotic systems. Phys. A Stat. Mech. Appl. 2020, 540, 123166. [Google Scholar] [CrossRef]
- Peng, Q.; Jian, J. Estimating the ultimate bounds and synchronization of fractional-order plasma chaotic systems. Chaos Solitons Fractals 2021, 150, 111072. [Google Scholar] [CrossRef]
- Huang, M.; Lu, S.; Shateyi, S.; Saberi-Nik, H. Ultimate boundedness and finite time stability for a high dimensional fractional-order Lorenz model. Fractal Fract. 2022, 6, 630. [Google Scholar] [CrossRef]
- Danca, M.; Kuznetsov, N. Matlab code for Lyapunov exponents of fractional-order systems. Int. J. Bifurc. Chaos 2018, 28, 1850067. [Google Scholar] [CrossRef] [Green Version]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, L.; Muhsen, S.; Shateyi, S.; Saberi-Nik, H. Dynamical Behaviour, Control, and Boundedness of a Fractional-Order Chaotic System. Fractal Fract. 2023, 7, 492. https://doi.org/10.3390/fractalfract7070492
Ren L, Muhsen S, Shateyi S, Saberi-Nik H. Dynamical Behaviour, Control, and Boundedness of a Fractional-Order Chaotic System. Fractal and Fractional. 2023; 7(7):492. https://doi.org/10.3390/fractalfract7070492
Chicago/Turabian StyleRen, Lei, Sami Muhsen, Stanford Shateyi, and Hassan Saberi-Nik. 2023. "Dynamical Behaviour, Control, and Boundedness of a Fractional-Order Chaotic System" Fractal and Fractional 7, no. 7: 492. https://doi.org/10.3390/fractalfract7070492
APA StyleRen, L., Muhsen, S., Shateyi, S., & Saberi-Nik, H. (2023). Dynamical Behaviour, Control, and Boundedness of a Fractional-Order Chaotic System. Fractal and Fractional, 7(7), 492. https://doi.org/10.3390/fractalfract7070492









