Exploration of Hermite–Hadamard-Type Integral Inequalities for Twice Differentiable h-Convex Functions
Abstract
:1. Introduction and Preliminaries
2. Main Results
3. Some Applications to the Main Results in Terms of Means
- (i)
- The arithmetic mean:
- (ii)
- The logarithmic mean:
4. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Loverro, A. Fractional Calculus: History, Definitions and Applications for the Engineer; Rapport Technique; Univeristy of Notre Dame, Department of Aerospace and Mechanical Engineering: Notre Dame, IN, USA, 2004; pp. 1–28. [Google Scholar]
- Samraiz, M.; Umer, M.; Abduljawad, T.; Naheed, S.; Rahman, G.; Shah, K. On Riemann-type weighted fractional operator and solution to cauchy problems. Comput. Model. Eng. Sci. 2023, 136, 901–919. [Google Scholar] [CrossRef]
- Singh, J.; Anastassiou, G.A.; Baleanu, D.; Kumar, D. On weighted fractional operators with applications to mathematical models arising in physics. In Advances in Mathematical Modelling, Applied Analysis and Computation; Lecture Notes in Networks and Systems; Springer: Cham, Switzerland, 2023; Volume 666. [Google Scholar]
- Ray, S.S.; Atangana, A.; Noutchie, S.C.; Kurulay, M.; Bildik, N.; Kilicman, A. Fractional calculus and its applications in applied mathematics and other sciences. Math. Probl. Eng. 2014, 2014, 849395. [Google Scholar] [CrossRef]
- Magin, R. Fractional calculus in bioengineering, Part 1. Crit. Rev. Biomed. Eng. 2004, 32, 104. [Google Scholar]
- Beckenbach, E.F. Convex functions. Bull. Am. Math. Soc. 1948, 54, 439–460. [Google Scholar] [CrossRef] [Green Version]
- Avriel, M. r-Convex functions. Math. Program. 1972, 2, 309–323. [Google Scholar] [CrossRef]
- Niculescu, C.P.; Persson, L.E. Convex Functions and Their Applications: A Contemporary Approach; CMC Books in Mathematics: New York, NY, USA, 2004. [Google Scholar]
- Ramli, A.A.; Watada, J.; Pedrycz, W. A combination of genetic algorithm-based fuzzy C-means with a convex hull-based regression for real-time fuzzy switching regression analysis: Application to industrial intelligent data analysis. IEEJ Trans. Electr. Electron. Eng. 2014, 9, 71–82. [Google Scholar] [CrossRef] [Green Version]
- Xu, J.; Noo, F. Convex optimization algorithms in medical image reconstruction in the age of AI. Phys. Med. Biol. 2022, 67, 07TR01. [Google Scholar] [CrossRef]
- Rockafellar, R.T. Convex Analysis; Princeton University Press: Princeton, NJ, USA, 1970. [Google Scholar]
- Yang, D.H. About inequality of geometrically convex function, Hebei university learned journal. Natur. Sci. Ed. 2002, 22, 325–328. [Google Scholar]
- Hudzik, H.; Maligranda, L. Some remarks on s-convex functions. Aequationes Math. 1994, 48, 100–111. [Google Scholar] [CrossRef]
- Bertsimas, D.; Brown, D.B.; Caramanis, C. Theory and applications of robust optimization. SIAM Rev. 2011, 53, 464–501. [Google Scholar] [CrossRef]
- Artacho, F.J.A.; Borwein, J.M.; Marquez, V.M.; Yao, L. Applications of convex analysis within mathematics. Math. Program. 2014, 148, 49–88. [Google Scholar] [CrossRef]
- Bullen, P.S. Handbook of Means and Their Inequalities; Springer Science and Business Media: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Dragomir, S.S. Operator Inequalities of Ostrowski and Trapezoidal Type; Springer: New York, NY, USA, 2011. [Google Scholar]
- Mitrinovic, D.S.; Pecaric, J.E.; Fink, A.M. Classical and New Inequalities in Analysis; Springer Science and Business Media: Berlin/Heidelberg, Germany, 1993. [Google Scholar]
- Gavrea, B.; Gavrea, I. On some Ostrowski type inequalities. Gen. Math. 2010, 18, 33–44. [Google Scholar]
- Gunawan, H. Fractional integrals and generalized Olsen inequalities. Kyungpook Math. J. 2009, 49, 31–39. [Google Scholar] [CrossRef] [Green Version]
- Sawano, Y.; Wadade, H. On the Gagliardo-Nirenberg type inequality in the critical Sobolev-Morrey space. J. Fourier Anal. Appl. 2013, 19, 20–47. [Google Scholar] [CrossRef]
- Ciatti, P.; Cowling, M.G.; Ricci, F. Hardy and uncertainty inequalities on stratified Lie groups. Adv. Math. 2015, 277, 365–387. [Google Scholar] [CrossRef]
- Hadamard, J. Etude sur les proprietes des fonctions entieres et en particulier dune fonction consideree par Riemann. J. Math. Pures Appl. 1893, 9, 171–216. [Google Scholar]
- Korus, P. Some Hermite-Hadamard type inequalities for functions of generalized convex derivative. Acta Math. Hungar. 2021, 165, 463–473. [Google Scholar] [CrossRef]
- Vivas-Cortez, M.; Ali, M.A.; Kashuri, A.; Budak, H. Generalizations of fractional Hermite-Hadamard-Mercer like inequalities for convex functions. AIMS Math. 2021, 6, 9397–9421. [Google Scholar] [CrossRef]
- Baleanu, D.; Samraiz, M.; Perveen, Z.; Iqbal, S.; Nisar, K.S.; Rahman, G. Hermite-Hadamard-Fejer type inequalities via fractional integral of a function concerning another function. AIMS Math. 2021, 6, 4280–4295. [Google Scholar] [CrossRef]
- Farid, G.; Yussouf, M.; Nonlaopon, K. Fejer-Hadamard type inequalities for (α,h-m)-p-convex functions via extended generalized fractional integrals. Fractal Fract. 2021, 5, 253. [Google Scholar] [CrossRef]
- Kang, S.M.; Farid, G.; Nazeer, W.; Tariq, B. Hadamard and Fejer-Hadamard inequalities for extended generalized fractional integrals involving special functions. J. Inequal. Appl. 2018, 2018, 119. [Google Scholar] [CrossRef] [PubMed]
- Vivas-Cortez, M.; Hernández, H.; Jorge, E. On some new generalized Hermite Hadamard Fejér-inequalities for product of two operator convex functions. Appl. Math. Inf. Sci. 2017, 11, 983–992. [Google Scholar] [CrossRef]
- Vivas-Cortez, M.; Ali, M.A.; Budak, H.; Kalsoom, H.; Agarwal, P. Some new Hermite–Hadamard and related inequalities for convex functions via (p, q)-integral. Entropy 2021, 23, 828. [Google Scholar] [CrossRef] [PubMed]
- Kalsoom, H.; Latif, M.A.; Khan, Z.A.; Vivas-Cortez, M. Some New Hermite-Hadamard-Fejér fractional type inequalities for h-convex and harmonically h-Convex interval-valued Functions. Mathematics 2021, 10, 74. [Google Scholar] [CrossRef]
- Kwun, Y.C.; Farid, G.; Nazeer, W.; Ullah, S.; Kang, S.M. Generalized riemann-liouville k-fractional integrals associated with Ostrowski type inequalities and error bounds of hadamard inequalities. IEEE Access 2018, 6, 64946–64953. [Google Scholar] [CrossRef]
- Budak, H.; Hezenci, F.; Kara, H. On generalized Ostrowski, Simpson and Trapezoidal type inequalities for co-ordinated convex functions via generalized fractional integrals. Adv. Differ. Equ. 2021, 2021, 312. [Google Scholar] [CrossRef]
- Khan, M.A.; Chu, Y.; Khan, T.U.; Khan, J. Some new inequalities of Hermite-Hadamard type for s-convex functions with applications. Open Math. 2017, 15, 1414–1430. [Google Scholar] [CrossRef]
- Rashid, S.; Kalsoom, H.; Hammouch, Z.; Ashraf, R.; Baleanu, D.; Chu, Y.M. New multi-parametrized estimates having pth-order differentiability in fractional calculus for predominating h-convex functions in Hilbert space. Symmetry 2020, 12, 222. [Google Scholar] [CrossRef] [Green Version]
- Mitrinović, D.S. Analytic Inequalities; Springer: Berlin, Germany, 1970. [Google Scholar]
- Davis, P.J. Leonhard euler’s integral: A historical profile of the gamma function: In memoriam: Milton abramowitz. Am. Math. Mon. 1959, 66, 849–869. [Google Scholar] [CrossRef]
- Mubeen, S.; Habibullah, G.M. k-Fractional integrals and application. Int. J. Contemp. Math. Sci. 2012, 7, 89–94. [Google Scholar]
- Chaudhry, M.A.; Qadir, A.; Rafique, M.; Zubair, S.M. Extension of Euler’s beta function. J. Comput. Appl. Math. 1997, 78, 19–32. [Google Scholar] [CrossRef] [Green Version]
- DiDonato, A.R.; Jarnagin, M.P. The efficient calculation of the incomplete beta-function ratio for half-integer values of the parameters a, b. Math. Comp. 1967, 21, 652–662. [Google Scholar] [CrossRef]
- Varosanec, S. On h-convexity. J. Math. Anal. Appl. 2007, 326, 303–311. [Google Scholar] [CrossRef] [Green Version]
- Mubeen, S.H.; Iqbal, S.; Iqbal, Z. On Ostrowski type inequalities for generalized k-fractional integrals. J. Inequal. Spec. Funct. 2017, 8, 107–118. [Google Scholar]
- Deng, J.; Wang, J. Fractional Hermite-Hadamard inequalities for (a,m)-logarithmically convex functions. J. Inequal. Appl. 2013, 2013, 364. [Google Scholar] [CrossRef] [Green Version]
- Hussain, R.; Ali, A.; Gulshan, G.; Latif, A.; Rauf, K. Hermite-Hadamard type inequalities for k-Riemann-Liouville fractional integrals via two kinds of convexity. Austral. J. Math. Anal. Appl. 2016, 13, 1–12. [Google Scholar]
- Liao, Y.; Deng, J.; Wang, J. Riemann-Liouville fractional Hermite-Hadamard inequalities. Part II: For twice differentiable geometric-arithmetically s-convex functions. J. Inequal. Appl. 2013, 2013, 517. [Google Scholar] [CrossRef] [Green Version]

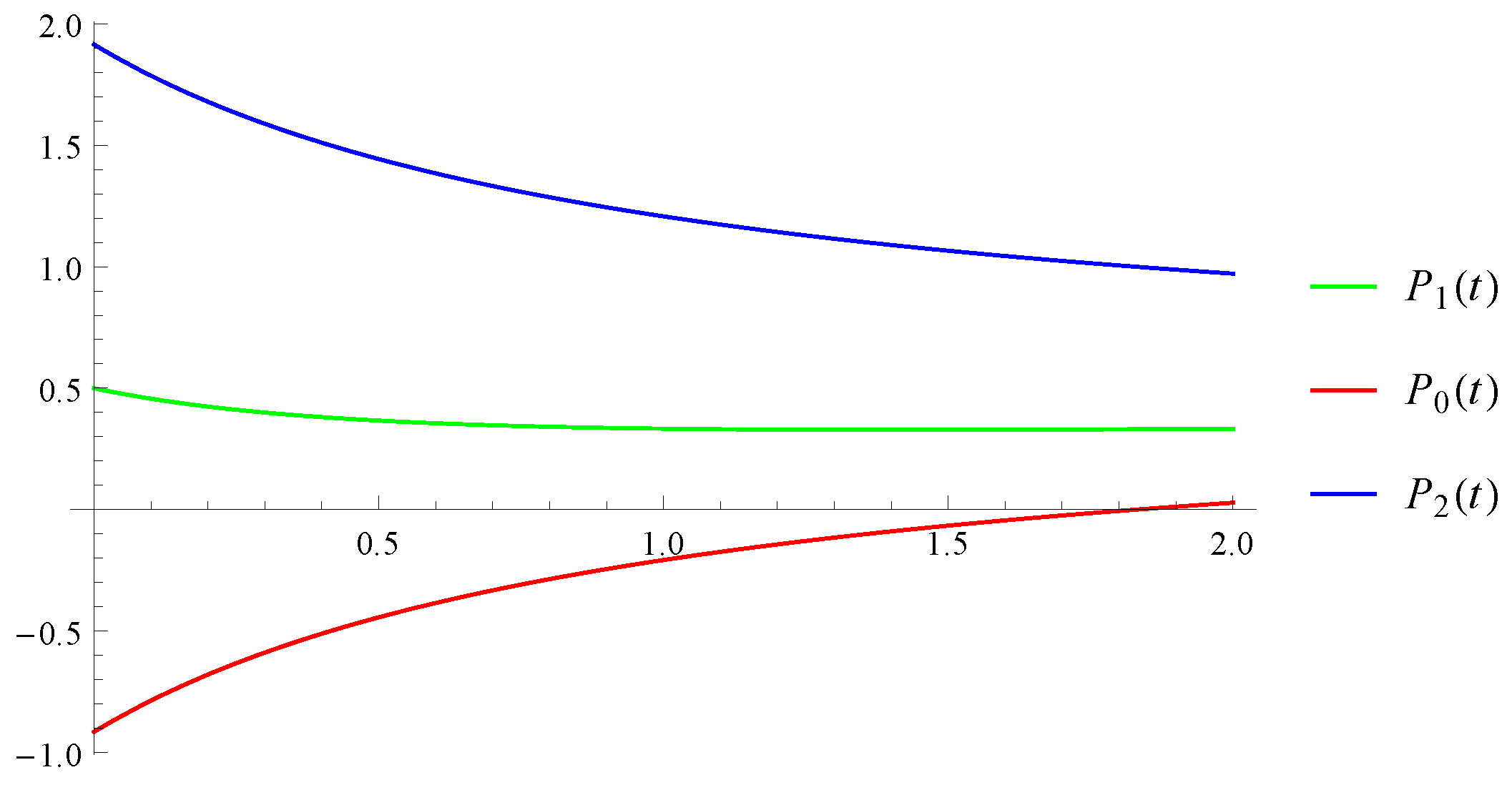
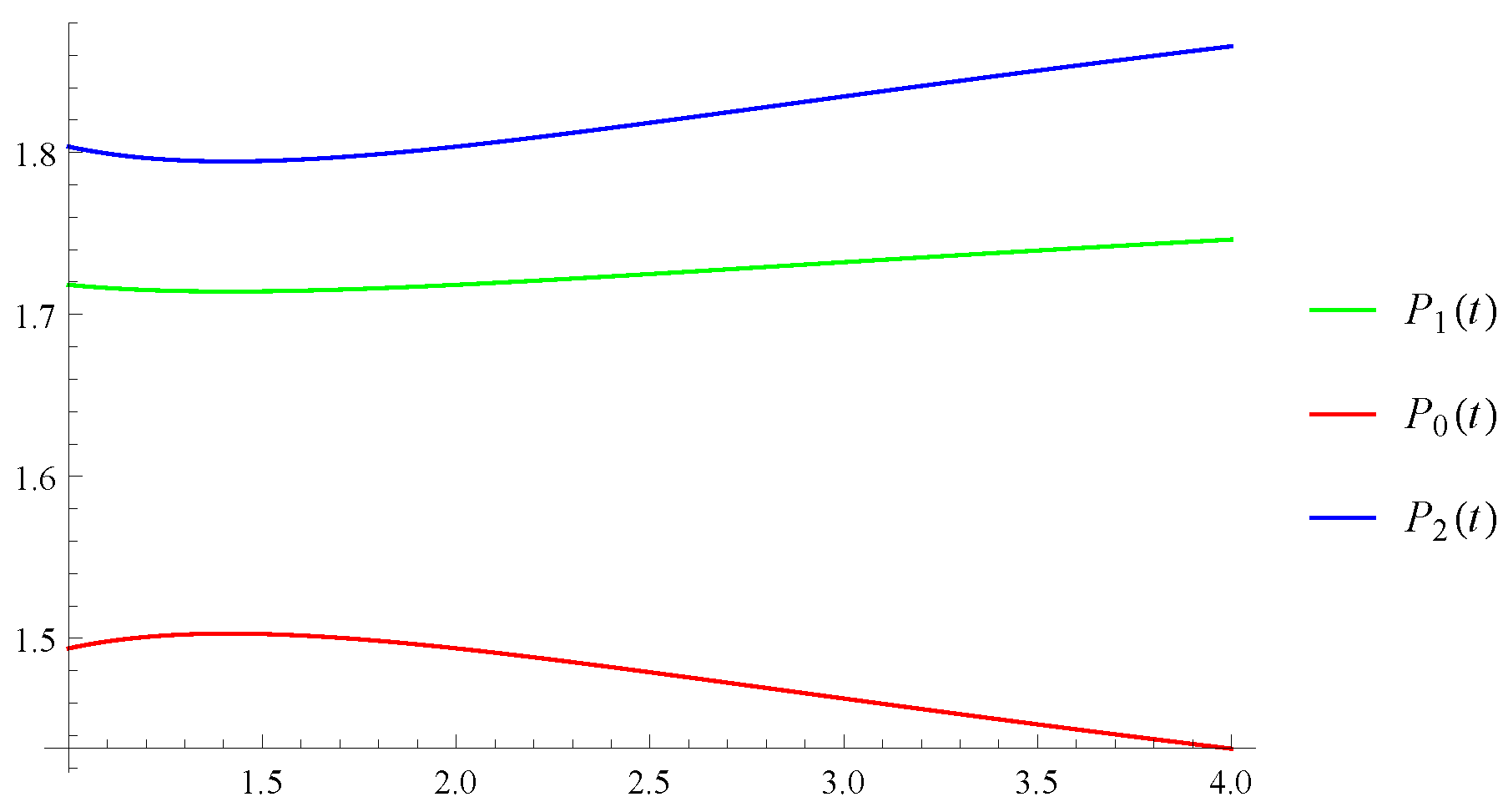


| Functions | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
|---|---|---|---|---|---|---|---|
| Functions | 0 | 0.4 | 0.8 | 1.2 | 1.6 | 2 |
|---|---|---|---|---|---|---|
| 0 | ||||||
| Functions | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
|---|---|---|---|---|---|---|---|
| Functions | 0 | 0.4 | 0.8 | 1.2 | 1.6 | 2 |
|---|---|---|---|---|---|---|
| 0 | ||||||
| Functions | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
|---|---|---|---|---|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vivas-Cortez, M.; Samraiz, M.; Ghaffar, M.T.; Naheed, S.; Rahman, G.; Elmasry, Y. Exploration of Hermite–Hadamard-Type Integral Inequalities for Twice Differentiable h-Convex Functions. Fractal Fract. 2023, 7, 532. https://doi.org/10.3390/fractalfract7070532
Vivas-Cortez M, Samraiz M, Ghaffar MT, Naheed S, Rahman G, Elmasry Y. Exploration of Hermite–Hadamard-Type Integral Inequalities for Twice Differentiable h-Convex Functions. Fractal and Fractional. 2023; 7(7):532. https://doi.org/10.3390/fractalfract7070532
Chicago/Turabian StyleVivas-Cortez, Miguel, Muhammad Samraiz, Muhammad Tanveer Ghaffar, Saima Naheed, Gauhar Rahman, and Yasser Elmasry. 2023. "Exploration of Hermite–Hadamard-Type Integral Inequalities for Twice Differentiable h-Convex Functions" Fractal and Fractional 7, no. 7: 532. https://doi.org/10.3390/fractalfract7070532
APA StyleVivas-Cortez, M., Samraiz, M., Ghaffar, M. T., Naheed, S., Rahman, G., & Elmasry, Y. (2023). Exploration of Hermite–Hadamard-Type Integral Inequalities for Twice Differentiable h-Convex Functions. Fractal and Fractional, 7(7), 532. https://doi.org/10.3390/fractalfract7070532











