A Chaos-Enhanced Fractional-Order Chaotic System with Self-Reproduction Based on a Memcapacitor and Meminductor
Abstract
1. Introduction
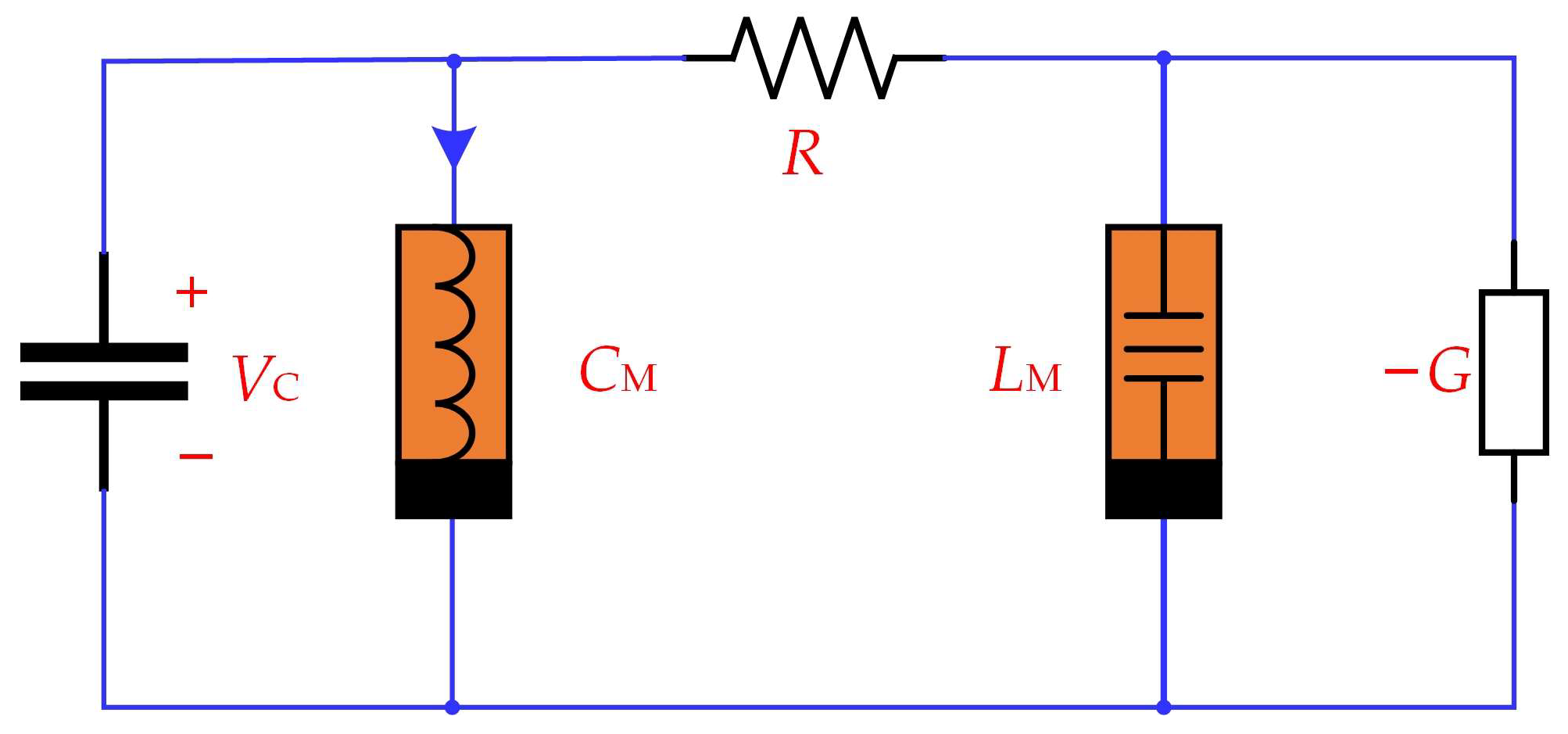
2. Circuit Models and System Equations
2.1. Caputo Differential Definition
2.2. Numerical Solution for FOMMS
2.3. Dissipation and Stability of the System
3. Dynamical Analysis
3.1. Existence of Asymptotic Periodic Solutions for FO Systems
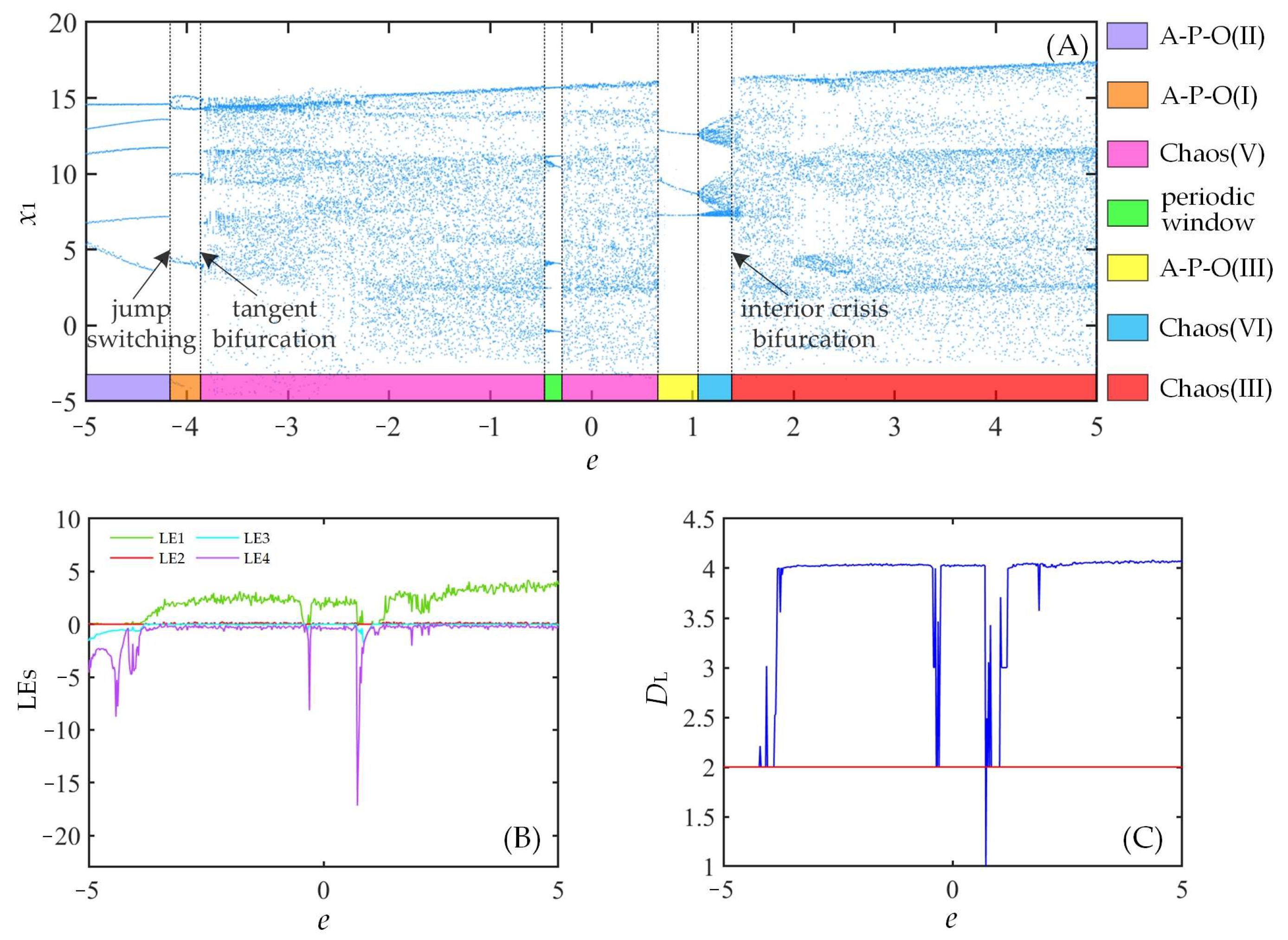
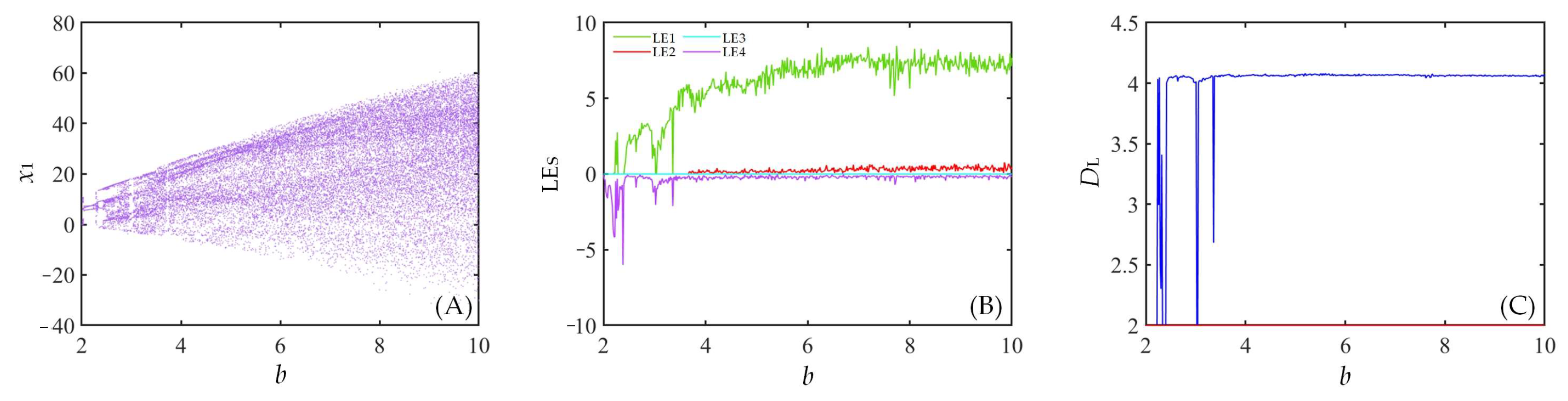
3.2. Bifurcation Diagrams (BD) and Lyapunov Exponent Spectrums (LEs) for Relevant Parameters
3.3. Multiple Stability
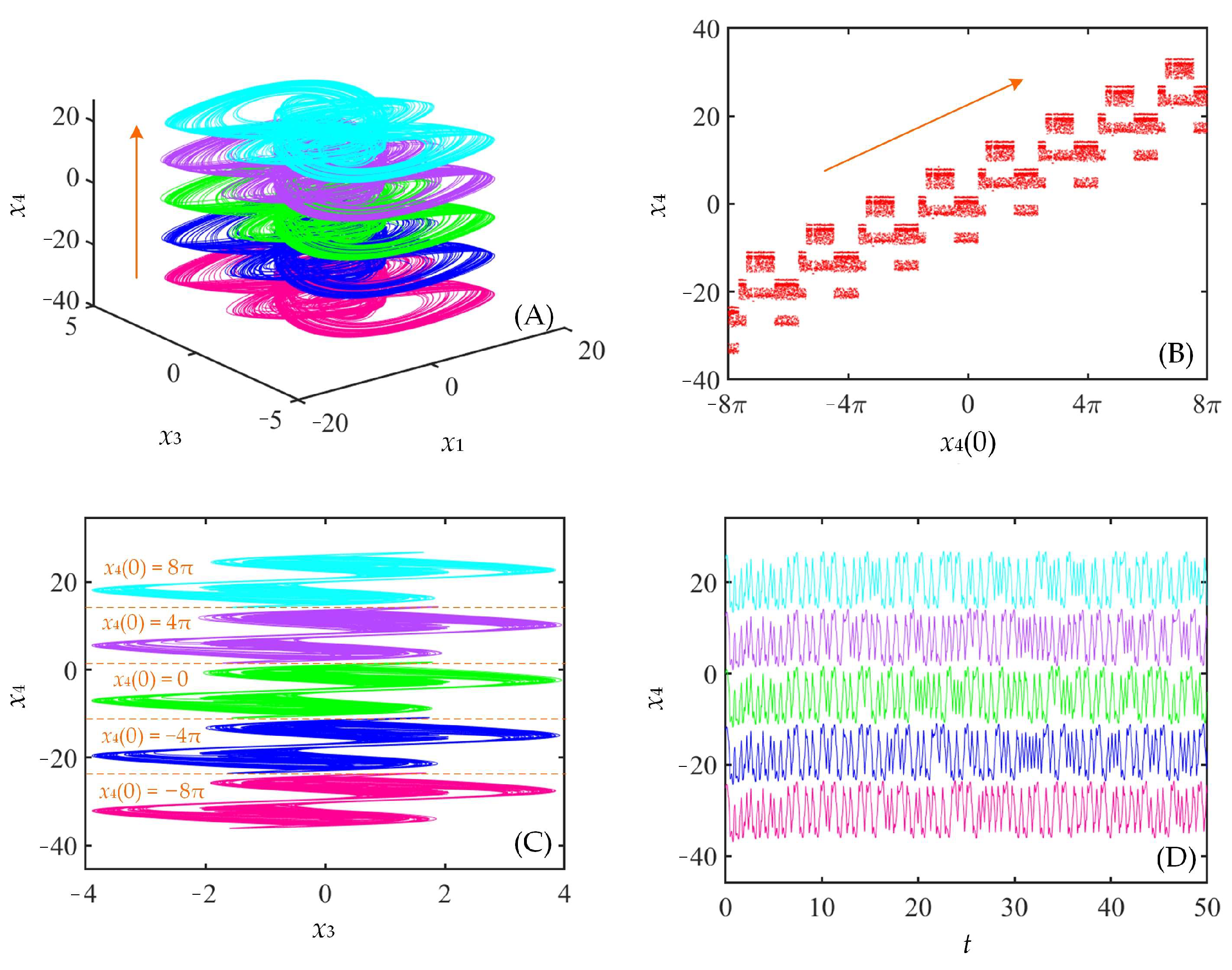
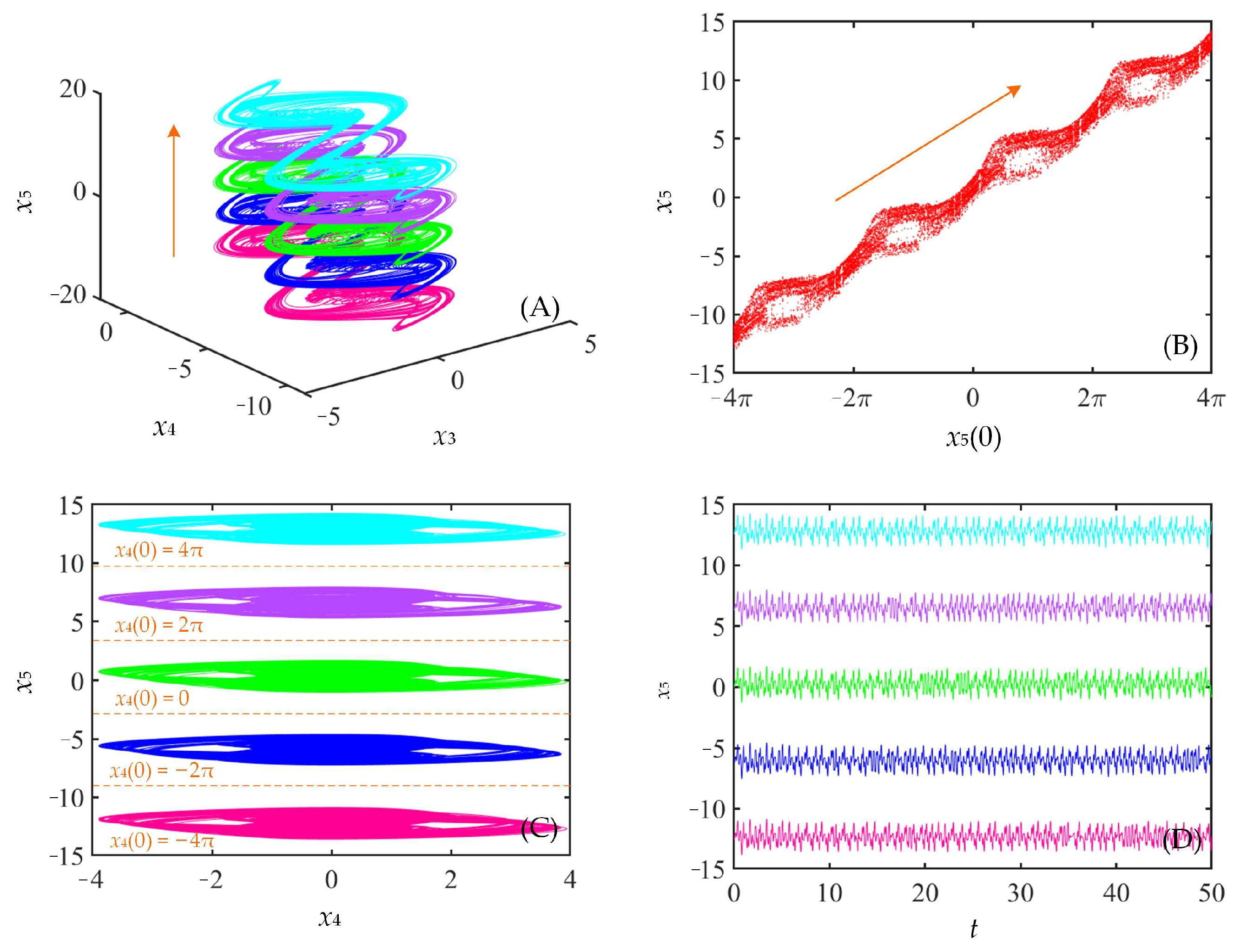
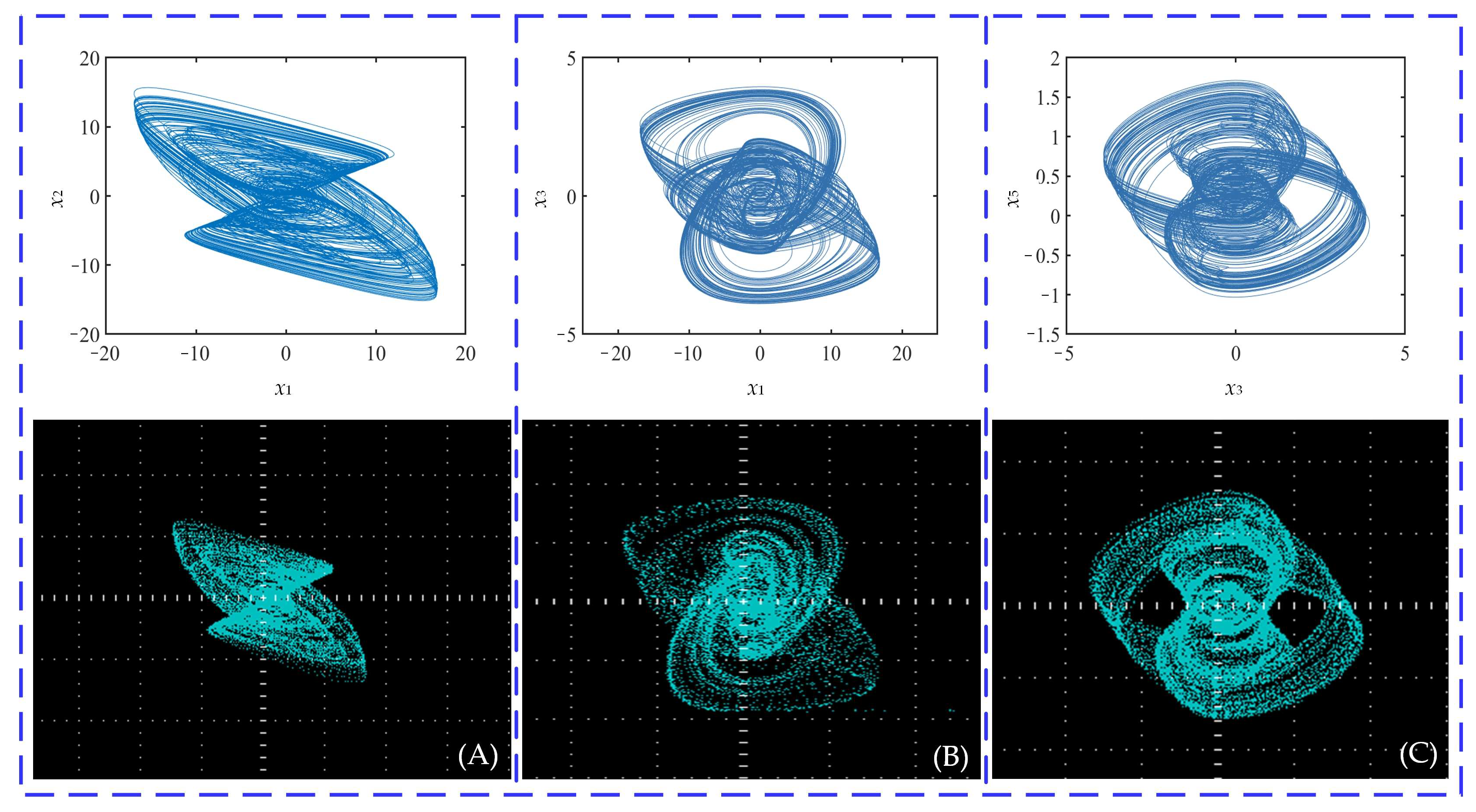
3.3.1. Self-Reproduction of Attractors
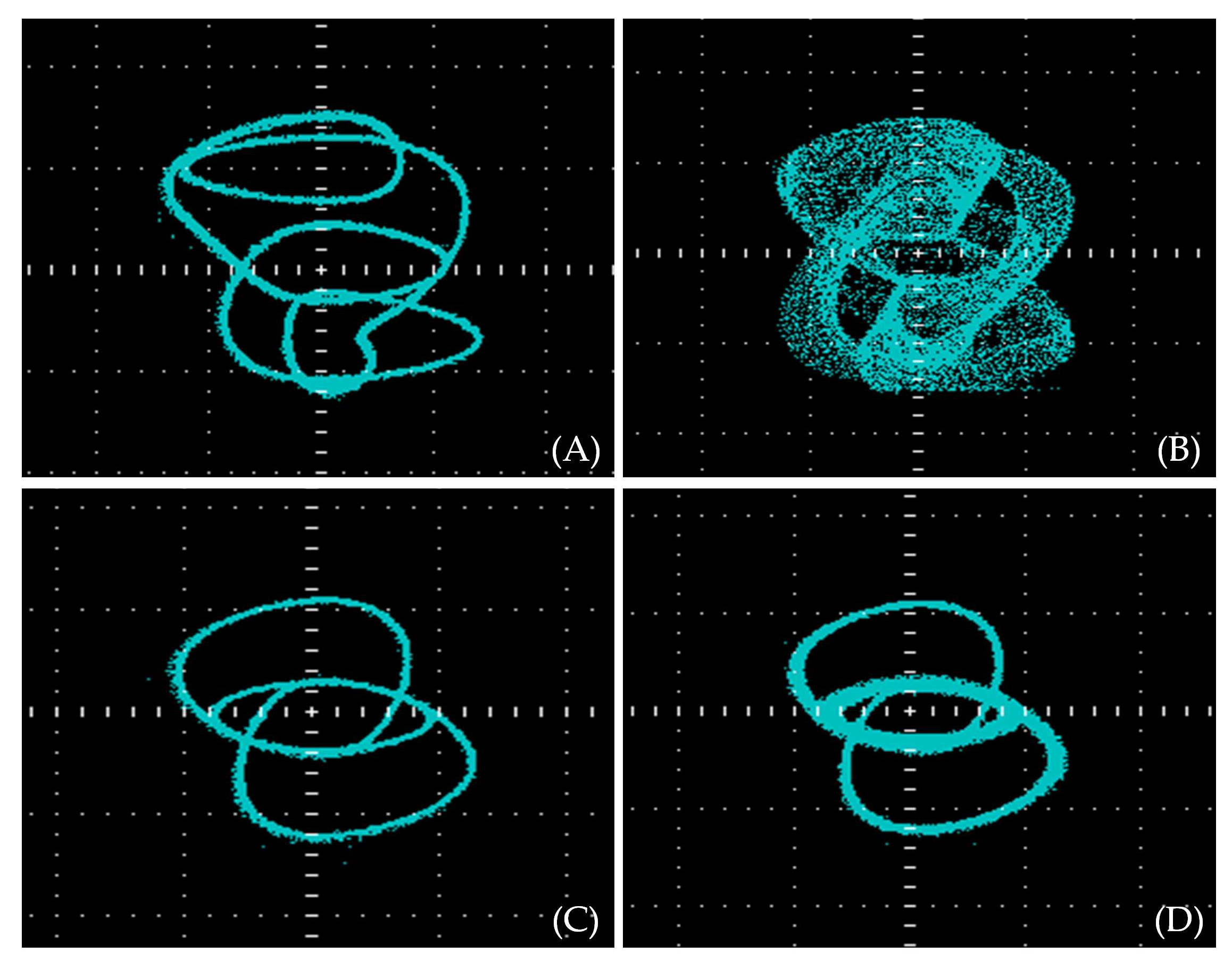
3.3.2. Coexisting Attractors
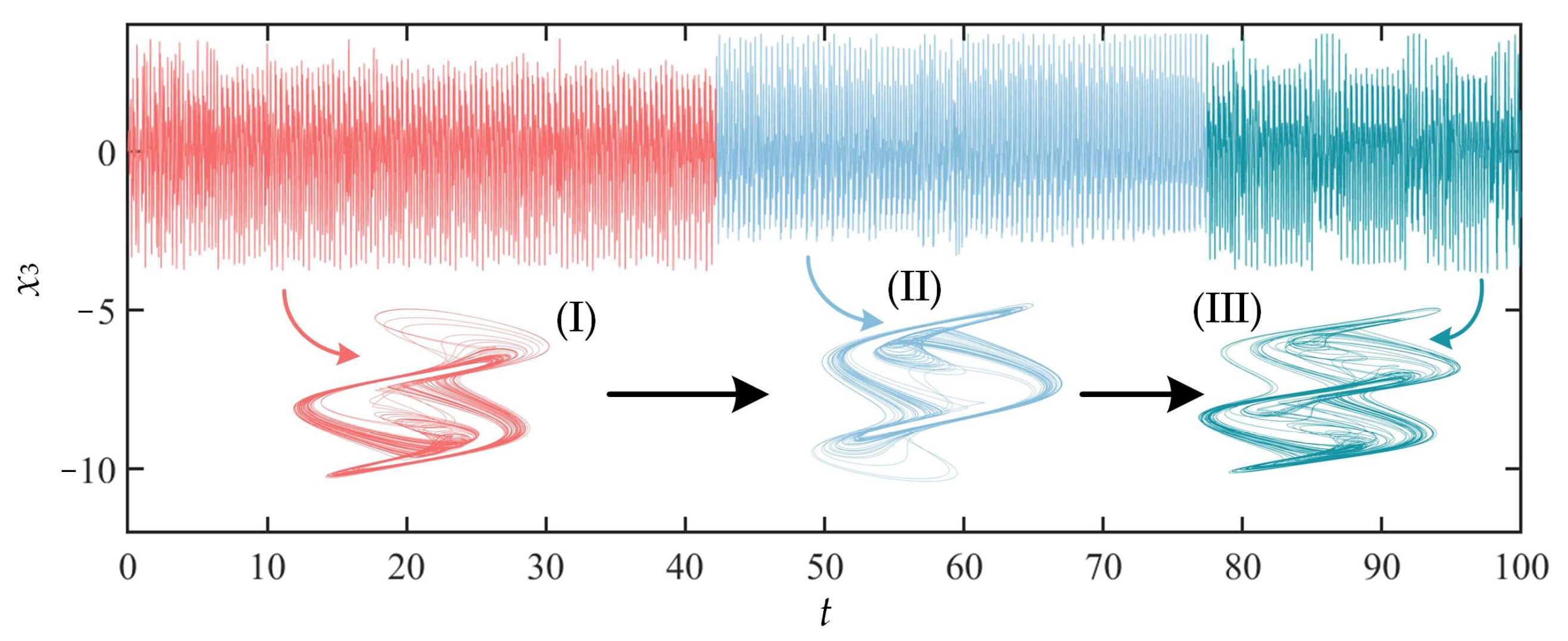
3.4. State Transition
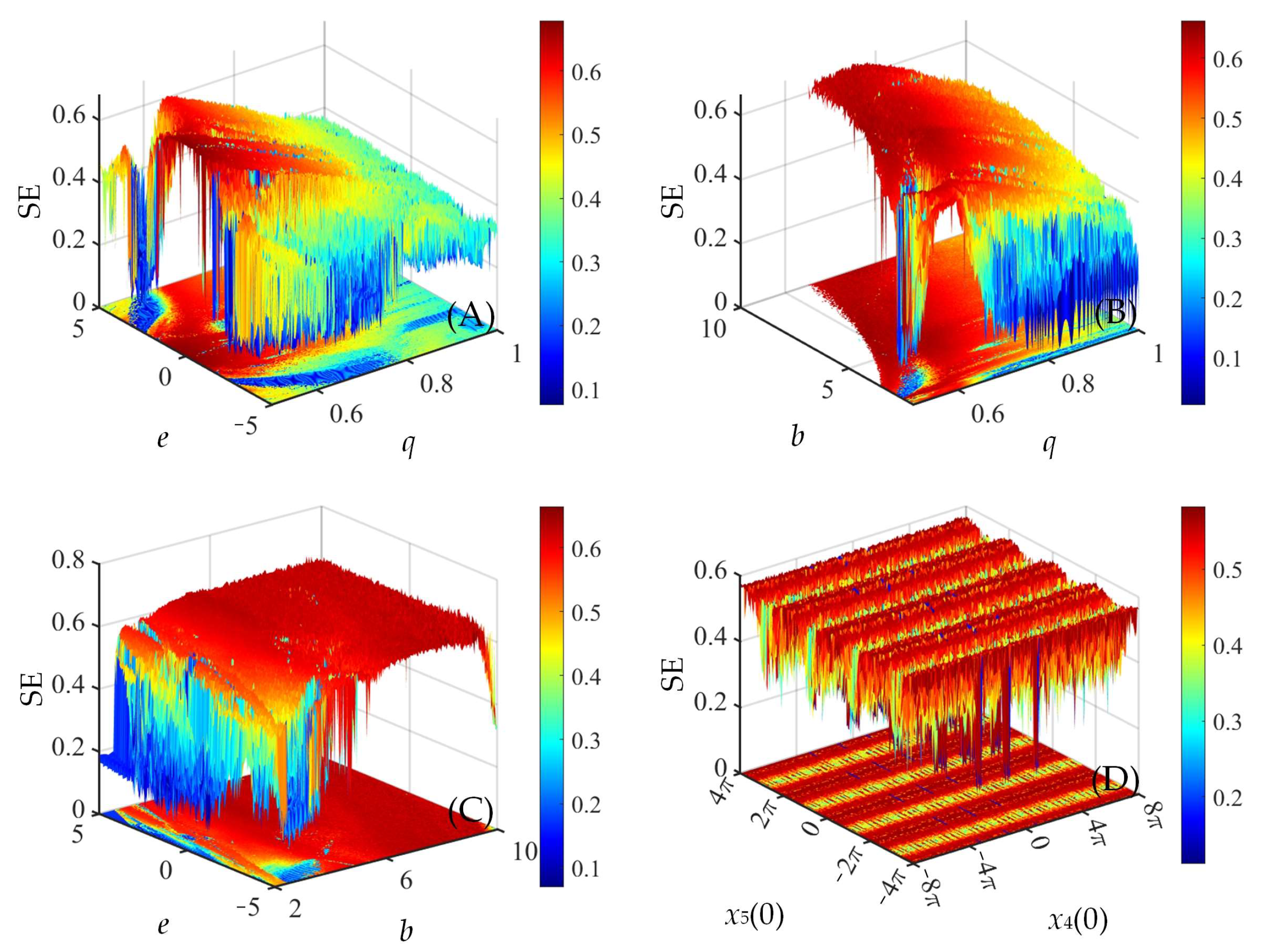
4. Complexity Analysis
5. Hardware Implementation Based on DSP
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Chua, L. Memristor-the missing circuit element. IEEE Trans. Circuit Theory 1971, 18, 507–519. [Google Scholar] [CrossRef]
- Di Ventra, M.; Pershin, Y.V.; Chua, L.O. Circuit elements with memory: Memristors, memcapacitors, and meminductors. Proc. IEEE 2009, 97, 1717–1724. [Google Scholar] [CrossRef]
- Ren, L.; Mou, J.; Banerjee, S.; Zhang, Y. A hyperchaotic map with a new discrete memristor model: Design, dynamical analysis, implementation and application. Chaos Solitons Fractals 2023, 167, 113024. [Google Scholar] [CrossRef]
- Xu, Q.; Lin, Y.; Bao, B.; Chen, M. Multiple attractors in a non-ideal active voltage-controlled memristor based Chua’s circuit. Chaos Solitons Fractals 2016, 83, 186–200. [Google Scholar] [CrossRef]
- Lin, H.; Wang, C.; Yu, F.; Sun, J.; Du, S.; Deng, Z.; Deng, Q. A review of chaotic systems based on memristive Hopfield neural networks. Mathematics 2023, 11, 1369. [Google Scholar] [CrossRef]
- Ma, Y.; Mou, J.; Lu, J.; Banerjee, S.; Cao, Y. A Discrete Memristor Coupled Two-Dimensional Generalized Square Hyperchaotic Maps. Fractals 2023, 31, 2340136. [Google Scholar] [CrossRef]
- Bao, H.; Chen, M.; Wu, H.; Bao, B. Memristor initial-boosted coexisting plane bifurcations and its extreme multi-stability reconstitution in two-memristor-based dynamical system. Sci. China Technol. Sci. 2020, 63, 603–613. [Google Scholar] [CrossRef]
- Ma, M.-L.; Xie, X.-H.; Yang, Y.; Li, Z.-J.; Sun, Y.-C. Synchronization coexistence in a Rulkov neural network based on locally active discrete memristor. Chin. Phys. B 2023, 32, 058701. [Google Scholar] [CrossRef]
- Guo, M.; Zhu, Y.; Liu, R.; Zhao, K.; Dou, G. An associative memory circuit based on physical memristors. Neurocomputing 2022, 472, 12–23. [Google Scholar] [CrossRef]
- Ma, T.; Mou, J.; Yan, H.; Cao, Y. A new class of Hopfield neural network with double memristive synapses and its DSP implementation. Eur. Phys. J. Plus 2022, 137, 1135. [Google Scholar] [CrossRef]
- Gao, X.; Sun, B.; Cao, Y.; Banerjee, S.; Mou, J. A color image encryption algorithm based on hyperchaotic map and DNA mutation. Chin. Phys. B 2023, 32, 030501. [Google Scholar] [CrossRef]
- de la Fraga, L.G.; Ovilla-Martínez, B. A chaotic PRNG tested with the heuristic Differential Evolution. Integration 2023, 90, 22–26. [Google Scholar] [CrossRef]
- Echenausía-Monroy, J.L.; Campos, E.; Jaimes-Reátegui, R.; García-López, J.H.; Huerta-Cuellar, G. Deterministic Brownian-like motion: Electronic approach. Electronics 2022, 11, 2949. [Google Scholar] [CrossRef]
- De la Fraga, L.G. Analyzing All the Instances of a Chaotic Map to Generate Random Numbers. Comput. Sci. Math. Forum 2022, 4, 6. [Google Scholar]
- Wang, L.; Cao, Y.; Jahanshahi, H.; Wang, Z.; Mou, J. Color image encryption algorithm based on Double layer Josephus scramble and laser chaotic system. Optik 2023, 275, 170590. [Google Scholar] [CrossRef]
- Ma, X.; Wang, C.; Qiu, W.; Yu, F. A fast hyperchaotic image encryption scheme. Int. J. Bifurc. Chaos 2023, 33, 2350061. [Google Scholar] [CrossRef]
- Sha, Y.; Mou, J.; Banerjee, S.; Zhang, Y. Exploiting Flexible and Secure Cryptographic Technique for Multi-Dimensional Image Based on Graph Data Structure and Three-Input Majority Gate. IEEE Trans. Ind. Inform. 2023. [Google Scholar] [CrossRef]
- Zhu, Y.; Wang, C.; Sun, J.; Yu, F. A chaotic image encryption method based on the artificial fish swarms algorithm and the DNA coding. Mathematics 2023, 11, 767. [Google Scholar] [CrossRef]
- Ma, X.; Wang, C. Hyper-chaotic image encryption system based on N+ 2 ring Joseph algorithm and reversible cellular automata. Multimed. Tools Appl. 2023. [Google Scholar] [CrossRef]
- Gao, X.; Mou, J.; Banerjee, S.; Zhang, Y. Color-Gray Multi-Image Hybrid Compression–Encryption Scheme Based on BP Neural Network and Knight Tour. IEEE Trans. Cybern. 2023, 53, 5037–5047. [Google Scholar] [CrossRef]
- Sha, Y.; Mou, J.; Wang, J.; Banerjee, S.; Sun, B. Chaotic image encryption with Hopfield neural network. Fractals 2023, 31, 2340107. [Google Scholar] [CrossRef]
- Sheng, Z.; Li, C.; Gao, Y.; Li, Z.; Chai, L. A Switchable Chaotic Oscillator with Multiscale Amplitude/Frequency Control. Mathematics 2023, 11, 618. [Google Scholar] [CrossRef]
- Ghanbari, B.; Günerhan, H.; Srivastava, H. An application of the Atangana-Baleanu fractional derivative in mathematical biology: A three-species predator-prey model. Chaos Solitons Fractals 2020, 138, 109910. [Google Scholar] [CrossRef]
- Han, X.; Mou, J.; Lu, J.; Banerjee, S.; Cao, Y. Two discrete memristive chaotic maps and its DSP implementation. Fractals 2023, 31, 2340104. [Google Scholar] [CrossRef]
- Xu, S.; Wang, X.; Ye, X. A new fractional-order chaos system of Hopfield neural network and its application in image encryption. Chaos Solitons Fractals 2022, 157, 111889. [Google Scholar] [CrossRef]
- Huang, P.; Chen, X.; Chai, Y.; Ma, L. A unified framework of fault detection and diagnosis based on fractional-order chaos system. Aerosp. Sci. Technol. 2022, 130, 107871. [Google Scholar] [CrossRef]
- Akgul, A.; Rajagopal, K.; Durdu, A.; Pala, M.A.; Yldz, M.Z. A simple fractional-order chaotic system based on memristor and memcapacitor and its synchronization application. Chaos Solitons Fractals 2021, 152, 111306. [Google Scholar] [CrossRef]
- Ma, T.; Mou, J.; Li, B.; Banerjee, S.; Yan, H. Study on the complex dynamical behavior of the fractional-order hopfield neural network system and its implementation. Fractal Fract. 2022, 6, 637. [Google Scholar] [CrossRef]
- Zhou, N.-R.; Tong, L.-J.; Zou, W.-P. Multi-image encryption scheme with quaternion discrete fractional Tchebyshev moment transform and cross-coupling operation. Signal Process. 2023, 211, 109107. [Google Scholar] [CrossRef]
- Liu, X.; Mou, J.; Wang, J.; Banerjee, S.; Li, P. Dynamical analysis of a novel fractional-order chaotic system based on memcapacitor and meminductor. Fractal Fract. 2022, 6, 671. [Google Scholar] [CrossRef]
- Echenausía-Monroy, J.; Jafari, S.; Huerta-Cuellar, G.; Gilardi-Velázquez, H. Predicting the emergence of multistability in a Monoparametric PWL system. Int. J. Bifurc. Chaos 2022, 32, 2250206. [Google Scholar] [CrossRef]
- Liu, X.; Mou, J.; Zhang, Y.; Cao, Y. A New Hyperchaotic Map Based on Discrete Memristor and Meminductor: Dynamics Analysis, Encryption Application, and DSP Implementation. IEEE Trans. Ind. Electron. 2023. [Google Scholar] [CrossRef]
- Li, Y.; Li, C.; Zhang, S.; Chen, G.; Zeng, Z. A self-reproduction hyperchaotic map with compound lattice dynamics. IEEE Trans. Ind. Electron. 2022, 69, 10564–10572. [Google Scholar] [CrossRef]
- Gao, X.; Mou, J.; Li, B.; Banerjee, S.; Sun, B. Multi-image hybrid encryption algorithm based on pixel substitution and gene theory. Fractals 2023, 31, 2340111. [Google Scholar] [CrossRef]
- Bao, H.; Hua, Z.; Wang, N.; Zhu, L.; Chen, M.; Bao, B. Initials-boosted coexisting chaos in a 2-D sine map and its hardware implementation. IEEE Trans. Ind. Inform. 2020, 17, 1132–1140. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Marzan, S.A. Nonlinear differential equations with the Caputo fractional derivative in the space of continuously differentiable functions. Differ. Equ. 2005, 41, 84–89. [Google Scholar] [CrossRef]
- Cherruault, Y.; Adomian, G. Decomposition methods: A new proof of convergence. Math. Comput. Model. 1993, 18, 103–106. [Google Scholar] [CrossRef]
- Wang, X.; Mou, J.; Jahanshahi, H.; Alotaibi, N.D.; Bi, X. Extreme multistability arising from periodic repetitive bifurcation behavior in a hyperchaotic oscillator. Nonlinear Dyn. 2023, 111, 13561–13578. [Google Scholar] [CrossRef]
- Matignon, D. Stability results for fractional differential equations with applications to control processing. In Proceedings of the Computational Engineering in Systems Applications, Lille, France, 9–12 July 1996; pp. 963–968. [Google Scholar]
- Danca, M.-F.; Fečkan, M.; Kuznetsov, N.V.; Chen, G. Complex dynamics, hidden attractors and continuous approximation of a fractional-order hyperchaotic PWC system. Nonlinear Dyn. 2018, 91, 2523–2540. [Google Scholar] [CrossRef]


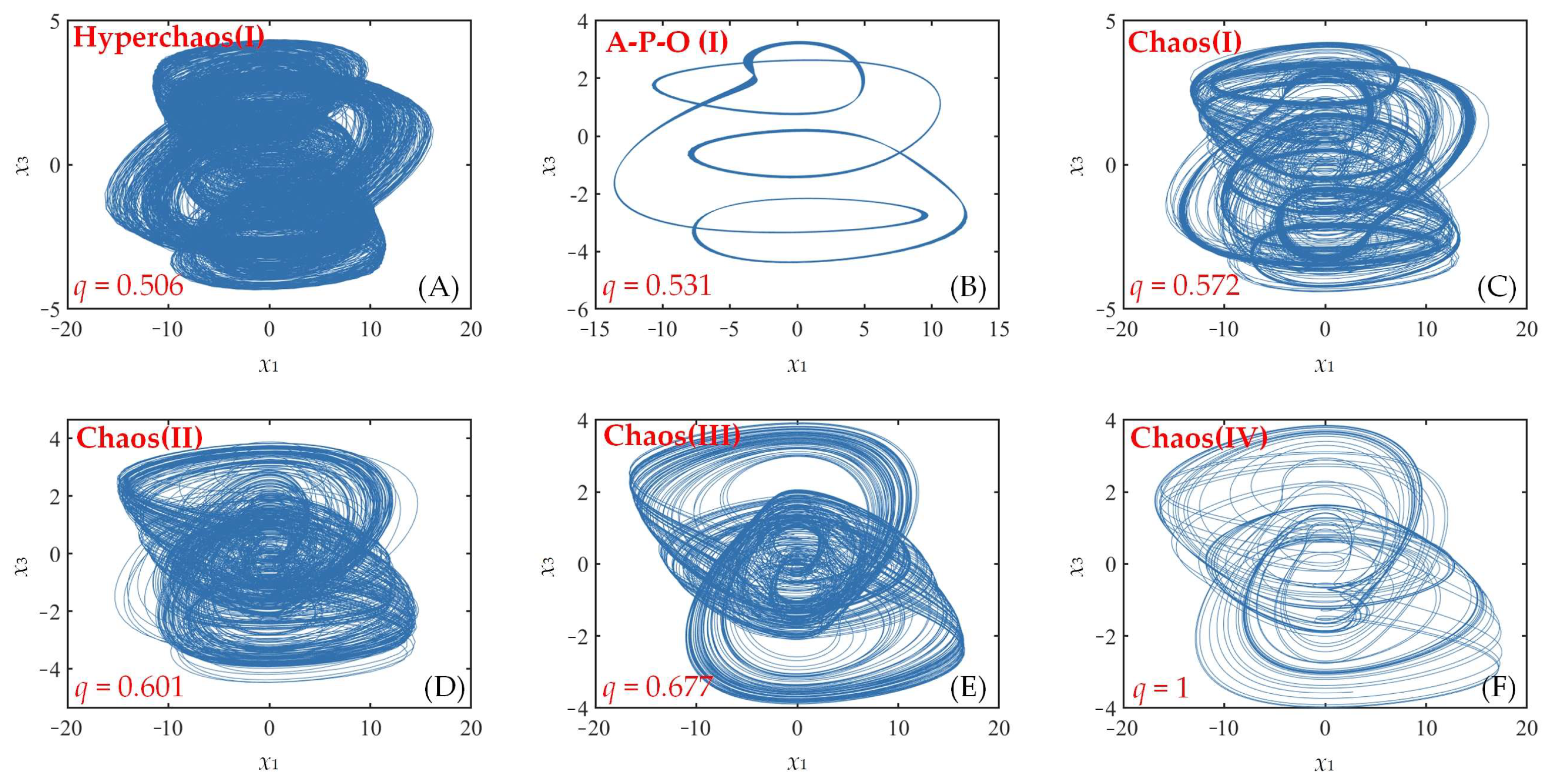



| q | Lyapunov Exponent | Lyapunov Dimension | Attractor Type |
|---|---|---|---|
| 0.506 | 7.3885, 0.1046, 0, −6.0704, −171.3690 | 4.0622 | Hyperchaos(I) |
| 0.531 | 0, −0.4533, −7.6863, −7.6691, −140.4726 | 2 | A-P-O(I) |
| 0.572 | 3.7954, 0, −0.1267, −2.5675, −137.2317 | 4.0450 | Chaos(I) |
| 0.601 | 4.3579, 0, 0, −1.0012, −117.5874 | 4.0285 | Chaos(II) |
| 0.677 | 3.2477, 0, 0, −0.2873, 65.8004 | 4.0279 | Chaos(III) |
| 1 | 0.3535, 0, 0, −0.1014, −9.0481 | 4.0189 | Chaos(IV) |
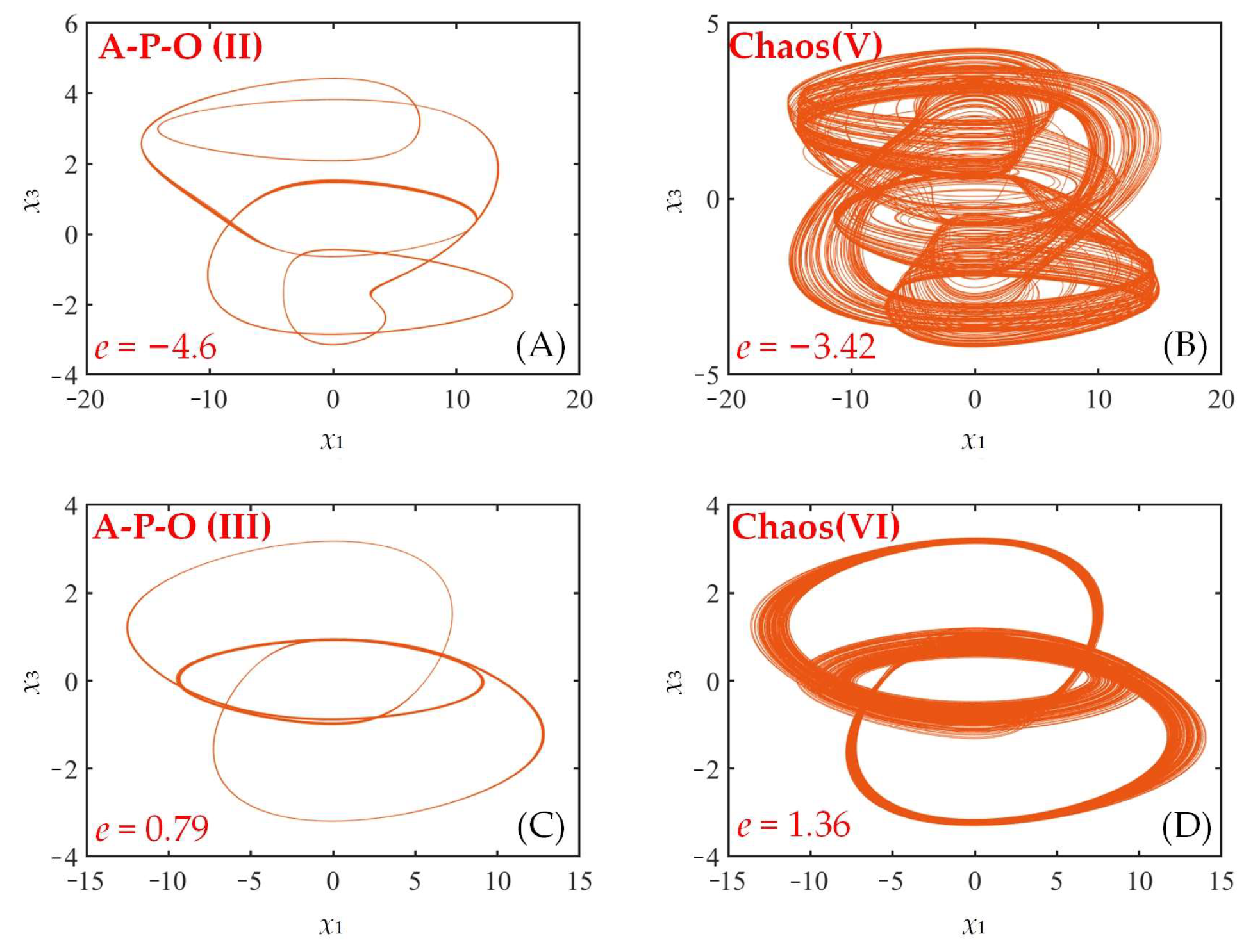
| e | Lyapunov Exponent | Lyapunov Dimension | Attractor Type |
|---|---|---|---|
| −4.6 | 0, 0, −0.7315, −2.5151, −59.7031 | 2 | A-P-O(II) |
| −3.42 | 1.6180, 0, 0, −0.3264, −68.7863 | 4.0245 | Chaos(V) |
| 0.79 | 0, 0, −0.7833, −9.3192, −41.8929 | 2 | A-P-O(III) |
| 1.36 | 1.0508, 0, 0, 0, −52.1427 | 4.0188 | Chaos(VI) |
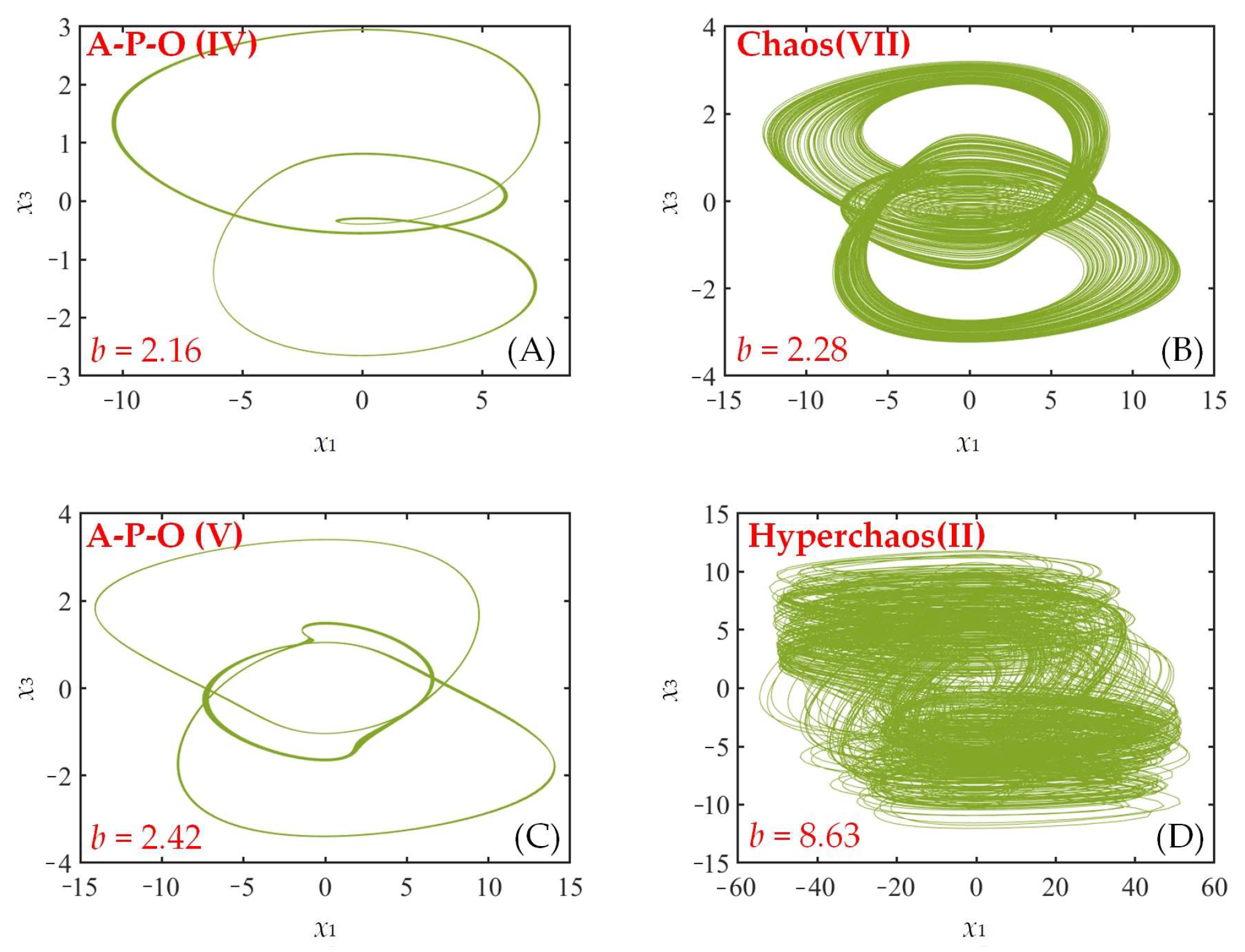
| b | Lyapunov Exponent | Lyapunov Dimension | Attractor Type |
|---|---|---|---|
| 2.16 | 0, 0, −0.4545, −0.7457, −48.3074 | 2 | A-P-O(IV) |
| 2.28 | 2.7585, 0, 0, −0.3099, −51.3781 | 4.0346 | Chaos(VII) |
| 2.42 | 0, 0, −0.7500, −0.6785, −37.9772 | 2 | A-P-O(V) |
| 8.63 | 7.6442, 0.4123, 0, 0, −128.7118 | 4.0687 | Hyperchaos(II) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Cao, Y.; Li, H.; Li, B. A Chaos-Enhanced Fractional-Order Chaotic System with Self-Reproduction Based on a Memcapacitor and Meminductor. Fractal Fract. 2023, 7, 582. https://doi.org/10.3390/fractalfract7080582
Wang X, Cao Y, Li H, Li B. A Chaos-Enhanced Fractional-Order Chaotic System with Self-Reproduction Based on a Memcapacitor and Meminductor. Fractal and Fractional. 2023; 7(8):582. https://doi.org/10.3390/fractalfract7080582
Chicago/Turabian StyleWang, Xuan, Yinghong Cao, Hongjie Li, and Bo Li. 2023. "A Chaos-Enhanced Fractional-Order Chaotic System with Self-Reproduction Based on a Memcapacitor and Meminductor" Fractal and Fractional 7, no. 8: 582. https://doi.org/10.3390/fractalfract7080582
APA StyleWang, X., Cao, Y., Li, H., & Li, B. (2023). A Chaos-Enhanced Fractional-Order Chaotic System with Self-Reproduction Based on a Memcapacitor and Meminductor. Fractal and Fractional, 7(8), 582. https://doi.org/10.3390/fractalfract7080582





