Dynamics of the Three-Compartment Financial Bubble Model under the Mittag-Leffler Operator
Abstract
1. Introduction
2. Fundamental Results
3. Theoretical Results
4. Numerical Scheme
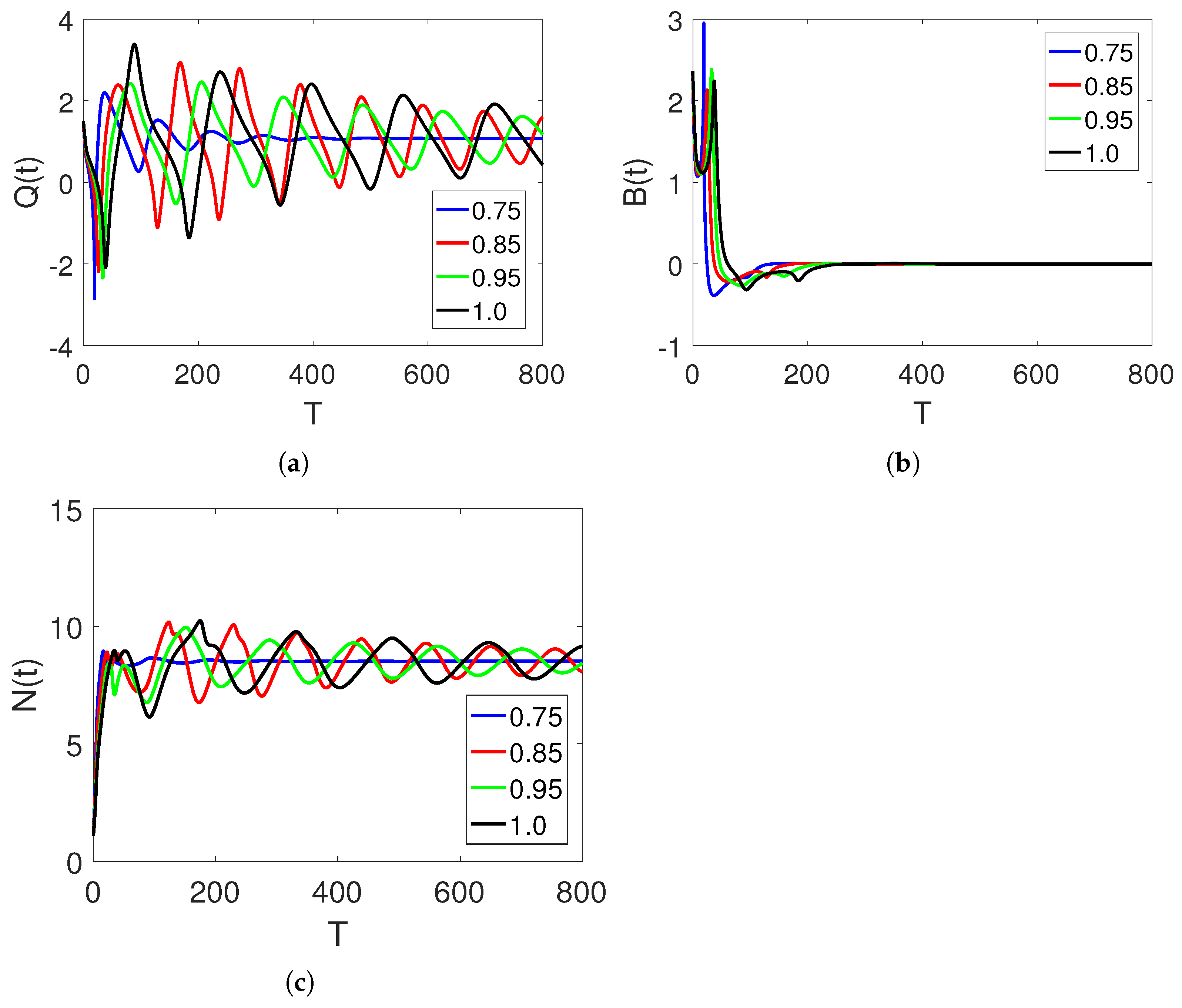
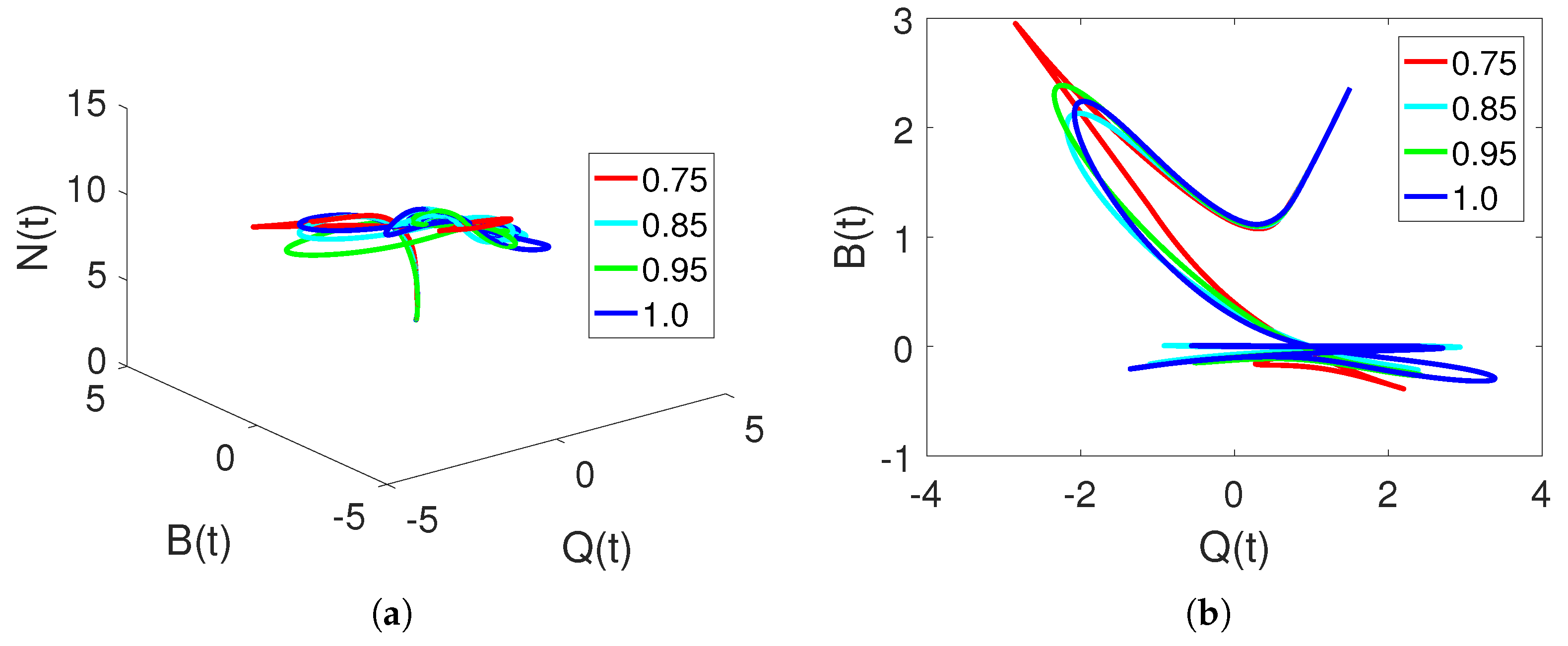
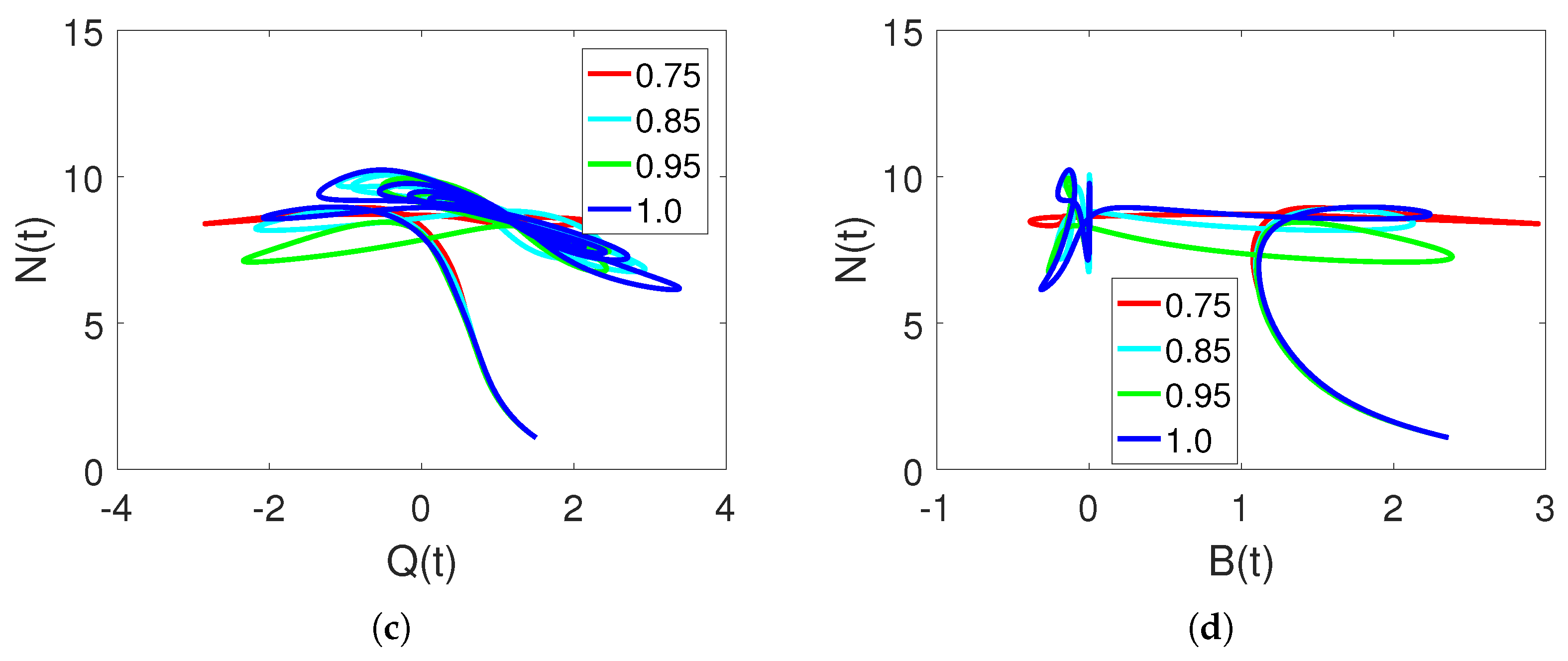
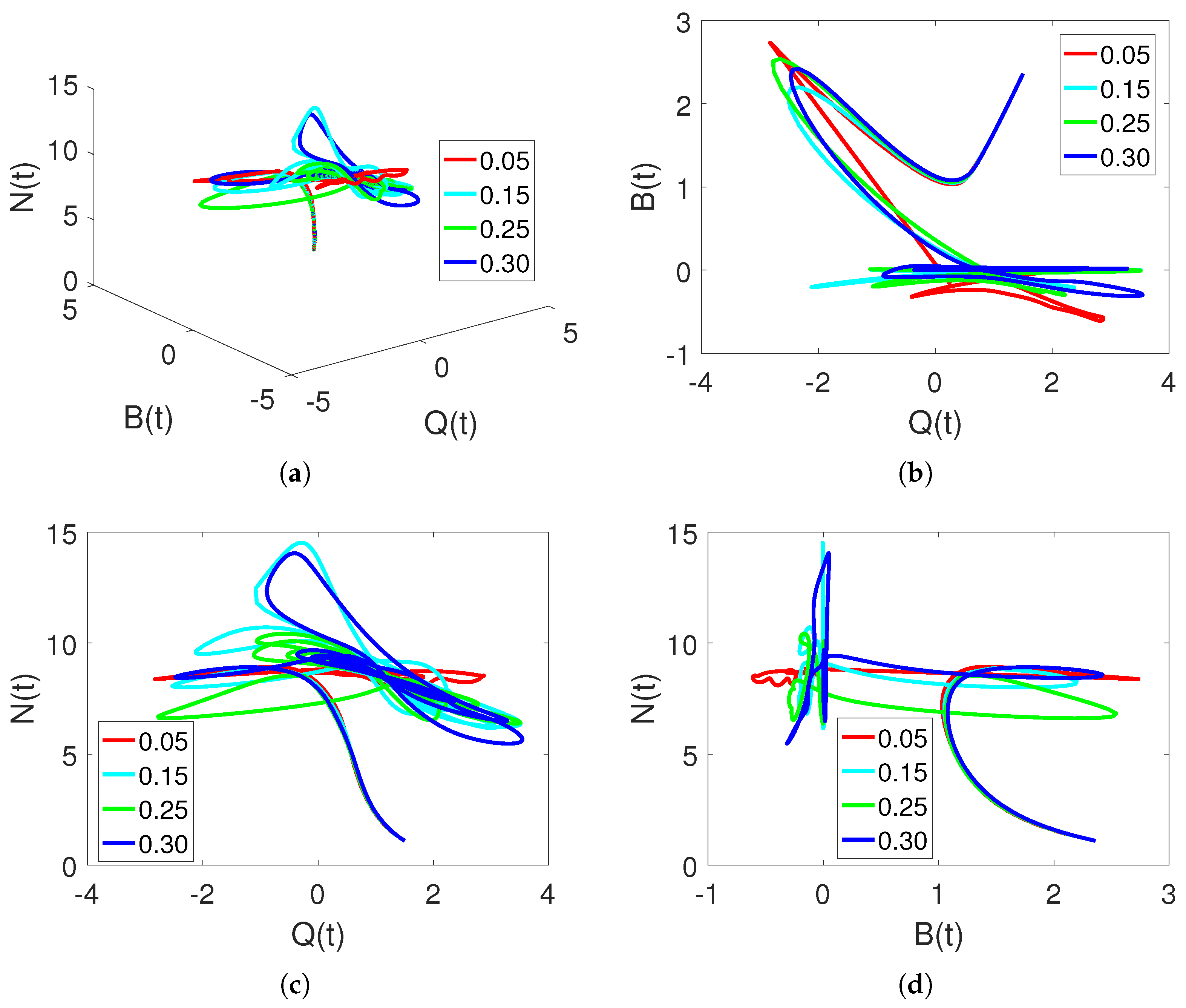
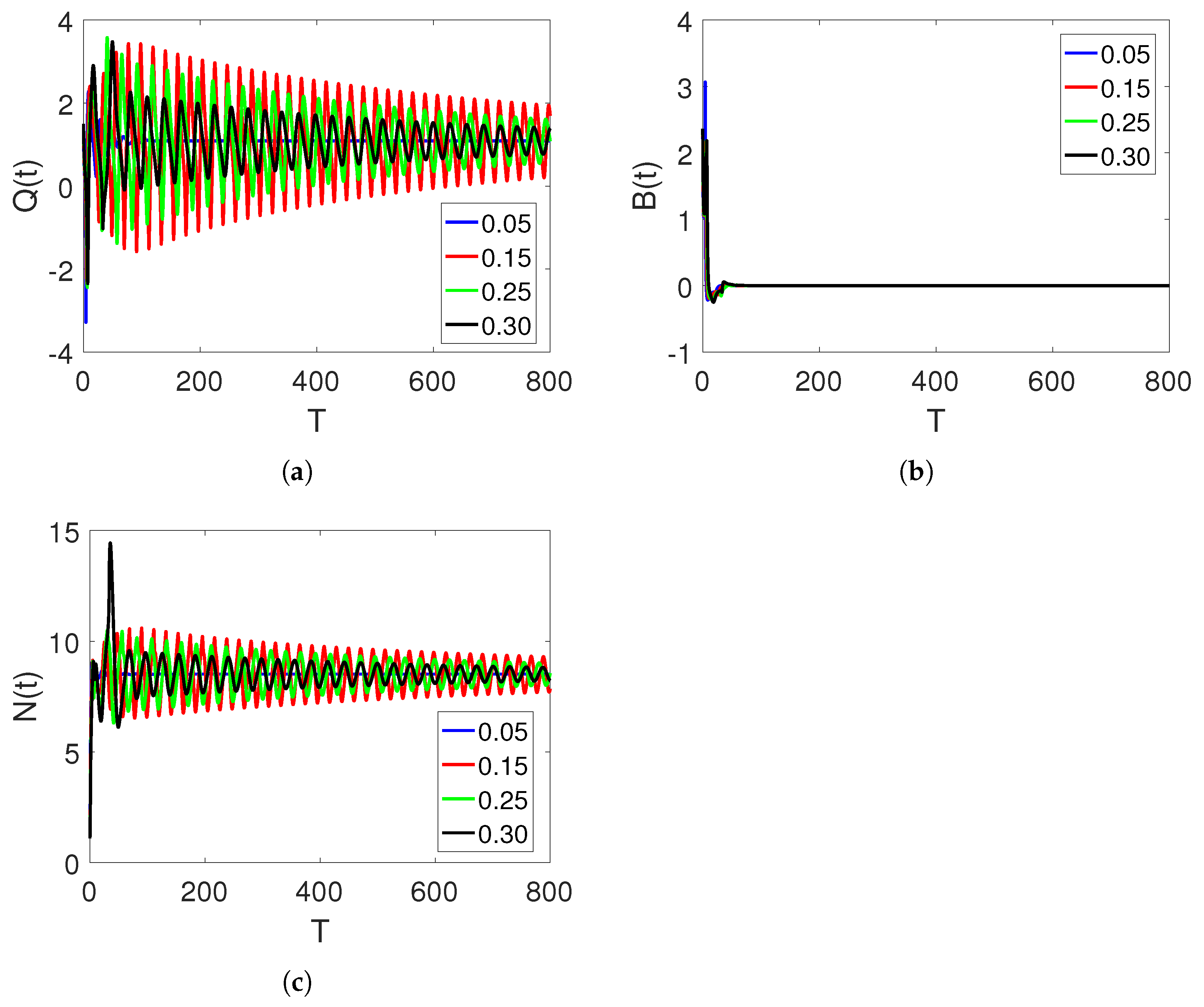
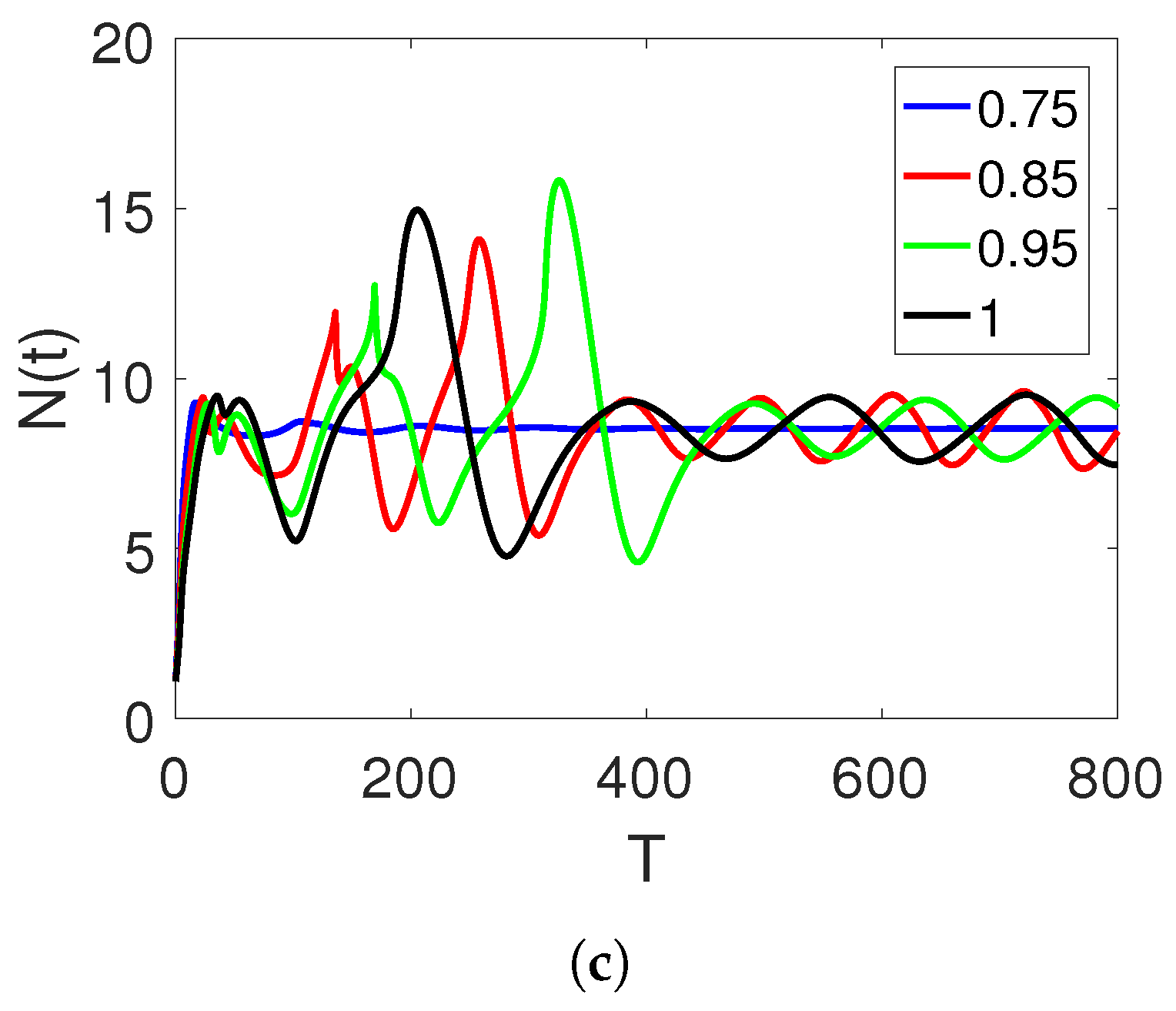
5. Discussion and Simulations
Sensitivity of Parameters
6. Summary
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shilnikov Pavlovich, L. A case of the existence of a denumerable set of periodic motions. In Doklady Akademii Nauk; Russian Academy of Sciences: Moscow, Russia, 1965; Volume 160, pp. 558–561. [Google Scholar]
- Bella, G.; Mattana, P.; Venturi, B. Shilnikov chaos in the Lucas model of endogenous growth. J. Econ. Theory 2017, 172, 451–477. [Google Scholar] [CrossRef]
- Ben, B.; Gertler, M. VAgency costs. Net Worth Bus. Fluct. Am. Econ. Rev. 1989, 79, 14–31. [Google Scholar]
- Carlstrom, C.T.; Fuerst, T.S. Agency costs, net worth, and business fluctuations: A computable general equilibrium analysis. Am. Econ. Rev. 1997, 87, 893–910. [Google Scholar]
- Nobuhiro, K.; Moore, J. Credit cycles. J. Political Econ. 1997, 105, 211–248. [Google Scholar]
- Bernanke, B.S.; Gertler, M.; Gilchrist, S. The financial accelerator in a quantitative business cycle framework. Handb. Macroecon. 1999, 1, 1341–1393. [Google Scholar]
- He, Q.; Xia, P.; Hu, C.; Li, B. PUBLIC Information, Actual Intervention and Inflation Expectations. Transform. Bus. Econ. 2022, 21, 644–666. [Google Scholar]
- He, Q.; Zhang, X.; Xia, P.; Zhao, C.; Li, S. A Comparison Research on Dynamic Characteristics of Chinese and American Energy Prices. J. Glob. Inf. Manag. (JGIM) 2023, 31, 1–16. [Google Scholar] [CrossRef]
- Giovanni, B.; Mattana, P. Chaos control in presence of financial bubbles. Econ. Lett. 2020, 193, 109314. [Google Scholar]
- Miao, J.; Wang, P. Banking bubbles and financial crises. J. Econ. Theory 2015, 157, 763–792. [Google Scholar] [CrossRef]
- Podlubny, I. Geometric and physical interpretation of fractional integration and fractional differentiation. J. Fract. Calc. Appl. 2002, 5, 367–386. [Google Scholar]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley: Hoboken, NJ, USA, 1993. [Google Scholar]
- Machado, J.T.; Kiryakova, V.; Mainardi, F. Recent history of fractional calculus. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 1140–1153. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Lakshmikantham, V.; Leela, S.; Devi, J.V. Theory of Fractional Dynamic Systems; CSP: St. Paul, MN, USA, 2009. [Google Scholar]
- Baleanu, D.; Diethelm, K.; Scalas, E.; Trujillo, J.J. Fractional Calculus: Models and Numerical Methods; World Scientific: Singapore, 2012; Volume 3. [Google Scholar]
- Yang, X.-J. Advanced Local Fractional Calculus and Its Applications; World Scientific: Singapore, 2012; Volume 1. [Google Scholar]
- Hilfer, R. (Ed.) Applications of Fractional Calculus in Physics; World Scientific: Singapore, 2000. [Google Scholar]
- Rahman, M.; Althobaiti, A.; Riaz, M.B.; Al-Duais, F.S. A Theoretical and Numerical Study on Fractional Order Biological Models with Caputo Fabrizio Derivative. Fractal Fract. 2022, 6, 446. [Google Scholar] [CrossRef]
- Khan, S.A.; Shah, K.; Zaman, G.; Jarad, F. Existence theory and numerical solutions to smoking model under Caputo-Fabrizio fractional derivative. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 013128. [Google Scholar] [CrossRef] [PubMed]
- Baleanu, D.; Jajarmi, A.; Mohammadi, H.; Rezapour, S. A new study on the mathematical modelling of human liver with Caputo–Fabrizio fractional derivative. Chaos Solitons Fractals 2020, 134, 109705. [Google Scholar] [CrossRef]
- Ahmad, S.; Dong, Q.; Rahman, M. Dynamics of a fractional-order COVID-19 model under the nonsingular kernel of Caputo-Fabrizio operator. Math. Model. Numer. Simul. Appl. 2022, 2, 228–243. [Google Scholar] [CrossRef]
- Abdon, A.; Baleanu, D. New fractional derivatives with non-local and non-singular kernel: Theory and application to heat transfer model. Therm. Sci. 2016, 20, 763–769. [Google Scholar]
- Zhang, L.; Rahman, M.; Arfan, M.; Ali, A. Investigation of mathematical model of transmission co-infection TB in HIV community with a non-singular kernel. Results Phys. 2021, 8, 104559. [Google Scholar] [CrossRef]
- ur Rahman, M.; Arfan, M.; Shah, Z.; Alzahrani, E. Evolution of fractional mathematical model for drinking under Atangana-Baleanu Caputo derivatives. Phys. Scr. 2021, 96, 115203. [Google Scholar] [CrossRef]
- Liu, X.; Arfan, M.; Rahman, M.U.; Fatima, B. Analysis of SIQR type mathematical model under Atangana-Baleanu fractional differential operator. Comput. Methods Biomech. Biomed. Eng. 2023, 26, 98–112. [Google Scholar] [CrossRef]
- Ghanbari, B.; Atangana, A. A new application of fractional Atangana–Baleanu derivatives: Designing ABC-fractional masks in image processing. Phys. Stat. Mech. Its Appl. 2020, 542, 123516. [Google Scholar] [CrossRef]
- Dokuyucu, M.A. Analysis of a novel finance chaotic model via ABC fractional derivative. Numer. Methods Partial. Differ. Equ. 2021, 37, 1583–1590. [Google Scholar] [CrossRef]
- Li, B.; Liang, H.; He, Q. Multiple and generic bifurcation analysis of a discrete Hindmarsh-Rose model. Chaos Solitons Fractals 2021, 146, 110856. [Google Scholar] [CrossRef]
- Li, B.; Liang, H.; Shi, L.; He, Q. Complex dynamics of Kopel model with nonsymmetric response between oligopolists. Chaos Solitons Fractals 2022, 156, 111860. [Google Scholar] [CrossRef]
- Li, B.; Zhang, T.; Zhang, C. Investigation of financial bubble mathematical model under fractal-fractional Caputo derivative. Fractals 2023, 31, 2350050. [Google Scholar] [CrossRef]
- Li, B.; Zhang, Y.; Li, X.; Eskandari, Z.; He, Q. Bifurcation analysis and complex dynamics of a Kopel triopoly model. J. Comput. Appl. Math. 2023, 426, 115089. [Google Scholar] [CrossRef]
- Özdemir, N.; Uçar, E. Investigating of an immune system-cancer mathematical model with Mittag-Leffler kernel. AIMS Math. 2020, 5, 1519–1531. [Google Scholar] [CrossRef]
- Uçar, E.; Özdemir, N. A fractional model of cancer-immune system with Caputo and Caputo–Fabrizio derivatives. Eur. Phys. J. Plus 2021, 136, 43. [Google Scholar] [CrossRef] [PubMed]
- Evirgen, F.; Ucar, E.; Özdemir, N.; Altun, E.; Abdeljawad, T. The impact of nonsingular memory on the mathematical model of Hepatitis C virus. Fractals 2023, 31, 2340065. [Google Scholar] [CrossRef]
- Atangana, A.; Araz, S.I. New Numerical Scheme with Newton Polynomial: Theory, Methods, and Applications; Academic Press: Cambridge, MA, USA, 2021. [Google Scholar]
- Toufik, M.; Atangana, A. New numerical approximation of fractional derivative with non-local and non-singular kernel: Application to chaotic models. Eur. Phys. J. Plus 2017, 132, 444. [Google Scholar] [CrossRef]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, B.; Chen, K.; Zhang, B. Dynamics of the Three-Compartment Financial Bubble Model under the Mittag-Leffler Operator. Fractal Fract. 2023, 7, 608. https://doi.org/10.3390/fractalfract7080608
Li B, Chen K, Zhang B. Dynamics of the Three-Compartment Financial Bubble Model under the Mittag-Leffler Operator. Fractal and Fractional. 2023; 7(8):608. https://doi.org/10.3390/fractalfract7080608
Chicago/Turabian StyleLi, Bo, Kaiwen Chen, and Bo Zhang. 2023. "Dynamics of the Three-Compartment Financial Bubble Model under the Mittag-Leffler Operator" Fractal and Fractional 7, no. 8: 608. https://doi.org/10.3390/fractalfract7080608
APA StyleLi, B., Chen, K., & Zhang, B. (2023). Dynamics of the Three-Compartment Financial Bubble Model under the Mittag-Leffler Operator. Fractal and Fractional, 7(8), 608. https://doi.org/10.3390/fractalfract7080608





