Abstract
We introduce the concept of controlled extended Branciari quasi-b-metric spaces, as well as a -implicit type mapping. Under this new space setting, we derive some new fixed points, periodic points, right and left Ulam–Hyers stability, right and left weak well-posed properties, and right and left weak limit shadowing results. Additionally, we use these findings to solve the fractional differential equations of a Riesz–Caputo type with integral anti-periodic boundary values, as well of nonlinear matrix equations. All ideas, results, and applications are properly illustrated with examples.
1. Extended Branciari Quasi-b-Distance
In the process of the rapid development of fixed-point theory, many new spaces have been emerged with their applications and the study of the newly emerged spaces. Such developments have been an interesting topic among the mathematical research community. A very interesting notion of b-metric space was introduced by Bakhtin [1] (later used by Czerwik in [2,3]). Branciari [4] developed the notion of Branciari distance space via substituting triangle inequality by quadrilateral inequality, while Kamran et al. [5] introduced the notion of extended b-metric space. Mlaiki et al. [6] introduced the concept of controlled metric type space by using two controlled functions in triangle inequality, and thus extended the work of Kamran et al. [5].
Definition 1
([6]). Let be a set and . A function is said to be a controlled metric type if, for all :
- (dc1)
- if and only if ,
- (dc2)
- ,
- (dc3)
- .
The pair is called a controlled metric-type space.
Recently, Abdeljawad et al. [7] have defined the notion of extended Branciari b-metric space by combining extended b-metric and Branciari distances.
Definition 2
([7]). Let be a set and . A function is said to be an extended Branciari b-metric (-metric, for short) if it satisfies, for all , :
- (ebb1)
- if and only if ,
- (ebb2)
- ,
- (ebb3)
- .
The pair will be called an extended Branciari b-metric space (EBbMS for short). If , then will be called a Branciari b-metric space.
In [8], Zubair et al. combined the work of Mlaiki et al. [6] and Abdeljawad et al. [7], and introduced the controlled b-Branciari metric-type space as follows:
Definition 3
([8]). Let be a set and . A function is said to be a controlled b-Branciari metric type if it satisfies, for all distinct :
- (dcb1)
- if and only if ,
- (dcb2)
- ,
- (dcb3)
- .
The pair is called a controlled b-Branciari metric-type space.
On the other hand, the notion of b-metric space was generalized to quasi-b-metric space in [9], and the concepts of right and left quasi-b-metric spaces were established in [10]. Jain et al. [11] recently introduced the idea of extended Branciari quasi-b-metric spaces and right and left completeness in these spaces, which represent an extension of the quasi-b-metric spaces notion.
Definition 4.
Let be a set and . A function is called an extended Branciari quasi-b-metric, if for all , and all distinct :
- (qeb1)
- ,
- (qeb2)
- .
The triplet is then called an extended Branciari quasi-b-metric space (EBQbMS for short) with the coefficient .
Inspired by the above discussion, in the following sections, we are going to introduce the controlled extended Branciari quasi-b-metric spaces and its related notions.
Definition 5.
Let be a set and . A function is said to be a controlled extended Branciari quasi-b-metric if it satisfies the following:
- (q1)
- ,
- (q2)
for all distinct . The pair is called a controlled extended Branciari quasi-b-metric space (controlled EBQbMS for short).
Definition 6.
Let be a controlled EBQbMS and let be a sequence in ϝ and . The sequence converges to ϖ if and only if .
Remark 1.
In a controlled EBQbMS, the uniqueness of limit is for a convergent sequence.
Definition 7.
Let be a controlled EBQbMS and let be a sequence in ϝ. The sequence is said to be as follows:
- (i)
- left--Cauchy if for every , there exists such that for all ,
- (ii)
- right--Cauchy if for every , there exists such that for all ,
- (iii)
- -Cauchy if for every , there exists such that for all .
Definition 8.
Let be a controlled EBQbMS. Then is called the following:
- (i)
- left--complete if every left--Cauchy sequence in ϝ is convergent,
- (ii)
- right--complete if every right--Cauchy sequence in ϝ is convergent,
- (iii)
- -complete if every -Cauchy sequence in ϝ is convergent.
Definition 9.
Let be a controlled EBQbMS. The mapping is continuous if each sequence for in ϝ is convergent to and the sequence converges to , that is,
Example 1.
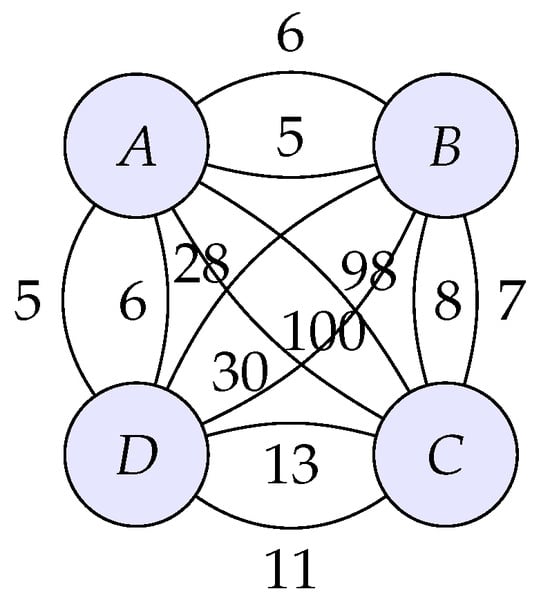
Let be four cities of India, and suppose that there is only a one-way inter-city connection. Then, we define a set of nodes as . Denote as the fare between the cities, which is defined as
Next, we denote the inter-city distances as and define
In Figure 1, is demonstrated.

Figure 1.
Distance graph, .
It can be readily ascertained that is a controlled EBQbMS but not an EBQbMS as
Example 2.
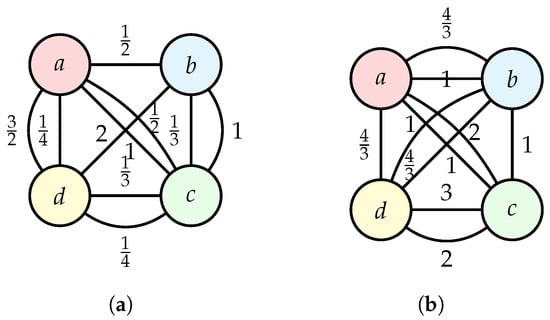
Let . Define by

Figure 2.
(a) Distance graph, . (b) Weight graph, .
It can be readily ascertained that is a controlled EBQbMS as
but not an EBQbMS as
The importance of this work lies in the fact that, in the context of right completeness (or left completeness), a new implicit relation makes it easier to demonstrate fixed-point results in a controlled EBQbMS space. In the context of underlining space, we also present novel ideas such as right and left Ulam–Hyers stability, right and left weak well-posed properties, right and left weak-limit shadowing properties, as well as their associated results. The two graphics depict a novel application to nonlinear matrix equations when using two illustrations. This demonstrates that our matrix equation solution assurance criteria are “weaker" than those previously derived in the literature. In addition, we used these findings to solve the fractional differential Riesz–Caputo equations with integral antiperiodic boundary values in the underlying space, and this was followed by an example demonstrating the validity of the result.
2. -Implicit Relations
The following notion was inspired by [12]. Let be a nonempty set. As denoted by , the set of all functions satisfy the following conditions:
- (i)
- is increasing and ;
- (ii)
- there exists such that, for all , and , where denotes the n-th iterate of .
It is clear that and the class .
Example 3.
Let be a controlled EBQbMS, where and . Consider the mapping , where . Note that . Thus,
Therefore, and hence .
We start by introducing a modified implicit relation, as in [13,14].
Let be the set of all functions satisfying the following conditions:
- (Ω1)
- for all and , implies that there exists such that ;
- (Ω2)
- If , then .
Example 4.
Let , and .
- (Ω1)
- Let , and .Now, if , then we obtain , which gives as and , i.e., a contradiction. Therefore, we obtain , where so that .
- (Ω2)
- If , that is, , then gives , which is a contradiction. Therefore, .
Example 5.
Let , , and .
- (Ω1)
- Let , and .Then, . Hence, , where , . It is easy to check that , with , and can be chosen so that .
- (Ω2)
- If , then it is a contradiction as . Therefore, .
3. Main Results
We introduced -implicit type mappings on a controlled EBbQMS.
Definition 10.
Let be a controlled EBQbMS and . We then say that ℑ is a -implicit type mapping if there exists such that for ,
For a self-mapping ℑ on a set , it is denoted as .
Theorem 1.
Let be a right--complete controlled EBQbMS with , and let be a continuous -implicit-type mapping where . Then, is a singleton set.
Proof.
Let and define a sequence by for all . If for some , and we then come to the conclusion. Thus, assume that for all . Using (1) with and , we have
that is,
Using , we obtain that there is a such that
and so
With the successive use of (1) with , we have
Similarly, if we take and , then we obtain
Next, we prove is a right--Cauchy sequence, that is, . We then discuss the two possible cases.
Case I. Let , . Then, by (q2), we have
that is, .
Case II. Let , . Then, by (q2), we have
that is, . Thus, by combining both cases, for all ; hence, the sequence is a right--Cauchy one.
Using the right--completeness of , we can deduce that there exists such that as , that is,
Using (q2), we have
Since ℑ is continuous, by taking , we obtain , that is, .
At last, we can show that is a set of one. Assume, however, that there are different . Through using (1), we have
i.e.,
It follows from that , which implies that . □
Example 6.
Let and be as in Example 1, and let us denote ℑ on ϝ as the toll tax of the city and define
Only Condition (1) of Theorem 1 has to be checked. When using Example 4, we have to check
for and , where .
Consider the following cases:
Case() If and (or and ; and ; or and ), then (5) holds trivially.
Case() Let and . Then,
and
so (5) reduces to .
Case() Let and . Then,
and
so (5) reduces to .
Case() Let and . Then,
and
so (5) reduces to .
Case() Let and . Then,
and
so (5) reduces to .
Case() Let and . Then, we have
and
so (5) reduces to .
Case() Let and . Then,
and
so (5) reduces to .
Case() Let and . Then,
and
so (5) reduces to .
Case() Let and . Then,
and
so (5) reduces to .
If we take and , then in all the cases the contractive Condition (5) holds true. Hence, ℑ is a -implicit type mapping.
Thus, all the conditions of Theorem 1 are fulfilled and is the unique fixed point of ℑ.
By choosing from Examples 4 and 5, we obtain the following consequences.
Corollary 1.
Let all the conditions of Theorem 1 be satisfied, except that the -implicit type condition is replaced by condition of the form (for all , with ). Thus, we have the following:
- (I)
- where and , or
- (II)
- where and
Then, is a singleton.
4. A Periodic Point Result
It is self-evident that if and , then , for an arbitrary . Nonetheless, it is evident that the opposite is not true, that is, a self-map may have a “periodic" point (a point satisfying for some ) that is not its fixed point.
Definition 11
([15]). A mapping is said to have the property (P) if it has no periodic points, i.e., if for every .
Theorem 2.
Under the assumptions of Theorem 1, ℑ has the property (P).
Proof.
Let , then . If , as in the proof of Theorem 1, we obtain such that . Using (1), we have
which is a contradiction. Therefore, for all . □
5. Results of the Ulam–Hyers Stability
This section provides a definition of the right and left Ulam–Hyers stability of the fixed-point problem (FPP) in controlled EBQbMS, which is an extension of the EBQbMS case discussed in [11] (see also [16,17,18]).
Definition 12.
Let be a controlled EBQbMS and . Then, the fixed-point equation (FPE)
is said to be as follows:
- 1.
- The right Ulam–Hyers is stable in the setting of EBQbMS if there exists such that for all and for all ε-solutions , that is,wherein there exists a solution of (6) such that
- 2.
- The left Ulam–Hyers is stable in the setting of EBQbMS if there exists such that for all and for all ε-solutions , that is,wherein there exists a solution of (6) such that
Theorem 3.
Let be a right -complete controlled EBQbMS with , and let be a continuous mapping satisfying the following:
for all , where and . Then, the FPE (6) is right Ulam–Hyers stable.
6. Right and Left Weak Well-Posed Properties (Right and Left Weak Limit Shadowing)
The concept of a well posited fixed-point problem (FPP) has captured the attention of numerous mathematicians, including Popa [19,20] and others. The authors of the paper [21] defined a weak well posed (wwp) property in a BbDS. In the following section, we will extend this concept to a controlled EBQbMS.
Definition 13.
Let be a controlled EBQbMS, and let . The FPP of ℑ is said to be right [resp. left-] if it satisfies the following:
- 1.
- ;
- 2.
- for any sequence in ϝ with and, one has[resp. for any sequence in ϝ with and, one has ].
Theorem 5.
Let be a right -complete controlled EBQbMS with , and let be continuous and satisfy Condition (9). Then, the FPP of ℑ is right wwp.
Proof.
Let be a (unique) fixed point of ℑ, and let be a sequence in such that and , for . Owing to (q2), we have
By letting in the above inequality, we obtain
WLOG. It is reasonable to presume that a subsequence of having distinct elements exists. Alternatively, there exists and such that for . As , . If , then since there is only one fixed point of ℑ. For , we obtain .
Using (9) for , we obtain
By letting and using , we have
which is not true. Thus, there exists such that . Then,
Therefore, from (12), we have
Again, by using (9), we obtain
i.e.,
By letting and using the continuity of ℑ, we obtain
which implies that
Therefore, from (13), we obtain
which is a contradiction. Therefore, . □
Theorem 6.
Let be a left -complete controlled EBQbMS with , and let be continuous and satisfy Condition (9). Then, the FPP of ℑ is left wwp.
There are some pieces of literature on the limit shadowing property of fpps ([22,23]). In order to investigate the right and left weak limit shadowing property (right wlsp/left wlsp) in a controlled EBQbMS, we first need to define these terms.
Definition 14.
Let be a controlled EBQbMS and .
- 1.
- The fpp of ℑ is said to have right wlsp in ϝ if assuming that in ϝ satisfies as and as . Thus, it follows that there exists such that as .
- 2.
- The fpp of ℑ is said to have left wlsp in ϝ if assuming that in ϝ satisfies as and as . Thus, it follows that there exists such that as .
Theorem 7.
Let be a right -complete controlled EBQbMS, and let be continuous and satisfy Condition (9) Then, ℑ has the right wlsp.
Proof.
Let , and let in be such that and . Since , , then, owing to Theorem 5, . Therefore, we obtain . □
Theorem 8.
Let be a left -complete controlled EBQbMS, and let be continuous and satisfy (9). Then, ℑ has the left wlsp.
7. Applications to Riesz–Caputo Fractional Derivatives
In comparison to integer-order models, fractional-order models provide a more plausible account of memory and genetic processes. Riemann–Liouville and Riesz derivatives have been frequently used in the research on fractional boundary/initial value problems (FBVP/FIVP) in recent years. These fractional operators, however, are one-sided and can only alter the past or the future. The Riesz space fractional operator, in contrast to the other fractional operators, is a two-sided operator that captures both past and present non-local memory effects. This is critical because present states in the mathematical models of physical processes on finite domains are affected by both past and future memory effects. In the anomalous diffusion problem, for example, the Riesz fractional derivative has been utilized to account for memory effects in both past and future concentrations. The authors of [24,25,26] addressed the solution of Riesz–Caputo fractional type BVP.
In this section, we investigate the uniqueness of a solution for an integral-type anti-periodic boundary value problem (APBVP) that is of a Riesz–Caputo fractional type of the form
where is the Riesz–Caputo derivative, is a continuous function, and (where X is a Banach space).
Before a discussion on the solutions of APBVP, we introduce the related notions.
Definition 15
([27]). Let . The left and right Riemann–Liouville fractional integral of a function of order ζ is defined as follows:
Definition 16.
Let . The Riesz fractional integral of a function of order ζ is defined as follows:
Definition 17
([27]). Let , . Then, the left and right Caputo fractional derivatives of a function of order ζ are defined as follows:
where is the ordinary differential operator.
Definition 18.
Let , . Then, the Riesz–Caputo fractional derivative of order ζ of a function is defined by
Lemma 1
([27]). Let and . Then, the following relations hold:
Therefore, we obtain
When and , we have
Lemma 2.
Suppose that and . Then, the fractional APBVP of order ζ in is
which is equivalent to the integral equation of the form
Proof.
We are now able to bring up, with the appropriate conditions for our APBVP, a unique solution. Let be the space of continuous functions , which are defined on with the norm .
Theorem 9.
Let be a continuous function. Assume that there exist non-negative real numbers , , such that for all , we have the following:
- (A1)
- (A2)
- for all ,
- (A3)
Then, Problem (14) has a unique solution on .
Proof.
Remark 2.
Lemma 2 and Theorem 9 generalize the work that is discussed in Wang and Wang [28]. Also, we used the generalized Banach fixed-point theorem 1 in a controlled EBQbMS to prove these results.
Example 7.
Consider the following nonlinear FDE with a Riesz–Caputo derivative:
Here, , , , , and
Therefore, (A1) and (A2) are satisfied with , and . Further,
Thus, by Theorem 9, Problem (23) has a unique solution on .
Example 8.
Consider the following nonlinear FDE with a Riesz–Caputo derivative:
Here, , , , , and
Therefore, (A1) and (A2) are satisfied with , and . Further,
Thus, by Theorem 9, Problem (24) has a unique solution on .
8. Application to Nonlinear Matrix Equations
A Hermitian matrix is a square matrix that is equal to its conjugate transposed matrix. Let denote the set of all Hermitian matrices over , and let be the set of all matrices over . Denote by any singular value of a matrix (singular values are the absolute values of the eigenvalues of a matrix ) and the trace norm of by . On , we define ( or ) if and only if is a positive semi-definite matrix (both of which are positive definites).
In [29], Ran and Reurings discussed the existence of solutions for the equation of
in , where , is a positive definite (PD), and ℏ is a mapping from into . Note that is a solution of (25) if and only if it is a fixed point of the mapping .
In [30], Sawangsup and Sintunavarat discussed the nonlinear matrix equation (NME) for the spectral norm of a matrix. For other variants on NMEs, one is referred to the studies of [31,32,33,34].
Theorem 10.
Consider the equation
where , , , and the operator is continuous in the trace norm. For some , and for any with , , let them hold for all singular values of .
Assume the following:
- 1.
- , where ;
- 2.
- For any with , holds;
- 3.
- For any with , holds;
- 4.
- There exists , so thatholds, wherefor all with and .
Then, Equation (26) has a unique solution of with . Moreover, the solution can be obtained as the limit of the iterative sequence , where, for , we have
and is an arbitrary element of satisfying .
Proof.
Denote as being a closed subset of . According to (2), any solution of (26) in has to be PD. For any , we have
For all , it follows that . Thus, (30) implies
Now, define an operator by
for . Consequently, finding the PDS of Equation (26) is equivalent to finding the fixed point(s) of ℑ.
For all can be expressed as
Thus, for all , we have
For some fixed , from (27) and (28), we have
that is,
Therefore, from (31), we have
Let be defined by
Then, is a complete controlled EBQbMS with the coefficient . It follows from (32) that
Let , and in (33). Thus, we have
Then, the formulated results follow from Theorem 1. □
9. Numerical Experiments
The experiment was conducted on an macOS Mojave version 10.14.6 CPU1.6 GHz Intel core i5 8GB with the programming language MATLAB R2020b (Online). The error is the symbol for the trace norm of the residual (), and CPU is the estimate time. In all of the investigations, was allocated.
Example 9.
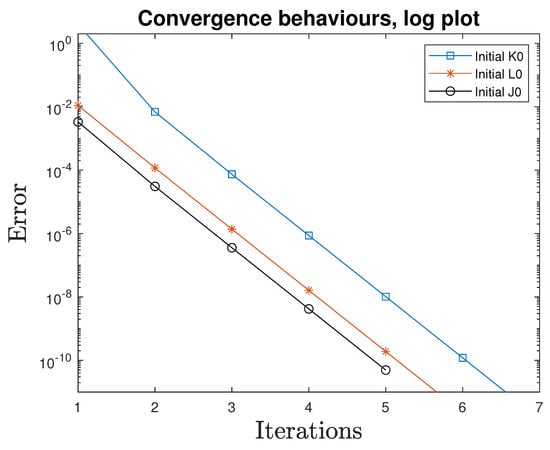
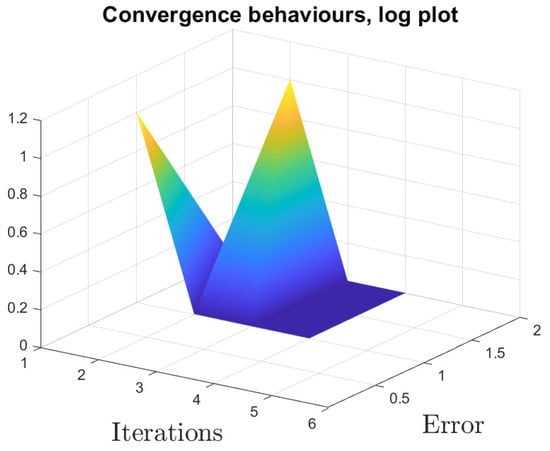
Consider matrices with coefficients that are constructed at random by
where . For , we obtain
We used the initial values
where . For , , the PDS is
The graphical view of convergence and the surface plot of are shown in Figure 3 and Figure 4, respectively.

Figure 3.
Iteration vs. error graph.

Figure 4.
Solution surface plot.
Example 10.

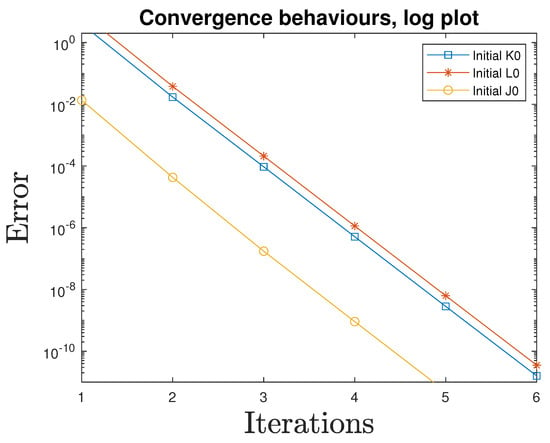
Consider the matrices as follows:
We began with the following initializations to demonstrate the convergence of the sequence , which was specified in (29) as follows:
where . Table 1 shows the details of the iteration, where the PDS is given by , and the convergence graph is shown in Figure 5.

Table 1.
Three initialization based analysis.

Figure 5.
Iteration vs. error graph.
10. Conclusions
In this work, a new concept of controlled extended Branciari quasi-b -metric spaces and a -implicit-type mapping were introduced. Further, we derived some new fixed-point, periodic-point, right and left Ulam-Hyers stability, right and left weak well-posed properties, and right and left weak limit shadowing results under the new space settings. We applied the results to find the solutions to the Riesz-Caputo fractional differential equations with integral anti-periodic boundary values and nonlinear matrix equations. All ideas, results, and applications are properly illustrated with examples.
Author Contributions
Conceptualization, H.K.N., writing—original draft preparation, R.J., H.K.N., and R.G.; writing—review and editing, H.K.N. and R.G.; software, H.K.N.; validation, H.K.N.; formal analysis, H.K.N.; investigation, H.K.N.; visualization, H.K.N.; funding acquisition, R.G. All authors have read and agreed to the published version of the manuscript.
Funding
The authors extend their appreciation to Prince Sattam bin Abdulaziz University for funding this research work through project number PSAU/2023/01/25637.
Data Availability Statement
Data are contained within the article.
Acknowledgments
We thank the editor for their kind support. The authors are thankful to the learned reviewers for their valuable comments.
Conflicts of Interest
The authors declare that they have no competing interest.
References
- Bakhtin, I.A. The contraction mapping principle in quasi metric spaces. Funkc. Anal. Ulianowsk Gos. Ped. Inst. 1999, 30, 243–253. [Google Scholar]
- Czerwik, S. Contraction mappings in b-metric spaces. Acta Math. Inform. Univ. Ostraviensis. 1993, 5, 5–11. [Google Scholar]
- Czerwik, S. Nonlinear set-valued contraction mappings in b-metric spaces. Atti Sem. Mat. Fis. Univ. Modena 1998, 46, 263–276. [Google Scholar]
- Branciari, A. A fixed point theorem for mappings satisfying a general contractive condition of integral type. Int. J. Math. Math. Sci. 2002, 29, 531–536. [Google Scholar] [CrossRef]
- Kamran, T.; Samreen, M.; Ain, O.U. A generalization of b-metric space and some fixed point theorems. Mathematics 2017, 5, 19. [Google Scholar] [CrossRef]
- Mlaiki, N.; Aydi, H.; Souayah, N.; Abdeljawad, T. Controlled metric type spaces and the related contraction principle. Mathematics 2018, 6, 194. [Google Scholar] [CrossRef]
- Abdeljawad, T.; Karapinar, E.; Panda, S.K.; Mlaiki, N. Solutions of boundary value problems on extended-Branciari b-distance. J. Ineq. Appl. 2020, 2020, 103. [Google Scholar] [CrossRef]
- Tasneem, Z.S.; Kalpana, G.; Abdeljawad, T. Controlled b-Branciari metric-type spaces and related fixed-point theorems with applications. Filomat 2020, 34, 4253–4269. [Google Scholar]
- Shah, M.H.; Hussain, N. Nonlinear contractions in partially ordered quasi b-metric spaces. Commun. Korean Math. Soc. 2012, 27, 117–128. [Google Scholar] [CrossRef]
- Hussain, N.; Vetro, C.; Vetro, F. Fixed point results for α-implicit contractions with application to integral equations. Nonlinear Anal. Model. Control 2016, 21, 362–378. [Google Scholar] [CrossRef]
- Jain, R.; Nashine, H.K.; Parvaneh, V. Extended Branciari quasi-b-distance spaces, implicit relations and application to nonlinear matrix equations. J. Inequalities Appl. 2021, 2021, 200. [Google Scholar] [CrossRef]
- Shatanawi, W.; Abodayeh, K.; Mukheimer, A. Some fixed point theorems in extended b-metric spaces. UPB Sci. Bull. Ser. A 2018, 80, 71–78. [Google Scholar]
- Popa, V.; Mocanu, M. Altering distance and common fixed points under implicit relations. Hacettepe J. Math. Stat. 2009, 38, 329–337. [Google Scholar]
- Aliouche, A.; Djoudi, A. Common fixed point theorems for mappings satisfying an implicit relation without decreasing assumption. Hacettepe J. Math. Stat. 2007, 36, 11–18. [Google Scholar]
- Jeong, G.S.; Rhoades, B.E. Maps for which F(T) = F(Tn). Fixed Point Theory Appl. 2005, 6, 87–131. [Google Scholar]
- Felhi, A.; Sahmim, S.; Aydi, H. Ulam-Hyers stability and well-posedness of fixed point problems for α-λ-contractions on quasi b-metric spaces. 1973 Fixed Point Theory Appl. 2016, 2016, 1. [Google Scholar] [CrossRef]
- Nashine, H.K.; Kadelburg, Z. Existence of solutions of cantilever beam problem via α-β-FG-contractions in b-metric-like spaces. Filomat 2017, 31, 3057–3074. [Google Scholar] [CrossRef]
- Phiangsungnoen, S.; Sintunavarat, W.; Kumam, P. Fixed point results, generalized Ulam-Hyers stability and well-posedness via α-admissible mappings in b-metric spaces. Fixed Point Theory Appl. 2012, 2014, 188. [Google Scholar] [CrossRef]
- Popa, V. Well-posedness of fixed point problems in orbitally complete metric spaces. Stud. Cerc. St. Ser. Mat. Univ. 2006, 16, 18–20. [Google Scholar]
- Popa, V. Well-posedness of fixed point problems in compact metric spaces. Bul. Univ. Petrol-Gaze, Ploiesti Sec. Mat. Inform. Fiz. 2008, 60, 1–4. [Google Scholar]
- Chen, L.; Huang, S.; Li, C.; Zhao, Y. Several fixed-point theorems for F-contractions in complete Branciari b-metrics, and applications. J. Funct. Spaces 2020, 2020, 7963242. [Google Scholar]
- Păcurar, M.; Rus, I.A. Fixed point theory for cyclic ϕ-contractions. Nonlinear Anal. 2010, 72, 1181–1187. [Google Scholar] [CrossRef]
- Rus, I.A. The theory of a metrical fixed point theorem: Theoretical and applicative relevances. Fixed Point Theory 2008, 9, 541–559. [Google Scholar]
- Chen, F.; Baleanu, D.; Wu, G. Existence results of fractional differential equations with Riesz-Caputo derivative. Eur. Phys. J. Spec. Top. 2017, 226, 3411–3425. [Google Scholar] [CrossRef]
- Chen, F.; Chen, A.; Wu, X. Anti-periodic boundary value problems with Riesz-Caputo derivative. Adv. Differ. Equ. 2019, 2019, 119. [Google Scholar] [CrossRef]
- Toprakseven, S. On the solutions of the higher order fractional differential equations of Riesz space derivative with anti-periodic boundary conditions. Commun. Adv. Math. Sci. 2021, 4, 171–179. [Google Scholar] [CrossRef]
- Kilbas, A.; Srivastava, H.H.; Trujillo, J. Theory and Applications of Fractional Differential Equations; North-Holland Mathematics Studies; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Wang, S.; Wang, Z. Existence results for fractional differential equations with the Riesz-Caputo derivative. J. Nonlinear Model. Anal. 2022, 4, 114–128. [Google Scholar]
- Ran, A.C.M.; Reurings, M.C.B. On the matrix equation X + A*F(X)A = Q: Solutions and perturbation theory. Linear Alg. Appl. 2002, 346, 15–26. [Google Scholar] [CrossRef]
- Sawangsup, K.; Sintunavarat, W. Fixed point and multidimensional fixed point theorems with applications to nonlinear matrix equations in terms of weak altering distance functions. Open Math. 2017, 15, 111–125. [Google Scholar] [CrossRef]
- Bera, A.; Dey, L.K.; Garai, H.; Raha, S. Common fixed points via asymptotic contraction and application to matrix equations. Comput. Appl. Math. 2020, 39, 301. [Google Scholar] [CrossRef]
- Garai, H.; Dey, L.K. Common solution to a pair of nonlinear matrix equations via fixed point results. J. Fixed Point Theory Appl. 2019, 21, 1–18. [Google Scholar] [CrossRef]
- Garai, H.; Dey, L.K.; Sintunavarat, W.; Som, S.; Raha, S. On new existence of a unique common solution to a pair of nonlinear matrix equations. arXiv 2020, arXiv:2006.10863. [Google Scholar]
- Nashine, H.K.; Shil, S.; Garai, H.; Dey, L.K.; Parvaneh, V. Common fixed point results in ordered left (right) quasi b-metric spaces and applications. J. Math. 2020, 2020, 8889453. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).