Privacy Preservation of Nabla Discrete Fractional-Order Dynamic Systems
Abstract
1. Introduction
- In contrast to the existing privacy-preserving literature that only concentrates on integer-order systems, this paper introduces a differential privacy mechanism for nabla discrete fractional-order dynamic systems. This method introduces Gaussian random noise into the output to prevent sensitive information from being inferred by malicious attackers.
- A connection between the differential privacy of initial values and the observability of nabla discrete fractional-order systems is provided. Furthermore, the paper proposes a sufficient condition for maintaining differential privacy via the observability Gramian matrix, effectively addressing the analytical challenges introduced by random noise in nabla fractional-order systems.
- An optimal Gaussian noise distribution is derived from an optimization problem. This distribution ensures the achievement of the desired privacy level while maintaining system performance.
2. Preliminaries
2.1. Notations
2.2. Discrete Fractional Calculus
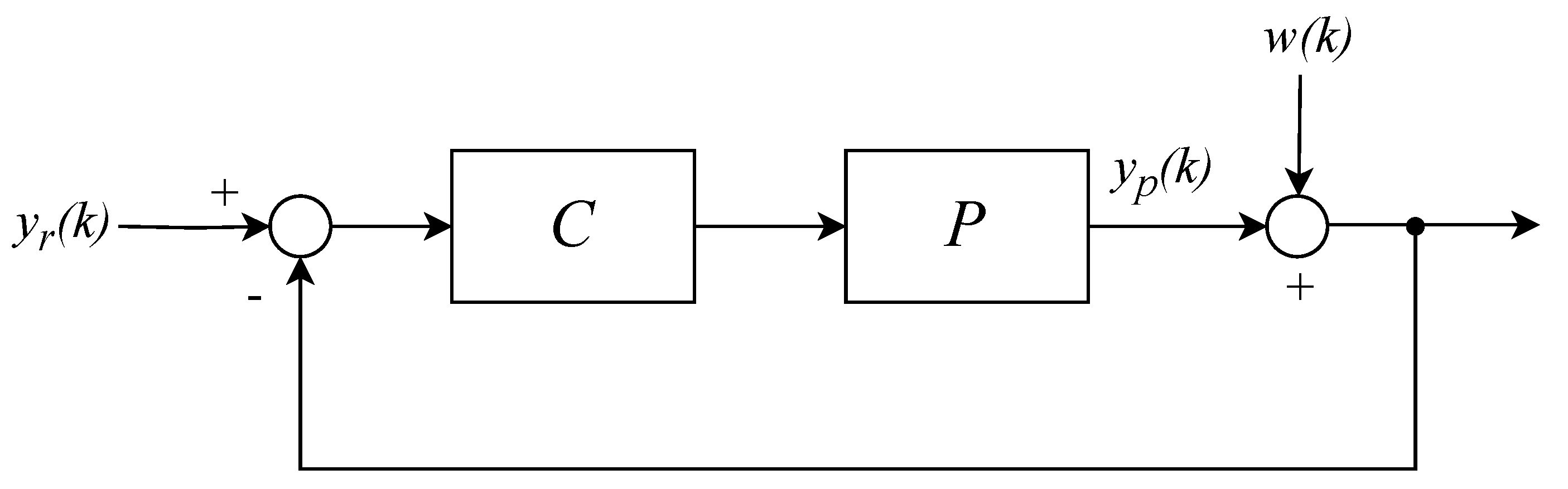
3. Problem Statement
4. Differential Privacy for Nabla Discrete Fractional-Order Systems
4.1. Differential Privacy with Output Noise
4.2. Connection with Observability
- 1
- The initial states of system (8) is observable in a finite time .
- 2
- The observability matrix has rank n.
- 3
- The observability Gramian matrix has rank n.
4.3. Minimization of the Noise
5. Numerical Example
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yamni, M.; Daoui, A.; El Ogri, O.; Karmouni, H.; Sayyouri, M.; Qjidaa, H.; Flusser, J. Fractional Charlier moments for image reconstruction and image watermarking. Signal Process. 2020, 171, 107509. [Google Scholar] [CrossRef]
- Wu, J.; Xu, Z.; Zhang, Y.; Su, C.Y.; Wang, Y. Modeling and tracking control of dielectric elastomer actuators based on fractional calculus. ISA Trans. 2023, 138, 687–695. [Google Scholar] [CrossRef] [PubMed]
- Traver, J.E.; Nuevo-Gallardo, C.; Tejado, I.; Fernández-Portales, J.; Ortega-Morán, J.F.; Pagador, J.B.; Vinagre, B.M. Cardiovascular circulatory system and left carotid model: A fractional approach to disease modeling. Fractal Fract. 2022, 6, 64. [Google Scholar] [CrossRef]
- Yousefpour, A.; Jahanshahi, H.; Munoz-Pacheco, J.M.; Bekiros, S.; Wei, Z. A fractional-order hyper-chaotic economic system with transient chaos. Chaos Solitons Fractals 2020, 130, 109400. [Google Scholar] [CrossRef]
- Yin, Y.; Guo, J.; Peng, G.; Yu, X.; Kong, Y. Fractal operators and fractional dynamics with 1/2 order in Biological Systems. Fractal Fract. 2022, 6, 378. [Google Scholar] [CrossRef]
- Chen, P.; Luo, Y.; Zheng, W.; Gao, Z.; Chen, Y. Fractional order active disturbance rejection control with the idea of cascaded fractional order integrator equivalence. ISA Trans. 2021, 114, 359–369. [Google Scholar] [CrossRef]
- Belkhatir, Z.; Laleg-Kirati, T.M. High-order sliding mode observer for fractional commensurate linear systems with unknown input. Automatica 2017, 82, 209–217. [Google Scholar] [CrossRef]
- Qi, F.; Qu, J.; Chai, Y.; Chen, L.; Lopes, A.M. Synchronization of incommensurate fractional-order chaotic systems based on linear feedback control. Fractal Fract. 2022, 6, 221. [Google Scholar] [CrossRef]
- Alessandretti, A.; Pequito, S.; Pappas, G.J.; Aguiar, A.P. Finite-dimensional control of linear discrete-time fractional-order systems. Automatica 2020, 115, 108512. [Google Scholar] [CrossRef]
- Stanisławski, R.; Latawiec, K.J. A modified Mikhailov stability criterion for a class of discrete-time noncommensurate fractional-order systems. Commun. Nonlinear Sci. Numer. Simul. 2021, 96, 105697. [Google Scholar] [CrossRef]
- Baleanu, D.; Wu, G.C.; Bai, Y.R.; Chen, F.L. Stability analysis of Caputo–like discrete fractional systems. Commun. Nonlinear Sci. Numer. Simul. 2017, 48, 520–530. [Google Scholar] [CrossRef]
- Wei, Y.; Su, N.; Zhao, L.; Cao, J. LMI based stability condition for delta fractional order system with sector approximation. Chaos Solitons Fractals 2023, 174, 113816. [Google Scholar] [CrossRef]
- Zhu, Z.; Lu, J.G. LMI-based robust stability analysis of discrete-time fractional-order systems with interval uncertainties. IEEE Trans. Circuits Syst. I-Regul. Pap. 2021, 68, 1671–1680. [Google Scholar] [CrossRef]
- Atici, F.M.; Eloe, P.W. Linear systems of fractional nabla difference equations. Rocky Mt. J. Math. 2011, 41, 353–370. [Google Scholar] [CrossRef]
- Wei, Y.; Chen, Y.; Liu, T.; Wang, Y. Lyapunov functions for nabla discrete fractional order systems. ISA Trans. 2019, 88, 82–90. [Google Scholar] [CrossRef]
- Wei, Y.; Zhao, L.; Wei, Y.; Cao, J. Lyapunov theorem for stability analysis of nonlinear nabla fractional order systems. Commun. Nonlinear Sci. Numer. Simul. 2023, 126, 107443. [Google Scholar] [CrossRef]
- Wei, Y.; Wei, Y.; Chen, Y.; Wang, Y. Mittag–Leffler stability of nabla discrete fractional-order dynamic systems. Nonlinear Dyn. 2020, 101, 407–417. [Google Scholar] [CrossRef]
- Hioual, A.; Ouannas, A.; Grassi, G.; Oussaeif, T.E. Nonlinear nabla variable-order fractional discrete systems: Asymptotic stability and application to neural networks. J. Comput. Appl. Math. 2023, 423, 114939. [Google Scholar] [CrossRef]
- Wei, Y.; Zhao, L.; Zhao, X.; Cao, J. Enhancing the Mathematical Theory of Nabla Tempered Fractional Calculus: Several Useful Equations. Fractal Fract. 2023, 7, 330. [Google Scholar] [CrossRef]
- Stanisławski, R.; Rydel, M.; Li, Z. A new reduced-order implementation of discrete-time fractional-order pid controller. IEEE Access 2022, 10, 17417–17429. [Google Scholar] [CrossRef]
- Zhao, M.; Li, H.L.; Zhang, L.; Hu, C.; Jiang, H. Quasi-projective synchronization of discrete-time fractional-order quaternion-valued neural networks. J. Frankl. Inst. 2023, 360, 3263–3279. [Google Scholar] [CrossRef]
- Gao, P.; Zhang, H.; Ye, R.; Stamova, I.; Cao, J. Quasi-uniform synchronization of fractional fuzzy discrete-time delayed neural networks via delayed feedback control design. Commun. Nonlinear Sci. Numer. Simul. 2023, 126, 107507. [Google Scholar] [CrossRef]
- Ma, J.; Hu, J.; Zhao, Y.; Ghosh, B.K. Leader-Following Consensus Control of Nabla Discrete Fractional Order Multi-Agent Systems. IFAC-PapersOnLine 2020, 53, 2897–2902. [Google Scholar] [CrossRef]
- Yuan, X.; Mo, L.; Yu, Y.; Ren, G. Containment control of fractional discrete-time multi-agent systems with nonconvex constraints. Appl. Math. Comput. 2021, 409, 126378. [Google Scholar] [CrossRef]
- Hong, X.; Zeng, Y.; Zhou, S.; Wei, Y. Nabla fractional distributed optimization algorithm with directed communication topology. In Proceedings of the 2023 6th International Symposium on Autonomous Systems (ISAS), Nanjing, China, 23–25 June 2023; pp. 1–6. [Google Scholar]
- Wang, J.; Cai, Z.; Yu, J. Achieving personalized k-anonymity-based content privacy for autonomous vehicles in CPS. IEEE Trans. Ind. Inform. 2019, 16, 4242–4251. [Google Scholar] [CrossRef]
- Ashkouti, F.; Khamforoosh, K.; Sheikhahmadi, A. DI-Mondrian: Distributed improved Mondrian for satisfaction of the L-diversity privacy model using Apache Spark. Inf. Sci. 2021, 546, 1–24. [Google Scholar] [CrossRef]
- Cramer, R.; Damgård, I.B.; Nielsen, J.B. Secure Multiparty Computation; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Dwork, C. Differential privacy: A survey of results. In Proceedings of the International Conference on Theory and Applications of Models of Computation, Xi’an, China, 25–29 April 2008; Springer: Berlin/Heidelberg, Germany, 2008; pp. 1–19. [Google Scholar]
- Le Ny, J.; Pappas, G.J. Differentially private filtering. IEEE Trans. Automat. Contr. 2013, 59, 341–354. [Google Scholar] [CrossRef]
- Liu, X.K.; Zhang, J.F.; Wang, J. Differentially private consensus algorithm for continuous-time heterogeneous multi-agent systems. Automatica 2020, 122, 109283. [Google Scholar] [CrossRef]
- Yazdani, K.; Jones, A.; Leahy, K.; Hale, M. Differentially private LQ control. IEEE Trans. Automat. Contr. 2022, 68, 1061–1068. [Google Scholar] [CrossRef]
- Wang, Y.; Nedić, A. Tailoring gradient methods for differentially-private distributed optimization. IEEE Trans. Automat. Contr. 2023, 1–16. [Google Scholar] [CrossRef]
- Chen, B.; Leahy, K.; Jones, A.; Hale, M. Differential privacy for symbolic systems with application to Markov Chains. Automatica 2023, 152, 110908. [Google Scholar] [CrossRef]
- Kawano, Y.; Cao, M. Design of privacy-preserving dynamic controllers. IEEE Trans. Automat. Contr. 2020, 65, 3863–3878. [Google Scholar] [CrossRef]
- Wang, L.; Manchester, I.R.; Trumpf, J.; Shi, G. Differential initial-value privacy and observability of linear dynamical systems. Automatica 2023, 148, 110722. [Google Scholar] [CrossRef]
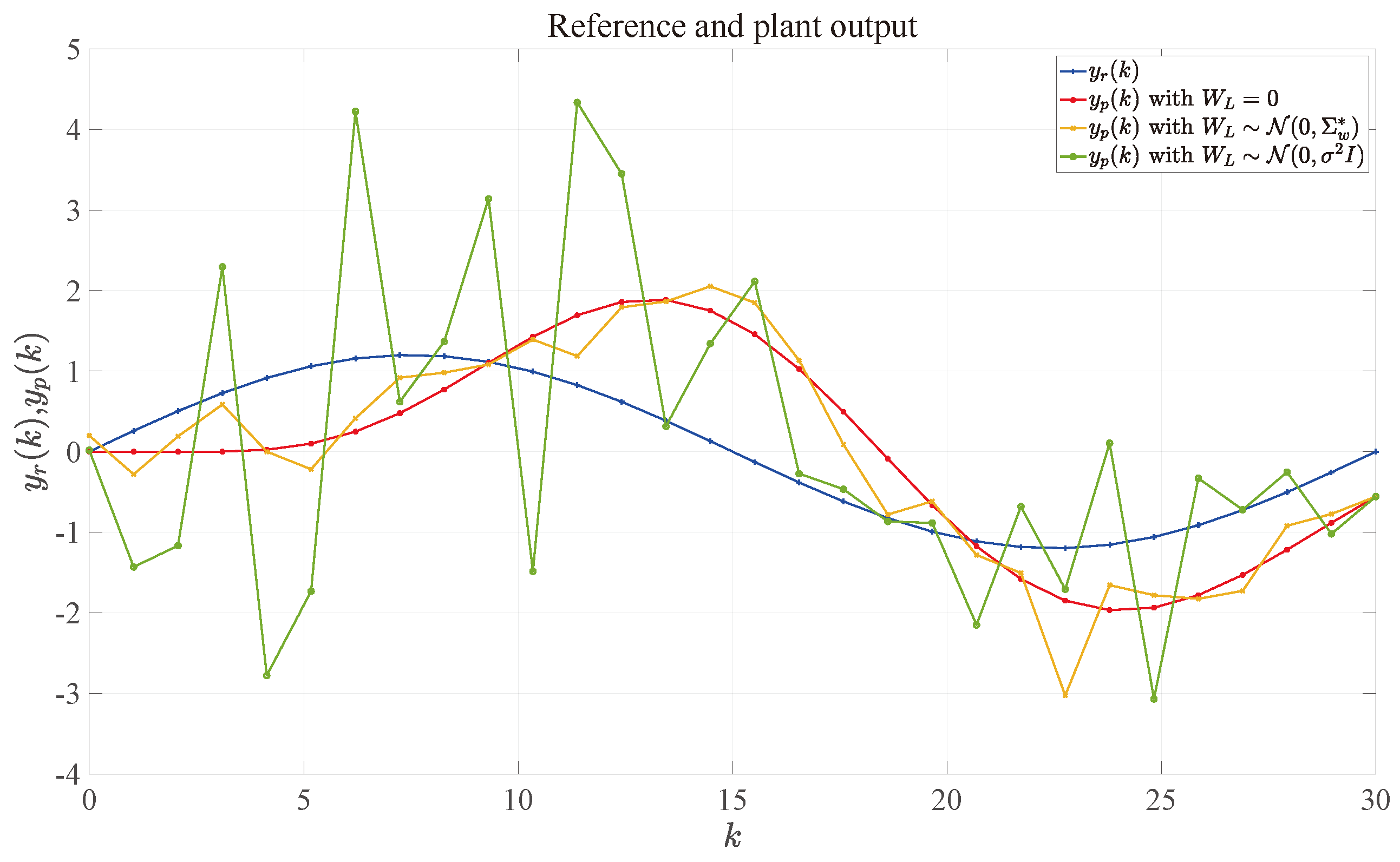
| Noise-Free | i.i.d. Noise | The Minimum Noise |
|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, J.; Hu, J.; Peng, Z. Privacy Preservation of Nabla Discrete Fractional-Order Dynamic Systems. Fractal Fract. 2024, 8, 46. https://doi.org/10.3390/fractalfract8010046
Ma J, Hu J, Peng Z. Privacy Preservation of Nabla Discrete Fractional-Order Dynamic Systems. Fractal and Fractional. 2024; 8(1):46. https://doi.org/10.3390/fractalfract8010046
Chicago/Turabian StyleMa, Jiayue, Jiangping Hu, and Zhinan Peng. 2024. "Privacy Preservation of Nabla Discrete Fractional-Order Dynamic Systems" Fractal and Fractional 8, no. 1: 46. https://doi.org/10.3390/fractalfract8010046
APA StyleMa, J., Hu, J., & Peng, Z. (2024). Privacy Preservation of Nabla Discrete Fractional-Order Dynamic Systems. Fractal and Fractional, 8(1), 46. https://doi.org/10.3390/fractalfract8010046









