Some Fractional Stochastic Models for Neuronal Activity with Different Time-Scales and Correlated Inputs
Abstract
1. Introduction
2. The General Fractional Model
2.1. Some Biological and Modeling Justifications
2.2. The Mathematical Setting for Fractional SDEs and Solutions
- (i)
- There exists such that
- (ii)
- ess
3. Model 1: The FNM Model without Leakage with a Correlated Input:
4. Model 2: The FNM Model with Leakage and a Correlated Input:
5. Model 3: The General FNM Model with Leakage and a Fractional Correlated Input:
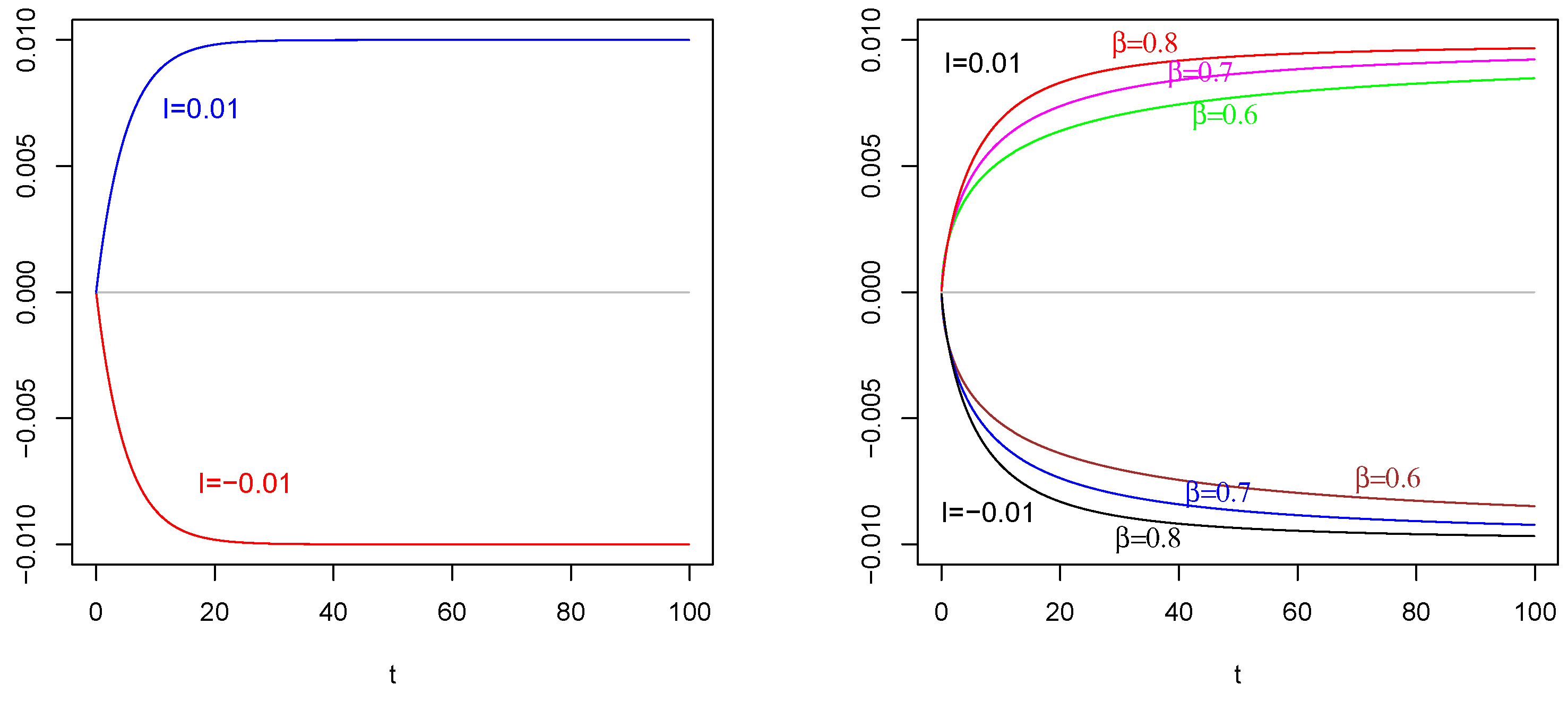
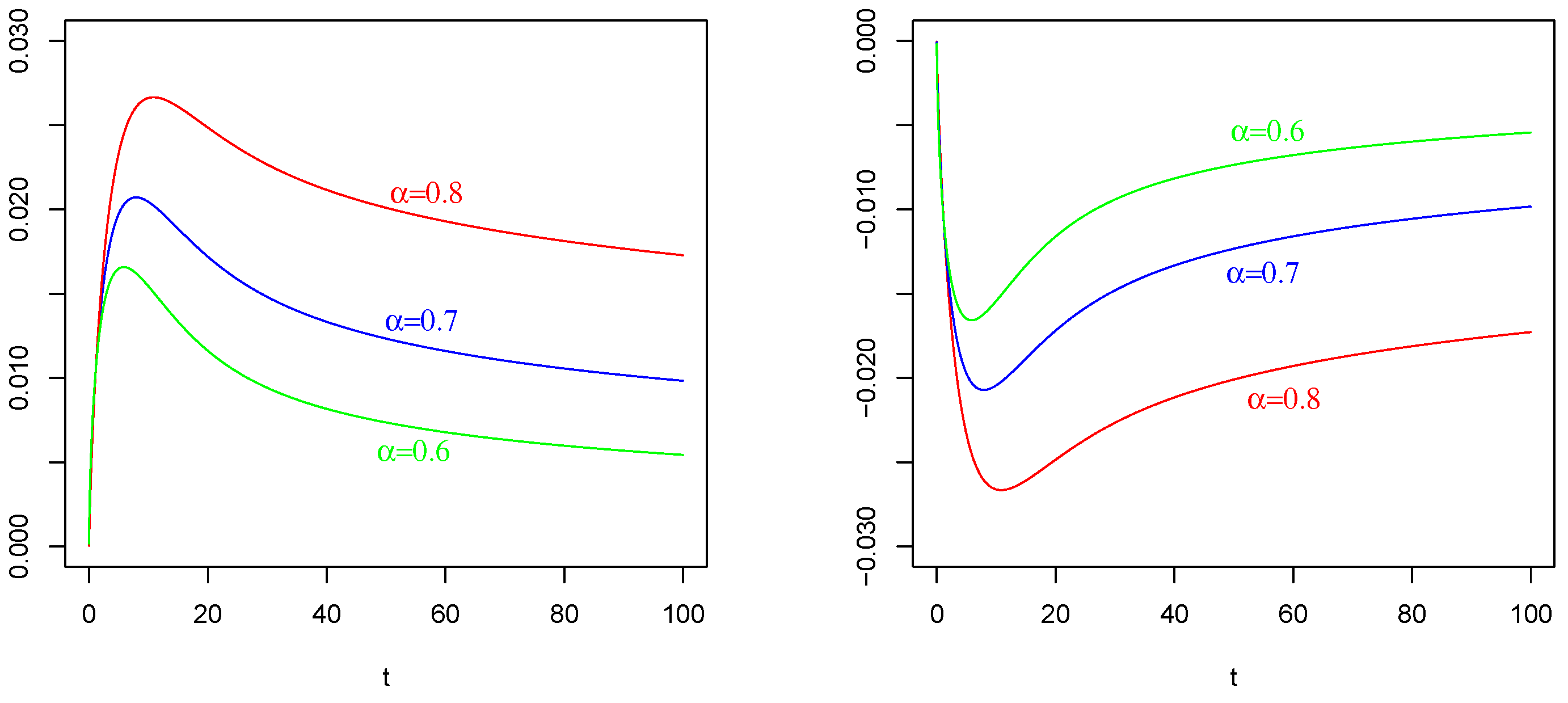
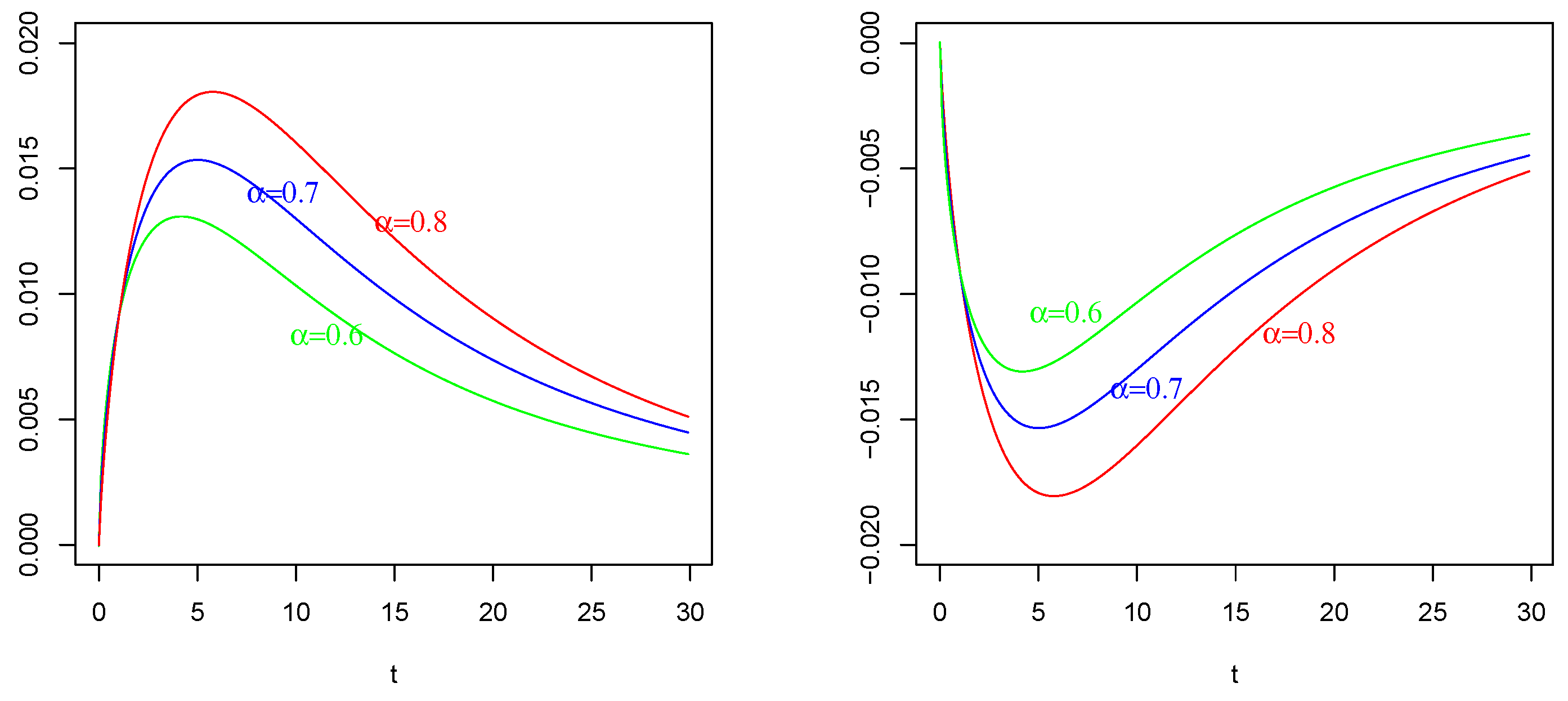
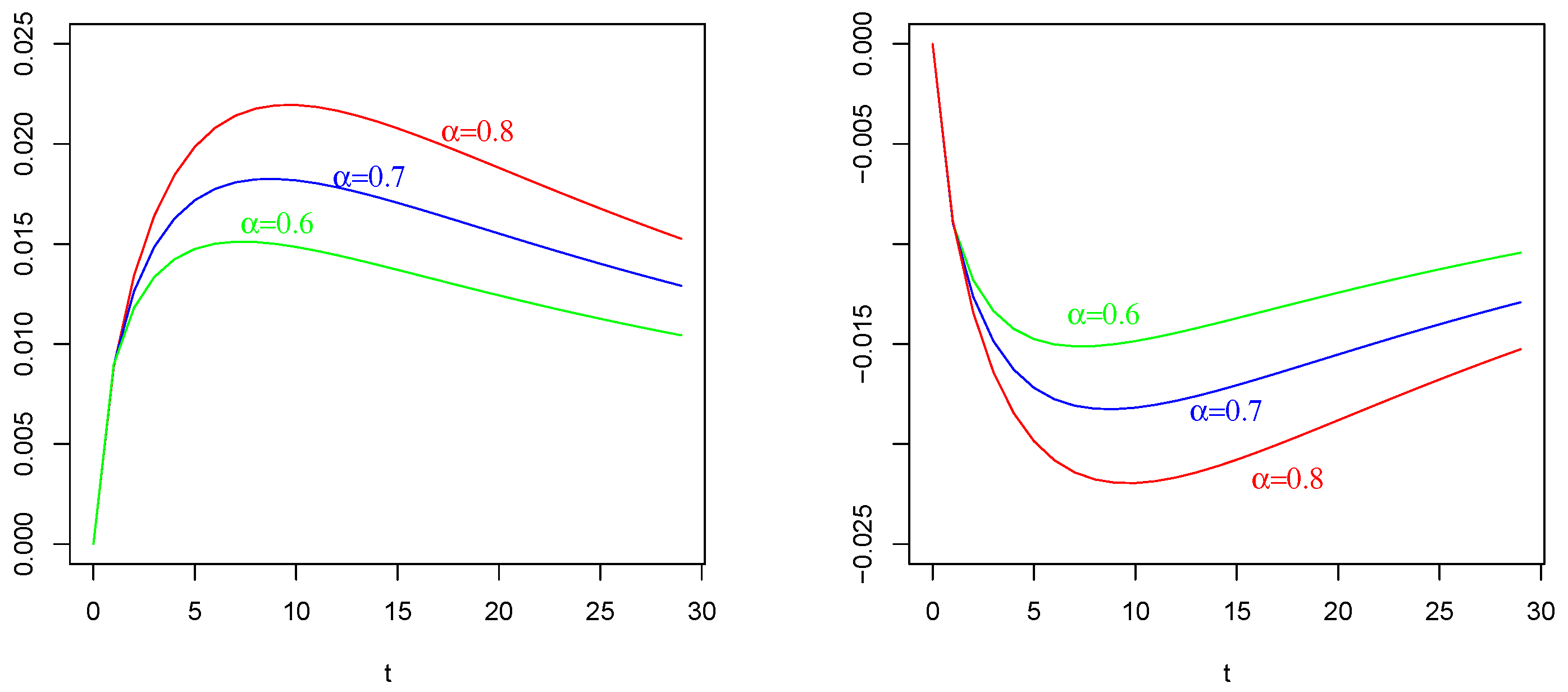
6. Numerical Results and Comparisons
7. Concluding Remarks
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives: Theory and Applications; Gordon and Breach Science Publishers: Philadelphia, PA, USA, 1993. [Google Scholar]
- Ascione, G.; Mishura, Y.; Pirozzi, E. Fractional Deterministic and Stochastic Calculus; De Gruyter: Berlin, Germany, 2024. [Google Scholar]
- Benedetto, E.; Polito, F.; Sacerdote, L. On firing rate estimation for dependent interspike intervals. Neural Comput. 2015, 27, 699–724. [Google Scholar] [CrossRef]
- Kobayashi, R.; Kitano, K. Impact of slow K+ currents on spike generation can be described by an adaptive threshold model. J. Comput. Neurosci. 2016, 40, 347–362. [Google Scholar] [CrossRef] [PubMed]
- Stevens, C.F.; Zador, A.M. Novel integrate-and-fire-like model of repetitive firing in cortical neurons. In Proceedings of the 5th Joint Symposium on Neural Computation, San Diego, CA, USA, 16 May 1998; University of California: La Jolla, CA, USA, 1998; Volume 8, pp. 172–177. [Google Scholar]
- Tuckwell, H.C. Spatial neuron model with two-parameter Ornstein-Uhlenbeck input current. Phys. A Stat. Mech. Appl. 2006, 368, 495–510. [Google Scholar] [CrossRef]
- Burkitt, A.N. A review of the integrate-and-fire neuron model: I. Homogeneous synaptic input. Biol. Cybern. 2006, 95, 1–19. [Google Scholar] [CrossRef]
- Shinomoto, S.; Sakai, Y.; Funahashi, S. The Ornstein-Uhlenbeck process does not reproduce spiking statistics of cortical neurons. Neural Comput. 1997, 11, 935–951. [Google Scholar] [CrossRef] [PubMed]
- Bazzani, A.; Bassi, G.; Turchetti, G. Diffusion and memory effects for stochastic processes and fractional Langevin equations. Phys. A Stat. Mech. Appl. 2003, 324, 530–550. [Google Scholar] [CrossRef]
- Kim, H.; Shinomoto, S. Estimating nonstationary inputs from a single spike train based on a neuron model with adaptation. Math. Bios. Eng. 2014, 11, 49–62. [Google Scholar] [CrossRef] [PubMed]
- Abundo, M.; Pirozzi, E. Fractionally integrated Gauss-Markov processes and applications. In Communications in Nonlinear Science and Numerical Simulation; Elsevier: Amsterdam, The Netherlands, 2021; Volume 101, p. 105862. ISSN 1007-5704. [Google Scholar]
- Ascione, G.; Toaldo, B. A Semi-Markov Leaky Integrate-and-Fire model. Mathematics 2019, 7, 1022. [Google Scholar] [CrossRef]
- Pirozzi, E. On the Integration of Fractional Neuronal Dynamics Driven by Correlated Processes. In Computer Aided Systems Theory–EUROCAST 2019: Proceedings of the 17th International Conference, Las Palmas de Gran Canaria, Spain, 17–22 February 2019, Revised Selected Papers, Part I 17; Springer: Berlin/Heidelberg, Germany, 2020; pp. 211–219. [Google Scholar]
- Pirozzi, E. Colored noise and a stochastic fractional model for correlated inputs and adaptation in neuronal firing. Biol. Cybern. 2018, 112, 25–39. [Google Scholar] [CrossRef]
- Sakai, Y.; Funahashi, S.; Shinomoto, S. Temporally correlated inputs to leaky integrate-and-fire models can reproduce spiking statistics of cortical neurons. Neural Netw. 1999, 12, 1181–1190. [Google Scholar] [CrossRef]
- Teka, W.; Marinov, T.M.; Santamaria, F. Neuronal Spike Timing Adaptation Described with a Fractional Leaky Integrate-and-Fire Model. PLoS Comput. Biol. 2014, 10, e1003526. [Google Scholar] [CrossRef] [PubMed]
- Ascione, G.; Pirozzi, E. On a stochastic neuronal model integrating correlated inputs. Math. Biosci. Eng. 2019, 16, 5206–5225. [Google Scholar] [CrossRef] [PubMed]
- Baldi, P. Stochastic Calculus. In Universitext; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Diethelm, K. The Analysis of Fractional Differential Equations. In Lecture Notes in Mathematics 2004; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Ascione, G.; Pirozzi, E. Generalized Fractional Calculus for Gompertz-Type Models. Mathematics 2021, 9, 2140. [Google Scholar] [CrossRef]
- Burkitt A., N. A review of the integrate-and-fire neuron model: II. Inhomogeneous synaptic input and network properties. Biol. Cybern. 2006, 95, 97–112. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Xu, J.; Kloeden, P.E. Asymptotic behavior of stochastic lattice systems with a Caputo fractional time derivative. Nonlinear Anal. 2016, 135, 205–222. [Google Scholar] [CrossRef]
- Doan, T.S.; Kloeden, P.; Huong, P.; Tuan, H.T. Asymptotic separation between solutions of Caputo fractional stochastic differential equations. Stoch. Anal. Appl. 2018, 36, 654–664. [Google Scholar]
- Anh, P.T.; Doan, T.S.; Huong, P.T. A variation of constant formula for Caputo fractional stochastic differential equations. Stat. Probab. Lett. 2019, 145, 351–358. [Google Scholar] [CrossRef]
- Garrappa, R.; Kaslik, E.; Popolizio, M. Evaluation of Fractional Integrals and Derivatives of Elementary Functions: Overview and Tutorial. Mathematics 2019, 7, 407. [Google Scholar] [CrossRef]
- Li, K.; Peng, J. Laplace transform and fractional differential equations. Appl. Math. Lett. 2011, 24, 2019–2023. [Google Scholar]
- Kazem, S. Exact Solution of Some Linear Fractional Differential Equation by Laplace Transform. Int. J. Nonlinear Sci. 2013, 16, 3–11. [Google Scholar]
- Lansky, P. Sources of periodical force in noisy integrate-and-remodels of neuronal dynamics. Phys. Rev. E 1997, 55, 2040–2043. [Google Scholar] [CrossRef]
- Haugh, M. Generating Random Variables and Stochastic Processes; Monte Carlo Simulation; Columbia University: New York, NY, USA, 2017. [Google Scholar]
- Doan, T.S.; Huong, P.T.; Kloeden, P.E.; Vu, A.M. Euler–Maruyama scheme for Caputo stochastic fractional differential equations. J. Comput. Appl. Math. 2020, 380, 112989. [Google Scholar] [CrossRef]
| Membrane capacitance | = 1 F |
| Resting membrane potential | mV |
| Initial membrane potential | mV |
| Leak conductance | mS |
| Characteristic time of the membrane | ms |
| Initial input value | nA |
| Input characteristic time | ms |
| Constant current | nA |
| Intensity parameter | = 1 nAms |
| Fractional order for the input |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pirozzi, E. Some Fractional Stochastic Models for Neuronal Activity with Different Time-Scales and Correlated Inputs. Fractal Fract. 2024, 8, 57. https://doi.org/10.3390/fractalfract8010057
Pirozzi E. Some Fractional Stochastic Models for Neuronal Activity with Different Time-Scales and Correlated Inputs. Fractal and Fractional. 2024; 8(1):57. https://doi.org/10.3390/fractalfract8010057
Chicago/Turabian StylePirozzi, Enrica. 2024. "Some Fractional Stochastic Models for Neuronal Activity with Different Time-Scales and Correlated Inputs" Fractal and Fractional 8, no. 1: 57. https://doi.org/10.3390/fractalfract8010057
APA StylePirozzi, E. (2024). Some Fractional Stochastic Models for Neuronal Activity with Different Time-Scales and Correlated Inputs. Fractal and Fractional, 8(1), 57. https://doi.org/10.3390/fractalfract8010057






