Optimal Design of Fractional-Order PID Controllers for a Nonlinear AWS Wave Energy Converter Using Hybrid Jellyfish Search and Particle Swarm Optimization
Abstract
:1. Introduction
1.1. Background and Motivation
1.2. Literature Overview
1.3. Objectives and Contributions
- A thorough mathematical modeling of the grid-connected AWS, including the back-to-back converter controllers, is presented, together with all of the system’s parameter values.
- The proposed FOPID controllers, the number of gains that must be tuned, and the HJSPSO method utilized for selecting the best gains are all detailed.
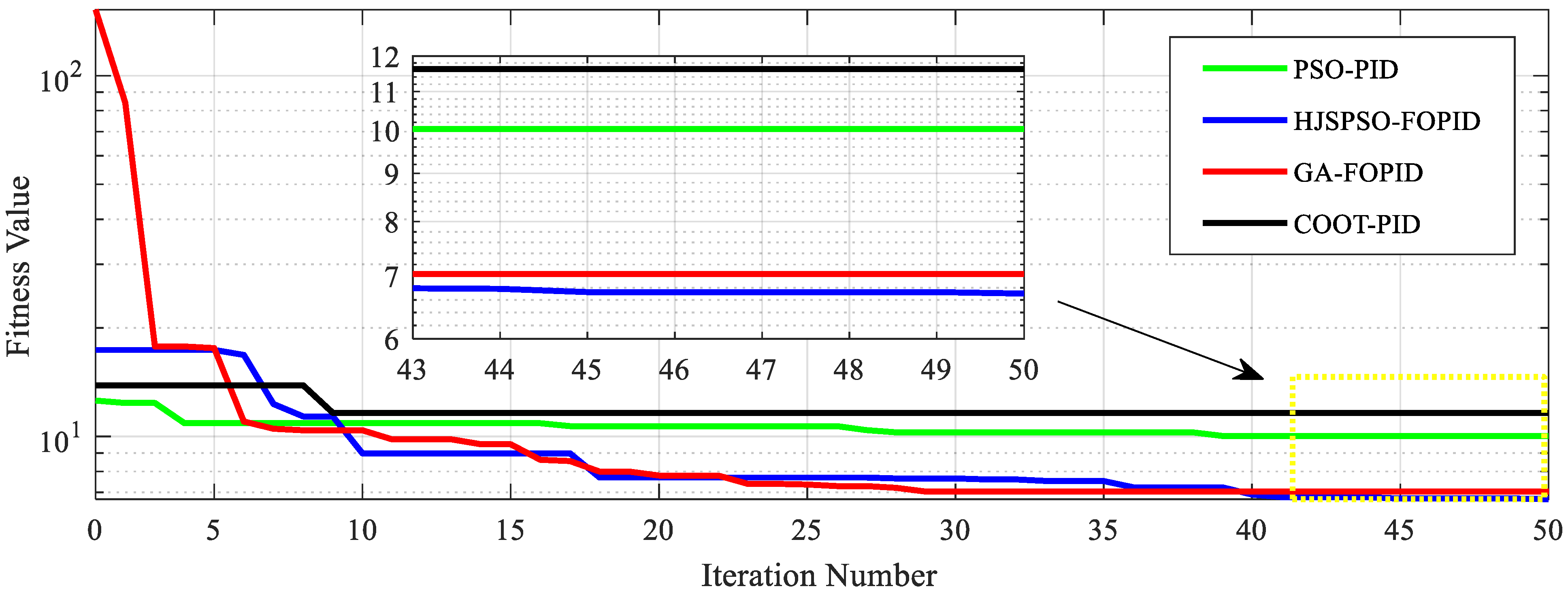
- The HJSPSO-FOPID controllers were compared with two conventional PID controllers that were tuned using PSO and COOT, in addition to FOPID controllers that were tuned using the GA.
- The controllers’ effectiveness and reliability were demonstrated by subjecting the grid-connected system to various unsymmetrical and symmetrical fault disturbances.
1.4. Organization
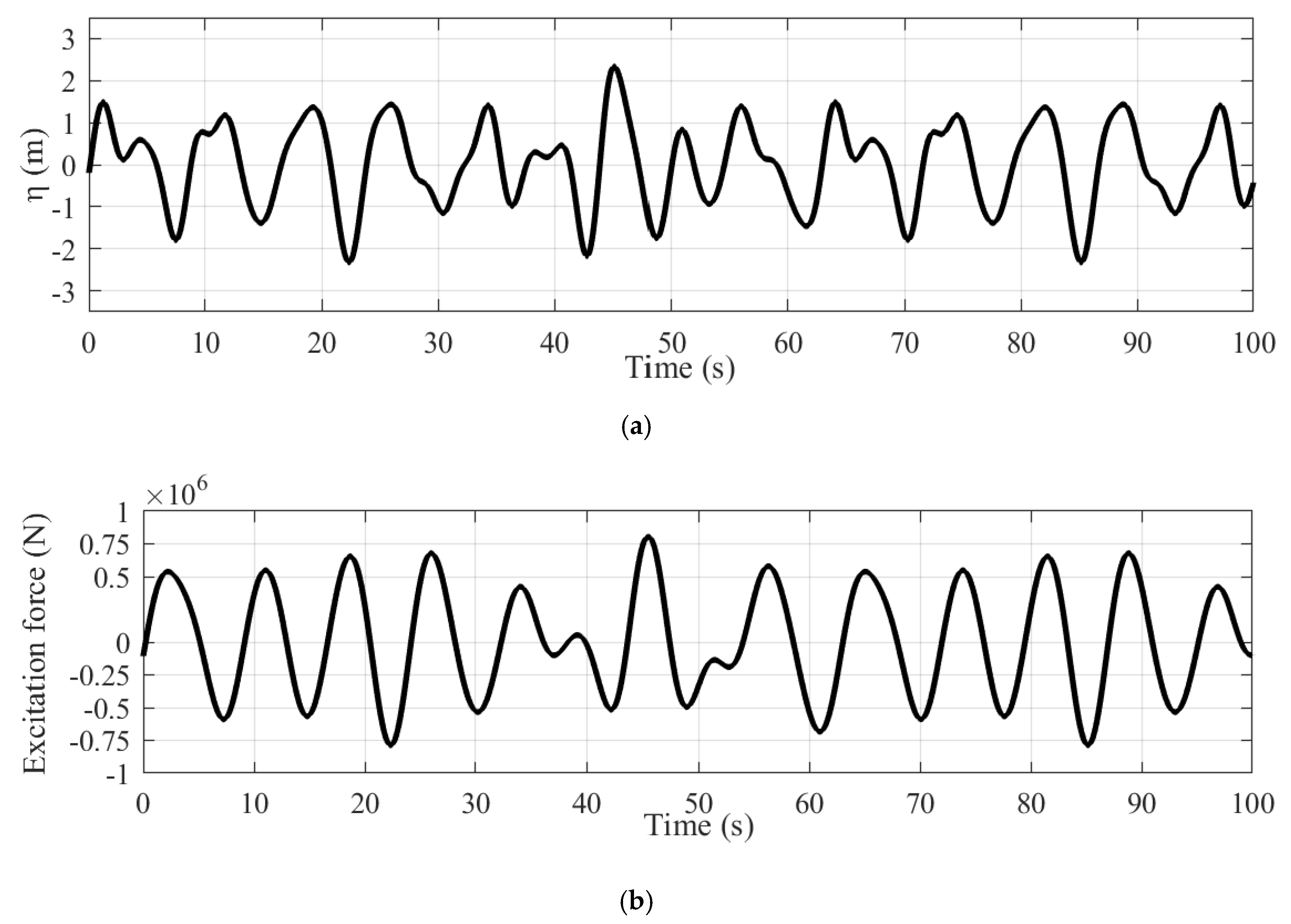
2. Modeling of the AWS Wave Energy Conversion System
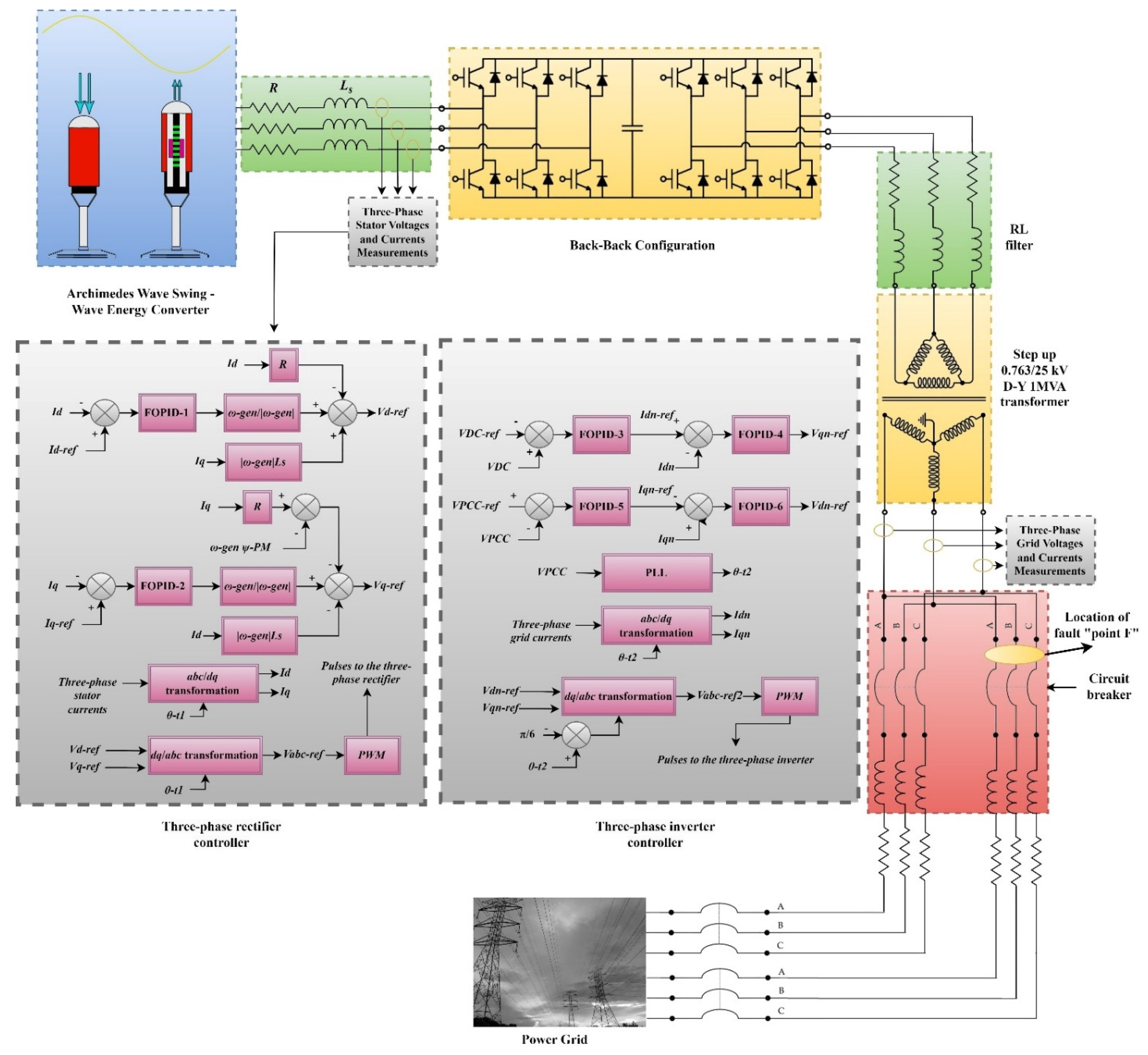
3. The Grid-Connected System: Block Diagram
3.1. The Fractional PID (FOPID) Control Strategy
3.2. The Back-to-Back Converter Configuration
4. Hybrid Jellyfish Search Optimizer and Particle Swarm Optimization (HJSPSO)
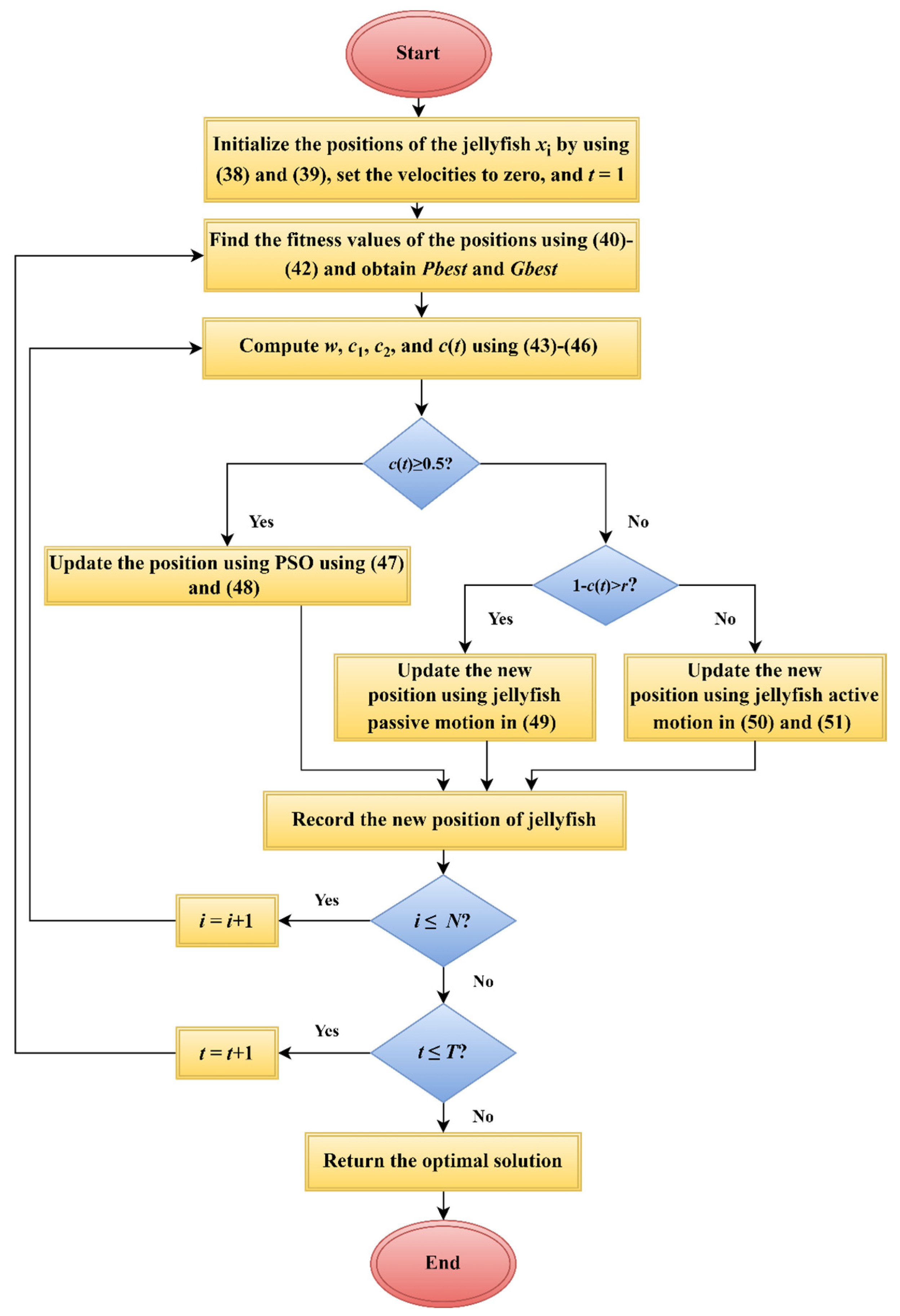
4.1. HJSPSO Algorithm Steps
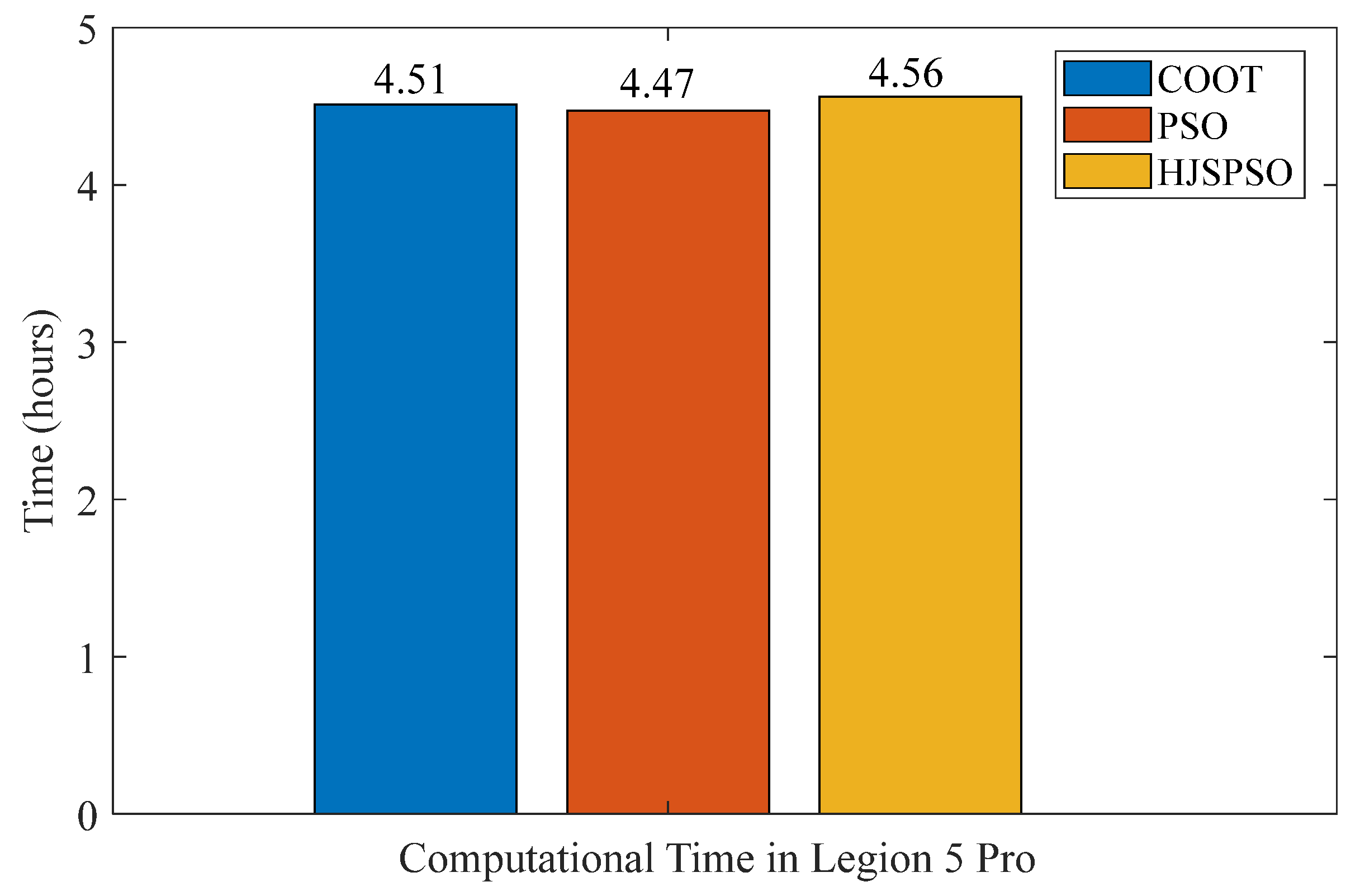
4.2. HJSPSO Algorithm Computational Complexity
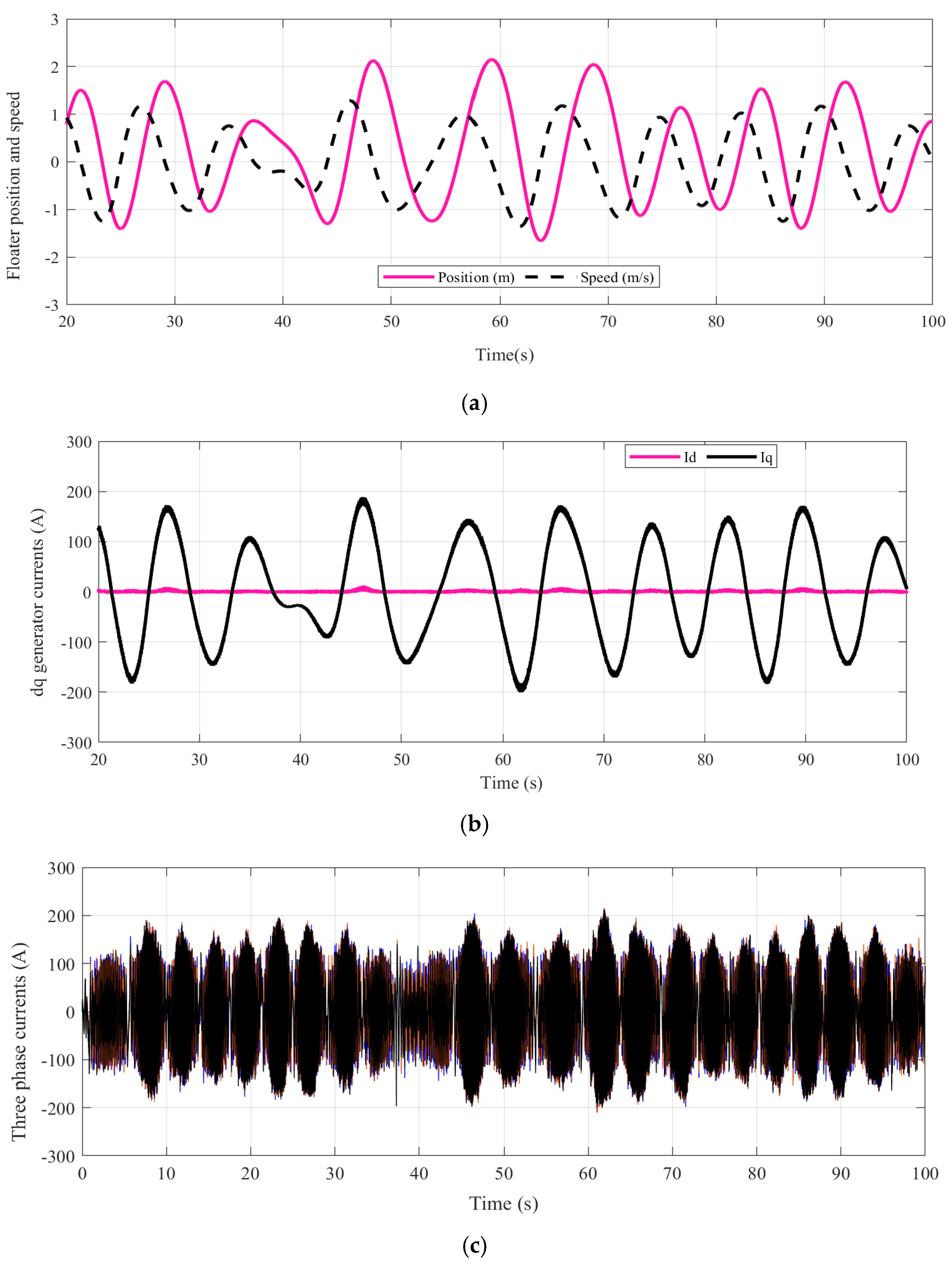
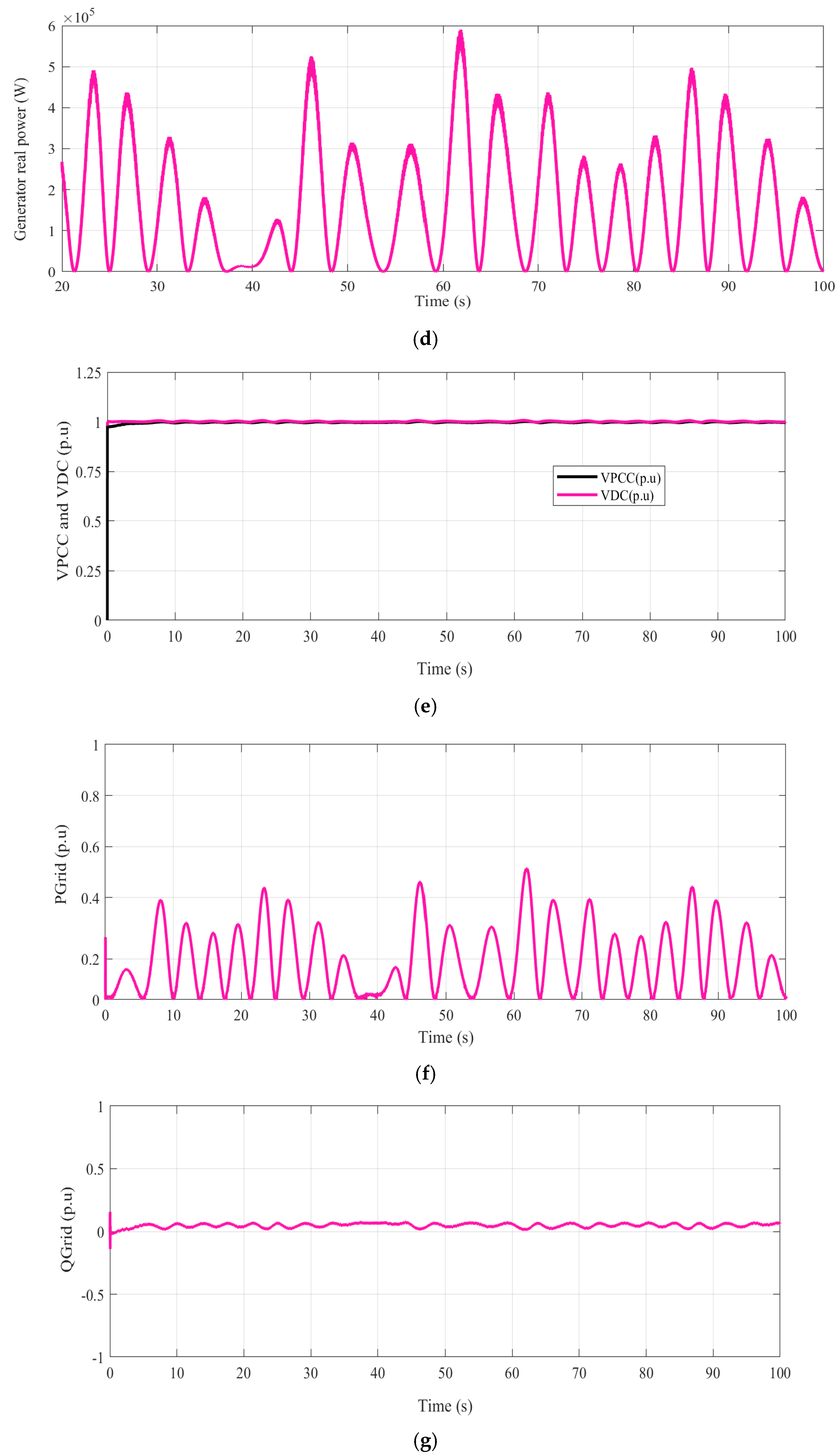
5. Nonlinear Grid-Connected AWS System Steady and Transient Responses
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Boyle, G. Renewable Energy: Power for a Sustainable Future, 2nd ed.; Oxford University Press: Oxford, UK, 2004; ISBN 0199261784. [Google Scholar]
- Mahdy, A.; Hasanien, H.M.; Aleem, S.H.E.A.; Al-Dhaifallah, M.; Zobaa, A.F.; Ali, Z.M. State-of-the-Art of the Most Commonly Adopted Wave Energy Conversion Systems. Ain Shams Eng. J. 2023, 15, 102322. [Google Scholar] [CrossRef]
- Archimedes Waveswing—AWS Ocean Energy. Available online: https://awsocean.com/archimedes-waveswing/ (accessed on 29 July 2023).
- Polinder, H.; Mecrow, B.C.; Jack, A.G.; Dickinson, P.; Mueller, M.A. Linear Generators for Direct-Drive Wave Energy Conversion. In Proceedings of the IEEE International Electric Machines and Drives Conference, IEMDC’03, Madison, WI, USA, 1–4 June 2003; Volume 2, pp. 798–804. [Google Scholar]
- De Sousa Prado, M.G.; Gardner, F.; Damen, M.; Polinder, H. Modelling and Test Results of the Archimedes Wave Swing. Proc. Inst. Mech. Eng. Part A J. Power Energy 2006, 220, 855–868. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, H.; Jiang, X.; Yang, X. A High-Order and Efficient Numerical Technique for the Nonlocal Neutron Diffusion Equation Representing Neutron Transport in a Nuclear Reactor. Ann. Nucl. Energy 2024, 195, 110163. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhang, H.; Yang, X. H1-Norm Error Analysis of a Robust ADI Method on Graded Mesh for Three-Dimensional Subdiffusion Problems. Numer. Algorithms 2023, 1–19. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, Q.; Yuan, G.; Sheng, Z. On Positivity Preservation in Nonlinear Finite Volume Method for Multi-Term Fractional Subdiffusion Equation on Polygonal Meshes. Nonlinear Dyn. 2018, 92, 595–612. [Google Scholar] [CrossRef]
- Sá da Costa, J.; Sarmento, A.J.N.; Gardner, F.; Beirão, P.; Brito-Melo, A. Time Domain Model of the AWS Wave Energy Converter. In Proceedings of the 6th European Wave and Tidal Energy Conference, Glasgow, UK, 29 August–2 September 2005; pp. 91–98. [Google Scholar]
- Gieske, P. Model Predictive Control of a Wave Energy Converter: Archimedes Wave Swing. Master’s Thesis, TU Delft, Delft, The Netherlands, 2007; p. 101. [Google Scholar]
- Mahdy, A.; Hasanien, H.M.; Hameed, W.H.A.; Turky, R.A.; Aleem, S.H.E.A.; Ebrahim, E.A. Nonlinear Modeling and Real-Time Simulation of a Grid-Connected AWS Wave Energy Conversion System. IEEE Trans. Sustain. Energy 2022, 13, 1744–1755. [Google Scholar] [CrossRef]
- Wu, F.; Zhang, X.P.; Ju, P.; Sterling, M.J.H. Optimal Control for AWS-Based Wave Energy Conversion System. IEEE Trans. Power Syst. 2009, 24, 1747–1755. [Google Scholar] [CrossRef]
- Hasanien, H.M. Transient Stability Augmentation of a Wave Energy Conversion System Using a Water Cycle Algorithm-Based Multiobjective Optimal Control Strategy. IEEE Trans. Ind. Inform. 2019, 15, 3411–3419. [Google Scholar] [CrossRef]
- Eskandar, H.; Sadollah, A.; Bahreininejad, A.; Hamdi, M. Water Cycle Algorithm—A Novel Metaheuristic Optimization Method for Solving Constrained Engineering Optimization Problems. Comput. Struct. 2012, 110–111, 151–166. [Google Scholar] [CrossRef]
- Mahdy, A.; Hasanien, H.M.; Helmy, W.; Turky, R.A.; Abdel Aleem, S.H.E. Transient Stability Improvement of Wave Energy Conversion Systems Connected to Power Grid Using Anti-Windup-Coot Optimization Strategy. Energy 2022, 245, 123321. [Google Scholar] [CrossRef]
- Naruei, I.; Keynia, F. A New Optimization Method Based on COOT Bird Natural Life Model. Expert Syst. Appl. 2021, 183, 115352. [Google Scholar] [CrossRef]
- Turky, R.A.; Hasanien, H.M.; Alkuhayli, A. Dynamic Stability Improvement of AWS-Based Wave Energy Systems Using a Multiobjective Salp Swarm Algorithm-Based Optimal Control Scheme. IEEE Syst. J. 2022, 16, 79–87. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A Bio-Inspired Optimizer for Engineering Design Problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Rasool, S.; Islam, M.R.; Muttaqi, K.M.; Sutanto, D. Coupled Modeling and Advanced Control for Smooth Operation of a Grid-Connected Linear Electric Generator Based Wave-To-Wire System. IEEE Trans. Ind. Appl. 2020, 56, 5575–5584. [Google Scholar] [CrossRef]
- Mahdy, A.; Hasanien, H.M.; Turky, R.A.; Abdel Aleem, S.H.E. Modeling and Optimal Operation of Hybrid Wave Energy and PV System Feeding Supercharging Stations Based on Golden Jackal Optimal Control Strategy. Energy 2023, 263, 125932. [Google Scholar] [CrossRef]
- Chopra, N.; Mohsin Ansari, M. Golden Jackal Optimization: A Novel Nature-Inspired Optimizer for Engineering Applications. Expert Syst. Appl. 2022, 198, 116924. [Google Scholar] [CrossRef]
- Hasanien, H.M. Gravitational Search Algorithm-based Optimal Control of Archimedes Wave Swing-based Wave Energy Conversion System Supplying a DC Microgrid under Uncertain Dynamics. IET Renew. Power Gener. 2017, 11, 763–770. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-pour, H.; Saryazdi, S. GSA: A Gravitational Search Algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Sharma, S.; Kapoor, R.; Dhiman, S. A Novel Hybrid Metaheuristic Based on Augmented Grey Wolf Optimizer and Cuckoo Search for Global Optimization. In Proceedings of the 2021 2nd International Conference on Secure Cyber Computing and Communications (ICSCCC), Jalandhar, India, 21–23 May 2021; pp. 376–381. [Google Scholar]
- Adaryani, M.R.; Taher, S.A.; Guerrero, J.M. Model Predictive Control of Direct-Drive Wave Power Generation System Connected to DC Microgrid through DC Cable. Int. Trans. Electr. Energy Syst. 2020, 30, etep12484. [Google Scholar] [CrossRef]
- Valério, D.; Mendes, M.J.G.C.; Beirão, P.; Sá da Costa, J. Identification and Control of the AWS Using Neural Network Models. Appl. Ocean Res. 2008, 30, 178–188. [Google Scholar] [CrossRef]
- Ataşlar-Ayyıldız, B. Robust Trajectory Tracking Control for Serial Robotic Manipulators Using Fractional Order-Based PTID Controller. Fractal Fract. 2023, 7, 250. [Google Scholar] [CrossRef]
- Frikh, M.L.; Soltani, F.; Bensiali, N.; Boutasseta, N.; Fergani, N. Fractional Order PID Controller Design for Wind Turbine Systems Using Analytical and Computational Tuning Approaches. Comput. Electr. Eng. 2021, 95, 107410. [Google Scholar] [CrossRef]
- Yang, B.; Yu, T.; Shu, H.; Zhu, D.; Zeng, F.; Sang, Y.; Jiang, L. Perturbation Observer Based Fractional-Order PID Control of Photovoltaics Inverters for Solar Energy Harvesting via Yin-Yang-Pair Optimization. Energy Convers. Manag. 2018, 171, 170–187. [Google Scholar] [CrossRef]
- Silaa, M.Y.; Barambones, O.; Derbeli, M.; Napole, C.; Bencherif, A. Fractional Order PID Design for a Proton Exchange Membrane Fuel Cell System Using an Extended Grey Wolf Optimizer. Processes 2022, 10, 450. [Google Scholar] [CrossRef]
- Rosas-Jaimes, O.A.; Munoz-Hernandez, G.A.; Mino-Aguilar, G.; Castaneda-Camacho, J.; Gracios-Marin, C.A. Evaluating Fractional PID Control in a Nonlinear MIMO Model of a Hydroelectric Power Station. Complexity 2019, 2019, 9367291. [Google Scholar] [CrossRef]
- Zheng, W.; Luo, Y.; Chen, Y.; Wang, X. A Simplified Fractional Order PID Controller’s Optimal Tuning: A Case Study on a PMSM Speed Servo. Entropy 2021, 23, 130. [Google Scholar] [CrossRef]
- Zamani, M.; Karimi-Ghartemani, M.; Sadati, N.; Parniani, M. Design of a Fractional Order PID Controller for an AVR Using Particle Swarm Optimization. Control Eng. Pract. 2009, 17, 1380–1387. [Google Scholar] [CrossRef]
- Noman, A.M.; Almutairi, S.Z.; Aly, M.; Alqahtani, M.H.; Aljumah, A.S.; Mohamed, E.A. A Marine-Predator-Algorithm-Based Optimum FOPID Controller for Enhancing the Stability and Transient Response of Automatic Voltage Regulators. Fractal Fract. 2023, 7, 690. [Google Scholar] [CrossRef]
- El-Sousy, F.F.M.; Alqahtani, M.H.; Aljumah, A.S.; Aly, M.; Almutairi, S.Z.; Mohamed, E.A. Design Optimization of Improved Fractional-Order Cascaded Frequency Controllers for Electric Vehicles and Electrical Power Grids Utilizing Renewable Energy Sources. Fractal Fract. 2023, 7, 603. [Google Scholar] [CrossRef]
- Daraz, A.; Malik, S.A.; Basit, A.; Aslam, S.; Zhang, G. Modified FOPID Controller for Frequency Regulation of a Hybrid Interconnected System of Conventional and Renewable Energy Sources. Fractal Fract. 2023, 7, 89. [Google Scholar] [CrossRef]
- Nayyef, H.M.; Ibrahim, A.A.; Mohd Zainuri, M.A.A.; Zulkifley, M.A.; Shareef, H. A Novel Hybrid Algorithm Based on Jellyfish Search and Particle Swarm Optimization. Mathematics 2023, 11, 3210. [Google Scholar] [CrossRef]
- Chou, J.-S.; Truong, D.-N. A Novel Metaheuristic Optimizer Inspired by Behavior of Jellyfish in Ocean. Appl. Math. Comput. 2021, 389, 125535. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Herber, D.R.; Allison, J.T. Wave Energy Extraction Maximization in Irregular Ocean Waves Using Pseudospectral Methods. In Proceedings of the Volume 3A: 39th Design Automation Conference; American Society of Mechanical Engineers, Portland, OR, USA, 4–7 August 2013. [Google Scholar]
- Wu, F.; Ju, P.; Zhang, X.-P.; Qin, C.; Peng, G.J.; Huang, H.; Fang, J. Modeling, Control Strategy, and Power Conditioning for Direct-Drive Wave Energy Conversion to Operate With Power Grid. Proc. IEEE 2013, 101, 925–941. [Google Scholar] [CrossRef]
- Shah, P.; Agashe, S. Review of Fractional PID Controller. Mechatronics 2016, 38, 29–41. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional-Order Systems and PI/Sup/Spl Lambda//D/Sup/Spl Mu//-Controllers. IEEE Trans. Automat. Contr. 1999, 44, 208–214. [Google Scholar] [CrossRef]
- Warrier, P.; Shah, P. Optimal Fractional Pid Controller for Buck Converter Using Cohort Intelligent Algorithm. Appl. Syst. Innov. 2021, 4, 50. [Google Scholar] [CrossRef]
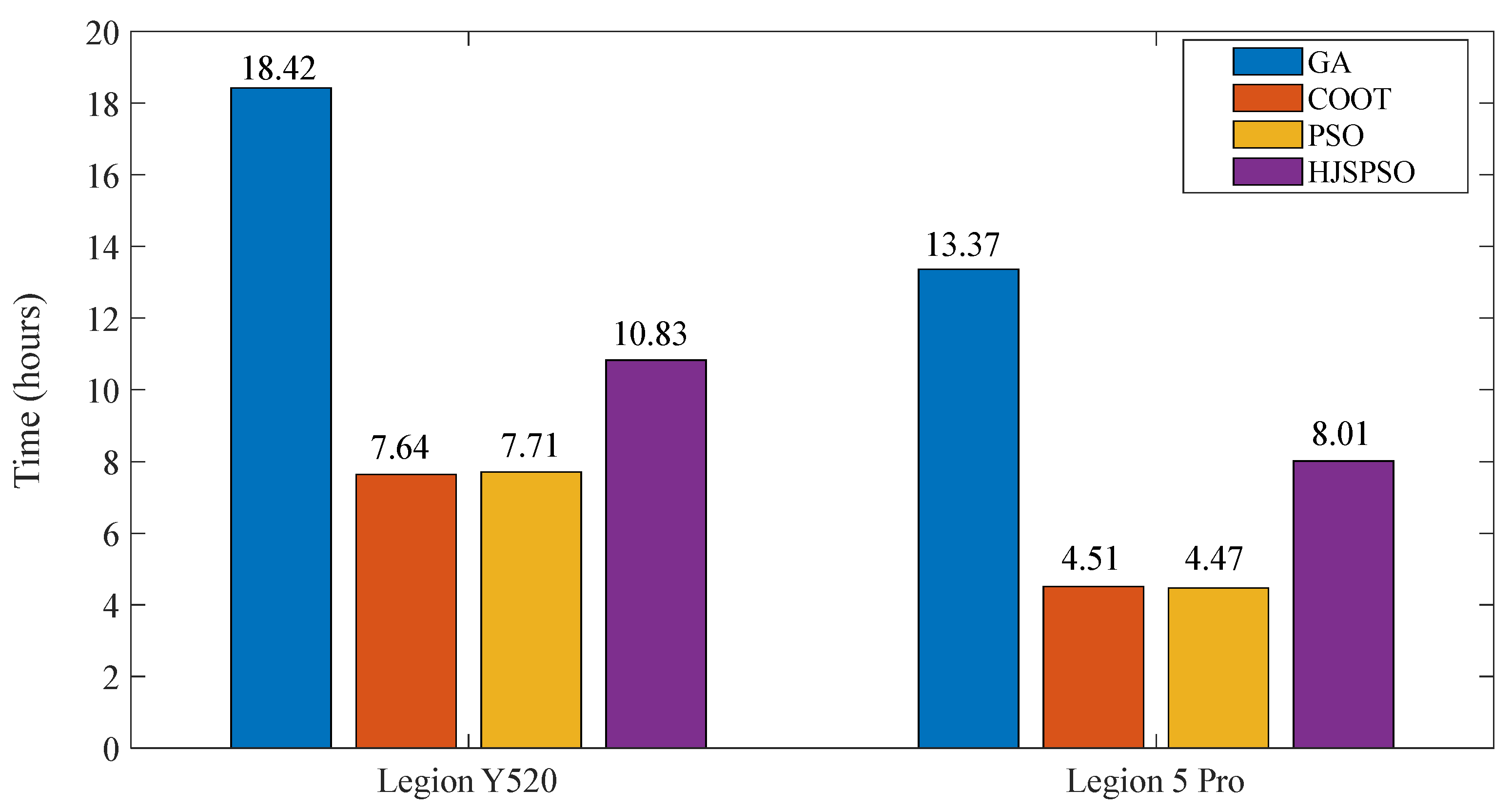
| Parameter | Value | Parameter | Value | Parameter | Value |
|---|---|---|---|---|---|
| 4 × kg | γ | 1.4 | 23 Wb | ||
| 3.55 × kg | θ | 4.5 m | 0.1 m | ||
| ρ | 1025 kg/ | 4 m | 0.4 | ||
| 1 × N/m2 | 8 s | 0.2 | |||
| 1.5 × kg/m | ψ | 4 m | R | 0.29 Ω | |
| 43 m | μ | 0.1 | 0.031 H | ||
| 11 m | η | 0 | 28.5 m | ||
| 1 | 2 | 11 m | |||
| 9.8 m/ | 79 | 95 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| DC link capacitance | 15 mF | Frequency | 50 Hz |
| j0.05 p.u | Base power | 1 MVA | |
| Filter’s resistance and inductance | R = 0.01 Ω and L = 0.0072 H | 0.02 + j0.14 p.u |
| Controller | Algorithm | Gains |
|---|---|---|
| FOPID | HJSPSO | r = [519.27 438 0.065 1.022 0.95 542.46 792 0.24 0.82 0.93 4.22 61.31 0.14 0.32 0.27 0.32 3.44 1.33 0.004 0.19 19.92 2.01 0.14 1.05 0.34 0.11 0.22 0.88 0.18 0.33] |
| FOPID | GA | r = [667.16 570.88 0.085 1.76 0.62 494.42 610.30 0.44 1.75 0.7 1.91 87.02 0.03 0.88 0.79 0.94 3.49 1.44 0.09 0.15 16.99 3.17 0.11 1.17 0.3 0.08 0.46 0.82 0.2 0.22] |
| PID | COOT | r = [554 694.4 1 0 1 728 1355 1 0 1 7.6 90 1 0 1 1.17 21.8 1 0 1 2.88 239.1 1 0 1 2.43 27.8 1 0 1] |
| PID | PSO | r = [374 878 1 0 1 747 1364 1 0 1 6.65 76 1 0 1 1.08 23.7 1 0 1 4.3 216.11 1 0 1 2.3 24.16 1 0 1] |
| Point of Comparison (p.u) | PSO-PID | COOT-PID | GA-FOPID | HJSPSO-FOPID | Optimal Controller |
|---|---|---|---|---|---|
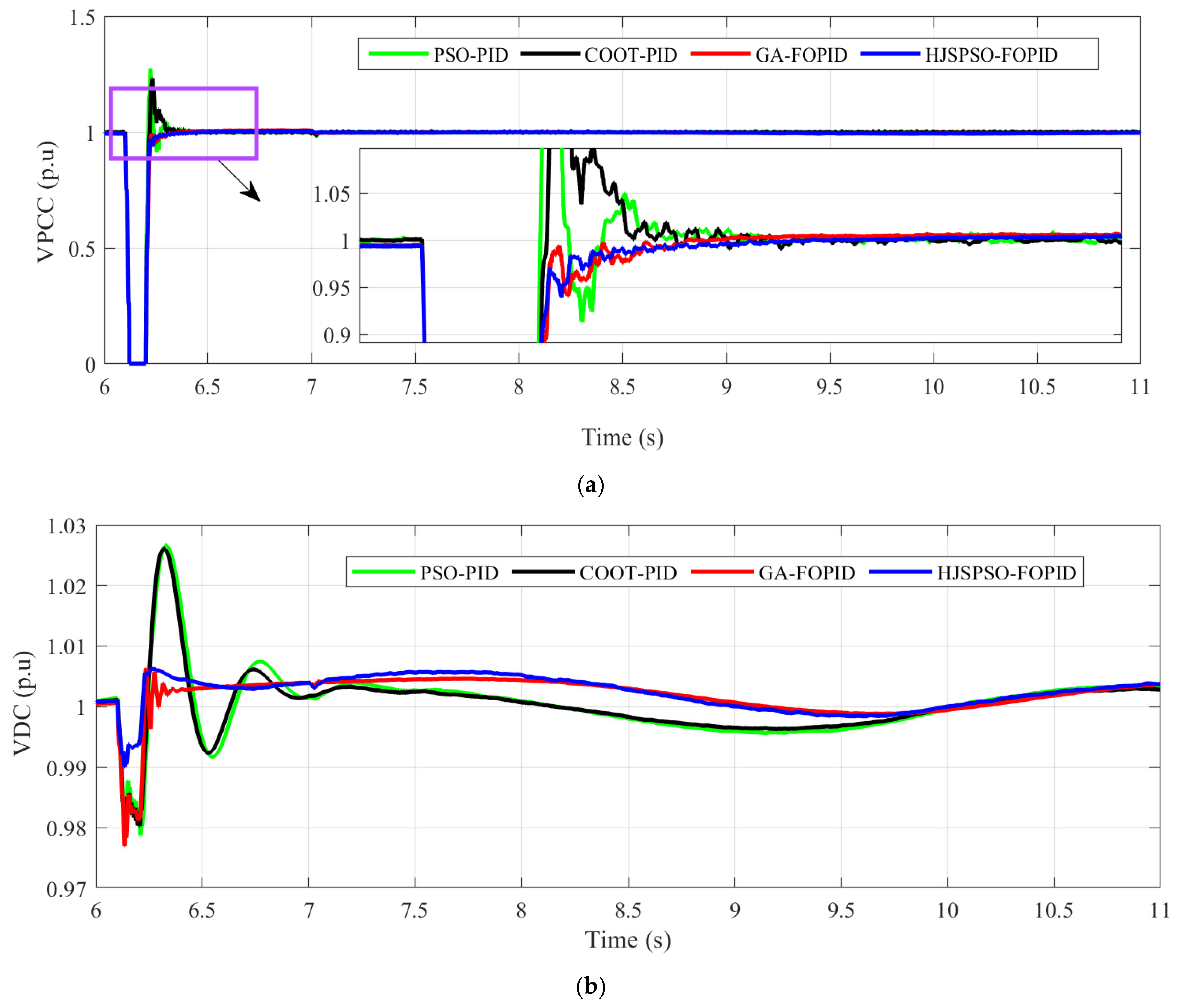
| Overshooting in | ~0.28 p.u | ~0.23 p.u | ~0.0 p.u | ~0.0 p.u | HJSPSO- and GA-FOPID |
| Overshooting in | ~0.03 p.u | ~0.03 p.u | ~0.007 p.u | ~0.006 p.u | HJSPSO-FOPID |
| Undershooting in | ~0.02 p.u | ~0.02 p.u | ~0.02 p.u | ~0.01 p.u | HJSPSO-FOPID |
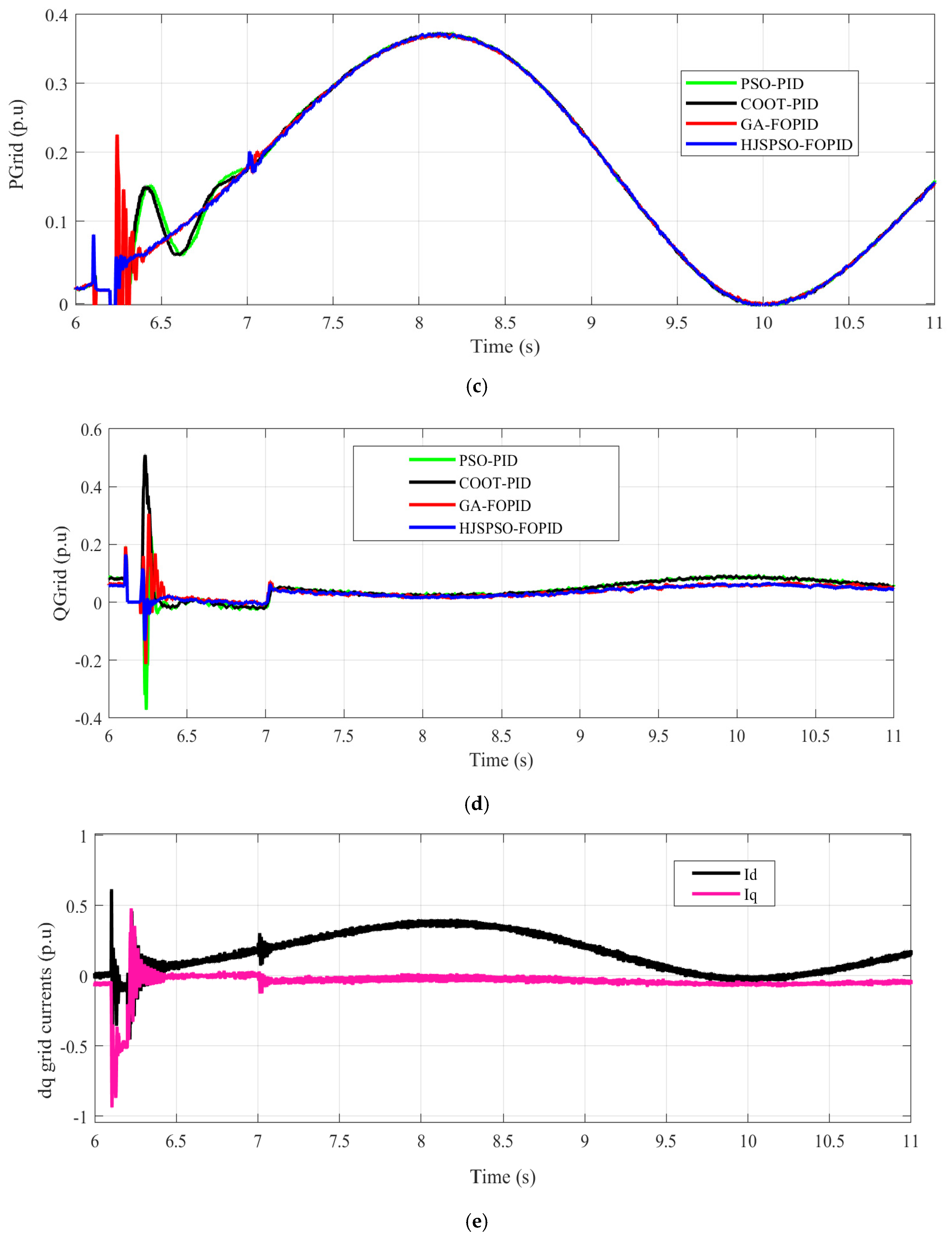
| Overshooting in | ~0.23 p.u | ~0.5 p.u | ~0.3 p.u | ~0.1 p.u | HJSPSO-FOPID |
| Undershooting in | ~0.37 p.u | ~0.02 p.u | ~0.22 p.u | ~0.13 p.u | COOT-PID |
| Point of Comparison (p.u) | PSO-PID | COOT-PID | GA-FOPID | HJSPSO-FOPID | Optimal Controller |
|---|---|---|---|---|---|
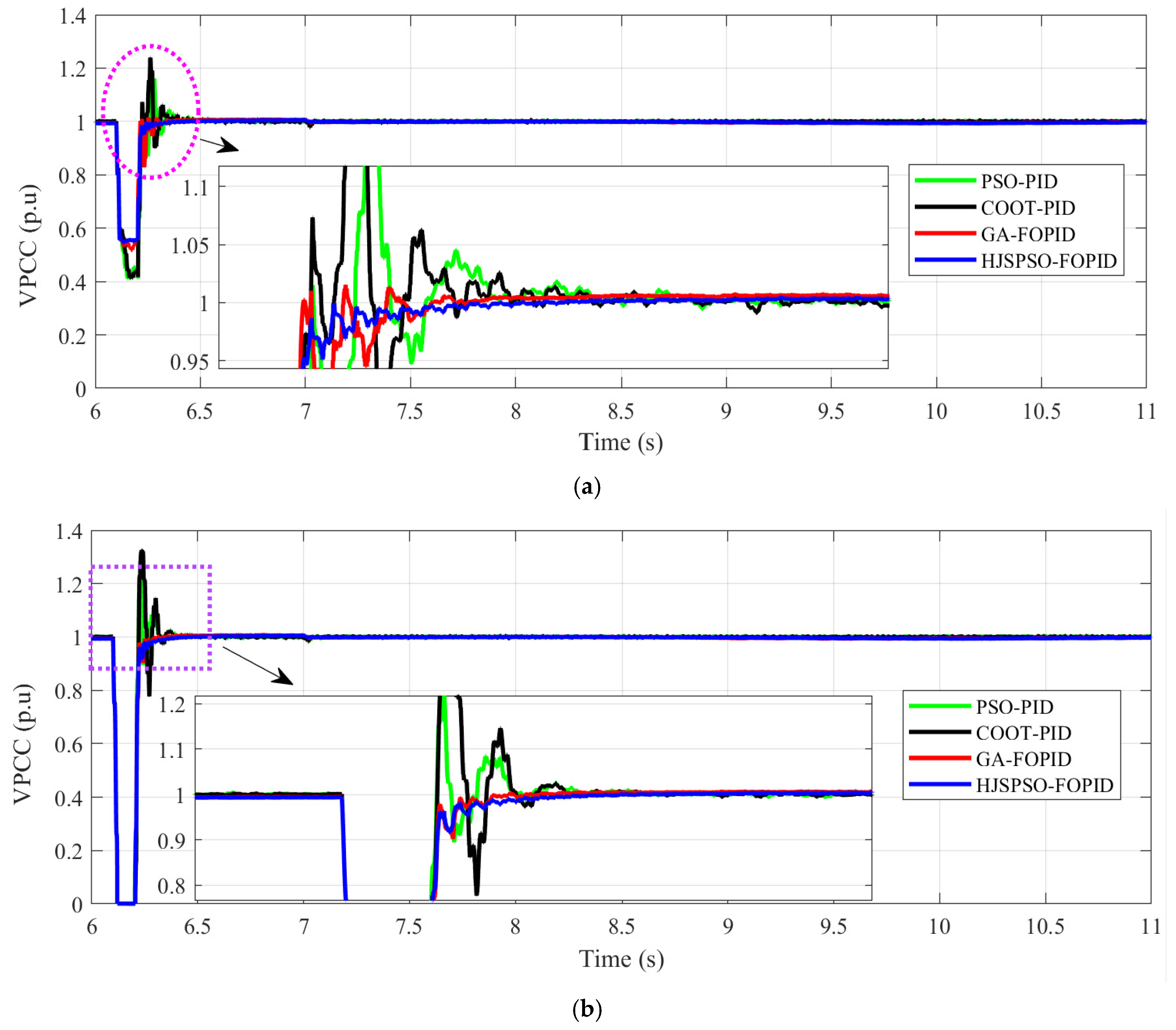
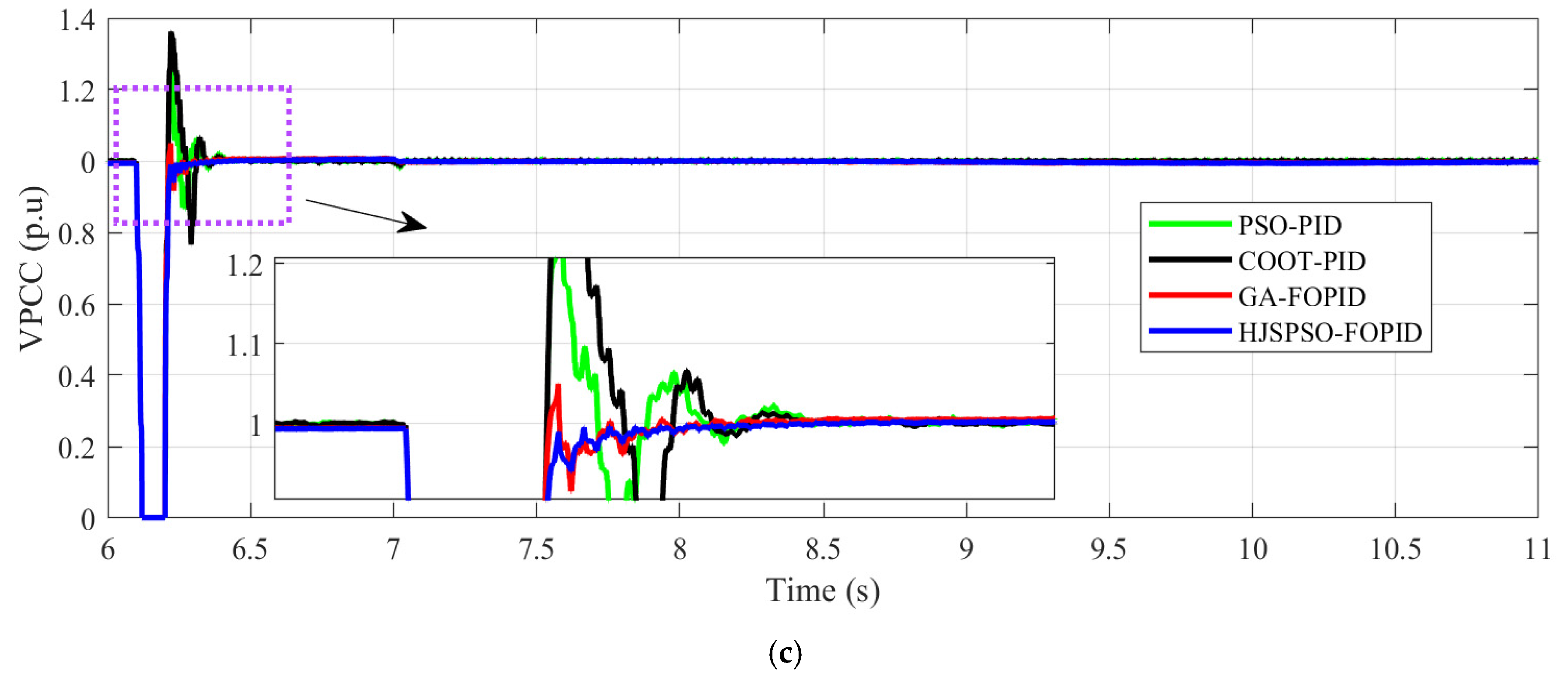
| Overshooting in during LG fault | ~0.16 p.u | ~0.25 p.u | ~0.2 p.u | ~0.0 p.u | HJSPSO-FOPID |
| Undershooting in during LG fault | ~0.59 p.u | ~0.58 p.u | ~0.48 p.u | ~0.46 p.u | HJSPSO-FOPID |
| Overshooting in during LLG fault | ~0.23 p.u | ~33% p.u | ~0.2% p.u | ~0.0 p.u | HJSPSO- and GA-FOPID |
| Overshooting in during LL fault | ~0.3 p.u | ~0.36 p.u | ~0.05 p.u | ~0.0 p.u | HJSPSO-FOPID |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, Z.M.; Ahmed, A.M.; Hasanien, H.M.; Aleem, S.H.E.A. Optimal Design of Fractional-Order PID Controllers for a Nonlinear AWS Wave Energy Converter Using Hybrid Jellyfish Search and Particle Swarm Optimization. Fractal Fract. 2024, 8, 6. https://doi.org/10.3390/fractalfract8010006
Ali ZM, Ahmed AM, Hasanien HM, Aleem SHEA. Optimal Design of Fractional-Order PID Controllers for a Nonlinear AWS Wave Energy Converter Using Hybrid Jellyfish Search and Particle Swarm Optimization. Fractal and Fractional. 2024; 8(1):6. https://doi.org/10.3390/fractalfract8010006
Chicago/Turabian StyleAli, Ziad M., Ahmed Mahdy Ahmed, Hany M. Hasanien, and Shady H. E. Abdel Aleem. 2024. "Optimal Design of Fractional-Order PID Controllers for a Nonlinear AWS Wave Energy Converter Using Hybrid Jellyfish Search and Particle Swarm Optimization" Fractal and Fractional 8, no. 1: 6. https://doi.org/10.3390/fractalfract8010006
APA StyleAli, Z. M., Ahmed, A. M., Hasanien, H. M., & Aleem, S. H. E. A. (2024). Optimal Design of Fractional-Order PID Controllers for a Nonlinear AWS Wave Energy Converter Using Hybrid Jellyfish Search and Particle Swarm Optimization. Fractal and Fractional, 8(1), 6. https://doi.org/10.3390/fractalfract8010006











