Numerical Simulation and Parameter Estimation of the Space-Fractional Magnetohydrodynamic Flow and Heat Transfer Coupled Model
Abstract
1. Introduction
2. Mathematical Model
3. Preliminary
4. Materials and Methods
5. Parameter Estimation
| Algorithm 1: Parameter estimation method. |
| Require: Initialize . |
| Ensure: |
| for to -1 do |
| for to 3 do |
| Sample , |
| Sample . |
| if , then |
| , |
| else |
| . |
| end if |
| end for |
| end for |
6. Numerical Examples
6.1. Example 1
6.2. Example 2
6.3. Example 3
7. Conclusions
- The numerical method is stable and convergent with an accuracy of .
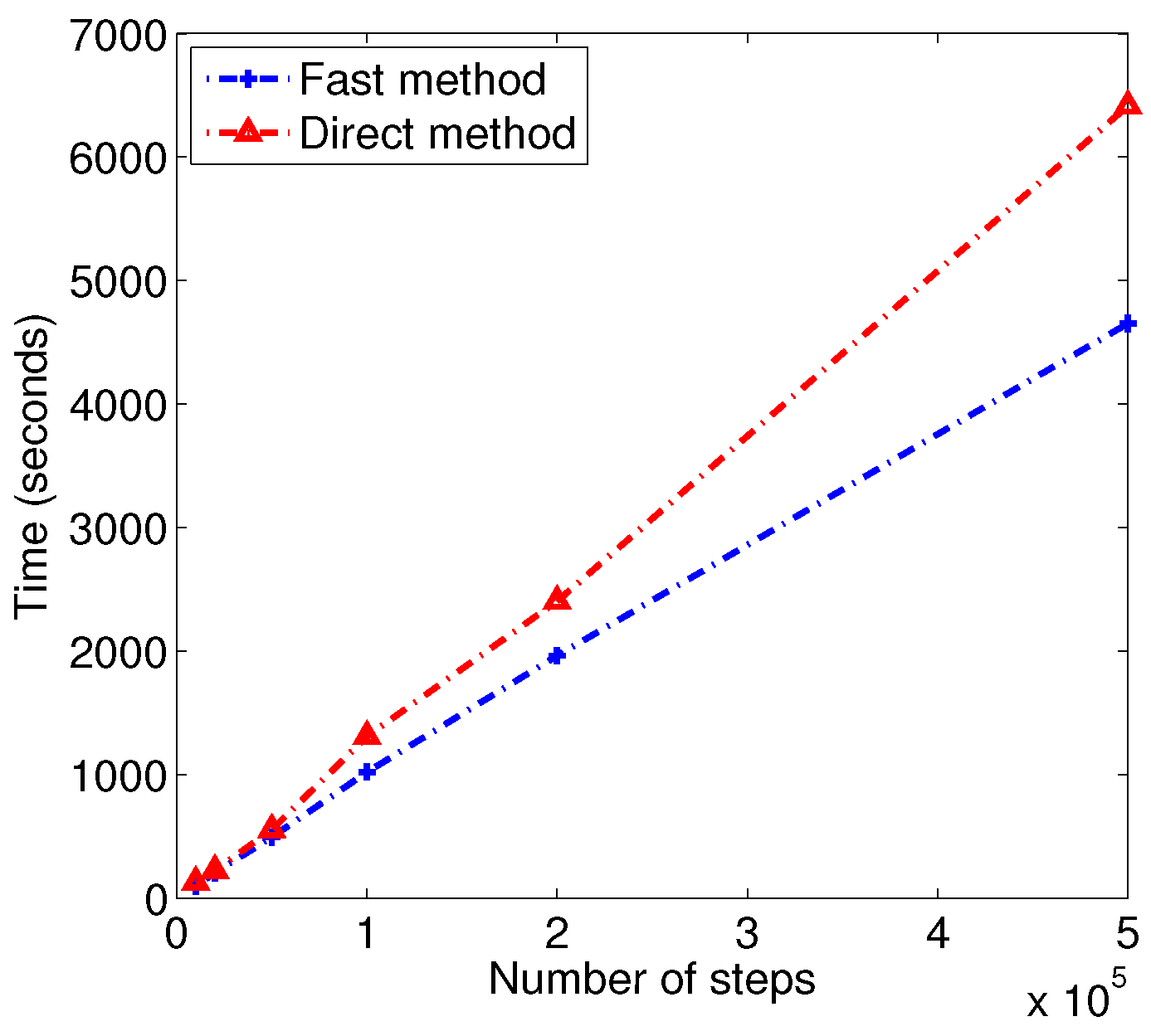
- The fast method is effective in reducing the computational time.
- Under different conditions, the parameter estimation method we propose can effectively estimate fractional derivative parameters and solve the problem of multi-parameter estimation in the coupled model.
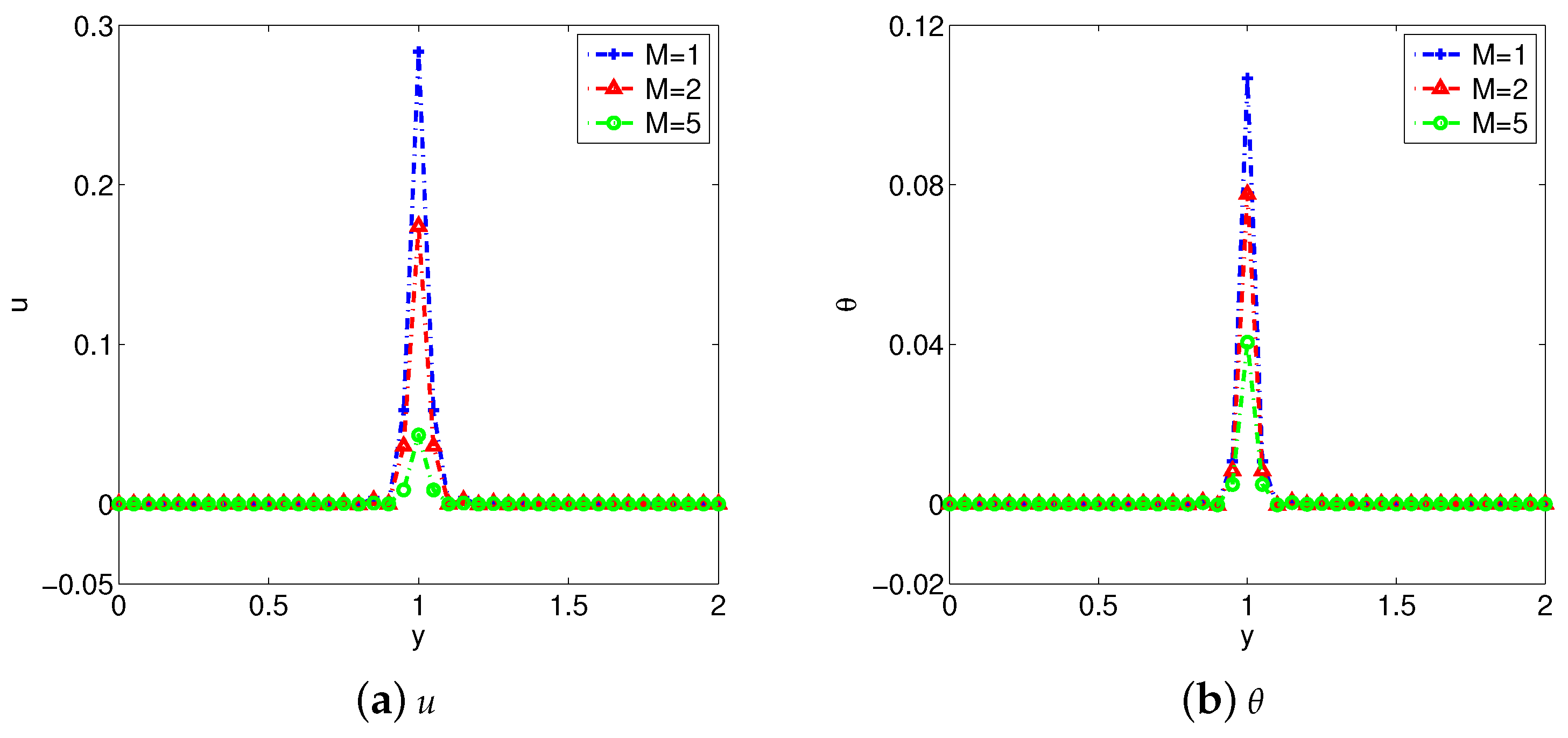
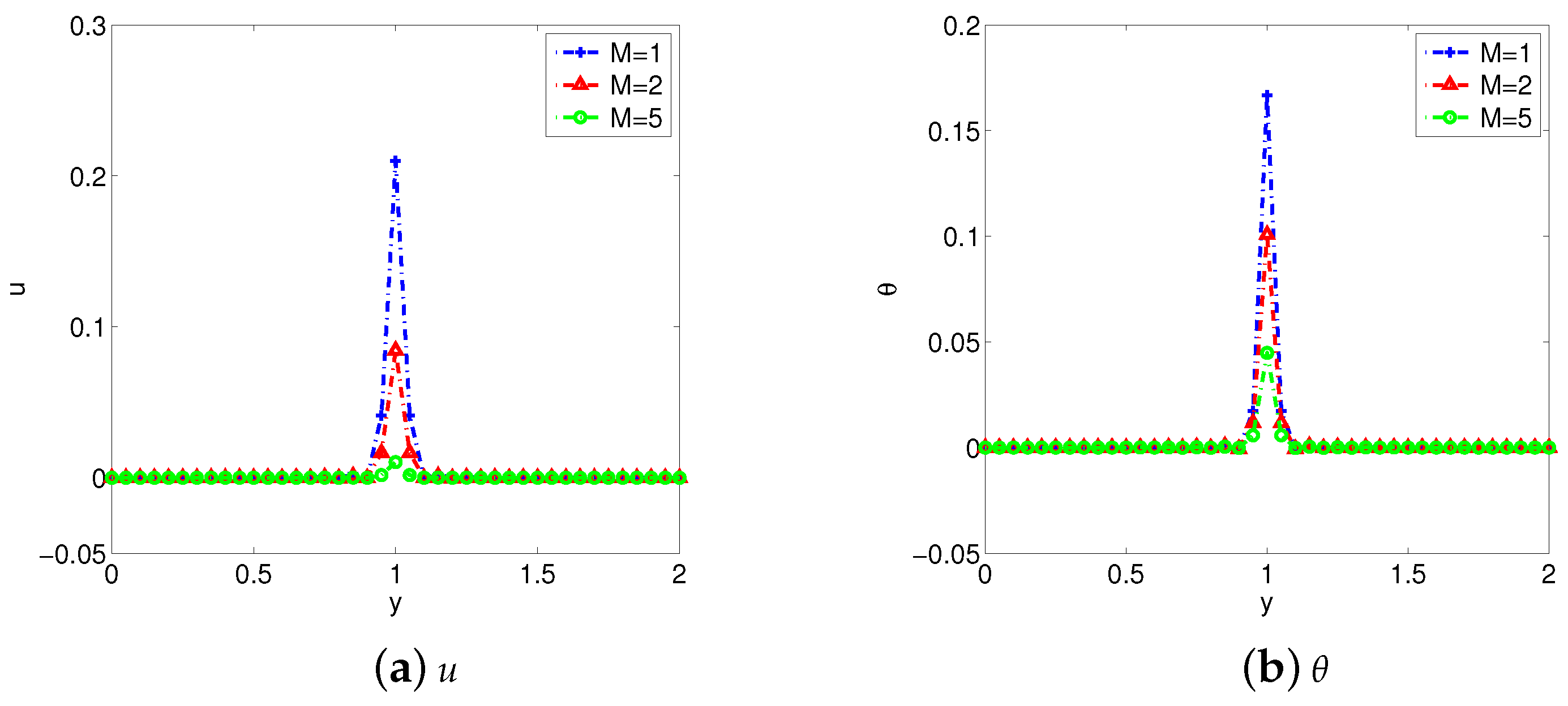
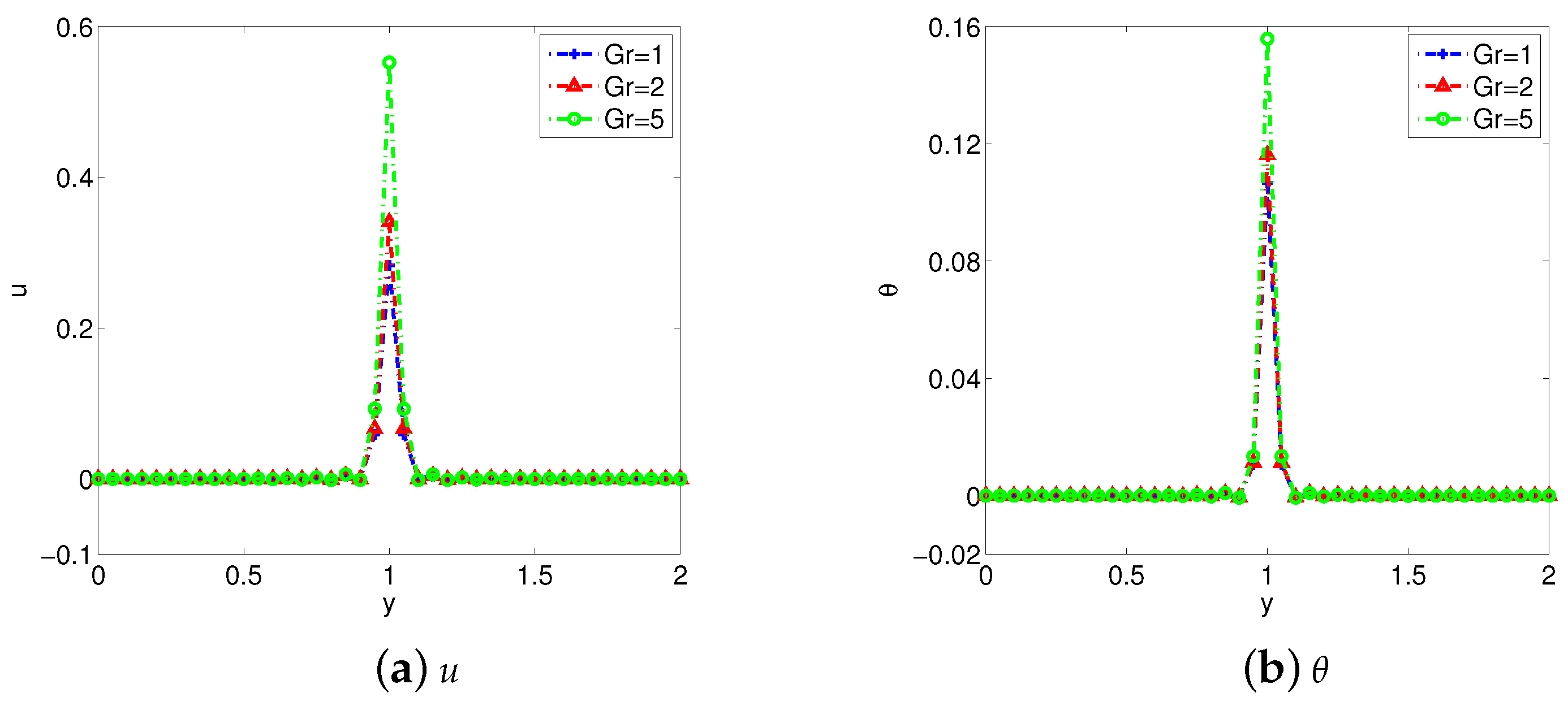
- The Lorentz force produced by the MHD flow will block the movement of the fluid and prolong the time for the fluid to reach a stable state. But the Hall parameter m will weaken this hindrance.
- The Joule heating effects play a negative role in heat transfer.
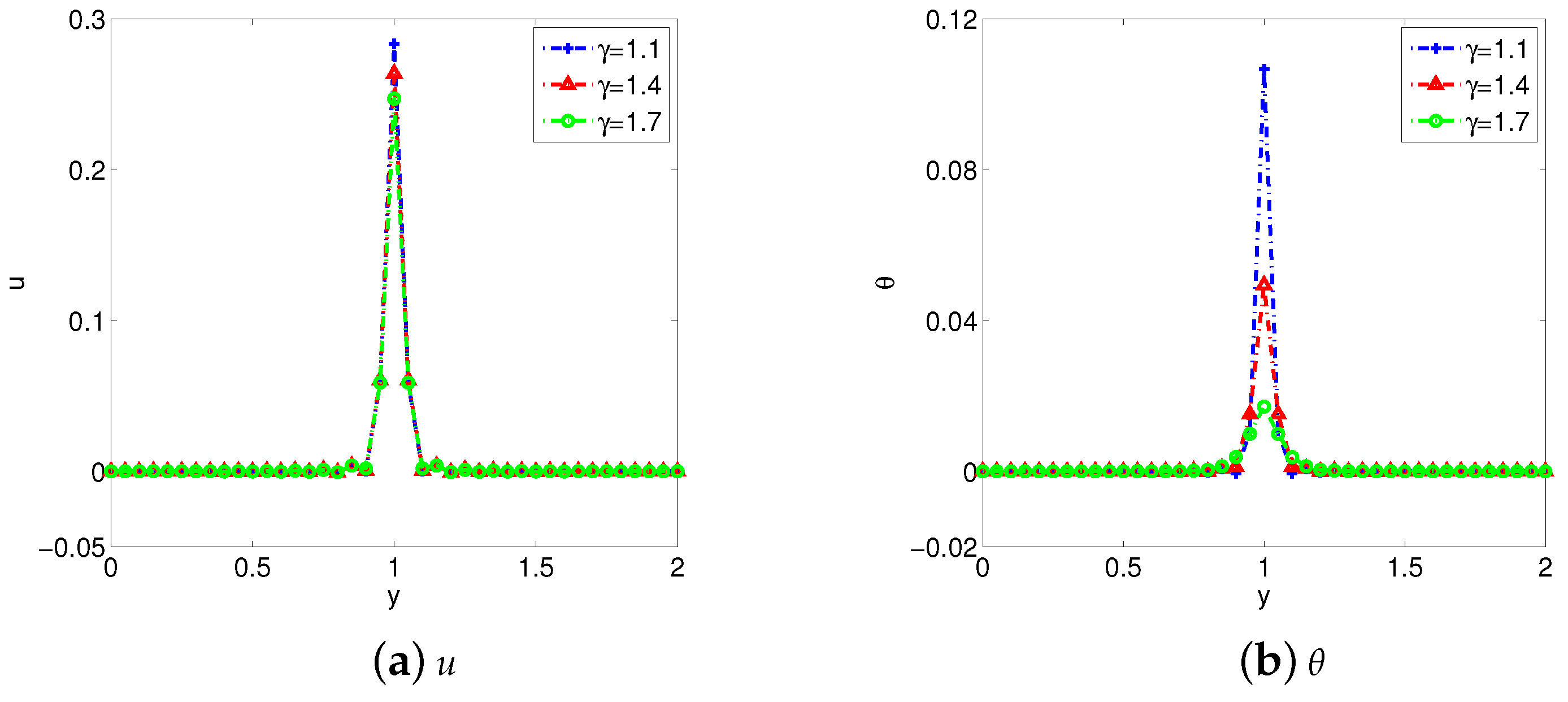
- Increasing the fractional derivative parameters , , and can promote the heat transfer, and make the flow become gentle in a short time.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbol | Meaning | Units |
| velocity vector | m/s | |
| magnetic field vector | A/m | |
| length | m | |
| t | time | s |
| Cauchy stress tensor | N/ | |
| T | temperature | °C |
| density of fluid | kg/ | |
| gravitational acceleration | m/ | |
| current density vector | A/ | |
| conductivity of fluid | S(Siemens) | |
| heat capacity | J/(kg·°C) | |
| dynamic viscosity | (kg·)/s | |
| magnetic field viscosity | /s | |
| thermal conductivity | (J·)/(s·°C) | |
| thermal expansion | 1/(°C) | |
| Hall effects parameter | m/A |
References
- Zheng, R.; Guo, B. Global solutions to the ideal MHD system with a strong magnetic background. Nonlinear Anal. Real World Appl. 2021, 61, 103334. [Google Scholar] [CrossRef]
- Iftikhar, N.; Riaz, M.B.; Awrejcewicz, J.; Akgül, A. Effect of magnetic field with parabolic motion on fractional second grade fluid. Fractal Fract. 2021, 5, 163. [Google Scholar] [CrossRef]
- Madhura, K.; Atiwali, B.; Iyengar, S. Influence of nanoparticle shapes on natural convection flow with heat and mass transfer rates of nanofluids with fractional derivative. Math. Methods Appl. Sci. 2021, 46, 8089–8105. [Google Scholar] [CrossRef]
- Rehman, A.U.; Jarad, F.; Riaz, M.B.; Shah, Z.H. Generalized Mittag-Leffler Kernel form solutions of free convection heat and mass transfer flow of Maxwell fluid with Newtonian heating: Prabhakar fractional derivative approach. Fractal Fract. 2022, 6, 98. [Google Scholar] [CrossRef]
- Chen, X.; Yang, W.; Zhang, X.; Liu, F. Unsteady boundary layer flow of viscoelastic MHD fluid with a double fractional Maxwell model. Appl. Math. Lett. 2019, 95, 143–149. [Google Scholar] [CrossRef]
- Jiang, X.; Zhang, H.; Wang, S. Unsteady magnetohydrodynamic flow of generalized second grade fluid through porous medium with Hall effects on heat and mass transfer. Phys. Fluids 2020, 32, 113105. [Google Scholar] [CrossRef]
- Huang, Y.Y.; Gu, X.M.; Gong, Y.; Li, H.; Zhao, Y.L.; Carpentieri, B. A fast preconditioned semi-implicit difference scheme for strongly nonlinear space-fractional diffusion equations. Fractal Fract. 2021, 5, 230. [Google Scholar] [CrossRef]
- Kumar, D.; Nama, H.; Singh, J.; Kumar, J. An Efficient Numerical Scheme for Fractional Order Mathematical Model of Cytosolic Calcium Ion in Astrocytes. Fractal Fract. 2024, 8, 184. [Google Scholar] [CrossRef]
- Yang, Z.; Zeng, F. A corrected L1 method for a time-fractional subdiffusion equation. J. Sci. Comput. 2023, 95, 85. [Google Scholar] [CrossRef]
- Wang, X.; Qi, H.; Yang, X.; Xu, H. Analysis of the time-space fractional bioheat transfer equation for biological tissues during laser irradiation. Int. J. Heat Mass Transf. 2021, 177, 121555. [Google Scholar] [CrossRef]
- Jia, J.; Xu, H.; Jiang, X. Fast evaluation for the two-dimensional nonlinear coupled time–space fractional Klein-Gordon-Zakharov equations. Appl. Math. Lett. 2021, 118, 107148. [Google Scholar] [CrossRef]
- Jian, H.Y.; Huang, T.Z.; Ostermann, A.; Gu, X.M.; Zhao, Y.L. Fast numerical schemes for nonlinear space-fractional multidelay reaction-diffusion equations by implicit integration factor methods. Appl. Math. Comput. 2021, 408, 126360. [Google Scholar] [CrossRef]
- Koleva, M.N.; Vulkov, L.G. Parameters Estimation in a Time-Fractiona Parabolic System of Porous Media. Fractal Fract. 2023, 7, 443. [Google Scholar] [CrossRef]
- Zhang, H.; Jiang, X. Spectral method and Bayesian parameter estimation for the space fractional coupled nonlinear Schrödinger equations. Nonlinear Dyn. 2019, 95, 1599–1614. [Google Scholar] [CrossRef]
- Qin, H.; Li, L.; Li, Y.; Chen, X. Time-Stepping Error Estimates of Linearized Grünwald–Letnikov Difference Schemes for Strongly Nonlinear Time-Fractional Parabolic Problems. Fractal Fract. 2024, 8, 390. [Google Scholar] [CrossRef]
- Yang, X.; Liu, Y.; Park, G.K. Parameter estimation of uncertain differential equation with application to financial market. Chaos Solitons Fractals 2020, 139, 110026. [Google Scholar] [CrossRef]
- Yang, X.; Jiang, X.; Kang, J. Parameter identification for fractional fractal diffusion model based on experimental data. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 083134. [Google Scholar] [CrossRef]
- Chi, X.; Yu, B.; Jiang, X. Parameter estimation for the time fractional heat conduction model based on experimental heat flux data. Appl. Math. Lett. 2020, 102, 106094. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. MHD flow and heat transfer of a hybrid nanofluid past a permeable stretching/shrinking wedge. Appl. Math. Mech. 2020, 41, 507–520. [Google Scholar] [CrossRef]
- Chi, X.; Zhang, H. Numerical study for the unsteady space fractional magnetohydrodynamic free convective flow and heat transfer with Hall effects. Appl. Math. Lett. 2021, 120, 107312. [Google Scholar] [CrossRef]
- Dai, M. Local well-posedness of the Hall-MHD system in Hs(n) with s > . Math. Nachrichten 2020, 293, 67–78. [Google Scholar] [CrossRef]
- Ghani, M. Local well-posedness of Boussinesq equations for MHD convection with fractional thermal diffusion in sobolev space Hs(n) × Hs+1−ϵ(n) × Hs+α−ϵ(n). Nonlinear Anal. Real World Appl. 2021, 62, 103355. [Google Scholar] [CrossRef]
- Xu, T.; Liu, F.; Lü, S.; Anh, V.V. Numerical approximation of 2D multi-term time and space fractional Bloch–Torrey equations involving the fractional Laplacian. J. Comput. Appl. Math. 2021, 393, 113519. [Google Scholar] [CrossRef]
- Farquhar, M.E.; Moroney, T.J.; Yang, Q.; Turner, I.W. GPU accelerated algorithms for computing matrix function vector products with applications to exponential integrators and fractional diffusion. SIAM J. Sci. Comput. 2016, 38, C127–C149. [Google Scholar] [CrossRef]
- Urschel, J.C. Uniform error estimates for the Lanczos method. SIAM J. Matrix Anal. Appl. 2021, 42, 1423–1450. [Google Scholar] [CrossRef]
- Jia, X.; Liang, X.; Shen, C.; Zhang, L.H. Solving the cubic regularization model by a nested restarting Lanczos method. SIAM J. Matrix Anal. Appl. 2022, 43, 812–839. [Google Scholar] [CrossRef]
- Zheng, R.; Jiang, X.; Zhang, H. Efficient and accurate spectral method for the time-fractional dual-phase-lag heat transfer model and its parameter estimation. Math. Methods Appl. Sci. 2020, 43, 2216–2232. [Google Scholar] [CrossRef]
- Li, Y.; Cao, G.; Wang, T.; Cui, Q.; Wang, B. A novel local region-based active contour model for image segmentation using Bayes theorem. Inform. Sci. 2020, 506, 443–456. [Google Scholar] [CrossRef]
- Demkowicz-Dobrzański, R.; Górecki, W.; Guţă, M. Multi-parameter estimation beyond quantum Fisher information. J. Phys. A Math. Theor. 2020, 53, 363001. [Google Scholar] [CrossRef]
- van de Schoot, R.; Depaoli, S.; King, R.; Kramer, B.; Märtens, K.; Tadesse, M.G.; Vannucci, M.; Gelman, A.; Veen, D.; Willemsen, J.; et al. Bayesian statistics and modelling. Nat. Rev. Methods Prim. 2021, 1, 1. [Google Scholar] [CrossRef]


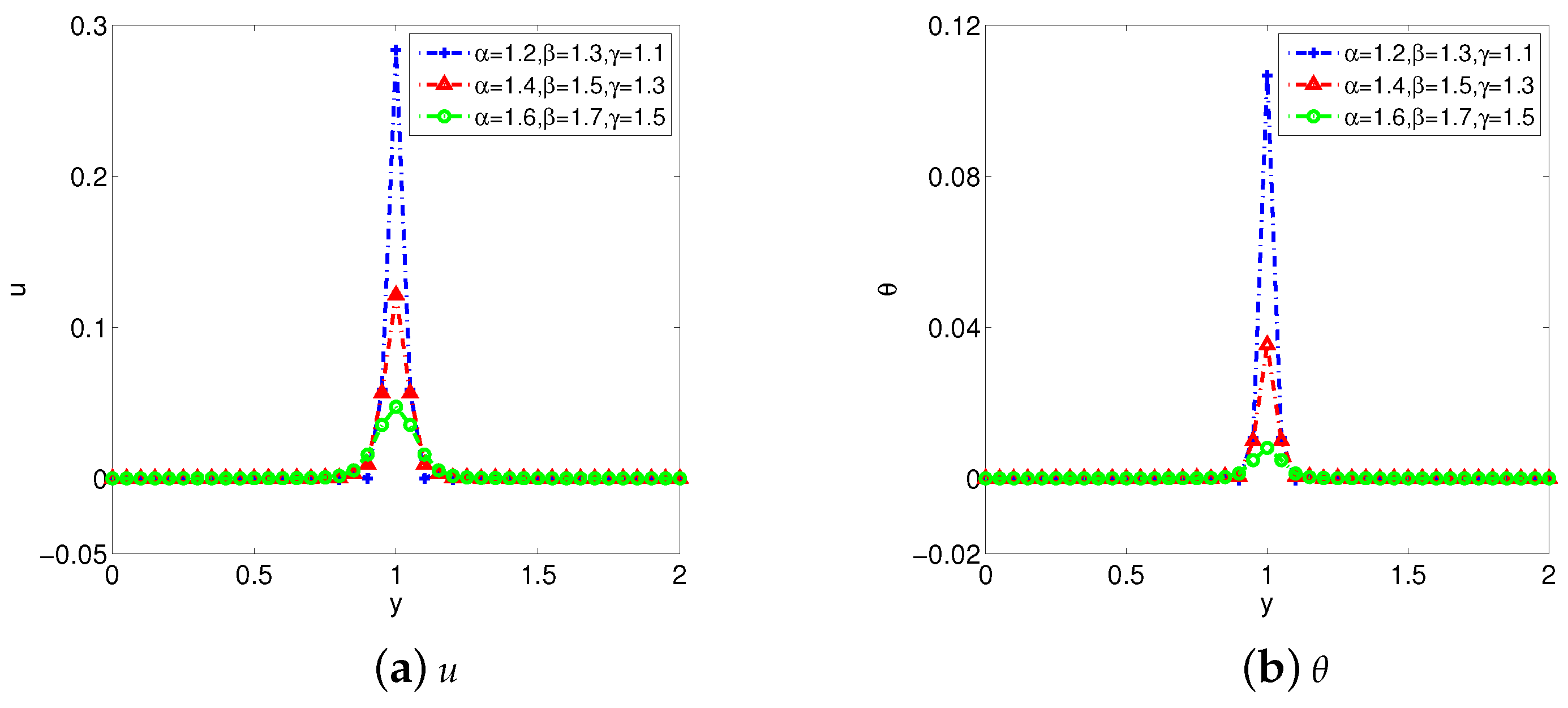


| u | b | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Error | Rate | Error | Rate | Error | Rate | ||||
| - | - | - | |||||||
| 1.9696 | 1.9445 | 2.0213 | |||||||
| 2.0008 | 1.9609 | 1.9296 | |||||||
| - | - | - | |||||||
| 1.9696 | 1.9445 | 2.0213 | |||||||
| 2.0009 | 1.9610 | 1.9296 | |||||||
| u | |||||
| b | |||||
| Exact Value | Measurement Error | Initial Guess | Iteration Times | Estimate Value |
|---|---|---|---|---|
| (1.3,1.7,1.4) | 0% | (1.5,1.4,1.6) | 1000 | (1.3098,1.7075,1.3990) |
| (1.5,1.4,1.6) | 2000 | (1.2962,1.7083,1.3812) | ||
| (1.2,1.8,1.1) | 1000 | (1.2894,1.7023,1.4071) | ||
| 2% | (1.5,1.4,1.6) | 1000 | (1.2988,1.6914,1.3971) | |
| (1.5,1.4,1.6) | 2000 | (1.2980,1.6921,1.4080) | ||
| (1.2,1.8,1.1) | 1000 | (1.3033,1.7113,1.4057) | ||
| 5% | (1.5,1.4,1.6) | 1000 | (1.3201,1.6952,1.3940) | |
| (1.5,1.4,1.6) | 2000 | (1.3022,1.7073,1.4053) | ||
| (1.2,1.8,1.1) | 1000 | (1.2936,1.7006,1.3914) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Jiang, X.; Jia, J. Numerical Simulation and Parameter Estimation of the Space-Fractional Magnetohydrodynamic Flow and Heat Transfer Coupled Model. Fractal Fract. 2024, 8, 557. https://doi.org/10.3390/fractalfract8100557
Liu Y, Jiang X, Jia J. Numerical Simulation and Parameter Estimation of the Space-Fractional Magnetohydrodynamic Flow and Heat Transfer Coupled Model. Fractal and Fractional. 2024; 8(10):557. https://doi.org/10.3390/fractalfract8100557
Chicago/Turabian StyleLiu, Yi, Xiaoyun Jiang, and Junqing Jia. 2024. "Numerical Simulation and Parameter Estimation of the Space-Fractional Magnetohydrodynamic Flow and Heat Transfer Coupled Model" Fractal and Fractional 8, no. 10: 557. https://doi.org/10.3390/fractalfract8100557
APA StyleLiu, Y., Jiang, X., & Jia, J. (2024). Numerical Simulation and Parameter Estimation of the Space-Fractional Magnetohydrodynamic Flow and Heat Transfer Coupled Model. Fractal and Fractional, 8(10), 557. https://doi.org/10.3390/fractalfract8100557






