Distributed Consensus Fuzzy Control Method and Fractional Order Control for Power Sharing in Field Medical Microgrids under FDI Attacks
Abstract
1. Introduction
- A system model of a multi-bus DC microgrid displaying a power coupling relationship between distributed power sources and loads in a region is developed. The microgrid system model is further switched into a linear heterogeneous MAS with unknown attacks. A distributed consensus secondary control method based on local communication network structure information is proposed to achieve accurate power distribution in the microgrid.
- In order to mitigate the impact of FDI attacks on the consistency of MASs, a security control protocol is proposed. The security controller is designed to reduce the impact of FDI attacks on sensors and actuators on the control commands of agents, and ensure the consistency of the MASs’ output.
- In order to reduce the communication burden, a fully distributed fuzzy control method is proposed, which emphasizes the discontinuous communication mode between distributed generators. This method effectively reduces the update frequency of the controller and the communication bandwidth under the condition of ensuring the control effect.
2. Research Background
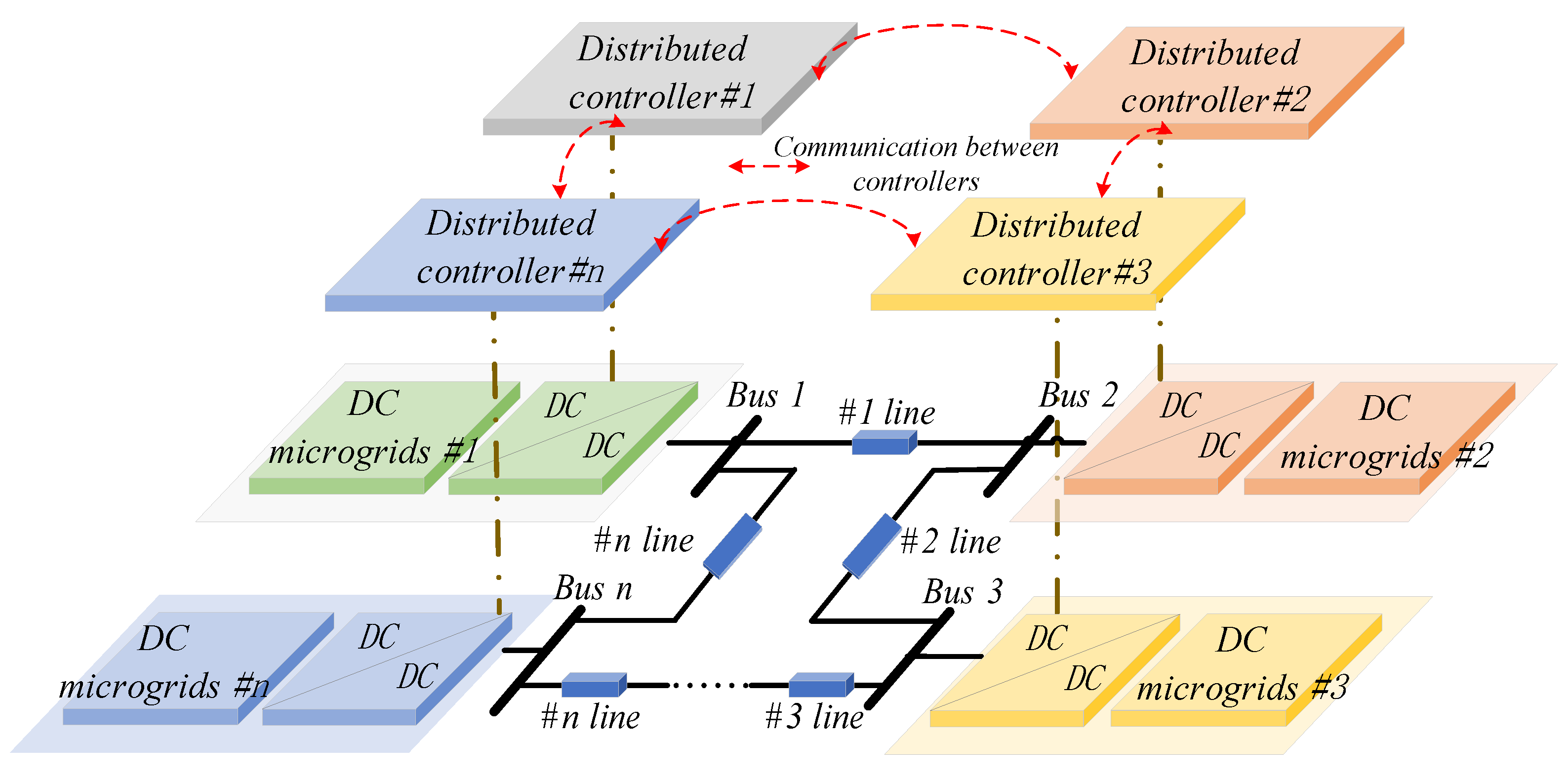
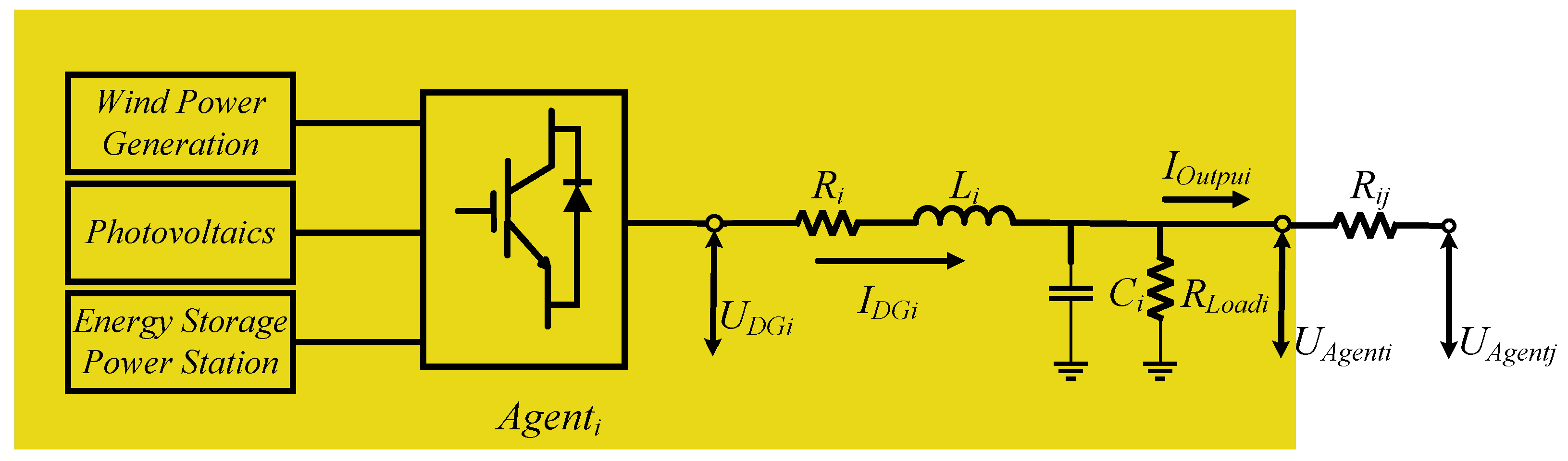
3. Modeling of Multi-Bus DC Microgrid System
4. Fuzzy Control Strategy for Current Sharing with FDI Attacks
4.1. Types of FDI Attack and Design of Adaptive Compensator
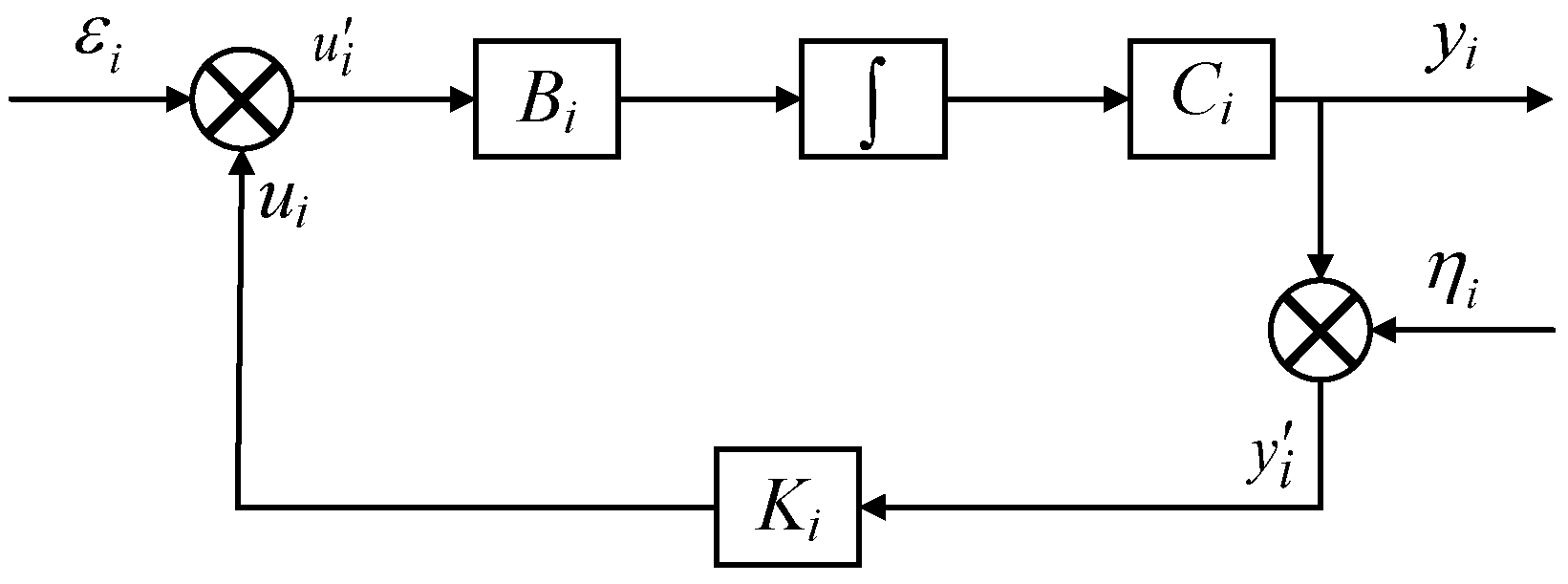
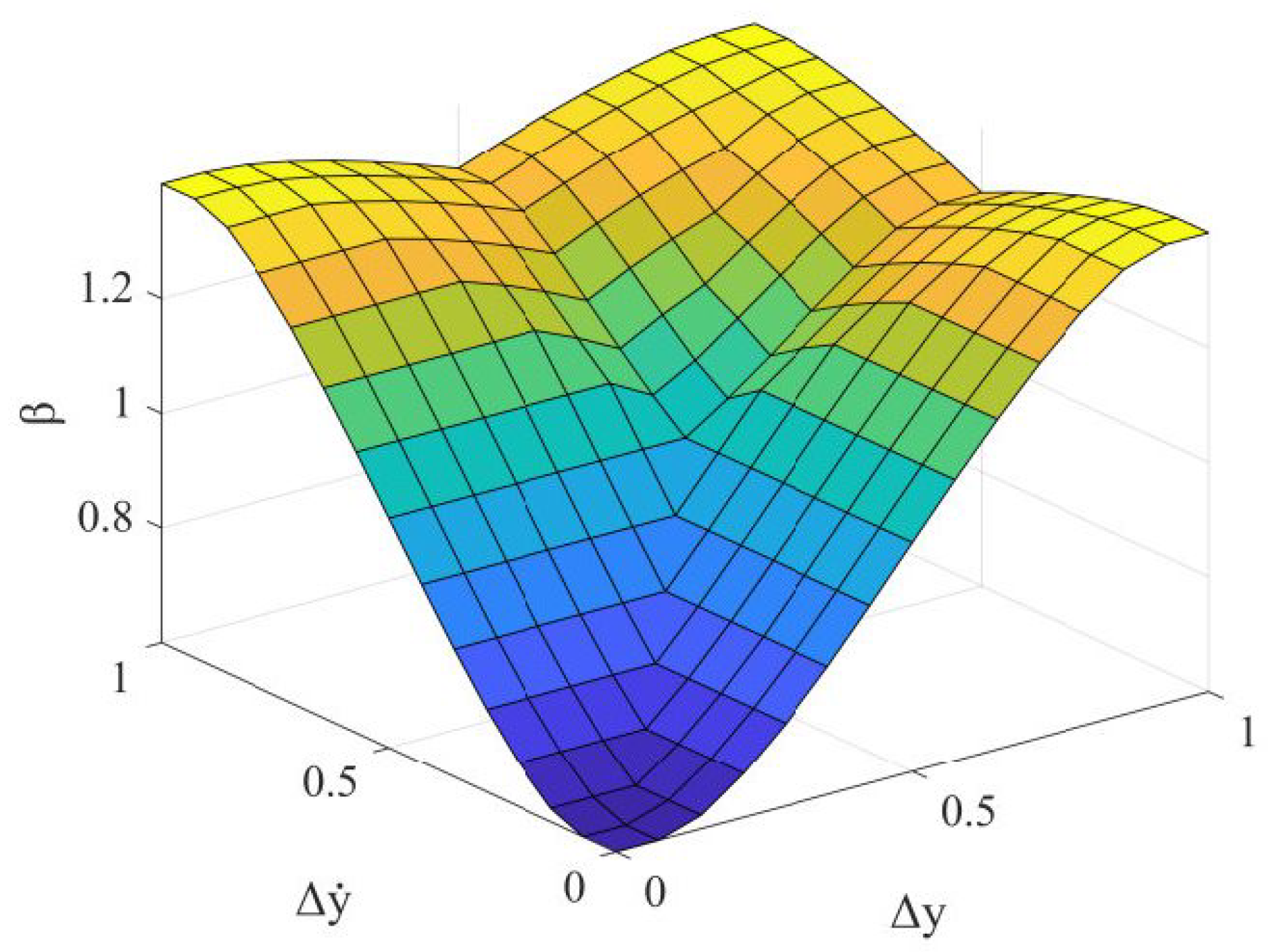
4.2. Design of Fuzzy Logic Controller
4.3. Criteria for Consistency of Continuous Linear Heterogeneous Multi-Agent Systems
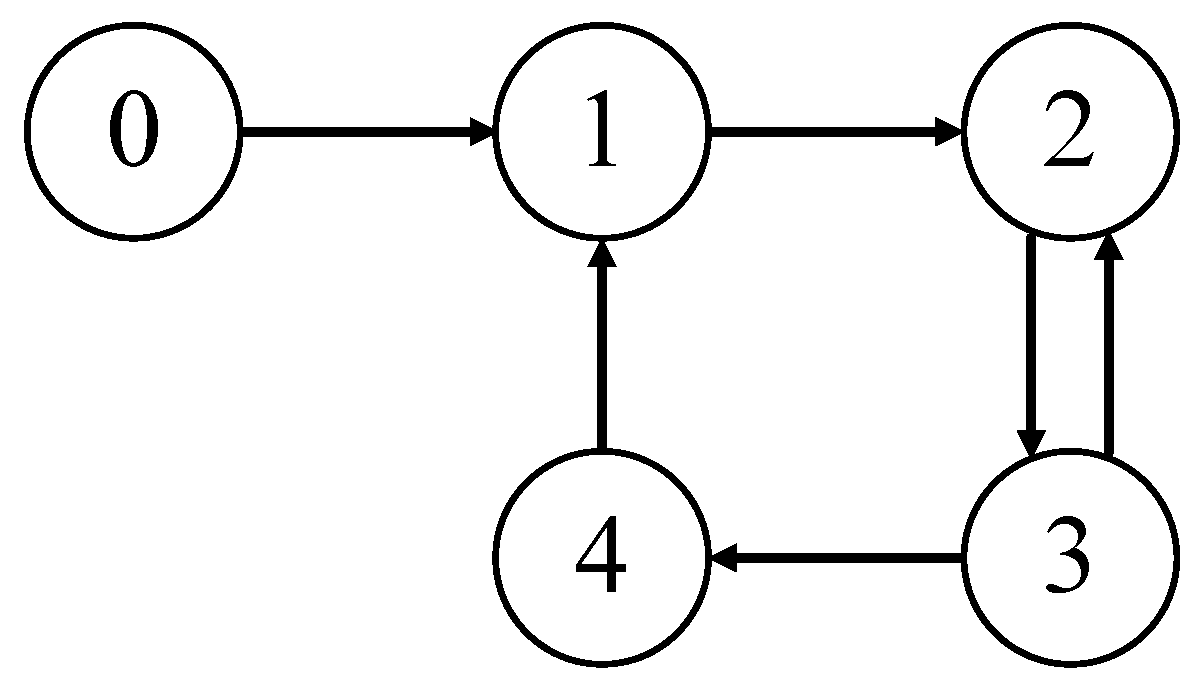
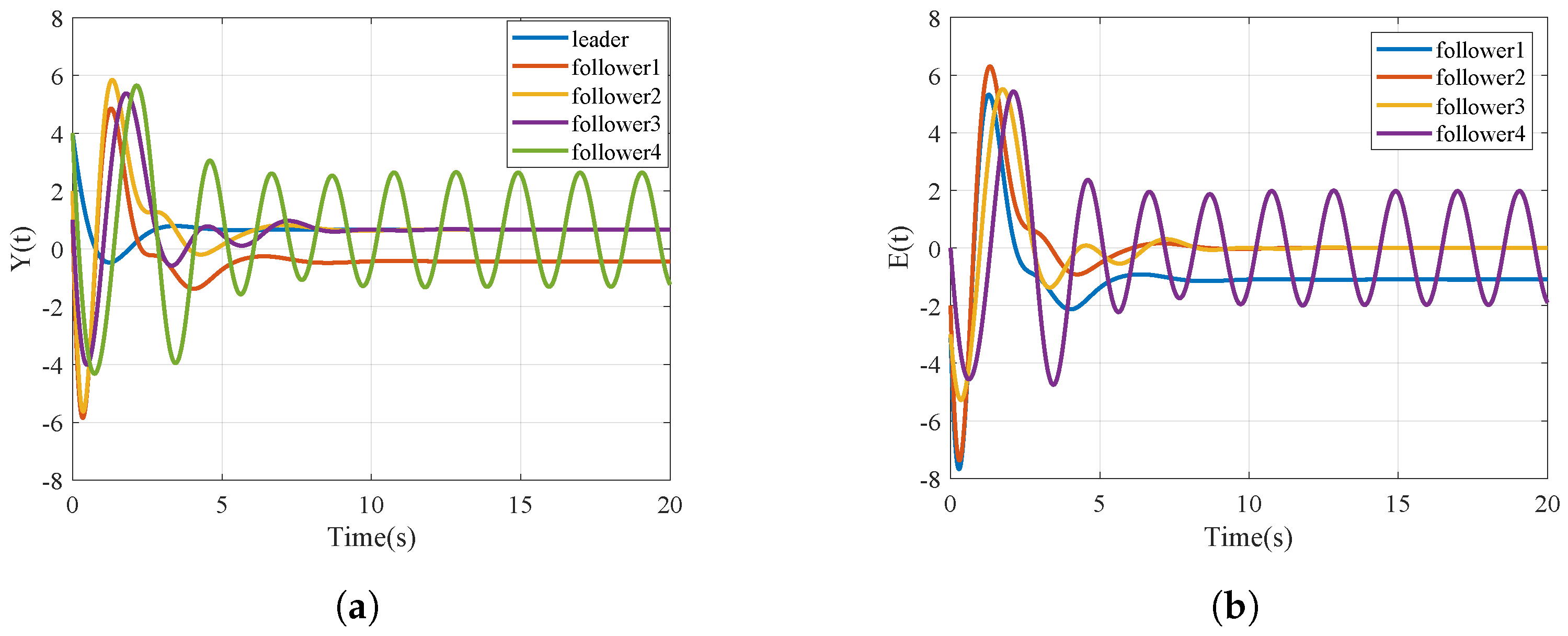
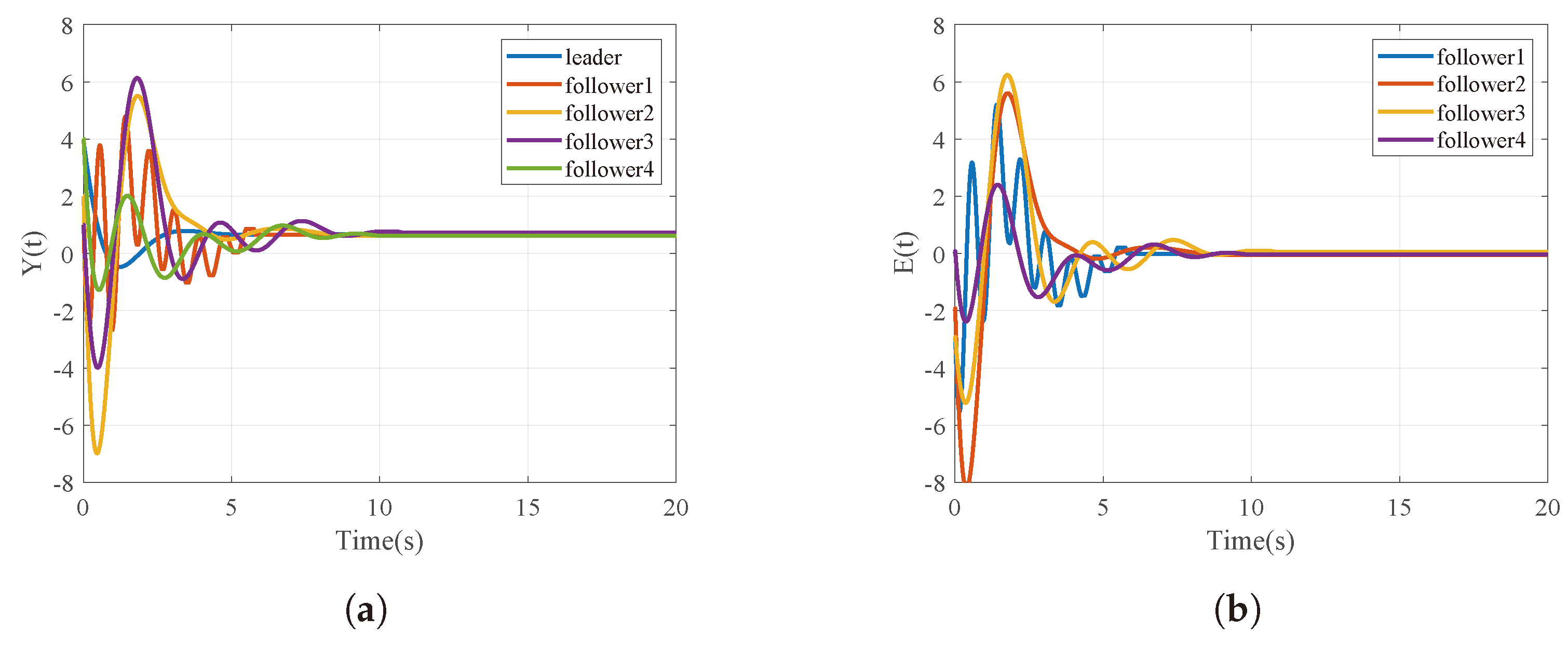
5. Simulation Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhirong, X.; Xingyun, R.; Rongjun, W. Introduction to medical care system for field battle. Southwest Def. Med. 2005, 15, 540–542. [Google Scholar] [CrossRef]
- Ningning, Y.; Yuchao, H.; Lulin, T.; Rong, J.; Chaojun, W. Research on variable order fractional PIλ controller based on fuzzy rules. J. Xi’an Univ. Technol. 2017, 33, 304–309. [Google Scholar] [CrossRef]
- Wang, R.; Yu, X.; Sun, Q.; Li, D.; Gui, Y.; Wang, P. The Integrated Reference Region Analysis for Parallel DFIGs’ Interfacing Inductors. IEEE Trans. Power Electron. 2024, 39, 7632–7642. [Google Scholar] [CrossRef]
- Liu, G.; Liu, J.; Xiao, X.; Sun, C.; Wang, R.; Sun, Q. Voltage Current Cooperative Control for DC Microgrid Under Input Unknown. In Proceedings of the IECON 2023—49th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 16–19 October 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Dingyu, X.; Chunna, Z. Fractional order PID controller design for fractional order system. Control. Theory Appl. 2007, 24, 771–776. [Google Scholar] [CrossRef]
- Xiao, M.; Tao, B.; Zheng, W.X.; Jiang, G. Fractional-Order PID Controller Synthesis for Bifurcation of Fractional-Order Small-World Networks. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 4334–4346. [Google Scholar] [CrossRef]
- Stanisławski, R.; Rydel, M.; Li, Z. A New Reduced-Order Implementation of Discrete-Time Fractional-Order PID Controller. IEEE Access 2022, 10, 17417–17429. [Google Scholar] [CrossRef]
- Zhang, N.; Yang, D.; Zhang, H.; Luo, Y. Distributed control strategy of DC microgrid based on consistency theory. Energy Rep. 2022, 8, 739–750. [Google Scholar] [CrossRef]
- Che, L.; Shahidehpour, M.; Alabdulwahab, A.; Al-Turki, Y. Hierarchical Coordination of a Community Microgrid with AC and DC Microgrids. IEEE Trans. Smart Grid 2015, 6, 3042–3051. [Google Scholar] [CrossRef]
- Peng, H.; Luan, L.; Xu, Z.; Mo, W.; Wang, Y. Event-Triggered Mechanism Based Control Method of SMES to Improve Microgrids Stability Under Extreme Conditions. IEEE Trans. Appl. Supercond. 2021, 31, 5403604. [Google Scholar] [CrossRef]
- Liu, S.; Siano, P.; Wang, X. Intrusion-Detector-Dependent Frequency Regulation for Microgrids Under Denial-of-Service Attacks. IEEE Syst. J. 2020, 14, 2593–2596. [Google Scholar] [CrossRef]
- Tan, S.; Xie, P.; Guerrero, J.M.; Vasquez, J.C.; Alcala, J.M.; Carreño, J.E.M.; Guerrero-Zapata, M. Lyapunov-Based Resilient Cooperative Control for DC Microgrid Clusters Against False Data Injection Cyber-Attacks. IEEE Trans. Smart Grid 2024, 15, 3208–3222. [Google Scholar] [CrossRef]
- Zhai, M.; Sun, Q.; Wang, R.; Wang, B.; Liu, S.; Zhang, H. Fully Distributed Fault-Tolerant Event-Triggered Control of Microgrids Under Directed Graphs. IEEE Trans. Netw. Sci. Eng. 2022, 9, 3570–3579. [Google Scholar] [CrossRef]
- Tahim, A.P.N.; Pagano, D.J.; Lenz, E.; Stramosk, V. Modeling and Stability Analysis of Islanded DC Microgrids Under Droop Control. IEEE Trans. Power Electron. 2015, 30, 4597–4607. [Google Scholar] [CrossRef]
- Wang, R.; Sun, Q.; Hu, W.; Li, Y.; Ma, D.; Wang, P. SoC-Based Droop Coefficients Stability Region Analysis of the Battery for Stand-Alone Supply Systems With Constant Power Loads. IEEE Trans. Power Electron. 2021, 36, 7866–7879. [Google Scholar] [CrossRef]
- Rui, W.; Qiuye, S.; Dazhong, M.; Xuguang, H. Line Impedance Cooperative Stability Region Identification Method for Grid-Tied Inverters Under Weak Grids. IEEE Trans. Smart Grid 2020, 11, 2856–2866. [Google Scholar] [CrossRef]
- Peyghami, S.; Davari, P.; Mokhtari, H.; Loh, P.C.; Blaabjerg, F. Synchronverter-Enabled DC Power Sharing Approach for LVDC Microgrids. IEEE Trans. Power Electron. 2017, 32, 8089–8099. [Google Scholar] [CrossRef]
- Kirakosyan, A.; El-Saadany, E.F.; Moursi, M.S.E.; Yazdavar, A.H.; Al-Durra, A. Communication-Free Current Sharing Control Strategy for DC Microgrids and Its Application for AC/DC Hybrid Microgrids. IEEE Trans. Power Syst. 2020, 35, 140–151. [Google Scholar] [CrossRef]
- Yang, Q.; Jiang, L.; Zhao, H.; Zeng, H. Autonomous Voltage Regulation and Current Sharing in Islanded Multi-Inverter DC Microgrid. IEEE Trans. Smart Grid 2018, 9, 6429–6437. [Google Scholar] [CrossRef]
- Nasirian, V.; Moayedi, S.; Davoudi, A.; Lewis, F.L. Distributed Cooperative Control of DC Microgrids. IEEE Trans. Power Electron. 2015, 30, 2288–2303. [Google Scholar] [CrossRef]
- Jinfeng, C.; Ke, J.; Zhenwen, X.; Rui, Z. Voltage Control Strategy of DC Microgrid Based on Discrete Consensus Algorithm. Zhejiang Electric Power 2019, 38, 65–71. [Google Scholar] [CrossRef]
- Liu, X.K.; He, H.; Wang, Y.W.; Xu, Q.; Guo, F. Distributed Hybrid Secondary Control for a DC Microgrid via Discrete-Time Interaction. IEEE Trans. Energy Convers. 2018, 33, 1865–1875. [Google Scholar] [CrossRef]
- Guo, F.; Xu, Q.; Wen, C.; Wang, L.; Wang, P. Distributed Secondary Control for Power Allocation and Voltage Restoration in Islanded DC Microgrids. IEEE Trans. Sustain. Energy 2018, 9, 1857–1869. [Google Scholar] [CrossRef]
- Yang, X.; Zhao, P.; Zhang, X.; Lin, J.; Yu, W. Toward a Gaussian-Mixture Model-Based Detection Scheme Against Data Integrity Attacks in the Smart Grid. IEEE Internet Things J. 2017, 4, 147–161. [Google Scholar] [CrossRef]
- Wang, H.; Ruan, J.; Wang, G.; Zhou, B.; Liu, Y.; Fu, X.; Peng, J. Deep Learning-Based Interval State Estimation of AC Smart Grids Against Sparse Cyber Attacks. IEEE Trans. Ind. Inform. 2018, 14, 4766–4778. [Google Scholar] [CrossRef]
- Zeng, W.; Chow, M.Y. Resilient Distributed Control in the Presence of Misbehaving Agents in Networked Control Systems. IEEE Trans. Cybern. 2014, 44, 2038–2049. [Google Scholar] [CrossRef] [PubMed]
- Teixeira, A.; Shames, I.; Sandberg, H.; Johansson, K.H. Distributed Fault Detection and Isolation Resilient to Network Model Uncertainties. IEEE Trans. Cybern. 2014, 44, 2024–2037. [Google Scholar] [CrossRef] [PubMed]
- Pasqualetti, F.; Bicchi, A.; Bullo, F. Consensus Computation in Unreliable Networks: A System Theoretic Approach. IEEE Trans. Autom. Control. 2012, 57, 90–104. [Google Scholar] [CrossRef]
- Sundaram, S.; Hadjicostis, C.N. Distributed Function Calculation via Linear Iterative Strategies in the Presence of Malicious Agents. IEEE Trans. Autom. Control. 2011, 56, 1495–1508. [Google Scholar] [CrossRef]
- Ding, D.; Wang, Z.; Ho, D.W.C.; Wei, G. Observer-Based Event-Triggering Consensus Control for Multiagent Systems with Lossy Sensors and Cyber-Attacks. IEEE Trans. Cybern. 2017, 47, 1936–1947. [Google Scholar] [CrossRef]
- Cui, Y.; Liu, Y.; Zhang, W.; Alsaadi, F.E. Sampled-Based Consensus for Nonlinear Multiagent Systems with Deception Attacks: The Decoupled Method. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 561–573. [Google Scholar] [CrossRef]
- Li, X.M.; Zhou, Q.; Li, P.; Li, H.; Lu, R. Event-Triggered Consensus Control for Multi-Agent Systems against False Data-Injection Attacks. IEEE Trans. Cybern. 2020, 50, 1856–1866. [Google Scholar] [CrossRef]
- Modares, H.; Kiumarsi, B.; Lewis, F.L.; Ferrese, F.; Davoudi, A. Resilient and Robust Synchronization of Multiagent Systems Under Attacks on Sensors and Actuators. IEEE Trans. Cybern. 2020, 50, 1240–1250. [Google Scholar] [CrossRef] [PubMed]
- Mustafa, A.; Modares, H. Attack Analysis and Resilient Control Design for Discrete-Time Distributed Multi-Agent Systems. IEEE Robot. Autom. Lett. 2020, 5, 369–376. [Google Scholar] [CrossRef]
- Rui, W.; Qiuye, S.; Pinjia, Z.; Yonghao, G.; Dehao, Q.; Peng, W. Reduced-Order Transfer Function Model of the Droop-Controlled Inverter via Jordan Continued-Fraction Expansion. IEEE Trans. Energy Convers. 2020, 35, 1585–1595. [Google Scholar] [CrossRef]
- Zhou, J.; Xu, Y.; Sun, H.; Wang, L.; Chow, M.Y. Distributed Event-Triggered H∞ Consensus Based Current Sharing Control of DC Microgrids Considering Uncertainties. IEEE Trans. Ind. Inform. 2020, 16, 7413–7425. [Google Scholar] [CrossRef]
- Huo, S.; Huang, D.; Zhang, Y. Secure output synchronization of heterogeneous multi-agent systems against false data injection attacks. Sci. China-Inf. Sci. 2022, 65, 162204. [Google Scholar] [CrossRef]
- Han, J.; Zhang, H.; Wang, Y.; Ren, H. Output Consensus Problem for Linear Heterogeneous Multiagent Systems with Dynamic Event-Based Impulsive Control. IEEE Trans. Syst. Man, Cybern. Syst. 2023, 53, 334–345. [Google Scholar] [CrossRef]
- El Ghaoui, L.; Oustry, F.; AitRami, M. A cone complementarity linearization algorithm for static output-feedback and related problems. IEEE Trans. Autom. Control 1997, 42, 1171–1176. [Google Scholar] [CrossRef]


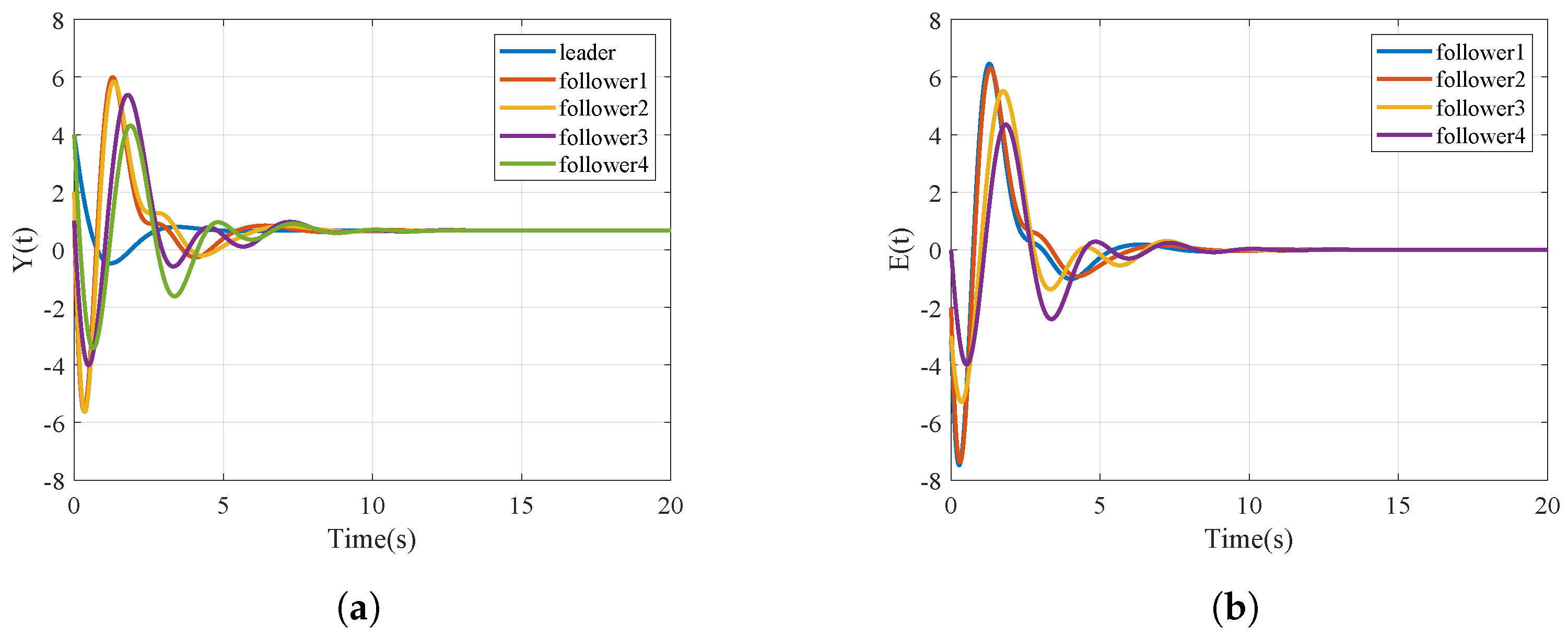


| Small | Big | |
|---|---|---|
| Small | N | U |
| Big | U | U |
| Parameter values | 0.6100 | 0.6008 | 0.6008 | 0.6007 |
| RLC Filter Resistance | Value | RLC Filter Capacitance | Value | RLC Filter Inductance | Value |
|---|---|---|---|---|---|
| 0.4 | 4 mF | 1 mH | |||
| 0.8 | 3 mF | 2/3 mH | |||
| 0.6 | 1 mF | 1/3 mH | |||
| 0.4 | 2 mF | 2/3 mH | |||
| 0.4 | 4 mF | 1/3 mH |
| Parameter Values | Parameter Values | Parameter Values | |||
|---|---|---|---|---|---|
| −7.6 | 3 | 4 | |||
| −8.2 | −11 | 6 | |||
| −2.4 | −1 | 1 | |||
| −3.1 | −3 | 2 | |||
| −6.6 | −3 | 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Zhao, W.; Liu, L.; Wang, R. Distributed Consensus Fuzzy Control Method and Fractional Order Control for Power Sharing in Field Medical Microgrids under FDI Attacks. Fractal Fract. 2024, 8, 561. https://doi.org/10.3390/fractalfract8100561
Wang C, Zhao W, Liu L, Wang R. Distributed Consensus Fuzzy Control Method and Fractional Order Control for Power Sharing in Field Medical Microgrids under FDI Attacks. Fractal and Fractional. 2024; 8(10):561. https://doi.org/10.3390/fractalfract8100561
Chicago/Turabian StyleWang, Chenyu, Wenyue Zhao, Lu Liu, and Rui Wang. 2024. "Distributed Consensus Fuzzy Control Method and Fractional Order Control for Power Sharing in Field Medical Microgrids under FDI Attacks" Fractal and Fractional 8, no. 10: 561. https://doi.org/10.3390/fractalfract8100561
APA StyleWang, C., Zhao, W., Liu, L., & Wang, R. (2024). Distributed Consensus Fuzzy Control Method and Fractional Order Control for Power Sharing in Field Medical Microgrids under FDI Attacks. Fractal and Fractional, 8(10), 561. https://doi.org/10.3390/fractalfract8100561







