New Event-Triggered Synchronization Criteria for Fractional-Order Complex-Valued Neural Networks with Additive Time-Varying Delays
Abstract
:1. Introduction
2. Preliminaries
3. Main Results
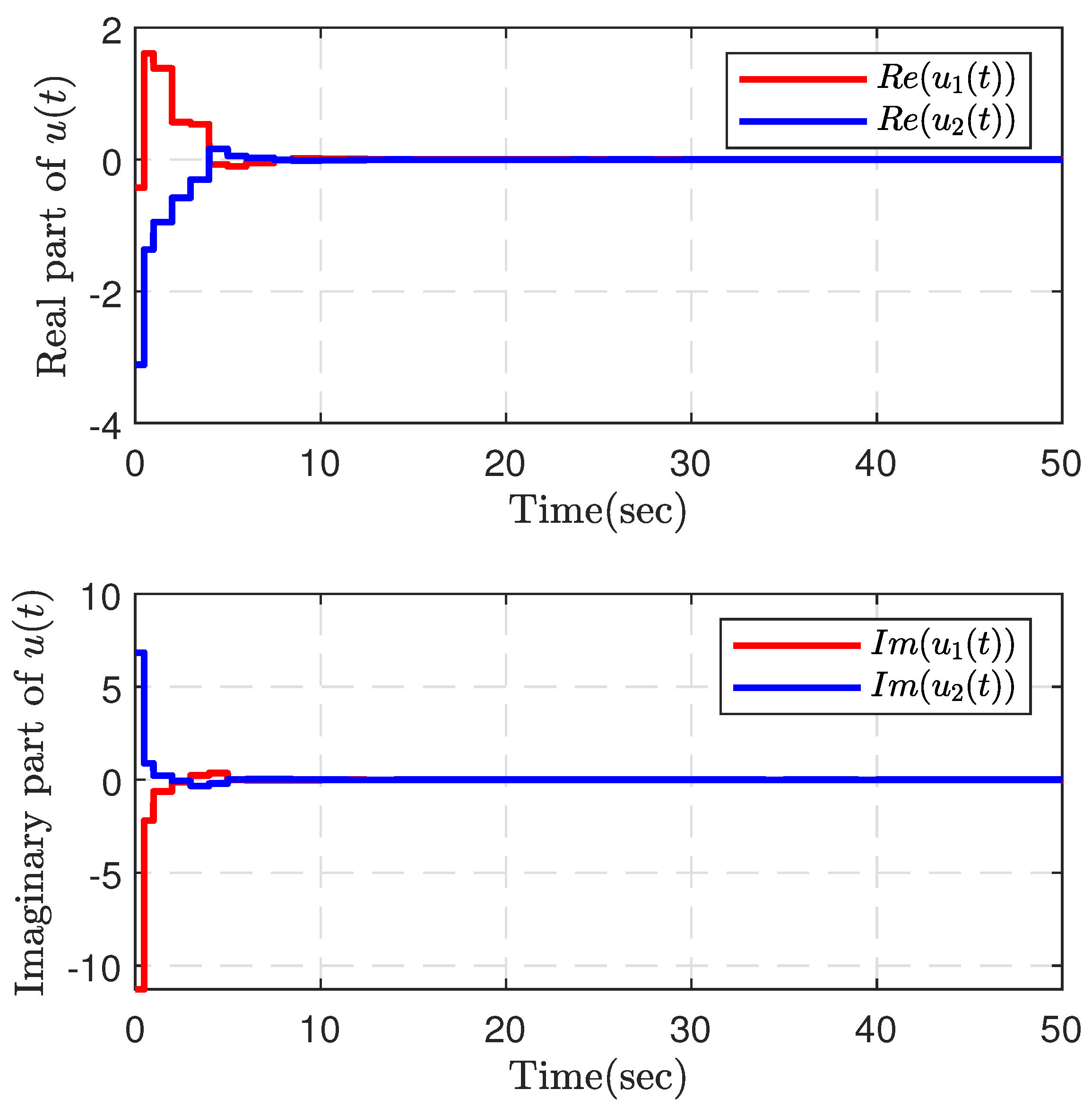
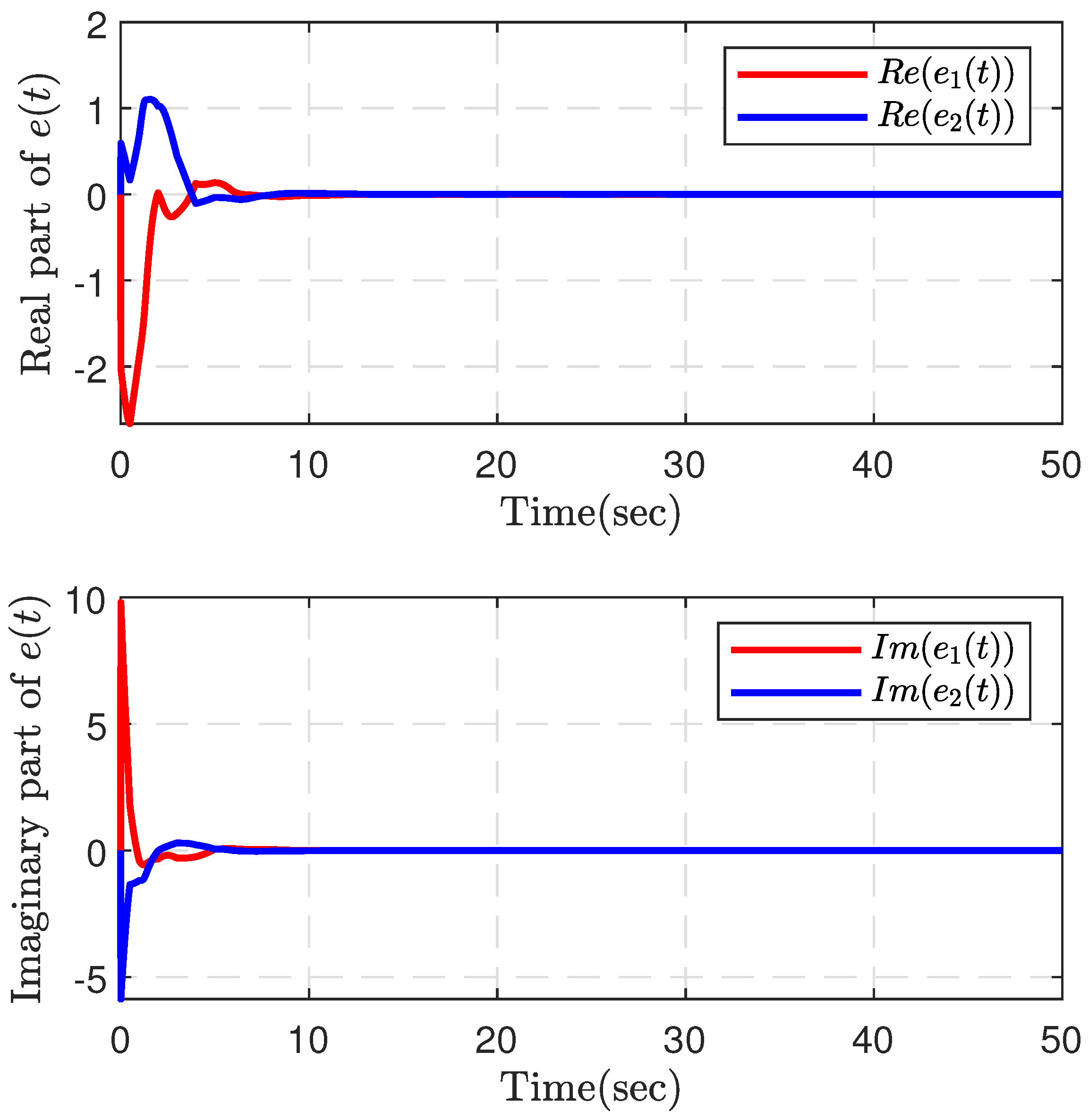
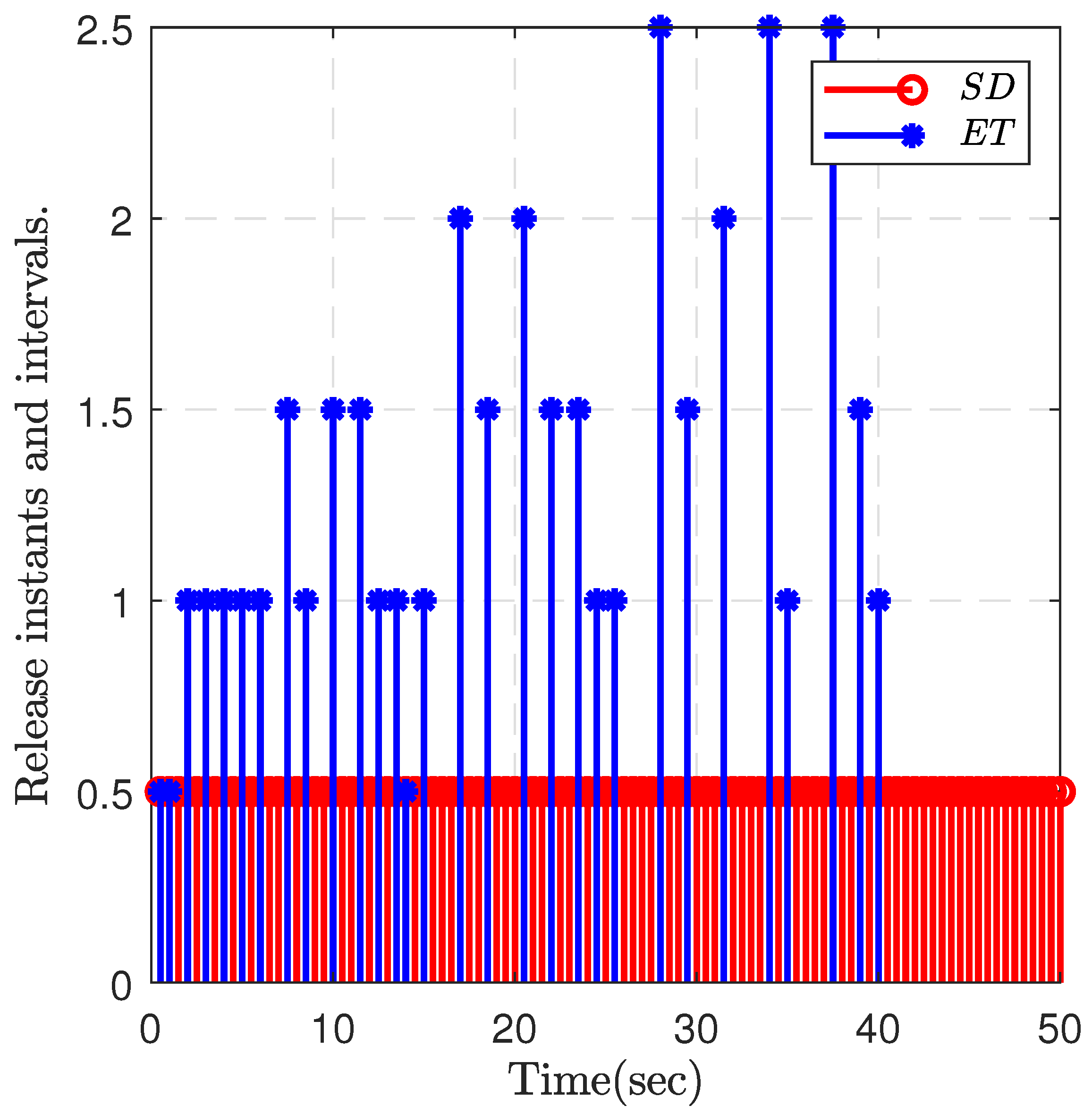
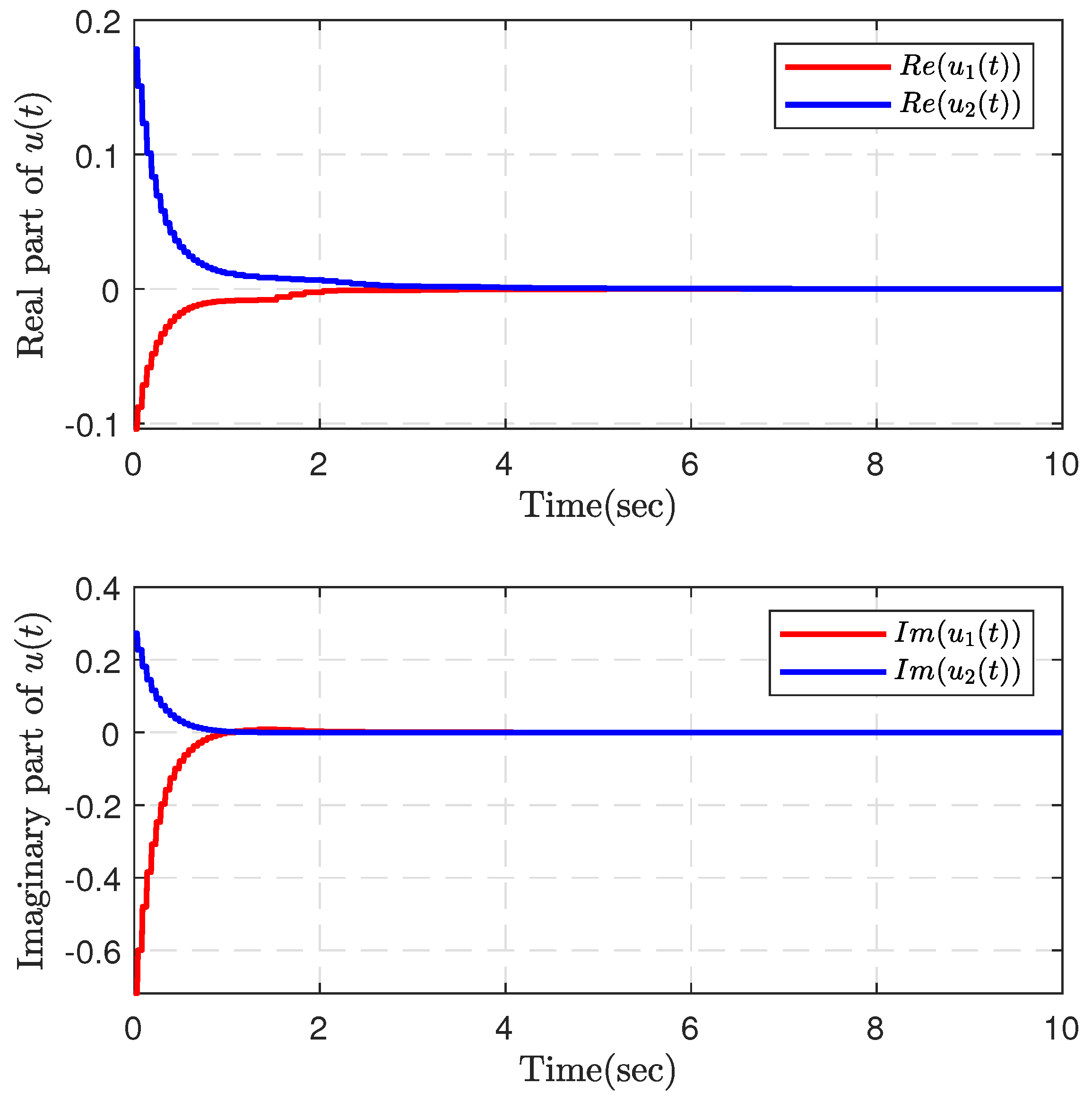
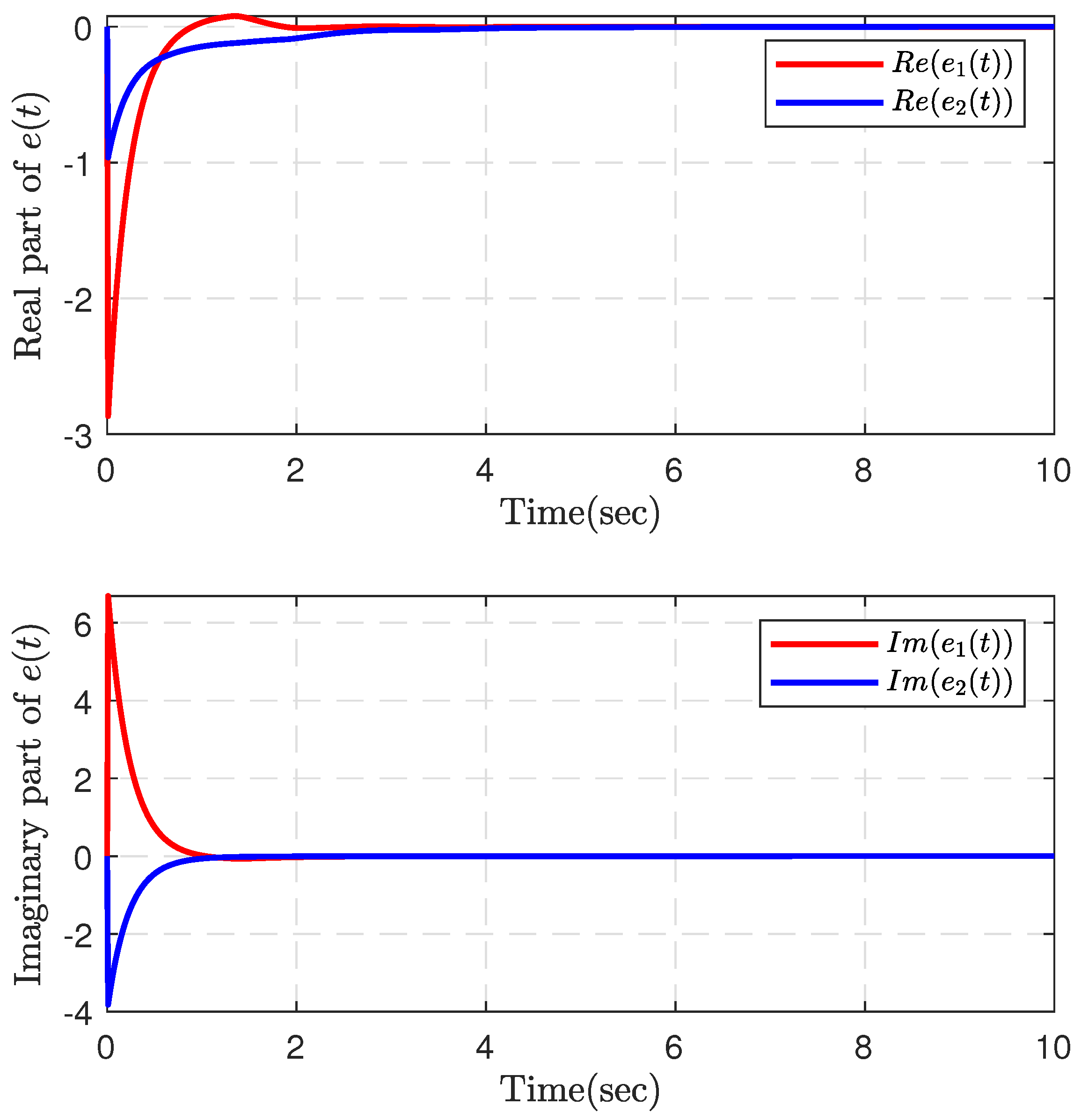
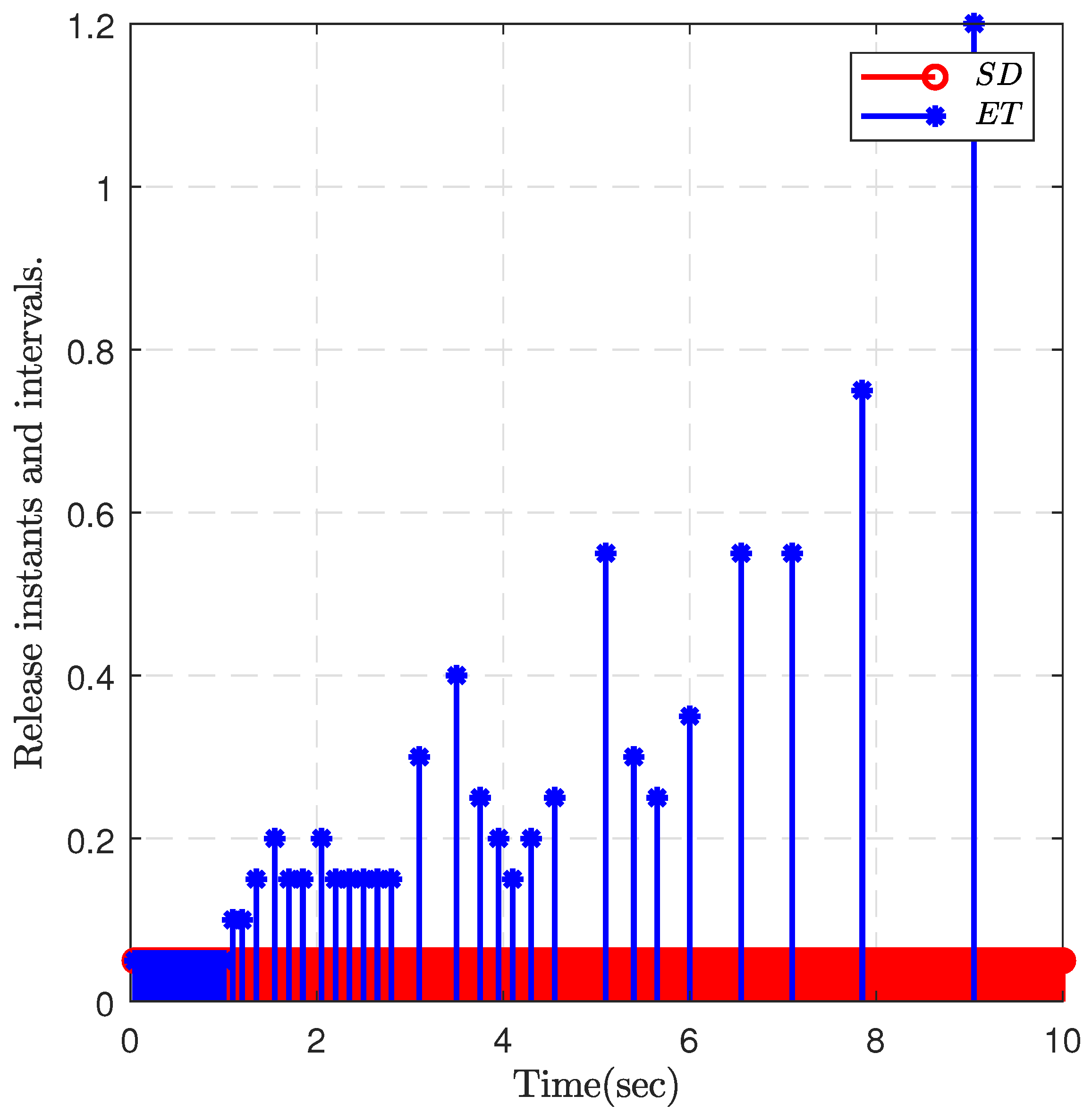
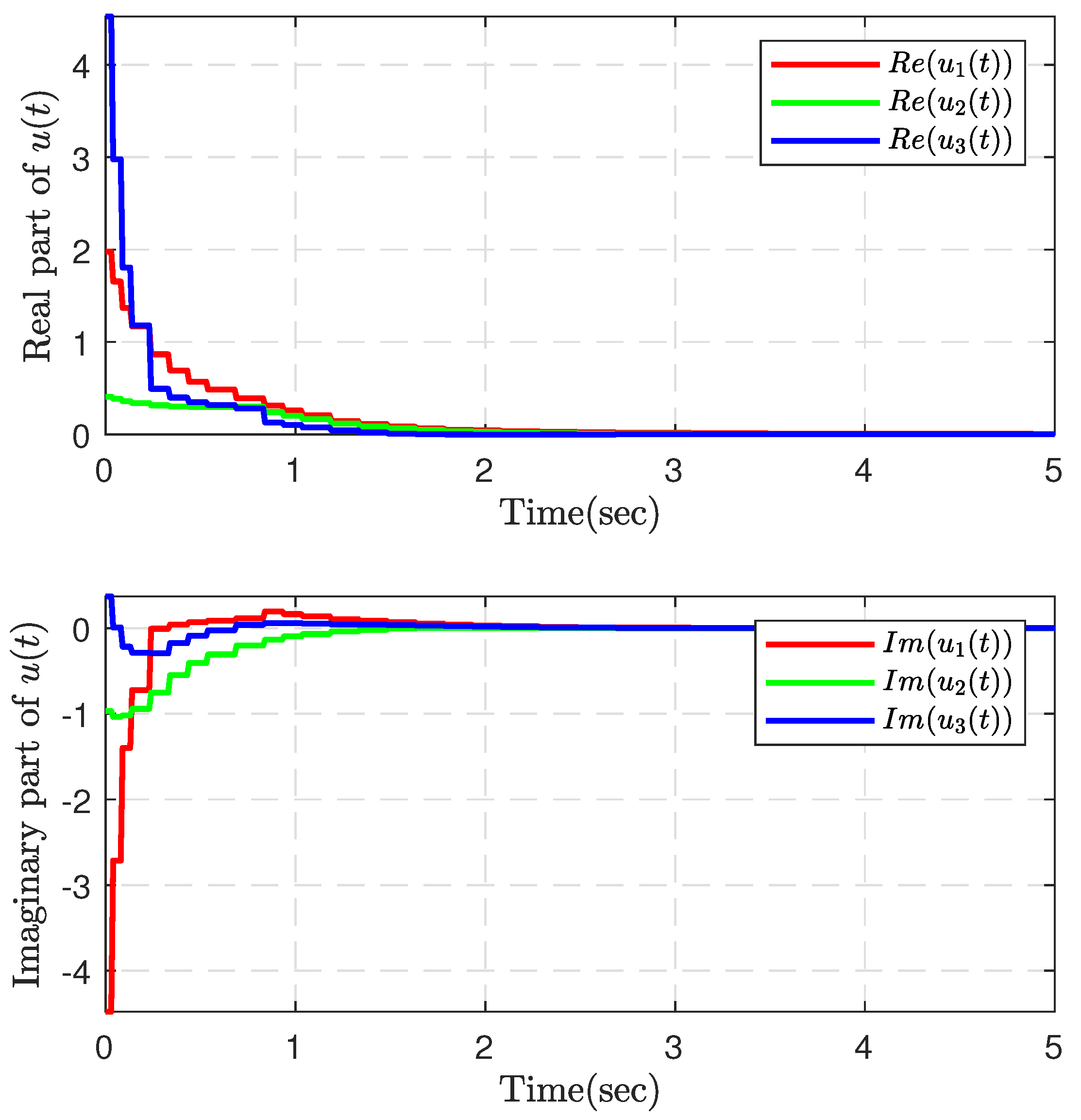
4. Numerical Examples
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kiruthika, R.; Krishnasamy, R.; Lakshmanan, S.; Prakash, M.; Manivannan, A. Non-fragile sampled-data control for synchronization of chaotic fractional-order delayed neural networks via LMI approach. Chaos Solitons Fractals 2023, 169, 113252. [Google Scholar] [CrossRef]
- Mukdasai, K. Synchronization of Fractional-Order Uncertain Delayed Neural Networks with an Event-Triggered Communication Scheme. Fractal Fract. 2022, 6, 641. [Google Scholar] [CrossRef]
- Bao, H.; Cao, J.; Kurths, J. State estimation of fractional-order delayed memristive neural networks. Nonlinear Dyn. 2018, 94, 1215–1225. [Google Scholar] [CrossRef]
- Padmaja, N.; Balasubramaniam, P. Design of H/passive state feedback control for delayed fractional order gene regulatory networks via new improved integral inequalities. Commun. Nonlinear Sci. Numer. Simul. 2022, 111, 106507. [Google Scholar] [CrossRef]
- Liang, J.; Li, K.; Song, Q.; Zhao, Z.; Liu, Y.; Alsaadi, F.E. State estimation of complex-valued neural networks with two additive time-varying delays. Neurocomputing 2018, 309, 54–61. [Google Scholar] [CrossRef]
- Wei, X.; Zhang, Z.; Lin, C.; Chen, J. Synchronization and anti-synchronization for complex-valued inertial neural networks with time-varying delays. Appl. Math. Comput. 2021, 403, 126194. [Google Scholar] [CrossRef]
- Pan, J.; Zhang, Z. Finite-time synchronization for delayed complex-valued neural networks via the exponential-type controllers of time variable. Chaos Solitons Fractals Appl. Sci. Eng. Interdiscip. J. Nonlinear Sci. 2021, 146, 110897. [Google Scholar] [CrossRef]
- Subramanian, K.; Muthukumar, P. Global asymptotic stability of complex-valued neural networks with additive time-varying delays. Cogn. Neurodynamics 2017, 11, 293–306. [Google Scholar] [CrossRef]
- Yao, L.; Wang, Z.; Wang, Q.; Xia, J.; Shen, H. Exponential Stabilization of Delayed Complex-valued Neural Networks with Aperiodic Sampling: A Free-matrix-based Time-dependent Lyapunov Functional Method. Int. J. Control Autom. Syst. 2020, 18, 1894–1903. [Google Scholar] [CrossRef]
- Aghayan, Z.S.; Alfi, A.; Mousavi, Y.; Fekih, A. Stability analysis of a class of variable fractional-order uncertain neutral-type systems with time-varying delay. J. Frankl. Inst. 2023, 360, 10517–10535. [Google Scholar] [CrossRef]
- Aghayan, Z.S.; Alfi, A.; Mousavi, Y.; Kucukdemiral, I.B.; Fekih, A. Guaranteed cost robust output feedback control design for fractional-order uncertain neutral delay systems. Chaos Solitons Fractals 2022, 163, 112523. [Google Scholar] [CrossRef]
- Aghayan, Z.S.; Alfi, A.; Mousavi, Y.; Fekih, A. Criteria for stability and stabilization of variable fractional-order uncertain neutral systems with time-varying delay: Delay-dependent analysis. IEEE Trans. Circuits Syst. II Express Briefs 2023, 70, 3393–3397. [Google Scholar] [CrossRef]
- Xiong, M.; Ju, G.; Tan, Y. Robust State Estimation for Fractional-Order Nonlinear Uncertain Systems via Adaptive Event-Triggered Communication Scheme. IEEE Access 2019, 7, 115002–115009. [Google Scholar] [CrossRef]
- Chen, S.; Song, Q.; Zhao, Z.; Liu, Y.; Alsaadi, F.E. Global asymptotic stability of fractional-order complex-valued neural networks with probabilistic time-varying delays. Neurocomputing 2021, 450, 311–318. [Google Scholar] [CrossRef]
- Aravind, R.V.; Balasubramaniam, P. Stochastic stability of fractional-order Markovian jumping complex-valued neural networks with time-varying delays. Neurocomputing 2021, 439, 122–133. [Google Scholar] [CrossRef]
- Zhang, H.; Qiu, Z.; Xiong, L. Stochastic stability criterion of neutral-type neural networks with additive time-varying delay and uncertain semi-Markov jump. Neurocomputing 2019, 333, 395–406. [Google Scholar] [CrossRef]
- Cao, Y.; Sriraman, R.; Shyamsundarraj, N.; Samidurai, R. Robust stability of uncertain stochastic complex-valued neural networks with additive time-varying delays. Math. Comput. Simul. 2020, 171, 207–220. [Google Scholar] [CrossRef]
- Felipe, A.; Oliveira, R.C. An LMI-based algorithm to compute robust stabilizing feedback gains directly as optimization variables. IEEE Trans. Autom. Control 2020, 66, 4365–4370. [Google Scholar] [CrossRef]
- Nguyen, T.H.; Nguyen, V.C.; Bui, D.Q.; Dao, P.N. An efficient Min/Max Robust Model Predictive Control for nonlinear discrete-time systems with dynamic disturbance. Chaos Solitons Fractals 2024, 180, 114551. [Google Scholar] [CrossRef]
- Seuret, A.; Gouaisbaut, F. Jensen’s and Wirtinger’s inequalities for time-delay systems. IFAC Proc. Vol. 2013, 46, 343–348. [Google Scholar] [CrossRef]
- Zeng, H.B.; He, Y.; Wu, M.; She, J. Free-matrix-based integral inequality for stability analysis of systems with time-varying delay. IEEE Trans. Autom. Control 2015, 60, 2768–2772. [Google Scholar] [CrossRef]
- Hu, T.; He, Z.; Zhang, X.; Zhong, S. Leader-following consensus of fractional-order multi-agent systems based on event-triggered control. Nonlinear Dyn. 2020, 99, 2219–2232. [Google Scholar] [CrossRef]
- Hu, T.; He, Z.; Zhang, X.; Zhong, S. Global synchronization of time-invariant uncertainty fractional-order neural networks with time delay. Neurocomputing 2019, 339, 45–58. [Google Scholar] [CrossRef]
- Hu, T.; Park, J.H.; Liu, X.; He, Z.; Zhong, S. Sampled-data-based event-triggered synchronization strategy for fractional and impulsive complex networks with switching topologies and time-varying delay. IEEE Trans. Syst. Man, Cybern. Syst. 2021, 52, 3568–3580. [Google Scholar] [CrossRef]
- Wen, G.; Chen, M.Z.; Yu, X. Event-triggered master–slave synchronization with sampled-data communication. IEEE Trans. Circuits Syst. II Express Briefs 2015, 63, 304–308. [Google Scholar] [CrossRef]
- Zhou, L.; Liu, C.; Pan, R.; Xiao, X. Event-triggered synchronization of switched nonlinear system based on sampled measurements. IEEE Trans. Cybern. 2020, 52, 3531–3538. [Google Scholar] [CrossRef] [PubMed]
- Guan, C.; Sun, D.; Fei, Z.; Ren, C. Synchronization for switched neural networks via variable sampled-data control method. Neurocomputing 2018, 311, 325–332. [Google Scholar] [CrossRef]
- Li, H.; Li, C.; Ouyang, D.; Nguang, S.K. Impulsive synchronization of unbounded delayed inertial neural networks with actuator saturation and sampled-data control and its application to image encryption. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 1460–1473. [Google Scholar] [CrossRef]
- Xiao, L.; Li, L.; Cao, P.; He, Y. A fixed-time robust controller based on zeroing neural network for generalized projective synchronization of chaotic systems. Chaos Solitons Fractals 2023, 169, 113279. [Google Scholar] [CrossRef]
- Li, H.L.; Hu, C.; Cao, J.; Jiang, H.; Alsaedi, A. Quasi-projective and complete synchronization of fractional-order complex-valued neural networks with time delays. Neural Netw. 2019, 118, 102–109. [Google Scholar] [CrossRef]
- Liu, D.; Zhu, S.; Sun, K. Global anti-synchronization of complex-valued memristive neural networks with time delays. IEEE Trans. Cybern. 2018, 49, 1735–1747. [Google Scholar] [CrossRef] [PubMed]
- Xu, B.; Li, B. Event-Triggered State Estimation for Fractional-Order Neural Networks. Mathematics 2022, 10, 325. [Google Scholar] [CrossRef]
- Xing, X.; Wu, H.; Cao, J. Event-triggered impulsive control for synchronization in finite time of fractional-order reaction–diffusion complex networks. Neurocomputing 2023, 557, 126703. [Google Scholar] [CrossRef]
- Yu, N.; Zhu, W. Exponential stabilization of fractional-order continuous-time dynamic systems via event-triggered impulsive control. Nonlinear Anal. Model. Control 2022, 27, 592–608. [Google Scholar] [CrossRef]
- Liu, F.; Yang, Y.; Wang, F.; Zhang, L. Synchronization of fractional-order reaction–diffusion neural networks with Markov parameter jumping: Asynchronous boundary quantization control. Chaos Solitons Fractals 2023, 173, 113622. [Google Scholar] [CrossRef]
- Sun, Y.; Hu, C.; Yu, J.; Shi, T. Synchronization of fractional-order reaction-diffusion neural networks via mixed boundary control. Appl. Math. Comput. 2023, 450, 127982. [Google Scholar] [CrossRef]
- Fan, Q.Y.; Yang, G.H. Sampled-data output feedback control based on a new event-triggered control scheme. Inf. Sci. 2017, 414, 306–318. [Google Scholar] [CrossRef]
- Peng, C.; Han, Q.L. A Novel Event-Triggered Transmission Scheme and L_2 Control Co-Design for Sampled-Data Control Systems. IEEE Trans. Autom. Control 2013, 58, 2620–2626. [Google Scholar] [CrossRef]
- Yang, Y.; Tu, Z.; Wang, L.; Cao, J.; Shi, L.; Qian, W. H infinity synchronization of delayed neural networks via event-triggered dynamic output control. Neural Netw. 2021, 142, 231–237. [Google Scholar] [CrossRef]
- Qiu, Q.; Su, H. Sampling-based event-triggered exponential synchronization for reaction-diffusion neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2021, 34, 1209–1217. [Google Scholar] [CrossRef]
- Zhao, L.N.; Ma, H.J.; Xu, L.X.; Wang, X. Observer-based adaptive sampled-data event-triggered distributed control for multi-agent systems. IEEE Trans. Circuits Syst. II Express Briefs 2019, 67, 97–101. [Google Scholar] [CrossRef]
- Hu, T.; He, Z.; Zhang, X.; Zhong, S. Finite-time stability for fractional-order complex-valued neural networks with time delay. Appl. Math. Comput. 2020, 365, 124715. [Google Scholar] [CrossRef]
- Hu, T.; He, Z.; Zhang, X.; Zhong, S.; Yao, X. New fractional-order integral inequalities: Application to fractional-order systems with time-varying delay. J. Frankl. Inst. 2021, 358, 3847–3867. [Google Scholar] [CrossRef]
- Padmaja, N.; Balasubramaniam, P. Results on passivity analysis of delayed fractional-order neural networks subject to periodic impulses via refined integral inequalities. Comput. Appl. Math. 2022, 41, 136. [Google Scholar] [CrossRef]
- Gunasekaran, N.; Zhai, G. Sampled-data state-estimation of delayed complex-valued neural networks. Int. J. Syst. Sci. 2020, 51, 303–312. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Z.; Song, Q.; Shen, H.; Huang, X. A waiting-time-based event-triggered scheme for stabilization of complex-valued neural networks. Neural Netw. 2020, 121, 329–338. [Google Scholar] [CrossRef] [PubMed]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Zhao, Y.; Xiong, L.; Dai, J.; Zhang, Y. New Event-Triggered Synchronization Criteria for Fractional-Order Complex-Valued Neural Networks with Additive Time-Varying Delays. Fractal Fract. 2024, 8, 569. https://doi.org/10.3390/fractalfract8100569
Zhang H, Zhao Y, Xiong L, Dai J, Zhang Y. New Event-Triggered Synchronization Criteria for Fractional-Order Complex-Valued Neural Networks with Additive Time-Varying Delays. Fractal and Fractional. 2024; 8(10):569. https://doi.org/10.3390/fractalfract8100569
Chicago/Turabian StyleZhang, Haiyang, Yi Zhao, Lianglin Xiong, Junzhou Dai, and Yi Zhang. 2024. "New Event-Triggered Synchronization Criteria for Fractional-Order Complex-Valued Neural Networks with Additive Time-Varying Delays" Fractal and Fractional 8, no. 10: 569. https://doi.org/10.3390/fractalfract8100569






