Abstract
In this paper, we aim to investigate corrected Euler–Maclaurin inequalities involving pre-invex mappings within the framework of fractional calculus. We want to find a number of important results for differentiable pre-invex mappings and Riemann–Liouville (RL) fractional integrals so that we can make more accurate error estimates. Additionally, we present examples with graphical illustrations to substantiate our major findings and deduce several special cases under certain conditions. Afterwards, we introduce applications such as the linear combination of means, composite corrected Maclaurin’s rule, modified Bessel mappings, and novel iterative methods for solving nonlinear equations.
1. Introduction
The concept of convexity is fundamental and intrinsic. A mapping is said to be convex if
where is a convex set and is a set of real numbers. Convexity plays a crucial role in several domains of physical sciences, including economics, finance, optimization, and engineering. Mathematical inequality and optimization have gained significant advancements from many interesting extensions and generalizations of classical convexity. Generalized convex mappings, such as -vex, sub--convex, pre-invex, and -pre-invex, are extensively used in optimization and inequalities to tackle with non-convex mappings. Using invex sets, Weir and Mond [1] introduced a class of mappings known as pre-invex, which is explored as follows.
A mapping is said to be a pre-invex on an invex set with respect to bifunction , if
where .
Moreover, Weir and Mond [2] investigated the situations and circumstances in which pre-invex mappings could take the role of convex mappings. Some properties of pre-invex mappings were presented by Mohan and Neogy [3]. Now, we enlist some significant contributions related to pre-invex mappings, which are crucial to conduct further investigation. Matloka [4] implemented the pre-invexity to examine some classic inequalities. Noor et al. [5] employed general pre-invex mappings to analyze trapezium-like inequalities. In 2014, Ozan [6] explored the classic inequalities concerning trapezium inequality incorporated with multiplicative pre-invexity. Lakhdari and Meftah [7] demonstrated some weighted Hadamard-like inequalities through h-pre-invexity. In 2021, Tariq and his group [8] explored various inequalities through a new unified pre-invexity of mappings. For more details, see [9,10]. The increasing interest in fractional calculus is driven by its diverse applications across scientific fields; for more details, see [11]. Mathematicians have explored various fractional integral inequalities to obtain more rectified bounds for existing quantities, such as Hermite–Hadamard’s and Simpson-type inequalities, as well as Newton and Euler–Maclaurin’s. There is no denying that fractional calculus can be used to solve a wide range of complex issues in science, engineering, and mathematics [12]. In fractional calculus, the RL fractional integral is the primary operator and is defined as follows.
Let . The RL integrals and of order with are defined by
and
respectively. Here, is the Gamma mapping and . For more details, see [13,14,15].
The concept of generalized fractional integrals was developed by Sarikaya and Ertural [16], who also derived Hadamard-type inequalities. As a result, mathematicians have extensively studied Hermite–Hadamard-type inequalities, as well as related ones like the trapezoid, midpoint, and Simpson’s inequalities.
Integral inequalities are the primary source for developing novel bounds for the remainder of the terms associated with Newton–Cotes schemes for differentiable convex mapping and various other classes of mapping. Furthermore, certain writers have set additional limits by utilizing the idea of fractional calculus. For example, Dragomir and Agarwal [17] examined the error inequalities of the trapezoidal rule by taking into account the first-order differentiability of convex mappings. In 2013, Alomari [18] investigated trapezoidal inequalities using Lipschitzian mappings and bounded variation mappings. Furthermore, Sarikaya and Yildirim [19] delivered some general versions of Hadamard’s inequalities by utilizing fractional operators and convexity strategies. Dragomir [20] computed the midpoint inequalities using bounded variation and Lipschitzian mapping. Set et al. [21] investigated the fractional Simpson-like inequalities by utilizing the concept of Riemann–Liouville fractional operators. Zhu et al. [22] explored the various error inequalities of quadrature processes through convex functions within multiplicative calculus. Hussain et al. [23] also analyzed Simpson-like inequalities through generalized fractional operators and the convexity properties of functions. Likewise, several approaches and bounds regarding Simpson-type inequalities are formulated in [24,25].
Using pre-invex mappings, Ali et al. [26] explored Simpson-like inequalities by leveraging the concepts of quantum calculus. Bin-Mohsin et al. [27] investigated Milne’s kinds of inequalities associated with Mercer’s inequality for convex mappings. You et al. [28] provided more variants and insights into Simpson’s kinds of inequalities, considering twice differentiable mappings in a fractional environment.
The Euler-corrected Maclaurin rule is given in [29] as
And the corresponding Maclaurin’s inequality is given as
Suppose that is a fourth-order continuous differentiable mapping on and . Then, the inequality
Franji and Peari [30] have demonstrated the corrected Euler–Maclaurin’s inequalities. In 2024, Hezenci and Budak [31], explored the Euler–Maclaurin-like inequalities through various classes of mappings.
In this work, by employing the concept of fractional operators, we shall construct fractional analogues of Maclaurin’s inequality through pre-invex mappings. The primary goal of looking at these inequalities is to forecast more robust and precise bounds of error terms. Initially, we will demonstrate the integral equality, which is essential to proving the article’s main findings. Additionally, using RL fractional integrals, several corrected Euler–Maclaurin-type inequalities for the case of differentiable pre-invex mappings will be established. In addition, we will present some examples with graphical representations to illustrate and confirm the validity of the recently derived inequalities. The last section will demonstrate the implications for means, composite error bounds, modified Bessel mappings, and iterative rules having an order of convergence of three to determine the roots of nonlinear equations.
2. Auxiliary Result
In this section, we derive an auxiliary result, which helps us to find our main results.
Lemma 1.
Let be an absolutely continuous mapping so that with , then
Here,
3. Main Results
In the following segment of this study, we prove some novel error boundaries of Euler-corrected Maclaurin’s procedure through a larger space of functions known as pre-invex mappings, auxiliary lemma, and some elementary inequalities from the theory of inequalities.
Theorem 1.
If the requirements of Lemma 1 are satisfied and the mapping is pre-invex on , then
where
Here,
and
Proof.
By taking the benefit of the modulus property, Lemma 1 and the pre-invexity of , we have
After some computations, the required result can be achieved. □
Corollary 1.
Selecting in Theorem 1,
Remark 1.
Inserting in Theorem 1, we obtain Theorem 5, which is proven in [32].
Example 1.
Let , given by , satisfying the requirements of Theorem 1 with , and then left-hand-side transform into the following form:
The right-hand side is given as
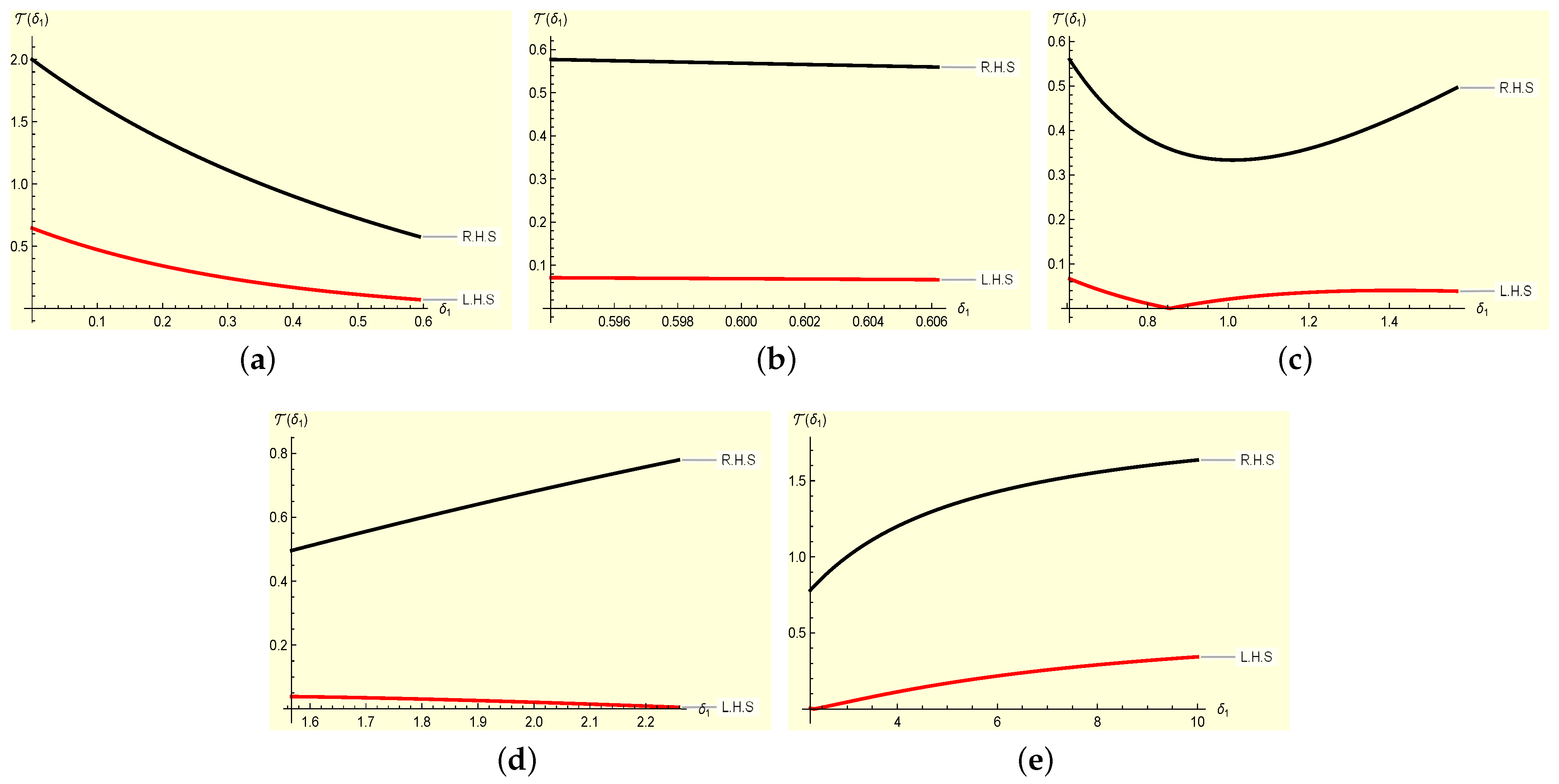
Figure 1 clearly affirms that the left-hand-side is less than the right-hand-side of Theorem 1. This shows that the result is accurate for .
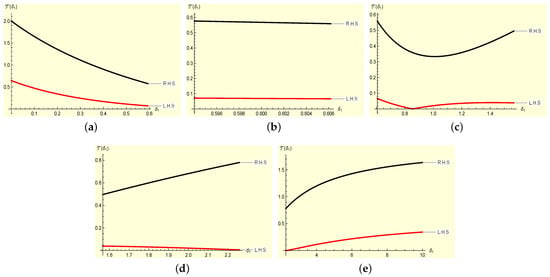
Figure 1.
Visuals of both sides of Theorem 1 based on are plotted with Mathematica. (a) Graph with interval . (b) Graph with interval . (c) Graph with interval . (d) Graph with interval . (e) Graph with interval .
Theorem 2.
If the requirements of Lemma 1 are satisfied and the mapping is pre-invex on , then
is valid. Here, is given by (10) and
Proof.
By taking the benefit of modulus property, Lemma 1, Hölder’s inequality, and pre-invexity of the mapping, we obtain
Since is pre-invex, then
Hence, the proof is completed. □
Corollary 2.
Selecting in Theorem 2,
Example 2.
Let , given by , satisfying the requirements of Theorem 2 with , then the left-hand-side transforms into the following form:
The right-hand-side then becomes
where
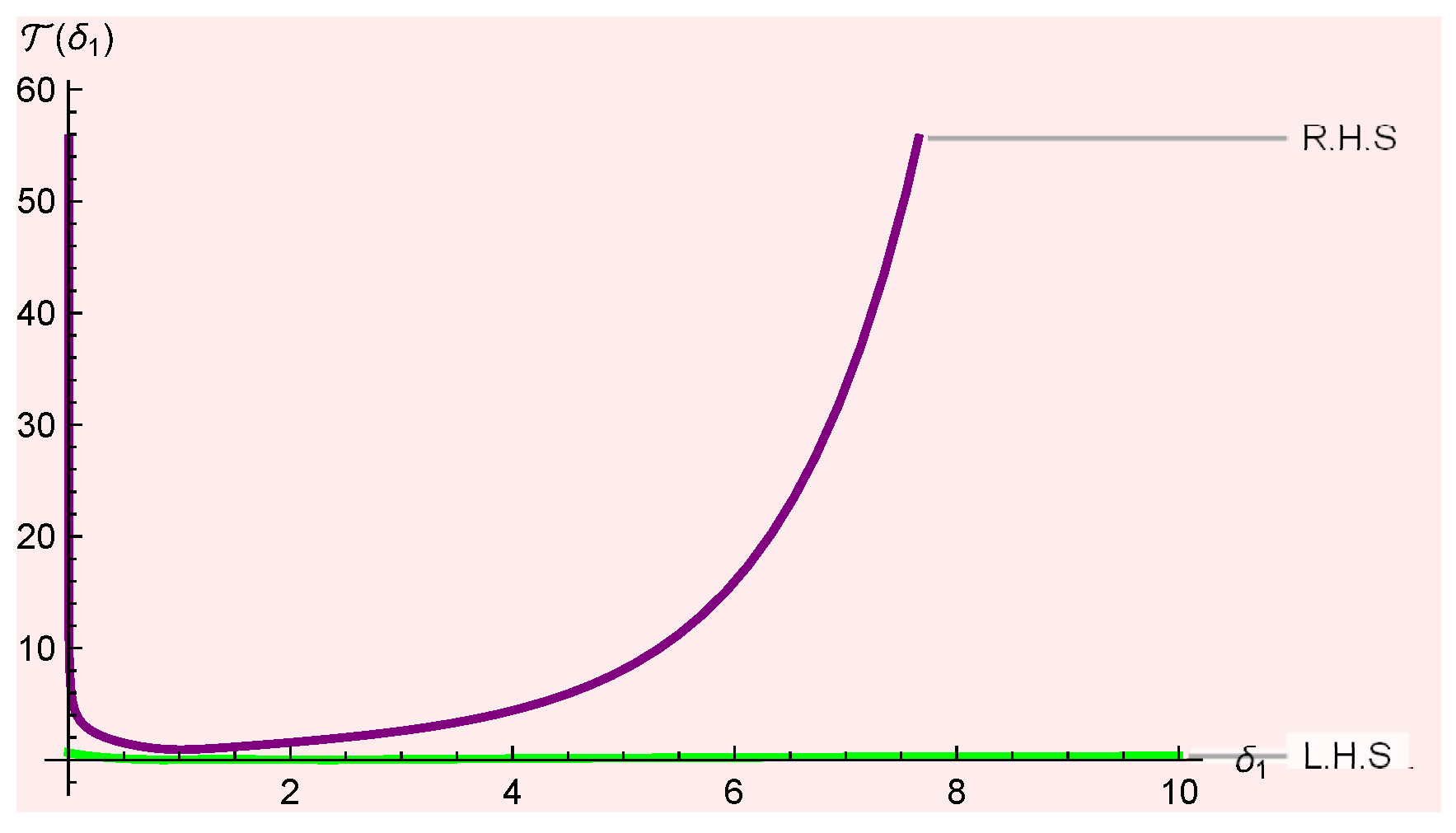
Figure 2 clearly affirms that the left-hand-side is less than the right-hand-side of Theorem 2. This shows that the result is accurate for .
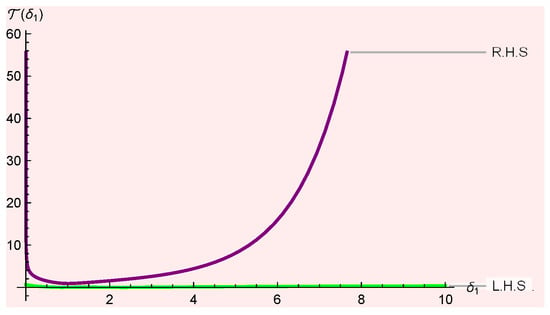
Figure 2.
Visual of both sides of Theorem 2 based on are plotted in Mathematica.
Theorem 3.
If the requirements of Lemma 1 are satisfied and the mapping is pre-invex on , then we have
where is given by (10), and , and are defined in Theorem 1 and
and
Proof.
By taking advantage of the power mean inequality and pre-invexity of , we obtain
Since is pre-invex,
Hence, the desired result is obtained. □
Corollary 3.
Let us consider in Theorem 3, then the following corrected Euler–Maclaurin-type inequality holds:
Remark 2.
Inserting in Theorem 3, we obtain Theorem 6, which is proven in [32].
Example 3.
Let , given by , satisfying the requirements of Theorem 3 with , then left-hand-side transforms into the following form:
For the right-hand-side, 3 is reduced to
where
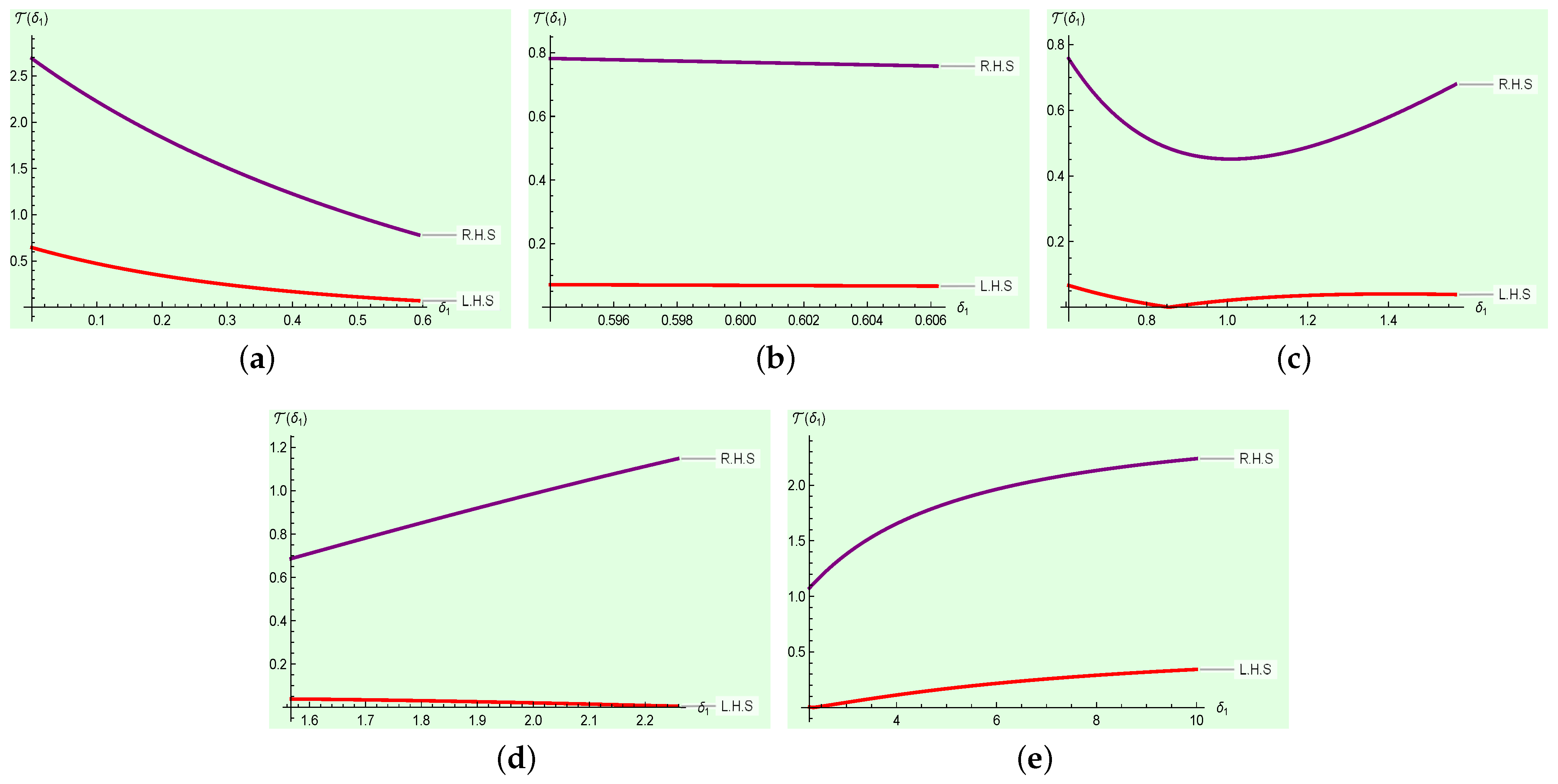
Figure 3 clearly affirms that the left-hand-side is less than the right-hand-side of Theorem 3. This shows that the result is accurate for .
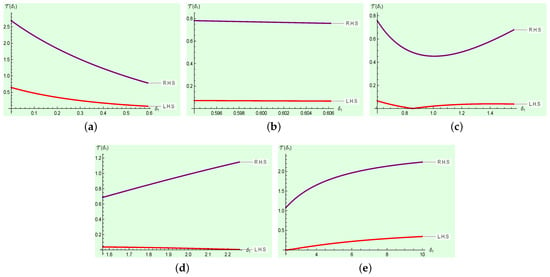
Figure 3.
Graph of both sides of Theorem 3 in Example 3, depending on , computed and plotted with Mathematica. (a) Graph with interval . (b) Graph with interval . (c) Graph with interval . (d) Graph with interval . (e) Graph with interval .
4. Applications
4.1. Application to Means
Here, we provide novel applications of our primary findings to linear combinations of means. Let us revisit some well-known binary means of any two non-negative numbers:
- .
- .
- .
Proposition 1.
Let and . Then,
Proof.
The proof is obvious from Theorem 1 with for and . □
Proposition 2.
Let and . Then,
Proof.
The proof is obvious from Theorem 2 with for and . □
4.2. Applications to Error Bounds
In the current portion of the study, we establish error bounds for the composite-corrected Euler–Maclaurin procedure. Let P be a division of such that , where .
- Taking the quadrature scheme into consideration,
Proposition 3.
Let be as in Theorem 1; then, we have
Proof.
By applying Theorem 1 with and to , multiplying the result by and then taking the sum from to , we achieve our desired result. □
Proposition 4.
Let be as in Theorem 2, then we have
Proof.
By applying Theorem 2 with and on , and multiplying the result by , the sum is taken from to . □
4.3. Applications to Matrices
Next, we explain the impacts of our created outcomes in matrices. In this setting, indicates the collection of complex matrices, symbolizes the algebra of all complex matrices, and refers to the subset of comprising strictly positive matrices. A matrix satisfies for every non-zero vector . The theory of matrices and convexity was consolidated by Sababheh in [33].
Proposition 5.
By using Theorem 2, we have
where ; furthermore, , and are defined in Theorem 2.
4.4. Iterative Methods
We provide applications of our conclusions in nonlinear analysis in the next section of the paper. Examine the following nonlinear equation:
One exciting area of study is the computation of roots of nonlinear equations. In the recent literature, several techniques have been discussed, such as quadrature formulas, Taylor’s expansion, interpolation, and decomposition techniques. We present an application of our proposed result through an iterative process. Newton’s integral representation is given as
Iterative Scheme 1.
For any , such that is a nonlinear equation, then
where
Proof.
From (11), we acquire our result. □
Now, we provide the order of convergence of Iterative Scheme 1.
Theorem 4.
Let be a differentiable mapping and be zero of order one. If approaches , then Iterative Scheme 1 has an order of convergence of three.
4.5. Examples and Visual Explanation of Iterative Scheme 1
First, we investigate a number of physical scenarios in the context of Iterative Scheme 1.
- In the first example, we investigate the topic linked to the plug flow of Casson fluids in blood using the Rheology and Fractional Nonlinear Equations Model [34]. The decline in flow rate can be calculated by the following equation:Here, we pick , and by picking the initial value , Iterative Scheme 1 with predicts the desired root in the third iteration.
- We look into the issue of porosity in biogels ([34]). The subsequent equation illustrates the dependence between pressure and velocity:where , , and are the initial values. Then, Iterative Scheme 1 with determines the root in 13 iterations.
In order to illustrate the effectiveness of our offered scheme, we conducted an analysis to compare it with traditional techniques such as Newton’s method (NM) [35], Abbasbandy’s method (AM) [36], Halley’s method (HM) [35], and Chun’s method (CM) [37]. In order to proceed, consider the following test mappings:
- .
- .
- .
- .
We fixed the tolerance of and
- ;
- .
The numerical outcomes were generated utilizing an Intel(R) Core(TM) i5 CPU at 1.60 GHz and 16 GB RAM. Maple 2020 was utilized for coding, with Matlab 2021 for visual depiction. After performing numerical tests on software, we presented tabular depictions of strategies for the above listed examples.
The above Table 1 provides a detailed comparative analysis of different non-linear examples for various methods.

Table 1.
Numerical outcomes of above mentioned examples.
4.6. Basins of Attraction
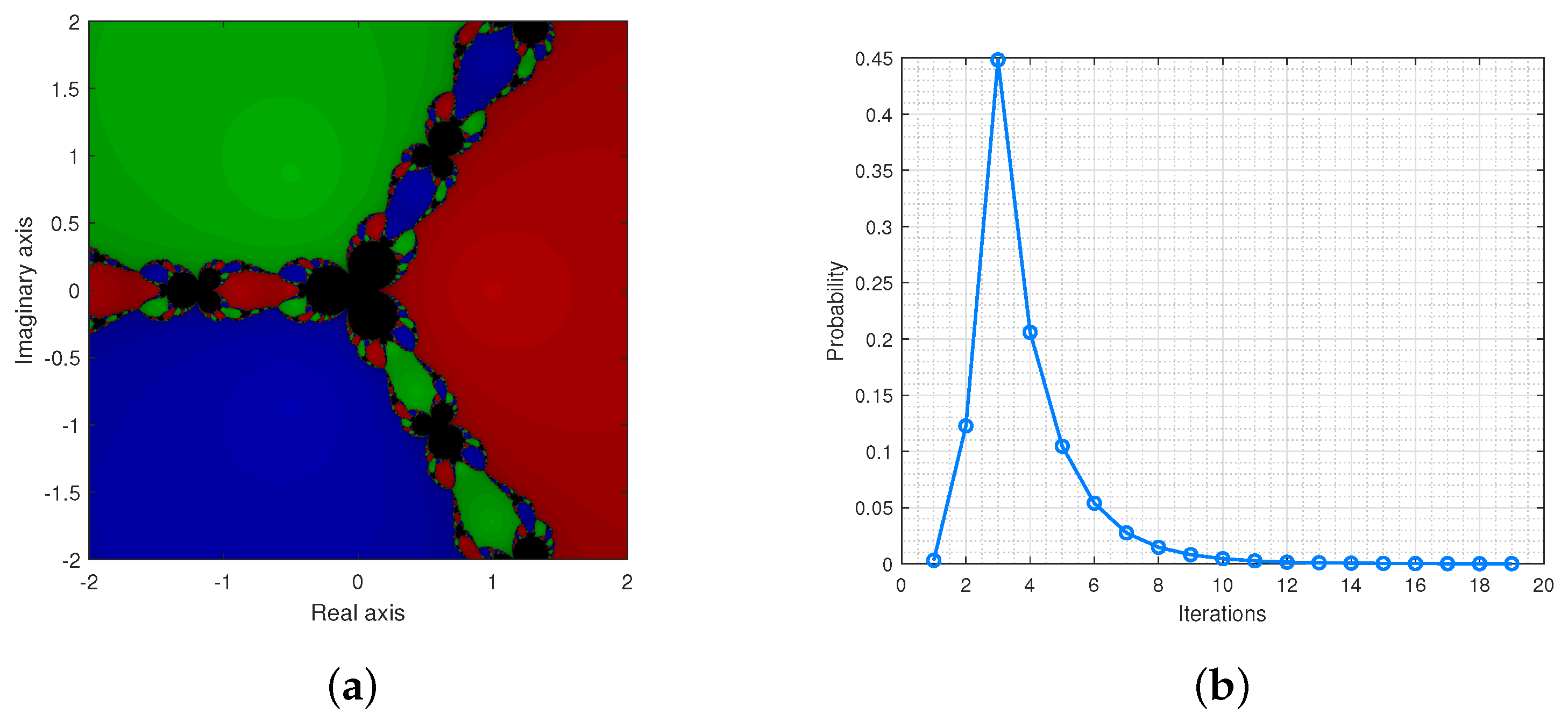
Here, we briefly describe Iterative Scheme 1 through the basin of attraction and some illustrations corresponding to CPU time to generate the basin of attractions. We deploy our proposed algorithm on with a point grid by fixing the tolerance , and the maximum number of iterations is 20. In addition, we present the probability distributions of the algorithm. The process of obtaining the basins of attraction required several iterations. The red line in the plots indicate the most probable number of iterations. For this purpose, we consider the following examples:
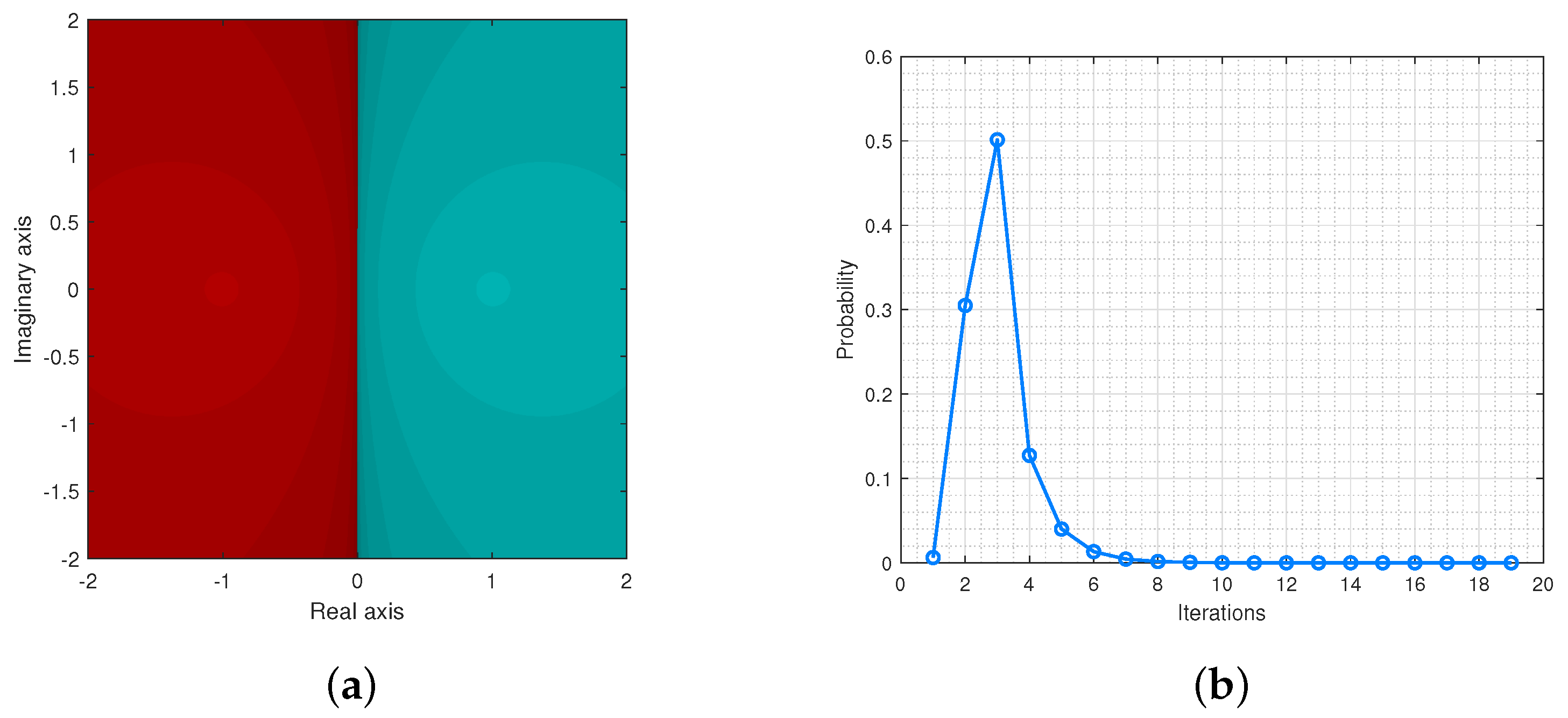
The Figure 4a,b provide the basin of attractions and the probability distribution for .
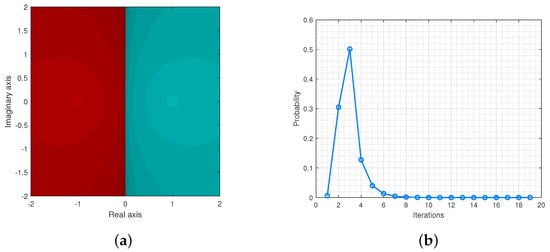
Figure 4.
(a) is the basin of attraction for and (b) illustrates the probability distributions.
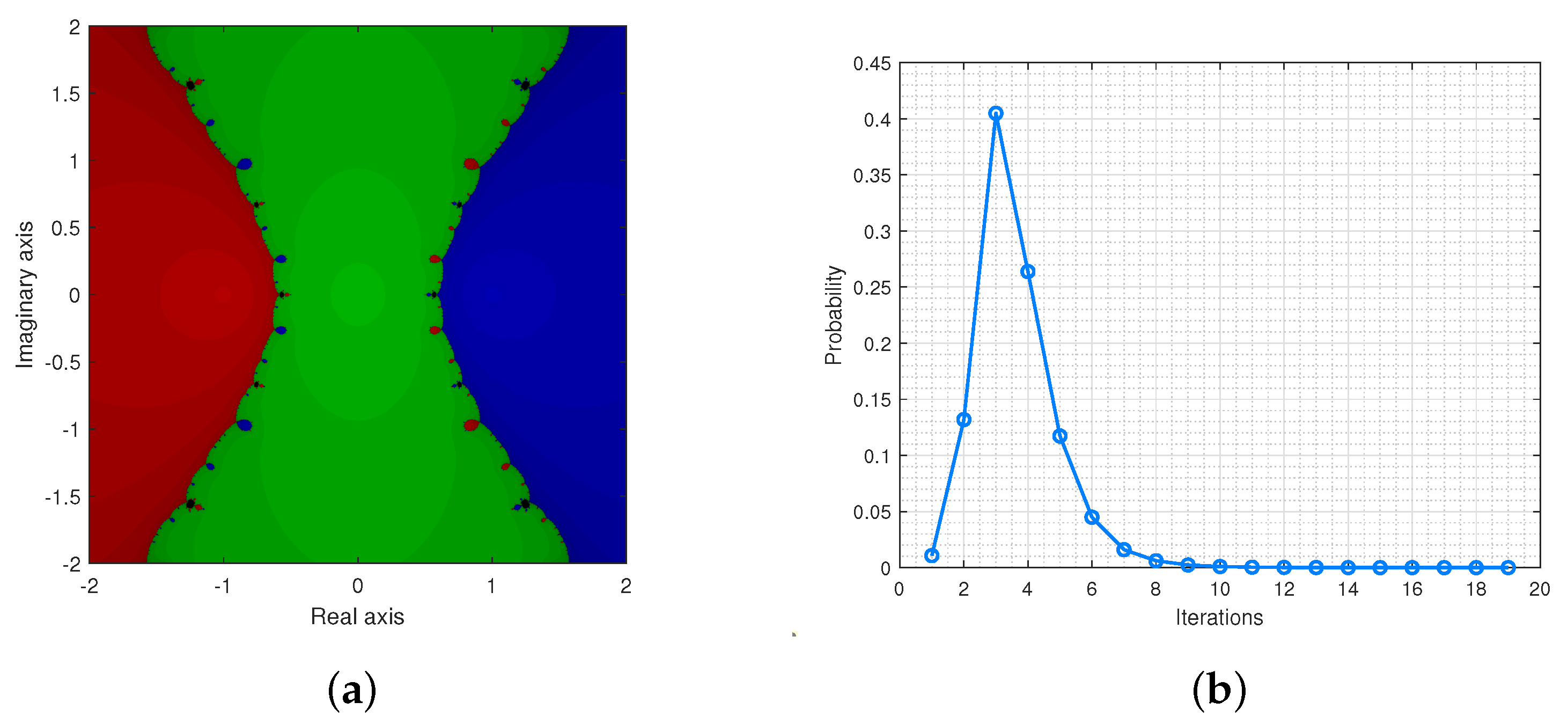
The Figure 5a,b provide the basin of attractions and the probability distribution for .
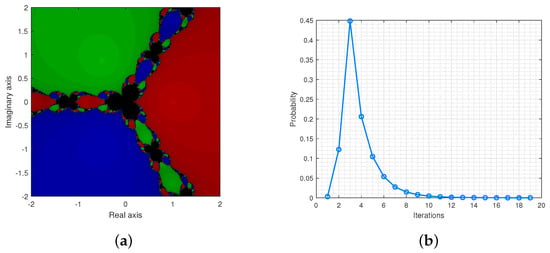
Figure 5.
(a) is the basin of attraction for and (b) illustrates the probability distributions.
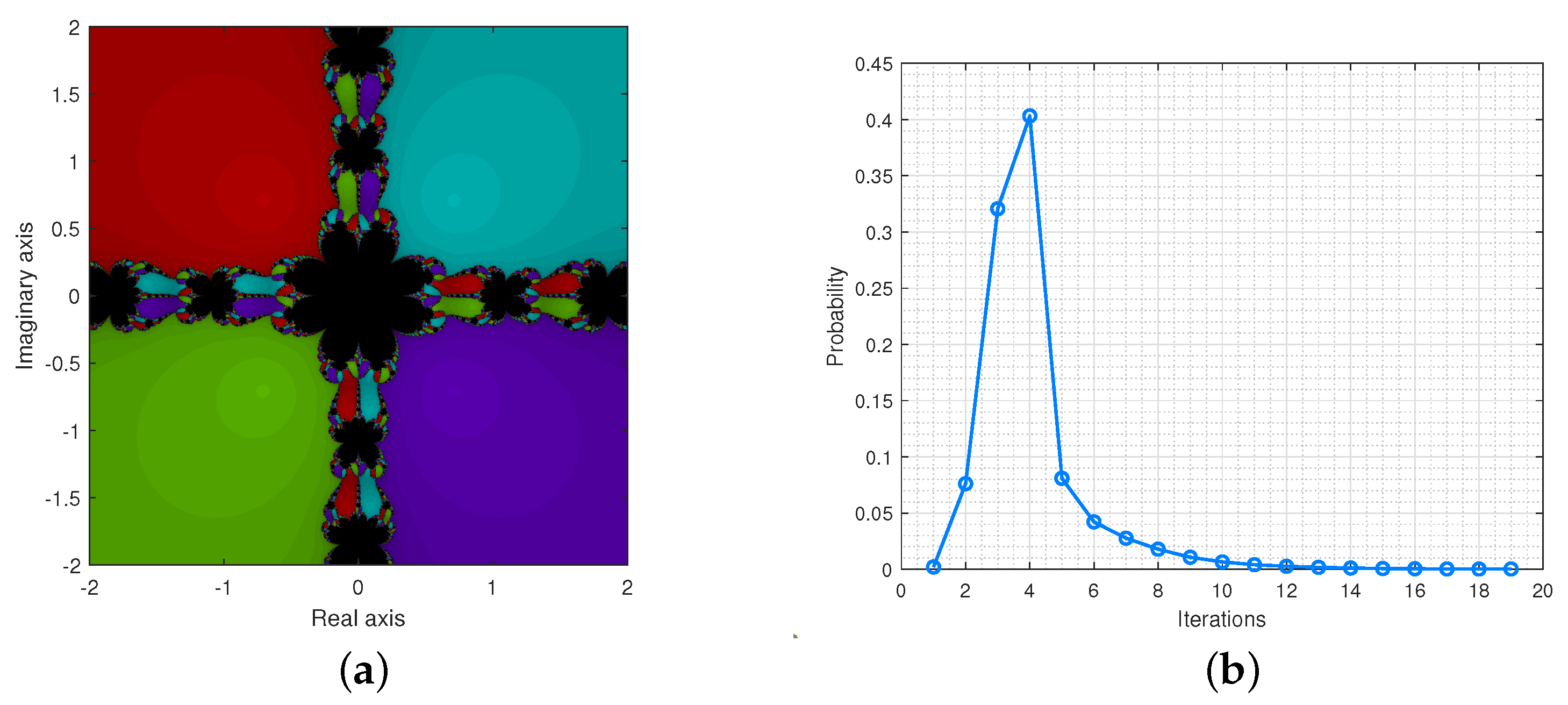
The Figure 6a,b provide the basin of attractions and the probability distribution for .
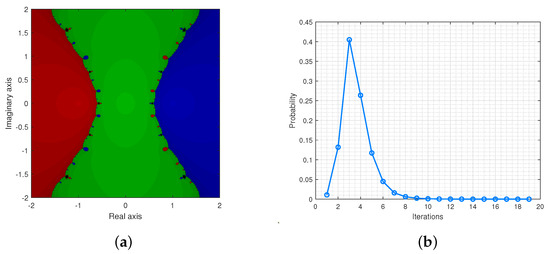
Figure 6.
(a) is the basin of attraction for and (b) illustrates the probability distributions.
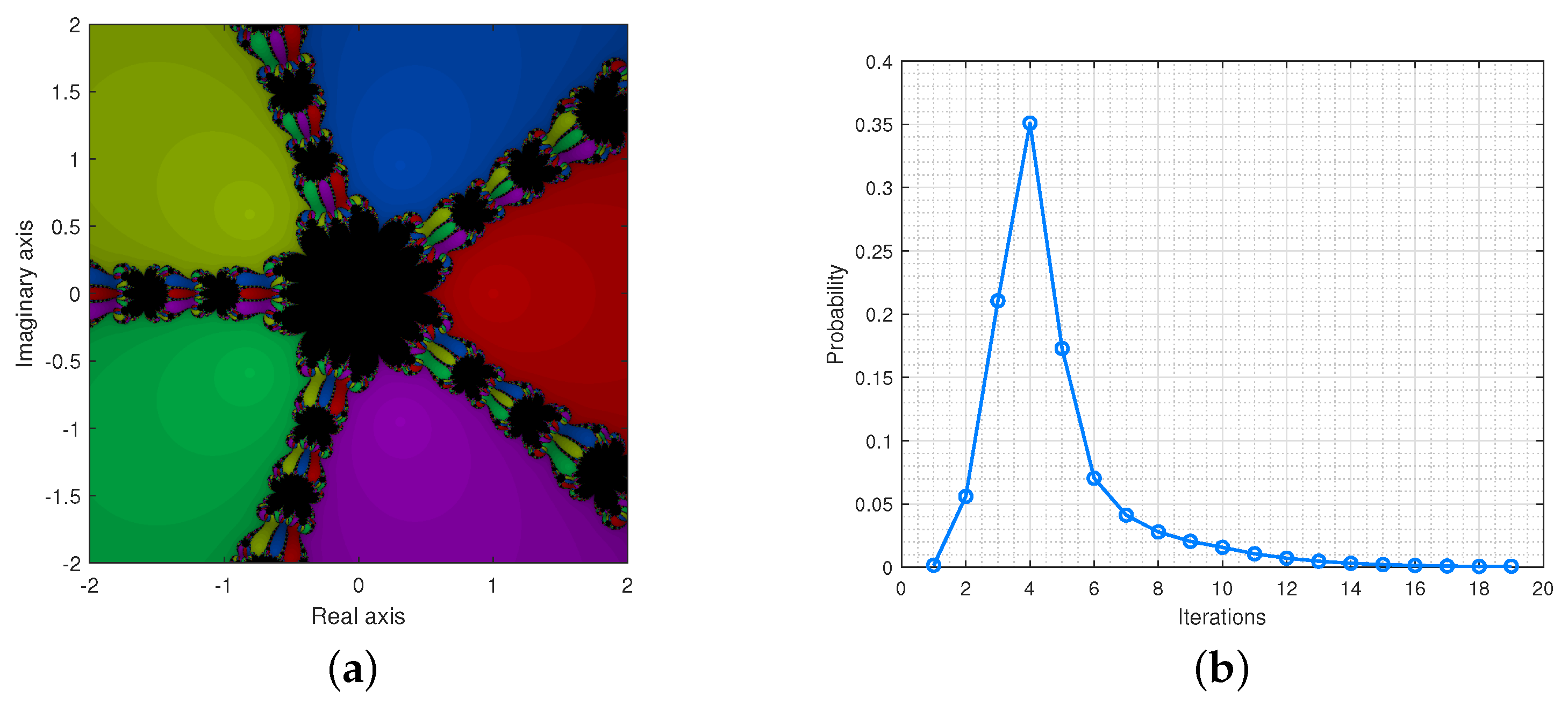
The Figure 7a,b provide the basin of attractions and the probability distribution for .
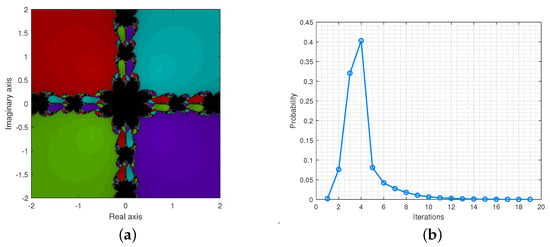
Figure 7.
(a) is the basin of attraction for and (b) illustrates the probability distributions.
The Figure 8a,b provide the basin of attractions and the probability distribution for .
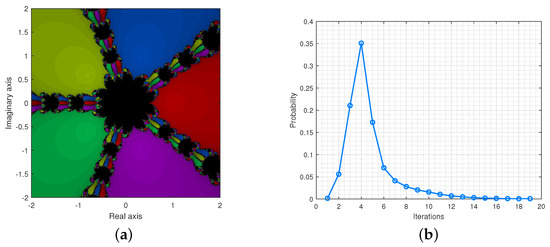
Figure 8.
(a) is the basin of attraction for and (b) illustrates the probability distributions.
Now, we present a visual of cumulative CPU time for the basin of attraction computation for each example and a tabular form of cumulative CPU times for each function across five iterations.
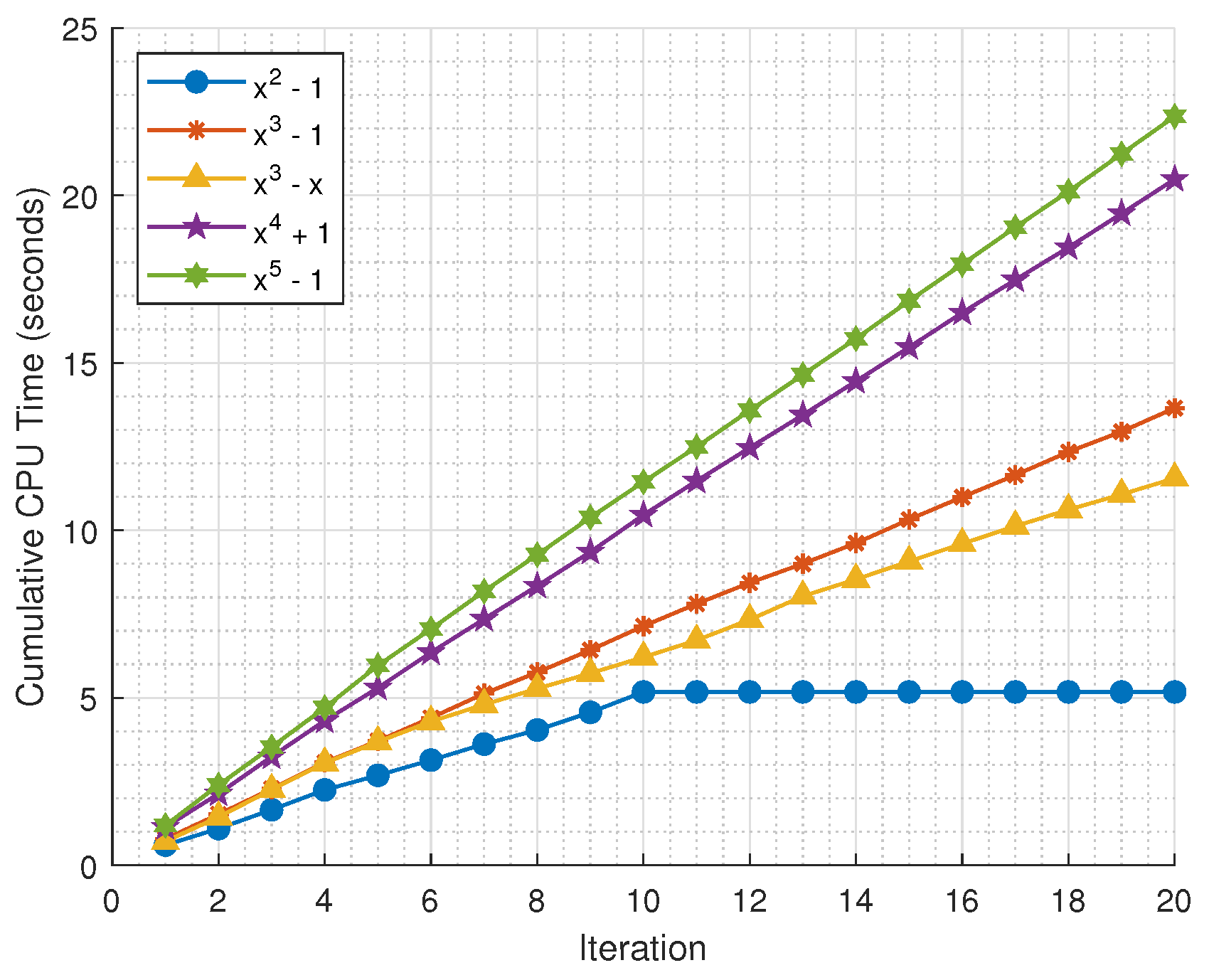
The above Figure 9 illustrates the comparison of CPU time taken across iterations.
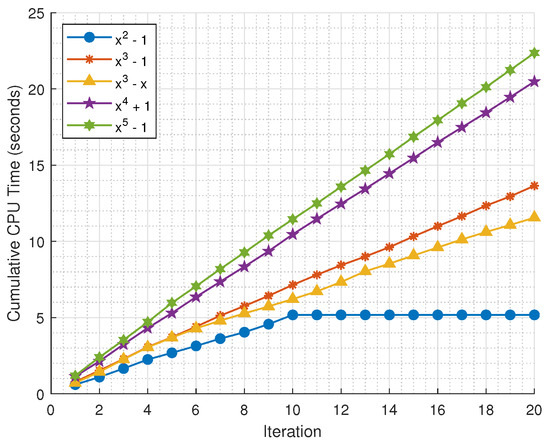
Figure 9.
Cumulative CPU time for basin of attraction computation.
The above Table 2 presenting the cumulative CPU time analysis depending of different nonlinear examples.

Table 2.
Cumulative CPU times for each function across iterations.
5. Conclusions
In the current article, we have developed some new generic Euler-corrected integral inequalities through RL fractional operators and pre-invex mappings. It is a large space of functions containing convex and several non-convex function classes. It is worth mentioning that our results are generic in nature because by substituting bi-mapping and such that and , we obtain the inequalities for various integral inequalities of Maclaurin-type for convex mappings, generalized convexity involving Raina’s function, and hypergeometric functions, respectively. Moreover, through examples, we conclude that Theorem 3 provides the better estimation compared to Theorems 1 and 2. From our proposed identity and pre-invex mappings, several bounds can be obtained by utilizing Young’s inequality, improved Hölder’s inequality, improved inequality, and other classes of convexity such as strong convexity, uniform convexity, and log convex mappings. In the future, we will try to obtain some sharp bounds for twice or higher-order differentiable convex functions within classical and fractional integral operators. One of the important targets is to investigate this inequality through quantum calculus. We hope that researchers can use the ideas and strategies we have used to reach our conclusions about corrected Euler–Maclaurin-type inequalities via RL fractional integrals to open up new directions for further research in this area.
Author Contributions
Conceptualization, Q.L., R., M.U.A., M.Z.J., L.C. and B.M.; methodology, M.U.A., R., M.Z.J., L.C. and B.M.; software, Q.L., R., M.U.A., M.Z.J., L.C. and B.M.; validation, Q.L., R., M.U.A., M.Z.J., L.C. and B.M.; formal analysis, M.U.A., M.Z.J., L.C. and B.M.; investigation, Q.L., R., M.U.A., M.Z.J., L.C. and B.M.; writing—original draft preparation, R. and M.Z.J.; writing—review and editing, Q.L., R., M.U.A., B.B.-M., M.Z.J., L.C. and B.M.; visualization, Q.L., R., M.U.A., M.Z.J. and L.C.; supervision, M.U.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article, further inquiries can be directed to the corresponding author.
Acknowledgments
The authors are thankful to the editor and the anonymous reviewers for their valuable comments and suggestions.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ben-Israel, A.; Mond, B. What is invexity? ANZIAM J. 1986, 28, 1–9. [Google Scholar] [CrossRef]
- Weir, T.; Mond, B. Pre-invex functions in multiple objective optimization. J. Math. Anal. Appl. 1988, 136, 29–38. [Google Scholar] [CrossRef]
- Mohan, S.R.; Neogy, S.K. On invex sets and preinvex functions. J. Math. Anal. Appl. 1995, 189, 901–908. [Google Scholar] [CrossRef]
- Matloka, M. Inequalities for h-preinvex functions. Appl. Math. Comput. 2014, 234, 52–57. [Google Scholar] [CrossRef]
- Noor, M.A.; Noor, K.I.; Awan, M.U.; Li, J. On Hermite-Hadamard inequalities for h-preinvex functions. Filomat 2014, 28, 1463–1474. [Google Scholar] [CrossRef]
- Ozcan, S. Some integral inequalities of Hermite-Hadamard type for multiplicatively preinvex functions. AIMS Math. 2020, 5, 1505–1518. [Google Scholar] [CrossRef]
- Lakhdari, A.; Meftah, B. Some fractional weighted trapezoid type inequalities for preinvex functions. Int. J. Nonlinear Anal. Appl. 2022, 13, 3567–3587. [Google Scholar]
- Tariq, M.; Shaikh, A.A.; Sahoo, S.K.; Ahmad, H.; Sitthiwirattham, T.; Reunsumrit, J. New integral inequalities via generalized preinvex functions. Axioms 2021, 10, 296. [Google Scholar] [CrossRef]
- Meftah, B. New integral inequalities for s-preinvex functions. Int. J. Nonlinear Anal. Appl. 2017, 8, 331–336. [Google Scholar]
- Du, T.S.; Liao, J.G.; Li, Y.J. Properties and integral inequalities of Hadamard-Simpson type for the generalized (s,m)-preinvex functions. J. Nonlinear Sci. Appl. 2016, 9, 3112–3126. [Google Scholar] [CrossRef]
- Gorenflo, R.; Mainardi, F. Fractional Calculus: Integral and Differential Equations of Fractional Order; Springer: Vienna, Austria, 1997; pp. 223–276. [Google Scholar]
- Sun, H.; Zhang, Y.; Baleanu, D.; Chen, W.; Chen, Y. A new collection of real world applications of fractional calculus in science and engineering. Commun. Nonlinear Sci. Numer. Simul. 2018, 64, 213–231. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Hyder, A.A.; Barakat, M.A.; Fathallah, A. Enlarged integral inequalities through recent fractional generalized operators. J. Inequalities Appl. 2022, 2022, 95. [Google Scholar] [CrossRef]
- Hyder, A.A.; Barakat, M.A.; Soliman, A.H. A new class of fractional inequalities through the convexity concept and enlarged Riemann-Liouville integrals. J. Inequalities Appl. 2023, 2023, 137. [Google Scholar] [CrossRef]
- Sarikaya, M.Z.; Ertugral, F. On the generalized Hermite-Hadamard inequalities. Ann. Univ.-Craiova-Math. Comput. Sci. Ser. 2020, 47, 193–213. [Google Scholar]
- Dragomir, S.S.; Agarwal, R. Two inequalities for differentiable mappings and applications to special means of real numbers and to trapezoidal formula. Appl. Math. Lett. 1998, 11, 91–95. [Google Scholar] [CrossRef]
- Alomari, M.W. A companion of the generalized trapezoid inequality and applications. J. Math. Appl. 2013, 36, 5–15. [Google Scholar]
- Sarikaya, M.Z.; Yildirim, H. On Hermite-Hadamard type inequalities for Riemann-Liouville fractional integrals. Miskolc Math. Notes 2016, 17, 1049–1059. [Google Scholar] [CrossRef]
- Dragomir, S.S. On the midpoint quadrature formula for mappings with bounded variation and applications. Kragujev. J. Math. 2000, 22, 13–19. [Google Scholar]
- Set, E.; Akdemir, A.O.; Ozdemir, E.M. Simpson type integral inequalities for convex functions via Riemann-Liouville integrals. Filomat 2017, 31, 4415–4420. [Google Scholar] [CrossRef]
- Zhu, W.S.; Meftah, B.; Xu, H.; Jarad, F.; Lakhdari, A. On parameterized inequalities for fractional multiplicative integrals. Demonstr. Math. 2024, 57, 20230155. [Google Scholar] [CrossRef]
- Hussain, S.; Khalid, J.; Chu, Y.M. Some generalized fractional integral Simpson’s type inequalities with applications. AIMS Math. 2020, 5, 5859–5883. [Google Scholar] [CrossRef]
- Saleh, W.; Lakhdari, A.; Abdeljawad, T.; Meftah, B. On fractional biparameterized Newton-type inequalities. J. Inequalities Appl. 2023, 2023, 122. [Google Scholar] [CrossRef]
- Dragomir, S.S.; Agarwal, R.P.; Cerone, P. On Simpson’s inequality and applications. J. Inequal. Appl. 2000, 2000, 891030. [Google Scholar] [CrossRef]
- Ali, M.A.; Abbas, M.; Budak, H.; Agarwal, P.; Murtaza, G.; Chu, Y.M. New quantum boundaries for quantum Simpson’s and quantum Newton’s type inequalities for preinvex functions. Adv. Differ. Equations 2021, 2021, 1–21. [Google Scholar] [CrossRef]
- Bin-Mohsin, B.; Javed, M.Z.; Awan, M.U.; Khan, A.G.; Cesarano, C.; Noor, M.A. Exploration of quantum Milne-Mercer-type inequalities with applications. Symmetry 2023, 15, 1096. [Google Scholar] [CrossRef]
- You, X.; Hezenci, F.; Budak, H.; Kara, H. New Simpson type inequalities for twice differentiable functions via generalized fractional integrals. AIMS Math. 2022, 7, 3959–3971. [Google Scholar] [CrossRef]
- Davis, P.J.; Rabinowitz, P. Methods of Numerical Integration; Courier Corporation: North Chelmsford, MA, USA, 2007. [Google Scholar]
- Franjić, I.; Pećarić, J. Corrected Euler-Maclaurin’s formulae. Rend. Del Circ. Mat. Palermo 2005, 54, 259–272. [Google Scholar]
- Hezenci, F.; Budak, H. Fractional Euler-Maclaurin-type inequalities for various function classes. Comput. Appl. Math. 2024, 43, 261. [Google Scholar] [CrossRef]
- Hezenci, F.; Budak, H. Some Riemann-Liouville fractional integral inequalities of corrected Euler-Maclaurin-type. J. Anal. 2024, 32, 1309–1330. [Google Scholar] [CrossRef]
- Sababheh, M. Convex functions and means of matrices. Math. Inequal. Appl. 2017, 20, 29–47. [Google Scholar] [CrossRef]
- Fournier, R.L. Basic Transport Phenomena in Biomedical Engineering; Taylor & Francis: New York., NY, USA, 2007. [Google Scholar]
- Burden, R.K.; Faires, J.D. Numerical Analysis, 9th ed.; Brooks/Cole, Cengage Learning: Boston, MA, USA, 2011. [Google Scholar]
- Abbasbandy, S. Improving Newton–Raphson method for nonlinear equations by modified Adomian decomposition method. Appl. Math. Comput. 2003, 145, 887–893. [Google Scholar] [CrossRef]
- Chun, C. Iterative methods improving Newton’s method by the decomposition method. Comput. Math. Appl. 2005, 50, 1559–1568. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).