An Efficient Numerical Method Based on Bell Wavelets for Solving the Fractional Integro-Differential Equations with Weakly Singular Kernels

Abstract

A novel numerical scheme based on the Bell wavelets is proposed to obtain numerical solutions of the fractional integro-differential equations with weakly singular kernels. Bell wavelets are first proposed and their properties are studied, and the fractional integration operational matrix is constructed. The convergence analysis of Bell wavelets approximation is discussed. The fractional integro-differential equations can be simplified to a system of algebraic equations by using a truncated Bell wavelets series and the fractional operational matrix. The proposed method’s efficacy is supported via various examples.

1. Introduction

In recent years, fractional calculus has become increasingly significant in science and engineering, as it plays a crucial role in modeling numerous physical and mathematical problems. Examples of these problems include viscoelasticity, electromagnetic waves, and dielectric polarization [1,2]. The research object of fractional calculus is fractional integration and differentiation. The definition of fractional calculus is obtained by integrating and unifying fractional integration and fractional differentiation. There are usually three definitions of fractional calculus: Riemann–Liouville fractional calculus, Grünwald–Letnikov’s fractional calculus, and Caputo fractional calculus. In recent years, many studies have focused on the existence, regularity, and convergence of solutions to fractional differential equations [3,4,5,6]. However, it is difficult to obtain analytical solutions for fractional differential equations or fractional integral differential equations. Therefore, it is not surprising that many different numerical methods have been proposed and analyzed for the fractional differential/integral equations, including the homotopy analysis method [7], variational iteration method [8], reproducing kernel method [9], pseudospectral method [10], Adomian decomposition method [11], and wavelet methods [12,13,14,15,16,17,18,19,20].

In this paper, the fractional Fredholm-Volterra integro-differential equations are considered as follows:

$$D_{\mathrm{*}}^{\alpha }y\left(t\right)={\lambda }_1{\int }_0^t\frac{y\left(s\right)}{{(x-t)}^{\beta }}\mathrm{d}s+{\lambda }_2{\int }_0^{1}k(t,s)y\left(s\right)\mathrm{d}s+g\left(t\right),$$

(1)

with initial condition

$$y\left(0\right)=0,$$

(2)

where $k(t,s)\in L^2([0,1]\times [0,1])$ and $g\left(t\right)$ are known functions, and ${\lambda }_1,{\lambda }_2$ are real constants. Here, $D_{\mathrm{*}}^{\alpha }$ denotes the fractional-order derivative of order $\alpha$ in the sense of Caputo and $0<\alpha ,\beta <1$.

Many numerical techniques have been studied for solving fractional integro-differential equations (FIDE). Yi [21] proposed CAS wavelets to solve the fractional FIDE with a weakly singular kernel, and the second Chebyshev wavelet (SCW) method [22] was used to improve the accuracy of the numerical methods. Nemati [23] solved the nonlinear FIDE with weakly singular kernels by using the modification of hat functions, and then the Legendre wavelets [24] were used for the equations. Recently, Taylor wavelets (TW) [25] and Euler wavelets (EW) [26] were proposed to solve the fractional Fredholm–Volterra integro-differential equations (FFVIDE). Compared with the extensively studied fractional differential/integral equations, the more difficult FFVIDE with weakly singular kernels still requires great efforts for the development and analysis of stable, accurate, and efficient numerical methods.

Bell polynomials are combinatorial-type polynomials. Since the mathematician E.T. Bell first proposed Bell polynomials, they have been a hot issue in the field of combinatorics. Now, Bell polynomials have become an important part of combinatorics, with applications in differential equations, theoretical physics, and stochastic processes. In [27], the Bell polynomials were used for solving the nonlinear Fredholm–Volterra integral equations. However, Bell polynomials do not have sparsity, and the coefficient matrix of the system of equations obtained by solving integral or differential equations is full-rank. As is well known, wavelets have locality and sparsity. Therefore, we attempt to construct wavelet functions by using Bell polynomials and use them to obtain the approximate solution. In this paper, the Bell wavelets (BWs) are first presented and their fractional integration operational matrix is first derived, and then the convergence of the Bell wavelets approximation is described. We used a truncated Bell wavelets series together with the operational matrix to reduce the equations to a system of algebraic equations. The coefficient matrix of the algebraic equations is sparse, which greatly reduces computational complexity. Bell wavelet functions have advantages and can provide better approximate solutions for equations.

This article is structured as follows. In Section 2, we introduce the definitions of fractional integration in the sense of the Riemann–Liouville and Caputo, and then the Bell wavelets are proposed. In Section 3, the fractional integration operational matrix of the Bell wavelet is presented. The analysis of the convergence of the Bell wavelets expansion is discussed in Section 4. The proposed scheme is presented in Section 5. The numerical experiments are provided to validate the Bell wavelets method in Section 6. The conclusions are given in the last section.

2. Preliminaries

2.1. Fractional Calculus

The commonly used definitions of fractional calculus include two situations: in the sense of the Riemann–Liouville and Caputo.

Definition 1. 

The Riemann–Liouville fractional integration of order α for a given function $f\left(t\right)$ is defined as

$$I^{\alpha }f\left(t\right)=\left\{\begin{array}{c}\frac{1}{\mathrm{\Gamma }\left(\alpha \right)}{\int }_0^t{(t-\tau )}^{\alpha -1}f\left(\tau \right)\mathrm{d}\tau ,\alpha >0,t>0,\hfill \\ f\left(t\right),\alpha =0.\hfill \end{array}\right.$$

(3)

The integral operator $I^{\alpha }$ has the following properties:

(i)

$I^{\alpha }{I}^{\beta }f\left(t\right)=I^{\alpha +\beta }f\left(t\right)$;

(ii)

$I^{\beta }{I}^{\alpha }f\left(t\right)=I^{\alpha +\beta }f\left(t\right)$;

(iii)

$I^{\alpha }{t}^{\nu }=[\mathrm{\Gamma }(\nu +1)/\mathrm{\Gamma }(\nu +\alpha +1)]t^{\alpha +\nu }$.

Definition 2. 

Let $D_{\mathrm{*}}^{\alpha }$ represent the fractional differential operator in the sense of Caputo, It is defined as

$$D_{\mathrm{*}}^{\alpha }f\left(t\right)=\left\{\begin{array}{c}\frac{d^{l}f\left(t\right)}{d{t}^l},\alpha =l\in N,\hfill \\ \frac{1}{\mathrm{\Gamma }(l-\alpha )}{\int }_0^t\frac{f^{\left(l\right)}\left(\tau \right)}{{(t-\tau )}^{\alpha -l+1}}\mathrm{d}\tau ,0\le l-1<\alpha <l.\hfill \end{array}\right.$$

(4)

The relation between the Riemann–Liouville operator and the Caputo operator is given as

$$D_{\mathrm{*}}^{\alpha }{I}^{\alpha }f\left(t\right)=f\left(t\right),$$

(5)

$$I^{\alpha }{D}_{\mathrm{*}}^{\alpha }f\left(t\right)=f\left(t\right)-\sum _{k=0}^{l-1}{f}^{\left(k\right)}\left(0^{+}\right)\frac{t^k}{k!},t>0.$$

(6)

2.2. Bell Wavelets

The Bell wavelets ${\psi }_{nm}\left(t\right)=\psi (k,n,m,t)$ have four arguments: k is any positive integer, $n=1,\cdots ,2^{k-1}$, m is the degree of the Bell polynomials, and t is the normalized time. The Bell wavelets are described on the interval $[0,1)$ as

$${\psi }_{nm}\left(t\right)=\left\{\begin{array}{c}{2}^{\frac{k-1}{2}}{\mathrm{B}}_{\mathrm{m}}(2^{k-1}t-n+1),\frac{n-1}{2^{k-1}}\le t<\frac{n}{2^{k-1}},\hfill \\ 0,\mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}\mathrm{.}\hfill \end{array}\right.$$

(7)

Here, $B_m\left(t\right)$ are the Bell polynomials of order m, which are defined as [27]

$$B_m\left(t\right)=\sum _{r=0}^{m}S(m,r)t^r,$$

where $S(m,r)$ shows the Stirling number of the second kind and is defined by

$$S(m,r)=\sum _{j=0}^r\frac{{(-1)}^j}{r!}\left(\genfrac{}{}{0pt}{}{r}{j}\right){(r-j)}^m.$$

By using the property of the Bell polynomials, the vector $\mathbf{B}\left(t\right)=[B_0\left(t\right),\cdots ,B_m\left(t\right)]$, which consists of the Bell polynomials $B_i\left(t\right),i=0,1,\cdots ,m$, is represented by

$$\mathbf{B}\left(t\right)=\mathbf{S}\mathbf{X}\left(t\right),$$

where

$$\mathbf{X}\left(t\right)={[1,t,\cdots ,t^m]}^T,$$

and

$$\mathbf{S}=\left[\begin{array}{cccc}S(0,0)& 0& \cdots & 0\\ S(1,0)& S(1,1)& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ S(m,0)& S(m,1)& \cdots & S(m,m)\end{array}\right].$$

3. Bell Wavelets Approximation and Operational Matrix

3.1. Bell Wavelets Approximation

A function $f\left(t\right)\in L^2[0,1]$ can be rewritten by the Bell wavelets as follows:

$$f\left(t\right)=\sum _{n=0}^{\infty }\sum _{m\in Z}{c}_{nm}{\psi }_{nm}\left(t\right),$$

The above equation is written as a finite term

$$f\left(t\right)\simeq \sum _{n=1}^{2^{k-1}}\sum _{m=0}^{M-1}{c}_{nm}{\psi }_{nm}\left(t\right)=C^{\mathrm{T}}\mathrm{\Psi }\left(t\right),$$

(8)

where

$$C={[c_{10},c_{11},\cdots ,c_{1(M-1)},c_{20},\cdots ,c_{2(M-1)},\cdots ,c_{2^{k-1}0},\cdots ,c_{2^{k-1}(M-1)}]}^{\mathrm{T}}$$

(9)

$$\mathrm{\Psi }\left(t\right)={[{\psi }_{10},{\psi }_{11},\cdots ,{\psi }_{1(M-1)},{\psi }_{20},\cdots ,{\psi }_{2(M-1)},\cdots ,{\psi }_{2^{k-1}0},\cdots ,{\psi }_{2^{k-1}(M-1)}]}^{\mathrm{T}}.$$

(10)

For simplicity, the Equation (8) can also be written as

$$f\left(t\right)\simeq \sum _{i=0}^{\widehat{m}}{c}_i{\phi }_i\left(t\right)=C^{\mathrm{T}}\mathrm{\Psi }\left(t\right),$$

where ${\phi }_i\left(t\right)={\psi }_{nm}\left(t\right)$, $c_i=c_{nm}$, $\widehat{m}=2^{k-1}M$ and $i=M(n-1)+m+1$. Therefore,

$$C={[c_1,c_2,\cdots ,c_{\widehat{m}}]}^{\mathrm{T}}$$

$$\mathrm{\Psi }\left(t\right)={[{\phi }_2\left(t\right),{\phi }_2\left(t\right),\cdots ,{\phi }_{\widehat{m}}\left(t\right)]}^{\mathrm{T}}.$$

To evaluate C, we let

$$h_{ij}={\int }_0^{1}f\left(t\right){\psi }_{ij}\left(t\right)\mathrm{d}t.$$

By using Equation (8), we obtain

$$h_{ij}=\sum _{n=1}^{2^{k-1}}\sum _{m=0}^{M-1}{c}_{nm}{\int }_0^1{\psi }_{nm}\left(t\right){\psi }_{ij}\left(t\right)\mathrm{d}t=\sum _{n=1}^{2^{k-1}}\sum _{m=0}^{M-1}{c}_{nm}{d}_{nm}^{ij},$$

(11)

where $d_{nm}^{ij}={\int }_0^1{\psi }_{nm}\left(t\right){\psi }_{ij}\left(t\right)\mathrm{d}t$, $i=1,2,\cdots ,2^{k-1},j=0,1,\cdots ,M-1$.

Let

$$H={[h_{10},h_{11},\cdots ,h_{1(M-1)},h_{20},\cdots ,h_{2(M-1)},\cdots ,h_{2^{k-1}0},\cdots ,h_{2^{k-1}(M-1)}]}^{\mathrm{T}}$$

and

$$D={\left[d_{nm}^{ij}\right]}_{2^{k-1}M\times 2^{k-1}M},$$

(12)

From Equation (11), we have

$$C^T=H^T{D}^{-1}.$$

(13)

Similarly, the arbitrary bivariate function $k(s,t)\in L^2([0,1]\times [0,1])$ can be approximated by Bell wavelets

$$k(s,t)=\mathrm{\Psi }{\left(s\right)}^{\mathrm{T}}K\mathrm{\Psi }\left(t\right),$$

(14)

where K is a $\widehat{m}\times \widehat{m}$ matrix, and it is given by

$$K=D^{-1}\left[{\int }_0^1{\int }_0^{1}k(s,t)\mathrm{\Psi }\left(s\right)\mathrm{\Psi }\left(t\right)\mathrm{d}t\mathrm{d}t\right]D^{-1}.$$

(15)

3.2. Operational Matrix of the Fractional Integration

If $I^{\alpha }$ is the Bell wavelets fractional integration operator, one can obtain

$$I^{\alpha }\mathrm{\Psi }\left(t\right)\approx P^{\alpha }\mathrm{\Psi }\left(t\right),$$

(16)

where matrix $P^{\alpha }$ is fractional integration operational BW matrix. By using Equation (3), we have

$$I^{\alpha }\mathrm{\Psi }\left(t\right)=\frac{1}{\mathrm{\Gamma }\left(\alpha \right)}{\int }_0^t{(t-\tau )}^{\alpha -1}\mathrm{\Psi }\left(\tau \right)\mathrm{d}\tau .$$

(17)

Since the BW basis functions $\mathrm{\Psi }\left(t\right)$ are polynomials, we can calculate $\frac{1}{\mathrm{\Gamma }\left(\alpha \right)}{\int }_0^t{(t-\tau )}^{\alpha -1}{\tau }^m\mathrm{d}\tau$. By the properties of fractional integration in the sense of Riemann–Liouville, we have

$$\frac{1}{\mathrm{\Gamma }\left(\alpha \right)}{\int }_0^t{(t-\tau )}^{\alpha -1}{\tau }^m\mathrm{d}\tau =\frac{t^{m+\alpha }\mathrm{\Gamma }(m+1)}{\mathrm{\Gamma }(m+\alpha +1)}.$$

Thus, ${(t-\tau )}^{\alpha -1}\mathrm{\Psi }\left(\tau \right)$ can be integrated, and then it is expanded by the BW basis functions; we can obtain the fractional integration operational BW matrix $P^{\alpha }$.

In fact, from Equations (12) and (16), the matrix $P^{\alpha }$ can be obtained as follows

$$P^{\alpha }=\left({\int }_0^1\left(\frac{1}{\mathrm{\Gamma }\left(\alpha \right)}{\int }_0^t{(t-\tau )}^{\alpha -1}\mathrm{\Psi }\left(\tau \right)\mathrm{d}\tau \right){\mathrm{\Psi }}^T\left(t\right)\mathrm{d}t\right)D^{-1}$$

(18)

For $k=2,M=3$ and $\alpha =1$, we have

$$P=\left[\begin{array}{cccccc}0& 0.5& 0& 0.5& 0& 0\\ 0.0069444& -0.25& 0.25& 0.25& 0& 0\\ 0.0185185& -0.597222& 0.5& 0.412037& 0& 0\\ 0& 0& 0& 0& 0.5& 0\\ 0& 0& 0& 0.0069444& -0.25& 0.25\\ 0& 0& 0& 0.0185185& -0.597222& 0.5\end{array}\right],$$

and for $k=2,M=3$ and $\alpha =0.5$, we have

$$P^{0.5}=\left[\begin{array}{cccccc}0.14660& 1.42919& -0.39957& 0.65203& -0.98966& 0.34397\\ 0.00505& -0.09073& 0.31503& 0.38432& -0.693184& 0.24871\\ 0.02179& -0.78216& 0.86545& 0.65735& -1.227210& 0.44296\\ 0& 0& 0& 0.14660& 1.42919& -0.39957\\ 0& 0& 0& 0.00505& -0.09073& 0.31503\\ 0& 0& 0& 0.02179& -0.78216& 0.86545\end{array}\right].$$

4. Convergence Analysis

In order to discuss the convergence of Bell wavelets approximation, some basic results of Bell polynomials approximation are stated.

Let $\mathbf{B}\left(t\right)=[B_0\left(t\right),B_1\left(t\right),\dots ,B_m\left(t\right)]$, and any function $y\left(t\right)\in L^2[0,1]$ can be rewritten as

$$y\left(t\right)\approx y_m\left(t\right)=\sum _{i=0}^m{c}_i{B}_i\left(t\right)=C^T\mathbf{B}\left(t\right).$$

(19)

The convergence analysis of the Bell polynomials is given in Lemma 1.

Lemma 1 

([27]). Suppose that $y\left(t\right)\in L^2[0,1]$, $y_m\left(t\right)$, as defined in Equation (19), is the best approximation of the real function $y\left(t\right)$ by the Bell polynomials. Then, there exists a constant $\tilde{K}$ such that

$$\parallel y\left(t\right)-y_m{\left(t\right)\parallel }_2\le \frac{\tilde{K}}{(m+1)!2^{2m+1}}.$$

where $\tilde{K}={max}_{t\in [0,1]}\left|y^{m+1}\left(t\right)\right|$. From Lemma 1, if $m\to \infty$, then $\frac{1}{(m+1)!2^{2m+1}}\to 0$, which means $y_m\left(t\right)\to y\left(t\right)$.

Theorem 1. 

Suppose that ${\sum }_{n=1}^{2^{k-1}}{\sum }_{m=0}^{M-1}{c}_{nm}{\psi }_{nm}\left(t\right)={\sum }_{j=0}^{\widehat{m}}{c}_j{\phi }_j\left(t\right)=C^{\mathrm{T}}\mathrm{\Psi }\left(t\right)$ is the Bell wavelets expansion of the smooth function $y\left(t\right)$, then we have

$$\underset{\widehat{m}\to \infty }{lim}\parallel y\left(t\right)-\sum _{i=0}^{\widehat{m}}{c}_i{\phi }_i\left(t\right)\parallel =0,$$

where $\widehat{m}=2^{k-1}M$.

Proof. 

Divide the interval $[0,1]$ into subintervals $I_{k,n}=[\frac{n-1}{2^{k-1}},\frac{n}{2^{k-1}}]$, we can write

$$\begin{array}{ccc}\hfill {\int }_0^1{[y\left(t\right)-C^{\mathrm{T}}\mathrm{\Psi }\left(t\right)]}^2\mathrm{d}t& =& \sum _{n=1}^{2^{k-1}}{\int }_{\frac{n-1}{2^{k-1}}}^{\frac{n}{2^{k-1}}}{[y\left(t\right)-C^{\mathrm{T}}\mathrm{\Psi }\left(t\right)]}^2\mathrm{d}t\hfill \\ & =& \sum _{n=1}^{2^{k-1}}{\int }_{\frac{n-1}{2^{k-1}}}^{\frac{n}{2^{k-1}}}{[y\left(t\right)-y_{M-1}\left(t\right)]}^2\mathrm{d}t\hfill \\ & =& \sum _{n=1}^{2^{k-1}}{\parallel y\left(t\right)-y_{M-1}\left(t\right)\parallel }_{I_{k,n}}^2.\hfill \end{array}$$

(20)

By using the Lemma 1, we have

$$\underset{M\to \infty }{lim}{\parallel y\left(t\right)-y_{M-1}\left(t\right)\parallel }_{I_{k,n}}^2=0.$$

(21)

Notice that, when $k\to \infty$,

$$I_{k,n}\to 0;$$

thus, we have

$$\parallel y\left(t\right)-y_{M-1}{\left(t\right)\parallel }_{I_{k,n}}^2\to 0.$$

(22)

By using Equation (20), we have

$$\underset{k\to \infty }{lim}{\parallel y\left(t\right)-y_{\widehat{m}}\left(t\right)\parallel }^2=0.$$

(23)

Considering Equations (21) and (23), and combining with $\widehat{m}=2^{k-1}M$, we have

$$\underset{\widehat{m}\to \infty }{lim}{\parallel y\left(t\right)-y_{\widehat{m}}\left(t\right)\parallel }^2=0.$$

(24)

□

5. Implementation of the Bell Wavelets Scheme

Consider the weakly singular FIDE (1) and (2). To solve the equations, the functions $D_{\mathrm{*}}^{\alpha }y\left(t\right)$, $g\left(t\right)$, and $k(t,s)$ are approximated by using Bell wavelets as follows:

$$D_{\mathrm{*}}^{\alpha }y\left(t\right)\approx C^{\mathrm{T}}\mathrm{\Psi }\left(t\right),$$

(25)

$$g\left(t\right)\approx G^{\mathrm{T}}\mathrm{\Psi }\left(t\right),$$

(26)

and

$$k(t,s)\approx \mathrm{\Psi }{\left(t\right)}^{\mathrm{T}}K\mathrm{\Psi }\left(s\right),$$

(27)

where K is the $\widehat{m}\times \widehat{m}$ matrix as in Equation (15).

From Equation (16), we can obtain

$$y\left(t\right)=I^{\alpha }{D}_{\mathrm{*}}^{\alpha }y\left(t\right)\approx I^{\alpha }\left[C^{\mathrm{T}}\mathrm{\Psi }\left(t\right)\right]=C^{\mathrm{T}}{I}^{\alpha }\left[\mathrm{\Psi }\left(t\right)\right])=C^{\mathrm{T}}{P}^{\alpha }\mathrm{\Psi }\left(t\right).$$

(28)

Therefore,

$$\begin{array}{c}\hfill {\int }_0^t\frac{y\left(s\right)}{{(t-s)}^{\beta }}\mathrm{d}s=C^{\mathrm{T}}{\int }_0^t\frac{P^{\alpha }\mathrm{\Psi }\left(s\right)}{{(t-s)}^{\beta }}\mathrm{d}s=\mathrm{\Gamma }(1-\beta )C^{\mathrm{T}}{P}^{\alpha }{P}^{1-\beta }\mathrm{\Psi }\left(t\right).\end{array}$$

(29)

By using Equations (27) and (28), we obtain

$$\begin{array}{ccc}\hfill {\int }_0^{1}k(t,s)y\left(s\right)\mathrm{d}s& =& {\int }_0^1\mathrm{\Psi }{\left(t\right)}^{\mathrm{T}}K\mathrm{\Psi }\left(s\right)\mathrm{\Psi }{\left(s\right)}^{\mathrm{T}}{C}^{\mathrm{T}}{P}^{\alpha }\mathrm{d}s\hfill \\ & =& \mathrm{\Psi }{\left(t\right)}^{\mathrm{T}}KD{P^{\alpha }}^{\mathrm{T}}C\hfill \\ & =& C^{\mathrm{T}}{P}^{\alpha }{D}^{\mathrm{T}}{K}^{\mathrm{T}}\mathrm{\Psi }\left(t\right).\hfill \end{array}$$

(30)

By substituting Equations (25), (26), (29), and (30) into Equation (1), we obtain

$$C^{\mathrm{T}}\mathrm{\Psi }\left(t\right)={\lambda }_1\mathrm{\Gamma }(1-\beta )C^{\mathrm{T}}{P}^{\alpha }{P}^{1-\beta }\mathrm{\Psi }\left(t\right)+{\lambda }_2{C}^{\mathrm{T}}{P}^{\alpha }{D}^{\mathrm{T}}{K}^{\mathrm{T}}\mathrm{\Psi }\left(t\right)+G^{\mathrm{T}}\mathrm{\Psi }\left(t\right).$$

(31)

Then, we can obtain

$$C^{\mathrm{T}}={\lambda }_1\mathrm{\Gamma }(1-\beta )C^{\mathrm{T}}{P}^{\alpha }{P}^{1-\beta }+{\lambda }_2{C}^{\mathrm{T}}{P}^{\alpha }{D}^{\mathrm{T}}{K}^{\mathrm{T}}+G^{\mathrm{T}}.$$

(32)

By solving this equation, we can obtain C, and then use Equation (28) to obtain the solution of Equations (1) and (2).

6. Numerical Examples

In this section, five examples are presented to verify the effectiveness of the proposed method. As a test measure, the absolute errors between the numerical solutions and the true solution are defined as follows:

$$E_n\left(t\right)=|y\left(t\right)-\widehat{y}\left(t\right)|,$$

where $\widehat{y}\left(t\right)=C^{\mathrm{T}}{P}^{\alpha }\mathrm{\Psi }\left(t\right)$ represents the numerical solutions of the equations. In the following examples, we find that when M is fixed and k tends toward infinity, or when k is fixed and M becomes larger, the absolute errors will become smaller and smaller.

Example 1. 

For the first one, we consider the following equation [21]:

$$D_{\mathrm{*}}^{0.25}y\left(t\right)=\frac{1}{2}{\int }_0^t\frac{y\left(s\right)}{{(t-s)}^{1/2}}\mathrm{d}s+\frac{1}{3}{\int }_0^1(t-s)y\left(s\right)\mathrm{d}s+g\left(t\right),$$

(33)

with the condition $y\left(0\right)=0$. In this problem,

$$g\left(t\right)=\frac{\mathrm{\Gamma }\left(3\right)}{\mathrm{\Gamma }\left(2.75\right)}{t}^{1.75}+\frac{\mathrm{\Gamma }\left(4\right)}{\mathrm{\Gamma }\left(3.75\right)}{t}^{2.75}-\frac{\sqrt{\pi }\mathrm{\Gamma }\left(3\right)t^{2.5}}{2\mathrm{\Gamma }\left(3.5\right)}-\frac{\sqrt{\pi }\mathrm{\Gamma }\left(4\right)t^{3.5}}{2\mathrm{\Gamma }\left(4.5\right)}-\frac{7t}{36}+\frac{3}{20}.$$

The exact solution of Equation (33) is $y\left(t\right)=t^2+t^3$.

By applying the BW method, we approximate $D_{\mathrm{*}}^{0.25}y\left(t\right)$ as

$$D_{\mathrm{*}}^{0.25}y\left(t\right)\approx C^{\mathrm{T}}\mathrm{\Psi }\left(t\right),$$

(34)

From Equation (28), we can obtain

$$y\left(t\right)=C^{\mathrm{T}}{P}^{0.25}\mathrm{\Psi }\left(t\right).$$

(35)

Therefore,

$$\begin{array}{c}\hfill {\int }_0^t\frac{y\left(s\right)}{{(t-s)}^{1/2}}\mathrm{d}s=C^{\mathrm{T}}{P}^{0.25}{\int }_0^t\frac{\mathrm{\Psi }\left(s\right)}{{(t-s)}^{1/2}}\mathrm{d}s=\mathrm{\Gamma }\left(0.5\right)C^{\mathrm{T}}{P}^{0.25}{P}^{0.5}\mathrm{\Psi }\left(t\right).\end{array}$$

(36)

By using Equation (30), we obtain

$$\begin{array}{c}\hfill {\int }_0^1(t-s)y\left(s\right)\mathrm{d}s=C^{\mathrm{T}}{P}^{0.25}{D}^{\mathrm{T}}{K}^{\mathrm{T}}\mathrm{\Psi }\left(t\right).\end{array}$$

(37)

where K is the $\widehat{m}\times \widehat{m}$ matrix as given by Equation (15). Similarly, the function $g\left(t\right)$ can be written by the BWs as follows

$$g\left(t\right)\approx G^{\mathrm{T}}\mathrm{\Psi }\left(t\right).$$

(38)

Substituting Equations (34) and (36)–(38) into Equation (33), we have

$$C^{\mathrm{T}}\mathrm{\Psi }\left(t\right)=\frac{1}{2}\mathrm{\Gamma }\left(0.5\right)C^{\mathrm{T}}{P}^{0.25}{P}^{0.5}\mathrm{\Psi }\left(t\right)+\frac{1}{2}{C}^{\mathrm{T}}{P}^{0.25}{D}^{\mathrm{T}}{K}^{\mathrm{T}}\mathrm{\Psi }\left(t\right)+G^{\mathrm{T}}\mathrm{\Psi }\left(t\right).$$

(39)

Equation (39) is a system of algebraic equations about an unknown vector C. After solving C, combined with Equation (35), we can obtain the numerical solution $y\left(t\right)$.

The BW approach is applied with $k=2,3,4$. To demonstrate the effectiveness of the BW method, CAS wavelets ($m^{\prime }=2^k(2M+1)$) [21] and SCW [22] are compared with BWs; the absolute errors are shown in

Table 1. The absolute errors for Example 1 with $M=3$ and different k.

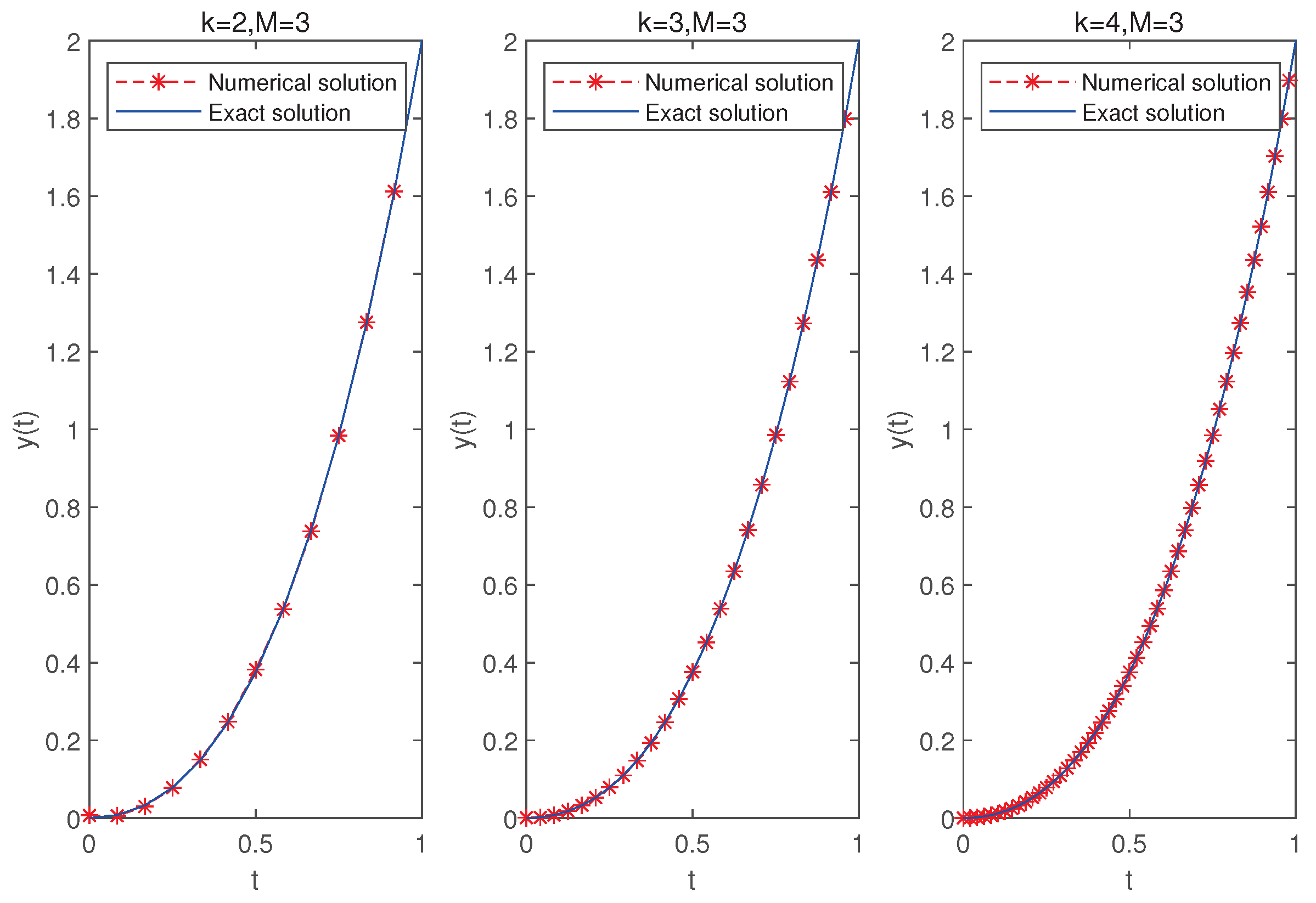
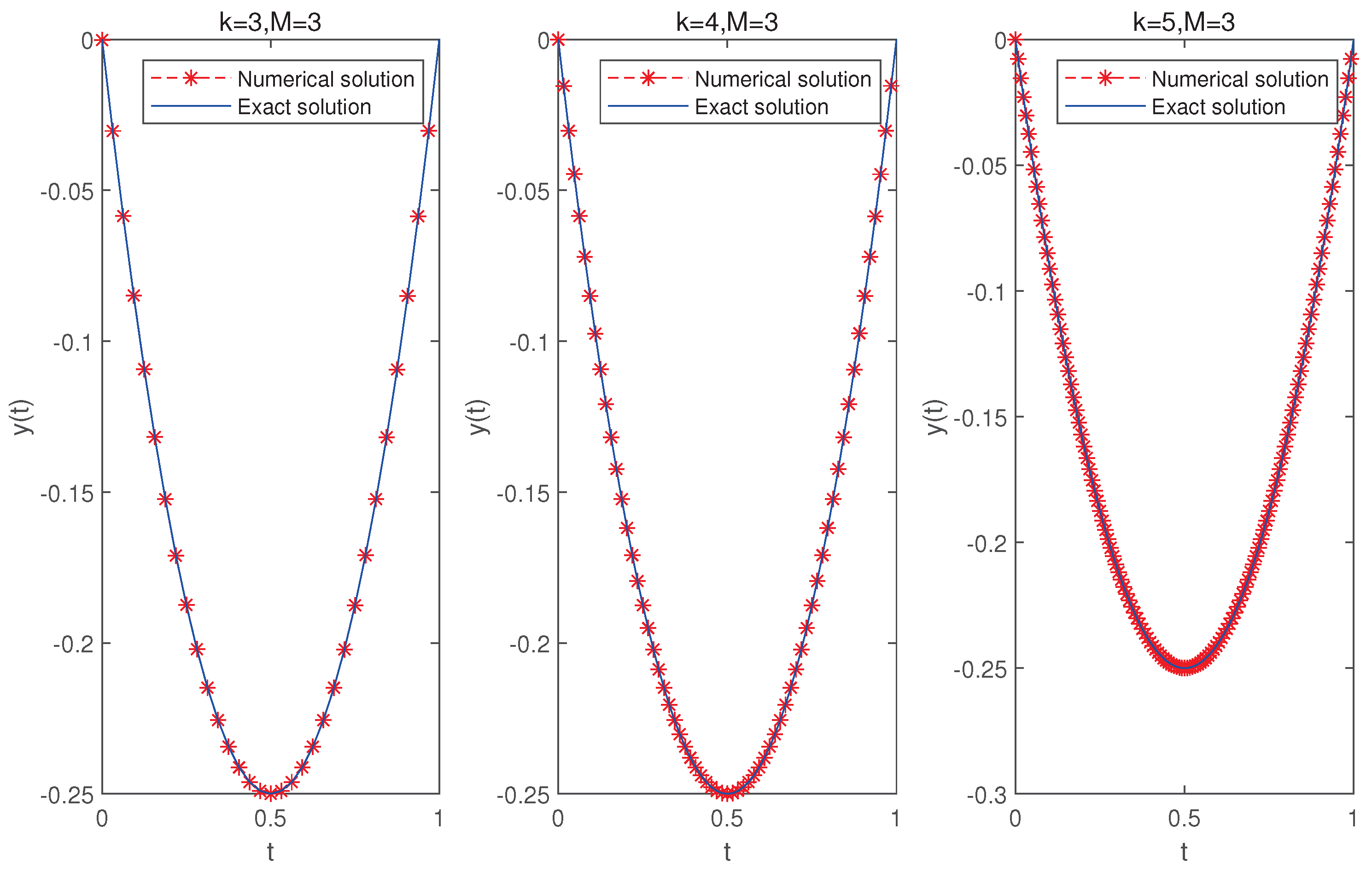
t	BW	SCW	CAS	BW	SCW	CAS	BW	SCW	CAS
	$\mathit{k}=\mathbf{2}$	$\mathit{k}=\mathbf{2}$	${\mathit{m}}^{\prime }=\mathbf{6}$	$\mathit{k}=\mathbf{3}$	$\mathit{k}=\mathbf{3}$	${\mathit{m}}^{\prime }=\mathbf{12}$	$\mathit{k}=\mathbf{4}$	$\mathit{k}=\mathbf{4}$	${\mathit{m}}^{\prime }=\mathbf{24}$
0	6.9313 × ${10}^{-3}$	8.3542 × ${10}^{-3}$	3.0586 × ${10}^{-2}$	8.1806 × ${10}^{-4}$	1.0620 × ${10}^{-3}$	1.4328 × ${10}^{-2}$	9.3735 × ${10}^{-5}$	1.4395 × ${10}^{-4}$	6.3492 × ${10}^{-3}$
1/6	2.8075 × ${10}^{-3}$	1.2599 × ${10}^{-3}$	4.4076 × ${10}^{-2}$	3.0810 × ${10}^{-4}$	1.1189 × ${10}^{-3}$	2.2762 × ${10}^{-2}$	4.1670 × ${10}^{-5}$	2.2617 × ${10}^{-4}$	1.1461 × ${10}^{-2}$
2/6	2.3585 × ${10}^{-3}$	9.3654 × ${10}^{-3}$	3.8707 × ${10}^{-2}$	3.4663 × ${10}^{-4}$	1.8879 × ${10}^{-3}$	1.9409 × ${10}^{-2}$	3.8572 × ${10}^{-5}$	5.9826 × ${10}^{-4}$	9.6983 × ${10}^{-3}$
3/6	6.7790 × ${10}^{-3}$	2.2406 × ${10}^{-2}$	1.5703 × ${10}^{-2}$	8.2215 × ${10}^{-4}$	4.7945 × ${10}^{-3}$	6.4173 × ${10}^{-3}$	1.0113 × ${10}^{-4}$	1.1274 × ${10}^{-3}$	2.9505 × ${10}^{-3}$
4/6	2.8546 × ${10}^{-3}$	1.9585 × ${10}^{-2}$	2.8551 × ${10}^{-2}$	3.0420 × ${10}^{-4}$	5.9543 × ${10}^{-3}$	1.8012 × ${10}^{-2}$	4.2679 × ${10}^{-5}$	1.4961 × ${10}^{-3}$	9.6732 × ${10}^{-3}$
5/6	2.3680 × ${10}^{-3}$	3.2596 × ${10}^{-2}$	9.8881 × ${10}^{-2}$	3.4753 × ${10}^{-4}$	8.0256 × ${10}^{-3}$	5.6450 × ${10}^{-2}$	3.8628 × ${10}^{-5}$	2.2056 × ${10}^{-3}$	2.9488 × ${10}^{-2}$

. In Figure 1, the comparisons between the exact solution and numerical solutions with some $k=2,3,4$ and $M=3$ are given. Figure 2 shows the absolute errors when k takes different values.

From Figure 1 and Figure 2, we can see that as the k value increases, the numerical solutions and exact solutions become closer and closer. Table 1 shows that the BW method performs better than the CAS wavelet method and SCW method.

Example 2. 

Take the equation [28]

$$D_{\mathrm{*}}^{0.15}y\left(t\right)=\frac{1}{4}{\int }_0^t\frac{y\left(s\right)}{{(t-s)}^{1/2}}\mathrm{d}s+\frac{1}{7}{\int }_0^1{e}^{t+s}y\left(s\right)\mathrm{d}s+g\left(t\right),$$

(40)

with the condition $y\left(0\right)=0$, $g\left(t\right)=\frac{\mathrm{\Gamma }\left(3\right)}{\mathrm{\Gamma }\left(2.85\right)}{t}^{1.85}-\frac{\mathrm{\Gamma }\left(2\right)}{\mathrm{\Gamma }\left(1.85\right)}{t}^{0.85}-\frac{\sqrt{\pi }\mathrm{\Gamma }\left(3\right)t^{2.5}}{4\mathrm{\Gamma }\left(3.5\right)}+\frac{\sqrt{\pi }\mathrm{\Gamma }\left(2\right)t^{1.5}}{4\mathrm{\Gamma }\left(2.5\right)}-\frac{e^{t+1}-3e^t}{7}$. The exact solution of Equation (40) is $y\left(t\right)=t^2-t$.

The evaluation of the numerical solutions of the BW method, the LWC (Legendre wavelets collocation), LW (Legendre wavelets) [28], and TW [25] is illustrated in

Table 2. Comparisons of the numerical solutions and exact solution with different k for Example 2.

t		$\mathit{k}=4$				$\mathit{k}=5$			Exact
	LWC	LW	TW	BW	LWC	LW	TW	BW	Solution
0	0.0025	0.0016	−0.0031	−0.00000	0.0011	0.0006	−0.0008	−0.00000	−0.00000
1/8	−0.1007	−0.1014	−0.1125	−0.10933	−0.1023	−0.1058	−0.1101	−0.10937	−0.10938
2/8	−0.1769	−0.1774	−0.1905	−0.18750	−0.1813	−0.1829	−0.1882	−0.18750	−0.18750
3/8	−0.2224	−0.2231	−0.2373	−0.23437	−0.2257	−0.2293	−0.2351	−0.23438	−0.23438
4/8	−0.2431	−0.2382	−0.2529	−0.25000	−0.2442	−0.2447	−0.2507	−0.25000	−0.25000
5/8	−0.2230	−0.2227	−0.2373	−0.23438	−0.2281	−0.2292	−0.2351	−0.23438	−0.23438
6/8	−0.1804	−0.1765	−0.1389	−0.18750	−0.1829	−0.1827	−0.1882	−0.18750	−0.18750
7/8	−0.1011	−0.0990	−0.1389	−0.10938	−0.1055	−0.1052	−0.1101	−0.10938	−0.10938

.

From Table 2, we can infer that the approximate solutions of all methods converge to the exact solution, but the BW method has better convergence. In Figure 3, the comparisons of the numerical solutions and the exact solution for various k are shown. Figure 4 shows the absolute errors with $k=3,4,5$. From Figure 3 and Figure 4, we can see that the numerical solutions become closer to the exact solution as k increases.

Example 3. 

Think about the integro-differential equation [29]

$$D_{\mathrm{*}}^{0.75}y\left(t\right)={\int }_0^t\frac{y\left(s\right)}{{(t-s)}^{1/2}}\mathrm{d}s+{\int }_0^{1}tsy\left(s\right)\mathrm{d}s+g\left(t\right),$$

(41)

with the condition $y\left(0\right)=0$. In this problem,

$$g\left(t\right)=\frac{105\sqrt{\pi }}{16\mathrm{\Gamma }\left(3.75\right)}{t}^{2.75}-\frac{35\pi }{128}{t}^4-\frac{2t}{11}.$$

The exact solution is $y\left(t\right)=t^{7/2}$.

The evaluation of the numerical solutions using the BW method with different M and $k=3$ is illustrated throughout

Table 3. The absolute errors of different $k=3$ and M for Example 3.

t	$\mathit{M}=2$	$\mathit{M}=3$	$\mathit{M}=4$
0	2.2305 × ${10}^{-3}$	6.2546 × ${10}^{-4}$	4.6293 × ${10}^{-5}$
1/6	1.1942 × ${10}^{-3}$	2.1897 × ${10}^{-4}$	1.4139 × ${10}^{-6}$
2/6	2.4926 × ${10}^{-3}$	4.4943 × ${10}^{-4}$	6.4363 × ${10}^{-7}$
3/6	2.3887 × ${10}^{-3}$	1.3856 × ${10}^{-3}$	1.9253 × ${10}^{-5}$
4/6	8.7406 × ${10}^{-3}$	5.3174 × ${10}^{-4}$	4.7829 × ${10}^{-8}$
5/6	1.0382 × ${10}^{-2}$	6.6994 × ${10}^{-4}$	2.8633 × ${10}^{-7}$

, Figure 5 and Figure 6. Table 3 shows that as the M value increases, the absolute errors decrease, that is, as M increases, the numerical solutions converge to the exact solution.

Example 4. 

We explore the following equation

$$D_{\mathrm{*}}^{\alpha }y\left(t\right)={\int }_0^t\frac{y\left(s\right)}{{(t-s)}^{1/2}}\mathrm{d}s+{\int }_0^1(t^2+s)y\left(s\right)\mathrm{d}s+g\left(t\right),$$

(42)

with condition $y\left(0\right)=0$, and

$$g\left(t\right)=-\frac{1}{2}t+e^t+2\sqrt{t}+(e-2)t^2-e^t\sqrt{\pi }Erf\left(\sqrt{t}\right),$$

where $Erf\left(t\right)=\frac{2}{\sqrt{\pi }}{\int }_0^t{e}^{-t^2}\mathrm{d}t$ is the Gauss error function. The exact solution is $y\left(t\right)=e^t-1$ for $\alpha =1$.

By setting $k=2,M=3$, the BW numerical solutions for $\alpha =0.85,0.9,0.95,1$ are obtained. From Figure 7 and

Table 4. The numerical solutions for different $\alpha$ for Example 4.

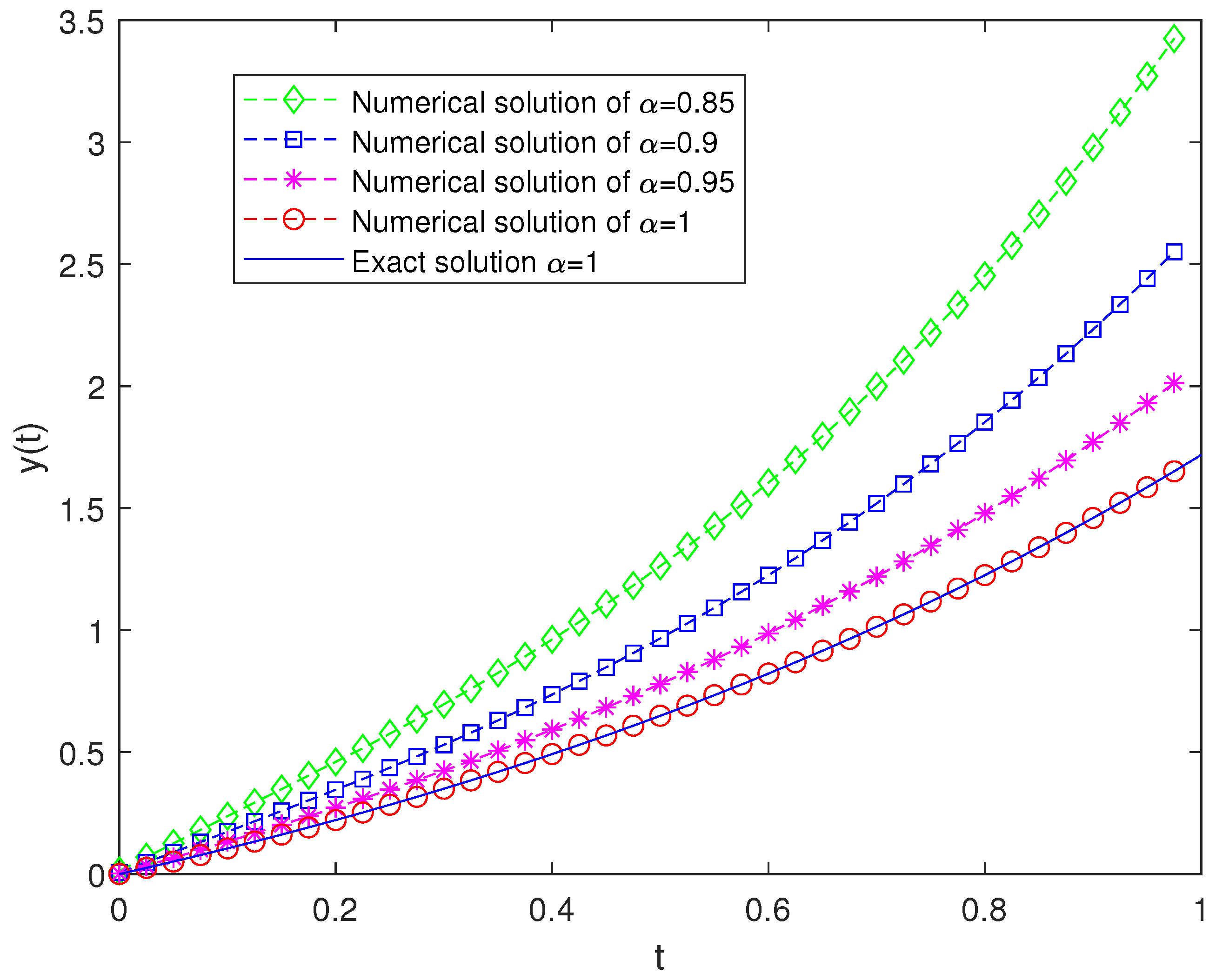
t	$\alpha =0.85$	$\alpha =0.9$	$\alpha =0.95$	$\alpha =1$	Exact Solution for $\alpha =1$
					0.0	0.012888	0.006038	0.002288	0.000148	0.000000
0.1	0.237160	0.173487	0.133091	0.105128	0.105171
0.2	0.459795	0.345549	0.272531	0.221457	0.221403
0.3	0.695967	0.530027	0.424025	0.349792	0.349859
0.4	0.961655	0.735810	0.592138	0.491875	0.491825
0.5	1.262802	0.966510	0.779070	0.648966	0.648721
0.6	1.604448	1.225164	0.986627	0.822048	0.822119
0.7	1.999504	1.519514	1.219497	1.013842	1.013753
0.8	2.453014	1.852598	1.479528	1.225431	1.225541
0.9	2.978791	2.232636	1.771674	1.459687	1.459603

, the numerical solutions by BW approach to the exact solution are concluded, as $\alpha$ is close to 1.

We considered the case of $0<\alpha <1$ in the first four examples. In fact, we can extend the proposed method to the case of $\alpha >1$.

Example 5. 

We explore the following fractional integro-differential equation:

$$D_{\mathrm{*}}^{1.25}y\left(t\right)={\int }_0^t\frac{y\left(s\right)}{{(t-s)}^{1/2}}\mathrm{d}s+{\int }_0^1(t^2+coss)y\left(s\right)\mathrm{d}s+g\left(t\right),$$

(43)

where $g\left(t\right)=\frac{2t^{0.75}}{\mathrm{\Gamma }\left(1.75\right)}-\frac{\sqrt{\pi }\mathrm{\Gamma }\left(3\right)t^{2.5}}{2\mathrm{\Gamma }\left(3.5\right)}-\frac{t^2}{3}-2cos1+sin1$, with initial conditions $y\left(0\right)=0,y^{\prime }\left(0\right)=0$. The exact solution of the Equation (43) is $y\left(t\right)=t^2$.

By setting $M=3$, BW solutions are obtained for various k. The absolute errors obtained by EW [26], and BW, respectively, are shown in

Table 5. Evaluation of the numerical solutions using the BWs and EW for Example 5.

t	BW	EW	BW	EW	BW	EW
	$\mathit{k}=\mathbf{2}$	$\mathit{k}=\mathbf{2}$	$\mathit{k}=\mathbf{3}$	$\mathit{k}=\mathbf{3}$	$\mathit{k}=\mathbf{4}$	$\mathit{k}=\mathbf{4}$
0	5.1239 × ${10}^{-4}$	7.3506 × ${10}^{-4}$	1.2797 × ${10}^{-4}$	5.6164 × ${10}^{-4}$	3.1983 × ${10}^{-5}$	6.7644 × ${10}^{-5}$
1/6	1.2863 × ${10}^{-4}$	3.3452 × ${10}^{-4}$	4.5853 × ${10}^{-5}$	4.5856 × ${10}^{-5}$	3.5506 × ${10}^{-7}$	1.7492 × ${10}^{-6}$
2/6	1.7512 × ${10}^{-4}$	5.6502 × ${10}^{-4}$	1.5776 × ${10}^{-6}$	1.6164 × ${10}^{-6}$	1.1317 × ${10}^{-7}$	6.6386 × ${10}^{-7}$
3/6	6.9527 × ${10}^{-5}$	7.9432 × ${10}^{-5}$	2.7632 × ${10}^{-6}$	4.5437 × ${10}^{-6}$	1.4772 × ${10}^{-7}$	2.8538 × ${10}^{-7}$
4/6	1.4217 × ${10}^{-5}$	3.4521 × ${10}^{-5}$	9.1782 × ${10}^{-8}$	6.7327 × ${10}^{-7}$	5.2470 × ${10}^{-9}$	4.8538 × ${10}^{-8}$
5/6	4.1377 × ${10}^{-6}$	2.8754 × ${10}^{-5}$	4.6553 × ${10}^{-7}$	1.0540 × ${10}^{-6}$	7.6072 × ${10}^{-9}$	6.8537 × ${10}^{-8}$

. In Figure 8, the comparisons between the exact solution and the numerical solutions with $M=3$ and some k are given. Table 5 displays that the BW method has smaller absolute errors than the EW method. Figure 9 shows that the absolute errors decrease as k increases.

7. Conclusions

A new numerical method with Bell wavelets and their operational matrix is first proposed for solving the FIDE with weakly singular kernels. This proposed method involves constructing the BWs and their fractional operational matrix to transform the FIDE into a linear algebraic system of equations. The error analysis of the BW function approximation is investigated. Furthermore, we demonstrate the efficiency and accuracy of our proposed scheme by solving several numerical simulations. After comparing the obtained results with other methods such as CAS wavelets, SCW, TW, and LW, the BW method performed the best.