A Bound-Preserving Numerical Scheme for Space–Time Fractional Advection Equations

Abstract

We develop and analyze an explicit finite difference scheme that satisfies a bound-preserving principle for space–time fractional advection equations with the orders of $0<\alpha$ and $\beta \le 1$. The stability (and convergence) of the method is discussed. Due to the nonlocal property of the fractional operators, the numerical method generates dense coefficient matrices with complex structures. In order to increase the effectiveness of the method, we use Toeplitz-like structures in the full coefficient matrix in a sparse form to reduce the costs of computation, and we also apply a fast evaluation method for the time–fractional derivative. Therefore, an efficient solver is constructed. Numerical experiments are provided for the utility of the method.

1. Introduction

It has been shown that fractional partial differential equations (FPDEs) [1,2] provide a powerful way through which to simulate challenging phenomena—including long-range spatial interactions [3,4,5,6,7] and anomalously diffusive transport [8,9,10,11] and memory effects [12]—and they have attracted extensive research [13,14,15,16,17,18]. The majority of the works in the literature have focused on FPDEs that model anomalously diffusive transport, including both subdiffusive transport and superdiffusive transport, or a combination of both [19,20,21,22,23]. Here, we discuss space–time fractional advection equations (stFAEs) in two space dimensions:

$$\begin{array}{c}{\partial }_t^{\alpha }u+v_x\left[{\kappa }_x{\partial }_x^{{\beta }_x,-}u+(1-{\kappa }_x){\partial }_x^{{\beta }_x,+}u\right]+v_y\left[{\kappa }_y{\partial }_y^{{\beta }_y,-}u+(1-{\kappa }_y){\partial }_y^{{\beta }_y,+}u\right]\hfill \\ {\displaystyle =f,in\Omega \times (0,T],}\hfill \\ u(x,y,0)=u_0(x,y),(x,y)\in \overline{\Omega },\hfill \\ u(x,y,t)=0,(x,y,t)\in \partial \Omega \times [0,T].\hfill \end{array}$$

(1)

Here, $v_x$ and $v_y$ are the components of the velocity field along the coordinate directions, which are assumed to be non-negative constants for simplicity of exposition. $0\le {\kappa }_x,{\kappa }_y\le 1$ represent the relative weights of the forward versus backward probabilities of the underlying particle jumps along coordinate directions, respectively. The rectangular domain $\Omega :=(x_d,x_u)\times (y_d,y_u)$, and fractional derivatives ${\partial }_x^{\gamma ,\pm }u$ of order $0<\gamma \le 1$ are defined by [2]

$$\begin{array}{c}{\partial }_x^{\gamma ,-}u:=\left\{\begin{array}{cc}{\displaystyle { }_{x_d}{I}_x^{1-\gamma }{\partial }_{x}u,}\hfill & \gamma \in (0,1),\hfill \\ {\displaystyle {\partial }_{x}u,}\hfill & \gamma =1,\hfill \end{array}\right.\hfill \\ {\partial }_x^{\gamma ,+}u:=\left\{\begin{array}{cc}{\displaystyle -{ }_x{I}_{x_u}^{1-\gamma }{\partial }_{x}u,}\hfill & \gamma \in (0,1),\hfill \\ {\displaystyle -{\partial }_{x}u,}\hfill & \gamma =1,\hfill \end{array}\right.\hfill \\ {\displaystyle { }_a{I}_x^{\gamma }g(x):=\frac{1}{\Gamma (\gamma )}{\int }_a^x\frac{g(z)}{{(x-z)}^{1-\gamma }}dz,{ }_x{I}_b^{\gamma }g(x):=\frac{1}{\Gamma (\gamma )}{\int }_x^b\frac{g(z)}{{(z-x)}^{1-\gamma }}dz.}\hfill \end{array}$$

(2)

If $\alpha =1$, then Equation (1) reduces to a space–fractional advection equation (sFAE)

$$\begin{array}{c}{\partial }_{t}u+v_x\left[{\kappa }_x{\partial }_x^{{\beta }_x,-}u+(1-{\kappa }_x){\partial }_x^{{\beta }_x,+}u\right]+v_y\left[{\kappa }_y{\partial }_y^{{\beta }_y,-}u+(1-{\kappa }_y){\partial }_y^{{\beta }_y,+}u\right]\hfill \\ {\displaystyle =f,in\Omega \times (0,T],}\hfill \\ u(x,y,0)=u_0(x,y),(x,y)\in \Omega ,\hfill \\ u(x,y,t)=0,(x,y,t)\in \partial \Omega \times (0,T].\hfill \end{array}$$

(3)

To understand the properties of the governing equations, we begin with the problem (3) in one-dimension and drop the subscript x as follows:

$$\begin{array}{c}{\partial }_{t}u+v\left[\kappa {\partial }_x^{\beta ,-}u+(1-\kappa ){\partial }_x^{\beta ,+}u\right]=f(x,t),(x,t)\in (x_d,x_u)\times (0,T],\\ u(x,0)=u_0(x),x\in [x_d,x_u],u(x_d,t)=u(x_u,t)=0,t\in [0,T].\end{array}$$

(4)

We consider the problem (4) with $(x_d,x_u)=(0,1)$, $v=1$, $\kappa =1$ and f being constant.

$${\partial }_x^{\beta ,-}u={ }_0{I}_x^{1-\beta }{\partial }_{x}u=f,x\in (0,1).$$

(5)

We utilized the semigroup property of ${ }_0{I}_x^{\beta }$ [2] and the formula

$${ }_0{I}_x^{\gamma }{x}^{\mu }=\frac{\Gamma (\mu +1)}{\Gamma (\gamma +\mu +1)}{x}^{\gamma +\mu },0<\gamma <1,\mu >-1$$

(6)

to obtain a closed-form expression of the solution u as

$$u(x)-u(0)={ }_0{I}_x{\partial }_{x}u={ }_0{I}_x^{\beta }{ }_0{I}_x^{1-\beta }{\partial }_{x}u={ }_0{I}_x^{\beta }f=\frac{f{x}^{1-\beta }}{\Gamma (2-\beta )}.$$

(7)

To uniquely determine a solution u to problem (5), one has to enforce a boundary condition $u(0)$ for Problem (5). In particular, $u(x)=u(0)$ for $f\equiv 0$ shows the advective nature of the problem.

We can similarly find a closed-form expression for the one-sided fractional diffusion equation of an order $1<\gamma <2$

$${\partial }_x^{\gamma ,-}u={ }_0{I}_x^{2-\gamma }{\partial }_{xx}u=1,x\in (0,1)$$

(8)

as follows:

$$u(x)=\frac{x^{\gamma }}{\gamma (\gamma -1)}+C_{1}x+C_2,x\in (0,1).$$

(9)

To uniquely determine a solution for Problem (8), one has to enforce the boundary condition for $u(0)$ and $u(1)$.

This partially explains why an implicit finite-difference approximation to Problem (8) is obtained by directly truncating the fractional derivative, which is unstable, as proved in [24]. The reason for this that the numerical approximation is uniquely determined by only the left-sided boundary condition, while the solution to the continuous Problem (9) can only be uniquely determined with the boundary condition at both of the endpoints of the interval.

We observed from (7) that the solution to the left-sided FAE (5) can be uniquely determined by the boundary condition at $x=x_d$. Via symmetry, we anticipated that the solution to the right-sided analog of Problem (5) can be uniquely determined by the right-end boundary condition. Consequently, the two-sided Problem (4) needed to be closed by boundary conditions at both the endpoints of the interval $(x_d,x_u)$. Unlike fractional diffusion problems, the two boundary conditions in the two-sided FAE Problem (4) work against each other in the sense that the two fronts generated by the two boundary conditions move toward each other as in the turning point problems in integer-order, advection–diffusion equations (which always produce numerical approximations with spurious oscillations, under and over shoot, as well as produce other numerical difficulties [25]).

Inspired by these considerations, we followed the ideas from [26,27,28,29,30] to develop a bound-preserving numerical method for fractional advection Equations (1) and (3), so that the resulting numerical approximations could remove the spurious numerical oscillations, as well as the under and over shoot. As we shall see, Problems (1) and (3) exhibited a combination of an advective and diffusive nature. This required further numerical and mathematical analysis. For instance, diffusion-dominated problems typically prefer an implicit temporal discretization, while advection-dominated problems prefer an explicit temporal discretization. We intended to develop an explicit numerical scheme for these problems.

Numerical discretizations of fractional differential operators involve dense matrices for their nonlocal nature, even if an explicit numerical discretization is used [31,32]. Further, the numerical discretizations of time-fractional differential operators contain numerical solutions at each time step. Their numerical solutions have a computational complexity of $O(M{N}^2+M^{2}N)$, as well as an $O(M{N}^2)$ memory requirement, where N is the number of spatial unknowns and M is the number of time steps. To improve the method, we followed the ideas from [33,34,35] to develop fast numerical methods for Problems (1) and (3).

The rest of the paper is organized as follows. An explicit finite difference method (EFDM) for the sFDE (3) is provided in Section 2, where we prove its boundary-preserving principle and error estimate. A fast implementation is also derived. In Section 3, we present an EFDM for stFDE (1). In a similar way, we prove its boundary-preserving principle and error estimate, as well as the fast implementation. In Section 4, we conduct numerical experiments to confirm the theoretical analysis, as well as study the performance of its fast implementation.

2. Derivation of Explicit Numerical Schemes

We derive numerical schemes for stFAEs (1) and sFAE (3) in this section. Let M, $N_x$ and $N_y$ be positive integers. We defined a space–time partition on $\Omega \times [0,T]$ by the following: $t_m:=m\tau$ for $m=0,1,\dots ,M$ with $\tau :=T/M$$x_i:=x_d+i{h}_x$, as well as $y_j:=y_d+j{h}_y$ for $i=0,1,\dots ,N_x$ and $j=0,1,\dots ,N_y$ with $h_x:=(x_u-x_d)/N_x$ and $h_y:=(y_u-y_d)/N_y$, respectively.

2.1. An Explicit Numerical Scheme for sFAE (3)

Let ${\delta }_{h}g(x):=(g(x+h)-g(x))/h$ and ${\delta }_{\tau }g(t):=(g(t+\tau )-g(t)/\tau$. We used an explicit Euler function to discretize ${\partial }_{t}u(x_i,t_m)$, as well as used the L-1 discretization to discretize ${\partial }_x^{{\beta }_x,-}u(x_i,t_m)$ and ${\partial }_x^{{\beta }_x,+}u(x_i,t_m)$ (where we have dropped the dummy variable $y_j$ for conciseness), as follows:

$$\begin{array}{c}{\displaystyle {\partial }_{t}u(x_i,t_m)={\delta }_{\tau }u(x_i,t_m)-R_{i,m}^t}\hfill \\ {\displaystyle {\partial }_x^{{\beta }_x,-}u(x_i,t_m)}\hfill \\ {\displaystyle =\frac{1}{\Gamma (1-{\beta }_x)}\sum _{k=0}^{i-1}{\int }_{x_k}^{x_{k+1}}\frac{{\delta }_{h_x}u(x_k,t_m)+\left({\partial }_{x}u(z,t_m)-{\delta }_{h_x}u(x_k,t_m)\right)}{{(x_i-z)}^{{\beta }_x}}dz}\hfill \\ {\displaystyle =\frac{1}{\Gamma (2-{\beta }_x)h_x^{{\beta }_x}}\sum _{k=0}^{i-1}\left(u(x_{k+1},t_m)-u(x_k,t_m)\right){\omega }_{i-k}^{{\beta }_x}+R_{i,m}^{{\beta }_x,-},}\hfill \\ =:{\delta }_{h_x}^{{\beta }_x,-}u(x_i,t_m)+R_{i,m}^{{\beta }_x,-},\hfill \\ {\displaystyle {\partial }_x^{{\beta }_x,+}u(x_i,t_m)}\hfill \\ {\displaystyle =\frac{-1}{\Gamma (1-{\beta }_x)}\sum _{k=i}^{N_x-1}{\int }_{x_k}^{x_{k+1}}\frac{{\delta }_{h_x}u(x_k,t_m)+\left({\partial }_{x}u(z,t_m)-{\delta }_{h_x}u(x_k,t_m)\right)}{{(z-x_i)}^{{\beta }_x}}dz}\hfill \\ {\displaystyle =\frac{-1}{\Gamma (2-{\beta }_x)h_x^{{\beta }_x}}\sum _{k=i}^{N_x-1}\left(u(x_{k+1},t_m)-u(x_k,t_m)\right){\omega }_{k-i+1}^{{\beta }_x}+R_{i,m}^{{\beta }_x,+},}\hfill \end{array}$$

(10)

where ${\omega }_k^{\beta }:=k^{1-\beta }-{(k-1)}^{1-\beta }$ and

$$\begin{array}{cc}\hfill {\displaystyle R_{i,m}^t}& {\displaystyle :=\frac{1}{\tau }{\int }_{t_m}^{t_{m+1}}{\partial }_{tt}u(x_i,t)\left(t_{m+1}-t\right)dt=\mathcal{O}(\tau ),}\hfill \\ \hfill {\displaystyle R_{i,m}^{{\beta }_x,-}}& {\displaystyle :=\frac{1}{\Gamma (1-\beta )}\sum _{k=0}^{i-1}{\int }_{x_k}^{x_{k+1}}{\partial }_{xx}u(s,t^m)\frac{(x_{k+1}+x_k-2s)}{{(x_i-s)}^{\beta }}ds+\mathcal{O}(h^2),}\hfill \\ \hfill {\displaystyle R_{i,m}^{{\beta }_x,+}}& {\displaystyle :=\frac{1}{\Gamma (1-\beta )}\sum _{k=i}^{N-1}{\int }_{x_k}^{x_{k+1}}{\partial }_{xx}u(s,t^m)\frac{(x_{k+1}+x_k-2s)}{{(s-x_i)}^{\beta }}ds+\mathcal{O}(h^2).}\hfill \end{array}$$

(11)

It was proved in [36] that ${\displaystyle |R_{i,m}^{{\beta }_x,-}|\le \mathcal{O}(h^{2-\beta }).}$ In fact, for the first term in the RHS of $R_{i,m}^{{\beta }_x,+}$ given above, we have

$$\begin{array}{c}{\displaystyle \frac{1}{\Gamma (1-\beta )}\sum _{k=i}^{N-1}{\int }_{x_k}^{x_{k+1}}\frac{(x_{k+1}+x_k-2s)}{{(s-x_i)}^{\beta }}ds}\hfill \\ {\displaystyle =\frac{h^{2-\beta }}{\Gamma (2-\beta )}\sum _{k=i}^{N-1}(2k+1)[{(k-i+1)}^{1-\beta }-{(k-i)}^{1-\beta }]}\hfill \\ {\displaystyle -\frac{2h^{2-\beta }}{\Gamma (2-\beta )}\sum _{k=i}^{N-1}[(k+1){(k-i+1)}^{1-\beta }-k{(k-i)}^{1-\beta }]}\hfill \\ {\displaystyle +\frac{2h^{2-\beta }}{\Gamma (3-\beta )}\sum _{k=i}^{N-1}[{(k-i+1)}^{2-\beta }-{(k-i)}^{2-\beta }]}\hfill \\ {\displaystyle =\frac{h^{2-\beta }}{\Gamma (2-\beta )}[(2N-1){(N-i)}^{1-\beta }-2(1^{1-\beta }+2^{1-\beta }+3^{1-\beta }+\cdots }\hfill \\ {\displaystyle +{(N-i-1)}^{1-\beta })]-\frac{2h^{2-\beta }}{\Gamma (2-\beta )}N{(N-i)}^{1-\beta }+\frac{2h^{2-\beta }}{\Gamma (3-\beta )}{(N-i)}^{2-\beta }}\hfill \\ {\displaystyle =\frac{h^{2-\beta }}{\Gamma (2-\beta )}[-{(N-i)}^{1-\beta }-2(1^{1-\beta }+2^{1-\beta }+3^{1-\beta }+\cdots }\hfill \\ {\displaystyle +{(N-i-1)}^{1-\beta })+\frac{2}{2-\beta }{(N-i)}^{2-\beta }]}\hfill \\ {\displaystyle =\frac{-h^{2-\beta }}{\Gamma (2-\beta )}S(N-i).}\hfill \end{array}$$

It was shown in [36] that $S(N-i)\le C$; thus, we obtained $|R_{i,m}^{{\beta }_x,+}|\le O(h^{2-\beta }).$

We discretized ${\partial }_y^{{\beta }_y,\pm }u$ by symmetry and reformulate sFAE (3) as the following reference equation:

$$\begin{array}{c}{\delta }_{\tau }u(x_i,y_j,t_m)+v_x\left[{\kappa }_x{\delta }_{h_x}^{{\beta }_x,-}+(1-{\kappa }_x){\delta }_{h_x}^{{\beta }_x,+}\right]u(x_i,y_j,t_m)\hfill \\ {\displaystyle +v_y\left[{\kappa }_y{\delta }_{h_y}^{{\beta }_y,-}+(1-{\kappa }_y){\delta }_{h_y}^{{\beta }_y,+}\right]u(x_i,y_j,t_m)=f(x_i,y_j,t_m)+R_{i,j,m},}\hfill \end{array}$$

(12)

where $R_{i,j,m}$ is given by

$$\begin{array}{cc}\hfill R_{i,j,m}:=& -R_{i,j,m}^t-v_x\left[{\kappa }_x{R}_{i,j,m}^{{\beta }_x,-}+(1-{\kappa }_x)R_{i,j,m}^{{\beta }_x,+}\right]\hfill \\ \hfill & -v_y\left[{\kappa }_y{R}_{i,j,m}^{{\beta }_y,-}+(1-{\kappa }_y)R_{i,j,m}^{{\beta }_y,+}\right]=\mathcal{O}\left(\tau +h_x^{2-{\beta }_x}+h_y^{2-{\beta }_y}\right).\hfill \end{array}$$

(13)

Let $u_{i,j}^m$ be the numerical approximation to $u(x_i,y_j,t_m)$ and $f_{i,j}^m:=f(x_i,y_j,t_m)$. We replaced $u(x_i,y_j,t_m)$ by $u_{i,j}^m$ in (13), and we dropped the local truncation error term to arrive at the following numerical scheme:

$$\begin{array}{c}{\delta }_{\tau }{u}_{i,j}^m+v_x\left[{\kappa }_x{\delta }_{h_x}^{{\beta }_x,-}+(1-{\kappa }_x){\delta }_{h_x}^{{\beta }_x,+}\right]u_{i,j}^m\hfill \\ {\displaystyle +v_y\left[{\kappa }_y{\delta }_{h_y}^{{\beta }_y,-}+(1-{\kappa }_y){\delta }_{h_y}^{{\beta }_y,+}\right]u_{i,j}^m=f_{i,j}^m.}\hfill \end{array}$$

(14)

2.2. An Explicit Numerical Scheme for stFAE (1)

To derive a numerical scheme for stFAE (1), we simply need to discretize ${\partial }_t^{\alpha }u$ at time step $t_m$ by an $L_1$ discretization as follows:

$$\begin{array}{c}{\displaystyle {\partial }_t^{\alpha }u(x_i,y_j,t_m)}\hfill \\ {\displaystyle =\frac{1}{\Gamma (1-\alpha )}\sum _{k=0}^{m-1}{\int }_{t_k}^{t_{k+1}}\frac{{\partial }_{t}u(x_i,y_j,t)}{{(t_m-t)}^{\alpha }}dt}\hfill \\ {\displaystyle =\frac{1}{\Gamma (1-\alpha )}\sum _{k=0}^{m-1}{\int }_{t_k}^{t_{k+1}}\frac{{\delta }_{\tau }u(x_i,y_j,t_k)}{{(t_m-t)}^{\alpha }}dt+R_{i,j,m}^{t,\alpha }}\hfill \\ {\displaystyle =\frac{1}{\Gamma (2-\alpha ){\tau }^{\alpha }}\sum _{k=0}^{m-1}\left(u(x_i,y_j,t_{k+1})-u(x_i,y_j,t_k)\right){\omega }_{m-k}^{\alpha }+R_{i,j,m}^{t,\alpha }}\hfill \\ {\displaystyle =:{\delta }_{\tau }^{\alpha }u(x_i,y_j,t_m)+R_{i,j,m}^{t,\alpha },}\hfill \end{array}$$

(15)

where the local truncation error $R_{i,j,m}^{t,\alpha }$ can be expressed as

$$\begin{array}{cc}\hfill R_{i,j,m}^{t,\alpha }& {\displaystyle =\frac{1}{\Gamma (1-\alpha )}\sum _{k=0}^{m-1}{\int }_{t_k}^{t_{k+1}}\frac{{\delta }_{\tau }u(x_i,y_j,t_k)-{\partial }_{t}u(x_i,y_j,t)}{{(t_m-t)}^{\alpha }}dt}\hfill \\ \hfill & {\displaystyle =\frac{1}{\Gamma (1-\alpha )\tau }\sum _{k=0}^{m-1}{\int }_{t_k}^{t_{k+1}}\frac{1}{{(t_m-t)}^{\alpha }}{\int }_{t_k}^{t_{k+1}}{\int }_t^s{\partial }_{\theta \theta }u(x_i,y_j,\theta )d\theta dsdt.}\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill & {\delta }_{h_x}^{{\beta }_x,-}{u}_{i,j}^m:=\frac{h_x^{-{\beta }_x}}{\Gamma (2-{\beta }_x)}\left[{\omega }_1^{{\beta }_x}{u}_{i,j}^m-\sum _{k=1}^{i-1}({\omega }_k^{{\beta }_x}-{\omega }_{k+1}^{{\beta }_x})u_{i-k,j}^m-{\omega }_i^{{\beta }_x}{u}_{0,j}^m\right],\hfill \\ \hfill & {\displaystyle {\delta }_{h_x}^{{\beta }_x,+}{u}_{i,j}^m:=\frac{h_x^{-{\beta }_x}}{\Gamma (2-{\beta }_x)}\left[{\omega }_1^{{\beta }_x}{u}_{i,j}^m-\sum _{k=1}^{N_x-i-1}({\omega }_k^{{\beta }_x}-{\omega }_{k+1}^{{\beta }_x})u_{i+k,j}^m-{\omega }_{N_x-i}^{{\beta }_x}{u}_{N_x,j}^m\right],}\hfill \\ \hfill & {\delta }_{h_y}^{{\beta }_y,-}{u}_{i,j}^m:=\frac{h_y^{-{\beta }_y}}{\Gamma (2-{\beta }_y)}\left[{\omega }_1^{{\beta }_y}{u}_{i,j}^m-\sum _{k=1}^{j-1}({\omega }_k^{{\beta }_y}-{\omega }_{k+1}^{{\beta }_y})u_{i,j-k}^m-{\omega }_j^{{\beta }_y}{u}_{i,0}^m\right],\hfill \\ \hfill & {\displaystyle {\delta }_{h_y}^{{\beta }_y,+}{u}_{i,j}^m:=\frac{h_y^{-{\beta }_y}}{\Gamma (2-{\beta }_y)}\left[{\omega }_1^{{\beta }_y}{u}_{i,j}^m-\sum _{k=1}^{N_y-i-1}({\omega }_k^{{\beta }_y}-{\omega }_{k+1}^{{\beta }_y})u_{i,j+k}^m-{\omega }_{N_y-i}^{{\beta }_y}{u}_{i,N_y}^m\right].}\hfill \end{array}$$

(17)

Here, ${\omega }_k^{\beta }:=k^{1-\beta }-{(k-1)}^{1-\beta }$, with $0<\beta <1$ having the following properties:

$$\begin{array}{c}{\displaystyle \left\{\begin{array}{c}{\omega }_k^{\beta }>0,k=1,2,\cdots ,N,\hfill \\ {\displaystyle 1={\omega }_1^{\beta }>{\omega }_2^{\beta }>\cdots >{\omega }_k^{\beta },{\omega }_k^{\beta }\to 0ask\to \infty ,}\hfill \\ {\displaystyle \sum _{k=1}^{i-1}({\omega }_k^{\beta }-{\omega }_{k+1}^{\beta })+{\omega }_i^{\beta }=1.}\hfill \end{array}\right.}\hfill \end{array}$$

(18)

From the above discretization, we can obtain the following EFDM for sFDE (3), which satisfies the bound-preserving principle as follows:

$$\begin{array}{cc}\hfill {\displaystyle u_{i,j}^m=}& {\displaystyle (1-{\lambda }_x-{\lambda }_y)u_{i,j}^{m-1}+{\lambda }_x{\kappa }_x\left[\sum _{k=1}^{i-1}({\omega }_k^{{\beta }_x}-{\omega }_{k+1}^{{\beta }_x})u_{i-k,j}^m+{\omega }_i^{{\beta }_x}{u}_{0,j}^m\right]}\hfill \\ \hfill & {\displaystyle +{\lambda }_x(1-{\kappa }_x)\left[\sum _{k=1}^{N_x-i-1}({\omega }_k^{{\beta }_x}-{\omega }_{k+1}^{{\beta }_x})u_{i+k,j}^m+{\omega }_{N_x-i}^{{\beta }_x}{u}_{N_x,j}^m\right]}\hfill \\ \hfill & {\displaystyle +{\lambda }_y{\kappa }_y\left[\sum _{k=1}^{j-1}({\omega }_k^{{\beta }_y}-{\omega }_{k+1}^{{\beta }_y})u_{i,j-k}^m+{\omega }_j^{{\beta }_y}{u}_{i,0}^m\right]}\hfill \\ \hfill & {\displaystyle +{\lambda }_y(1-{\kappa }_y)\left[\sum _{k=1}^{N_y-i-1}({\omega }_k^{{\beta }_y}-{\omega }_{k+1}^{{\beta }_y})u_{i,j+k}^m+{\omega }_{N_y-i}^{{\beta }_y}{u}_{i,N_y}^m\right]+f_{i,j}^m,}\hfill \end{array}$$

(19)

where ${\lambda }_x=v_x\frac{\tau }{\Gamma (2-{\beta }_x)h_x^{{\beta }_x}}$ and ${\lambda }_y=v_y\frac{\tau }{\Gamma (2-{\beta }_y)h_y^{{\beta }_y}}$.

2.3. Stability and Error Analysis of the EFDM for sFDE

Now, we are in the position to analyze the bound-preserving principle and the error estimate of the EFDM for sFDE (3). We begin with the bound-preserving principle, i.e., if $u_{i,j}^0$ is in the range $[l,L]$, then $u_{i,j}^m\in [l,L].$

Theorem 1.

If all the values of $u_{i,j}^0$ are in the range $[l,L]$, then $u_{i,j}^m\in [l,L]$ for any $i,j,m$ under the Courant–Friedrichs–Lewy (CFL) condition is $0<{\lambda }_x+{\lambda }_y<1$.

Proof. 

The theorem is proved by a mathematical induction. Firstly, when $m=1$, according to the explicit scheme (19), we have

$$\begin{array}{cc}\hfill {\displaystyle u_{i,j}^1=}& {\displaystyle (1-{\lambda }_x-{\lambda }_y)u_{i,j}^0+{\lambda }_x{\kappa }_x\left[\sum _{k=1}^{i-1}({\omega }_k^{{\beta }_x}-{\omega }_{k+1}^{{\beta }_x})u_{i-k,j}^0+{\omega }_i^{{\beta }_x}{u}_{0,j}^0\right]}\hfill \\ \hfill & {\displaystyle +{\lambda }_x(1-{\kappa }_x)\left[\sum _{k=1}^{N_x-i-1}({\omega }_k^{{\beta }_x}-{\omega }_{k+1}^{{\beta }_x})u_{i+k,j}^0+{\omega }_{N_x-i}^{{\beta }_x}{u}_{N_x,j}^0\right]}\hfill \\ \hfill & {\displaystyle +{\lambda }_y{\kappa }_y\left[\sum _{k=1}^{j-1}({\omega }_k^{{\beta }_y}-{\omega }_{k+1}^{{\beta }_y})u_{i,j-k}^0+{\omega }_j^{{\beta }_y}{u}_{i,0}^0\right]}\hfill \\ \hfill & {\displaystyle +{\lambda }_y(1-{\kappa }_y)\left[\sum _{k=1}^{N_y-j-1}({\omega }_k^{{\beta }_y}-{\omega }_{k+1}^{{\beta }_y})u_{i,j+k}^0+{\omega }_{N_y-j}^{{\beta }_y}{u}_{i,N_y}^0\right]}\hfill \\ \hfill {\displaystyle =:}& {\displaystyle \sum _{i=0}^{N_x}\sum _{j=0}^{N_y}{\eta }_{i,j}{u}_{i,j}^0.}\hfill \end{array}$$

(20)

We can conclude that all coefficients ${\eta }_{i,j}\ge 0$ are such using the properties of coefficients ${\omega }_k^{\beta }$ in (18) and the CFL condition [37] $0<{\lambda }_x+{\lambda }_y<1$. Then, we have

$$\begin{array}{cc}\hfill {\displaystyle \sum _{i=0}^{N_x}\sum _{j=0}^{N_y}{\eta }_{i,j}=}& {\displaystyle (1-{\lambda }_x-{\lambda }_y)+{\lambda }_x{\kappa }_x\left[\sum _{k=1}^{i-1}({\omega }_k^{{\beta }_x}-{\omega }_{k+1}^{{\beta }_x})+{\omega }_i^{{\beta }_x}\right]}\hfill \\ \hfill & {\displaystyle +{\lambda }_x(1-{\kappa }_x)\left[\sum _{k=1}^{N_x-i-1}({\omega }_k^{{\beta }_x}-{\omega }_{k+1}^{{\beta }_x})+{\omega }_{N_x-i}^{{\beta }_x}\right]}\hfill \\ \hfill & {\displaystyle +{\lambda }_y{\kappa }_y\left[\sum _{k=1}^{j-1}({\omega }_k^{{\beta }_y}-{\omega }_{k+1}^{{\beta }_y})+{\omega }_j^{{\beta }_y}\right]}\hfill \\ \hfill & {\displaystyle +{\lambda }_y(1-{\kappa }_y)\left[\sum _{k=1}^{N_y-j-1}({\omega }_k^{{\beta }_y}-{\omega }_{k+1}^{{\beta }_y})+{\omega }_{N_y-j}^{{\beta }_y}\right]}\hfill \\ \hfill =& {\displaystyle 1.}\hfill \end{array}$$

(21)

We combined (21) into (20) to bound $u_{i,j}^1$ as follows:

$${\displaystyle \underset{i,j}{min}{u}_{i,j}^0\le u_{i,j}^1=\sum _{i=0}^{N_x}\sum _{j=0}^{N_y}{\eta }_{i,j}{u}_{i,j}^0\le \underset{i,j}{max}{u}_{i,j}^0.}$$

As $u_{i,j}^0\in [l,L]$ for all $i,j$, then we have for all $i,j,$

$$u_{i,j}^1\in [l,L].$$

Secondly, suppose that all the values of $u_{i,j}^{m-1}$ are in the range $[l,L],$ then according to the explicit scheme (19), we have

$$\begin{array}{cc}\hfill {\displaystyle u_{i,j}^m=}& {\displaystyle \sum _{i=0}^{N_x}\sum _{j=0}^{N_y}{\eta }_{i,j}{u}_{i,j}^{m-1}.}\hfill \end{array}$$

The above equation has the same coefficients ${\eta }_{i,j}$ with Equation (20). Hence, we can conclude that $u_{i,j}^m\in [l,L]$ under the CFL condition is $0<{\lambda }_x+{\lambda }_y<1$. □

An error estimate of the explicit finite difference scheme (19) is proved as follows. Let

$$\begin{array}{c}\hfill {\displaystyle e_{i,j}^m:=u_{i,j}^m-u(x_i,y_j,t_m),(x_i,y_j)\in \Omega ,0\le m\le M.}\end{array}$$

(22)

Theorem 2.

Assume $u(x,y,t)\in L^{\infty }(0,T;H^3)$, then there is a constant C that is positive and independent of the mesh parameters $h_x,h_y$ and τ, such that

$${\displaystyle \underset{i,j}{sup}|e_{i,j}^m|\le C(\tau +h_x^{2-{\beta }_x}+h_y^{2-{\beta }_y}),}$$

under the CFL condition $0<{\lambda }_x+{\lambda }_y<1$.

Proof. 

From the truncation errors of the discretization in Equation (16) and the explicit scheme, we determined that the errors $e_{i,j}^m$ satisfy the following formulation:

$$\begin{array}{cc}\hfill & {\displaystyle e_{i,j}^m-e_{i,j}^{m-1}+{\lambda }_x{\kappa }_x\left[{\omega }_1^{{\beta }_x}{e}_{i,j}^{m-1}-\sum _{k=1}^{i-1}({\omega }_k^{{\beta }_x}-{\omega }_{k+1}^{{\beta }_x})e_{i-k,j}^{m-1}-{\omega }_i^{{\beta }_x}{e}_{0,j}^{m-1}\right]}\hfill \\ \hfill & {\displaystyle +{\lambda }_x(1-{\kappa }_x)\left[{\omega }_1^{{\beta }_x}{e}_{i,j}^{m-1}-\sum _{k=1}^{N_x-i-1}({\omega }_k^{{\beta }_x}-{\omega }_{k+1}^{{\beta }_x})e_{i+k,j}^{m-1}-{\omega }_{N_x-i}^{{\beta }_x}{e}_{N_x,j}^{m-1}\right],}\hfill \\ \hfill & {\displaystyle +{\lambda }_y{\kappa }_y\left[{\omega }_1^{{\beta }_y}{e}_{i,j}^{m-1}-\sum _{k=1}^{j-1}({\omega }_k^{{\beta }_y}-{\omega }_{k+1}^{{\beta }_y})e_{i,j-k}^{m-1}-{\omega }_j^{{\beta }_y}{e}_{i,0}^{m-1}\right]}\hfill \\ \hfill & {\displaystyle +{\lambda }_y(1-{\kappa }_y)\left[{\omega }_1^{{\beta }_y}{e}_{i,j}^{m-1}-\sum _{k=1}^{N_y-j-1}({\omega }_k^{{\beta }_y}-{\omega }_{k+1}^{{\beta }_y})e_{i,j+k}^{m-1}-{\omega }_{N_y-j}^{{\beta }_y}{e}_{i,N_y}^{m-1}\right],}\hfill \\ \hfill & =O({\tau }^2+\tau (h_x^{2-{\beta }_x}+h_y^{2-{\beta }_y})),\hfill \end{array}$$

(23)

and all $e_{i,j}^0=0$.

When the CFL condition is $0<{\lambda }_x+{\lambda }_y<1$, according to Theorem 1, we have

$$\begin{array}{ccc}\hfill {\displaystyle |e_{i,j}^m|}& \le \hfill & {\displaystyle (1-{\lambda }_x-{\lambda }_y)|e_{i,j}^{m-1}|+{\lambda }_x{\kappa }_x\sum _{k=1}^{i-1}({\omega }_k^{{\beta }_x}-{\omega }_{k+1}^{{\beta }_x})|e_{i-k,j}^{m-1}|+{\lambda }_x{\kappa }_x{\omega }_i^{{\beta }_x}|e_{0,j}^{m-1}|}\hfill \\ & & {\displaystyle +{\lambda }_x(1-{\kappa }_x)\sum _{k=1}^{N_x-i-1}({\omega }_k^{{\beta }_x}-{\omega }_{k+1}^{{\beta }_x})|e_{i+k,j}^{m-1}|+{\lambda }_x(1-{\kappa }_x){\omega }_{N_x-i}^{{\beta }_x}|e_{N_x,j}^{m-1}|}\hfill \\ & & {\displaystyle +{\lambda }_y{\kappa }_y\sum _{k=1}^{j-1}({\omega }_k^{{\beta }_y}-{\omega }_{k+1}^{{\beta }_y})|e_{i,j-k}^{m-1}|+{\lambda }_y{\kappa }_y{\omega }_j^{{\beta }_y}|e_{i,0}^{m-1}|}\hfill \\ & & {\displaystyle +{\lambda }_y(1-{\kappa }_y)\sum _{k=1}^{N_y-j-1}({\omega }_k^{{\beta }_y}-{\omega }_{k+1}^{{\beta }_y})|e_{i,j+k}^{m-1}|+{\lambda }_y(1-{\kappa }_y){\omega }_{N_y-j}^{{\beta }_y}|e_{i,N_y}^{m-1}|}\hfill \\ & & {\displaystyle +O({\tau }^2+\tau (h_x^{2-{\beta }_x}+h_y^{2-{\beta }_y}))}\hfill \\ & \le \hfill & {\displaystyle \underset{i,j}{sup}|e_{i,j}^{m-1}|+O({\tau }^2+\tau (h_x^{2-{\beta }_x}+h_y^{2-{\beta }_y}))}\hfill \end{array}$$

i.e.,

$$\begin{array}{ccc}\hfill {\displaystyle \underset{i,j}{sup}|e_{i,j}^m|}& \le \hfill & {\displaystyle \underset{i,j}{sup}|e_{i,j}^{m-1}|+O({\tau }^2+\tau (h_x^{2-{\beta }_x}+h_y^{2-{\beta }_y})).}\hfill \end{array}$$

(24)

By induction,

$$\begin{array}{ccc}\hfill {\displaystyle \underset{i,j}{sup}|e_{i,j}^m|}& \le \hfill & {\displaystyle \underset{i,j}{sup}|e_{i,j}^0|+m·O({\tau }^2+\tau (h_x^{2-{\beta }_1}+h_y^{2-{\beta }_2})).}\hfill \end{array}$$

(25)

For $m\le M,$$T=M\tau$, we can easily obtain $m\tau \le T.$

Therefore, ${\displaystyle \underset{i,j}{sup}|e_{i,j}^m|\le C(\tau +h_x^{2-{\beta }_x}+h_y^{2-{\beta }_y})}$ and C is a constant independent of $h_x,h_y$ and $\tau$. □

2.4. A Fast Implementation

We provide a demonstration of the complexity of computation of the fast finite difference method for sFDE (3) in this subsection.

We set

$$\begin{array}{c}{\mathbf{u}}^m={[u_{1,1}^m,\cdots ,u_{N_x,1}^m,u_{1,2}^m,\cdots ,u_{N_x,2}^m,\cdots ,u_{1,N_y}^m,\cdots ,u_{N_x,N_y}^m]}^T,\hfill \\ {\mathbf{f}}^m={[f_{1,1}^m,\cdots ,f_{N_x,1}^m,f_{1,2}^m,\cdots ,f_{N_x,2}^m,\cdots ,f_{1,N_y}^m,\cdots ,f_{N_x,N_y}^m]}^T.\hfill \end{array}$$

From the explicit finite difference scheme of sFDE (3), we can get obtain linear algebraic system

$$\begin{array}{c}\hfill {\displaystyle {\mathbf{u}}^m={\mathbf{u}}^{m-1}+\mathbf{A}{\mathbf{u}}^{m-1}+\tau {\mathbf{f}}^{m-1}.}\end{array}$$

(26)

Here, the stiffness of Matrix $\mathbf{A}$ is expressed by

$$\mathbf{A}=\left(\begin{array}{ccccc}{\mathbf{A}}_0& {\mathbf{A}}_1& \dots & {\mathbf{A}}_{N_y-2}& {\mathbf{A}}_{N_y-1}\\ {\mathbf{A}}_{-1}& {\mathbf{A}}_0& {\mathbf{A}}_1& \ddots & {\mathbf{A}}_{N_y-2}\\ ⋮& \ddots & \ddots & \ddots & ⋮\\ {\mathbf{A}}_{2-N_y}& \ddots & {\mathbf{A}}_{-1}& {\mathbf{A}}_0& {\mathbf{A}}_1\\ {\mathbf{A}}_{1-N_y}& {\mathbf{A}}_{2-N_y}& \dots & {\mathbf{A}}_{-1}& {\mathbf{A}}_0\end{array}\right),$$

(27)

where

$${\mathbf{A}}_0=\left(\begin{array}{ccccc}{a}_0& a_1& \dots & a_{N_x-2}& a_{N_x-1}\\ a_{-1}& a_0& a_1& \ddots & a_{N_x-2}\\ ⋮& \ddots & \ddots & \ddots & ⋮\\ a_{2-N_x}& \ddots & a_{-1}& a_0& a_1\\ a_{1-N_x}& a_{2-N_x}& \dots & a_{-1}& a_0\end{array}\right),$$

$$\begin{array}{ccc}{\mathbf{A}}_s(i,j)\hfill & =b_s\mathbf{E},\hfill & \\ {\mathbf{A}}_{-s}(i,j)\hfill & =b_{-s}\mathbf{E},\hfill & s=1,2,\cdots ,N_y-1.\hfill \end{array}$$

with $\mathbf{E}$ being the $N_x$-by-$N_x$ dimensional unit matrix and

$$\begin{array}{cc}{a}_0=-{\lambda }_x-{\lambda }_y,\hfill & \\ a_{-s}={\lambda }_x{\kappa }_x({\omega }_s^{{\beta }_x}-{\omega }_{s+1}^{{\beta }_x}),\hfill & s=1,2,\cdots ,N_x-1\hfill \\ a_s={\lambda }_x(1-{\kappa }_x)({\omega }_s^{{\beta }_x}-{\omega }_{s+1}^{{\beta }_x}),\hfill & s=1,2,\cdots ,N_x-1\hfill \\ b_{-s}={\lambda }_y{\kappa }_y({\omega }_s^{{\beta }_y}-{\omega }_{s+1}^{{\beta }_y}),\hfill & s=1,2,\cdots ,N_y-1\hfill \\ b_s={\lambda }_y(1-{\kappa }_y)({\omega }_s^{{\beta }_y}-{\omega }_{s+1}^{{\beta }_y}),\hfill & s=1,2,\cdots ,N_y-1.\hfill \end{array}$$

Through studying the structure of the stiffness Matrix $\mathbf{A}$, we found that the stiffness Matrix $\mathbf{A}$ had a block–Toeplitz–Toeplitz–block structure [38,39]. It was proved in [33,34] that, for any vector $\mathbf{u}\in {\mathbb{R}}^N,$ the computational cost of the matrix–vector multiplication $\mathbf{Au}$ has $O(NlogN)$ operations, with $N=N_x{N}_y$ being the spatial points number, which is obtained by embedding $\mathbf{A}$ into a $2N_y$-by-$2N_y$ block–circulant Matrix $\mathbf{C}$ and using a fast Fourier transform (FFT). Combining the linear algebraic system, we can easily obtain the following theorem.

Theorem 3.

The fast EFDM can be carried out in $O(MNlogN)$ operations and has an $O(MN)$ requirement by the fast Fourier transform.

3. A Finite Difference Approximation for stFDE (1)

We constructed an explicit monotone numerical scheme to solve stFDE (1), which satisfied the bound-preserving principle. And the error estimate of the EFDM for the stFDE was analyzed in the maximum-norm form. We also showed that a fast EFDM(FFDM) with the stiffness matrix of the EFDM has a Toeplitz-like structure, and the matrix–vector computation can be carried out by the FFT.

Combining the discretizations (17) with (15), a bound-principle-satisfying EFDM for the stFDE (1) can be given as

$$\begin{array}{ccc}\hfill & \hfill & {\displaystyle u_{i,j}^m=(1-{\lambda }_3-{\lambda }_4-{\omega }_1^{\alpha })u_{i,j}^{m-1}+\sum _{s=2}^{m-1}({\omega }_{s-1}^{\alpha }-{\omega }_s^{\alpha })u_{i,j}^{m-s}+{\omega }_{m-1}^{\alpha }{u}_{i,j}^0}\hfill \\ \hfill & \hfill & {\displaystyle +{\lambda }_3{\kappa }_x\left[\sum _{k=1}^{i-1}({\omega }_{k-1}^{{\beta }_x}-{\omega }_k^{{\beta }_x})u_{i-k,j}^{m-1}+{\omega }_{i-1}^{{\beta }_x}{u}_{0,j}^{m-1}\right]}\hfill \\ \hfill & \hfill & {\displaystyle +{\lambda }_3(1-{\kappa }_x)\left[\sum _{k=1}^{N_x-i-1}({\omega }_{k-1}^{{\beta }_x}-{\omega }_k^{{\beta }_x})u_{i+k,j}^{m-1}+{\omega }_{N_x-i-1}^{{\beta }_x}{u}_{N_x,j}^{m-1}\right]}\hfill \\ \hfill & \hfill & {\displaystyle +{\lambda }_4{\kappa }_y\left[\sum _{k=1}^{j-1}({\omega }_{k-1}^{{\beta }_y}-{\omega }_k^{{\beta }_x})u_{i,j-k}^{m-1}+{\omega }_{j-1}^{{\beta }_y}{u}_{i,0}^{m-1}\right]}\hfill \\ \hfill & \hfill & {\displaystyle +{\lambda }_4(1-{\kappa }_y)\left[\sum _{k=1}^{N_y-j-1}({\omega }_{k-1}^{{\beta }_y}-{\omega }_k^{{\beta }_y})u_{i,j+k}^{m-1}+{\omega }_{N_y-j-1}^{{\beta }_y}{u}_{i,N_y}^{m-1}\right]+f_{i,j}^m,}\hfill \end{array}$$

(28)

Here ${\lambda }_3=v_x\frac{\Gamma (2-\alpha ){\tau }^{\alpha }}{\Gamma (2-{\beta }_x)h_x^{{\beta }_x}}$ and ${\lambda }_4=v_y\frac{\Gamma (2-\alpha ){\tau }^{\alpha }}{\Gamma (2-{\beta }_y)h_y^{{\beta }_y}}$.

3.1. Error Analysis and Stability of the EFDM for stFDE

We analyze the bound-preserving principle and the error estimate of the explicit finite difference scheme for stFDE (1) in this subsection. We begin with the bound-preserving principle.

Theorem 4.

If the initial values $u_{i,j}^0$ are in the range $[l,L]$, then $u_{i,j}^m\in [l,L]$ for any $i,j,m$ under the CFL condition is $0<{\lambda }_3+{\lambda }_4<1-{\omega }_2^{\alpha }$.

Proof. 

The theorem is proved by mathematical induction. Firstly, the EFDM (28) of stFDE (1) can be formulated as

$$\begin{array}{cc}\hfill {\displaystyle u_{i,j}^1=}& {\displaystyle (1-{\lambda }_3-{\lambda }_4)u_{i,j}^0+{\lambda }_3{\kappa }_x\left[\sum _{k=1}^{i-1}({\omega }_k^{{\beta }_x}-{\omega }_{k+1}^{{\beta }_x})u_{i-k,j}^0+{\omega }_i^{{\beta }_x}{u}_{0,j}^0\right]}\hfill \\ \hfill & {\displaystyle +{\lambda }_3(1-{\kappa }_x)\left[\sum _{k=1}^{N_x-i-1}({\omega }_k^{{\beta }_x}-{\omega }_{k+1}^{{\beta }_x})u_{i+k,j}^0+{\omega }_{N_x-i}^{{\beta }_x}{u}_{N_x,j}^0\right],}\hfill \\ \hfill & {\displaystyle +{\lambda }_4{\kappa }_y\left[\sum _{k=1}^{j-1}({\omega }_k^{{\beta }_y}-{\omega }_{k+1}^{{\beta }_y})u_{i,j-k}^0+{\omega }_j^{{\beta }_y}{u}_{i,0}^0\right]}\hfill \\ \hfill & {\displaystyle +{\lambda }_4(1-{\kappa }_y)\left[\sum _{k=1}^{N_y-j-1}({\omega }_k^{{\beta }_y}-{\omega }_{k+1}^{{\beta }_y})u_{i,j+k}^0+{\omega }_{N_y-j}^{{\beta }_y}{u}_{i,N_y}^0\right],}\hfill \end{array}$$

(29)

This formulation is similar with (20) in Theorem 1, where ${\lambda }_x$ and ${\lambda }_y$ are replaced by ${\lambda }_3$ and ${\lambda }_4,$ respectively. According to Theorem 1, we can obtain all of the $u_{i,j}^1\in [l,L]$ if all the initial values $u_{i,j}^0$ are in the range of $[l,L]$.

Now, if we suppose that $u_{i,j}^{m-1}\in [l,L]$ and all the values at each time steps are in the range $[l,L]$, then we need prove $u_{i,j}^m\in [l,L]$ for Scheme (28).

$$\begin{array}{cc}\hfill {\displaystyle u_{i,j}^m=}& {\displaystyle (1-{\omega }_2^{\alpha }-{\lambda }_3-{\lambda }_4)u_{i,j}^{m-1}+\sum _{s=2}^{m-1}({\omega }_s^{\alpha }-{\omega }_{s+1}^{\alpha })u_{i,j}^{m-s}+{\omega }_m^{\alpha }{u}_{i,j}^0}\hfill \\ \hfill & +{\lambda }_3{\kappa }_x({\omega }_1^{{\beta }_x}-{\omega }_2^{{\beta }_x})u_{i-1,j}^{m-1}+\cdots +{\lambda }_3{\kappa }_x{\omega }_i^{{\beta }_x}{u}_{0,j}^{m-1}\hfill \\ \hfill & +{\lambda }_3(1-{\kappa }_x)({\omega }_1^{{\beta }_x}-{\omega }_2^{{\beta }_x})u_{i+1,j}^{m-1}+\cdots +{\lambda }_3(1-{\kappa }_x){\omega }_{N_x-i}^{{\beta }_x}{u}_{N_x,j}^{m-1}\hfill \\ \hfill & +{\lambda }_4{\kappa }_y({\omega }_1^{{\beta }_y}-{\omega }_2^{{\beta }_y})u_{i,j-1}^{m-1}++\cdots +{\lambda }_4{\kappa }_y{\omega }_j^{{\beta }_y}{u}_{i,0}^{m-1}\hfill \\ \hfill & +{\lambda }_4(1-{\kappa }_y)({\omega }_1^{{\beta }_y}-{\omega }_2^{{\beta }_y})u_{i,j+1}^{m-1}+\cdots +{\lambda }_4(1-{\kappa }_y){\omega }_{N_y-i}^{{\beta }_y}{u}_{i,N_y}^{m-1}.\hfill \\ \hfill =& {\displaystyle \sum _{k=0}^{N_x}\sum _{n=0}^{N_y}{\eta }_{k,n}{u}_{k,n}^{m-1}+\sum _{s=0}^{m-2}{\xi }_s{u}_{i,j}^s.}\hfill \end{array}$$

(30)

According to the CFL condition and the properties of the coefficients ${\omega }_k^{\beta }$, we can obtain all the coefficients ${\eta }_{k,l}\ge 0$ and ${\xi }_s\ge 0$; as such, we can only analyze the coefficients. From Equation (18), we have

$$\begin{array}{cc}\hfill {\displaystyle \sum _{k=0}^{N_x}\sum _{n=0}^{N_y}{\eta }_{k,n}=}& {\displaystyle (1-{\omega }_2^{\alpha }-{\lambda }_3-{\lambda }_4)+{\lambda }_3{\kappa }_x\left[\sum _{k=0}^{i-1}({\omega }_k^{{\beta }_x}-{\omega }_{k+1}^{{\beta }_x})+{\omega }_{i-1}^{{\beta }_x}\right]}\hfill \\ & {\displaystyle +{\lambda }_3(1-{\kappa }_x)\left[\sum _{k=0}^{N_x-i}({\omega }_{k-1}^{{\beta }_x}-{\omega }_k^{{\beta }_x})+{\omega }_{N_x-i}^{{\beta }_x}\right]}\hfill \\ & +{\lambda }_4{\kappa }_y\left[{\displaystyle \sum _{k=0}^{i-1}}({\omega }_{k-1}^{{\beta }_y}-{\omega }_k^{{\beta }_y})+{\omega }_{i-1}^{{\beta }_y}\right]\hfill \\ & {\displaystyle +{\lambda }_4(1-{\kappa }_y)\left[\sum _{k=0}^{N_y-j}({\omega }_{k-1}^{{\beta }_y}-{\omega }_k^{{\beta }_y})+{\omega }_{N_y-j}^{{\beta }_y}\right]}\hfill \\ \hfill =& {\displaystyle (1-{\omega }_2^{\alpha }-{\lambda }_3-{\lambda }_4)+{\lambda }_3{\kappa }_x+{\lambda }_3(1-{\kappa }_x)+{\lambda }_4{\kappa }_y+{\lambda }_4(1-{\kappa }_y)}\hfill \\ \hfill =& {\displaystyle 1-{\omega }_2^{\alpha },}\hfill \\ \hfill {\displaystyle {\displaystyle \sum _{s=0}^{m-2}}{\xi }_s=}& {\displaystyle \sum _{s=2}^{m-1}}({\omega }_s^{\alpha }-{\omega }_{s+1}^{\alpha })+{\omega }_m^{\alpha }={\omega }_2^{\alpha }.\hfill \end{array}$$

Hence, ${\displaystyle \sum _{k=0}^{N_x}\sum _{l=0}^{N_y}{\eta }_{k,l}+\sum _{s=0}^{m-2}{\xi }_s=1}$ is a convex combination and has

$${\displaystyle l\le \sum _{k=0}^{N_x}\sum _{l=0}^{N_y}{\eta }_{k,l}{u}_{k,l}^{m-1}+\sum _{s=0}^{m-2}{\xi }_s{u}_{i,j}^s\le L.}$$

Thus, the $u_{i,j}^m\in [l,L]$ under the CFL condition is $0<{\lambda }_3+{\lambda }_4<1-{\omega }_2^{\alpha }$. □

Next, we analyzed the error estimate of the EFDM for stFDE (2). The error $e_{i,j}^m$ was defined in the same way as in Section 2.

Theorem 5.

If we assume $u(x,y,t)\in L^{\infty }(0,T;H^2)$, then there is a positive constant C, which is independent of the mesh parameters $h_x,h_y$ and τ, such that

$${\displaystyle \underset{i,j}{sup}|e_{i,j}^m|\le C({\tau }^{2-\alpha }+h_x^{2-{\beta }_x}+h_y^{2-{\beta }_y})}$$

under the CFL condition is $0<{\lambda }_3+{\lambda }_4<1-{\omega }_2^{\alpha }$.

Proof. 

The error $e_{i,j}^m$ satisfies the following error equation:

$$\begin{array}{cc}\hfill {\displaystyle e_{i,j}^m}& {\displaystyle =(1-{\lambda }_3-{\lambda }_4-{\omega }_2^{\alpha })e_{i,j}^{m-1}+\sum _{s=2}^{m-1}({\omega }_s^{\alpha }-{\omega }_{s+1}^{\alpha })e_{i,j}^{m-s}+{\omega }_{m-1}^{\alpha }{e}_{i,j}^0}\hfill \\ \hfill & {\displaystyle +{\lambda }_3{\kappa }_x\left[\sum _{k=1}^{i-1}({\omega }_k^{{\beta }_x}-{\omega }_{k+1}^{{\beta }_x})e_{i-k,j}^{m-1}+{\omega }_i^{{\beta }_x}{e}_{0,j}^{m-1}\right]}\hfill \\ \hfill & {\displaystyle +{\lambda }_3(1-{\kappa }_x)\left[\sum _{k=1}^{N_x-i}({\omega }_k^{{\beta }_x}-{\omega }_{k+1}^{{\beta }_x})e_{i+k,j}^{m-1}+{\omega }_{N_x-i}^{{\beta }_x}{e}_{N_x,j}^{m-1}\right],}\hfill \\ \hfill & {\displaystyle +{\lambda }_4{\kappa }_y\left[\sum _{k=1}^{j-1}({\omega }_k^{{\beta }_y}-{\omega }_{k+1}^{{\beta }_y})e_{i,j-k}^{m-1}+{\omega }_j^{{\beta }_y}{e}_{i,0}^{m-1}\right]}\hfill \\ \hfill & {\displaystyle -{\lambda }_4(1-{\kappa }_y)\left[\sum _{k=1}^{N_y-j-1}({\omega }_k^{{\beta }_y}-{\omega }_{k+1}^{{\beta }_y})e_{i,j+k}^{m-1}+{\omega }_{N_y-j}^{{\beta }_y}{e}_{i,N_y}^{m-1}\right],}\hfill \\ \hfill & +\Gamma (2-\alpha )\Delta t^{\alpha }O(\Delta t^{2-\alpha }+\Delta t(h_x^{2-{\beta }_x}+h_y^{2-{\beta }_y})),\hfill \end{array}$$

(31)

where all $e_{i,j}^0=0$.

Firstly, when $m=1$, the above error equation can be formulated as follows:

$$\begin{array}{cc}\hfill e_{i,j}^1=& {\displaystyle (1-{\lambda }_3-{\lambda }_4-{\omega }_2^{\alpha })e_{i,j}^0+{\lambda }_3{\kappa }_x\left[\sum _{k=1}^{i-1}({\omega }_k^{{\beta }_x}-{\omega }_{k+1}^{{\beta }_x})e_{i-k,j}^0+{\omega }_i^{{\beta }_x}{e}_{0,j}^0\right]}\hfill \\ & {\displaystyle +{\lambda }_3(1-{\kappa }_x)\left[\sum _{k=1}^{N_x-i-1}({\omega }_k^{{\beta }_x}-{\omega }_{k+1}^{{\beta }_x})e_{i+k,j}^0+{\omega }_{N_x-i}^{{\beta }_x}{e}_{N_x,j}^0\right],}\hfill \\ & {\displaystyle +{\lambda }_4{\kappa }_y\left[\sum _{k=1}^{j-1}({\omega }_k^{{\beta }_y}-{\omega }_{k+1}^{{\beta }_y})e_{i,j-k}^0+{\omega }_j^{{\beta }_y}{e}_{i,0}^0\right]}\hfill \\ & {\displaystyle +{\lambda }_4(1-{\kappa }_y)\left[\sum _{k=1}^{N_y-j-1}({\omega }_k^{{\beta }_y}-{\omega }_{k+1}^{{\beta }_y})e_{i,j+k}^0+{\omega }_{N_y-j}^{{\beta }_y}{e}_{i,N_y}^0\right]}\hfill \\ & {\displaystyle +\Gamma (2-\alpha )\Delta t^{\alpha }O(\Delta t^{2-\alpha }+h_x^{2-{\beta }_x}+h_y^{2-{\beta }_y}).}\hfill \end{array}$$

The above formulation is similar to (20) in Theorem 1, with ${\lambda }_x$ and ${\lambda }_y$ being replaced by ${\lambda }_3$ and ${\lambda }_4,$ respectively. According to (18), all of the coefficients of errors are positive and the sum of all the coefficients is 1; thus, we can obtain

$$\begin{array}{ccc}\hfill {\displaystyle \underset{i,j}{sup}|e_{i,j}^1|}& \le \hfill & {\displaystyle \underset{i,j}{sup}|e_{i,j}^0|+\Gamma (2-\alpha )\Delta t^{\alpha }O(\Delta t^{2-\alpha }+h_x^{2-{\beta }_x}+h_y^{2-{\beta }_y})}\hfill \\ \hfill & \le \hfill & {\displaystyle \underset{i,j}{sup}|e_{i,j}^0|+\Gamma (1-\alpha )t_1^{\alpha }O(\Delta t^{2-\alpha }+h_x^{2-{\beta }_x}+h_y^{2-{\beta }_y}).}\hfill \end{array}$$

(32)

Secondly, suppose that, for all $s\le m-1,$ the error $e_i^s$ satisfies the following formulation:

$$\begin{array}{ccc}\hfill {\displaystyle \underset{i,j}{sup}|e_{i,j}^s|}& \le \hfill & {\displaystyle \underset{i,j}{sup}|e_{i,j}^0|+\Gamma (1-\alpha )t_1^{\alpha }O(\Delta t^{2-\alpha }+h_x^{2-{\beta }_x}+h_y^{2-{\beta }_y}).}\hfill \end{array}$$

(33)

Next, we proved that the error estimate holds when $s=m.$ Furthermore, if we note that the coefficients ${\displaystyle {\omega }_{k+1}^{\alpha }=(1-\alpha ){\int }_k^{k+1}{x}^{-\alpha }dx}$ and $x^{-\alpha }$ monotonically decrease for $x>0$, then

$$(1-\alpha ){(k+1)}^{-\alpha }<{\omega }_{k+1}^{\alpha }<(1-\alpha )k^{-\alpha }.$$

(34)

We can observe that the coefficients of errors are positive and the sum of all the coefficients is 1 from (18) and

$$\begin{array}{ccc}\hfill {\displaystyle |e_{i,j}^m|}& \le \hfill & {\displaystyle (1-{\omega }_1^{\alpha })\underset{i,j}{sup}|e_{i,j}^{m-1}|+\sum _{s=1}^{m-1}({\omega }_s^{\alpha }-{\omega }_{s+1}^{\alpha })\underset{i,j}{sup}|e_{i,j}^{m-s}|+{\omega }_{m-1}^{\alpha }\underset{i,j}{sup}|e_{i,j}^0|}\hfill \\ & & {\displaystyle +\Gamma (2-\alpha )\Delta t^{\alpha }O(\Delta t^{2-\alpha }+h_x^{2-{\beta }_x}+h_y^{2-{\beta }_y}).}\hfill \end{array}$$

With the supposed Equation (33) and Equation (18), we can obtain

$$\begin{array}{ccc}\hfill {\displaystyle \underset{i,j}{sup}|e_{i,j}^m|}& \le \hfill & {\displaystyle \underset{i,j}{sup}|e_{i,j}^0|+\Gamma (2-\alpha )\Delta t^{\alpha }O(\Delta t^{2-\alpha }+h_x^{2-{\beta }_x}+h_y^{2-{\beta }_y})}\hfill \\ \hfill & \hfill & {\displaystyle +\sum _{s=1}^{m-1}({\omega }_s^{\alpha }-{\omega }_{s+1}^{\alpha })\Gamma (1-\alpha )t_{m-s}^{\alpha }O(\Delta t^{2-\alpha }+h_x^{2-{\beta }_x}+h_y^{2-{\beta }_y}).}\hfill \end{array}$$

(35)

For the coefficients ${\omega }_{m-1}^{\alpha }$ that satisfy $(1-\alpha )m^{-\alpha }<{\omega }_{m-1}^{\alpha }$ and the time nodes $t_n^{\alpha }<t_m^{\alpha },n<m$, we obtain the result

$$\begin{array}{ccc}\hfill {\displaystyle \underset{i,j}{sup}|e_{i,j}^m|}& \le \hfill & {\displaystyle \underset{i,j}{sup}|e_{i,j}^0|+{\omega }_{m-1}^{\alpha }\Gamma (1-\alpha )t_m^{\alpha }O(\Delta t^{2-\alpha }+h_x^{2-{\beta }_x}+h_y^{2-{\beta }_y})}\hfill \\ & & {\displaystyle +\sum _{s=1}^{m-1}({\omega }_{s-1}^{\alpha }-{\omega }_s^{\alpha })\Gamma (1-\alpha )t_{m-s}^{\alpha }O(\Delta t^{2-\alpha }+h_x^{2-{\beta }_x}+h_y^{2-{\beta }_y})}\hfill \\ & \le \hfill & {\displaystyle \underset{i,j}{sup}|e_{i,j}^0|+\Gamma (1-\alpha )t_m^{\alpha }O(\Delta t^{2-\alpha }+h_x^{2-{\beta }_x}+h_y^{2-{\beta }_y}).}\hfill \end{array}$$

That is

$${\displaystyle \underset{i,j}{sup}|e_{i,j}^m|\le C(\Delta t^{2-\alpha }+h_x^{2-{\beta }_x}+h_y^{2-{\beta }_y})}$$

and C are constant independent of $h_x,h_y$ and $\tau$. □

3.2. A Fast-Evaluation-in-Time Implementation

Analogous to Section 2.4 and the EFDM for stFDE (1), we can rewrite the EFDM for stFDE into the matrix from the following:

$$\begin{array}{cc}\hfill {\displaystyle {\mathbf{u}}^m=}& {\displaystyle (1-{\omega }_2^{\alpha }){\mathbf{u}}^{m-1}+\sum _{s=2}^{m-1}({\omega }_s^{\alpha }-{\omega }_{s+1}^{\alpha }){\mathbf{u}}^{m-s}+{\omega }_m^{\alpha }{\mathbf{u}}^0+\mathbf{A}{\mathbf{u}}^{m-1}}\hfill \\ \hfill & {\displaystyle +{\tau }^{\alpha }\Gamma (2-\alpha ){\mathbf{f}}^{m-1}.}\hfill \end{array}$$

(36)

The stiffness Matrix $\mathbf{A}$ is identified with $\mathbf{A}$ in Section 2.4—where ${\lambda }_x$ and ${\lambda }_y$ are replaced by ${\lambda }_3$ and ${\lambda }_4$, respectively—such that the matrix–vector multiplication can be carried out in $O(NlogN)$ computation by FFT. Furthermore, we used the fast method in time developed in [40] to approximate the RHS of (36).

To obtain the definition of the time fractional derivative ${\partial }_t^{\alpha }u(x,y,t_m)$ at time step $t_m$, we decomposed the integrating range $(0,t_m)$ into the two integrating ranges of $(t_{m-1},t_m)$ and $(0,t_{m-1}).$ We evaluated the integral on the first range by the standard $L^1$ approximation and approximated the second term via integration by parts as follows:

$${\int }_0^{t_{m-1}}\frac{\partial u(x,y,s)}{\partial s}{(t_m-s)}^{-\alpha }ds=\frac{u(x,y,t_{m-1})}{{\tau }^{\alpha }}-\frac{u_0}{t_m^{\alpha }}-\alpha {\int }_0^{t_{m-1}}\frac{u(x,y,s)}{{(t_m-s)}^{\alpha +1}}ds.$$

We can find that the integral on the RHS can be approximated by the following recursive relation:

$$\begin{array}{c}{\displaystyle \sum _{k=1}^{M_{exp}}{w}_k{U}_{hist,k}(x_i,y_j,t_m)}\hfill \\ {\displaystyle \approx \sum _{k=1}^{M_{exp}}{w}_k\{e^{-s_k\tau }{U}_{hist,k}(x_i,y_j,t_{m-1})+\frac{e^{s_k\tau }}{s_k^2\tau }[\left(e^{-s_k\tau }-1+s_k\tau \right)u(x_i,y_j,t_{m-1})}\hfill \\ {\displaystyle +\left(1-e^{-s_k\tau }(1+s_k\tau )\right)u(x_i,y_j,t_{m-2})\left]\right\}.}\hfill \end{array}$$

Here, ${\left\{s_k\right\}}_{k=1}^{M_{exp}}$ and ${\left\{w_k\right\}}_{k=1}^{M_{exp}}$ are positive.

A fast-evaluation-in-time EFDM(TFFDM) is formulated as follows:

$$\begin{array}{cc}{\displaystyle {\mathbf{u}}^m}\hfill & =\mathbf{A}{\mathbf{u}}^{m-1}+\Gamma (2-\alpha ){\tau }^{\alpha }{\mathbf{f}}^m+\alpha {\mathbf{u}}^{m-1}+(1-\alpha ){\tau }^{\alpha }{\mathbf{u}}^0\hfill \\ {\displaystyle }\hfill & +\alpha (1-\alpha ){\tau }^{\alpha }{\displaystyle \sum _{k=1}^{M_{exp}}}\left(a_k{\mathbf{U}}_{hist,k}^{m-1}+b_k{\mathbf{u}}^{m-1}+c_k{\mathbf{u}}^{m-2}\right),\hfill \end{array}$$

(37)

with

$$\begin{array}{c}{a}_k:=w_k{e}^{-s_k\tau },\hfill \\ b_k:=w_{k}f{e}^{s_k\tau }{s}_k^2\tau (e^{-s_k\tau }-1+s_k\tau ),\hfill \\ c_k:=w_k\frac{e^{s_k\tau }}{s_k^2\tau }(1-e^{-s_k\tau }(1+s_k\tau )),\hfill \\ {\mathbf{U}}_{hist,k}^{m-1}:={\mathbf{U}}_{hist,k}(·,t_{m-1}).\hfill \end{array}$$

(38)

Theorem 6.

The TFFDM requires a memory of $O(NlogM)$ and costs a complexity of computation $O(MNlog(MN))$.

The detail proof can be find in [40], so we will not reiterate it here.

4. Numerical Experiments

We provide some numerical examples to illustrate the performance of the finite difference method in this section. We will also investigate the fast algorithm, which significantly reduces the computational complexity of the numerical method from $O(M{N}^2+M^{2}N)$ to $O(MNlog(MN))$ when compared with the traditional algorithm for the finite difference method. Furthermore, the TFFDM was found to reduce the memory requirement from $O(M{N}^2)$ to $O(NlogM)$.

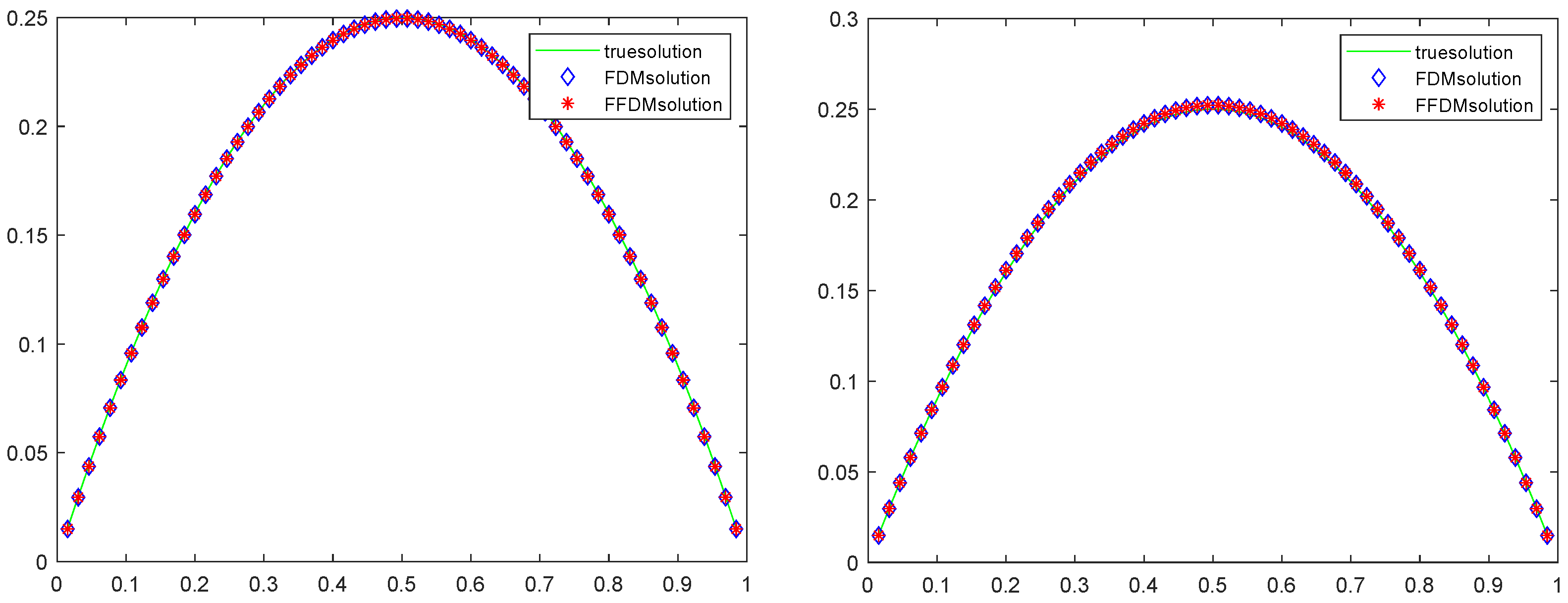
4.1. The Convergence and Performance of Both Methods

We considered the problems in Equations (3) and (1) with the spacial fractional order ${\beta }_x={\beta }_y=\beta$ and $\kappa =0.5$, as well as the diffusion coefficient $v_x=v_y=0.5.$ The spatial domain was $\Omega =(0,1)\times (0,1)$ and the time interval was $[0,T]=[0,1]$. The true solution was chosen to be $u(x,y,t)=t^2{x}^2{(1-x)}^2{y}^2{(1-y)}^2.$ The source term f, the initial condition $u_0$ and the boundary data could be computed accordingly. For convenience, we chose $N_x=N_y$, such that $h:=h_x=h_y$. The convergence rates $r_t$ and $r_s$ were measured such that

$$\parallel u-u_h{\parallel }_{L_{\infty }(0,T;L_2(\Omega ))}\le C({\tau }^{r_t}+h^{r_s}).$$

We present the results of both the FDM and FFDM for the sFDE in

Table 1. Results and convergence rates of $r_t$ for (3), with ${\beta }_x={\beta }_y=0.5$ and $N_x=N_y=2^8$.

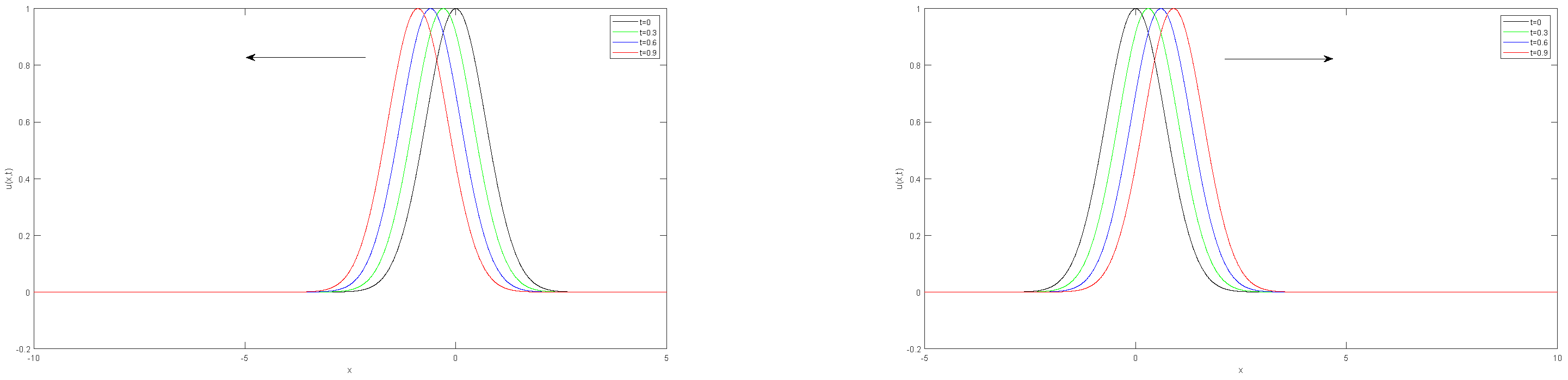
M	FDM			FFDM
	${\mathit{L}}^{\mathbf{2}}$ Error	${\mathit{r}}_{\mathit{t}}$	CPU Time	${\mathit{L}}^{\mathbf{2}}$ Error	${\mathit{r}}_{\mathit{t}}$	CPU Time
$2^4$	0.0021	-	14.25 s	0.0021	-	8.78 s
$2^5$	0.0010	1.0704	3 min 52 s	0.0010	1.0704	17.05 s
$2^6$	5.2135 $\times {10}^{-4}$	0.9397	10 min 27 s	5.2135 $\times {10}^{-4}$	0.9397	33.63 s
$2^7$	-	-	Out of memory	2.6067 $\times {10}^{-4}$	1.0000	66.67 s
$2^8$	-	-	Out of memory	1.3033 $\times {10}^{-4}$	1.0001	2 min 14 s

,

Table 2. Results and convergence rates $r_s$ for (3) with $M=2^{12}$.

${\mathit{\beta }}_{\mathit{x}}={\mathit{\beta }}_{\mathit{y}}$	${\mathit{N}}_{\mathit{x}}={\mathit{N}}_{\mathit{y}}$	FDM		FFDM
		${\mathit{L}}^{\mathbf{2}}$-Error	${\mathit{r}}_{\mathit{s}}$	${\mathit{L}}^{\mathbf{2}}$ -Error	${\mathit{r}}_{\mathit{s}}$
$0.3$	$2^3$	2.3313 $\times {10}^{-4}$	-	2.3313 $\times {10}^{-4}$	-
	$2^4$	7.9127 $\times {10}^{-5}$	1.5589	7.9127 $\times {10}^{-5}$	1.5589
	$2^5$	2.0332 $\times {10}^{-5}$	1.9604	2.0332 $\times {10}^{-5}$	1.9604
	$2^6$	3.1985 $\times {10}^{-6}$	2.6683	3.1985 $\times {10}^{-6}$	2.6683
$0.5$	$2^3$	6.6565 $\times {10}^{-4}$	-	6.6565 $\times {10}^{-4}$	-
	$2^4$	2.6633 $\times {10}^{-4}$	1.3215	2.6633 $\times {10}^{-4}$	1.3215
	$2^5$	9.5791 $\times {10}^{-5}$	1.4753	9.5791 $\times {10}^{-5}$	1.4753
	$2^6$	2.8968 $\times {10}^{-5}$	1.7254	2.8968 $\times {10}^{-5}$	1.7254
	$2^7$	4.9270 $\times {10}^{-6}$	2.5557	4.9270 $\times {10}^{-6}$	2.5557
$0.7$	$2^3$	0.0016	-	0.0016	-
	$2^4$	7.3537 $\times {10}^{-4}$	1.1215	7.3537 $\times {10}^{-4}$	1.1215
	$2^5$	3.1433 $\times {10}^{-4}$	1.2262	3.1433 $\times {10}^{-4}$	1.2262
	$2^6$	1.2657 $\times {10}^{-4}$	1.3123	1.2657 $\times {10}^{-4}$	1.3123
	$2^7$	4.6550 $\times {10}^{-5}$	1.4431	4.6550 $\times {10}^{-5}$	1.4431

and

Table 3. Results and CPU times for (3) with ${\beta }_x={\beta }_y=0.5$.($M=N_x=N_y$).

M	FDM			FFDM
	${\mathit{L}}^{\mathbf{2}}$ Error	Rate	CPU Time	${\mathit{L}}^{\mathbf{2}}$ Error	Rate	CPU Time
$2^5$	0.0013	-	1.43 s	0.0013	-	1.35 s
$2^6$	6.7777 $\times {10}^{-4}$	0.9392	15.0 s	6.7777 $\times {10}^{-4}$	0.9392	10.6 s
$2^7$	3.4326 $\times {10}^{-4}$	0.9820	4 min 38 s	3.4326 $\times {10}^{-4}$	0.9820	1 min 53 s
$2^8$	-	-	Out of memory	1.7335 $\times {10}^{-4}$	0.9856	10 min 56 s
$2^9$	-	-	Out of memory	8.7323 $\times {10}^{-5}$	0.9893	1 h 33 min 49 s
$2^{10}$	-	-	Out of memory	4.3901 $\times {10}^{-5}$	0.9921	12 h 51 min 6 s

and the stFDE in

Table 4. Results and convergence rates $r_t$ for (1) with ${\beta }_x={\beta }_y=0.5$ and $N_x=N_y=2^8$.

$\mathit{\alpha }$	M	FDM		FFDM
		${\mathit{L}}^{\mathbf{2}}$ Error	${\mathit{r}}_{\mathit{t}}$	${\mathit{L}}^{\mathbf{2}}$ Error	${\mathit{r}}_{\mathit{t}}$
0.3	$2^3$	2.7251 $\times {10}^{-4}$	-	2.7251 $\times {10}^{-4}$	-
	$2^4$	9.1584 $\times {10}^{-5}$	1.5669	9.1584 $\times {10}^{-5}$	1.5669
	$2^5$	3.0983 $\times {10}^{-5}$	1.5699	3.0983 $\times {10}^{-5}$	1.5699
	$2^6$	1.0531 $\times {10}^{-5}$	1.5568	1.0531 $\times {10}^{-5}$	1.5568
	$2^7$	3.6480 $\times {10}^{-6}$	1.5295	3.6480 $\times {10}^{-6}$	1.5295
0.5	$2^3$	6.9408 $\times {10}^{-4}$	-	6.9408 $\times {10}^{-4}$	-
	$2^4$	2.5789 $\times {10}^{-4}$	1.4283	2.5789 $\times {10}^{-4}$	1.4283
	$2^5$	9.4645 $\times {10}^{-5}$	1.4462	9.4645 $\times {10}^{-5}$	1.4462
	$2^6$	3.4528 $\times {10}^{-5}$	1.4548	3.4528 $\times {10}^{-5}$	1.4548
	$2^7$	1.2575 $\times {10}^{-5}$	1.4572	1.2575 $\times {10}^{-5}$	1.4572
0.7	$2^3$	0.0015	-	0.00154	-
	$2^4$	6.3110 $\times {10}^{-4}$	1.2490	6.3110 $\times {10}^{-4}$	1.2490
	$2^5$	2.6111 $\times {10}^{-4}$	1.2732	2.6111 $\times {10}^{-4}$	1.2732
	$2^6$	1.0735 $\times {10}^{-4}$	1.2823	1.0735 $\times {10}^{-4}$	1.2823
	$2^7$	4.3973 $\times {10}^{-5}$	1.2876	4.3973 $\times {10}^{-5}$	1.2876

,

Table 5. Results and convergence rates $r_s$ for (1) with $\alpha =0.5$ and $M=2^{12}$.

${\mathit{\beta }}_{\mathit{x}}={\mathit{\beta }}_{\mathit{y}}$	${\mathit{N}}_{\mathit{x}}={\mathit{N}}_{\mathit{y}}$	FDM		FFDM
		${\mathit{L}}^{\mathbf{2}}$-Error	${\mathit{r}}_{\mathit{s}}$	${\mathit{L}}^{\mathbf{2}}$-Error	${\mathit{r}}_{\mathit{s}}$
$0.3$	$2^3$	3.4169 $\times {10}^{-4}$	-	3.4169 $\times {10}^{-4}$	-
	$2^4$	1.2196 $\times {10}^{-4}$	1.4863	1.2196 $\times {10}^{-4}$	1.4863
	$2^5$	3.7410 $\times {10}^{-5}$	1.7049	3.7410 $\times {10}^{-5}$	1.7049
	$2^6$	7.9030 $\times {10}^{-6}$	2.2430	7.9030 $\times {10}^{-6}$	2.2430
$0.5$	$2^3$	9.6137 $\times {10}^{-4}$	-	9.6137 $\times {10}^{-4}$	-
	$2^4$	3.9324 $\times {10}^{-4}$	1.2897	3.9324 $\times {10}^{-4}$	1.2897
	$2^5$	1.4755 $\times {10}^{-4}$	1.4142	1.4755 $\times {10}^{-4}$	1.4142
	$2^6$	5.0551 $\times {10}^{-5}$	1.5454	5.0551 $\times {10}^{-5}$	1.5454
$0.7$	$2^3$	0.0023	-	0.0023	-
	$2^4$	0.0011	1.0641	0.0011	1.0641
	$2^5$	4.7942 $\times {10}^{-4}$	1.1981	4.7942 $\times {10}^{-4}$	1.1981
	$2^6$	1.9961 $\times {10}^{-4}$	1.2641	1.9961 $\times {10}^{-4}$	1.2641

and

Table 6. Results and CPU times for (1) with ${\beta }_x={\beta }_y=0.5$ ($M=N_x=N_y$).

$\mathit{\alpha }$	M	FDM			FFDM
		${\mathit{L}}^{\mathbf{2}}$ Error	Rate	CPU Time	${\mathit{L}}^{\mathbf{2}}$ Error	Rate	CPU Time
0.5	$2^5$	8.2859 $\times {10}^{-4}$	-	1.80 s	8.2859 $\times {10}^{-4}$	-	1.88 s
	$2^6$	4.2568 $\times {10}^{-4}$	0.9598	15.3 s	4.2568 $\times {10}^{-4}$	0.9598	12.3 s
	$2^7$	2.1763 $\times {10}^{-4}$	0.9690	3 min 59 s	2.1763 $\times {10}^{-4}$	0.9690	1 min 39 s
	$2^8$	1.1066 $\times {10}^{-4}$	0.9757	6 h 37 min 7 s	1.1066 $\times {10}^{-4}$	0.9757	12 min 43 s
	$2^9$	-	-	Out of memory	5.6020 $\times {10}^{-5}$	0.9821	1 h 42 min 2 s
	$2^{10}$	-	-	Out of memory	2.8261 $\times {10}^{-5}$	0.9871	14 h 45 min 9 s
0.7	$2^5$	8.8750 $\times {10}^{-4}$	-	1.56 s	8.8750 $\times {10}^{-4}$	-	1.47 s
	$2^6$	4.4614 $\times {10}^{-4}$	0.9923	15.9 s	4.4614 $\times {10}^{-4}$	0.9923	12.3 s
	$2^7$	2.2392 $\times {10}^{-4}$	0.9945	3 min 59 s	2.2392 $\times {10}^{-4}$	0.9945	1 m 39 s
	$2^8$	1.1212 $\times {10}^{-4}$	0.9979	6 h 34 min 35 s	1.1212 $\times {10}^{-4}$	0.9979	12 min 39 s
	$2^9$	-	-	Out of memory	5.6031 $\times {10}^{-5}$	1.0007	1 h 45 min 6 s
	$2^{10}$	-	-	Out of memory	2.7954 $\times {10}^{-5}$	1.0032	15 h 38 min 33 s

, respectively. The performance of the FDM and FFDM for each example with $\alpha =1$, as well as $\alpha =0.3,0.5$ and $0.7$ at fixed spatial meshes and the successively refined time steps are in Table 2 and Table 5, respectively. We present the performance of the FDM and FFDM for each an example with $\beta =0.3,0.5$ and $0.7$ at successively refined meshes in space and time in Table 2 and Table 5, respectively. In Table 3 and in Table 6, we respectively show the computational performance of both the methods with $\beta =0.5$, as well as $\alpha =0.5$ and $0.7$, at successively refined temporal meshes with fixed spatial grid points. And the results confirmed the theory analyzed in the Section 2 and Section 3.

By comparing the results that are shown in the tables, we obtained the following observations:

(i)

FFDM can effectively reduce the costs of computation and memory requirement, which is to say that FFDM has a much better efficiency than FDM.

(ii)

Both methods have the same accuracy and the convergence results that verify the theory analyzed in Section 2 and Section 3.

(iii)

In Table 4, one can see that we only show the two cases where $\alpha =0.5$ and $\alpha =0.7$ because the result is unsteady when $\alpha =0.3$ is for $\lambda >1$ as they did not satisfy the CFL condition, which strongly confirm the theories.

4.2. Anomalous Diffusive Transport

We simulated the anomalous diffusive transport described by a one-dimensional analog of Problems (1) and (3) with the homogeneous Dirichlet boundary condition, as well as with $\Omega =(0,1),[0,T]=[0,1],h=1/256,$ and $\tau =1/250.$

Example 1.

In order to figure out the connections and differences between the integer equation ${\partial }_{t}u+K{\partial }_{x}u=0$ and the fractional–order differential equation ${\partial }_{t}u+{\mathcal{L}}_x^{\beta }u=0$, K can be 1 or $-1$ and ${\mathcal{L}}_x^{\beta }$ can be the left–sided fractional operator ${\partial }_x^{\beta ,-}$ or the right–sided fractional operator ${\partial }_x^{\beta ,+}$, as defined in (2). We set the same function $u_0=exp(-x^2)$ as our initial condition. We used the Euler scheme to respectively obtain the numerical solutions.

In Figure 1 and Figure 2, we display the numerical solutions of the different models evaluated at $t=0,0.3,0.6$ and $0.9$. We can see that the moving direction is toward the coordinate directions in both figures. The difference is that the integer model moves in parallel, while the fractional model moves in a downward trend.

In Figure 3, we display a plot of the exact solutions (g-), the FDM solutions (bd) and the FFDM solutions (r*) in x and $t(t=1$) with $N=2^6$ and $M=N$ to show the accuracy of the method. We can see that the numerical solutions fit the exact solution accurately.

5. Discussion and Conclusions

We developed and analyzed an EFDM that satisfied a bound-preserving principle for space–time fractional advection equations with orders of $0<\alpha$ and $\beta \le 1$. Under the CFL condition, the EFDM is bound-preserved and convergent. And the FFDM for stFAE has the same accuracy with FDM. But, FFDM can reduce the costs of computation and the requirements of memory effectively, which is to say that the FFDM has a much better efficiency than FDM. However, both methods have a rate of time convergence of 1. To obtain a higher accuracy in the numerical method, the discontinuous Galerkin method [41,42,43] can be adopted for space and/or time derivatives, and this can lead to interesting outcomes. It could be that a compact finite difference method [44,45] can be adopted for time derivatives in our future work, which could thus lead to a better convergency.