Quantization-Based Event-Triggered H∞ Consensus for Discrete-Time Markov Jump Fractional-Order Multiagent Systems with DoS Attacks
Abstract
:1. Introduction
- Compared to MJMASs and FOMASs, we address the more generalized consensus problem for DTMJFOMASs, which takes into account incomplete probabilistic Markov processes and external disturbances.
- A mode-dependent distributed controller with quantized inputs is developed, and DoS attacks obeying a Bernoulli distribution are addressed to enhance the robustness of the system.
- Considering the high-frequency communication between MASs, a mode-dependent approach to quantization is introduced. Compared with the traditional triggering strategy, the QETM has both a lower triggering frequency and meets the system performance requirements.
2. Preliminaries
3. Materials and Methods
3.1. Problem Formulation
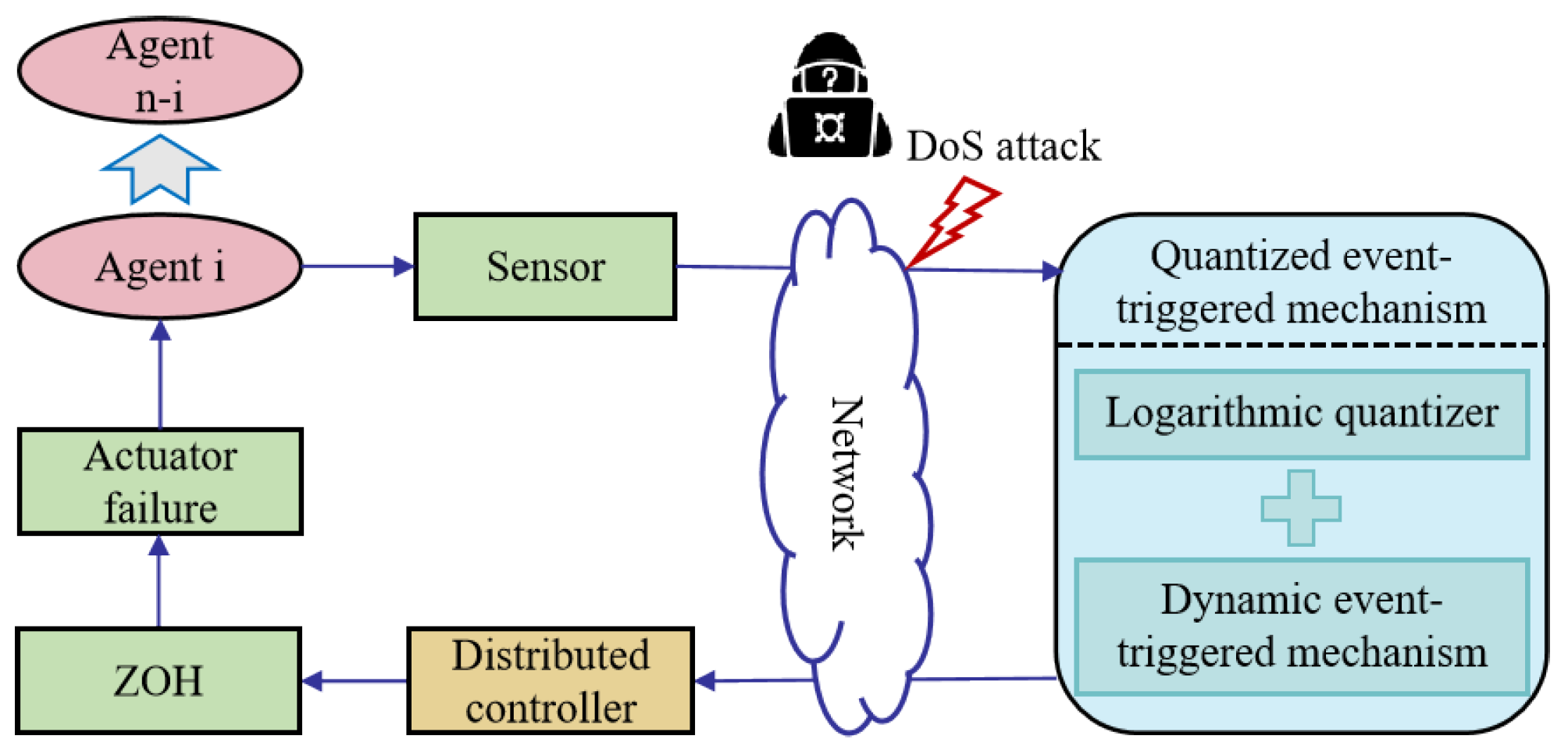
3.2. Quantized Event-Triggered Mechanism
- 1.
- 2.
- 3.
3.3. Mode-Dependent Distributed Control Protocol
3.4. Model Transformation
- 1.
- If , the system consensus is mean-square asymptotic stability, i.e., Definition (2) is met.
- 2.
- Under zero initial conditions, the following inequality holds for any non-zero :
4. Main Results
- ,
- , ,
- , .
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- .
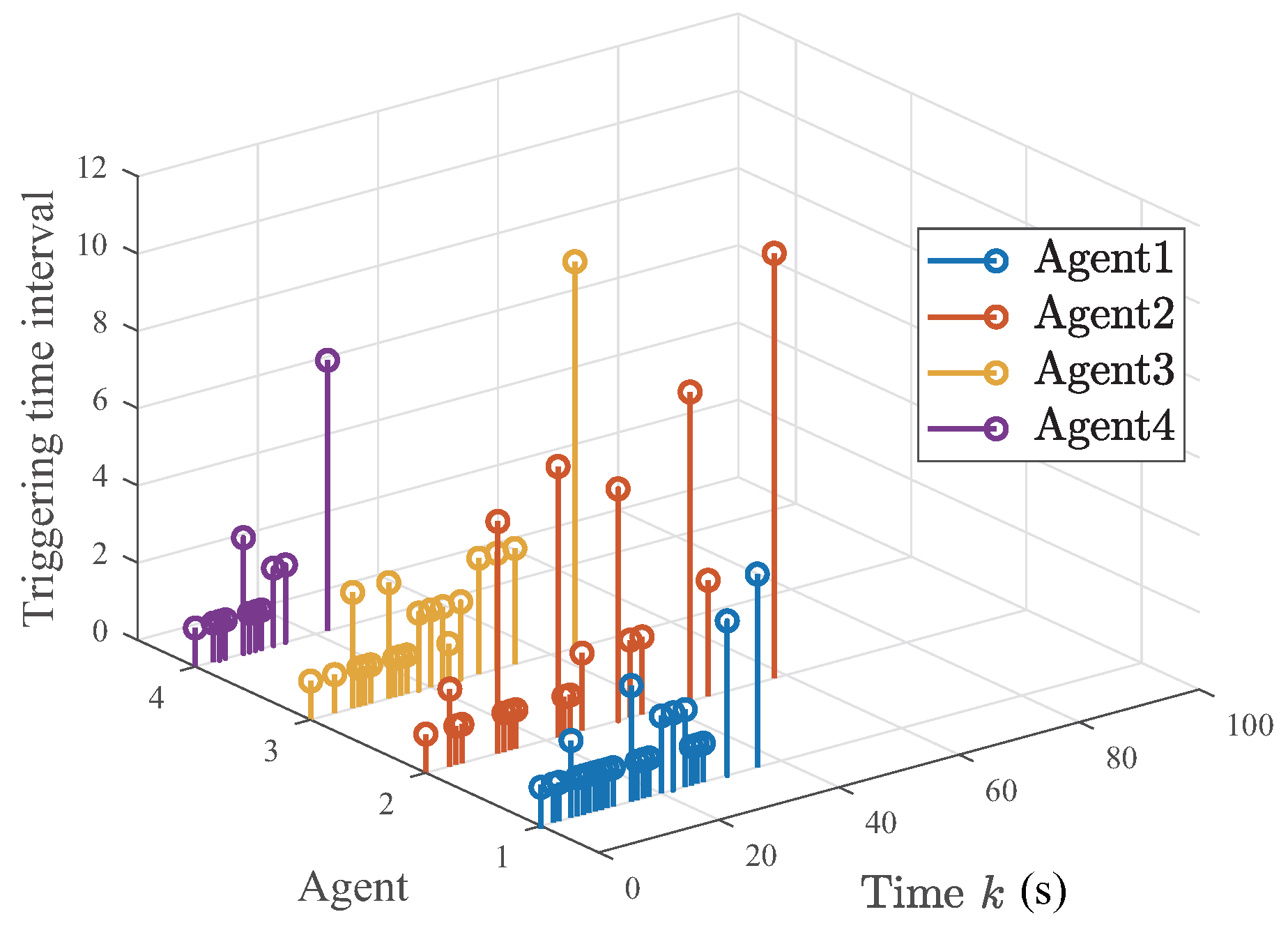
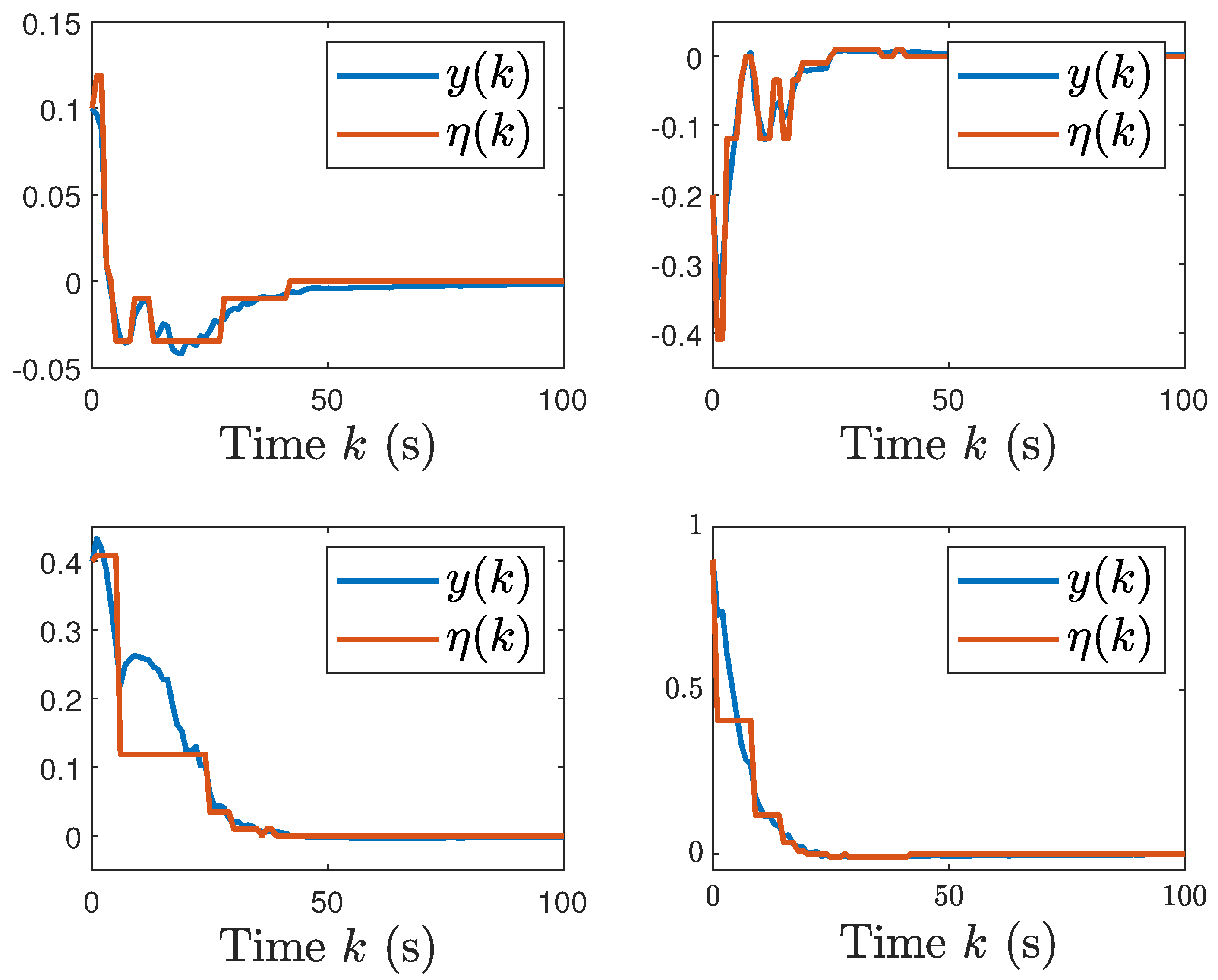
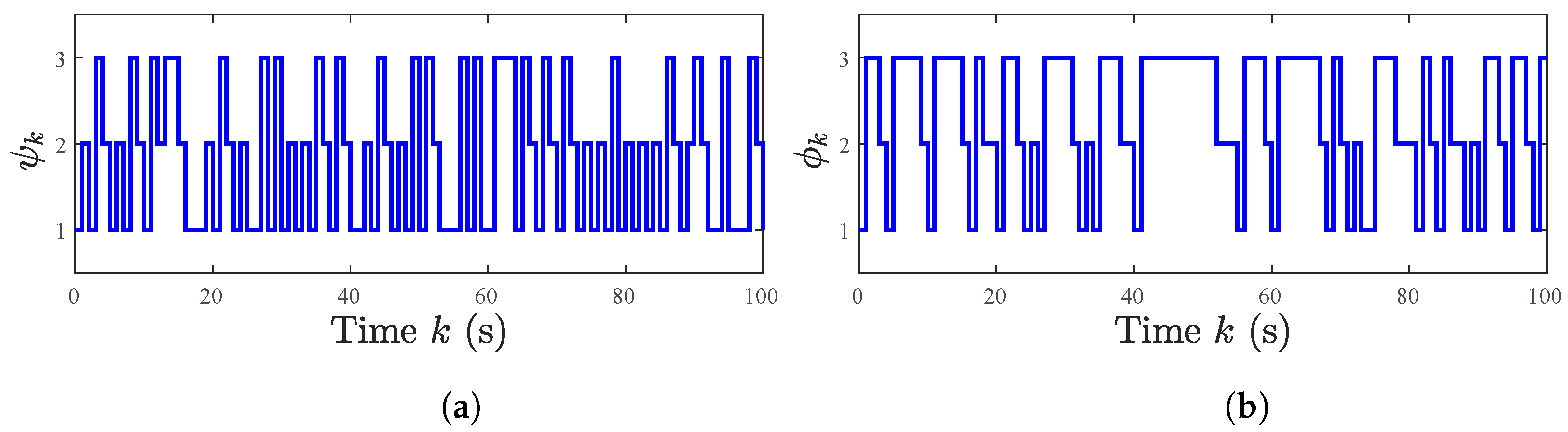
5. Simulation Examples
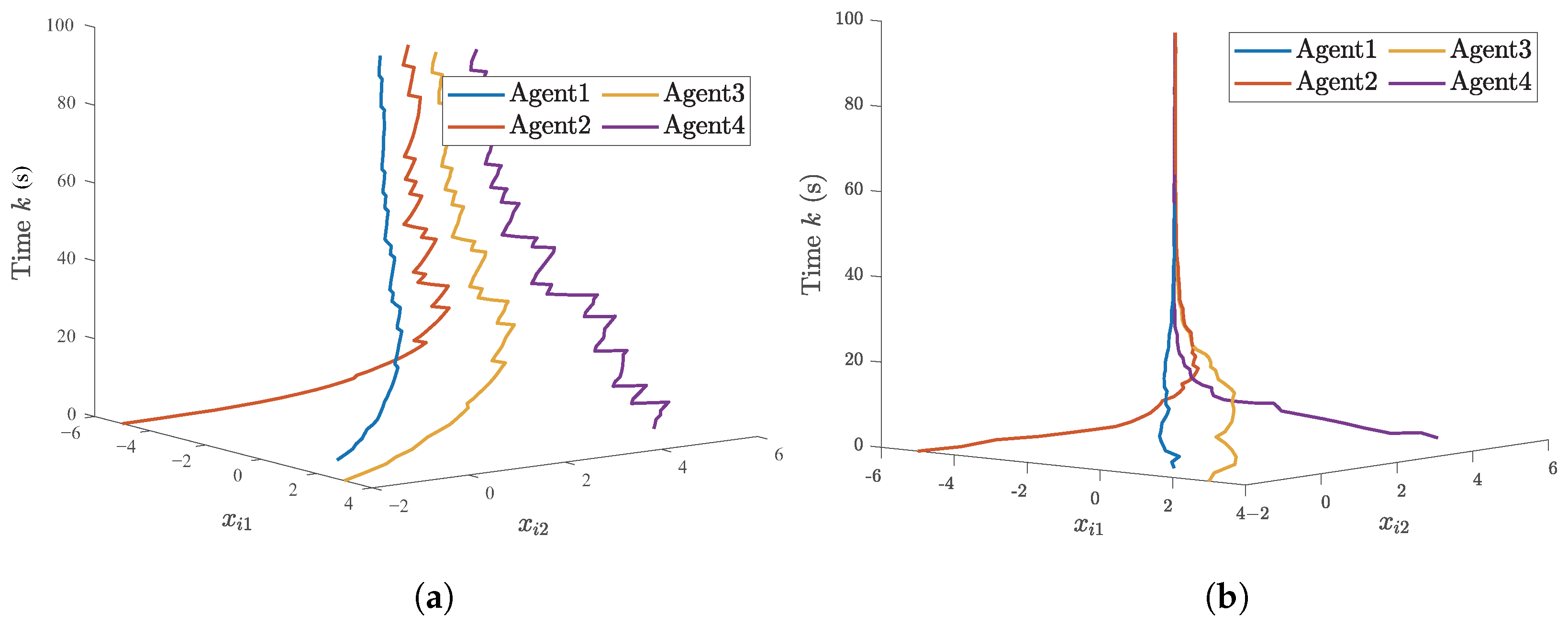
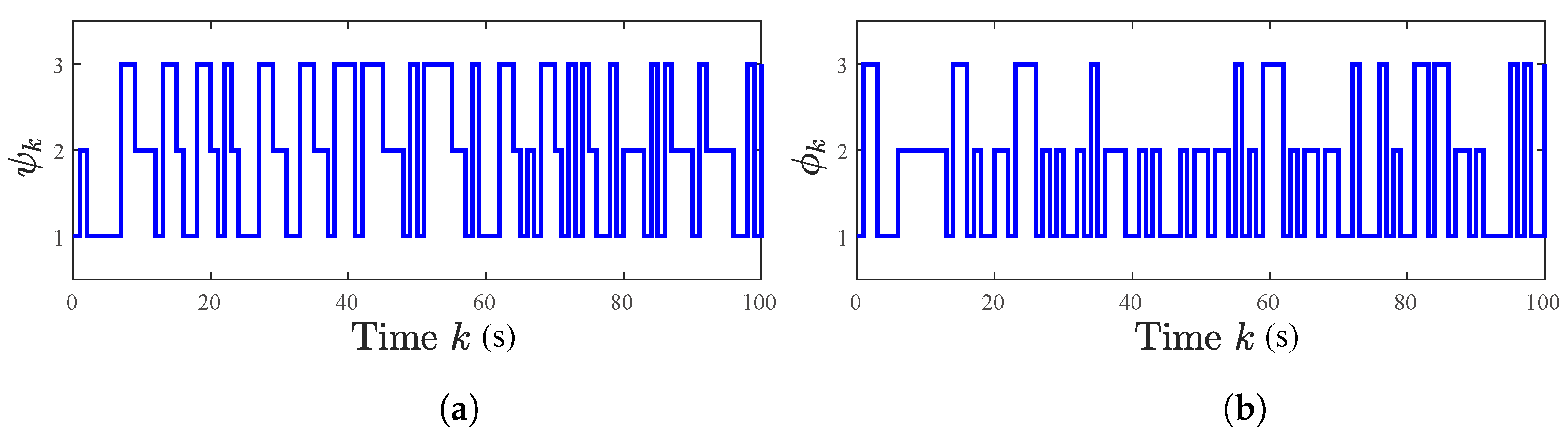
5.1. A Numerical Example
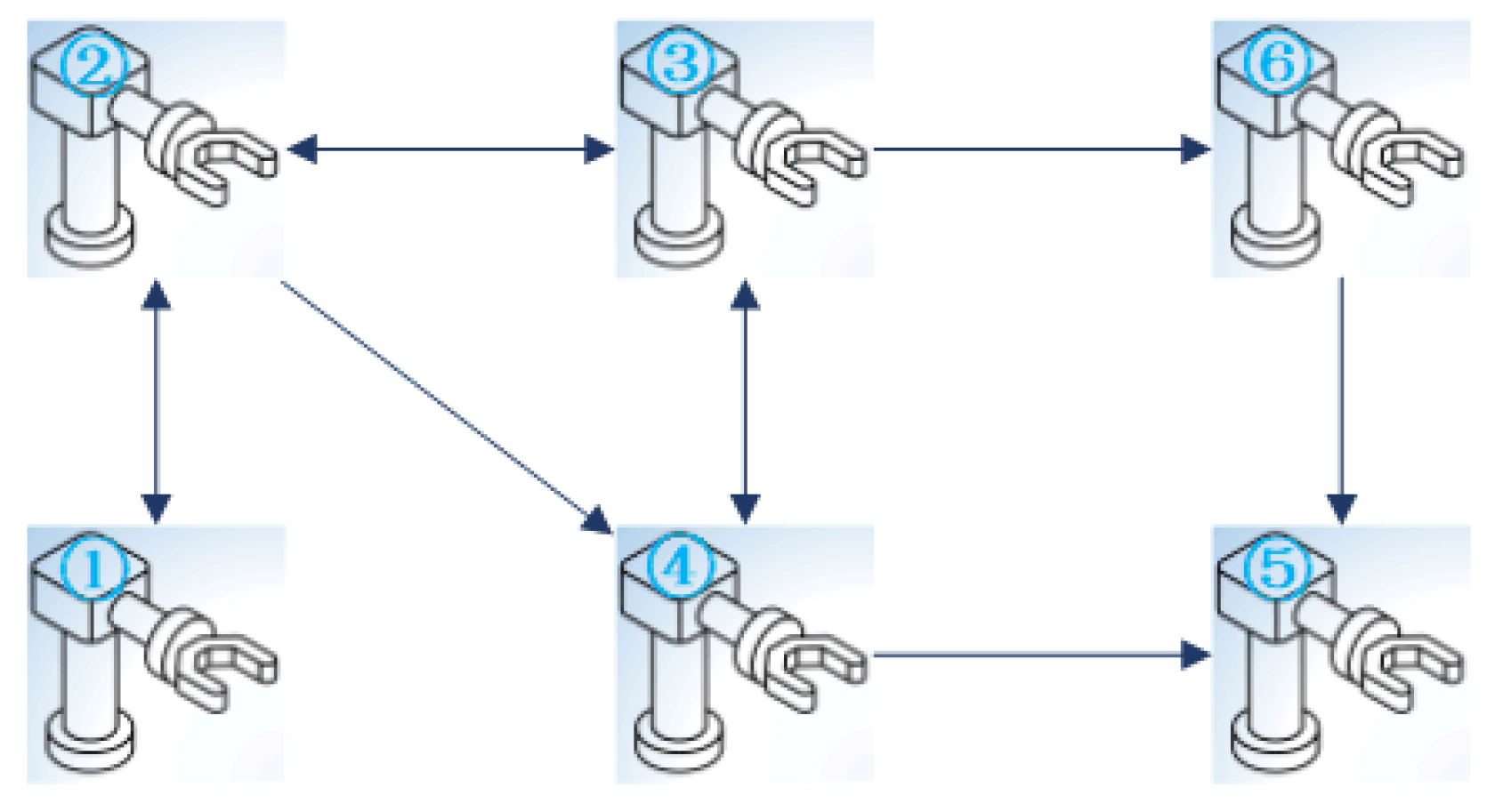
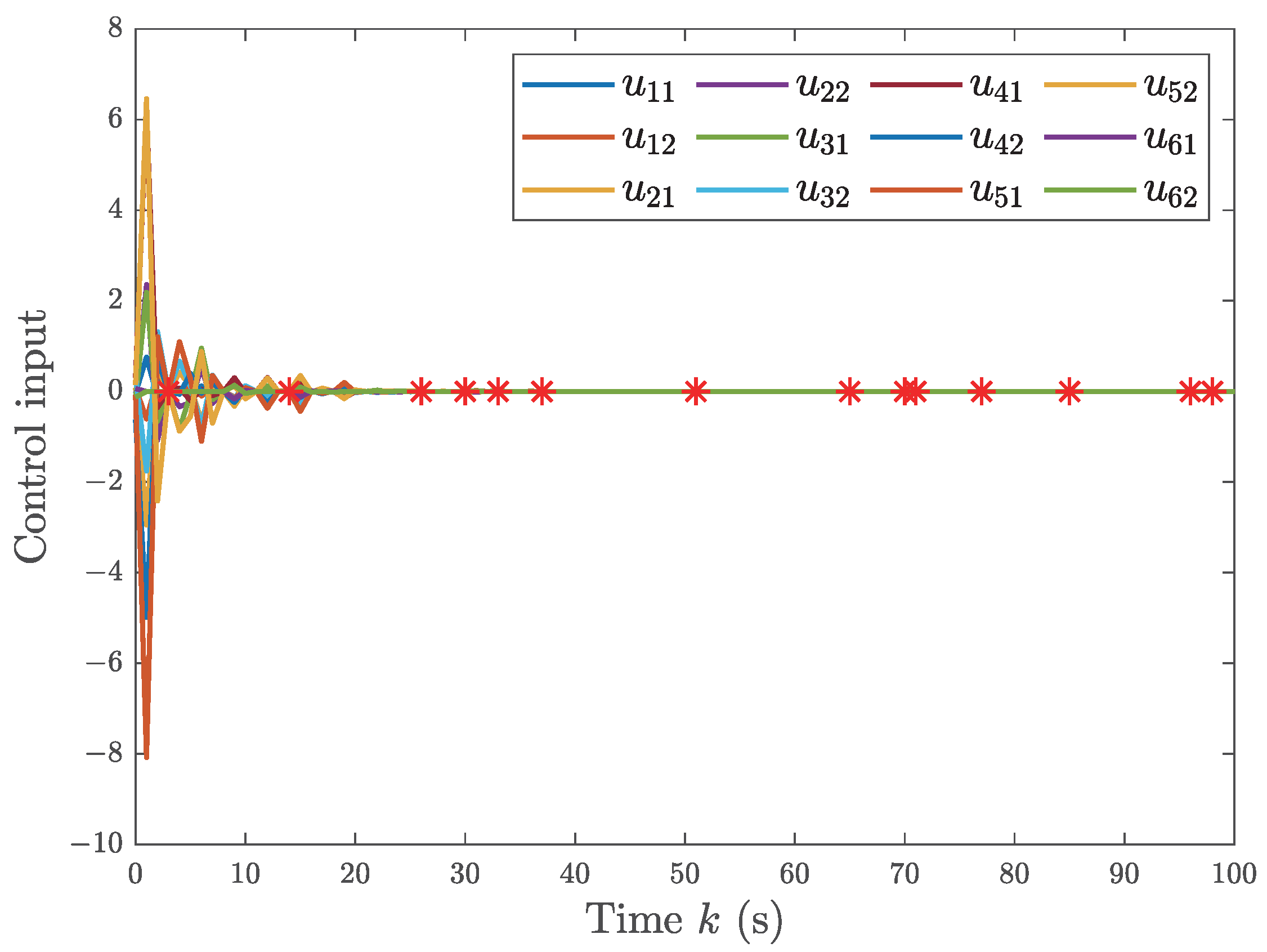
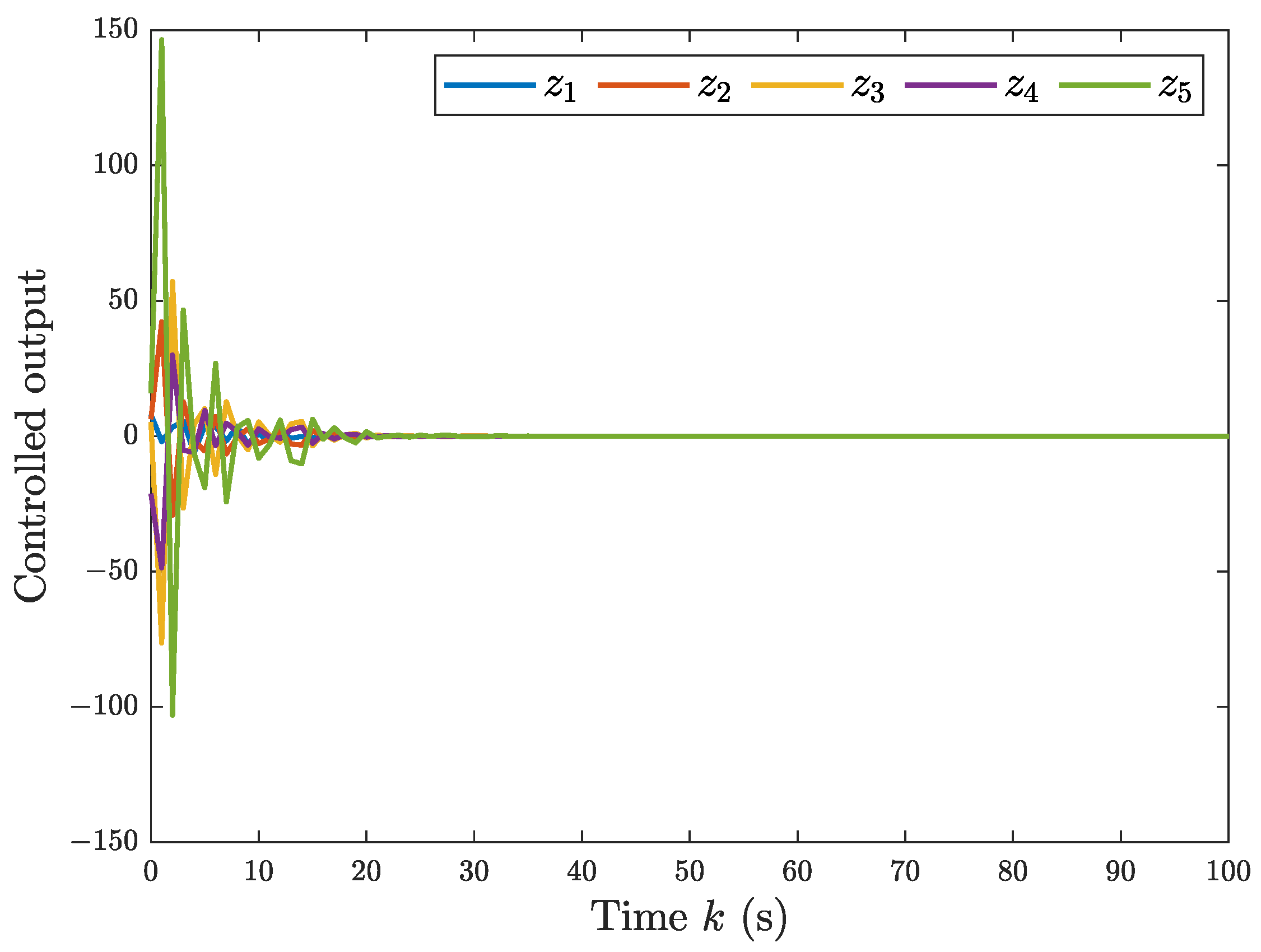
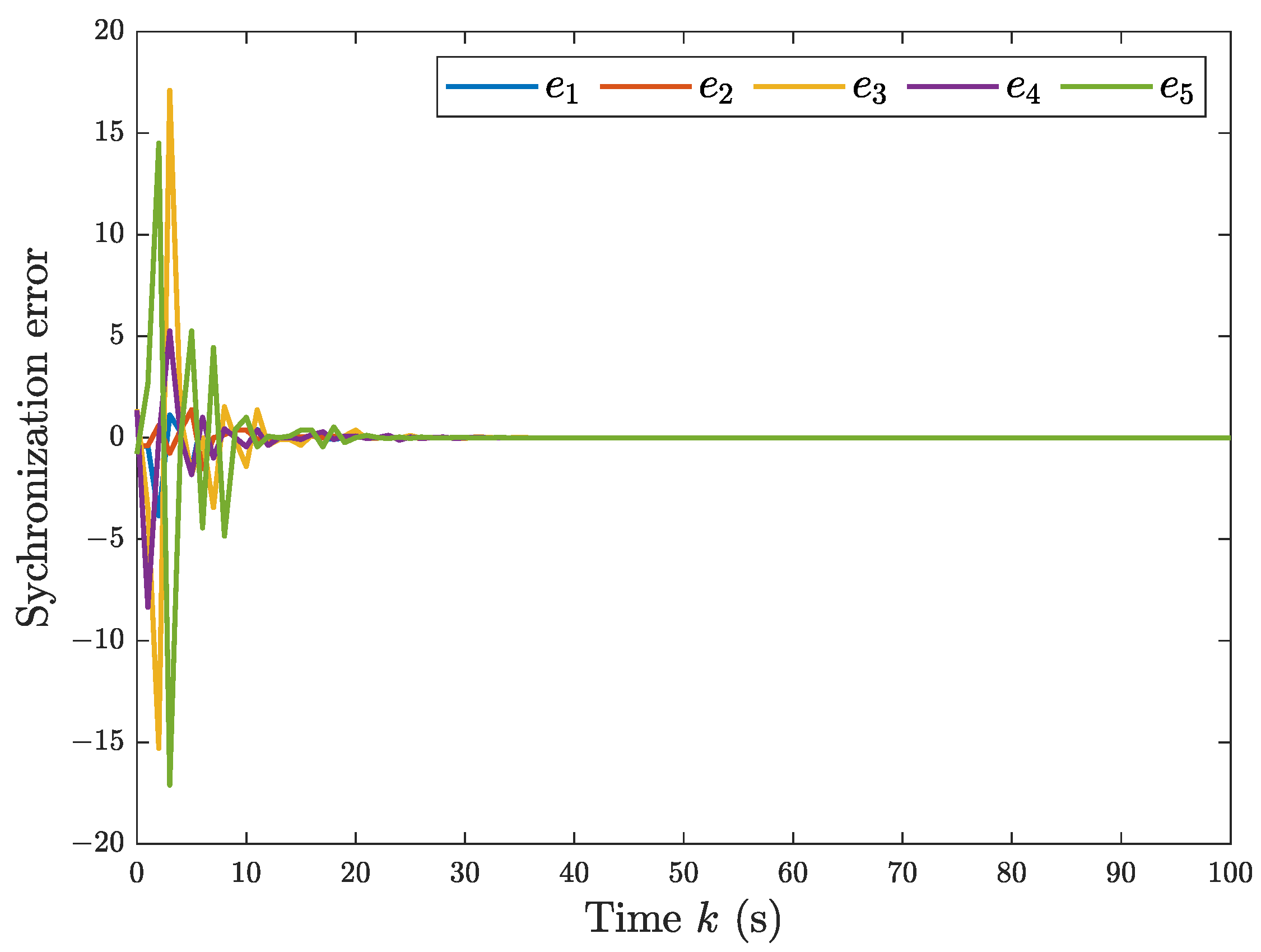
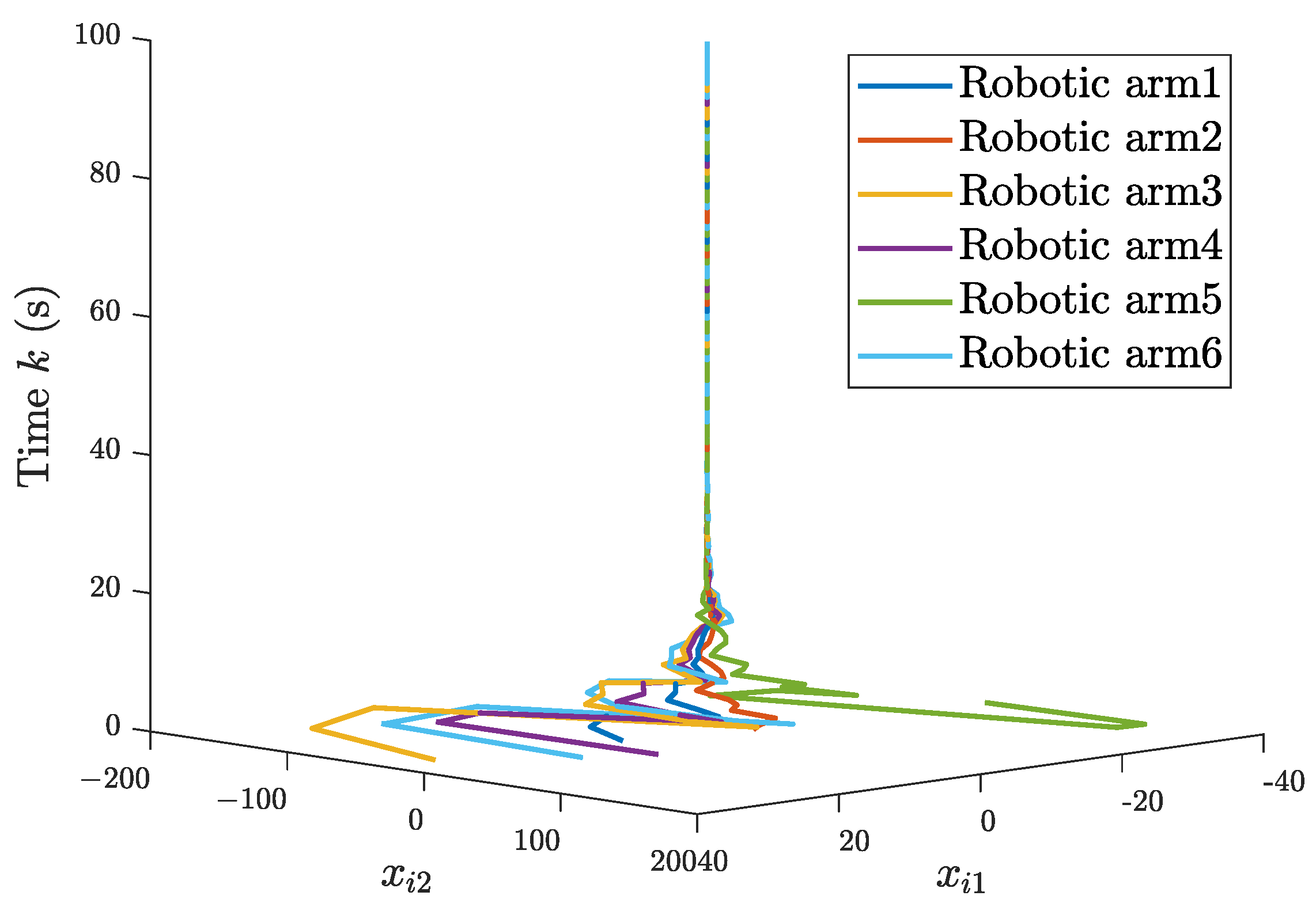
5.2. The Single-Link Robotic Arm Systems
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ren, W.; Sorensen, N. Distributed coordination architecture for multi-robot formation control. Rob. Auton. Syst. 2008, 56, 324–333. [Google Scholar] [CrossRef]
- Yang, X.; Yuan, J.; Chen, T.; Zhang, C.; Yang, H.; Hu, S. Distributed convex optimization of higher order nonlinear uncertain multi-agent systems with switched parameters and topologies. J. Vib. Control 2023. [Google Scholar] [CrossRef]
- Pipattanasomporn, M.; Feroze, H.; Rahman, S. Multi-agent systems in a distributed smart grid: Design and implementation. In Proceedings of the 2009 IEEE/PES Power Systems Conference and Exposition, Seattle, WA, USA, 15–18 March 2009; pp. 1–8. [Google Scholar]
- Pang, K.; Ma, L.; Bai, H.; Yi, X. Dynamic event-based finite-horizon H∞ secure consensus control of a class of nonlinear multi-agent systems. ISA Trans. 2022, 127, 168–177. [Google Scholar] [CrossRef]
- Ding, P.; Shen, H.; Xia, J.; Li, F. H∞ secure consensus of hidden Markov jump multi-agent systems subject to DoS attacks and disturbance. Int. J. Robust Nonlinear Control 2024. [Google Scholar] [CrossRef]
- Xue, A.; Wang, H.; Lu, R. Event-based H∞ control for discrete Markov jump systems. Neurocomputing 2016, 190, 165–171. [Google Scholar] [CrossRef]
- Yao, L.; Huang, X.; Wang, Z.; Liu, K. Secure control of Markovian jumping systems under deception attacks: An attack-probability-dependent adaptive event-trigger mechanism. IEEE Trans. Control Netw. Syst. 2023, 10, 1818–1830. [Google Scholar] [CrossRef]
- Li, S.; Chen, Y.; Liu, P.X. Fault estimation and fault-tolerant tracking control for multi-agent systems with Lipschitz nonlinearities using double periodic event-triggered mechanism. IEEE Trans. Signal Inf. Process. Netw. 2023, 9, 229–241. [Google Scholar] [CrossRef]
- Guo, S.; Zhao, X.; Wang, H.; Xu, N. Distributed consensus of heterogeneous switched nonlinear multiagent systems with input quantization and DoS attacks. Appl. Math. Comput. 2023, 456, 128127. [Google Scholar] [CrossRef]
- Wang, X.; Niu, B.; Gao, Y.; Shang, Z. Adaptive finite time output feedback bipartite tracking control for nonlinear multiagent systems. IEEE Trans. Autom. Sci. Eng. 2023. [Google Scholar] [CrossRef]
- Chai, J.; Lu, Q.; Tao, X.; Peng, D.; Zhang, B. Dynamic event-triggered fixed-time consensus control and its applications to magnetic map construction. IEEE/CAA J. Autom. Sin. 2023, 10, 2000–2013. [Google Scholar] [CrossRef]
- Costa, O.L.V.; Fragoso, M.D.; Marques, R.P. Discrete-time Markov jump linear systems; Springer Science & Business Media: Berlin, Germany, 2005. [Google Scholar]
- Lian, J.; Li, S. Fuzzy control of uncertain positive Markov jump fuzzy systems with input constraint. IEEE Trans. Cybern. 2021, 51, 2032–2041. [Google Scholar] [CrossRef] [PubMed]
- Sakthivel, R.; Parivallal, A.; Kaviarasan, B.; Lee, H.; Lim, Y. Finite-time consensus of Markov jumping multi-agent systems with time-varying actuator faults and input saturation. ISA Trans. 2018, 83, 89–99. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.; Zhang, H.; Wang, Z.; Yan, H. Reliable leader-following consensus of discrete-time semi-Markovian jump multi-agent systems. IEEE Trans. Netw. Sci. Eng. 2023, 10, 3505–3518. [Google Scholar] [CrossRef]
- Dong, S.; Ren, W.; Wu, Z.G.; Su, H. H∞ output consensus for Markov jump multiagent systems with uncertainties. IEEE Trans. Cybern. 2022, 50, 2264–2273. [Google Scholar] [CrossRef]
- Wang, H.; Xue, B.; Xue, A. Leader-following consensus control for semi-Markov jump multi-agent systems: An adaptive event-triggered scheme. J. Franklin Inst. 2021, 358, 428–447. [Google Scholar] [CrossRef]
- Huo, S.; Zhang, Y. H∞ consensus of Markovian jump multi-agent systems under multi-channel transmission via output feedback control strategy. ISA Trans. 2020, 99, 28–36. [Google Scholar] [CrossRef]
- Dong, S.; Liu, L.; Feng, G.; Liu, M.; Wu, Z.G.; Zheng, R. Cooperative output regulation quadratic control for discrete-time heterogeneous multiagent Markov jump systems. IEEE Trans. Cybern. 2022, 52, 9882–9892. [Google Scholar] [CrossRef]
- Wang, J.; Chen, X. H∞ consensus for stochastic Markov jump multi-agent systems with imperfect time-varying transition probabilities and multiplicative noise. Appl. Math. Comput. 2023, 436, 127504. [Google Scholar] [CrossRef]
- Abdelwahed, H.; El-Shewy, E.; Alghanim, S.; Abdelrahman, M.A. On the physical fractional modulations on Langmuir plasma structures. Fractal Fract. 2022, 6, 430. [Google Scholar] [CrossRef]
- Sharaf, M.; El-Shewy, E.; Zahran, M. Fractional anisotropic diffusion equation in cylindrical brush model. J. Taibah Univ. Sci. 2020, 14, 1416–1420. [Google Scholar] [CrossRef]
- An, C.; Su, H.; Chen, S. H∞ consensus for discrete-time fractional-order multi-agent systems with disturbance via Q-learning in zero-sum games. IEEE Trans. Netw. Sci. Eng. 2022, 9, 2803–2814. [Google Scholar] [CrossRef]
- Shahamatkhah, E.; Tabatabaei, M. Containment control of linear discrete-time fractional-order multi-agent systems with time-delays. Neurocomputing 2020, 385, 42–47. [Google Scholar] [CrossRef]
- Reed, E.; Chatterjee, S.; Ramos, G.; Bogdan, P.; Pequito, S. Fractional cyber-neural systems-A brief survey. Annu. Rev. Control 2022, 54, 386–408. [Google Scholar] [CrossRef]
- Xu, J.; Cheng, J.; Yan, H.; Park, J.H.; Qi, W. Dynamic event-triggered control for semi-Markov singularly perturbed systems with generally transition rates. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 225–235. [Google Scholar] [CrossRef]
- Shi, T.; Shi, P.; Chambers, J. Dynamic event-triggered model predictive control under channel fading and denial-of-service attacks. IEEE Trans. Autom. Sci. Eng. 2023, 54, 225–235. [Google Scholar] [CrossRef]
- Gao, X.; Deng, F.; Zhang, H.; Zeng, P. Observer-based event-triggered asynchronous control of networked Markovian jump systems under deception attacks. Sci. China Inf. Sci. 2023, 66, 159204. [Google Scholar] [CrossRef]
- Hu, Z.; Chen, B. Sliding mode control for multi-agent systems under event-triggering hybrid scheduling strategy. IEEE Trans. Circuits Syst. II Express Briefs 2023. [Google Scholar] [CrossRef]
- Wu, Z.G.; Xu, Y.; Pan, Y.J.; Shi, P.; Wang, Q. Event-triggered pinning control for consensus of multiagent systems with quantized information. IEEE Trans. Syst. Man Cybern. Syst. 2017, 48, 1929–1938. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, Z.G.; Shi, P.; Huang, T.; Chakrabarti, P. Quantization-based event-triggered consensus of multiagent systems against aperiodic DoS attacks. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 3774–3783. [Google Scholar] [CrossRef]
- Ren, H.; Liu, R.; Cheng, Z.; Ma, H.; Li, H. Data-driven event-triggered control for nonlinear multi-agent systems with uniform quantization. IEEE Trans. Circuits Syst. II Express Briefs 2023, 71, 712–716. [Google Scholar] [CrossRef]
- Yang, X.; Yuan, J.; Chen, T.; Yang, H. Distributed adaptive optimization algorithm for fractional high-order multiagent systems based on event-triggered strategy and input quantization. Fractal Fract. 2023, 7, 749. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, F. Distributed dynamic event-triggered control for multi-agent systems with quantization communication. IEEE Trans. Circuits Syst. II Express Briefs 2023. [Google Scholar] [CrossRef]
- Arbi, A. Controllability of delayed discret fornasini-marchesini model via quantization and random packet dropouts. Math. Model. Nat. Phenom. 2022, 17, 38. [Google Scholar] [CrossRef]
- Zhou, X.; Tang, Y.; Cheng, J.; Cao, J.; Xue, C.; Yan, D. Nonstationary quantized control for discrete-time Markov jump singularly perturbed systems against deception attacks. J. Franklin Inst. 2021, 358, 2915–2932. [Google Scholar] [CrossRef]
- Zhang, G.; Li, F.; Wang, J.; Shen, H. Mixed H∞ and passive consensus of Markov jump multi-agent systems under DoS attacks with general transition probabilities. J. Franklin Inst. 2023, 360, 5375–5391. [Google Scholar] [CrossRef]
- Li, W.; Niu, Y.; Lv, X. Dynamic event-triggering sliding mode resilient control for multi-agent systems. J. Franklin Inst. 2023, 360, 10. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Zhou, K.; Khargonekar, P.P. Robust stabilization of linear systems with norm-bounded time-varying uncertainty. Syst. Control Lett. 1988, 10, 17–20. [Google Scholar] [CrossRef]
- Ning, Z.; Zhang, L.; de Jesus Rubio, J.; Yin, X. Asynchronous filtering for discrete-time fuzzy affine systems with variable quantization density. IEEE Trans. Cybern. 2017, 47, 153–164. [Google Scholar] [CrossRef]
- Kaczorek, T. Selected Problems of Fractional Systems Theory; Springer Science & Business Media: Berlin, Germany, 2011. [Google Scholar]
- Wei, Y.; Gao, Y.; Liu, D.Y.; Wang, Y. Controllability and observability of linear nabla fractional order systems. In Proceedings of the 2018 37th Chinese Control Conference, Wuhan, China, 25–27 July 2018; pp. 25–27. [Google Scholar]
- Fu, M.; Xie, L. The sector bound approach to quantized feedback control. IEEE Trans. Autom. Control 2005, 50, 1698–1711. [Google Scholar]
- Wang, J.; He, W.; Fu, J.; Wang, Y.; Sun, J. Sampled-data consensus control of nonlinear multi-agent systems with Markovian switching topologies based on extended looped functional. IEEE Trans. Circuits Syst. II Express Briefs 2024, 71, 251–255. [Google Scholar] [CrossRef]
- Elahi, A.; Alfi, A.; Modares, H. H∞ consensus control of discrete-time multi-agent systems under network imperfections and external disturbance. IEEE/CAA J. Autom. Sin. 2019, 6, 667–675. [Google Scholar] [CrossRef]
- Zhao, D.; Dong, T.; Hu, W. Event-triggered consensus of discrete time second-order multi-agent network. Int. J. Control Autom. Syst. 2018, 16, 87–96. [Google Scholar] [CrossRef]
- Qi, W.; Zong, G.; Karimi, H.R. Finite-time observer-based sliding mode control for quantized semi-Markov switching systems with application. IEEE Trans. Ind. Inf. 2020, 16, 1259–1271. [Google Scholar] [CrossRef]
- Xue, M.; Yan, H.; Zhang, H.; Li, Z.; Chen, S.; Chen, C. Event-triggered guaranteed cost controller design for T-S fuzzy Markovian jump systems with partly unknown transition probabilities. IEEE Trans. Fuzzy Syst. 2021, 29, 1052–1064. [Google Scholar] [CrossRef]
- Liu, X.; Wei, X.; Li, Y. Observer-based finite-time fuzzy H∞ control for Markovian jump systems with time-delay and multiplicative noises. Int. J. Fuzzy Syst. 2023, 25, 1643–1655. [Google Scholar] [CrossRef]


| A | B | C | D | E | |
|---|---|---|---|---|---|
| Mode 1 | |||||
| Mode 2 | |||||
| Mode 3 |
| A | B | C | D | E | |
|---|---|---|---|---|---|
| Mode 1 | |||||
| Mode 2 | |||||
| Mode 3 |
| Trigger Frequency | Robotic Arm 1 | Robotic Arm 2 | Robotic Arm 3 | Robotic Arm 4 | Robotic Arm 5 | Robotic Arm 6 | Average |
|---|---|---|---|---|---|---|---|
| QETM | 18% | 23% | 21% | 19% | 24% | 23% | 21.33% |
| Method 1 * | 23% | 24% | 24% | 26% | 21% | 26% | 24.00% |
| Method 2 * | 38% | 35% | 40% | 33% | 30% | 33% | 34.83% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Y.; Wu, X.; Wang, Y.; Huang, L.; Wei, Q. Quantization-Based Event-Triggered H∞ Consensus for Discrete-Time Markov Jump Fractional-Order Multiagent Systems with DoS Attacks. Fractal Fract. 2024, 8, 147. https://doi.org/10.3390/fractalfract8030147
Lu Y, Wu X, Wang Y, Huang L, Wei Q. Quantization-Based Event-Triggered H∞ Consensus for Discrete-Time Markov Jump Fractional-Order Multiagent Systems with DoS Attacks. Fractal and Fractional. 2024; 8(3):147. https://doi.org/10.3390/fractalfract8030147
Chicago/Turabian StyleLu, Yi, Xiru Wu, Yaonan Wang, Lihong Huang, and Qingjin Wei. 2024. "Quantization-Based Event-Triggered H∞ Consensus for Discrete-Time Markov Jump Fractional-Order Multiagent Systems with DoS Attacks" Fractal and Fractional 8, no. 3: 147. https://doi.org/10.3390/fractalfract8030147
APA StyleLu, Y., Wu, X., Wang, Y., Huang, L., & Wei, Q. (2024). Quantization-Based Event-Triggered H∞ Consensus for Discrete-Time Markov Jump Fractional-Order Multiagent Systems with DoS Attacks. Fractal and Fractional, 8(3), 147. https://doi.org/10.3390/fractalfract8030147






