Fractal Numerical Investigation of Mixed Convective Prandtl-Eyring Nanofluid Flow with Space and Temperature-Dependent Heat Source
Abstract
:1. Introduction
- Cooling systems: Nanofluids have demonstrated potential in improving the thermal efficiency of cooling systems, specifically in electronic devices and microchips. Efforts are currently being made to commercialize nanofluids in order to enhance heat removal efficiency in these applications.
- Energy storage: It is worth noting that nanofluids have the potential to enhance the thermal efficiency of energy storage systems, including fuel cells. Efforts are being made to utilize the improved thermal conductivity of nanofluids to optimize energy storage and conversion processes.
- Catalysis: The unique features of nanofluids make them highly promising for catalytic applications, where they can significantly improve reaction speeds and selectivity. Pharmaceutical, chemical synthesis, and environmental remediation are some of the potential applications of nanofluids that are the focus of current research.
- Heat exchangers. Because of their exceptional thermal qualities, nanofluids are finding more and more uses as coolants in heat exchangers, where they greatly enhance performance and efficiency. Improvements in the preparation and use of nanofluids for different heat exchange purposes are the subject of continuing research.
- Vehicle thermal management: Vehicles, such as hybrid electric vehicles and chilled engines, can potentially benefit from nanofluids for heat management. Improving vehicle cooling and thermal management systems is the focus of research efforts. Nanofluids are being considered as potential solutions.
2. Proposed Fractal Numerical Scheme
3. Stability Analysis
4. Problem Formulation
- Understanding System Behavior: Our objective is to systematically examine the effects of changing various parameters on the profiles of velocity, temperature, and nanoparticle volume percentage in the boundary layer flow. These parameters include the Prandtl number, Eyring viscosity parameter, and heat generation parameters. Important for comprehending complicated fluid dynamics events, this sheds light on how alterations to these parameters impact the general behavior of the fluid’s flow and thermal properties.
- Validation of Computational Scheme: Parametric analysis validates our computational scheme. We may evaluate our computational approach’s correctness and dependability by comparing our numerical results to theoretical data for specific parameter values. Validating our numerical simulations and findings is crucial to their credibility and robustness.
- Practical Implications and Engineering Applications: Our parametric study lays the framework for understanding non-Newtonian nanofluid behavior under different conditions, but it does not explicitly address practical applications. Thermal management, nanofluid manufacturing, and renewable energy engineers and researchers benefit from such knowledge. Our study helps optimize and develop nanofluid systems by revealing how parameters affect fluid flow and heat transfer.
5. Results and Discussions
6. Conclusions
- The velocity profile was enhanced as the parameter I grew.
- The rising coefficient of the space-dependent heat generation term increased the temperature profile.
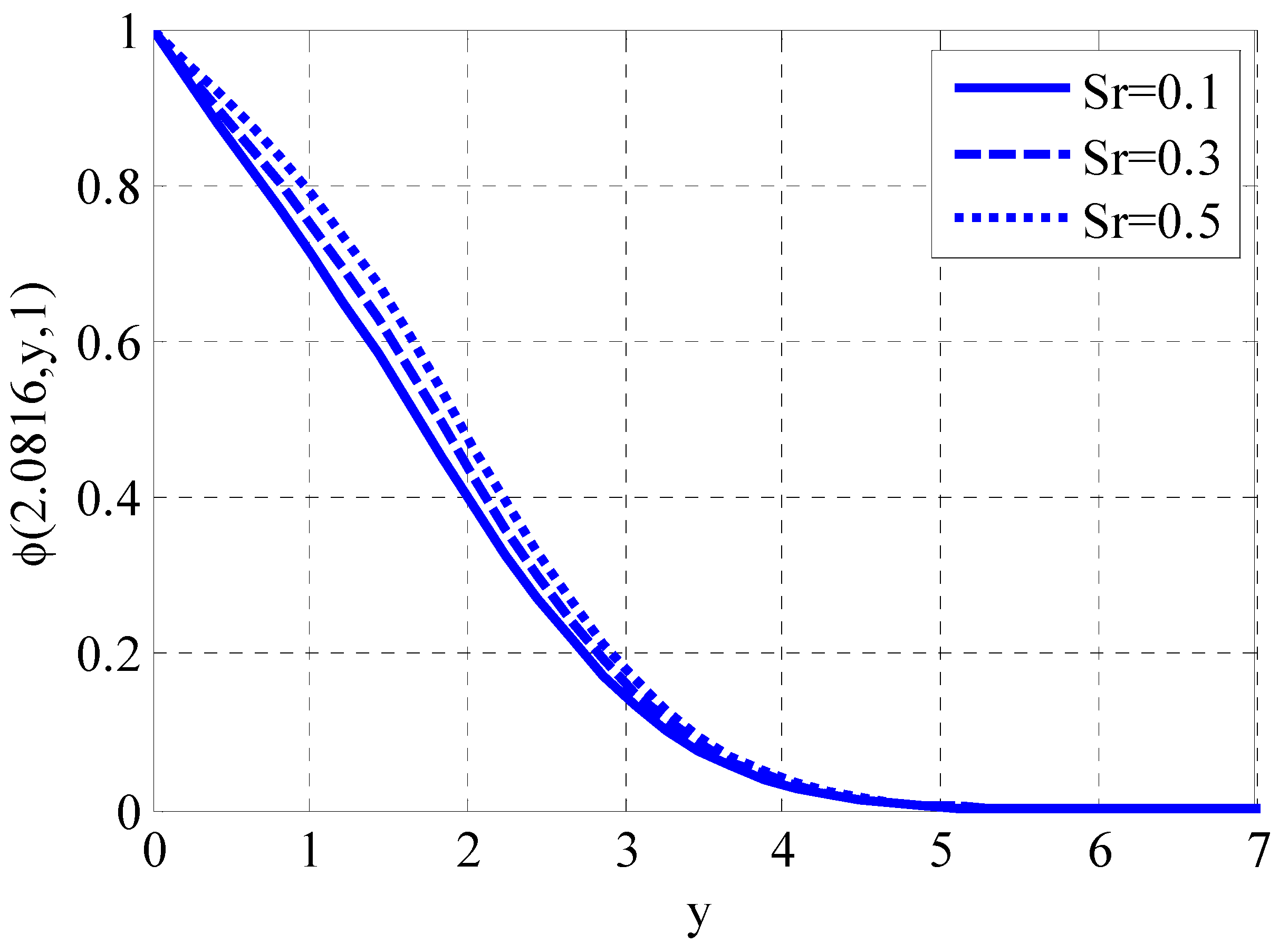
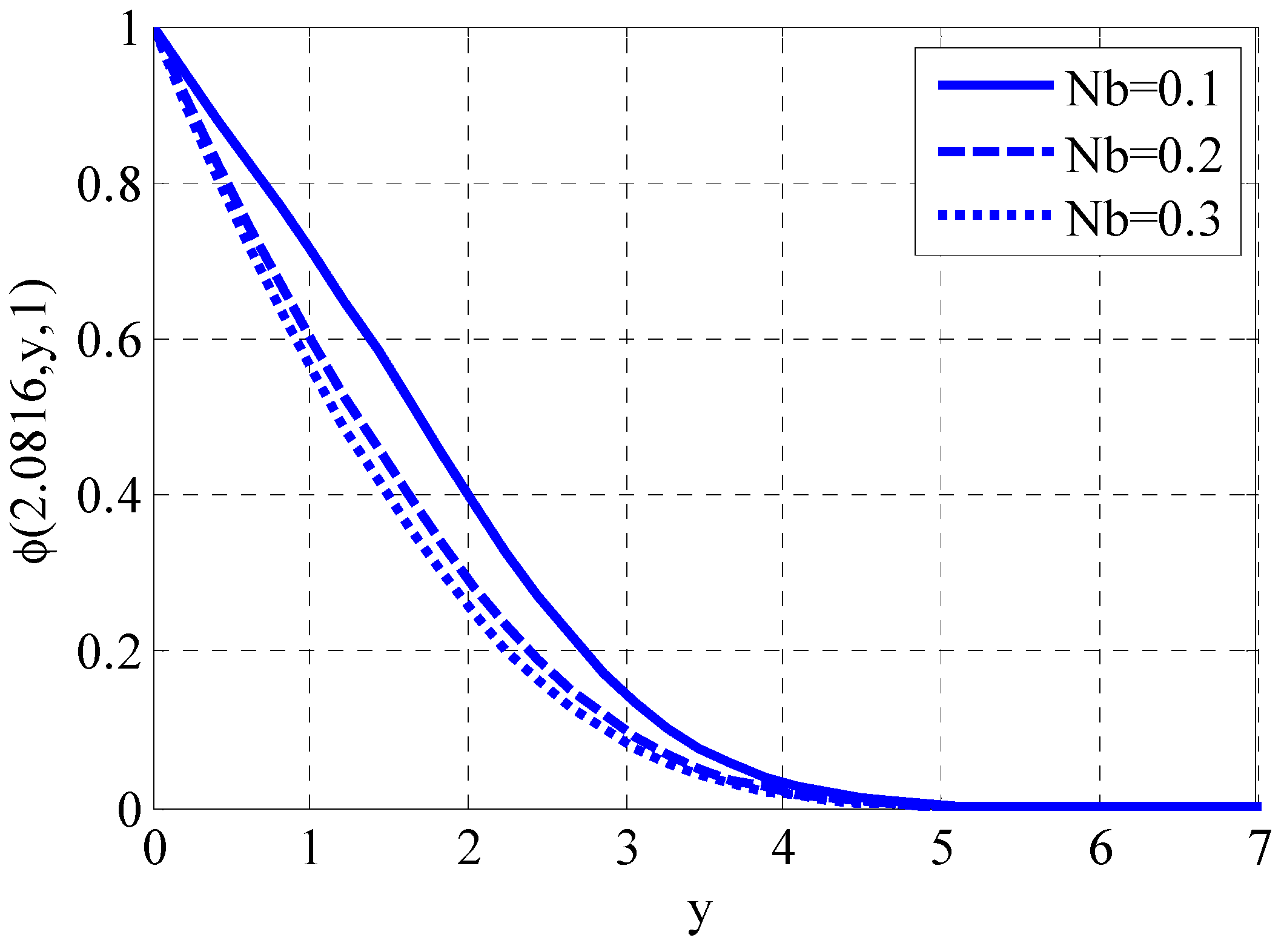
- The rising Brownian motion parameter declined the nanoparticle volume fraction.
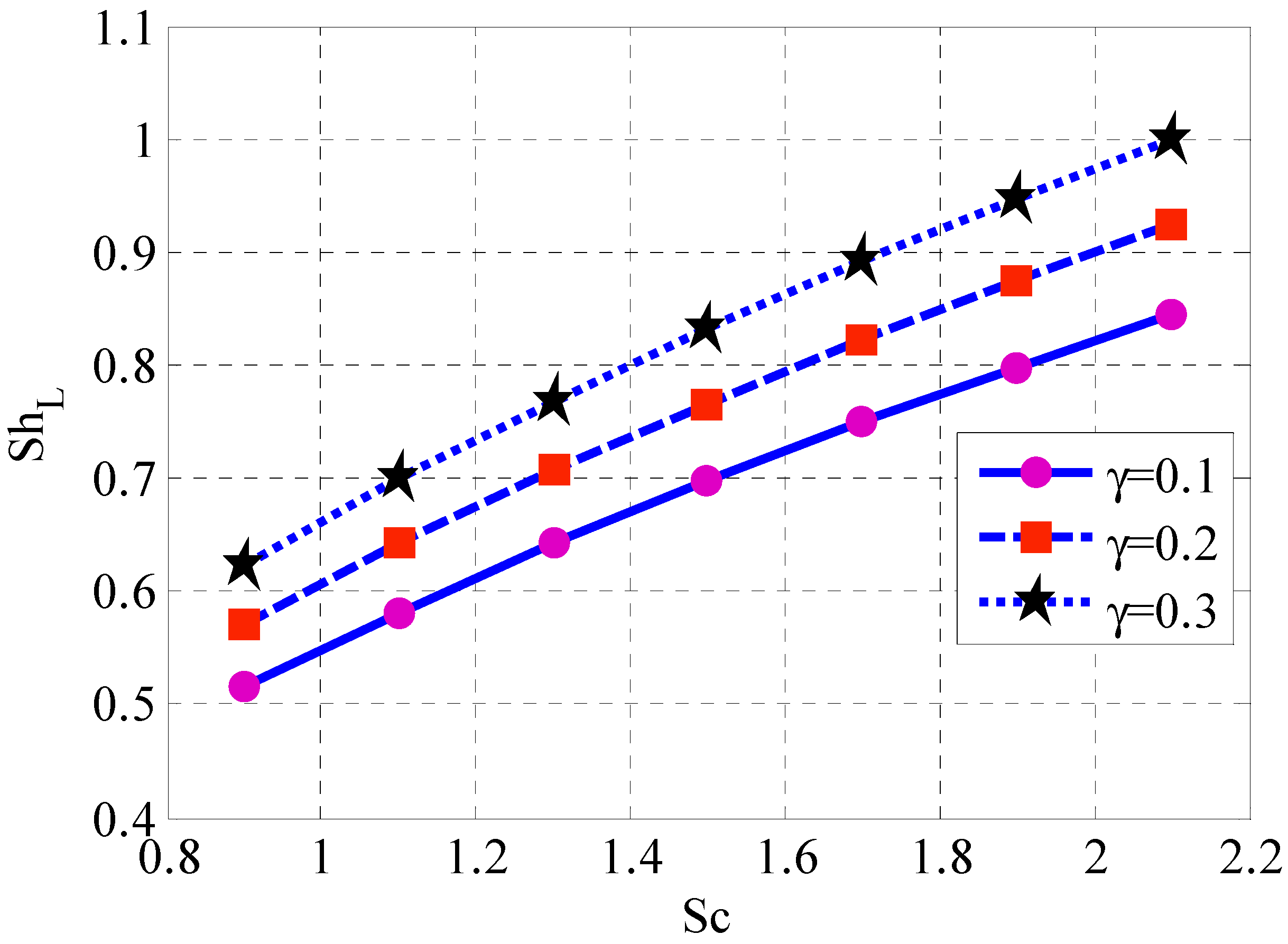
- Local Sherwood number increased with Schmidt number and response rate parameter.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Aziz, T.; Fatima, A.; Khalique, C.M.; Mahomed, F.M. Prandtl’s boundary layer equation for two-dimensional flow: Exact solutions via the simplest equation method. Math. Probl. Eng. 2013, 2013, 724385. [Google Scholar] [CrossRef]
- Sankad, G.; Ishwar, M.; Dhange, M. Varying wall temperature and thermal radiation effects on MHD boundary layer liquid flow containing gyrotactic microorganisms. Partial. Differ. Equ. Appl. Math. 2021, 4, 100092. [Google Scholar]
- Hussain, M.; Ghaffar, A.; Ali, A.; Shahzad, A.; Nisar, K.S.; Alharthi, M.R.; Jamshed, W. MHD thermal boundary layer flow of a Casson fluid over a penetrable stretching wedge in the existence of nonlinear radiation and convective boundary condition. Alex. Eng. J. 2021, 60, 5473–5483. [Google Scholar] [CrossRef]
- Abedi, H.; Sarkar, S.; Johansson, H. Numerical modelling of neutral atmospheric boundary layer flow through heterogeneous forest canopies in complex terrain (a case study of a Swedish wind farm). Renew. Energy 2021, 180, 806–828. [Google Scholar] [CrossRef]
- Yang, S.; Liu, L.; Long, Z.; Feng, L. Unsteady natural convection boundary layer flow and heat transfer past a vertical flat plate with novel constitution models. Appl. Math. Lett. 2021, 120, 107335. [Google Scholar] [CrossRef]
- Long, Z.; Liu, L.; Yang, S.; Feng, L.; Zheng, L. Analysis of Marangoni boundary layer flow and heat transfer with novel constitution relationships. Int. Commun. Heat Mass Transf. 2021, 127, 105523. [Google Scholar] [CrossRef]
- Zhang, X.; Tang, Y.; Zhang, F.; Lee, C.S. A novel aluminum—Graphite dual-ion battery. Adv. Energy Mater. 2016, 6, 1502588. [Google Scholar] [CrossRef]
- Hosseini, S.M.; Safaei, M.R.; Goodarzi, M.; Alrashed, A.A.; Nguyen, T.K. New temperature, interfacial shell dependent dimensionless model for thermal conductivity of nanofluids. Int. J. Heat Mass Transf. 2017, 114, 207–210. [Google Scholar] [CrossRef]
- Ahmadi, M.H.; Mohseni-Gharyehsafa, B.; Ghazvini, M.; Goodarzi, M.; Jilte, R.D.; Kumar, R. Comparing various machine learning approaches in modeling the dynamic viscosity of CuO/water nanofluid. J. Therm. Anal. Calorim. 2020, 139, 2585–2599. [Google Scholar] [CrossRef]
- Bahiraei, M.; Salmi, H.K.; Safaei, M.R. Effect of employing a new biological nanofluid containing functionalized graphene nanoplatelets on thermal and hydraulic characteristics of a spiral heat exchanger. Energy Convers. Manag. 2019, 180, 72–82. [Google Scholar] [CrossRef]
- Waqas, H.; Farooq, U.; Khan, S.A.; Alshehri, H.M.; Goodarzi, M. Numerical analysis of dual variable of conductivity in bioconvection flow of Carreau–Yasuda nanofluid containing gyrotactic motile microorganisms over a porous medium. J. Therm. Anal. Calorim. 2021, 145, 2033–2044. [Google Scholar] [CrossRef]
- Wang, X.; Li, C.; Zhang, Y.; Said, Z.; Debnath, S.; Sharma, S.; Yang, M.; Gao, T. Influence of texture shape and arrangement on nanofluid minimum quantity lubrication turning. Int. J. Adv. Manuf. Technol. 2021, 119, 631–646. [Google Scholar] [CrossRef]
- Xie, Y.; Meng, X.; Mao, D.; Qin, Z.; Wan, L.; Huang, Y. Homogeneously dispersed graphene nanoplatelets as long-term corrosion inhibitors for aluminum matrix composites. ACS Appl. Mater. Interfaces 2021, 13, 32161–32174. [Google Scholar] [CrossRef] [PubMed]
- Abu-Hamdeh, N.H.; Alsulami, R.A.; Rawa, M.J.; Alazwari, M.A.; Goodarzi, M.; Safaei, M.R. A Significant Solar Energy Note on Powell-Eyring Nanofluid with Thermal Jump Conditions: Implementing Cattaneo-Christov Heat Flux Model. Mathematics 2021, 9, 2669. [Google Scholar] [CrossRef]
- Sajid, T.; Jamshed, W.; Shahzad, F.; Eid, M.R.; Alshehri, H.M.; Goodarzi, M.; Akgül, E.K.; Nisar, K.S. Micropolar fluid past a convectively heated surface embedded with nth order chemical reaction and heat source/sink. Phys. Scr. 2021, 96, 104010. [Google Scholar] [CrossRef]
- Maleki, H.; Safaei, M.R.; Togun, H.; Dahari, M. Heat transfer and fluid flow of pseudo-plastic nanofluid over a moving permeable plate with viscous dissipation and heat absorption/generation. J. Therm. Anal. Calorim. 2019, 135, 1643–1654. [Google Scholar] [CrossRef]
- Shankar, U.; Naduvinamani, N. Magnetized squeezed flow of time-dependent Prandtl-Eyring fluid past a sensor surface. Heat Transf. Asian Res. 2019, 48, 2237–2261. [Google Scholar] [CrossRef]
- Al-Kaabi, W.; Al-Khafajy, D.G.S. Radiation and Mass Transfer Effects on Inclined MHD Oscillatory Flow for Prandtl-Eyring Fluid through a Porous Channel. Al-Qadisiyah J. Pure Sci. 2021, 26, 347–363. [Google Scholar]
- Hayat, T.; Ullah, I.; Muhammad, K.; Alsaedi, A. Gyrotactic microorganism and bio-convection during flow of Prandtl-Eyring nanomaterial. Nonlinear Eng. 2021, 10, 201–212. [Google Scholar] [CrossRef]
- Waqas, H.; Farooq, U.; Alshehri, H.M.; Goodarzi, M. Marangoni-bioconvectional flow of Reiner–Philippoff nanofluid with melting phenomenon and nonuniform heat source/sink in the presence of a swimming microorganisms. Math. Methods Appl. Sci. 2021. [Google Scholar] [CrossRef]
- Alazwari, M.A.; Abu-Hamdeh, N.H.; Goodarzi, M. Entropy Optimization of First-Grade Viscoelastic Nanofluid Flow over a Stretching Sheet by Using Classical Keller-Box Scheme. Mathematics 2021, 9, 2563. [Google Scholar] [CrossRef]
- Munjam, S.R.; Gangadhar, K.; Seshadri, R.; Rajeswar, M. Novel technique MDDIM solutions of MHD flow and radiative Prandtl-Eyring fluid over a stretching sheet with convective heating. Int. J. Ambient. Energy 2021, 43, 4850–4859. [Google Scholar] [CrossRef]
- Jamshed, W.; Kumar, V.; Kumar, V. Computational examination of Casson nanofluid due to a nonlinear stretching sheet subjected to particle shape factor: Tiwari and Das model. Numer. Methods Partial. Differ. Equ. 2020, 38, 848–875. [Google Scholar] [CrossRef]
- Jamshed, W.; Mishra, S.; Pattnaik, P.; Nisar, K.S.; Devi, S.S.U.; Prakash, M.; Shahzad, F.; Hussain, M.; Vijayakumar, V. Features of entropy optimization on viscous second grade nanofluid streamed with thermal radiation: A Tiwari and Das model. Case Stud. Therm. Eng. 2021, 27, 101291. [Google Scholar] [CrossRef]
- Abdelmalek, Z.; Hussain, A.; Bilal, S.; Sherif, E.-S.M.; Thounthong, P. Brownian motion and thermophoretic diffusion influence on thermophysical aspects of electrically conducting viscoinelastic nanofluid flow over a stretched surface. J. Mater. Res. Technol. 2020, 9, 11948–11957. [Google Scholar] [CrossRef]
- Pan, M.; Zheng, L.; Liu, F.; Zhang, X. Modeling heat transport in nanofluids with stagnation point flow using fractional calculus. Appl. Math. Model. 2016, 40, 8974–8984. [Google Scholar] [CrossRef]
- Li, S.N.; Cao, B.Y. Fractional Boltzmann transport equation for anomalous heat transport and divergent thermal conductivity. Int. J. Heat Mass Transf. 2019, 137, 84–89. [Google Scholar] [CrossRef]
- Santina, D.; Asif, M.; Aljawi, S.; Mlaiki, N. Application of the inverse Laplace transform techniques to solve the generalized Bagley–Torvik equation including Caputo’s fractional derivative. Partial. Differ. Equ. Appl. Math. 2024, 10, 100664. [Google Scholar] [CrossRef]
- Chen, X.; Ye, Y.; Zhang, X.; Zheng, L. Lie-group similarity solution and analysis for fractional viscoelastic MHD fluid over a stretching sheet. Comput. Math. Appl. 2018, 75, 3002–3011. [Google Scholar] [CrossRef]
- Caputo, M. Linear models of dissipation whose Q is almost frequency independent. Ann. Geophys. 1966, 19, 383–393. [Google Scholar] [CrossRef]
- Chakrabarty, A.K.; Roshid, M.M.; Rahaman, M.M.; Abdeljawad, T.; Osman, M.S. Dynamical analysis of optical soliton solutions for CGL equation with Kerr law nonlinearity in classical, truncated M-fractional derivative, beta fractional derivative, and conformable fractional derivative types. Results Phys. 2024, 60, 107636. [Google Scholar] [CrossRef]
- Asjad, M.I.; Sarwar, N.; Hafeez, M.B.; Sumelka, W.; Muhammad, T. Advancement of non-newtonian fluid with hybrid nanoparticles in a convective channel and prabhakar’s fractional derivative—Analytical solution. Fractal Fract. 2021, 5, 99. [Google Scholar] [CrossRef]
- Asjad, M.I.; Ali, R.; Iqbal, A.; Muhammad, T.; Chu, Y.M. Application of water based drilling clay-nanoparticles in heat transfer of fractional Maxwell fluid over an infinite flat surface. Sci. Rep. 2021, 11, 25. [Google Scholar] [CrossRef]
- Asjad, M.I.; Basit, A.; Iqbal, A.; Shah, N.A. Advances in transport phenomena with nanoparticles and generalized thermal process for vertical plate. Phys. Scr. 2021, 96, 15. [Google Scholar] [CrossRef]
- Pan, M.; Zheng, L.; Liu, F.; Liu, C.; Chen, X. A spatial-fractional thermal transport model for nanofluid in porous media. Appl. Math. Model. 2018, 53, 622–634. [Google Scholar] [CrossRef]
- Tassaddiq, A. MHD flow of a fractional second grade fluid over an inclined heated plate. Chaos Solitons Fractals 2019, 123, 341–346. [Google Scholar] [CrossRef]
- Chen, X.; Yang, W.; Zhang, X.; Liu, F. Unsteady boundary layer flow of viscoelastic MHD fluid with a double fractional Maxwell model. Appl. Math. Lett. 2019, 95, 143–149. [Google Scholar] [CrossRef]
- Yang, W.; Chen, X.; Zhang, X.; Zheng, L.; Liu, F. Flow and heat transfer of double fractional Maxwell fluids over a stretching sheet with variable thickness. Appl. Math. Model. 2020, 80, 204–216. [Google Scholar] [CrossRef]
- Li, B.; Liu, F. Boundary layer flows of viscoelastic fluids over a non-uniform permeable surface. Comput. Math. Appl. 2020, 79, 2376–2387. [Google Scholar] [CrossRef]
- Shen, M.; Chen, L.; Zhang, M.; Liu, F. A renovated Buongiorno’s model for unsteady Sisko nanofluid with fractional Cattaneo heat flux. Int. J. Heat Mass Transf. 2018, 126, 277–286. [Google Scholar] [CrossRef]
- Liu, L.; Feng, L.; Xu, Q.; Zheng, L.; Liu, F. Flow and heat transfer of generalized Maxwell fluid over a moving plate with distributed order time fractional constitutive models. Int. Commun. Heat Mass Transf. 2020, 116, 415. [Google Scholar] [CrossRef]
- Anwar, M.S.; Ahmad, R.T.M.; Shahzad, T.; Irfan, M.; Ashraf, M.Z. Electrified fractional nanofluid flow with suspended carbon nanotubes. Comput. Math. Appl. 2020, 80, 1375–1386. [Google Scholar] [CrossRef]
- Sun, Z.Z.; Wu, X. A fully discrete difference scheme for a diffusion-wave system. Appl. Numer. Math. 2006, 56, 193–209. [Google Scholar] [CrossRef]
- She, M.; Li, D.; Sun, H.W. A transformed L1 method for solving the multi-term time-fractional diffusion problem. Math. Comput. Simul. 2022, 193, 584–606. [Google Scholar] [CrossRef]
- Yuan, W.; Li, D.; Zhang, C. Linearized Transformed L1 Galerkin FEMs with Unconditional Convergence for Nonlinear Time Fractional Schrödinger Equations. Numer. Math. Theory Methods Appl. 2023, 16, 348–369. [Google Scholar] [CrossRef]
- Lu, Z.; Fan, W. A fast algorithm for multi-term time-space fractional diffusion equation with fractional boundary condition. Numer. Algorithms 2024, 1–24. [Google Scholar] [CrossRef]
- Chen, W.; Sun, H.; Zhang, X.; Korošak, D. Anomalous diffusion modeling by fractal and fractional derivatives. Comput. Math. Appl. 2010, 59, 1754–1758. [Google Scholar] [CrossRef]
- Khan, Z.A.; Shah, K.; Abdalla, B.; Abdeljawad, T. A numerical Study of Complex Dynamics of a Chemostat Model Under Fractal-Fractional Derivative. Fractals 2023, 31, 2340181. [Google Scholar] [CrossRef]
- Li, F.-l.; Wu, Z.-k.; Ye, C.-r. A finite difference solution to a two-dimensional parabolic inverse problem. Appl. Math. Model. 2012, 36, 2303–2313. [Google Scholar] [CrossRef]
- Arif, M.S.; Abodayeh, K.; Nawaz, Y. A finite difference explicit-implicit scheme for fractal heat and mass transportation of Williamson nanofluid flow in quantum calculus. Numer. Heat Transf. Part A Appl. 2024, 1–23. [Google Scholar] [CrossRef]
- Arif, M.S.; Abodayeh, K.; Nawaz, Y. The modified finite element method for heat and mass transfer of unsteady reacting flow with mixed convection. Front. Phys. 2022, 10, 952787. [Google Scholar] [CrossRef]
- Nawaz, Y.; Arif, M.S.; Abodayeh, K. An explicit-implicit numerical scheme for time fractional boundary layer flows. Int. J. Numer. Methods Fluids 2022, 94, 920–940. [Google Scholar] [CrossRef]
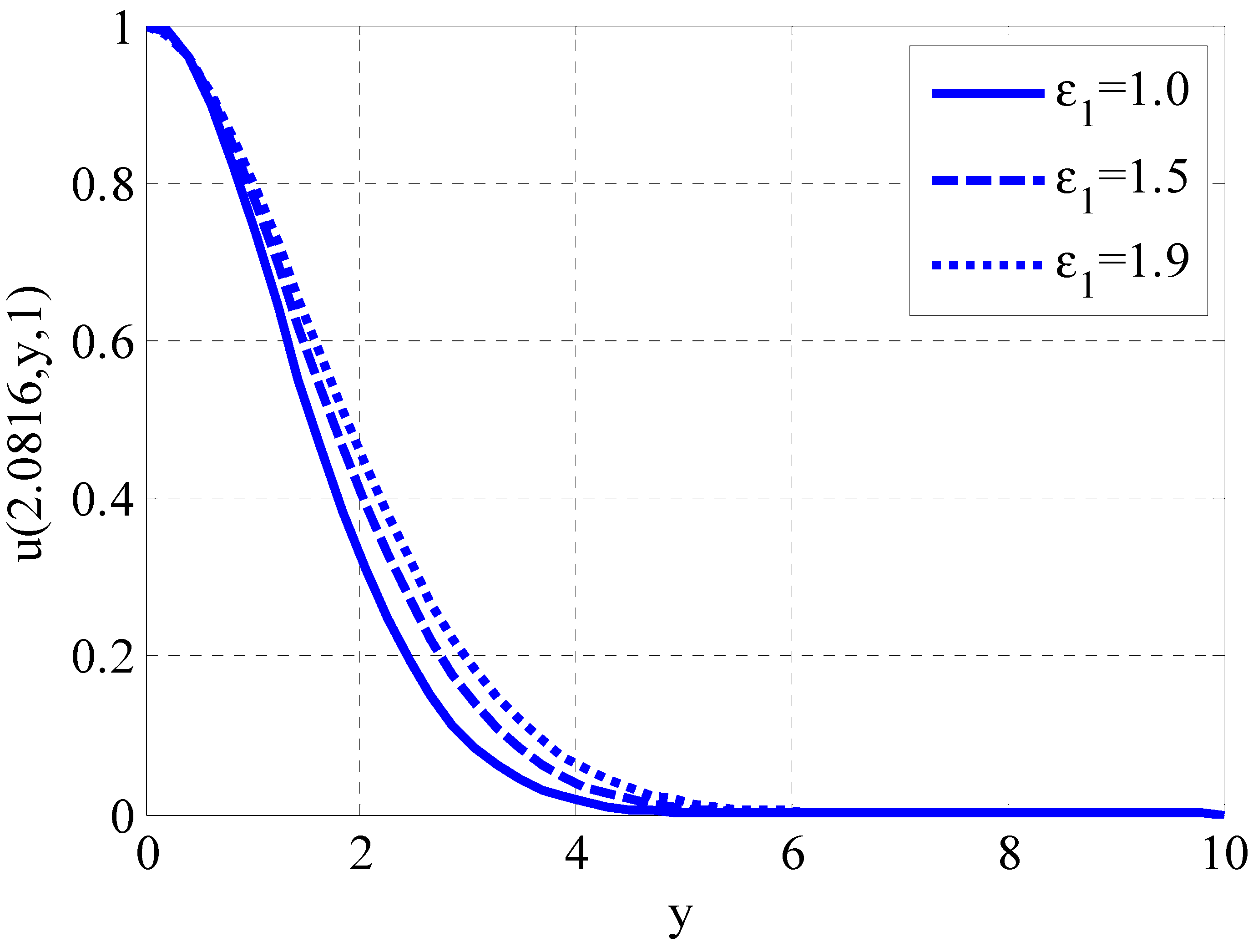

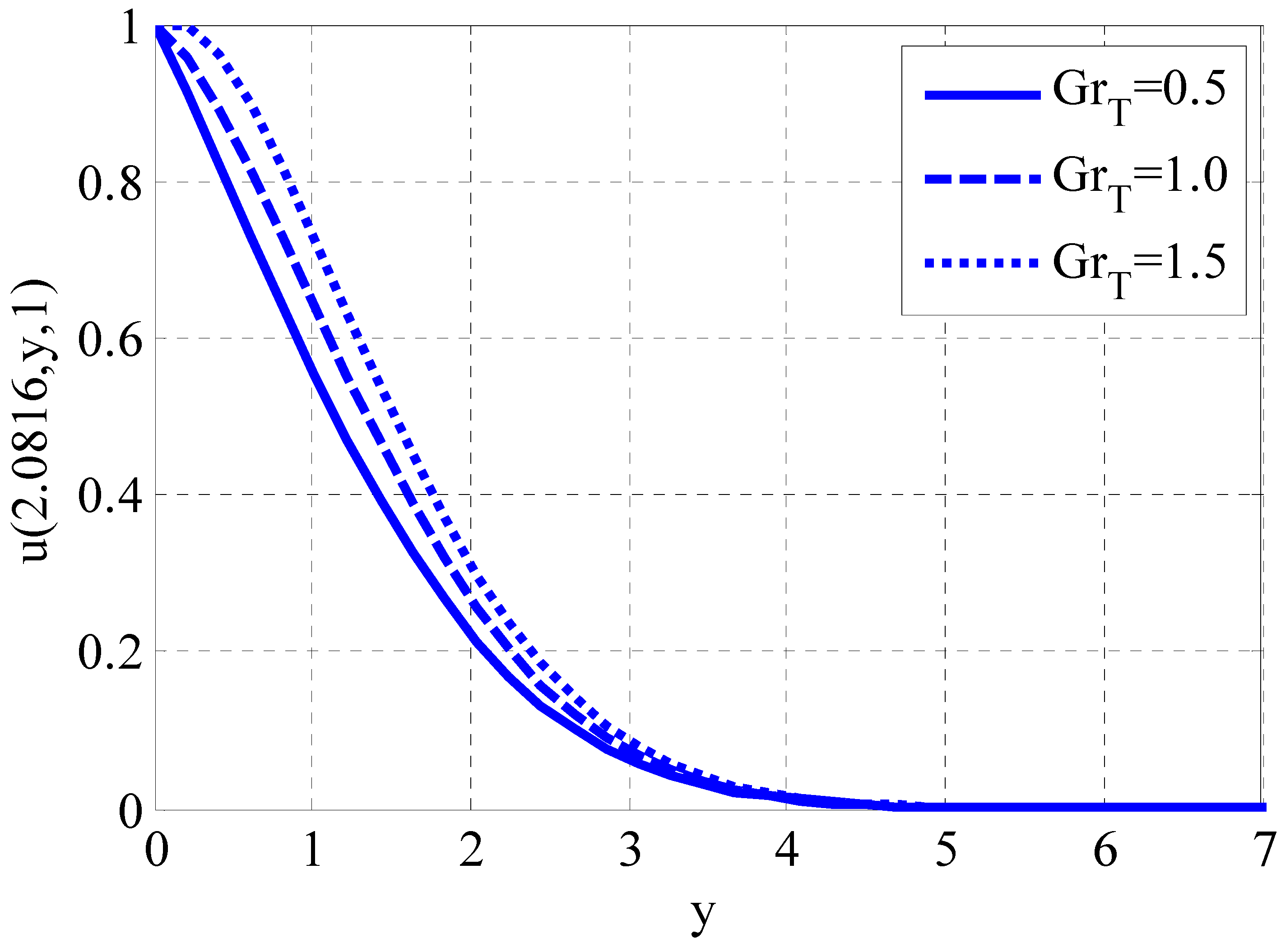
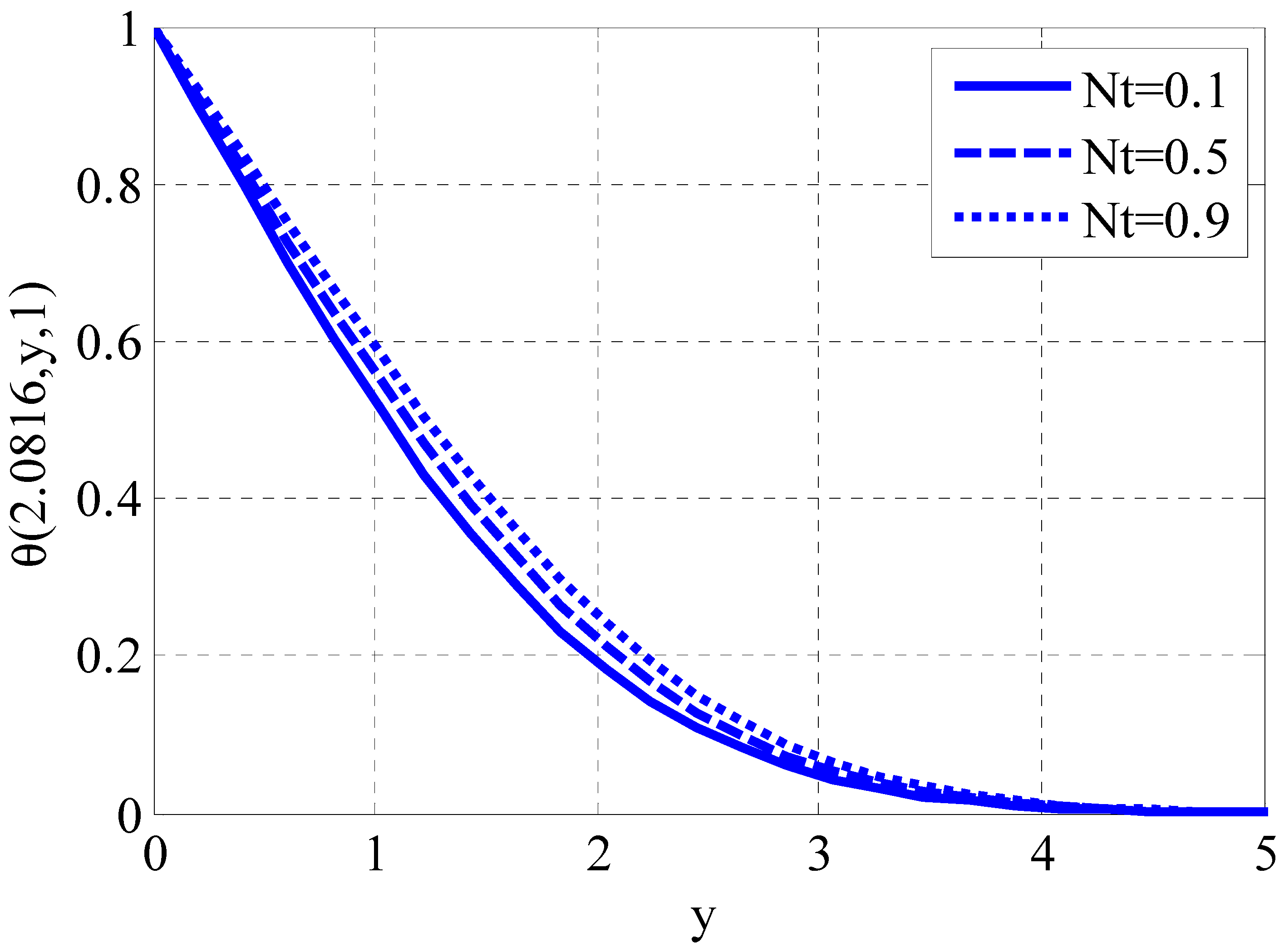
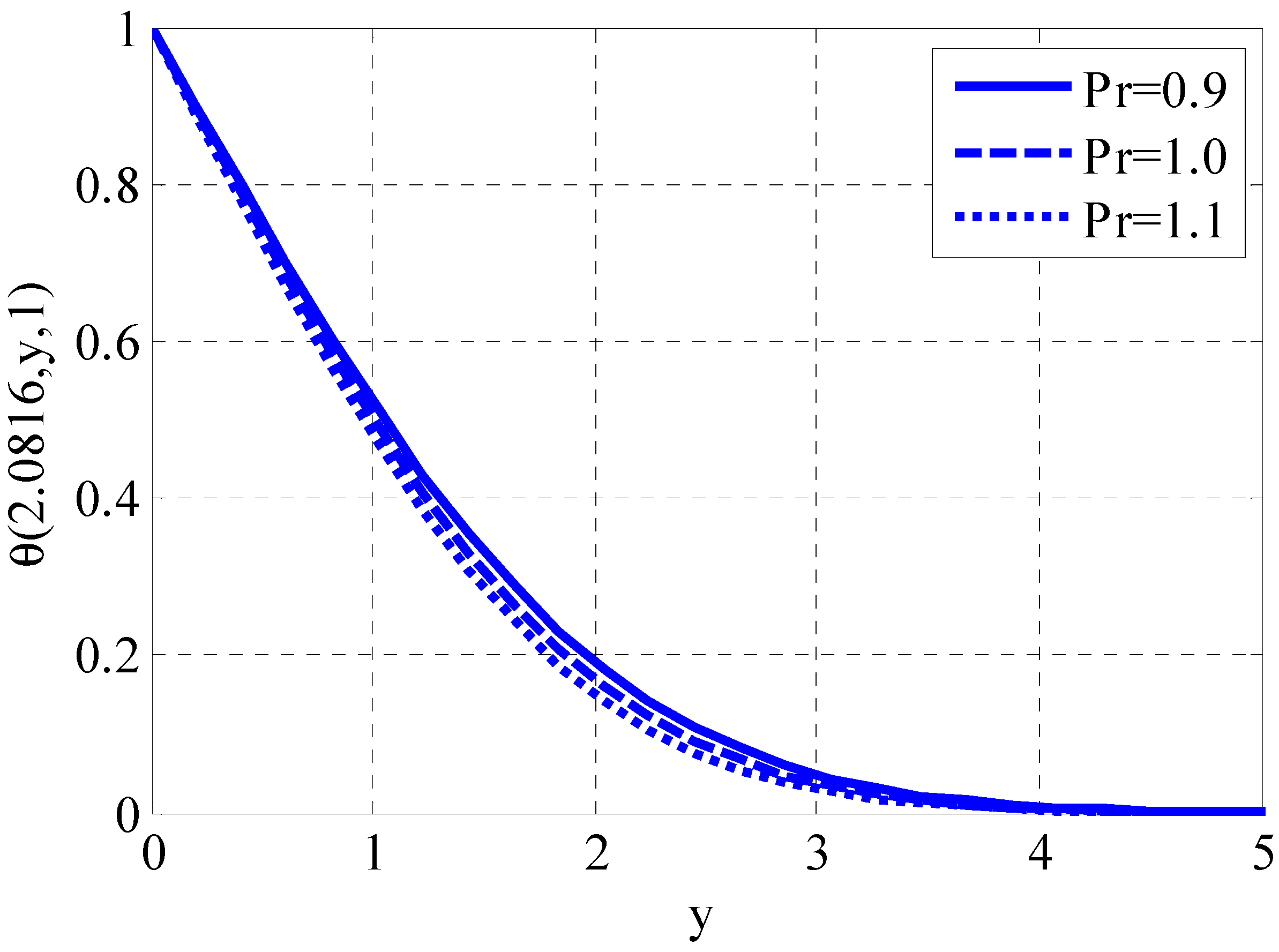



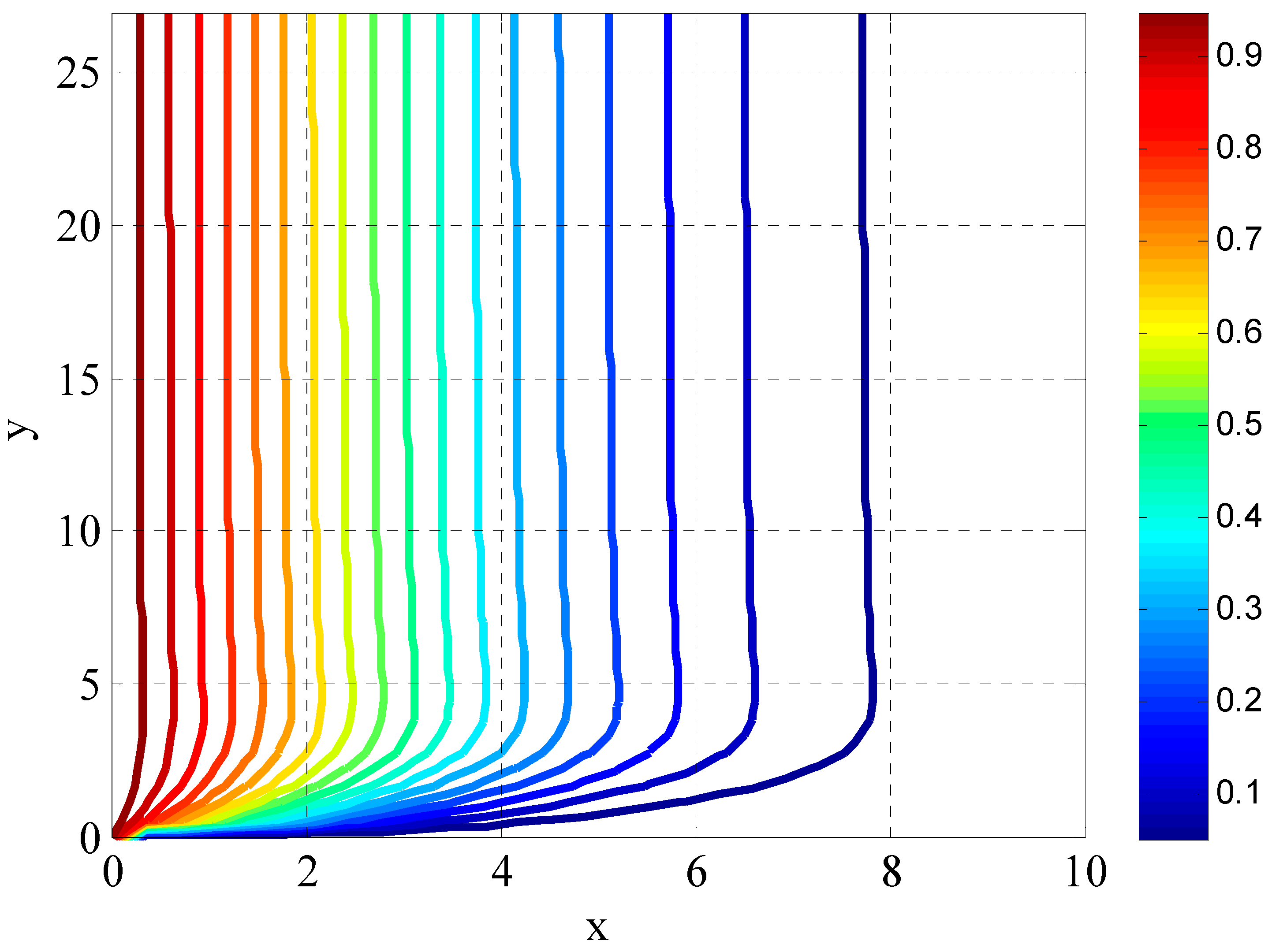
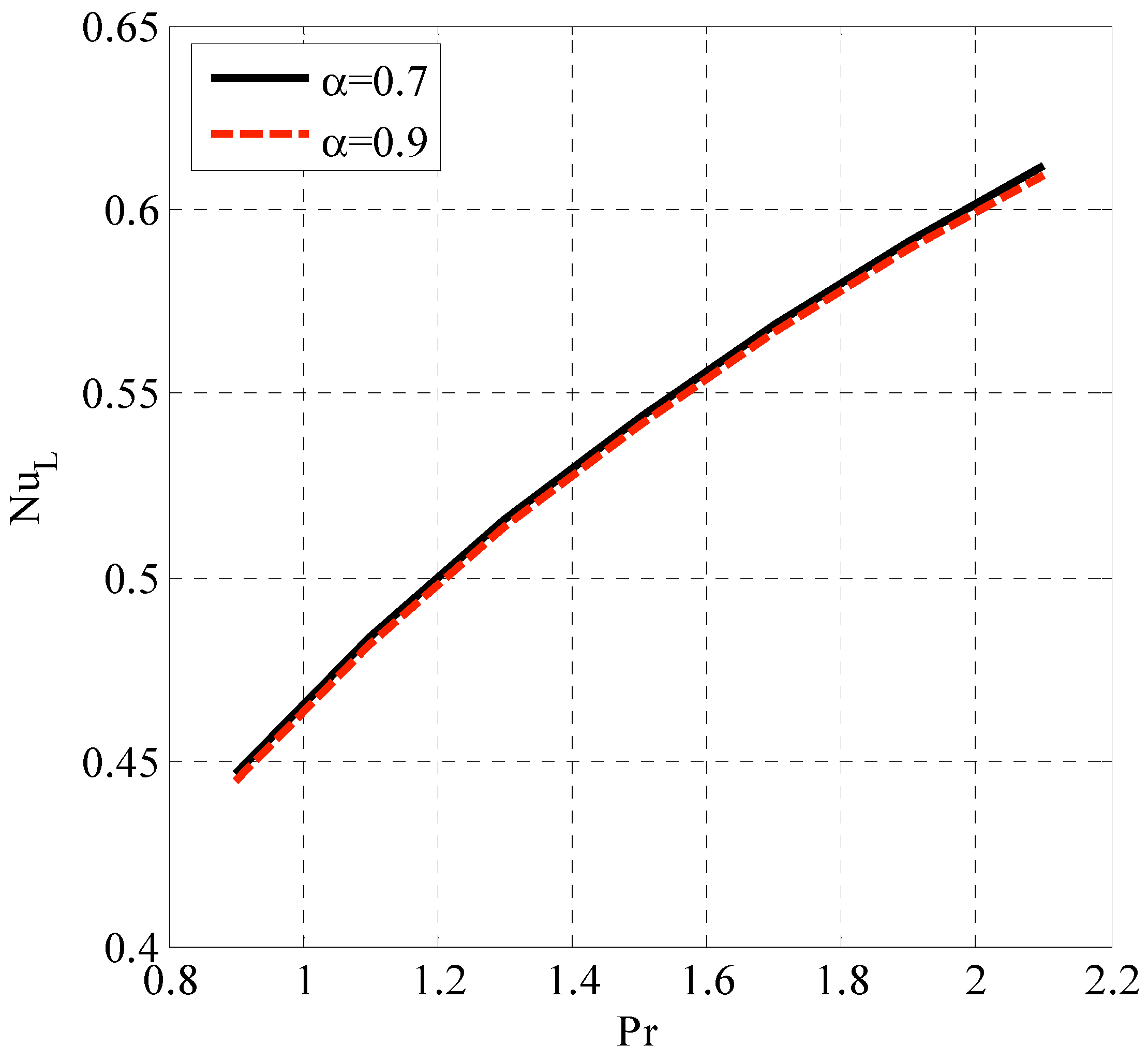
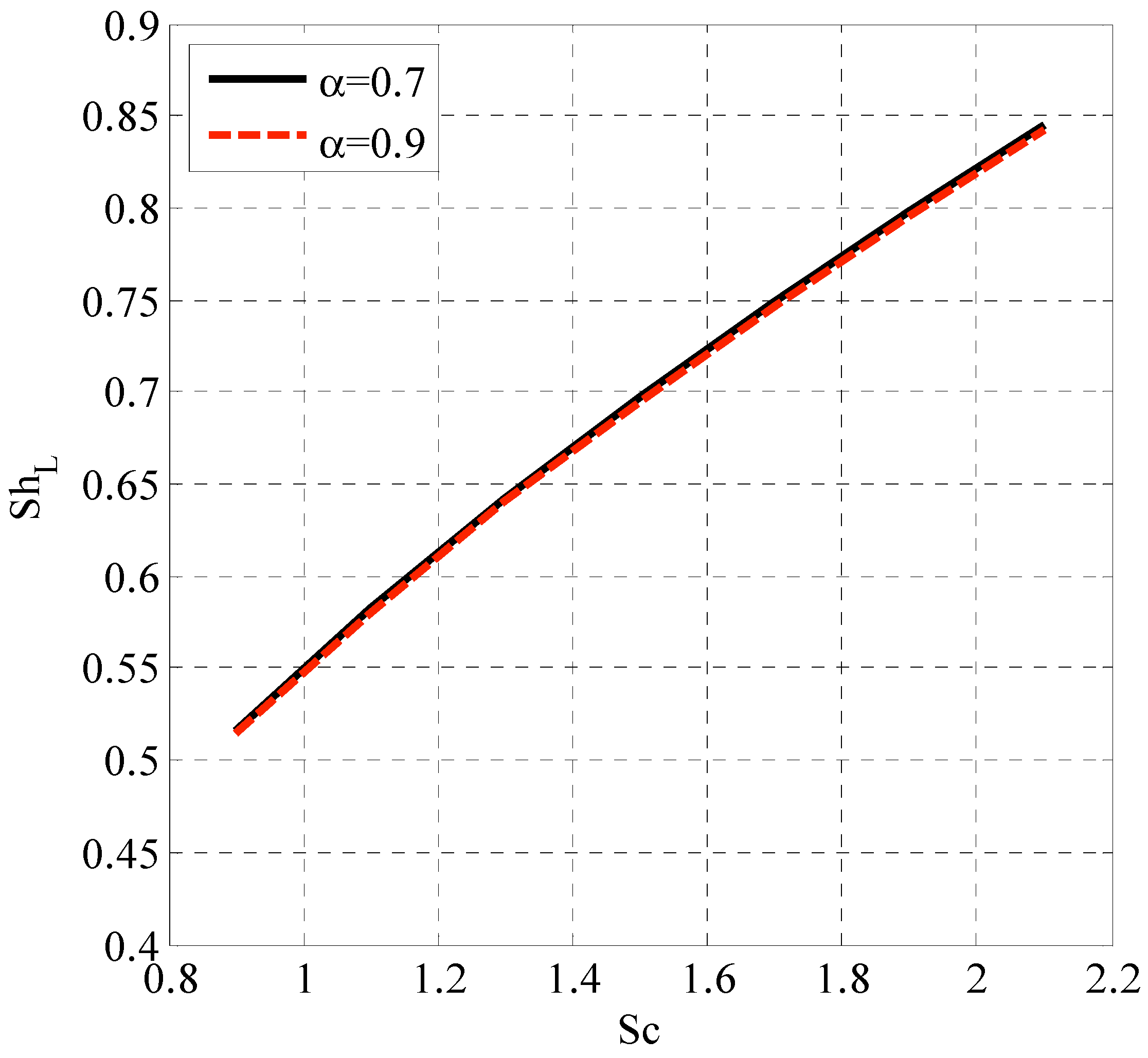
| Fluid | Type of Derivative | Type of Magnetic Field | Type of Solution | Researchers | Case Study |
|---|---|---|---|---|---|
| Single nanofluid (Water-CuWater-Ag Water- Water-) | Spatial fractional | Without magnetic field | Numerical (finite difference) | Pan et al. [35] | Boundary layer flow in a porous media |
| Second-grade fluid | Time fractional | Inclined magnetic field | Numerical (Laplace along with Zakian’s algorithm) | Tassaddiq [36] | Boundary layer flow along an inclined heated plate |
| Viscoelastic fluid | Time fractional | Vertical magnetic field | Numerical (finite difference) | Chen et al. [37] | Boundary layer flow over a stretching sheet |
| Maxwell fluid | Time fractional | Without magnetic field | Numerical (finite difference) | Yang et al. [38] | Stretching sheet with variable thickness |
| Viscoelastic fluid | Spatial fractional | Without magnetic field | Numerical (finite difference) | Li et al. [39] | Boundary layer over a permeable surface |
| Sisko nanofluid | Time fractional | Without magnetic field | Numerical (finite difference) | Shen et al. [40] | Boundary layer flow over a continuously moving plate |
| Maxwell fluid | Time fractional | Without magnetic field | Numerical (finite difference) | Liu et al. [41] | Boundary layer over a moving plate |
| Single nanofluid (Water-SWCNTs Water-MWCNTs) | Time fractional | Vertical magnetic field | Numerical (Joint of finite-difference discretization and L1 algorithm) | Anwar et al. [42] | Boundary layer flow induced due to a stretching sheet |
| Proposed | 1st Order Scheme | 2nd Order Scheme | ||||
|---|---|---|---|---|---|---|
| Error | Conv. Order | Error | Conv. Order | Error | Conv. Order | |
| 4.27 × 10−4 | - | 6.29 × 10−4 | - | 5.31 × 10−4 | - | |
| 4.19 × 10−4 | 0.1227 | 5.93 × 10−4 | 0.3823 | 5.09 × 10−4 | 0.2745 | |
| 4.13 × 10−4 | 0.1080 | 5.66 × 10−4 | 0.3490 | 4.92 × 10−4 | 1.2805 | |
| 4.09 × 10−4 | 0.0826 | 5.45 × 10−4 | 0.3210 | 4.79 × 10−4 | 0.2274 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nawaz, Y.; Arif, M.S.; Mansoor, M.; Abodayeh, K.; Baazeem, A.S. Fractal Numerical Investigation of Mixed Convective Prandtl-Eyring Nanofluid Flow with Space and Temperature-Dependent Heat Source. Fractal Fract. 2024, 8, 276. https://doi.org/10.3390/fractalfract8050276
Nawaz Y, Arif MS, Mansoor M, Abodayeh K, Baazeem AS. Fractal Numerical Investigation of Mixed Convective Prandtl-Eyring Nanofluid Flow with Space and Temperature-Dependent Heat Source. Fractal and Fractional. 2024; 8(5):276. https://doi.org/10.3390/fractalfract8050276
Chicago/Turabian StyleNawaz, Yasir, Muhammad Shoaib Arif, Muavia Mansoor, Kamaleldin Abodayeh, and Amani S. Baazeem. 2024. "Fractal Numerical Investigation of Mixed Convective Prandtl-Eyring Nanofluid Flow with Space and Temperature-Dependent Heat Source" Fractal and Fractional 8, no. 5: 276. https://doi.org/10.3390/fractalfract8050276
APA StyleNawaz, Y., Arif, M. S., Mansoor, M., Abodayeh, K., & Baazeem, A. S. (2024). Fractal Numerical Investigation of Mixed Convective Prandtl-Eyring Nanofluid Flow with Space and Temperature-Dependent Heat Source. Fractal and Fractional, 8(5), 276. https://doi.org/10.3390/fractalfract8050276









