Abstract
We study the critical behaviors of systems undergoing fractal time processes above the upper critical dimension. We derive a set of novel critical exponents, irrespective of the order of the fractional time derivative or the particular form of interaction in the Hamiltonian. For fractal time processes, we not only discover new universality classes with a dimensional constant but also decompose the dangerous irrelevant variables to obtain corrections for critical dynamic behavior and static critical properties. This contrasts with the traditional theory of critical phenomena, which posits that static critical exponents are unrelated to the dynamical processes. Simulations of the Landau–Ginzburg model for fractal time processes and the Ising model with temporal long-range interactions both show good agreement with our set of critical exponents, verifying its universality. The discovery of this new universality class provides a method for examining whether a system is undergoing a fractal time process near the critical point.
1. Introduction
Time effects play a crucial role in phase transitions, and have attracted widespread attention in recent years [1,2,3]. The Markov stochastic thermodynamics has been well established and proven [4,5], which is meaningful for phase transition in open systems only when the timescale for a system to reach equilibrium from a non-equilibrium state is much smaller than the timescale for the environment to reach a new equilibrium after the system’s state changes [6]. However, strong coupling between the system and the environment, initial-state correlations, and entanglement, as well as the coupling between quantum systems and an environment possessing a nanoscale structure, can lead to memory effects [7]. The quantum open system coupled to a sub-Ohmic Bosonic environment exhibits non-Markovian behavior during the integration of environmental degrees of freedom, leading to the reversed flow of past-time information back to the open system [8], and these critical phenomena have been extensively studied [9,10,11]. Although the quantum-classical correspondence of critical phenomena has been validated under the Markov approximation [12], the critical behavior of non-Markovian systems in classical systems remains an open question.
The study of critical phenomena inevitably involves an upper critical dimension that depends on the form of spatial interaction [13]. When the spatial dimension is below this upper critical dimension, the critical exponents depend on the form of spatial interaction [14]. However, when the spatial dimension is above this upper critical dimension, due to the presence of dangerous irrelevant variables (DIVs), the critical exponents exhibit a high degree of universality independent of the spatial interaction form [15]. Although additional corrections are required for size effects, mean-field exponents are effective in describing critical behavior for Markov processes [16]. In recent years, an effective way to describe non-Markovian behavior is by introducing fractional-order time derivatives into the evolution equation [17,18,19]. Although it has been found that the upper critical dimension also depends on the specific order of the fractional derivative [20], the influence of fractal time processes on critical phenomena is an open question. On one hand, in the past, critical properties were entirely dependent on spatial interactions and irrelevant to dynamics [21]; this phenomenon has also been proven in Markov processes [4]. On the other hand, fractal time processes lack practical proof and effective observational methods. Therefore, how fractal time processes affect critical properties remains a significant research question. Furthermore, it is essential to investigate how the critical behavior of fractal time processes manifests a highly universal behavior above the upper critical dimension and how to quantitatively verify these results.
This study aims to extend the research on critical properties above the upper critical dimension to the more general investigation of critical properties with fractal time processes. First, since the introduction of fractal time processes disrupts fundamental thermodynamic relations, we restore the disrupted thermodynamic relations by introducing a dimensional constant instead of a new environmental variable and found novel critical exponents. Then, based on mean-field theory and dangerous irrelevant variable theory, we propose decomposing the dangerous irrelevant variable into a temporal DIV. Consequently, we discover another set of highly universal critical exponents, independent of the fractional order, distinct from the standard mean-field exponents. Finally, we simulate the Landau–Ginzburg model for fractal time processes and the Ising model with temporal long-range interactions for describing ferromagnetic phase transitions to verify the relevant critical exponents. Additionally, due to the universality of critical phenomena [22], this study applies not only to ferromagnetic phase transitions for fractal time processes but also to continuous phase transitions such as gas–liquid transitions, mixture transitions, and super-conducting transitions.
This paper presents the following structure: Section 2 discusses a series of transformations resulting from the violation of thermodynamic relation caused by fractal time processes, and quantitatively calculates the static and dynamic critical exponents above the upper critical dimension. Section 3 introduces a method for obtaining critical exponents and gives the dynamic scaling forms. Section 4 simulates the Landau–Ginzburg model with temporal fractional-order derivatives and the Ising model with temporal long-range interactions to verify the related exponents. Finally, we summarize the research findings of the entire project and discuss potential areas for future investigation in Section 4.
2. Theory of Critical Behavior above the Upper Critical Dimension
In this paper, we study the critical exponents for systems undergoing a fractal time process above the upper critical dimension. We start by considering a generalized form of the time fractional Langevin equation.
Equation (1) is an expansion of the standard Langevin equation, where the Hamiltonian H is described by the Landau–Ginzburg model [23]:
In Equation (1), is the kinetic coefficient and is the fractional order, and in Equation (2), u is the coupling constant, h is the external field, is the deviation from the critical temperature , and is a random external force. For , one assumes the Gaussian distribution with zero mean and the correlation function , is the Caputo derivative operation and can be expressed as follows [24]:
where represents , and is the initial time. For , it recovers to the standard Langevin equation. We present a field-theoretic action for Equation (1) with the main field and the auxiliary field [25,26]:
We employ dimensional analysis to calculate critical exponents [21]. For instance, the renormalized can be expressed as , dominated by a Gaussian fixed point, where b is a renormalized factor, is the dimension of , and is a critical exponent. According to the relation between dimensions and critical exponents, we can determine the critical exponents by setting the dimension of the coordinate dimension as and assuming that are dimensionless. According to the dimensional analysis, the upper critical dimension corresponds to the dimensionlessness of u; the mean-field exponents , , , , , and can also be obtained from at , where , , , , , and are critical exponents. However, the hyperscaling law is only valid for at . For , due to , the hyperscaling law is not effective anymore at . In order to recover the hyperscaling law for the fractal time process at , it should be introduced to transform the original Hamiltonian Equation (2) into , where a is a dimensional constant. To avoid introducing a new scale field a in scaling functions, a series of transformations should be applied; the transformations are as follows:
After the transformations, the introduced dimensional constant a will not appear in the renormalization group equations [27]. Furthermore, due to the form in , the effective spatial dimension changes to in order to hold the accordance of spatial integrals between and ; it can be formed as . In other words, we assign to the spatial integral and to the time such that the former plays a role in generating an effective dimension , whereas the latter serves to further transform the time and dynamic exponent for .
Above the upper critical dimension, due to the influence of DIV, the hyperscaling law is broken, and the Gaussian exponents are no longer suitable to describe the system’s critical behavior [28]. Thus, a simple dimensional analysis is insufficient, and we need to introduce a series of transformations to eliminate the influence of DIV for a fractal time process, such as the following:
Indeed, in the past, the upper critical dimension was only dependent on the gradient term or the form of spatial long-range interactions and irrelevant to the dimension of t in the time-independent Hamiltonian [14,21]. However, the upper critical dimension depends on the form of spatial interaction and the temporal fractional order after considering the fractal time process. To express this more precisely, we decompose u into two components , where represents spatial DIV obtained entirely from the time-independent Hamiltonian as Equation (2), corresponding to the spatial upper critical dimension . According to effective-dimension theory, will be corrected to the spatial dimension demonstrating the mean-field exponents and changes the scaling form of lattice size L for [16]. On the other hand, represents a DIV caused by dynamics and is called temporal DIV. For , due to the real spatial dimension being below the spatial upper critical dimension , and , and the critical behavior of the system will be affected by the temporal DIV rather than the spatial DIV . On the other hand, for , the critical behavior of the system is affected by both the spatial DIV and the temporal DIV due to , . To this end, for , the dimensions of and are expressed as follows:
After transforming as Equation (6), due to the fact that can be regarded as a dimensionless constant, one fixes it at 1 for convenience; becomes as follows:
where
Then, we divide the integrals of space and time into two parts as follows:
Obviously, and correct the spatial dimension d and obtain the effective dimension , whereas will change the temporal dimension as follows:
Since is derived from dynamics rather than spatial interactions, the dimensional analysis should regard and as dimensionless. This makes the dimensions of the variables in Equation (8) change to the following:
Hence, the effective spatial dimension becomes derived from the spatial integral form in Equation (10). According to Equations (7) and (12), the relation between and d is as follows:
Due to the relation between critical exponents and the dimension of variables, the critical exponents for different spatial dimensions are reported in Table 1. It should be emphasized that although Equation (6) is different from the DIV theory, the critical exponents describing macroscopic properties, including related to magnetization, and related to magnetization susceptibility, and related to specific heat, are entirely identical. Moreover, they also have the same finite-size scaling and dynamics scaling (See Supplemental Material for details of dynamics scaling form above the upper critical dimension, 2023). The differences lie in considering the critical exponent , which accounts for the decay of correlations with distance, and the exponent , which defines the correlation length. Various definitions of correlation length just modify our observational approach to the system, without exerting any influence on the macroscopic properties of the system and the accompanying critical exponents.

Table 1.
Critical exponents for the fractal time process above the critical upper dimension.
3. Finite-Time Scaling
According to the analysis presented above, the scaling function of free energy density can be written as follows:
Equation (14) demonstrates that the critical exponents depend solely on the spatial dimension and are not influenced by the fractional order . This implies that the critical behavior, when considering the influence of the fractional derivative above the upper critical dimension, no longer relies on the specific form in the time direction. This is because the effects of fluctuations are constrained when enough past states are taken into account, and then a time-induced special critical behavior will be found. It displays properties similar to mean-field behavior, in which the critical exponents are independent on the details of spatial long-range interactions [29]. Additionally, the scaling forms of magnetization and susceptibility can also be obtained from Equation (14) and expressed as follows:
where and are scaling functions corresponding to magnetization and susceptibility, respectively.
To verify the exponents, we utilize finite-time scaling (FTS) [30], which is an effective method for observing critical dynamics and measuring the dynamic exponent z. FTS observes critical dynamics by linearly changing a parameter in the Hamiltonian. The linear rate R imposes a controllable external finite timescale on the system and replaces with the divergence of the timescale at a critical point. We change the reduced temperature and choose the rate R instead of as a scale field in the scaling function. Accordingly, Equation (14) becomes as follows:
where r is the driven exponent. Due to and , one finds , which can verify the dynamic exponent z. Setting , FTS is expressed as follows:
The others have FTS forms as follows:
In Equation (18), the peak of corresponds to temperature , . This yields a critical exponent and a critical temperature , where is the peak of , and and are values of magnetization and susceptibility at . These parameters are satisfied with , , and ; therefore, and can be obtained. , , , and are non-universal constants.
4. Numerical Results
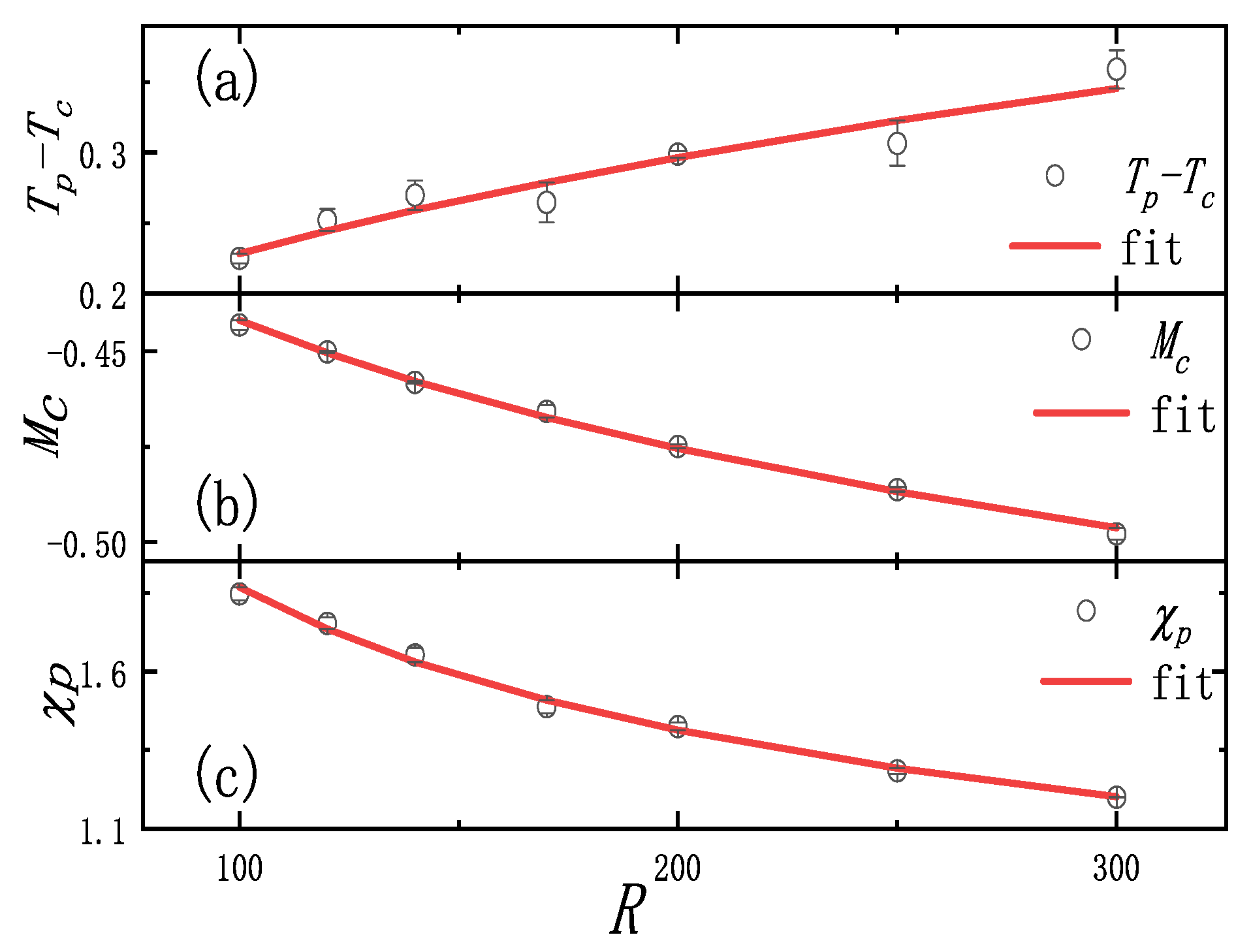
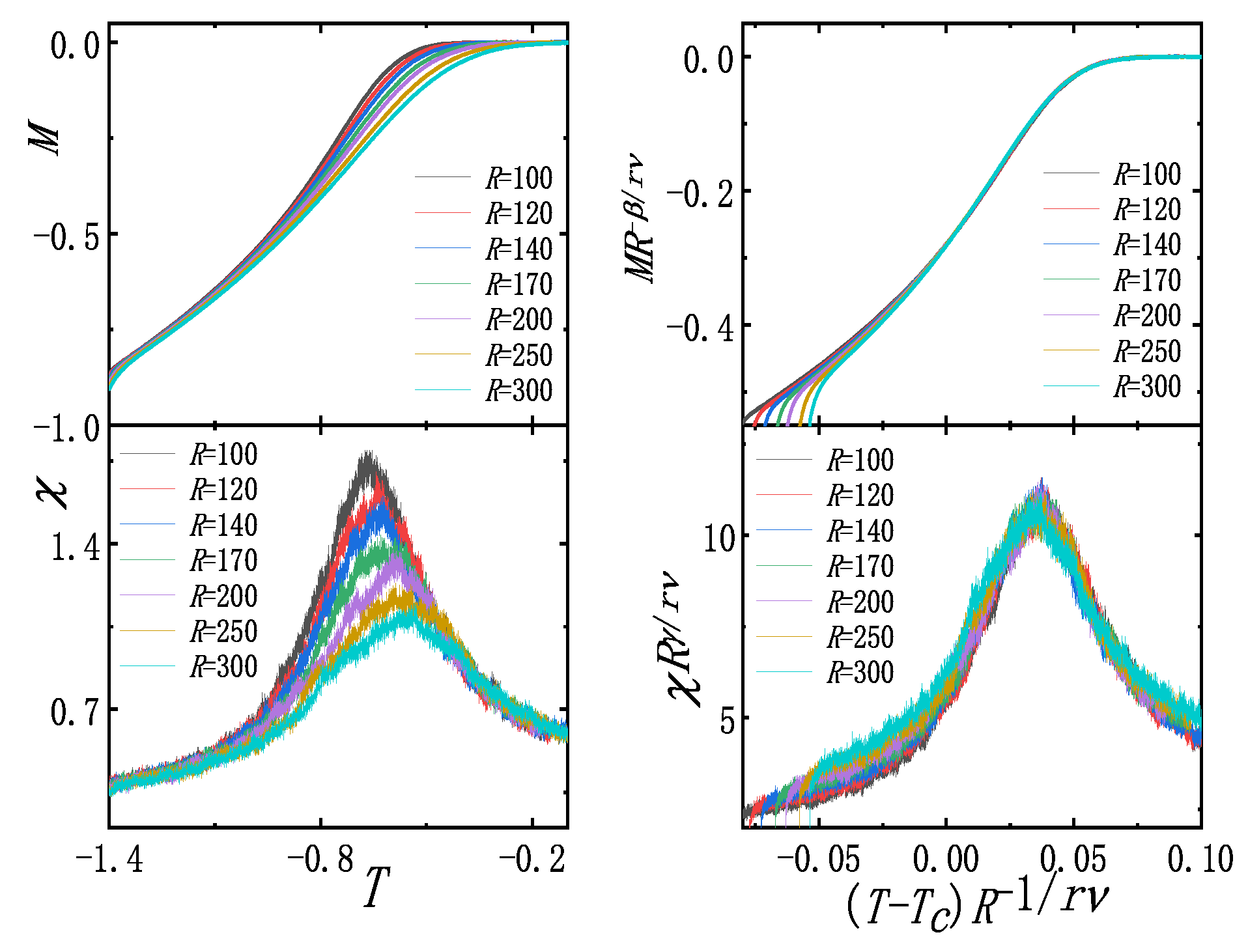
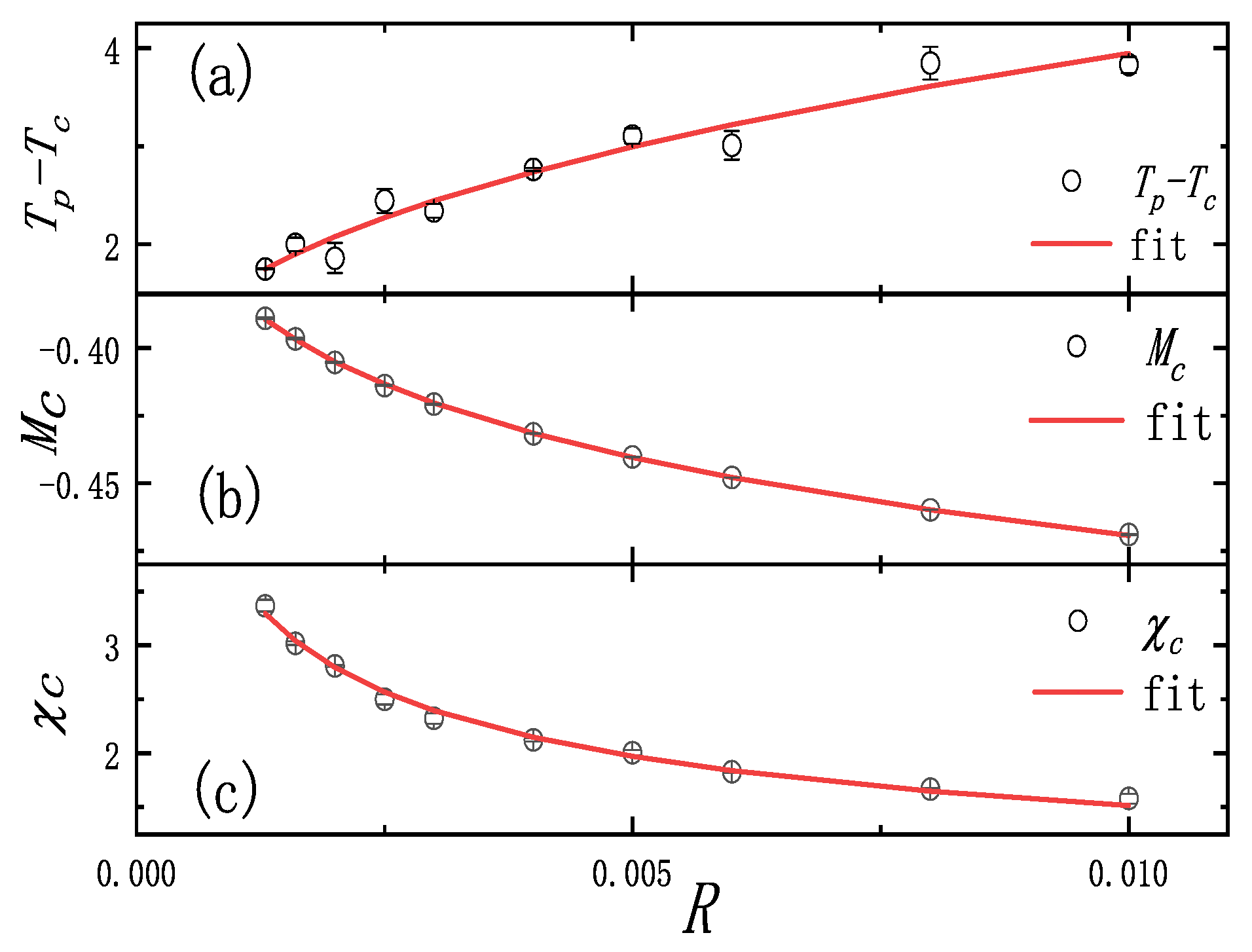
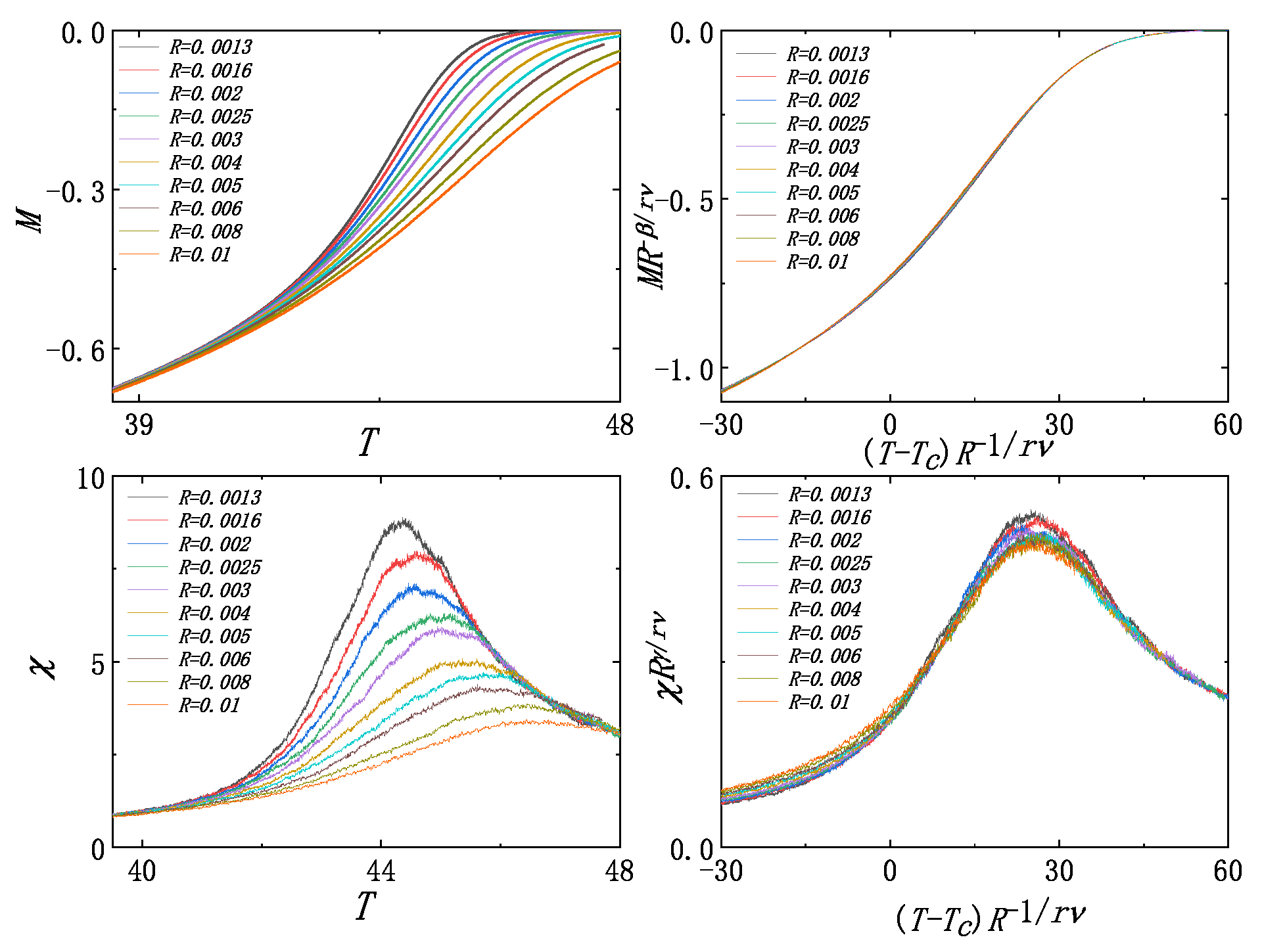
First, we simulate Equation (1) with and cut-off . For fractal time processes with fixed memory, a system will inevitably reach a stable distribution in the long-time limit. As time progresses and more memories accumulate, earlier memories have diminishing effects on the system. Therefore, the system will approach an asymptotic stable distribution, which can be approximated as the result of having a sufficiently large fixed . We use periodic boundary conditions and initial states far from the critical point throughout the heating process. Based on the previous discussion for , , and , the estimated critical temperature leads to Figure 1a–c. Figure 1a displays the fitting curve of and the linear heating rate R. The fitting result shows that . Figure 1b displays the fitting curve of magnetization obtained by linear interpolation at . The fitting curve of and the heating rate R show . Figure 1c displays that the fitting curve of derived from the peak of , the fitting curve of , and the heating rate R show . These fitting results are very close to the theoretical results. The critical exponent is derived from and ; another exponent can be obtained by and . Figure 2 depicts the curves before and after scaling using the theoretical critical exponents. The magnetization and susceptibility curves at different rates R collapse after rescaling. This implies that the critical exponents are effective for the Landau–Ginzburg model for the fractal time process. Furthermore, these exponents are also completely different from the standard 2D Landau–Ginzburg model and mean-field exponents. A slightly smaller has also been investigated, and we found that it did not impact on the measurement of the critical exponents.
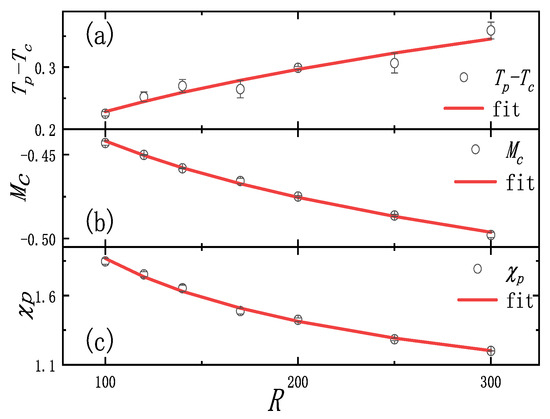
Figure 1.
Fitting curve between (a) and driving rate R, (b) and driving rate R, and (c) and driving rate R in the Landau–Ginzburg model for the fractal time process (average of 2000 samples).
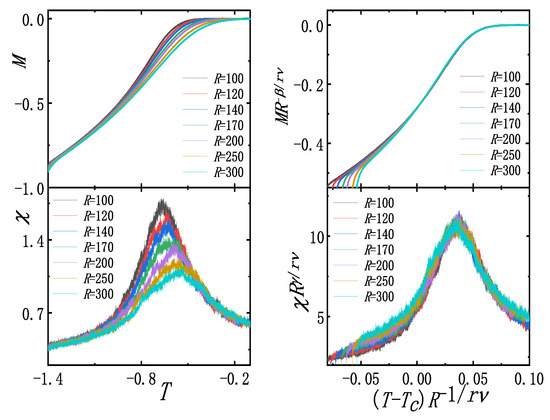
Figure 2.
The original curves of M and are on the left, and the rescaled curves of M and are on the right.
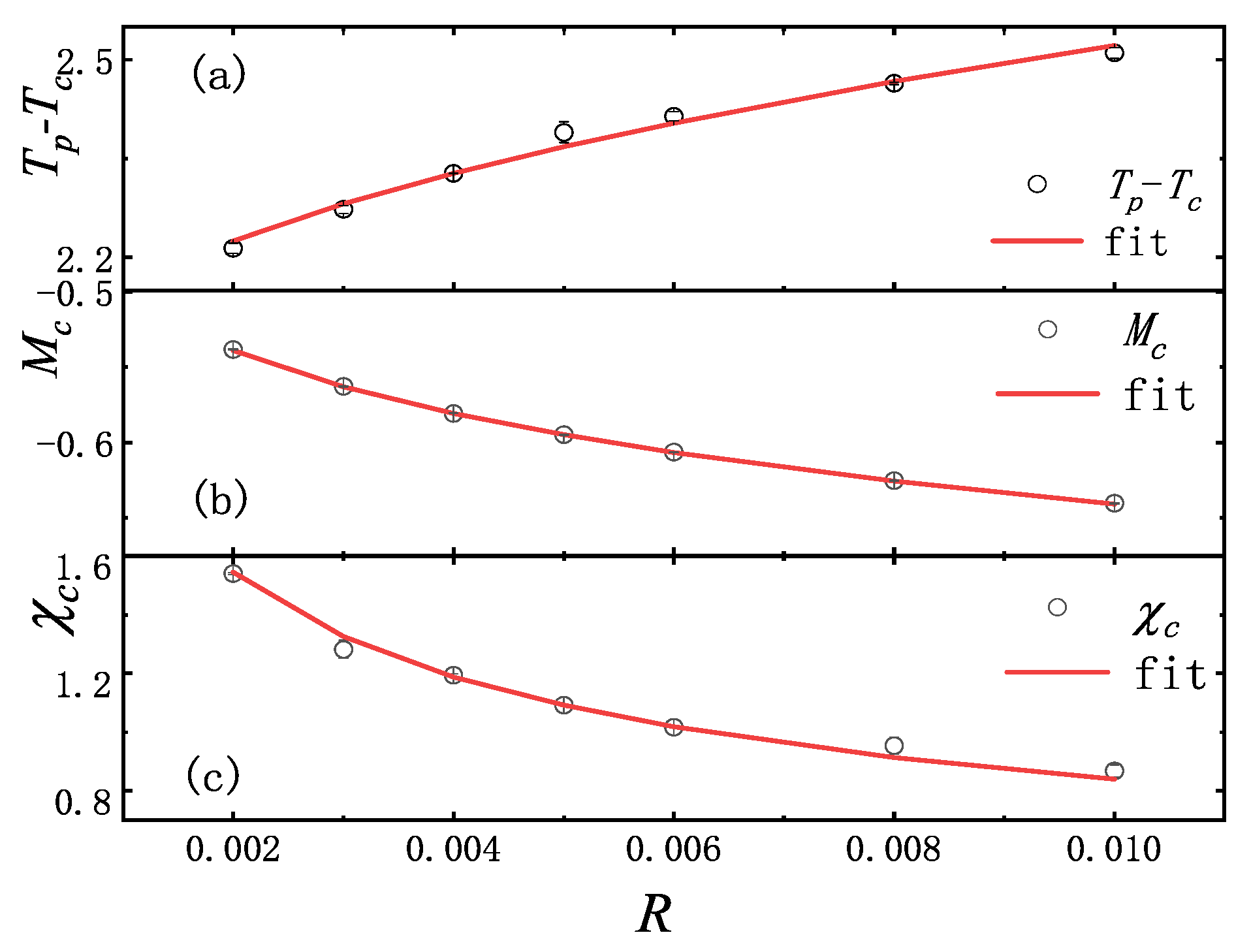
We also simulate the Ising model with temporal long-range interactions of power-law decay (See Supplemental Material for details of Ising model with temporal long-range interactions, 2023). We use linear heating to move the system from the ordered to the disordered phase through the critical point. Period boundary conditions have been applied throughout, and the initial ordered state is also far away from the critical point not to affect the results. The estimated leads to a fitting curve with and in Figure 3a,b. In order to decrease the range of corrections, is obtained through linear interpolation, where replaces , leading to the fitting curve with in Figure 3c. Accordingly, the critical exponents and . The curves are also close to the theoretical values, and these fitting exponents result in the rather good curve collapses around in Figure 4 after rescaling.
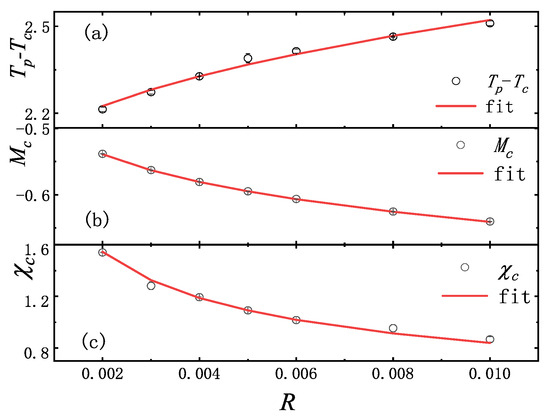
Figure 3.
Fitting curve between (a) and driving rate R, (b) and driving rate R, and (c) and driving rate R in 2D Ising model with temporal long-range interactions for , (average of 40,000 samples).
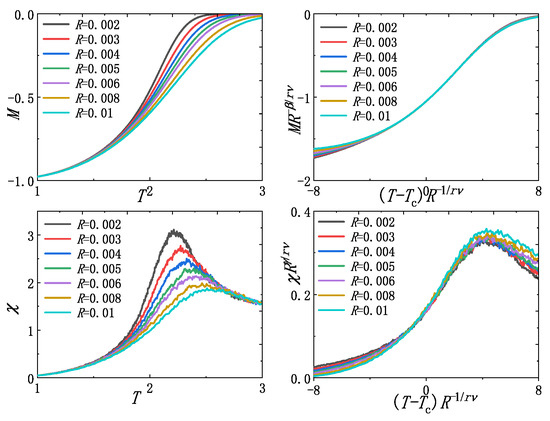
Figure 4.
Original curves of M and on the left and rescaled curves of M and on the right.
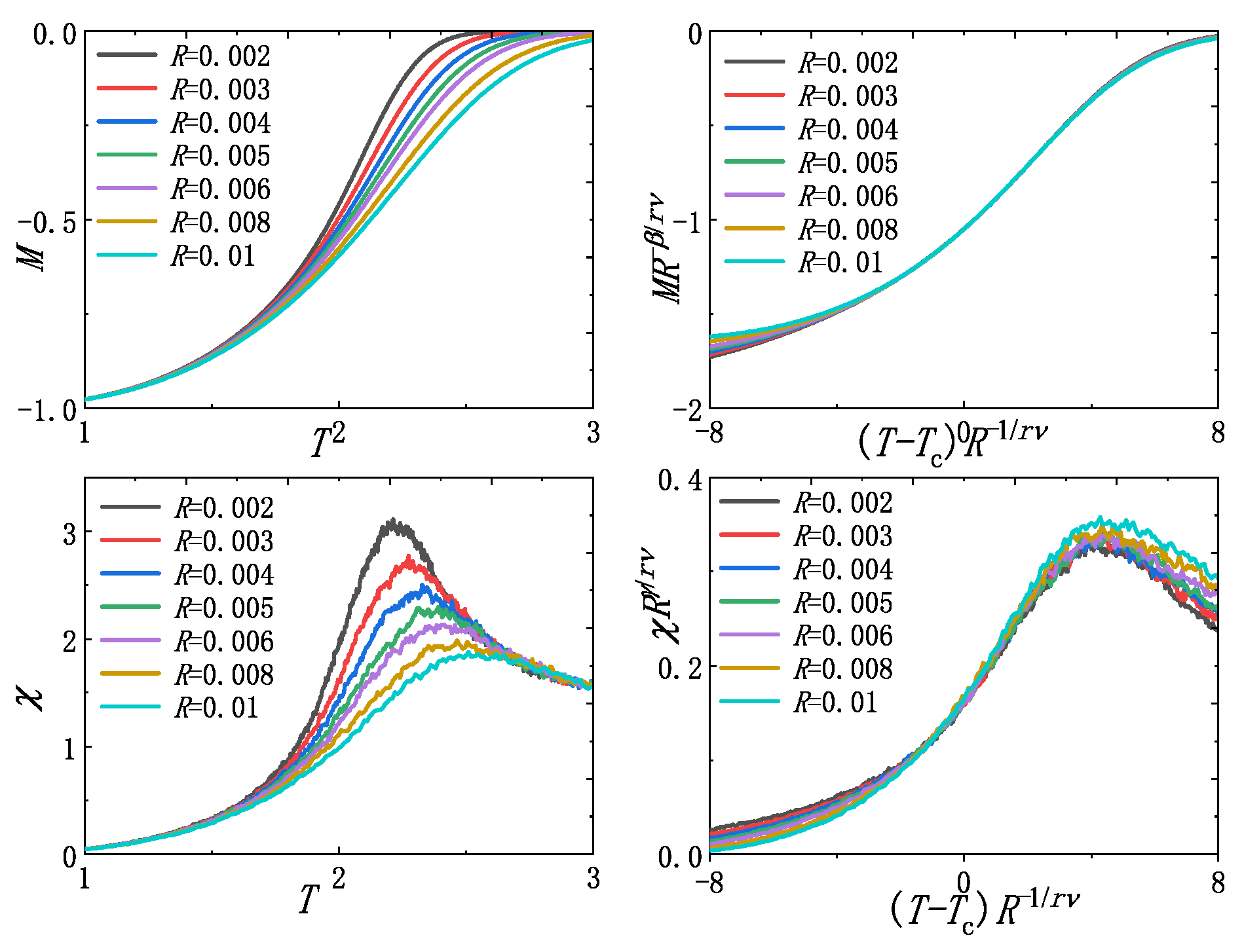
To verify the universality of exponents above the upper critical dimension, we also simulate the Ising model with an exponentially decaying temporal long-range interaction (See Supplemental Material for details of Ising model with temporal long-range interactions, 2023). Figure 5 and Figure 6 display the results of this model. The estimated leads to a fitting curve with , , and (Figure 5a–c), which are also close to the theoretical values , , and . Correspondingly, the critical exponents and are and , respectively. These fitting exponents also result in the rather good curve collapsing around (Figure 6).
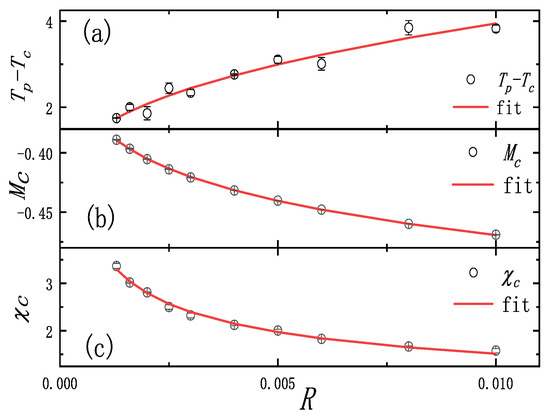
Figure 5.
Fitting curve between (a) and driving rate R, (b) and driving rate R and (c) and driving rate R in 2D Ising model with temporal long-range interactions for , (average of 40,000).
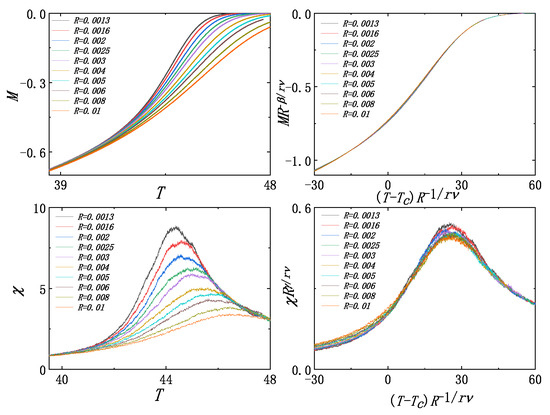
Figure 6.
Original curves of M and on the left and rescaled curves of M and on the right.
Consequently, we notice significant errors and cumulative errors in the computed results. One reason is the insufficient samples and the limited size of the simulated system. Since real phase transitions only occur in systems with an infinite volume, this leads to deviations between our numerical results and theoretical expectations. Additionally, errors unavoidably arise in the interpolation of magnetization and susceptibility at the critical temperature due to fluctuations. Finally, the finite memory size of computers imposes a truncation time for both the Landau–Ginzburg model for fractal time processes and the Ising model with temporal long-range interactions, contributing to the occurrence of errors. Nevertheless, the results of simulations under various interactions in the temporal direction reveal that all models exhibit similar critical exponents when the interaction decreases, being sufficiently slow in the time direction. In addition, we also observed that, after applying theoretical exponential scaling, curves with different rates collapse sufficiently well near the critical point. Therefore, these exponents are effective in describing the critical behavior of systems with fractal time processes. Finally, as mentioned in our theoretical framework, these exponents can be highly universal and completely different from the critical exponents of the standard Landau–Ginzburg model, regardless of the specific form of attenuation, representing a new time-induced universal class.
5. Conclusions
In conclusion, we have quantitatively determined the critical exponents for fractal time processes above the upper critical dimension, which also serve as an upper limit for critical exponents when considering temporal effects. These critical exponents, which are different with standard mean-field exponents, no longer depend on specific fractional orders or the details of temporal interactions, exhibiting a high degree of universality. Moreover, we also find a temporal DIV due to the influence of a temporal DIV. The dynamic exponent remains a fixed value and does not increase as decreases. These results not only demonstrate that fractal time processes can change the critical properties of a system but also imply that the macroscopic properties near the critical point can be modulated through the system’s dynamical behavior. Furthermore, measuring the non-Markovianity of classical systems requires considering the correlations of microscopic states at different times; it is a complex task. However, based on these results, it is a reasonable approach to experimentally measure the macroscopic properties of the system near the critical point to assess non-Markovianity. In fact, we have found similar results to the theory in some experimental results of low-dimensional materials [31,32,33]. Finally, these results have been numerically validated using both the Landau–Ginzburg model for fractal time processes and the Ising model with temporal long-range interactions.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/fractalfract8050294/s1, Supplemental Material for: Relation between DIV theory and effective-dimension theory and details of Ising model with temporal long-range interactions.
Author Contributions
Writing—original draft, S.Z.; Supervision, S.T.; Funding acquisition, Y.H. and B.W.; Writing—review and editing, S.Z. and Y.H.; All authors have read and agreed to the published version of the manuscript.
Funding
The work was supported by the NSFC (National Natural Science Foundation of China) through funds with Grant Nos. 12172090, 11772360, and 11832019.
Data Availability Statement
Data are contained within the article.
Acknowledgments
The authors thank the editors and reviewers for their hard work, who have made outstanding contributions to the improvement of the quality of this article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Heyl, M.; Polkovnikov, A.; Kehrein, S. Dynamical Quantum Phase Transitions in the Transverse-Field Ising Model. Phys. Rev. Lett. 2013, 110, 135704. [Google Scholar] [CrossRef]
- Quintana, M.; Berger, A. Experimental Observation of Critical Scaling in Magnetic Dynamic Phase Transitions. Phys. Rev. Lett. 2023, 131, 116701. [Google Scholar] [CrossRef]
- Bao, Y.; Block, M.; Altman, E. Finite-Time Teleportation Phase Transition in Random Quantum Circuits. Phys. Rev. Lett. 2024, 132, 030401. [Google Scholar] [CrossRef]
- Hohenberg, P.C.; Halperin, B.I. Theory of dynamic critical phenomena. Rev. Mod. Phys. 1977, 49, 435–479. [Google Scholar] [CrossRef]
- Seifert, U. Stochastic thermodynamics, fluctuation theorems and molecular machines. Rep. Prog. Phys. 2012, 75, 126001. [Google Scholar] [CrossRef]
- de Vega, I.; Alonso, D. Dynamics of non-Markovian open quantum systems. Rev. Mod. Phys. 2017, 89, 015001. [Google Scholar] [CrossRef]
- Breuer, H.P.; Laine, E.M.; Piilo, J.; Vacchini, B. Colloquium: Non-Markovian dynamics in open quantum systems. Rev. Mod. Phys. 2016, 88, 021002. [Google Scholar] [CrossRef]
- Caruso, F.; Giovannetti, V.; Lupo, C.; Mancini, S. Quantum channels and memory effects. Rev. Mod. Phys. 2014, 86, 1203–1259. [Google Scholar] [CrossRef]
- Kaur, K.; Sépulcre, T.; Roch, N.; Snyman, I.; Florens, S.; Bera, S. Spin-Boson Quantum Phase Transition in Multilevel Superconducting Qubits. Phys. Rev. Lett. 2021, 127, 237702. [Google Scholar] [CrossRef]
- Qian, X.; Sun, Z.; Zhou, N. Unveiling quantum entanglement and correlation of sub-Ohmic and Ohmic baths for quantum phase transitions in dissipative systems. Phys. Rev. A 2022, 105, 012431. [Google Scholar] [CrossRef]
- De Filippis, G.; de Candia, A.; Cangemi, L.M.; Sassetti, M.; Fazio, R.; Cataudella, V. Quantum phase transitions in the spin-boson model: Monte Carlo method versus variational approach à la Feynman. Phys. Rev. B 2020, 101, 180408. [Google Scholar] [CrossRef]
- Sachdev, S. Quantum Phase Transitions; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Wittmann, M.; Young, A.P. Finite-size scaling above the upper critical dimension. Phys. Rev. E 2014, 90, 062137. [Google Scholar] [CrossRef]
- Fisher, M.E.; Ma, S.k.; Nickel, B.G. Critical Exponents for Long-Range Interactions. Phys. Rev. Lett. 1972, 29, 917–920. [Google Scholar] [CrossRef]
- Luijten, E.; Blöte, H.W.J. Finite-Size Scaling and Universality above the Upper Critical Dimensionality. Phys. Rev. Lett. 1996, 76, 1557–1561. [Google Scholar] [CrossRef]
- Zeng, S.; Szeto, S.P.; Zhong, F. Effective-dimension theory of critical phenomena above upper critical dimensions. Physica Scripta 2022, 97, 125002. [Google Scholar] [CrossRef]
- Matignon, D. An Introduction to Fractional Calculus. In Scaling, Fractals and Wavelets; John Wiley and Sons, Ltd.: Hoboken, NJ, USA, 2009; Chapter 7; pp. 237–277. [Google Scholar] [CrossRef]
- Hattaf, K.; Mohsen, A.A.; Al-Husseiny, H.F. Gronwall inequality and existence of solutions for differential equations with generalized Hattaf fractional derivative. J. Math. Comput. Sci. 2022, 27, 18–27. [Google Scholar] [CrossRef]
- Al-Sa’di, S.; Bibi, M.; Muddassar, M.; Kermausuor, S. Generalized m-preinvexity on fractal set and related local fractional integral inequalities with applications. J. Math. Comput. Sci. 2023, 30, 352–371. [Google Scholar] [CrossRef]
- Batalov, L.; Batalova, A. Critical dynamics in systems controlled by fractional kinetic equations. Phys. A Stat. Mech. Its Appl. 2013, 392, 602–611. [Google Scholar] [CrossRef]
- Wilson, K.G. Renormalization Group and Critical Phenomena. I. Renormalization Group and the Kadanoff Scaling Picture. Phys. Rev. B 1971, 4, 3174–3183. [Google Scholar] [CrossRef]
- Kadanoff, L. Scaling laws for ising models near Tc. Phys. Phys. Fiz. 1966, 2, 263–272. [Google Scholar] [CrossRef]
- Hoffmann, K.; Tang, Q. Ginzburg-Landau Phase Transition Theory and Superconductivity; International Series of Numerical Mathematics; Birkhäuser: Basel, Switzerland, 2012. [Google Scholar]
- Li, C.; Deng, W. Remarks on fractional derivatives. Appl. Math. Comput. 2007, 187, 777–784. [Google Scholar] [CrossRef]
- Zinn-Justin, J. Quantum Field Theory and Critical Phenomena; Oxford University Press: Oxford, UK, 2021. [Google Scholar]
- Vasil’ev, A. The Field Theoretic Renormalization Group in Critical Behavior Theory and Stochastic Dynamics; Chapman and Hall/CRC: New York, NY, USA, 1998. [Google Scholar] [CrossRef]
- Zeng, S.; Szeto, S.P.; Zhong, F. Theory of Critical Phenomena with Memory. Chin. Phys. Lett. 2022, 39, 120501. [Google Scholar] [CrossRef]
- Berche, B.; Kenna, R.; Walter, J.C. Hyperscaling above the upper critical dimension. Nucl. Phys. B 2012, 865, 115–132. [Google Scholar] [CrossRef]
- Luijten, E.; Blöte, H.W.J. Classical critical behavior of spin models with long-range interactions. Phys. Rev. B 1997, 56, 8945–8958. [Google Scholar] [CrossRef]
- Zhong, F. Finite-Time Scaling and Its Applications to Continuous Phase Transitions; IntechOpen: Rijeka, Croatia, 2011; Chapter 18. [Google Scholar] [CrossRef]
- Lyuksyutov, I.; Fedorus, A. Critical exponents of the HW (011) system. Sov. Phys. Jetp 1981, 53, 1317. [Google Scholar]
- Taroni, A.; Bramwell, S.T.; Holdsworth, P.C.W. Universal window for two-dimensional critical exponents. J. Phys. Condens. Matter 2008, 20, 275233. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.H.; Bedoya-Pinto, A.; Blei, M.; Dismukes, A.H.; Hamo, A.; Jenkins, S.; Koperski, M.; Liu, Y.; Sun, Q.C.; Telford, E.J.; et al. The Magnetic Genome of Two-Dimensional van der Waals Materials. ACS Nano 2022, 16, 6960–7079. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).