Exploring the Exact Solution of the Space-Fractional Stochastic Regularized Long Wave Equation: A Bifurcation Approach
Abstract
:1. Introduction
2. Mathematical Analysis
3. Bifurcation Analysis
- (A)
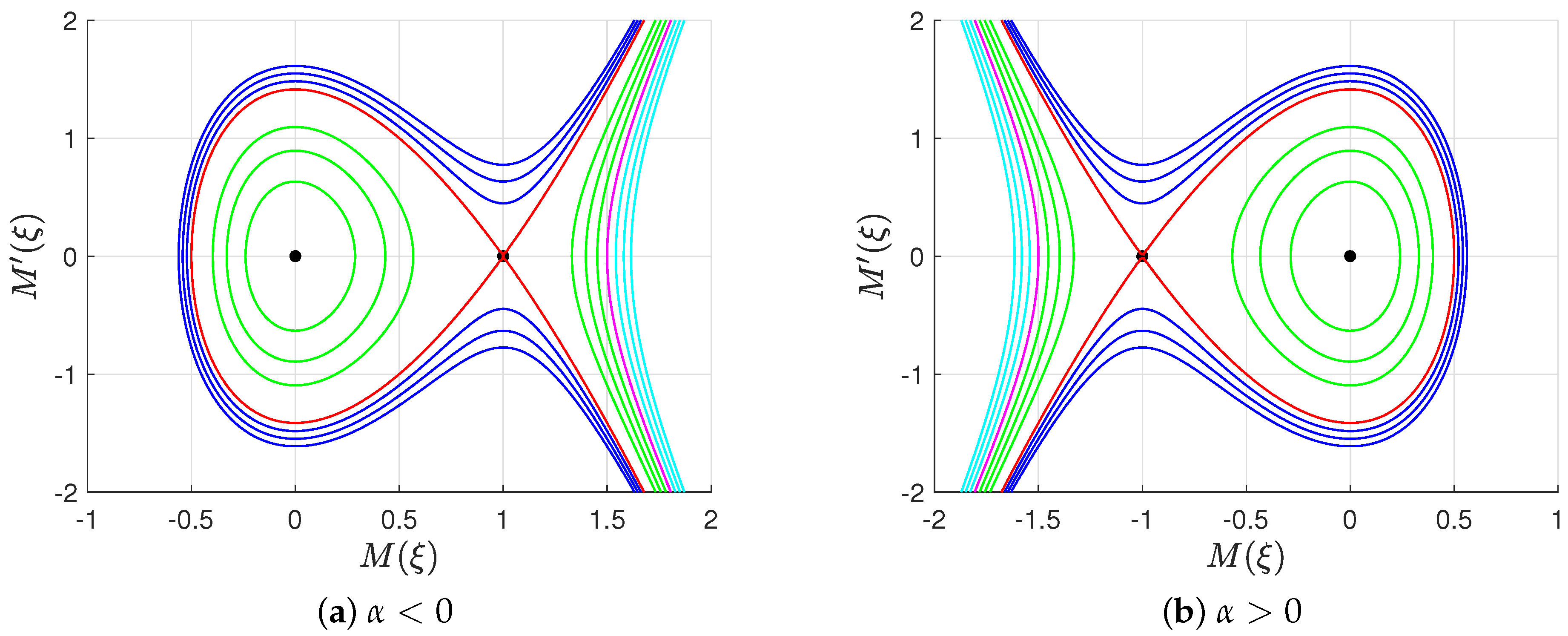
- Figure 1a illustrates the phase portrait corresponding to the system (9) when . In this figure, we see a family of unbounded blue orbits . At , the homoclinic red orbit emerges, connecting the saddle equilibrium point A with itself, in addition to two unbounded solutions. When , there are two families of orbits in green, denoted as . One of them is periodic, positioned inside the homoclinic orbit, while the other is unbounded, lying outside the homoclinic orbit. When , there is an unbounded orbit in pink and the equilibrium solution at B, and when , there is a family of unbounded orbits in cyan. The homoclinic orbit and the unbounded pink orbit are referred to as limiting orbits since the other orbits approach them as the value of f changes. This is called the degeneracy process. The periodic family of green orbits approaches the homoclinic orbit as . Similarly, the family of unbounded blue orbits also approaches the homoclinic red orbit as . A similar description applies to Figure 1b.
- (B)
- When , the phase portrait for system (9) is shown in Figure 2a. For , there is a family of unbounded orbits shown in blue. When , system (9) has a homoclinic orbit in red, connecting the saddle point B with itself, in addition to two unbounded orbits. If , there are two families of green orbits: one is a bounded periodic family located inside the homoclinic orbit, while the other is unbounded and appears outside the homoclinic orbit. For , there is a pink unbounded orbit and the equilibrium solution at A. For , there is an unbounded family of cyan orbits. The two orbits and are termed limiting orbits and play an essential role in studying the degeneracy property of the solutions, as we will see later. A similar description applies to Figure 2b.
4. Solutions Formulation
- (a)
- If , system (9) has unbounded orbit in blue intersecting the M-axis in a single point representing the only real root for the polynomial (14). The polynomial can be written as , where , , and * is the complex conjugation. The real solution interval is . Taking and integrating both sides of Equation (13), we obtainwhere , . By employing the transformation (3), we obtain a new solution for Equation (2) in the form
- (b)
- If , there is a homoclinic orbit in red and two unbounded orbits as illustrated in Figure 1a. Substituting in (14), we obtain . The real solution intervals are and . We examine each interval separately.
- (c)
- For , the system (9) has two different types of orbits in green, as shown in Figure 1a. These orbits intersect the M-axis at three points, namely, the real zeros of the polynomial (14). Hence, , where . The real solution intervals are . We obtain the solutions for each of these intervals separately.
- (d)
- When , in addition to the equilibrium solution at B, the system (9) has an unbounded pink orbit intersecting the M-axis in exactly one point. Hence, the polynomial (14) is written as , where and . Assuming and integrating both sides of Equation (13), we obtainwhere , . Using the transformation (3), a new solution for the SFLRW Equation (2) is constructed, given by
- (e)
- .
Solution Degeneracy
- (a)
- The family of periodic orbits in green shown in Figure 1a approaches the homoclinic orbit in red as the parameter f approaches zero. Thus, we can obtain the homoclinic solution by taking and , and the solution (25) becomeswhich agrees with solution (21). Likewise, the family of unbounded orbits in green will approach the unbounded orbit in pink when f approaches zero. Hence, for the later orbit, the solution in (27) becomes
- (b)
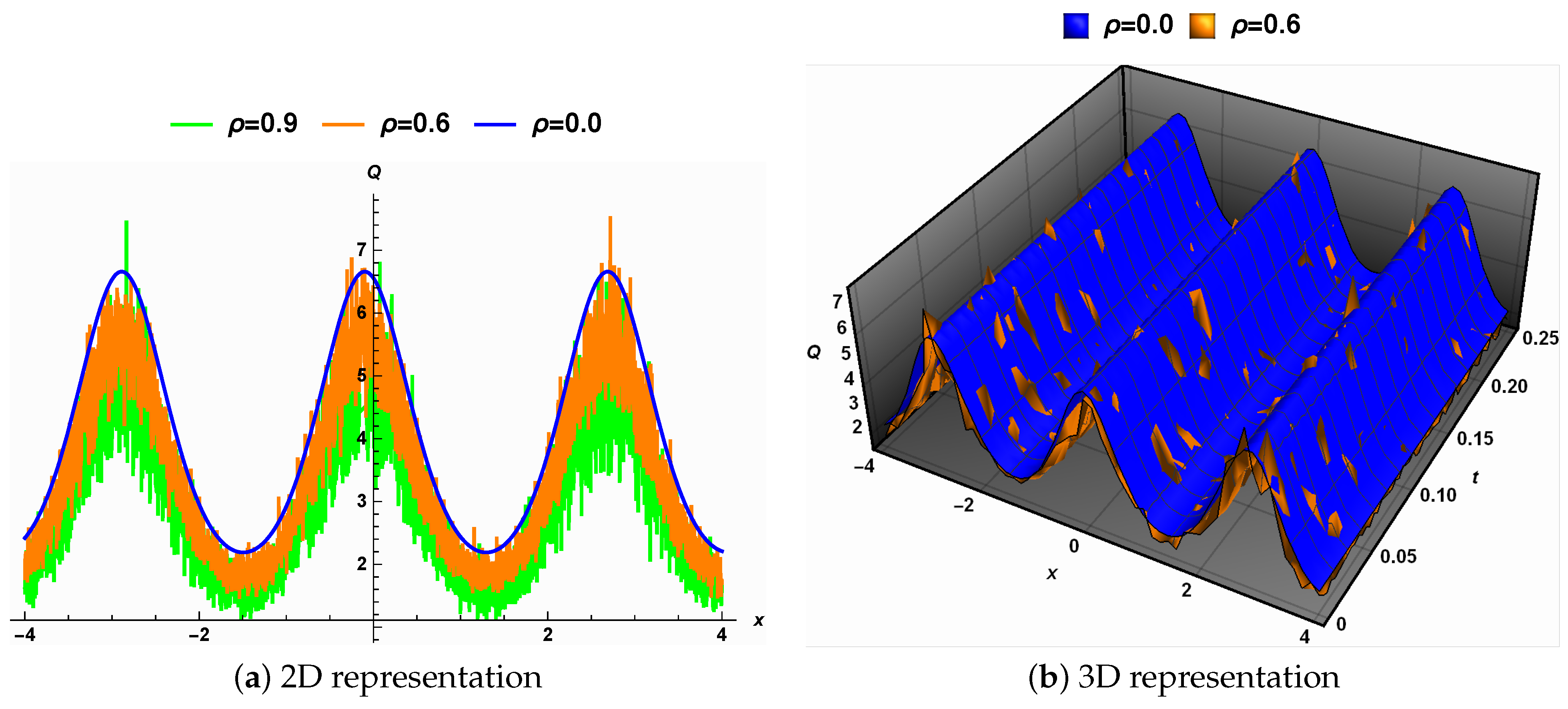
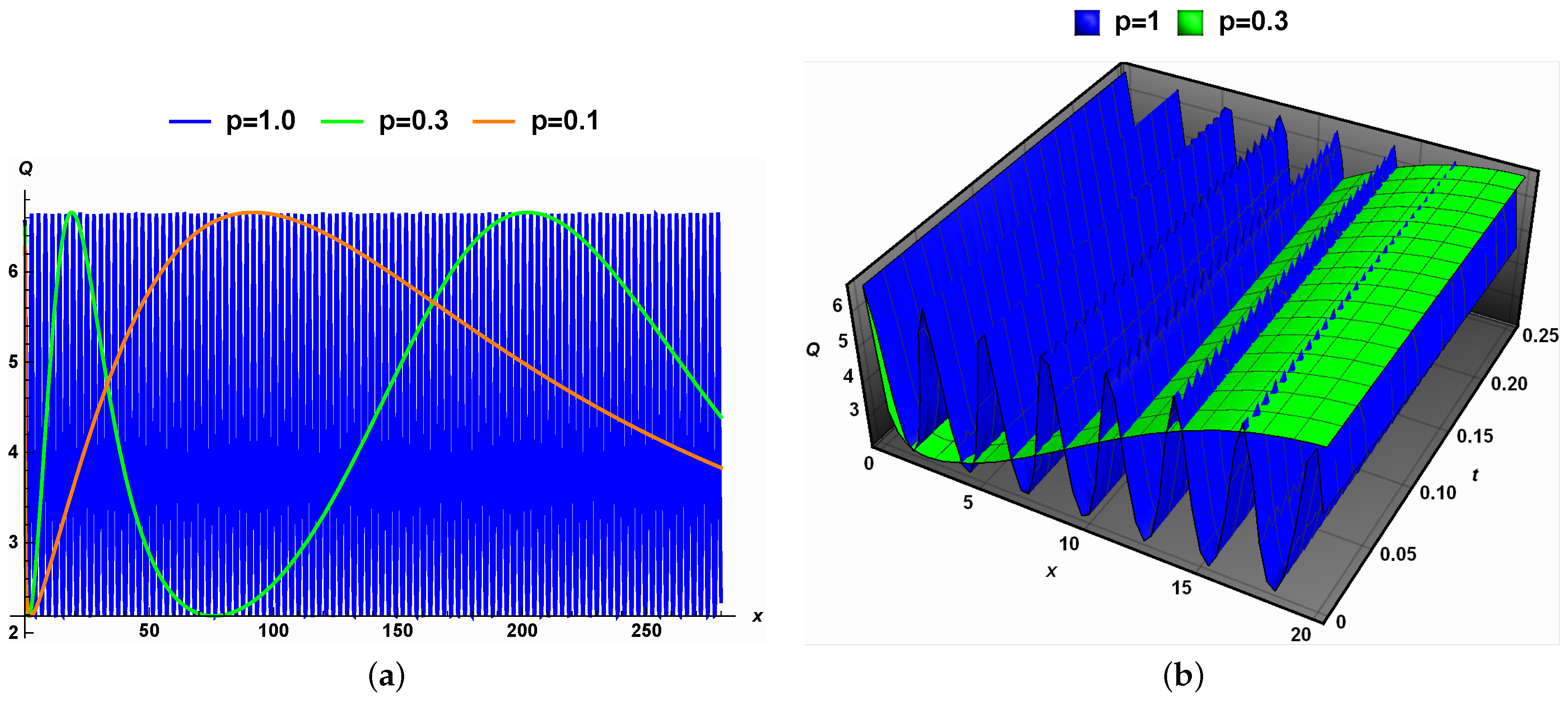
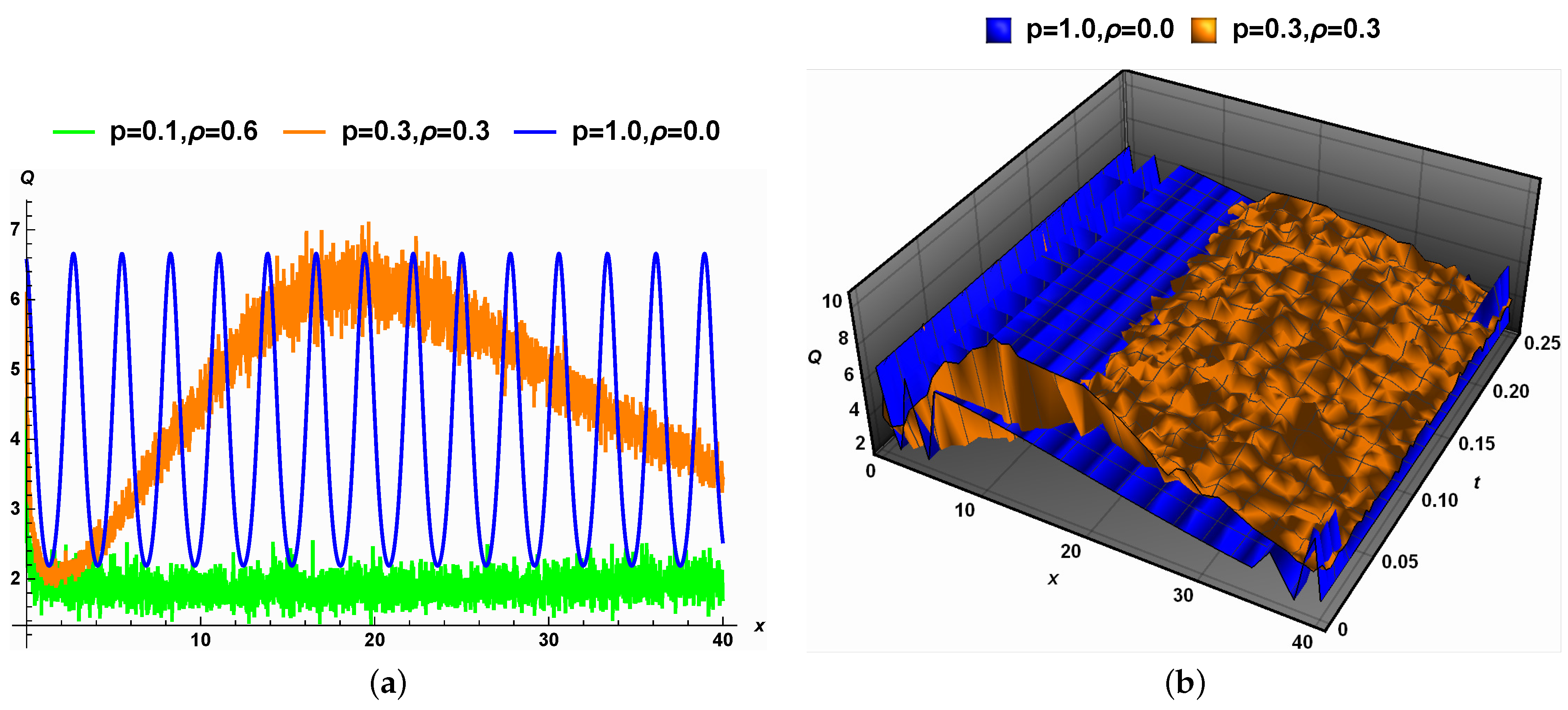
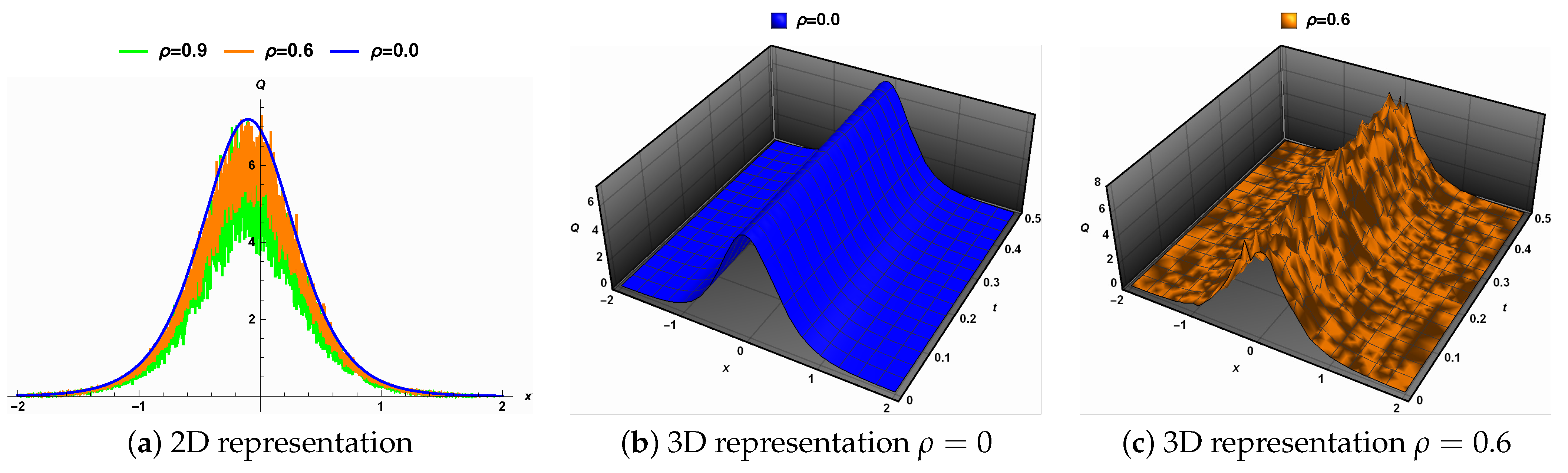
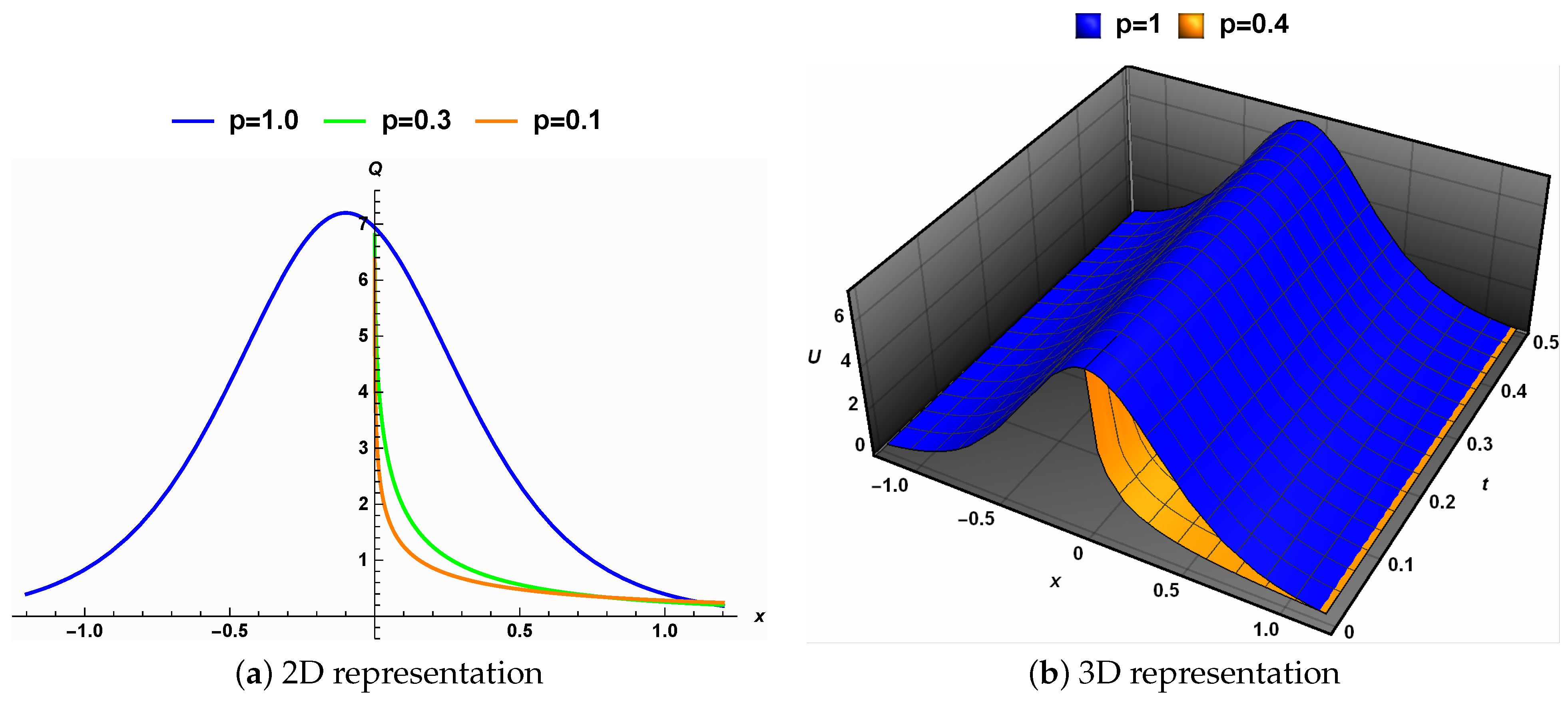
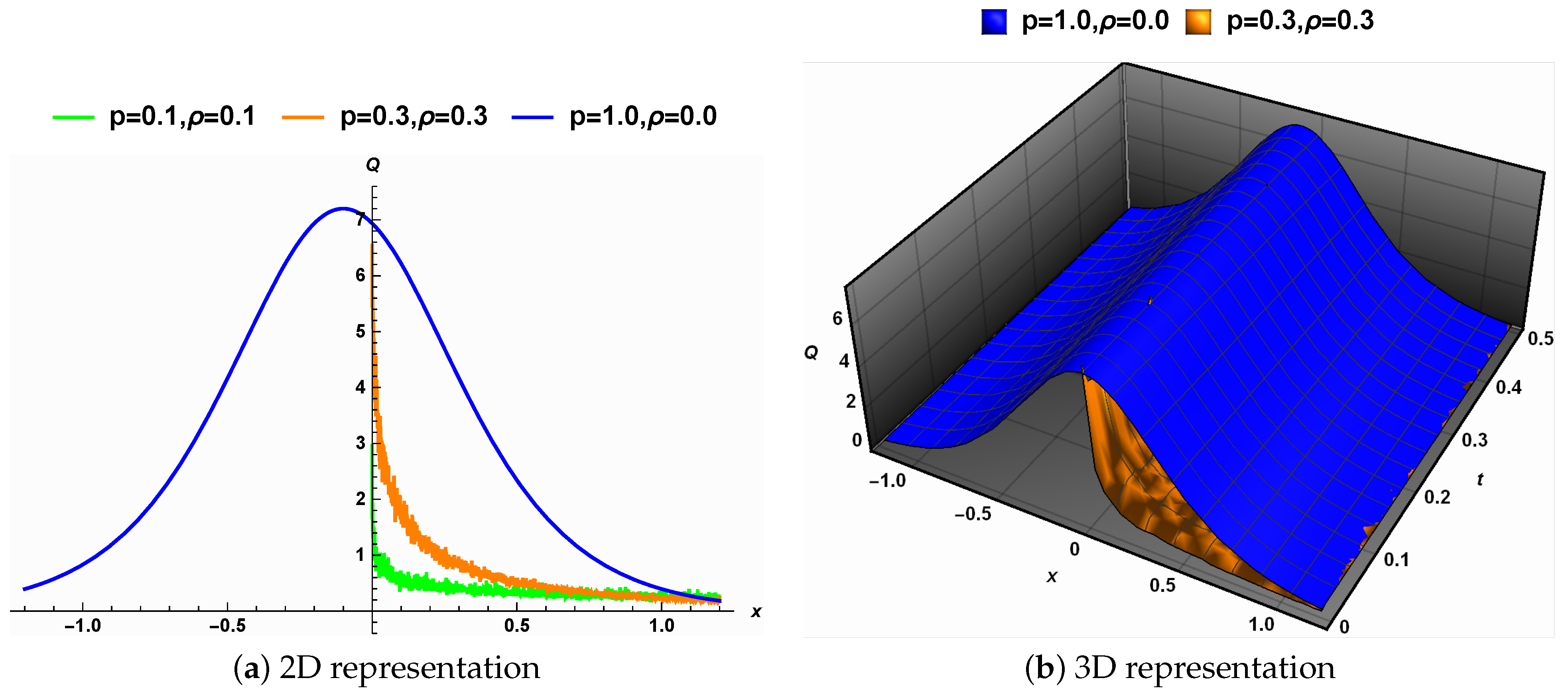
5. Physical Interpretations
- 2.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Jumarie’s Modified Riemann–Liouville Derivative and Standard Wiener Process
- ,
- ,
- is a continuous function for ,
- For and are independent,
- has a normal distribution with mean zero and variance .
References
- Peregrine, D.H. Calculations of the development of an undular bore. J. Fluid Mech. 1966, 25, 321–330. [Google Scholar] [CrossRef]
- Benjamin, T.B.; Bona, J.L.; Mahony, J.J. Model equations for long waves in nonlinear dispersive systems. Philos. Trans. R. Soc. London. Ser. A Math. Phys. Sci. 1972, 272, 47–78. [Google Scholar] [CrossRef]
- Bona, J.L.; Bryant, P.J. A mathematical model for long waves generated by wavemakers in non-linear dispersive systems. Math. Proc. Camb. Philos. Soc. 1973, 73, 391–405. [Google Scholar] [CrossRef]
- Eilbeck, J.; McGuire, G. Numerical study of the regularized long-wave equation I: Numerical methods. J. Comput. Phys. 1975, 19, 43–57. [Google Scholar] [CrossRef]
- El-Danaf, T.S.; Ramadan, M.A.; Abd Alaal, F.E. The use of adomian decomposition method for solving the regularized long-wave equation. Chaos Solitons Fractal. 2005, 26, 747–757. [Google Scholar] [CrossRef]
- Pshtiwan, O.M.; Alqudah, M.A.; Hamed, Y.S.; Kashuri, A.; Abualnaja, K.M. Solving the Modified Regularized Long Wave Equations via Higher Degree B-Spline Algorithm. J. Funct. Spaces 2021, 2021, 5580687. [Google Scholar] [CrossRef]
- Hirsch, M.W.; Smale, S.; Devaney, R.L. Differential Equations, Dynamical Systems, and an Introduction to Chaos; Academic Press: Cambridge, MA, USA; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar] [CrossRef]
- Farlow, S. Partial Differential Equations for Scientists and Engineers; Dover Publications: Mineola, NY, USA, 1993. [Google Scholar]
- Zhou, Y. Fractional Evolution Equations and Inclusions: Analysis and Control; Academic Press: Cambridge, MA, USA; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar] [CrossRef]
- Kubica, A.; Ryszewska, K.; Yamamoto, M. Time-Fractional Differential Equations, A Theoretical Introduction; Springer: Singapore, 2020. [Google Scholar] [CrossRef]
- Tarasov, V.E. Fractional Dynamics: Applications of Fractional Calculus to Dynamics of Particles, Fields and Media; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar] [CrossRef]
- AL Nuwairan, M. The exact solutions of the conformable time fractional version of the generalized Pochhammer–Chree equation. Math. Sci. 2023, 17, 305–316. [Google Scholar] [CrossRef]
- Magin, R.L. Fractional calculus models of complex dynamics in biological tissues. Comput. Math. Appl. 2010, 59, 1586–1593, Fractional Differentiation and Its Applications. [Google Scholar] [CrossRef]
- Butt, A.; Imran, M.; Batool, S.; AL Nuwairan, M. Theoretical Analysis of a COVID-19 CF-Fractional Model to Optimally Control the Spread of Pandemic. Symmetry 2023, 15, 380. [Google Scholar] [CrossRef]
- Braumann, C.A. Introduction to Stochastic Differential Equations with Applications to Modelling in Biology and Finance; Wiley: Hoboken, NJ, USA, 2019. [Google Scholar] [CrossRef]
- Baxendale, P.; Lototsky, S.V. Stochastic Differential Equations: Theory and Applications; World Scientific: Singapore, 2007. [Google Scholar] [CrossRef]
- Evans, L.C. An Introduction to Stochastic Differential Equations; American Mathematical Society: Providence, RI, USA, 2013. [Google Scholar]
- Swishchuk, A. Random Evolutions and Their Applications: New Trends; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 504. [Google Scholar]
- Weinan, E.; Li, X.; Vanden-Eijnden, E. Some recent progress in multiscale modeling. In Multiscale Modelling and Simulation; Springer: Berlin/Heidelberg, Germany, 2004; pp. 3–21. [Google Scholar]
- Kamrani, M. Numerical solution of stochastic fractional differential equations. J. Fluid Mech. 2015, 68, 81–93. [Google Scholar] [CrossRef]
- Ha, T.; Li, Z.; Kun, K. Exact solutions of the stochastic fractional long–short wave interaction system with multiplicative noise in generalized elastic medium. Results Phys. 2023, 44, 106174. [Google Scholar] [CrossRef]
- Al Nuwairan, M. Bifurcation and Analytical Solutions of the Space-Fractional Stochastic Schrödinger Equation with White Noise. Fractal Fract. 2023, 7, 157. [Google Scholar] [CrossRef]
- Yang, M. Existence uniqueness of mild solutions for Ψ-Caputo fractional stochastic evolution equations driven by fBm. J. Inequal. Appl. 2021, 2021, 170. [Google Scholar] [CrossRef]
- Yuan, C.; Mao, X. Convergence of the Euler–Maruyama method for stochastic differential equations with Markovian switching. Math. Comput. Simul. 2004, 64, 223–235. [Google Scholar] [CrossRef]
- Elbrolosy, M.; Alhamud, M.; Elmandouh, A. Analytical solutions to the fractional stochastic (3 + 1) equation of fluids with gas bubbles using an extended auxiliary function method. Alex. Eng. J. 2024, 92, 254–266. [Google Scholar] [CrossRef]
- Mohammed, W.W.; Cesarano, C.; Elmandouh, A.A.; Alqsair, I.; Sidaoui, R.; Alshammari, H.W. Abundant optical soliton solutions for the stochastic fractional fokas system using bifurcation analysis. Phys. Scr. 2024, 99, 045233. [Google Scholar] [CrossRef]
- Li, S.; Khan, S.; Riaz, M.; AlQahtani, S.A.; Alamri, M.M. Numerical simulation of a fractional stochastic delay differential equations using spectral scheme: A comprehensive stability analysis. Sci. Rep. 2024, 14, 6930. [Google Scholar] [CrossRef]
- Maarouf, N.; Maadan, H.; Hilal, K. Lie symmetry analysis and explicit solutions for the time-fractional regularized long-wave equation. Int. J. Differ. Equ. 2021, 2021, 6614231. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, J.; Baleanu, D.; Sushila. Analysis of regularized long-wave equation associated with a new fractional operator with Mittag-Leffler type kernel. Phys. A Stat. Mech. Its Appl. 2018, 492, 155–167. [Google Scholar] [CrossRef]
- Jhangeer, A.; Muddassar, M. andKousar, M.; Infal, B. Multistability and Dynamics of Fractional Regularized Long Wave equation with Conformable Fractional Derivatives. Ain Shams Eng. J. 2021, 12, 2153–2169. [Google Scholar] [CrossRef]
- Al-Askar, F.M.; Cesarano, C.; Mohammed, W.W. Effects of the wiener process and beta derivative on the exact solutions of the kadomtsev–petviashvili equation. Axioms 2023, 12, 748. [Google Scholar] [CrossRef]
- Mohammed, W.W.; Alshammari, M.; Cesarano, C.; Albadrani, S.; El-Morshedy, M. Brownian motion effects on the stabilization of stochastic solutions to fractional diffusion equations with polynomials. Mathematics 2022, 10, 1458. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Goldstein, H. Classical Mechanics; Addison-Wesley Series in Physics; Addison-Wesley USA: Boston, MA, USA, 1980. [Google Scholar]
- Saha, A.; Banerjee, S. Dynamical Systems and Nonlinear Waves in Plasmas; CRC Press: Boca Raton, FL, USA, 2021; p. x+207. [Google Scholar]
- Nemytskii, V.V. Qualitative Theory of Differential Equations; Princeton University Press: Princeton, NJ, USA, 2015; Volume 2083. [Google Scholar]
- Hand, L.N.; Finch, J.D. Analytical Mechanics; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Jumarie, G. Modified Riemann-Liouville derivative and fractional Taylor series of nondifferentiable functions further results. Comput. Math. Appl. 2006, 51, 1367–1376. [Google Scholar] [CrossRef]
- Platen, E.; Bruti-Liberati, N. Numerical Solution of Stochastic Differential Equations with Jumps in Finance; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010; Volume 64. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almutairi, B.; Al Nuwairan, M.; Aldhafeeri, A. Exploring the Exact Solution of the Space-Fractional Stochastic Regularized Long Wave Equation: A Bifurcation Approach. Fractal Fract. 2024, 8, 298. https://doi.org/10.3390/fractalfract8050298
Almutairi B, Al Nuwairan M, Aldhafeeri A. Exploring the Exact Solution of the Space-Fractional Stochastic Regularized Long Wave Equation: A Bifurcation Approach. Fractal and Fractional. 2024; 8(5):298. https://doi.org/10.3390/fractalfract8050298
Chicago/Turabian StyleAlmutairi, Bashayr, Muneerah Al Nuwairan, and Anwar Aldhafeeri. 2024. "Exploring the Exact Solution of the Space-Fractional Stochastic Regularized Long Wave Equation: A Bifurcation Approach" Fractal and Fractional 8, no. 5: 298. https://doi.org/10.3390/fractalfract8050298
APA StyleAlmutairi, B., Al Nuwairan, M., & Aldhafeeri, A. (2024). Exploring the Exact Solution of the Space-Fractional Stochastic Regularized Long Wave Equation: A Bifurcation Approach. Fractal and Fractional, 8(5), 298. https://doi.org/10.3390/fractalfract8050298






