Correlation between Agglomerates Hausdorff Dimension and Mechanical Properties of Denture Poly(methyl methacrylate)-Based Composites
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Processing of Composite Materials
2.3. Characterization of Samples
3. Results and Discussion
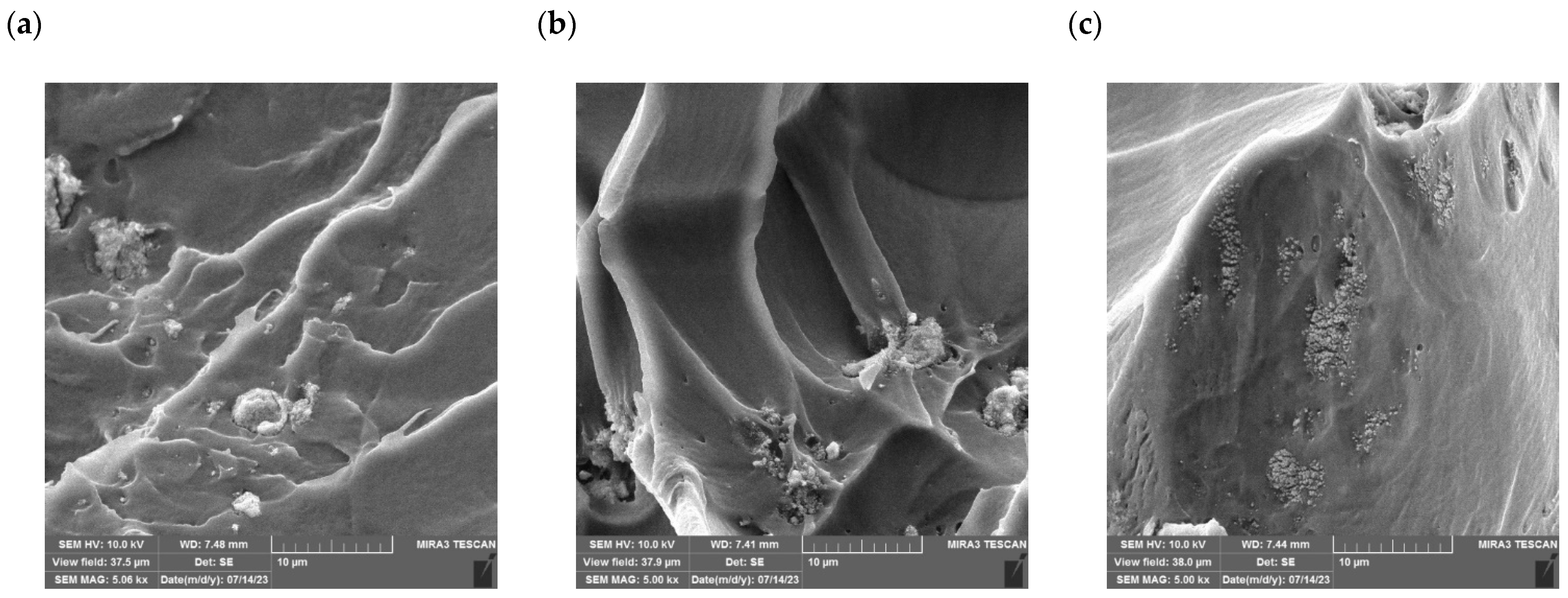
3.1. FESEM Analysis of Composites
3.2. Fractal Analysis
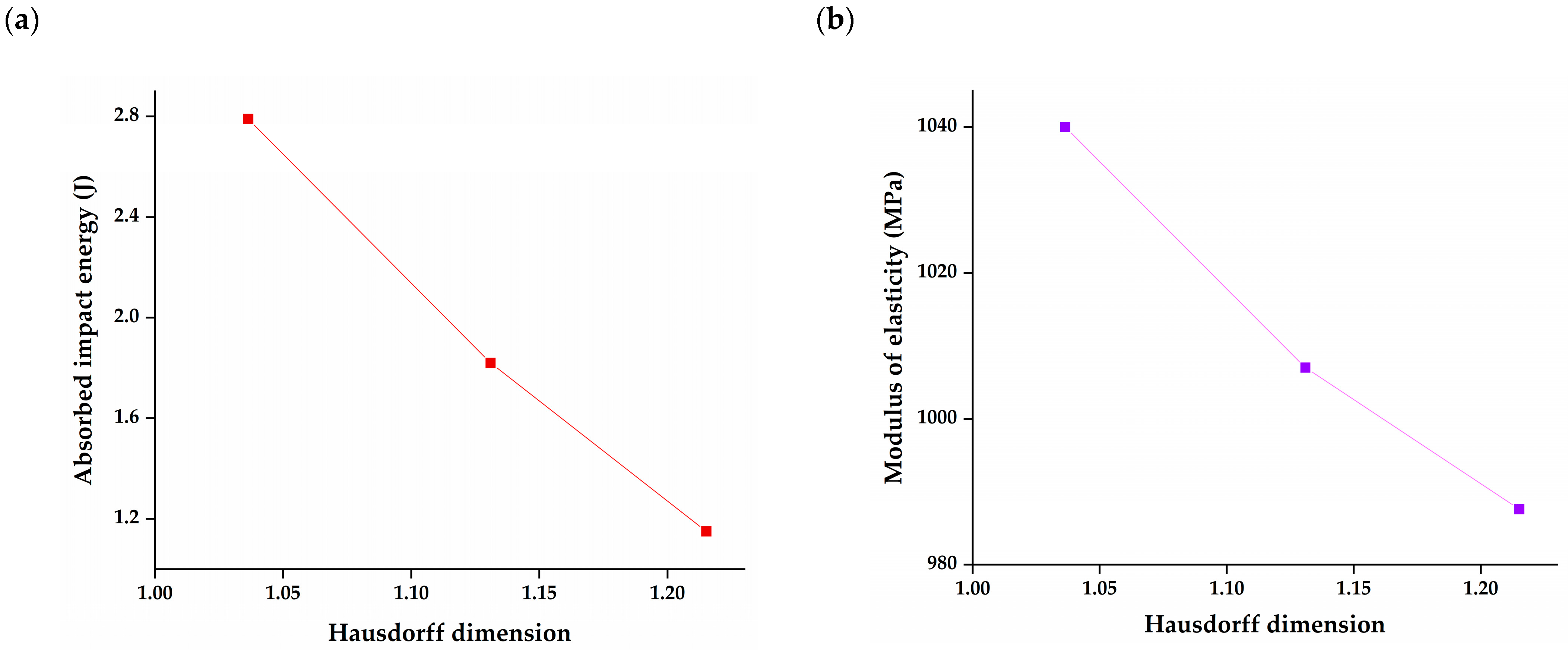
3.3. Dependence of Mechanical Properties on Agglomerate Hausdroff Dimension
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, H.-K.; Wu, W.-J.; Kang, Z.; Feng, X.-Q. Topology optimization method for the design of bioinspired self-similar hierarchical microstructures. Comput. Methods Appl. Mech. Eng. 2020, 372, 113399. [Google Scholar] [CrossRef]
- Ţălu, Ş.; Stach, S.; Lainović, T.; Vilotić, M.; Blažić, L.; Alb, S.F.; Kakaš, D. Surface roughness and morphology of dental nanocomposites polished by four different procedures evaluated by a multifractal approach. Appl. Surf. Sci. 2015, 330, 20–29. [Google Scholar] [CrossRef]
- Fu, S.-Y.; Feng, X.-Q.; Lauke, B.; Mai, Y.-W. Effects of particle size, particle/matrix interface adhesion and particle loading on mechanical properties of particulate–polymer composites. Compos. Part B Eng. 2008, 39, 933–961. [Google Scholar] [CrossRef]
- Feng, J.; Venna, S.R.; Hopkinson, D.P. Interactions at the interface of polymer matrix-filler particle composites. Polymer 2016, 103, 189–195. [Google Scholar] [CrossRef]
- Peterson, G.W.; Lee, D.T.; Barton, H.F.; Epps, T.H.; Parsons, G.N. Fibre-based composites from the integration of metal–organic frameworks and polymers. Nat. Rev. Mater. 2021, 6, 605–621. [Google Scholar] [CrossRef]
- Niccolini, G.; Rubino, A.; Carpinteri, A. Dimensional transitions in creeping materials due to nonlinearity and microstructural disorder. Chaos Solitons Fractals 2020, 141, 110345. [Google Scholar] [CrossRef]
- Zhang, Y.; Fu, H.; Xu, S.; Fan, J.A.; Hwang, K.-C.; Jiang, J.; Rogers, J.A.; Huang, Y. A hierarchical computational model for stretchable interconnects with fractal-inspired designs. J. Mech. Phys. Solids 2014, 72, 115–130. [Google Scholar] [CrossRef]
- Yaman, K. Fractal characterization of electrical conductivity and mechanical properties of copper particulate polyester matrix composites using image processing. Polym. Bull. 2022, 79, 3309–3332. [Google Scholar] [CrossRef]
- Ji, G.; Li, K.; Zhang, G.; Li, S.; Zhang, L. An assessment method for shale fracability based on fractal theory and fracture toughness. Eng. Fract. Mech. 2019, 211, 282–290. [Google Scholar] [CrossRef]
- Gurbuz, E.; Erdem, S.; Zhang, M. Mechanical properties and 3D fractal analysis of engineered cementitious composites with shape memory alloy fibres. Case Stud. Constr. Mater. 2023, 19, e02412. [Google Scholar] [CrossRef]
- Jodha, K.S.; Kaur, N.; Salazar Marocho, S.M.; Mecholsky, J.J.; Lirette, S.T.; Duan, Y.; Griggs, J.A. Relationship between fracture toughness and fractal dimensional increment in two types of dental glass-ceramics with different fracture surface roughness. Dent. Mater. 2022, 38, 1977–1988. [Google Scholar] [CrossRef]
- Zafar, M.S. Prosthodontic Applications of Polymethyl Methacrylate (PMMA): An Update. Polymers 2020, 12, 2299. [Google Scholar] [CrossRef] [PubMed]
- Al-Dwairi, Z.N.; Tahboub, K.Y.; Baba, N.Z.; Goodacre, C.J. A Comparison of the Flexural and Impact Strengths and Flexural Modulus of CAD/CAM and Conventional Heat-Cured Polymethyl Methacrylate (PMMA). J. Prosthodont. 2020, 29, 341–349. [Google Scholar] [CrossRef] [PubMed]
- Yerliyurt, K.; Taşdelen, T.B.; Eğri, Ö.; Eğri, S. Flexural Properties of Heat-Polymerized PMMA Denture Base Resins Reinforced with Fibers with Different Characteristics. Polymers 2023, 15, 3211. [Google Scholar] [CrossRef] [PubMed]
- Jiangkongkho, P.; Arksornnukit, M.; Takahashi, H. The synthesis, modification, and application of nanosilica in polymethyl methacrylate denture base. Dent. Mater. J. 2018, 37, 582–591. [Google Scholar] [CrossRef] [PubMed]
- Sharifianjazi, F.; Pakseresht, A.H.; Shahedi Asl, M.; Esmaeilkhanian, A.; Nargesi khoramabadi, H.; Jang, H.W.; Shokouhimehr, M. Hydroxyapatite Consolidated by Zirconia: Applications for Dental Implant. J. Compos. Compd. 2020, 2, 26–34. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, C.; Dong, S.; Zu, L.; Lan, T. The study on microstructure and mechanical properties of multi-component composite based on HDPE. Des. Monomers Polym. 2020, 23, 164–176. [Google Scholar] [CrossRef]
- Elhmali, H.T.; Stajcic, I.; Stajcic, A.; Pesic, I.; Jovanovic, M.; Petrovic, M.; Radojevic, V. Influence of Novel SrTiO3/MnO2 Hybrid Nanoparticles on Poly(methyl methacrylate) Thermal and Mechanical Behavior. Polymers 2024, 16, 278. [Google Scholar] [CrossRef]
- ISO 527-2:2012; Plastics—Determination of Tensile Properties Part 2: Test Conditions for Moulding and Extrusion Plastics. International Organization for Standardization: Geneva, Switzerland, 2012.
- Stajcic, I.; Stajcic, A.; Serpa, C.; Vasiljevic-Radovic, D.; Randjelovic, B.; Radojevic, V.; Fecht, H. Microstructure of Epoxy-Based Composites: Fractal Nature Analysis. Fractal Fract. 2022, 6, 741. [Google Scholar] [CrossRef]
- Mitic, V.V.; Lazovic, G.; Paunovic, V.; Cvetkovic, N.; Jovanovic, D.; Veljkovic, S.; Randjelovic, B.; Vlahovic, B. Fractal frontiers in microelectronic ceramic materials. Ceram. Int. 2019, 45, 9679–9685. [Google Scholar] [CrossRef]
- Serpa, C.; Buescu, J. Explicitly defined fractal interpolation functions with variable parameters. Chaos Solitons Fractals 2015, 75, 76–83. [Google Scholar] [CrossRef]
- Mitić, V.; Serpa, C.; Ilić, I.; Mohr, M.; Fecht, H.-J. Fractal Nature of Advanced Ni-Based Superalloys Solidified on Board the International Space Station. Remote Sens. 2021, 13, 1724. [Google Scholar] [CrossRef]




| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| −0.108 | −0.163 | −0.015 | 0.008 | 0.034 | −0.179 | −0.203 | −0.072 | −0.043 | 0.053 | 0.028 | −0.085 | |
| −0.094 | 0.005 | −0.292 | 0.055 | 0.504 | 0.288 | −0.04 | −0.685 | −0.101 | 0.534 | −0.044 | −0.077 | |
| 3.132 | 3.155 | 2.761 | 2.598 | 2.493 | 3.542 | 3.824 | 3.17 | 2.613 | 2.428 | 2.941 | 3.192 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| −0.111 | −0.063 | −0.177 | −0.018 | 0.017 | 0.143 | −0.145 | −0.107 | −0.27 | 0.056 | −0.095 | 0.147 | |
| 0.285 | 0.367 | −0.579 | 0.114 | −0.318 | −0.302 | 0.154 | 0.154 | 0.549 | −0.126 | 0.328 | −0.456 | |
| 2.333 | 2.503 | 3.419 | 1.995 | 2.244 | 1.578 | 2.224 | 2.233 | 2.553 | 2.042 | 2.356 | 2.258 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.006 | 0.173 | 0.05 | −0.023 | −0.031 | −0.075 | 0.007 | −0.01 | 0.004 | −0.008 | 0.058 | −0.039 | |
| 0.48 | −1.597 | 0.802 | 1.218 | −0.525 | −0.175 | −0.298 | 0.007 | 0.068 | −0.25 | 0.467 | 1.011 | |
| 2.731 | 2.825 | 1.383 | 2.529 | 3.542 | 2.872 | 2.118 | 1.563 | 1.376 | 1.428 | 0.746 | 2.035 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elhmali, H.T.; Serpa, C.; Radojevic, V.; Stajcic, A.; Petrovic, M.; Jankovic-Castvan, I.; Stajcic, I. Correlation between Agglomerates Hausdorff Dimension and Mechanical Properties of Denture Poly(methyl methacrylate)-Based Composites. Fractal Fract. 2024, 8, 314. https://doi.org/10.3390/fractalfract8060314
Elhmali HT, Serpa C, Radojevic V, Stajcic A, Petrovic M, Jankovic-Castvan I, Stajcic I. Correlation between Agglomerates Hausdorff Dimension and Mechanical Properties of Denture Poly(methyl methacrylate)-Based Composites. Fractal and Fractional. 2024; 8(6):314. https://doi.org/10.3390/fractalfract8060314
Chicago/Turabian StyleElhmali, Houda Taher, Cristina Serpa, Vesna Radojevic, Aleksandar Stajcic, Milos Petrovic, Ivona Jankovic-Castvan, and Ivana Stajcic. 2024. "Correlation between Agglomerates Hausdorff Dimension and Mechanical Properties of Denture Poly(methyl methacrylate)-Based Composites" Fractal and Fractional 8, no. 6: 314. https://doi.org/10.3390/fractalfract8060314
APA StyleElhmali, H. T., Serpa, C., Radojevic, V., Stajcic, A., Petrovic, M., Jankovic-Castvan, I., & Stajcic, I. (2024). Correlation between Agglomerates Hausdorff Dimension and Mechanical Properties of Denture Poly(methyl methacrylate)-Based Composites. Fractal and Fractional, 8(6), 314. https://doi.org/10.3390/fractalfract8060314






