A Dynamical Analysis and New Traveling Wave Solution of the Fractional Coupled Konopelchenko–Dubrovsky Model
Abstract
1. Introduction
2. Dynamical Analysis and Traveling Wave Solutions of Equation (1)
2.1. Traveling Wave Transformation
2.2. Dynamical Analysis
2.3. Traveling Wave Solutions of Equation (1)
- (i)
- If or , the traveling wave solutions of Equation (1) take the form:
- (ii)
- If , the traveling wave solutions of Equation (1) take the form:
- (i)
- If and , or and , the implicit traveling wave solutions of Equation (1) can be expressed as below:
- (ii)
- If and , or and , the implicit traveling wave solutions of Equation (1) can be expressed as below:
- (iii)
- If , the implicit traveling wave solutions of Equation (1) can be expressed as below:
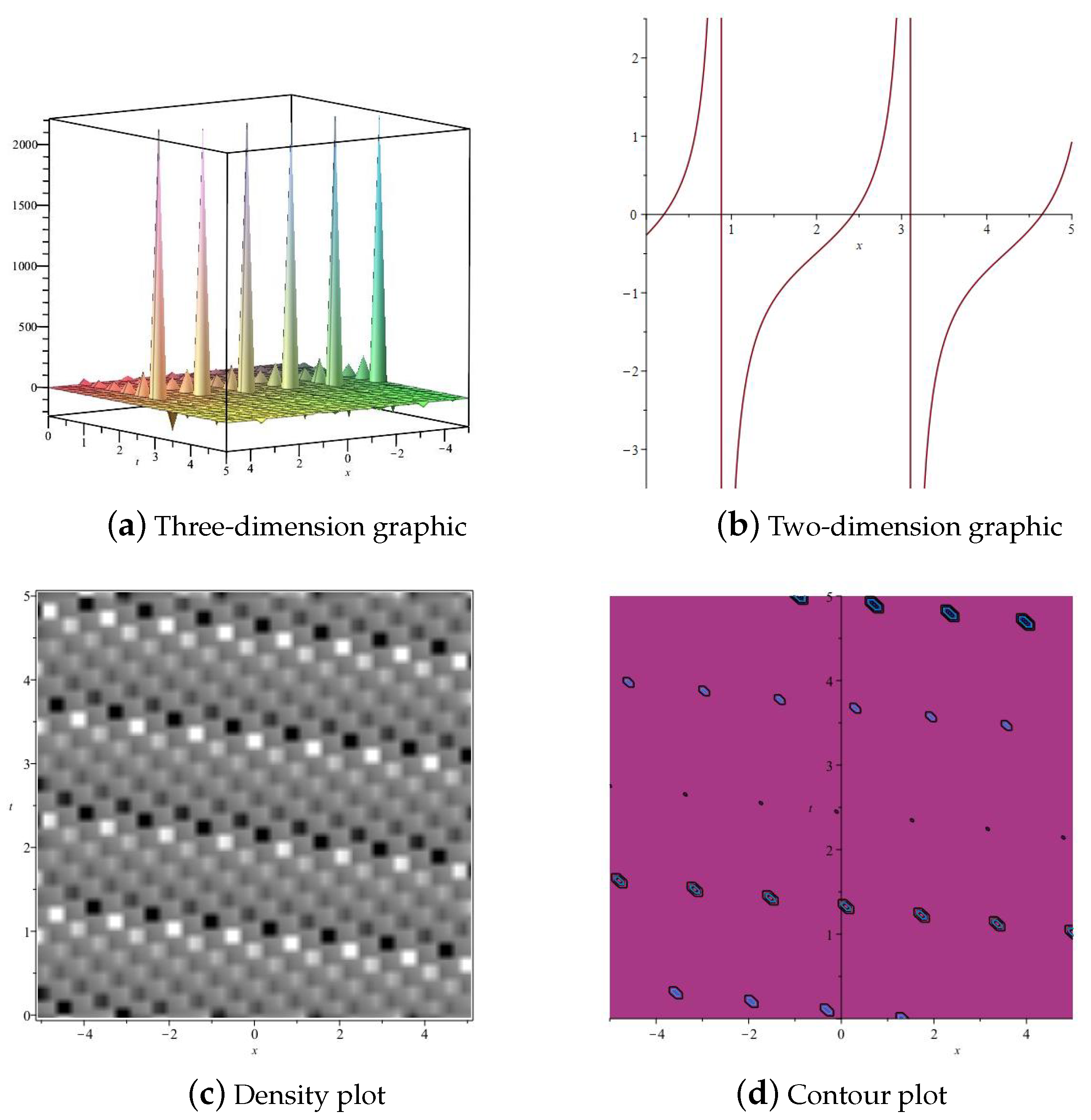
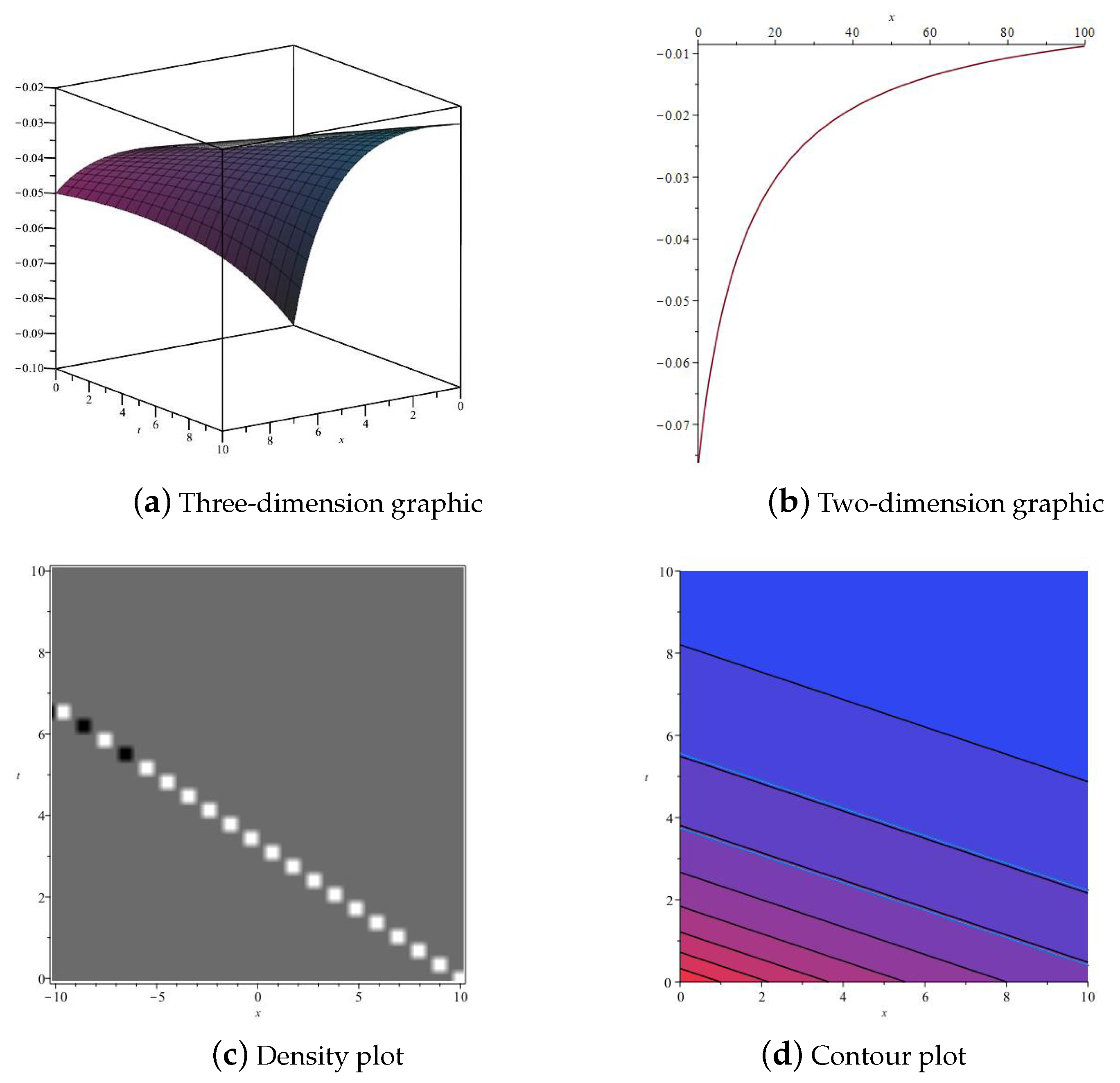
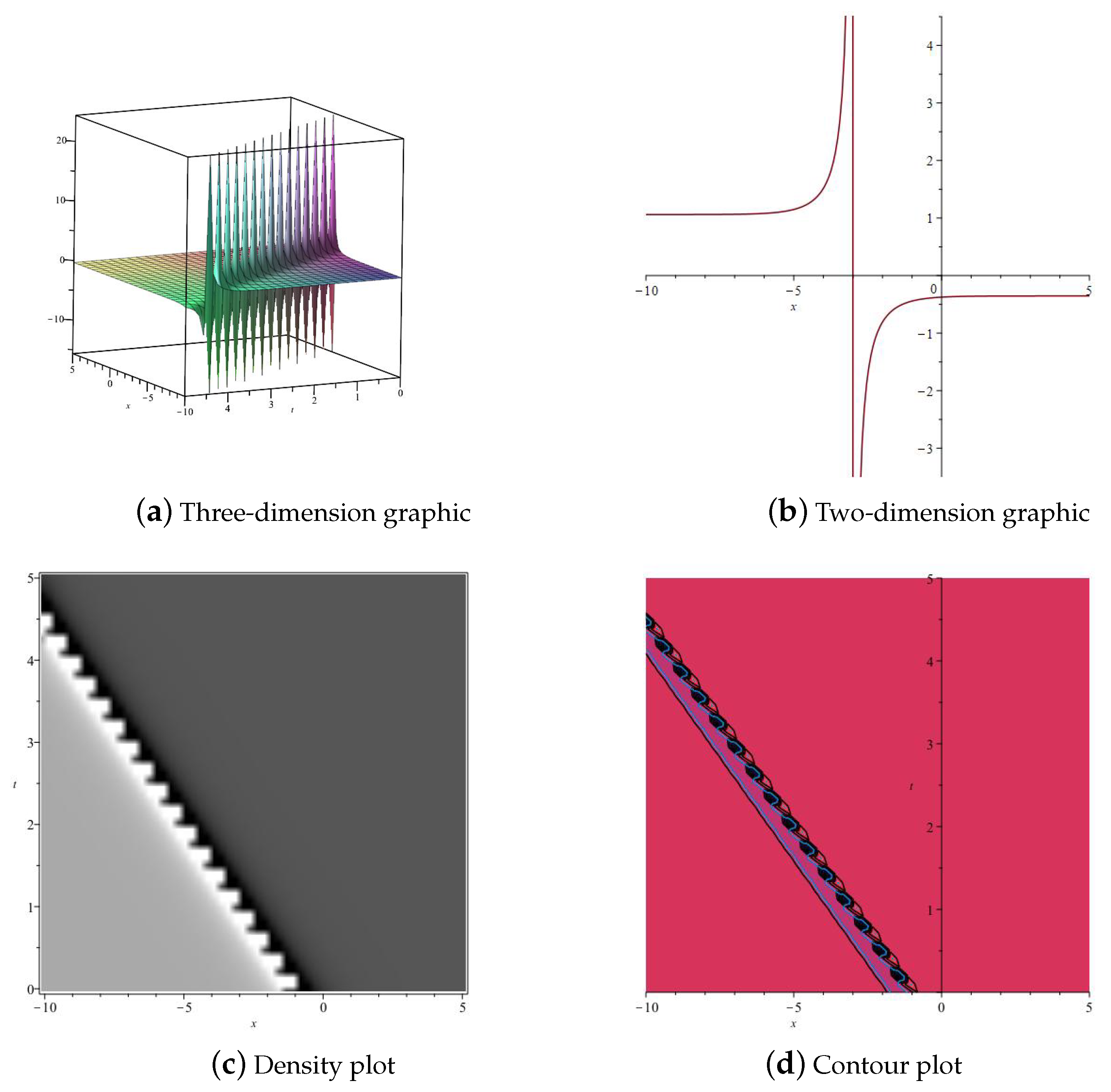
3. Numerical Simulation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gu, M.; Peng, C.; Li, Z. Traveling wave solution of (3+1)-dimensional negative-order KdV-Calogero-Bogoyavlenskii-Schiff equation. Aims Math. 2024, 9, 6699–6708. [Google Scholar] [CrossRef]
- Wu, J.; Huang, Y. Boundedness of solutions for an attraction-repulsion model with indirect signal production. Mathematics 2024, 12, 1143. [Google Scholar] [CrossRef]
- Liu, C.; Li, Z. The dynamical behavior analysis and the traveling wave solutions of the stochastic Sasa-Satsuma Equation. Qual. Theory Dyn. Syst. 2024, 23, 157. [Google Scholar] [CrossRef]
- Wu, J.; Yang, Z. Global existence and boundedness of chemotaxis-fluid equations to the coupled Solow-Swan model. Aims Math. 2023, 8, 17914–17942. [Google Scholar] [CrossRef]
- Tang, C.; Li, X.; Wang, Q. Mean-field stochastic linear quadratic optimal control for jump-diffusion systems with hybrid disturbances. Symmetry 2024, 16, 642. [Google Scholar] [CrossRef]
- Chen, T.; Chen, J.; Zhuang, B. Stabilization of coupled delayed nonlinear time fractional reaction diffusion systems using sampled-in-space sensing and actuation. Int. J. Adapt. Control. Signal Process. 2024. [Google Scholar] [CrossRef]
- Arfaoui, H.; Makhlouf, A.B. Stability of a time fractional advection-diffusion system. Chaos Solitons Fractals 2022, 157, 111949. [Google Scholar] [CrossRef]
- Khater, M.M.A. In solid physics equations, accurate and novel soliton wave structures for heating a single crystal of sodium fluoride. Int. J. Mod. Phys. 2023, 37, 2350068. [Google Scholar] [CrossRef]
- Li, Z.; Liu, C. Chaotic pattern and traveling wave solution of the perturbed stochastic nonlinear Schrödinger equation with generalized anti-cubic law nonlinearity and spatio-temporal dispersion. Results Phys. 2024, 56, 107305. [Google Scholar] [CrossRef]
- Arafat, S.M.Y.; Fatema, K.; Islam, M.E.; Akbar, M.A. Promulgation on various genres soliton of Maccari system in nonlinear optics. Opt. Quantum Electron. 2022, 54, 206. [Google Scholar] [CrossRef]
- Khater, M.M.A.; Alfalqi, S.H.; Alzaidi, J.F.; Attia, R.A.M. Analytically and numerically, dispersive, weakly nonlinear wave packets are presented in a quasi-monochromaticmedium. Results Phys. 2023, 46, 106312. [Google Scholar] [CrossRef]
- Akinyemi, L.; Rezazadeh, H.; Shi, Q.H.; Inc, M.; Khater, M.M.; Ahmad, H.; Jhangeer, A.; Akbar, M.A. New optical solitons of perturbed nonlinear Schrodinger-Hirota equation with spatio-temporal dispersion. Results Phys. 2021, 29, 104656. [Google Scholar] [CrossRef]
- Li, Z.; Peng, C. Bifurcation, phase portrait and traveling wave solution of time-fractional thin-film ferroelectric material equation with beta fractional derivative. Phys. Lett. 2023, 484, 129080. [Google Scholar] [CrossRef]
- Zhang, K.; Li, Z.; Cao, J. Qualitative analysis and modulation instability for the extended (3+1)-dimensional nonlinear Schrödinger equation with conformable derivative. Results Phys. 2024, 61, 107713. [Google Scholar] [CrossRef]
- Ma, H.; Gao, Y.; Deng, A. Nonlinear superposition of the (2+1)-dimensional generalized Konopelchenko-Dubrovsky-Kaup-Kupershmidt equation. Nonlinear Dyn. 2023, 111, 619–632. [Google Scholar] [CrossRef]
- Khater, M.M.A. Novel computational simulation of the propagation of pulses in optical fibers regarding the dispersion effect. Int. J. Mod. Phys. 2023, 37, 2350083. [Google Scholar] [CrossRef]
- Feng, W.; Chen, L.; Ma, G.; Zhou, Q. Study on weakening optical soliton interaction in nonlinear optics. Nonlinear Dyn. 2022, 108, 2483–2488. [Google Scholar] [CrossRef]
- Ma, H.; Gao, Y.; Deng, A. Fission and fusion solutions of the (2+1)-dimensional generalized Konopelchenko-Dubrovsky-Kaup-Kupershmidt equation: Case of fluid mechanics and plasma physics. Nonlinear Dyn. 2022, 108, 4123–4137. [Google Scholar] [CrossRef]
- Han, T.; Jiang, Y.; Lyu, J. Chaotic behavior and optical soliton for the concatenated model arising in optical communication. Results Phys. 2024, 58, 107467. [Google Scholar] [CrossRef]
- Khater, M.M.A. A hybrid analytical and numerical analysis of ultra-short pulse phase shifts. Chaos Solitons Fractals 2023, 169, 113232. [Google Scholar] [CrossRef]
- Horvath, D.X.; Calabrese, P.; Castro-Alvaredo, O.A. Branch point twist field form factors in the sine-Gordon model II: Composite twist fields and symmetry resolved entanglement. Sci Post Phys. 2022, 12, 88. [Google Scholar] [CrossRef]
- Ismael, H.F.; Bulut, H.; Park, C.; Osman, M.S. M-lump, N-soliton solutions, and the collision phenomena for the (2+1)-dimensional Date-Jimbo-Kashiwara-Miwa equation. Results Phys. 2020, 19, 103329. [Google Scholar] [CrossRef]
- Akbulut, A.; Kaplan, M.; Bekir, A. Auxiliary equation method for fractional differential equations with modified Riemann-Liouville derivative. Int. J. Nonlinear Sci. Numer. Simul. 2016, 17, 413–420. [Google Scholar] [CrossRef]
- He, J.; Wu, X. Exp-function method for nonlinear wave equations. Chaos Solitons Fractals 2006, 30, 700–708. [Google Scholar] [CrossRef]
- Ma, W. N-soliton solution and the Hirota condition of a (2+1)-dimensional combined equation. Math. Comput. Simul. 2021, 190, 270–279. [Google Scholar] [CrossRef]
- Ma, W. N-soliton solution of a combined pKP-BKP equation. J. Geom. Phys. 2021, 165, 104191. [Google Scholar] [CrossRef]
- Li, W.; Chen, H.; Zhang, G. The (w/g)-expansion method and its application to Vakhnenko equation. Chin. Phys. 2009, 18, 400. [Google Scholar]
- Arafat, S.M.Y.; Khan, K.; Islam, S.M.R.; Rahman, M.M. Parametric effects on paraxial nonlinear Schrodinger equation in Kerr media. Chin. J. Phys. 2023, 83, 361–378. [Google Scholar] [CrossRef]
- Arafat, S.M.Y.; Islam, S.M.R.; Rahman, M.M.; Saklayen, M.A. On nonlinear optical solitons of fractional Biswas-Arshed Model with beta derivative. Results Phys. 2023, 48, 106426. [Google Scholar] [CrossRef]
- Wazwaz, A.-M. The tanh method: Solitons and periodic solutions for the Dodd-Bullough-Mikhailov and the Tzitzeica-Dodd-Bullough equations. Chaos Solitons Fractals 2005, 25, 55–63. [Google Scholar] [CrossRef]
- Seadawy, A.R.; Iqbal, M. Propagation of the nonlinear damped Korteweg-de Vries equation in an unmagnetized collisional dusty plasma via analytical mathematical methods. Math. Methods Appl. Sci. 2021, 44, 737–748. [Google Scholar] [CrossRef]
- Yiasir Arafat, S.M.; Fatema, K.; Rayhanul Islam, S.M.; Islam, M.E.; Ali Akbar, M.; Osman, M.S. The mathematical and wave profile analysis of the Maccari system in nonlinear physical phenomena. Opt. Quantum Electron. 2023, 55, 136. [Google Scholar] [CrossRef]
- Aslam, A.; Majeed, A.; Kamran, M.; Inc, M.; Alqahtani, T.R. Dynamical behavior of the fractional coupled Konopelchenko-Dubrovsky and (3+1)-dimensional modified Korteweg-de Vries-Zakharov-Kuznestsov equations. Opt. Quantum Electron. 2023, 55, 543. [Google Scholar] [CrossRef]
- Arafat, S.M.Y.; Rahman, M.M.; Karim, M.F.; Amin, M.R. Wave profile analysis of the (2+1)-dimensional Konopelchenko-Dubrovsky model in mathematical physics. Partial. Differ. Equ. Appl. Math. 2023, 8, 100573. [Google Scholar] [CrossRef]
- Khalil, R.R.; Horani, M.A.H.H.; Yousef, A.; Sababheh, M. A new definition of fractional derivative. J. Comput. Appl. Math. 2014, 264, 65–70. [Google Scholar] [CrossRef]
- Li, Z.; Han, T.; Huang, C. Exact single traveling wave solutions for generalized fractional Gardner equation. Math. Probl. Eng. 2020, 2020, 8842496. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Li, Z. A Dynamical Analysis and New Traveling Wave Solution of the Fractional Coupled Konopelchenko–Dubrovsky Model. Fractal Fract. 2024, 8, 341. https://doi.org/10.3390/fractalfract8060341
Wang J, Li Z. A Dynamical Analysis and New Traveling Wave Solution of the Fractional Coupled Konopelchenko–Dubrovsky Model. Fractal and Fractional. 2024; 8(6):341. https://doi.org/10.3390/fractalfract8060341
Chicago/Turabian StyleWang, Jin, and Zhao Li. 2024. "A Dynamical Analysis and New Traveling Wave Solution of the Fractional Coupled Konopelchenko–Dubrovsky Model" Fractal and Fractional 8, no. 6: 341. https://doi.org/10.3390/fractalfract8060341
APA StyleWang, J., & Li, Z. (2024). A Dynamical Analysis and New Traveling Wave Solution of the Fractional Coupled Konopelchenko–Dubrovsky Model. Fractal and Fractional, 8(6), 341. https://doi.org/10.3390/fractalfract8060341





