Actor-Critic Neural-Network-Based Fractional-Order Sliding Mode Control for Attitude Tracking of Spacecraft with Uncertainties and Actuator Faults
Abstract
:1. Introduction
2. Model Description and Preliminaries
2.1. Spacecraft Dynamics
2.2. Preliminaries
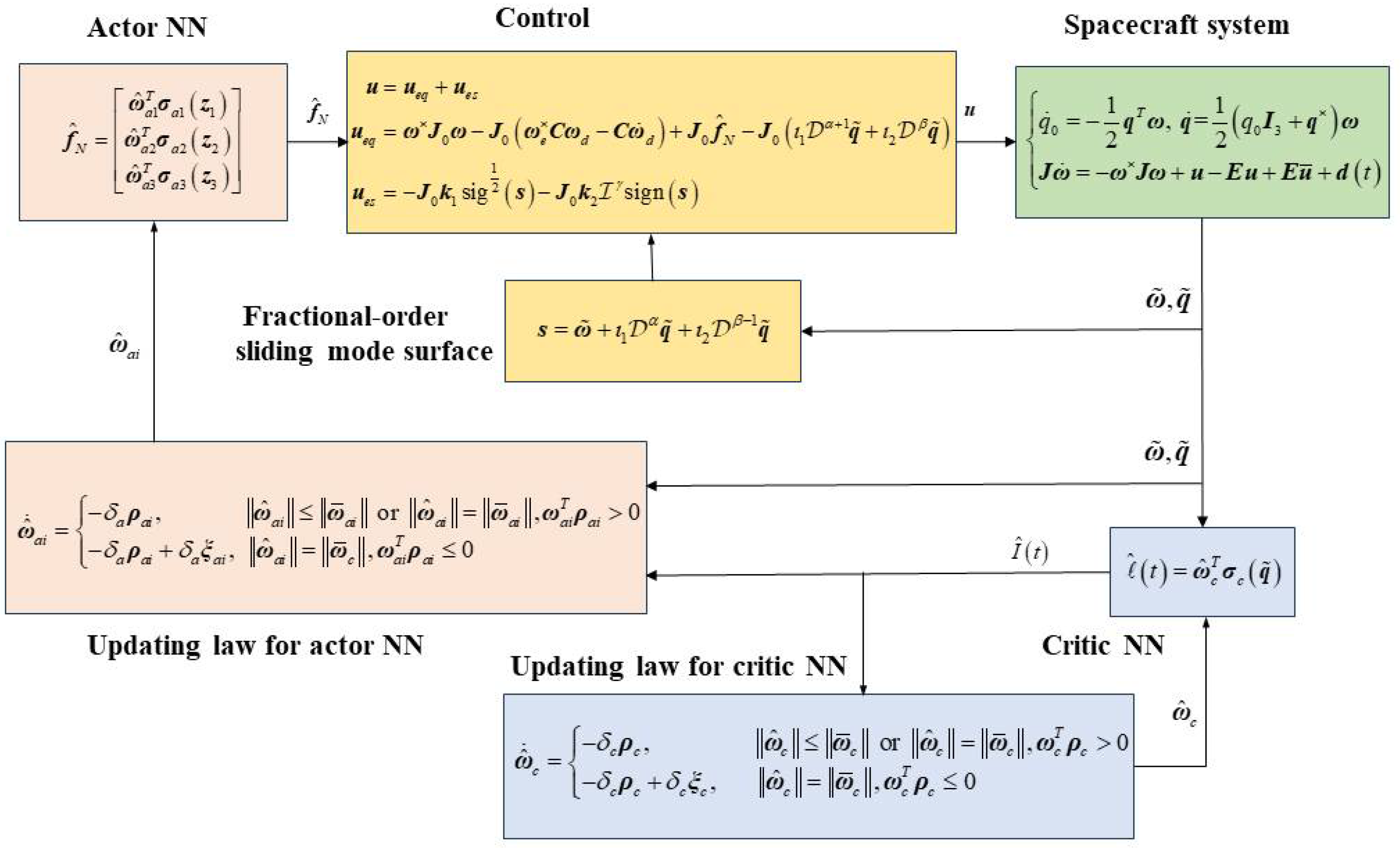
3. Controller Design
3.1. Uncertainty Estimation Using Actor-Critic NN
3.1.1. Critic NN
3.1.2. Actor NN
3.2. Fractional-Order Super-Twisting Sliding Mode Control
4. Stability Analysis
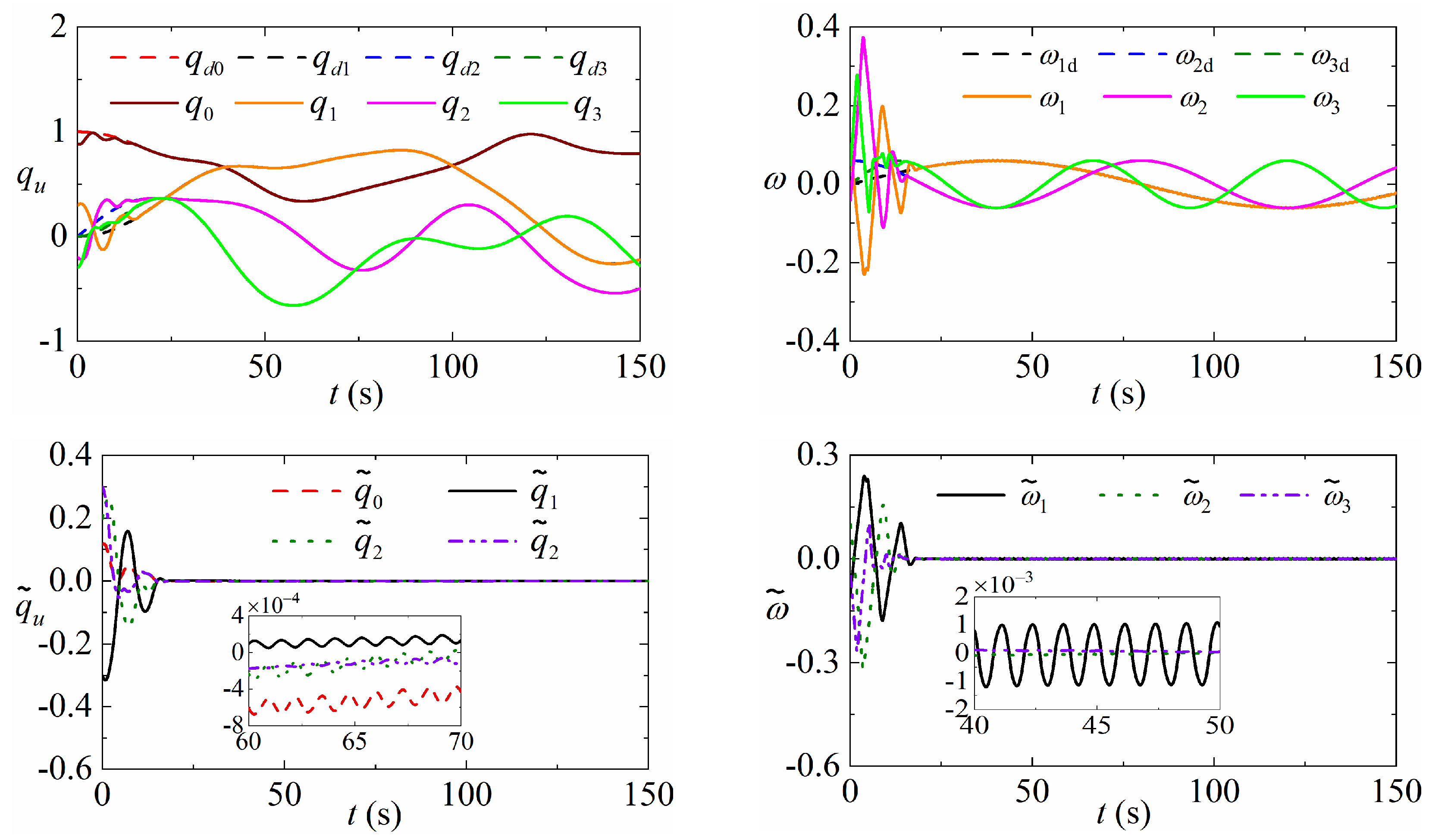
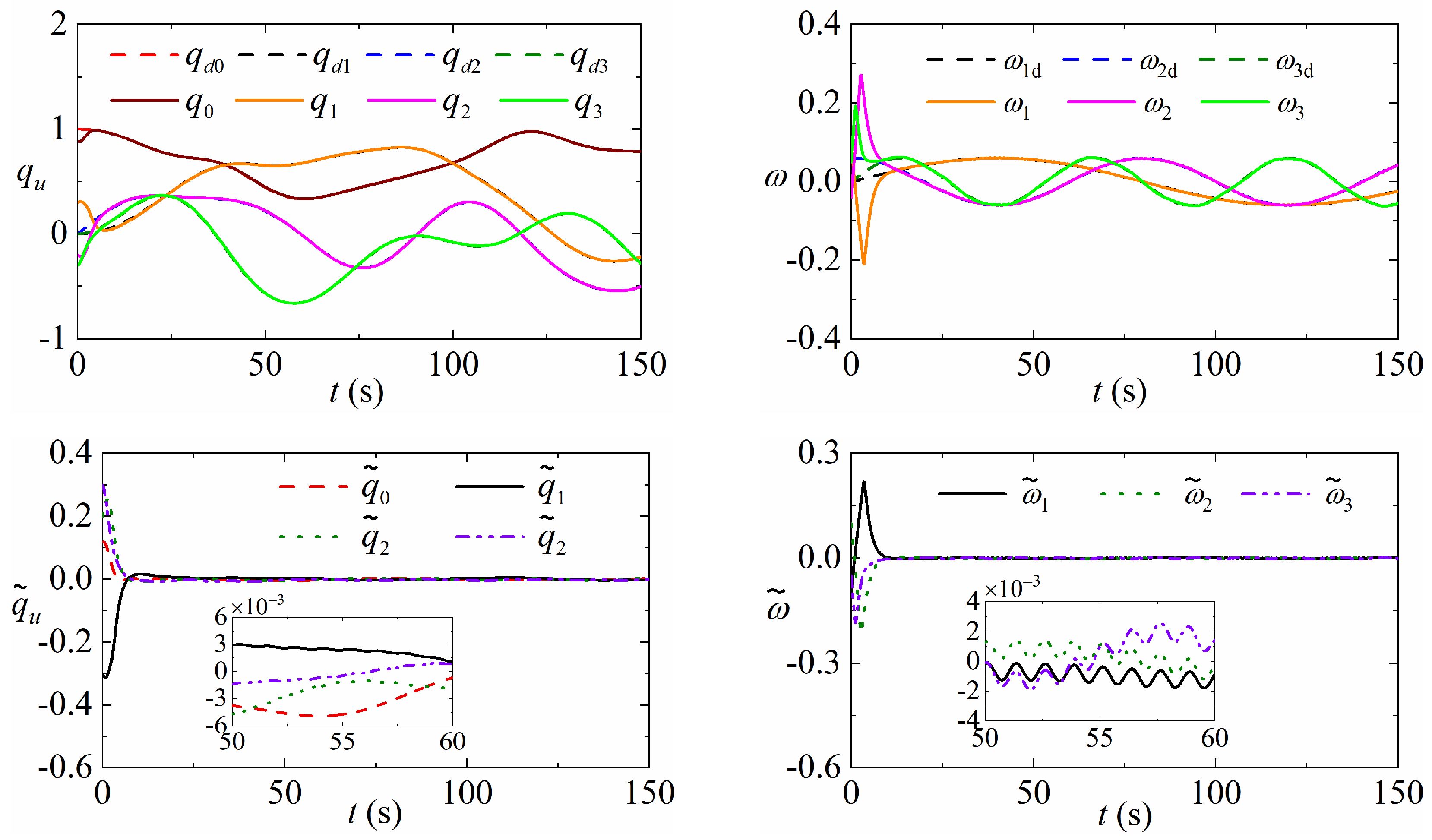
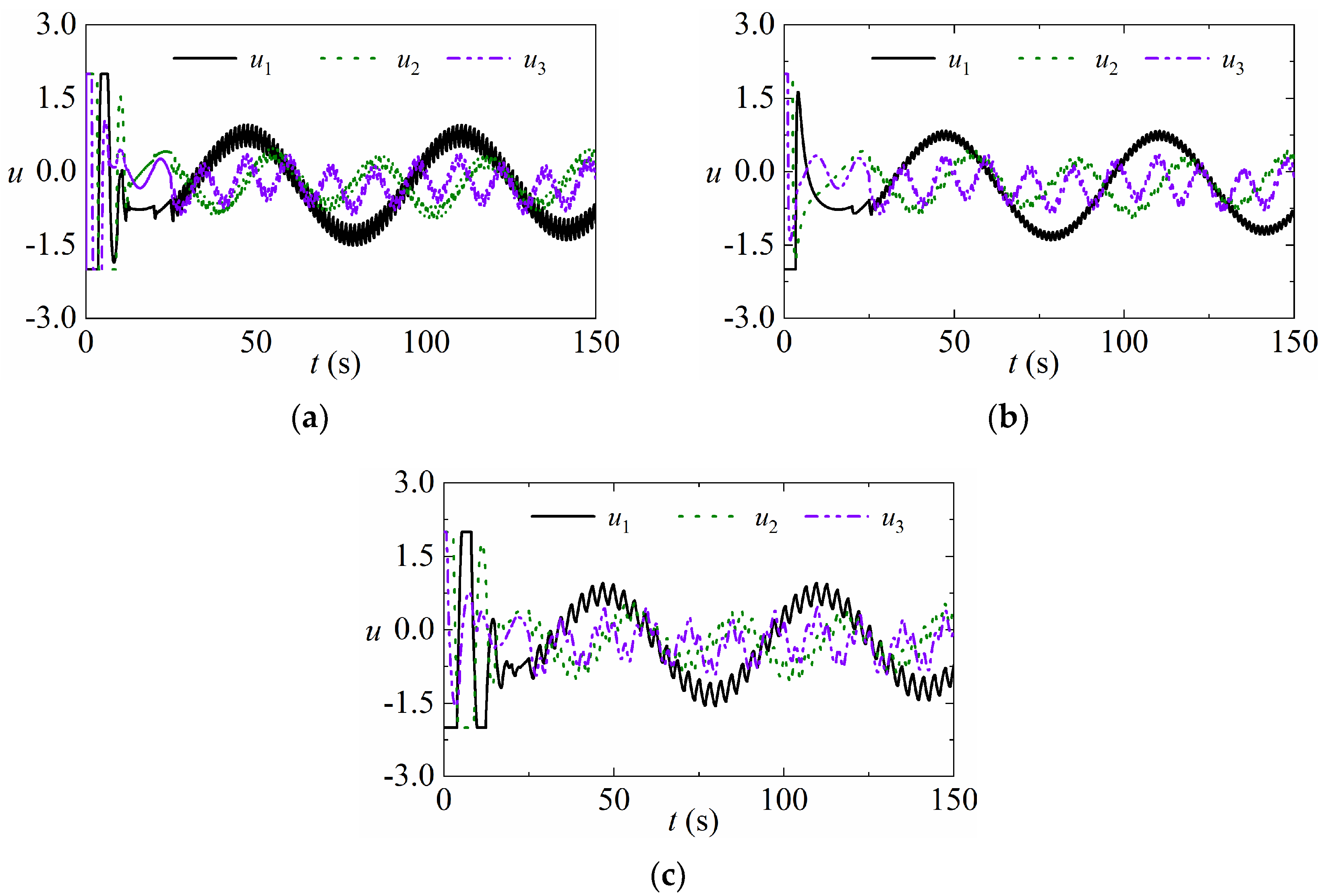
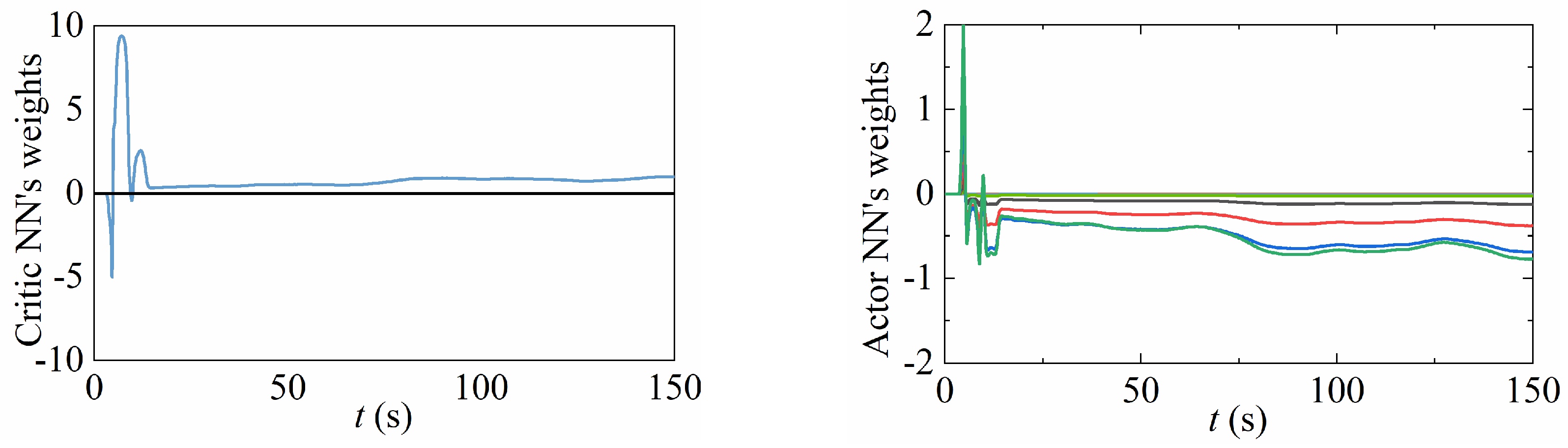
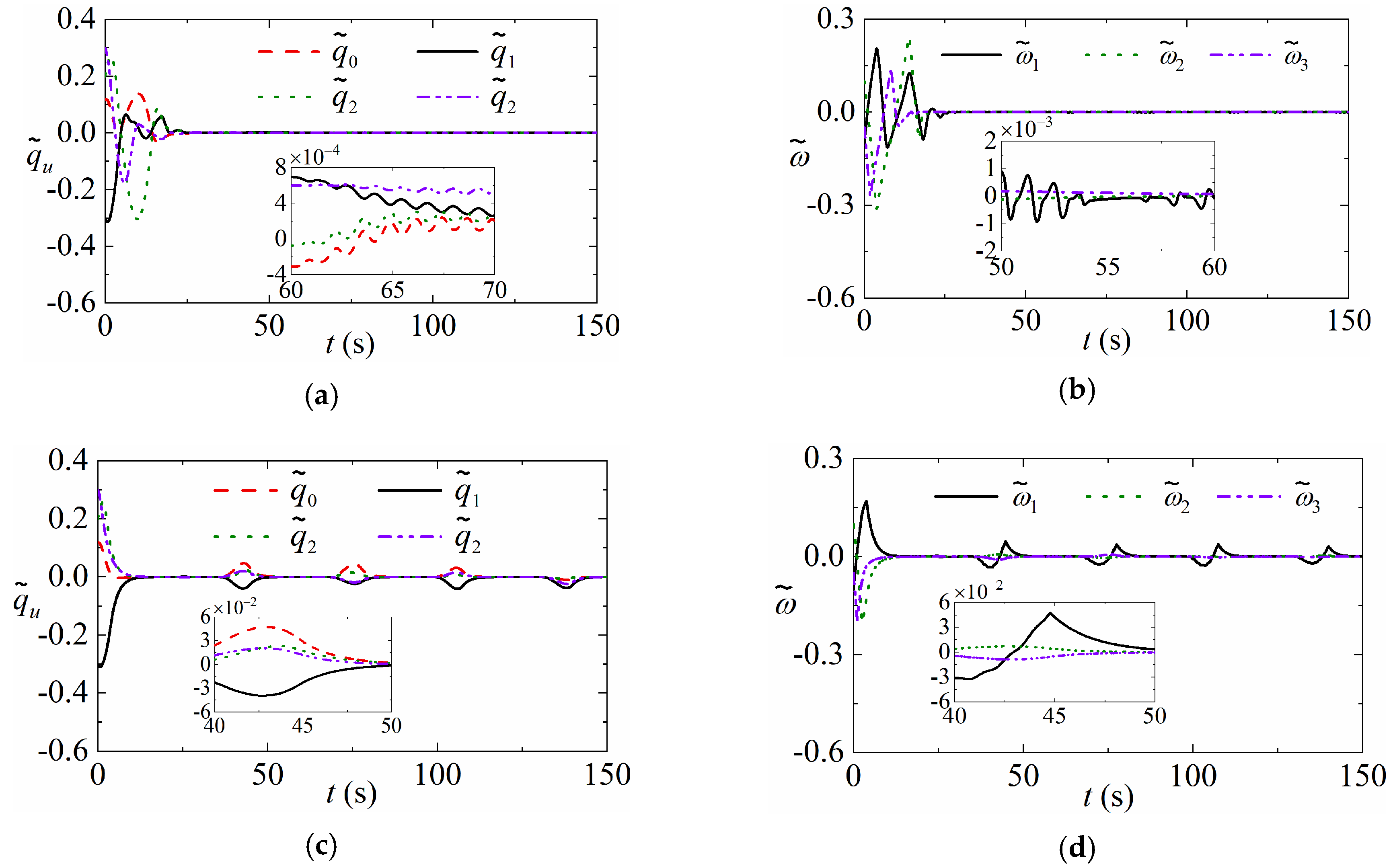
5. Simulations
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, S.; Zhou, Y.; Cai, S. Fractional-Order PD Attitude Control for a Type of Spacecraft with Flexible Appendages. Fractal Fract. 2022, 6, 601. [Google Scholar] [CrossRef]
- Hasan, M.N.; Haris, M.; Qin, S. Fault-tolerant spacecraft attitude control: A critical assessment. Prog. Aerosp. Sci. 2022, 130, 100806. [Google Scholar] [CrossRef]
- Jin, T.; Kang, G.; Cai, J.; Jia, S.; Yang, J.; Zhang, X.; Liu, F. Disturbance Attenuation and Pointing Control System Design for an Improved Disturbance-Free Payload Spacecraft. Aerospace 2023, 10, 530. [Google Scholar] [CrossRef]
- Golestani, M.; Zhang, W.; Yang, Y.; Xuan-Mung, N. Disturbance observer-based constrained attitude control for flexible spacecraft. IEEE T. Aero. Elec. Sys. 2022, 59, 963–972. [Google Scholar] [CrossRef]
- Jing, C.; Du, H.; Liu, Y. Immersion and invariance based adaptive robust control for attitude tracking of spacecraft with input saturation. Adv. Space Res. 2023, 72, 3606–3618. [Google Scholar] [CrossRef]
- Guo, Y.; Zhou, J.; Liu, Y. Distributed RISE control for spacecraft formation reconfiguration with collision avoidance. J. Franklin I. 2019, 356, 5332–5352. [Google Scholar] [CrossRef]
- Tiwari, M.; Prazenica, R.; Henderson, T. Direct adaptive control of spacecraft near asteroids. Acta Astronaut. 2023, 202, 197–213. [Google Scholar] [CrossRef]
- Nadafi, R.; Kabganian, M. Robust backstepping attitude tracking control of an underactuated spacecraft with saturation and time-variant perturbations. P. I. Mech. Eng. G-J Aer. 2022, 236, 502–516. [Google Scholar] [CrossRef]
- Yao, Q. Robust adaptive iterative learning control for high-precision attitude tracking of spacecraft. J. Aerospace Eng. 2021, 34, 04020108. [Google Scholar] [CrossRef]
- Wang, Z.; Li, Y. Rigid spacecraft nonlinear robust H∞ attitude controller design under actuator misalignments. Nonlinear Dynam. 2023, 111, 15037–15054. [Google Scholar] [CrossRef]
- Pukdeboon, C.; Siricharuanun, P. Nonsingular terminal sliding mode-based finite-time control for spacecraft attitude tracking. Int. J. Control Autom. 2014, 12, 530–540. [Google Scholar] [CrossRef]
- Moradi, R.; Alikhani, A.; Fathi Jegarkandi, M. Spacecraft attitude fault tolerant control based on multi-objective optimization. J. Theor. App. Mech-Pol. 2020, 58, 983–996. [Google Scholar] [CrossRef] [PubMed]
- Hajnorouzali, Y.; Malekzadeh, M.; Ataei, M. Finite-time disturbance observer based-control of flexible spacecraft. J. Vib. Control 2023, 29, 346–361. [Google Scholar] [CrossRef]
- Esmaeilzadeh, S.M.; Golestani, M.; Fekih, A. Adaptive attitude stabilization of flexible spacecraft with fast fixed-time convergence. IJST-T. Mech. Eng. 2022, 46, 195–208. [Google Scholar] [CrossRef]
- Han, Z.; Wang, M.; Yan, X.; Qian, H. Adaptive fixed-time nonsingular terminal sliding mode attitude tracking control for spacecraft with actuator saturations and faults. Int. J. Aerospace Eng. 2021, 1, 8838784. [Google Scholar] [CrossRef]
- Eshghi, S.; Varatharajoo, R. Nonsingular terminal sliding mode control technique for attitude tracking problem of a small satellite with combined energy and attitude control system (CEACS). Aerosp. Sci. Technol. 2018, 76, 14–26. [Google Scholar] [CrossRef]
- Xuan-Mung, N.; Golestani, M. Energy-efficient disturbance observer-based attitude tracking control with fixed-time convergence for spacecraft. IEEE T. Aero. Elec. Sys. 2022, 59, 3659–3668. [Google Scholar] [CrossRef]
- Esmaeilzadeh, S.M.; Golestani, M.; Mobayen, S. Chattering-free fault-tolerant attitude control with fast fixed-time convergence for flexible spacecraft. Int. J. Control Autom. 2021, 19, 767–776. [Google Scholar] [CrossRef]
- Xuan-Mung, N.; Golestani, M.; Hong, S.K. Constrained nonsingular terminal sliding mode attitude control for spacecraft: A funnel control approach. Mathematics 2023, 11, 247. [Google Scholar] [CrossRef]
- Pukdeboon, C. Finite-Time Second-Order Sliding Mode Controllers for Spacecraft Attitude Tracking. Math. Probl. Eng. 2013, 930269. [Google Scholar] [CrossRef]
- Lu, K.F.; Xia, Y.Q. Finite-time attitude control for rigid spacecraft-based on adaptive super-twisting algorithm. IET Control Theory A. 2014, 8, 1465–1477. [Google Scholar] [CrossRef]
- Ahmed, S.; Azar, A.T.; Tounsi, M.; Ibraheem, I.K. Adaptive Control Design for Euler–Lagrange Systems Using Fixed-Time Fractional Integral Sliding Mode Scheme. Fractal Fract. 2023, 7, 712. [Google Scholar] [CrossRef]
- Yu, Y.; Liu, X. Model-free fractional-order sliding mode control of electric drive system based on nonlinear disturbance observer. Fractal Fract. 2022, 6, 603. [Google Scholar] [CrossRef]
- Alipour, M.; Malekzadeh, M.; Ariaei, A. Practical fractional-order nonsingular terminal sliding mode control of spacecraft. ISA T. 2022, 128, 162–173. [Google Scholar] [CrossRef]
- Zhang, X.; Gao, Z.; Qian, M.; Bai, L. Integrated fault estimation and fault-tolerant control for rigid spacecraft attitude system with multiple actuator faults. Int. J. Innov. Comput. I. 2019, 15, 1255–1270. [Google Scholar]
- Qian, M.; Shi, Y.; Gao, Z.; Zhang, X. Integrated fault tolerant tracking control for rigid spacecraft using fractional order sliding mode technique. J. Franklin I. 2020, 357, 10557–10583. [Google Scholar] [CrossRef]
- Fang, Y.; Li, S.; Fei, J. Adaptive Intelligent High-Order Sliding Mode Fractional Order Control for Harmonic Suppression. Fractal Fract. 2022, 6, 482. [Google Scholar] [CrossRef]
- Cao, S.; Sun, L.; Jiang, J.; Zuo, Z. Reinforcement learning-based fixed-time trajectory tracking control for uncertain robotic manipulators with input saturation. IEEE T. Neur. Net. Lear. 2021, 34, 4584–4595. [Google Scholar] [CrossRef] [PubMed]
- Chen, R.Z.; Li, Y.X.; Ahn, C.K. Reinforcement-learning-based fixed-time attitude consensus control for multiple spacecraft systems with model uncertainties. Aerosp. Sci. Technol. 2023, 132, 108060. [Google Scholar] [CrossRef]
- Wang, X.; Shi, P.; Wen, C.; Zhao, Y. Design of parameter-self-tuning controller based on reinforcement learning for tracking noncooperative targets in space. IEEE T. Aero. Elec. Sys. 2020, 56, 4192–4208. [Google Scholar] [CrossRef]
- Muduli, R.; Jena, D.; Moger, T. Application of Reinforcement Learning-Based Adaptive PID Controller for Automatic Generation Control of Multi-Area Power System. IEEE T. Autom. Sci. Eng. 2024, 1–12. [Google Scholar] [CrossRef]
- Nohooji, H.R.; Zaraki, A.; Voos, H. Actor–critic learning based PID control for robotic manipulators. Appl. Soft Comput. 2024, 151, 111153. [Google Scholar] [CrossRef]
- Ouyang, Y.; Dong, L.; Wei, Y.; Sun, C. Neural network-based tracking control for an elastic joint robot with input constraint via actor-critic design. Neurocomputing 2020, 409, 286–295. [Google Scholar] [CrossRef]
- Patel, B.M.; Dwivedy, S.K. Manoeuvring of underwater snake robot with tail thrust using the actor-critic neural network super-twisting sliding mode control in the uncertain environment and disturbances. Neural. Comput. Appl. 2023, 1–15. [Google Scholar] [CrossRef]
- Wang, N.; Gao, Y.; Zhao, H.; Ahn, C.K. Reinforcement learning-based optimal tracking control of an unknown unmanned surface vehicle. IEEE T. Neur. Net. Lear. 2020, 32, 3034–3045. [Google Scholar] [CrossRef] [PubMed]
- Zheng, M.; Wu, Y.; Li, C. Reinforcement learning strategy for spacecraft attitude hyperagile tracking control with uncertainties. Aerosp. Sci. Technol. 2021, 119, 107126. [Google Scholar] [CrossRef]
- Cao, J.; Zhang, Y.; Ju, C.; Xue, X.; Zhang, J. A New Force Control Method by Combining Traditional PID Control with Radial Basis Function Neural Network for a Spacecraft Low-Gravity Simulation System. Aerospace 2023, 10, 520. [Google Scholar] [CrossRef]
- Yu, B.; Du, H.; Ding, L.; Wu, D.; Li, H. Neural network-based robust finite-time attitude stabilization for rigid spacecraft under angular velocity constraint. Neural. Comput. Appl. 2022, 34, 5107–5117. [Google Scholar] [CrossRef]
- Jing, C.; Du, H.; Liu, Y.; Yan, B.; Liu, C. Immersion and invariance sliding mode control with time-delay estimation for rigid spacecraft with uncertainties and actuator faults. T. I. Meas. Control 2023, 45, 3138–3146. [Google Scholar] [CrossRef]
- Muñoz-Vázquez, A.J.; Sánchez-Torres, J.D.; Parra-Vega, V.; Sánchez-Orta, A.; Martínez-Reyes, F. A fractional super-twisting control of electrically driven mechanical systems. T. I. Meas. Control 2020, 42, 485–492. [Google Scholar] [CrossRef]

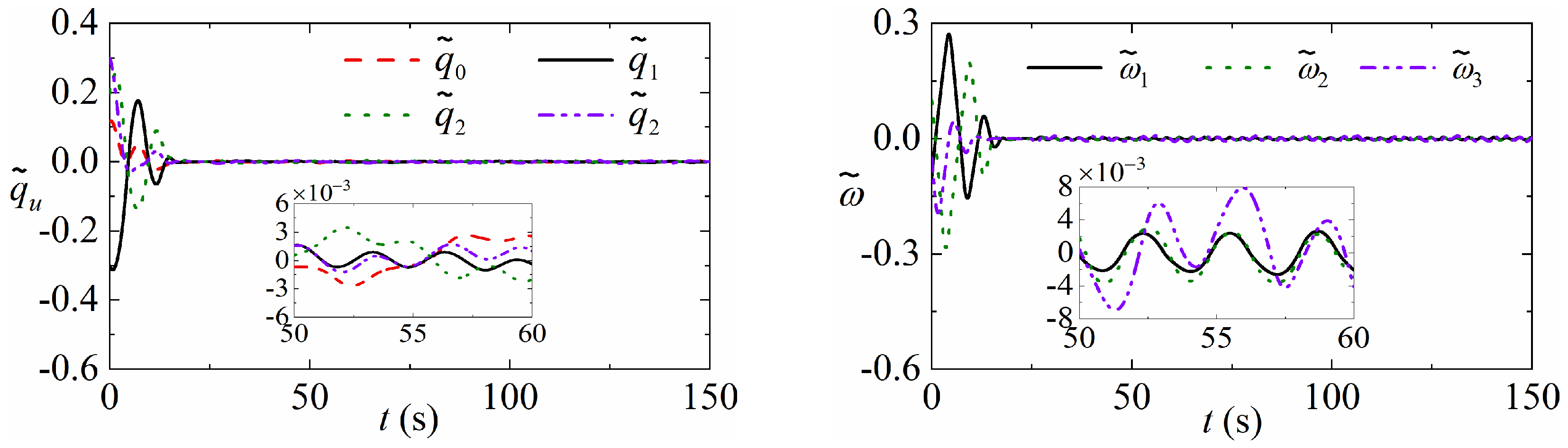

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jing, C.; Ma, X.; Zhang, K.; Wang, Y.; Yan, B.; Hui, Y. Actor-Critic Neural-Network-Based Fractional-Order Sliding Mode Control for Attitude Tracking of Spacecraft with Uncertainties and Actuator Faults. Fractal Fract. 2024, 8, 385. https://doi.org/10.3390/fractalfract8070385
Jing C, Ma X, Zhang K, Wang Y, Yan B, Hui Y. Actor-Critic Neural-Network-Based Fractional-Order Sliding Mode Control for Attitude Tracking of Spacecraft with Uncertainties and Actuator Faults. Fractal and Fractional. 2024; 8(7):385. https://doi.org/10.3390/fractalfract8070385
Chicago/Turabian StyleJing, Chenghu, Xiaole Ma, Kun Zhang, Yanfeng Wang, Bingsheng Yan, and Yanbo Hui. 2024. "Actor-Critic Neural-Network-Based Fractional-Order Sliding Mode Control for Attitude Tracking of Spacecraft with Uncertainties and Actuator Faults" Fractal and Fractional 8, no. 7: 385. https://doi.org/10.3390/fractalfract8070385




