Employing the Laplace Residual Power Series Method to Solve (1+1)- and (2+1)-Dimensional Time-Fractional Nonlinear Differential Equations
Abstract
:1. Introduction
2. Basic Concepts
- 1.
- .
- 2.
- .
- 3.
- 4.
- .
- (i)-
- ;
- (ii)-
- ;
- (iii)-
- ;
- (iv)-
- .
3. Derivation LRPS Method
3.1. The (1+1)-Dimensional Time-Fractional Coupled Differential Equation
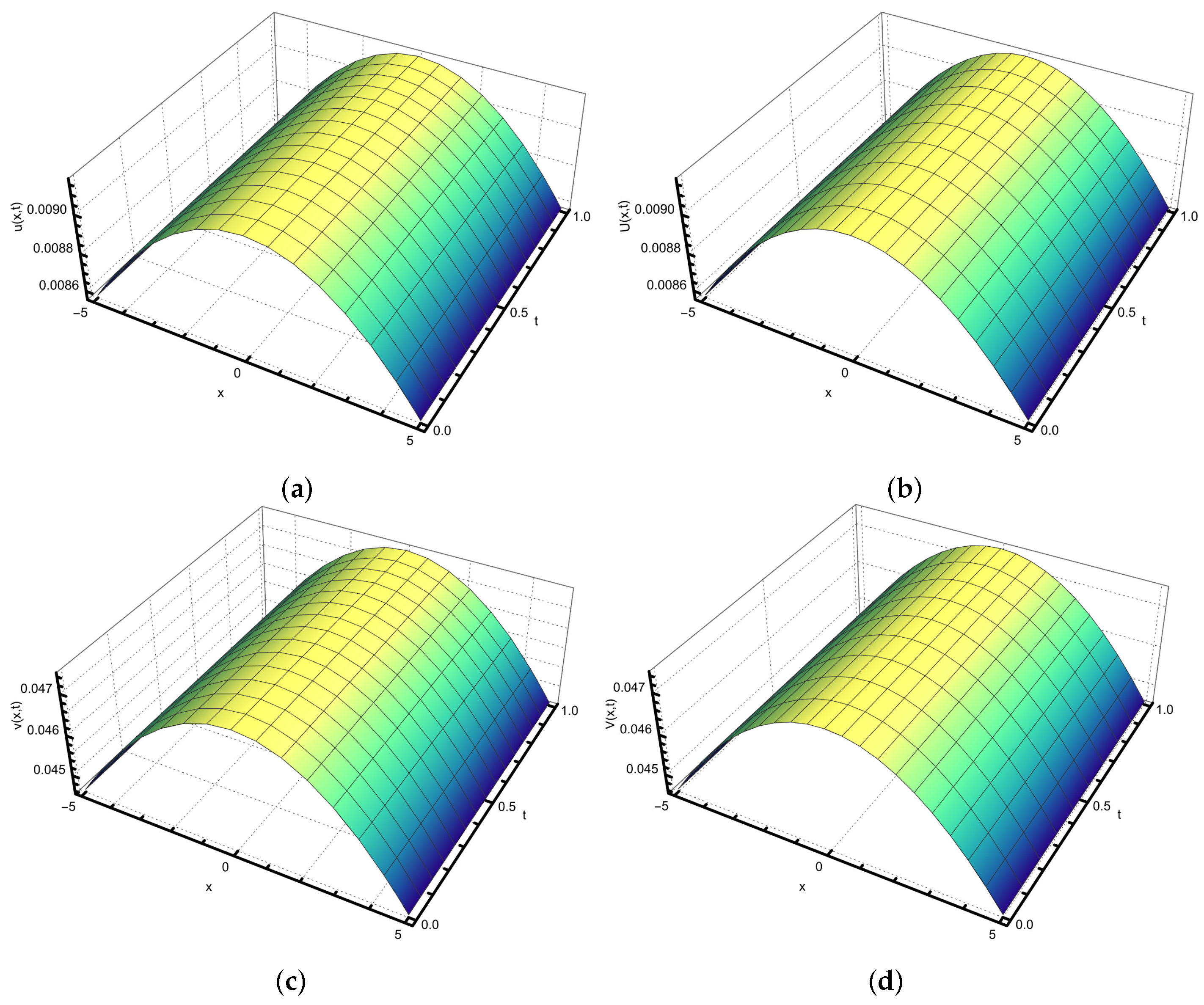
3.2. Illustrative Examples
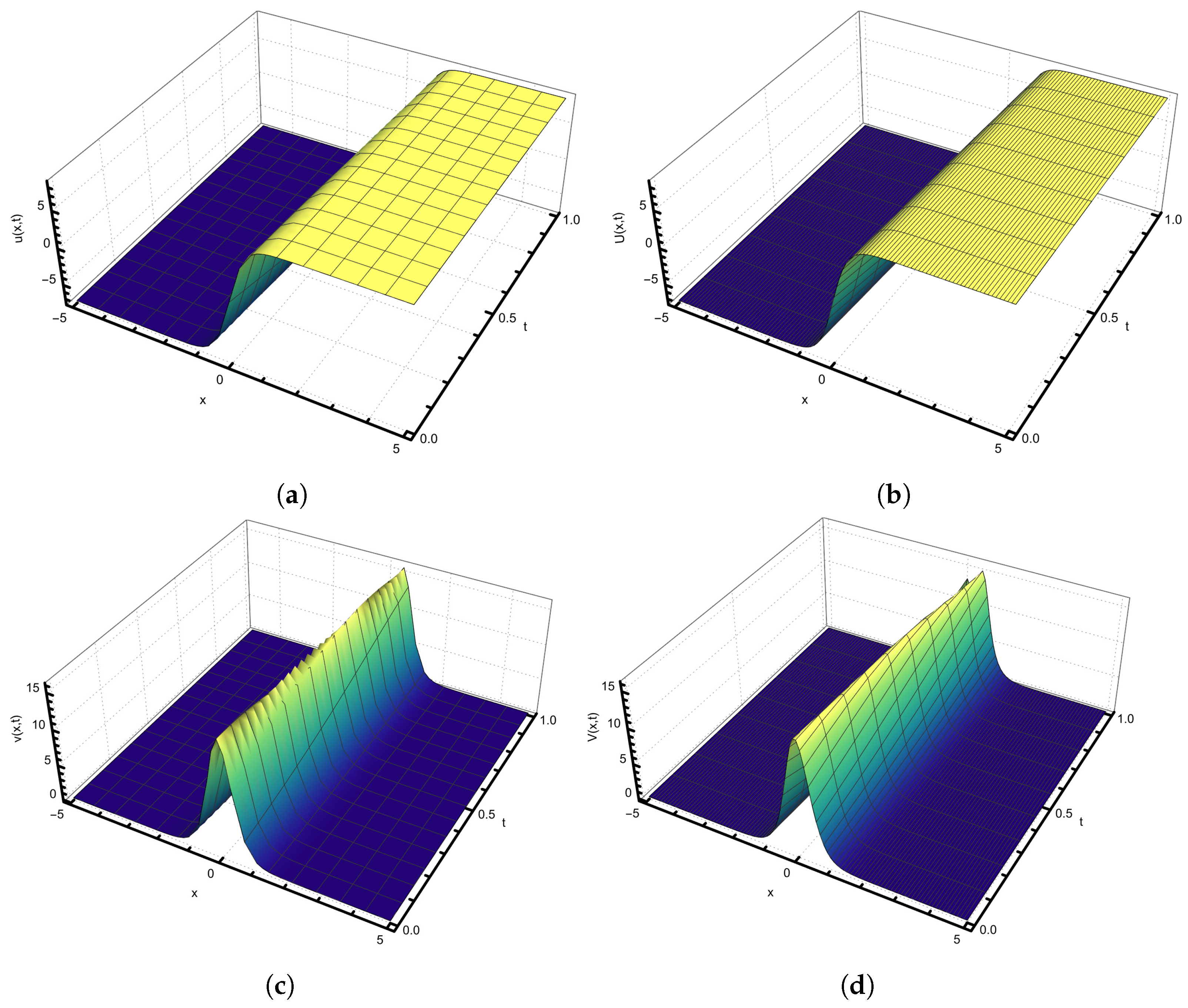
4. The (2+1)-Dimensional Time-Fractional Coupled Differential Equation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Hadhoud, A.R.; Rageh, A.A. Redefined Quintic B-Spline Collocation Method to Solve the Time-Fractional Whitham-Broer-Kaup Equations. Comput. Math. Methods 2024, 2024, 7326616. [Google Scholar] [CrossRef]
- Hadhoud, A.R.; Rageh, A.A.; Radwan, T. Computational solution of the time-fractional Schrödinger equation by using trigonometric B-spline collocation method. Fractal Fract. 2022, 6, 127. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Oldham, K.; Spanier, J. The Fractional Calculus Theory and Applications of Differentiation and Integration to Arbitrary Order; Elsevier: Amsterdam, The Netherlands, 1974. [Google Scholar]
- Al-Smadi, M.; Arqub, O.A.; Hadid, S. An attractive analytical technique for coupled system of fractional partial differential equations in shallow water waves with conformable derivative. Commun. Theor. Phys. 2020, 72, 085001. [Google Scholar] [CrossRef]
- Hadhoud, A.R.; Agarwal, P.; Rageh, A.A. Numerical treatments of the nonlinear coupled time-fractional Schrödinger equations. Math. Methods Appl. Sci. 2022, 45, 7119–7143. [Google Scholar] [CrossRef]
- Hadhoud, A.R.; Rageh, A.A.; Agarwal, P. Numerical method for solving two-dimensional of the space and space–time fractional coupled reaction-diffusion equations. Math. Methods Appl. Sci. 2023, 46, 6054–6076. [Google Scholar] [CrossRef]
- Sene, N.; Fall, A.N. Homotopy perturbation ρ-laplace transform method and its application to the fractional diffusion equation and the fractional diffusion-reaction equation. Fractal Fract. 2019, 3, 14. [Google Scholar] [CrossRef]
- Tamsir, M.; Srivastava, V.K. Analytical study of time-fractional order Klein–Gordon equation. Alex. Eng. J. 2016, 55, 561–567. [Google Scholar] [CrossRef]
- Sahu, I.; Jena, S.R. SDIQR mathematical modelling for COVID-19 of Odisha associated with influx of migrants based on Laplace Adomian decomposition technique. Model. Earth Syst. Environ. 2023, 9, 4031–4040. [Google Scholar] [CrossRef]
- Owolabi, K.M.; Pindza, E.; Karaagac, B.; Oguz, G. Laplace transform-homotopy perturbation method for fractional time diffusive predator–prey models in ecology. Partial Differ. Equ. Appl. Math. 2024, 9, 100607. [Google Scholar] [CrossRef]
- Jawarneh, Y.; Alsheekhhussain, Z.; Al-Sawalha, M.M. Fractional View Analysis System of Korteweg–de Vries Equations Using an Analytical Method. Fractal Fract. 2024, 8, 40. [Google Scholar] [CrossRef]
- Eriqat, T.; El-Ajou, A.; Moa’ath, N.O.; Al-Zhour, Z.; Momani, S. A new attractive analytic approach for solutions of linear and nonlinear neutral fractional pantograph equations. Chaos Solitons Fractals 2020, 138, 109957. [Google Scholar] [CrossRef]
- Alquran, M.; Ali, M.; Alsukhour, M.; Jaradat, I. Promoted residual power series technique with Laplace transform to solve some time-fractional problems arising in physics. Results Phys. 2020, 19, 103667. [Google Scholar] [CrossRef]
- Shqair, M.; Ghabar, I.; Burqan, A. Using Laplace Residual Power Series Method in Solving Coupled Fractional Neutron Diffusion Equations with Delayed Neutrons System. Fractal Fract. 2023, 7, 219. [Google Scholar] [CrossRef]
- Oqielat, M.N.; Eriqat, T.; Ogilat, O.; El-Ajou, A.; Alhazmi, S.E.; Al-Omari, S. Laplace-Residual Power Series Method for Solving Time-Fractional Reaction–Diffusion Model. Fractal Fract. 2023, 7, 309. [Google Scholar] [CrossRef]
- Aljarrah, H.; Alaroud, M.; Ishak, A.; Darus, M. Approximate solution of nonlinear time-fractional PDEs by Laplace residual power series method. Mathematics 2022, 10, 1980. [Google Scholar] [CrossRef]
- Albalawi, W.; Shah, R.; Nonlaopon, K.; El-Sherif, L.S.; El-Tantawy, S.A. Laplace Residual Power Series Method for Solving Three-Dimensional Fractional Helmholtz Equations. Symmetry 2023, 15, 194. [Google Scholar] [CrossRef]
- Burqan, A.; Sarhan, A.; Saadeh, R. Constructing Analytical Solutions of the Fractional Riccati Differential Equations Using Laplace Residual Power Series Method. Fractal Fract. 2022, 7, 14. [Google Scholar] [CrossRef]
- Sarhan, A.; Burqan, A.; Saadeh, R.; Al-Zhour, Z. Analytical Solutions of the Nonlinear Time-Fractional Coupled Boussinesq-Burger Equations Using Laplace Residual Power Series Technique. Fractal Fract. 2022, 6, 631. [Google Scholar] [CrossRef]
- Heydari, M.H.; Avazzadeh, Z. Numerical study of non-singular variable-order time fractional coupled Burgers’ equations by using the Hahn polynomials. Eng. Comput. 2022, 38, 101–110. [Google Scholar] [CrossRef]
- Albuohimad, B.; Adibi, H. On a hybrid spectral exponential Chebyshev method for time-fractional coupled Burgers equations on a semi-infinite domain. Adv. Differ. Equ. 2017, 2017, 85. [Google Scholar] [CrossRef]
- Ahmed, H.F.; Bahgat, M.; Zaki, M. Analytical approaches to space-and time-fractional coupled Burgers’ equations. Pramana 2019, 92, 38. [Google Scholar] [CrossRef]
- Albuohimad, B.; Adibi, H.; Kazem, S. A numerical solution of time-fractional coupled Korteweg-de Vries equation by using spectral collection method. Ain Shams Eng. J. 2018, 9, 1897–1905. [Google Scholar] [CrossRef]
- Alomari, A.; Massoun, Y. Numerical Solution of Time Fractional Coupled Korteweg-de Vries Equation with a Caputo Fractional Derivative in Two Parameters. IAENG Int. J. Comput. Sci. 2023, 50, 388–393. [Google Scholar]
- Khater, A.; Temsah, R.; Callebaut, D. Numerical solutions for some coupled nonlinear evolution equations by using spectral collocation method. Math. Comput. Model. 2008, 48, 1237–1253. [Google Scholar] [CrossRef]
- Bhrawy, A.; Doha, E.; Ezz-Eldien, S.; Abdelkawy, M. A numerical technique based on the shifted Legendre polynomials for solving the time-fractional coupled KdV equations. Calcolo 2016, 53, 1–17. [Google Scholar] [CrossRef]
- Yasmin, H. Numerical analysis of time-fractional Whitham-Broer-Kaup equations with exponential-decay kernel. Fractal Fract. 2022, 6, 142. [Google Scholar] [CrossRef]
- Chen, S.; Li, M.; Guan, B.; Li, Y.; Wang, Y.; Lin, X.; Liu, T. Abundant variant wave patterns by coupled Boussinesq–Whitham–Broer–Kaup equations. Chin. J. Phys. 2022, 78, 485–494. [Google Scholar] [CrossRef]
- Shah, R.; Khan, H.; Baleanu, D. Fractional Whitham–Broer–Kaup equations within modified analytical approaches. Axioms 2019, 8, 125. [Google Scholar] [CrossRef]
- Prakash, A.; Veeresha, P.; Prakasha, D.; Goyal, M. A new efficient technique for solving fractional coupled Navier–Stokes equations using q-homotopy analysis transform method. Pramana 2019, 93, 6. [Google Scholar] [CrossRef]
- Singh, B.K.; Kumar, P. FRDTM for numerical simulation of multi-dimensional, time-fractional model of Navier–Stokes equation. Ain Shams Eng. J. 2018, 9, 827–834. [Google Scholar] [CrossRef]


| LADM [24] | LVIM [24] | RDTM [24] | Present Method | |
|---|---|---|---|---|
| 0.01 | ||||
| 0.05 | ||||
| 0.10 | ||||
| 0.50 | ||||
| 1.00 |
| −5 | 0.1 | ||
| 0.4 | |||
| 0.7 | |||
| 1 | |||
| −2.5 | 0.1 | ||
| 0.4 | |||
| 0.7 | |||
| 1 | |||
| 0 | 0.1 | ||
| 0.4 | |||
| 0.7 | |||
| 1 | |||
| 2.5 | 0.1 | ||
| 0.4 | |||
| 0.7 | |||
| 1 | |||
| 5 | 0.1 | ||
| 0.4 | |||
| 0.7 | |||
| 1 |
| Present Method | Chebyshev Method [25] | |||
|---|---|---|---|---|
| 0.1 | ||||
| 0.2 | ||||
| 0.3 | ||||
| 0.4 | ||||
| 0.5 | ||||
| 0.6 | ||||
| 0.7 | ||||
| 0.8 | ||||
| 0.9 | ||||
| −5 | 0.1 | ||
| 0.2 | |||
| 0.3 | |||
| 0.4 | |||
| −2 | 0.1 | ||
| 0.2 | |||
| 0.3 | |||
| 0.4 | |||
| 1 | 0.1 | ||
| 0.2 | |||
| 0.3 | |||
| 0.4 | |||
| 4 | 0.1 | ||
| 0.2 | |||
| 0.3 | |||
| 0.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hadhoud, A.R.; Rageh, A.A.M.; Radwan, T. Employing the Laplace Residual Power Series Method to Solve (1+1)- and (2+1)-Dimensional Time-Fractional Nonlinear Differential Equations. Fractal Fract. 2024, 8, 401. https://doi.org/10.3390/fractalfract8070401
Hadhoud AR, Rageh AAM, Radwan T. Employing the Laplace Residual Power Series Method to Solve (1+1)- and (2+1)-Dimensional Time-Fractional Nonlinear Differential Equations. Fractal and Fractional. 2024; 8(7):401. https://doi.org/10.3390/fractalfract8070401
Chicago/Turabian StyleHadhoud, Adel R., Abdulqawi A. M. Rageh, and Taha Radwan. 2024. "Employing the Laplace Residual Power Series Method to Solve (1+1)- and (2+1)-Dimensional Time-Fractional Nonlinear Differential Equations" Fractal and Fractional 8, no. 7: 401. https://doi.org/10.3390/fractalfract8070401
APA StyleHadhoud, A. R., Rageh, A. A. M., & Radwan, T. (2024). Employing the Laplace Residual Power Series Method to Solve (1+1)- and (2+1)-Dimensional Time-Fractional Nonlinear Differential Equations. Fractal and Fractional, 8(7), 401. https://doi.org/10.3390/fractalfract8070401







