Analysis of Non-Local Integro-Differential Equations with Hadamard Fractional Derivatives: Existence, Uniqueness, and Stability in the Context of RLC Models
Abstract
1. Introduction
2. Preliminaries and Problem Statement
| Symbol | Definition |
|---|---|
| Space of continuous functions from to | |
| Norm: | |
| Product | |
| Banach space with Norm: |
Problem Formulation
3. Main Results
4. Ulam Stability Results
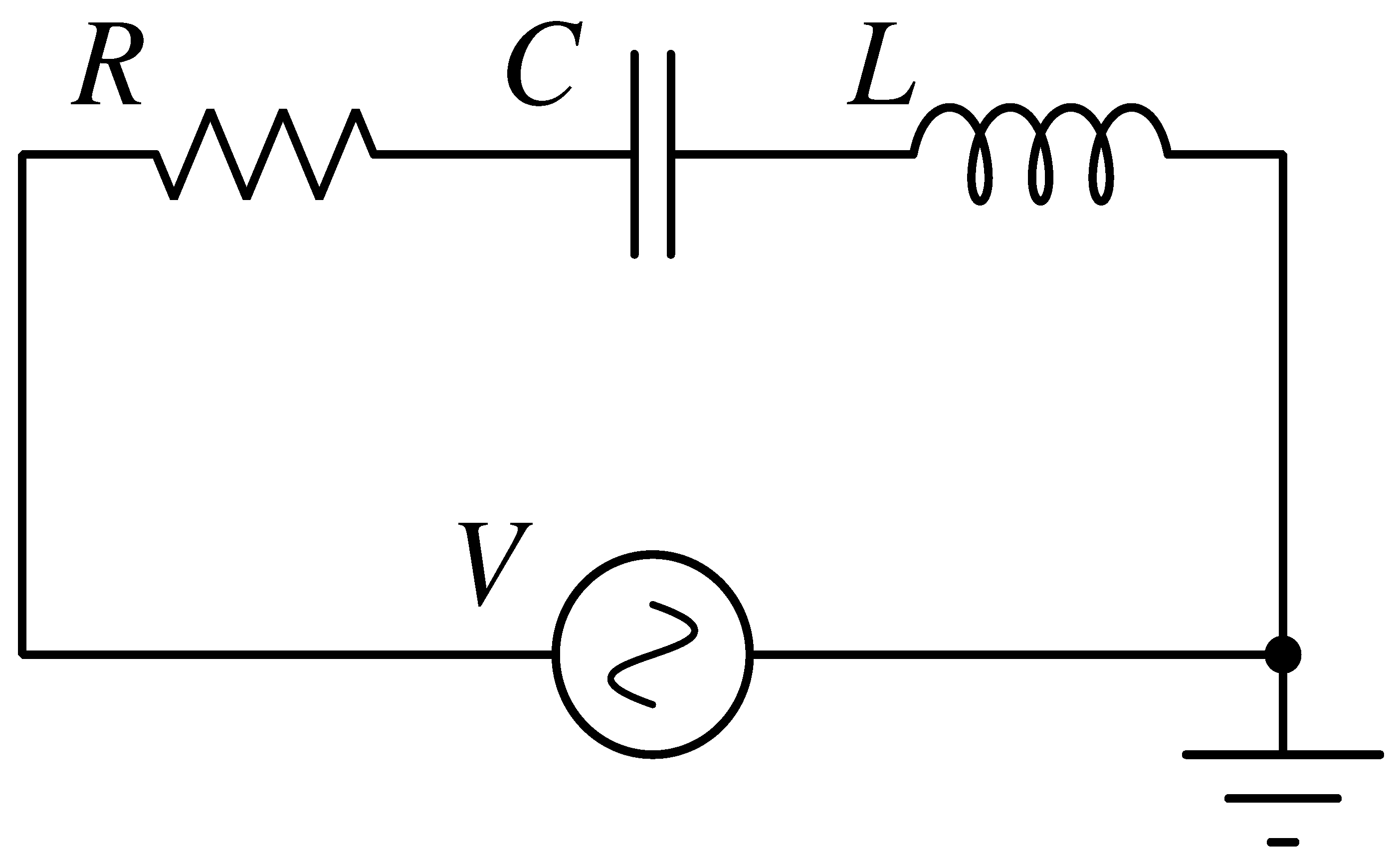
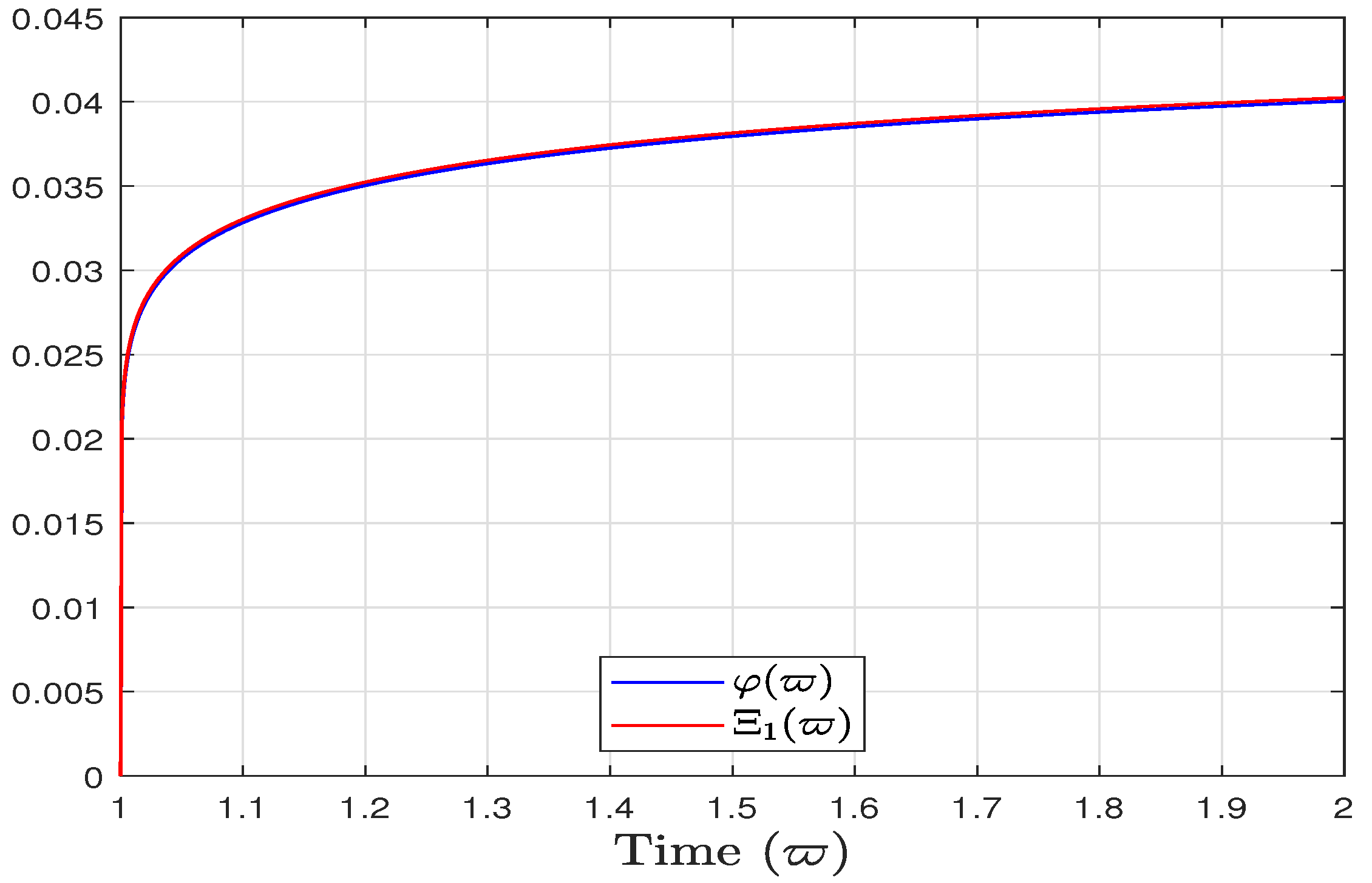
5. Example
6. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sudsutad, W.; Ntouyas, S.K.; Tariboon, J. Systems of fractional Langevin equations of Riemann-Liouville and Hadamard types. Adv. Differ. Equ. 2015, 2015, 1–24. [Google Scholar] [CrossRef]
- Ntouyas, S.K.; Sitho, S.; Khoployklang, T.; Tariboon, J. Sequential Riemann–Liouville and Hadamard–Caputo fractional differential equation with iterated fractional integrals conditions. Axioms 2021, 10, 277. [Google Scholar] [CrossRef]
- Borisut, P.; Kumam, P.; Ahmed, I.; Sitthithakerngkiet, K. Nonlinear Caputo fractional derivative with nonlocal Riemann-Liouville fractional integral condition via fixed point theorems. Symmetry 2019, 11, 829. [Google Scholar] [CrossRef]
- Shah, K.; Arfan, M.; Ullah, A.; Al-Mdallal, Q.; Ansari, K.J.; Abdeljawad, T. Computational study on the dynamics of fractional order differential equations with applications. Chaos Solitons Fractals 2022, 157, 111955. [Google Scholar] [CrossRef]
- Mohamed, S.A. A fractional differential quadrature method for fractional differential equations and fractional eigenvalue problems. Math. Methods Appl. Sci. 2020. [Google Scholar] [CrossRef]
- Dzherbashian, M.; Nersesian, A. Fractional derivatives and Cauchy problem for differential equations of fractional order. Fract. Calc. Appl. Anal. 2020, 23, 1810–1836. [Google Scholar] [CrossRef]
- Sevinik Adigüzel, R.; Aksoy, Ü.; Karapinar, E.; Erhan, İ.M. On the solution of a boundary value problem associated with a fractional differential equation. Math. Methods Appl. Sci. 2020. [Google Scholar] [CrossRef]
- Jalili, B.; Jalili, P.; Shateri, A.; Ganji, D.D. Rigid plate submerged in a Newtonian fluid and fractional differential equation problems via Caputo fractional derivative. Partial Differ. Equ. Appl. Math. 2022, 6, 100452. [Google Scholar] [CrossRef]
- Ding, W.; Patnaik, S.; Sidhardh, S.; Semperlotti, F. Applications of distributed-order fractional operators: A review. Entropy 2021, 23, 110. [Google Scholar] [CrossRef]
- Tlelo-Cuautle, E.; Pano-Azucena, A.D.; Guillén-Fernández, O.; Silva-Juárez, A. Analog/Digital Implementation of Fractional Order Chaotic Circuits and Applications; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Yang, F.; Mou, J.; Liu, J.; Ma, C.; Yan, H. Characteristic analysis of the fractional-order hyperchaotic complex system and its image encryption application. Signal Process. 2020, 169, 107373. [Google Scholar] [CrossRef]
- Wang, S.; He, S.; Yousefpour, A.; Jahanshahi, H.; Repnik, R.; Perc, M. Chaos and complexity in a fractional-order financial system with time delays. Chaos Solitons Fractals 2020, 131, 109521. [Google Scholar] [CrossRef]
- Shanmugam, S.; Narayanan, G.; Rajagopal, K.; Ali, M.S. Finite-time synchronization of complex-valued neural networks with reaction-diffusion terms: An adaptive intermittent control approach. Neural Comput. Appl. 2024, 36, 7389–7404. [Google Scholar] [CrossRef]
- Ahmad, S.; Ullah, A.; Akgül, A. Investigating the complex behaviour of multi-scroll chaotic system with Caputo fractal-fractional operator. Chaos Solitons Fractals 2021, 146, 110900. [Google Scholar] [CrossRef]
- Klimek, M. Sequential fractional differential equations with Hadamard derivative. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 4689–4697. [Google Scholar] [CrossRef]
- Gohar, M.; Li, C.; Li, Z. Finite difference methods for Caputo–Hadamard fractional differential equations. Mediterr. J. Math. 2020, 17, 194. [Google Scholar] [CrossRef]
- Benkerrouche, A.; Souid, M.S.; Karapınar, E.; Hakem, A. On the boundary value problems of Hadamard fractional differential equations of variable order. Math. Methods Appl. Sci. 2023, 46, 3187–3203. [Google Scholar] [CrossRef]
- Guo, L.; Li, C.; Zhao, J. Existence of Monotone Positive Solutions for Caputo–Hadamard Nonlinear Fractional Differential Equation with Infinite-Point Boundary Value Conditions. Symmetry 2023, 15, 970. [Google Scholar] [CrossRef]
- Subramanian, M.; Manigandan, M.; Gopal, T.N. Fractional differential equations involving Hadamard fractional derivatives with nonlocal multi-point boundary conditions. Discontinuity Nonlinearity Complex. 2020, 9, 421–431. [Google Scholar] [CrossRef]
- Manigandan, M.; Subramanian, M.; Duraisamy, P.; Gopal, T.N. On Caputo-Hadamard type fractional differential equations with nonlocal discrete boundary conditions. Discontinuity Nonlinearity Complex. 2021, 10, 185–194. [Google Scholar] [CrossRef]
- Van Mieghem, P. Origin of the fractional derivative and fractional non-Markovian continuous-time processes. Phys. Rev. Res. 2022, 4, 023242. [Google Scholar] [CrossRef]
- Li, C.; Zhu, C.; Zhang, N.; Sui, S.; Zhao, J. Free vibration of self-powered nanoribbons subjected to thermal-mechanical-electrical fields based on a nonlocal strain gradient theory. Appl. Math. Model. 2022, 110, 583–602. [Google Scholar] [CrossRef]
- Zhu, C.; Chen, Y.; Zhao, J.; Li, C.; Lei, Z. On Nonlocal Vertical and Horizontal Bending of a Micro-Beam. Math. Probl. Eng. 2022, 2022, 5121377. [Google Scholar] [CrossRef]
- Garra, R.; Orsingher, E.; Polito, F. A note on Hadamard fractional differential equations with varying coefficients and their applications in probability. Mathematics 2018, 6, 4. [Google Scholar] [CrossRef]
- Fan, E.; Li, C.; Li, Z. Numerical approaches to Caputo–Hadamard fractional derivatives with applications to long-term integration of fractional differential systems. Commun. Nonlinear Sci. Numer. Simul. 2022, 106, 106096. [Google Scholar] [CrossRef]
- Mirzaee, F.; Samadyar, N. Extension of Darbo fixed-point theorem to illustrate existence of the solutions of some nonlinear functional stochastic integral equations. Int. J. Nonlinear Anal. Appl. 2020, 11, 413–421. [Google Scholar]
- Al Elaiw, A.; Awadalla, M.; Manigandan, M.; Abuasbeh, K. A novel implementation of Mönch’s fixed point theorem to a system of nonlinear Hadamard fractional differential equations. Fractal Fract. 2022, 6, 586. [Google Scholar] [CrossRef]
- Karapınar, E.; Abdeljawad, T.; Jarad, F. Applying new fixed point theorems on fractional and ordinary differential equations. Adv. Differ. Equ. 2019, 2019, 1–25. [Google Scholar] [CrossRef]
- Shen, G.; Sakthivel, R.; Ren, Y.; Li, M. Controllability and stability of fractional stochastic functional systems driven by Rosenblatt process. Collect. Math. 2020, 71, 63–82. [Google Scholar] [CrossRef]
- Almutairi, A.; El-Metwally, H.; Sohaly, M.; Elbaz, I. Lyapunov stability analysis for nonlinear delay systems under random effects and stochastic perturbations with applications in finance and ecology. Adv. Differ. Equ. 2021, 2021, 1–32. [Google Scholar]
- Shen, G.; Xiao, R.; Yin, X. Averaging principle and stability of hybrid stochastic fractional differential equations driven by Lévy noise. Int. J. Syst. Sci. 2020, 51, 2115–2133. [Google Scholar] [CrossRef]
- Abdo, M.S.; Panchal, S.K.; Wahash, H.A. Ulam–Hyers–Mittag-Leffler stability for a ψ-Hilfer problem with fractional order and infinite delay. Results Appl. Math. 2020, 7, 100115. [Google Scholar] [CrossRef]
- Arshad, U.; Sultana, M.; Ali, A.H.; Bazighifan, O.; Al-Moneef, A.A.; Nonlaopon, K. Numerical solutions of fractional-order electrical rlc circuit equations via three numerical techniques. Mathematics 2022, 10, 3071. [Google Scholar] [CrossRef]
- Lavenda, B. Concepts of stability and symmetry in irreversible thermodynamics. I. Found. Phys. 1972, 2, 161–179. [Google Scholar] [CrossRef]
- Gallavotti, G. Breakdown and regeneration of time reversal symmetry in nonequilibrium statistical mechanics. Phys. D Nonlinear Phenom. 1998, 112, 250–257. [Google Scholar] [CrossRef]
- Russo, G.; Slotine, J.J.E. Symmetries, stability, and control in nonlinear systems and networks. Phys. Rev. E 2011, 84, 041929. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Qassim, M.; Furati, K.M.; Tatar, N.E. On a differential equation involving Hilfer-Hadamard fractional derivative. In Abstract and Applied Analysis; Hindawi: London, UK, 2012; Volume 2012, p. 391062. [Google Scholar]
- Rus, I.A. Ulam Stability of Ordinary Differential Equations; Studia Universitatis Babes-Bolyai, Mathematica: Cluj-Napoca, Romania, 2009. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Murugesan, M.; Shanmugam, S.; Rhaima, M.; Ravi, R. Analysis of Non-Local Integro-Differential Equations with Hadamard Fractional Derivatives: Existence, Uniqueness, and Stability in the Context of RLC Models. Fractal Fract. 2024, 8, 409. https://doi.org/10.3390/fractalfract8070409
Murugesan M, Shanmugam S, Rhaima M, Ravi R. Analysis of Non-Local Integro-Differential Equations with Hadamard Fractional Derivatives: Existence, Uniqueness, and Stability in the Context of RLC Models. Fractal and Fractional. 2024; 8(7):409. https://doi.org/10.3390/fractalfract8070409
Chicago/Turabian StyleMurugesan, Manigandan, Saravanan Shanmugam, Mohamed Rhaima, and Ragul Ravi. 2024. "Analysis of Non-Local Integro-Differential Equations with Hadamard Fractional Derivatives: Existence, Uniqueness, and Stability in the Context of RLC Models" Fractal and Fractional 8, no. 7: 409. https://doi.org/10.3390/fractalfract8070409
APA StyleMurugesan, M., Shanmugam, S., Rhaima, M., & Ravi, R. (2024). Analysis of Non-Local Integro-Differential Equations with Hadamard Fractional Derivatives: Existence, Uniqueness, and Stability in the Context of RLC Models. Fractal and Fractional, 8(7), 409. https://doi.org/10.3390/fractalfract8070409







