Enhancing Transient Stability in Multi-Machine Power Systems through a Model-Free Fractional-Order Excitation Stabilizer
Abstract
:1. Introduction
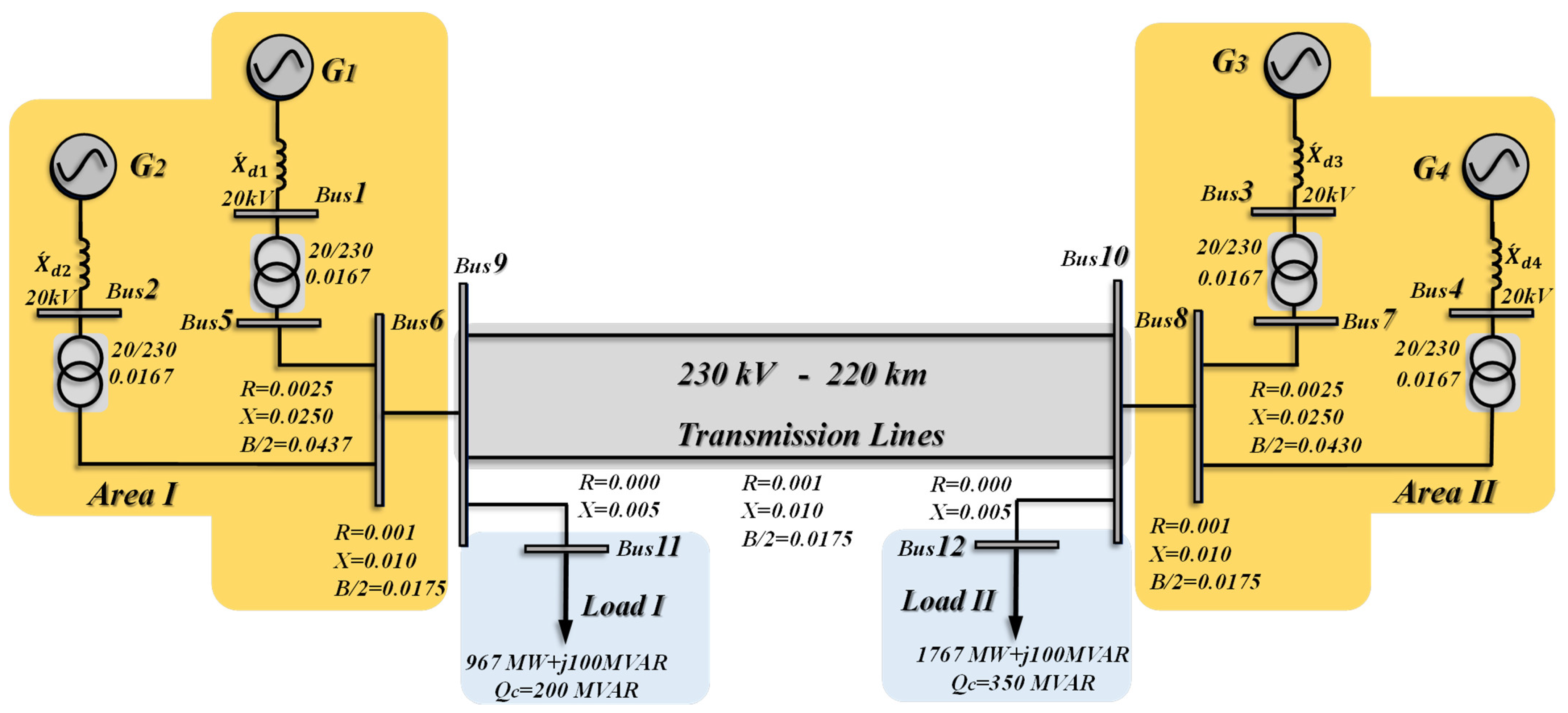
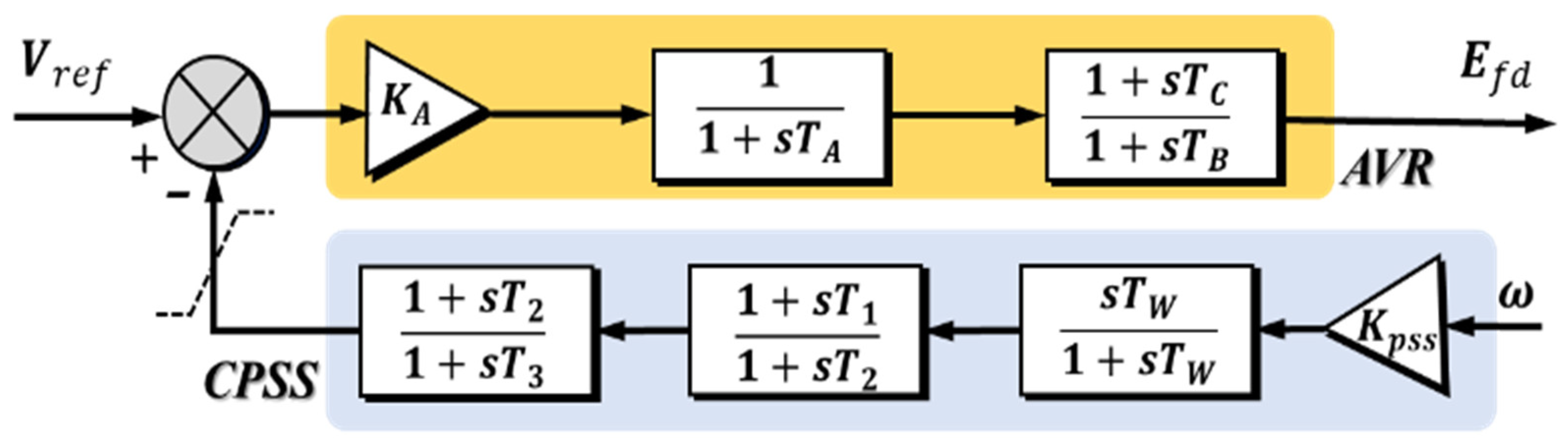
2. Dynamic Model of a Multi-Machine Power System
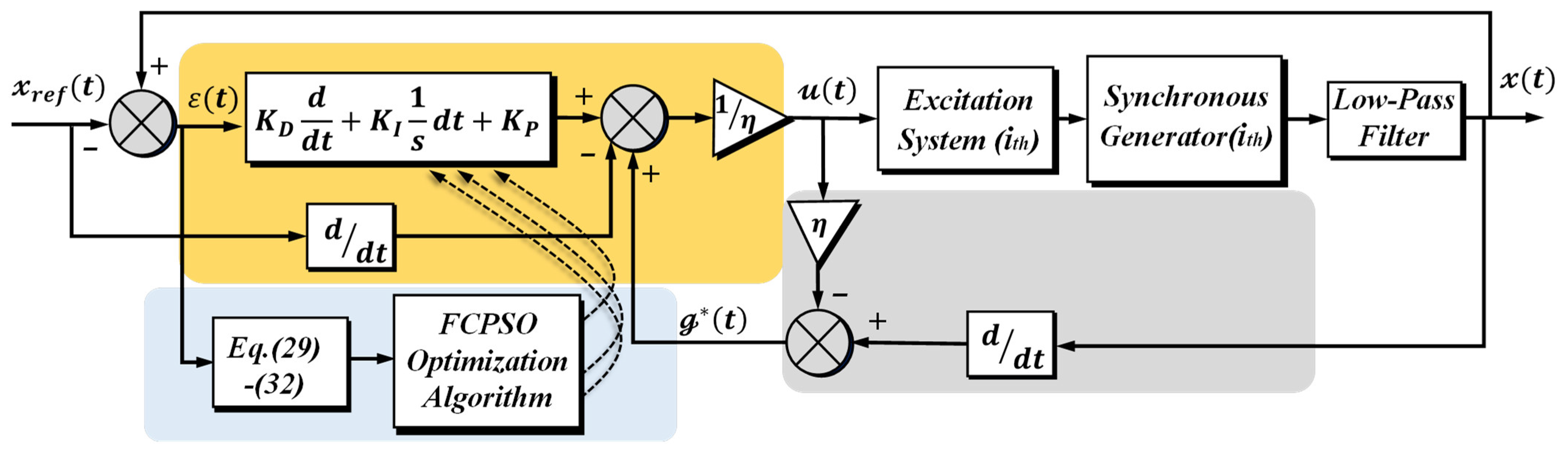
3. Model-Free Excitation System Stabilizer Using the Fractional Calculus Optimization Algorithm
3.1. Design of an Ultra-Local Controller
3.2. Fractional Calculus-Based Particle Swarm Optimization (FCPSO) Algorithm
| Algorithm 1 |
| set the population size and dimension set the searching space initialize swarm repeat for all particles do calculate fitness function values end for all particles do end until stopping rule |
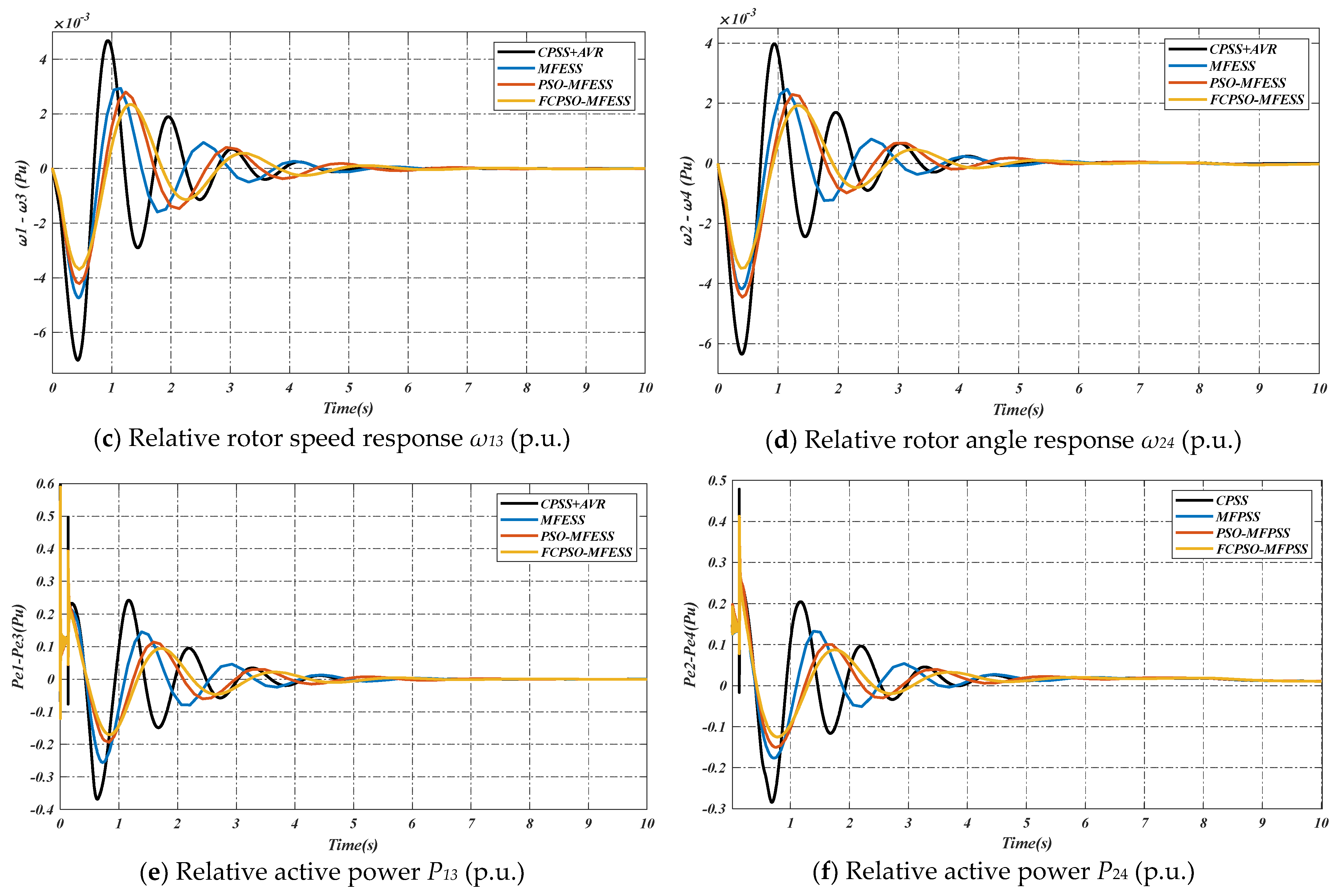
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. List of Symbols of the Dynamic Model of a Multi-Machine Power System
| D-axis open circuit field time constant | |
| Rotor speed of the jth synchronous generator | |
| Synchronous speed of the synchronous generators | |
| Rotor speed reference value of the jth synchronous generator | |
| Rotor angle of the jth synchronous generator | |
| Mechanical damping coefficient of the jth synchronous generator | |
| Inertia constant of the jth synchronous generator | |
| Mechanical power input to the jth synchronous generator shaft | |
| Active electrical power output of the jth synchronous generator | |
| Transient q-axis electromechanical force (EMF) of the jth synchronous generator | |
| Equivalent electro-motive force (EMF) in excitation winding of the jth synchronous generator | |
| Direct-axis reactance of the jth synchronous generator | |
| Direct-axis transient reactance of the jth synchronous generator | |
| Direct-axis stator current of the jth synchronous generator | |
| Quadrature-axis stator current of the jth synchronous generator | |
| Terminal voltage of the jth synchronous generator | |
| , | q and d-axis of the jth synchronous generator stator voltages |
References
- Zhang, N.; Jia, H.; Hou, Q.; Zhang, Z.; Xia, T.; Cai, X.; Wang, J. Data-Driven Security and Stability Rule in High Renewable Penetrated Power System Operation. Proc. IEEE 2023, 111, 788–805. [Google Scholar] [CrossRef]
- Du, W.; Fu, Q.; Wang, H.F. Power System Small-Signal Angular Stability Affected by Virtual Synchronous Generators. IEEE Trans. Power Syst. 2019, 34, 3209–3219. [Google Scholar] [CrossRef]
- Prakash, A.; Moursi, M.S.E.; Parida, S.K.; Kumar, K.; El-Saadany, E.F. Damping of Inter-Area Oscillations with Frequency Regulation in Power Systems Considering High Penetration of Renewable Energy Sources. IEEE Trans. Ind. Appl. 2024, 60, 1665–1679. [Google Scholar] [CrossRef]
- Liccardo, A.; Tessitore, S.; Bonavolontà, F.; Cristiano, S.; Noia, L.P.D.; Giannuzzi, G.M.; Pisani, C. Detection and Analysis of Inter-Area Oscillations Through a Dynamic-Order DMD Approach. IEEE Trans. Instrum. Meas. 2022, 71, 1–14. [Google Scholar] [CrossRef]
- Fathollahi, A.; Andresen, B. Deep Deterministic Policy Gradient for Adaptive Power System Stabilization and Voltage Regulation. E-Prime Adv. Electr. Eng. Electron. Energy 2024, 9, 100675. [Google Scholar] [CrossRef]
- Alaraifi, S.; Djouadi, S.; Moursi, M.S.E. Domain of Stability Characterization for Power Systems: A Novel Individual Invariance Method. IEEE Trans. Power Syst. 2024, 39, 14–27. [Google Scholar] [CrossRef]
- Oshnoei, S.; Fathollahi, A.; Oshnoei, A.; Khooban, M.H. Microgrid Frequency Regulation Based on a Fractional Order Cascade Controller. Fractal Fract. 2023, 7, 343. [Google Scholar] [CrossRef]
- Mira-Gebauer, N.; Rahmann, C.; Álvarez-Malebrán, R.; Vittal, V. Review of Wide-Area Controllers for Supporting Power System Stability. IEEE Access 2023, 11, 8073–8095. [Google Scholar] [CrossRef]
- Wang, G.; Tang, Y.; Li, Y.; Ai, D.; Chen, G.; Wei, W. Control Method for Additional Damper in Hydro-turbine Speed Governor of Hydro-dominant Power Systems. CSEE J. Power Energy Syst. 2023, 9, 589–598. [Google Scholar] [CrossRef]
- Zamani, M.; Shahgholian, G.; Fathollahi, A.; Mosavi, A.; Felde, I. Improving Interarea Mode Oscillation Damping in Multi-Machine Energy Systems through a Coordinated PSS and FACTS Controller Framework. Sustainability 2023, 15, 16070. [Google Scholar] [CrossRef]
- Du, W.; Dong, W.; Wang, Y.; Wang, H. A Method to Design Power System Stabilizers in a Multi-Machine Power System Based on Single-Machine Infinite-Bus System Model. IEEE Trans. Power Syst. 2021, 36, 3475–3486. [Google Scholar] [CrossRef]
- Shahgholian, G.; Fattollahi, A. Improving power system stability using transfer function: A comparative analysis. Eng. Technol. Appl. Sci. Res. 2017, 7, 1946–1952. [Google Scholar] [CrossRef]
- Bhadu, M.; Senroy, N.; Narayan Kar, I.; Sudha, G.N. Robust linear quadratic Gaussian-based discrete mode wide area power system damping controller. IET Gener. Transm. Distrib. 2016, 10, 1470–1478. [Google Scholar] [CrossRef]
- Fregene, K.; Kennedy, D. Stabilizing control of a high-order generator model by adaptive feedback linearization. IEEE Trans. Energy Convers. 2003, 18, 149–156. [Google Scholar] [CrossRef]
- Mansour, M.Z.; Ravanji, M.H.; Karimi, A.; Bahrani, B. Small-Signal Synchronization Stability Enhancement of Grid-Following Inverters via a Feedback Linearization Controller. IEEE Trans. Power Deliv. 2022, 37, 4335–4344. [Google Scholar] [CrossRef]
- Bento, M.E.C.; Ramos, R.A. A Method Based on Linear Matrix Inequalities to Design a Wide-Area Damping Controller Resilient to Permanent Communication Failures. IEEE Syst. J. 2021, 15, 3832–3840. [Google Scholar] [CrossRef]
- Zucco, J.P.T.; Ramirez, H.; Wu, Y.; Gorrec, Y.L. Linear Matrix Inequality Design of Exponentially Stabilizing Observer-Based State Feedback Port-Hamiltonian Controllers. IEEE Trans. Autom. Control 2023, 68, 6184–6191. [Google Scholar] [CrossRef]
- Sun, Z.; Cao, Y.; Wen, Z.; Song, Y.; Sun, Z. A Grey Wolf Optimizer algorithm based fuzzy logic power system stabilizer for single machine infinite bus system. Energy Rep. 2023, 9, 847–853. [Google Scholar] [CrossRef]
- Ansari, J.; Abbasi, A.R.; Heydari, M.H.; Avazzadeh, Z. Simultaneous design of fuzzy PSS and fuzzy STATCOM controllers for power system stability enhancement. Alex. Eng. J. 2022, 61, 2841–2850. [Google Scholar] [CrossRef]
- Kumar, A. Power System Stabilizers Design for Multimachine Power Systems Using Local Measurements. IEEE Trans. Power Syst. 2016, 31, 2163–2171. [Google Scholar] [CrossRef]
- Fattollahi, A.; Dehghani, M.; Yousefi, M.R. Analysis and simulation dynamic behavior of power system equipped with PSS and excitation system stabilizer. Signal Process. Renew. Energy 2022, 6, 99–111. [Google Scholar]
- Roy, T.K.; Mahmud, M.A.; Shen, W.; Oo, A.M.T. A non-linear adaptive excitation control scheme for feedback linearized synchronous generations in multimachine power systems. IET Gener. Transm. Distrib. 2021, 15, 1501–1520. [Google Scholar] [CrossRef]
- Shi, L.; Lee, K.Y.; Wu, F. Robust ESS-Based Stabilizer Design for Damping Inter-Area Oscillations in Multimachine Power Systems. IEEE Trans. Power Syst. 2016, 31, 1395–1406. [Google Scholar] [CrossRef]
- Han, W.; Stanković, A.M. Model-Predictive Control Design for Power System Oscillation Damping via Excitation—A Data-Driven Approach. IEEE Trans. Power Syst. 2023, 38, 1176–1188. [Google Scholar] [CrossRef]
- Halder, A.; Pal, N.; Mondal, D. Higher order sliding mode STATCOM control for power system stability improvement. Math. Comput. Simul. 2020, 177, 244–262. [Google Scholar] [CrossRef]
- Farahani, M.; Ganjefar, S. Intelligent power system stabilizer design using adaptive fuzzy sliding mode controller. Neurocomputing 2017, 226, 135–144. [Google Scholar] [CrossRef]
- Musarrat, M.N.; Fekih, A. A fractional order sliding mode control-based topology to improve the transient stability of wind energy systems. Int. J. Electr. Power Energy Syst. 2021, 133, 107306. [Google Scholar] [CrossRef]
- Liao, K.; He, Z.; Xu, Y.; Chen, G.; Dong, Z.Y.; Wong, K.P. A Sliding Mode Based Damping Control of DFIG for Interarea Power Oscillations. IEEE Trans. Sustain. Energy 2017, 8, 258–267. [Google Scholar] [CrossRef]
- Lee, S.S.; Li, S.Y.; Park, J.K. Nonlinear adaptive back-stepping controller design for power system stabilizer in multi-machine power systems. In Proceedings of the 2008 American Control Conference, Seattle, WA, USA, 11–13 June 2008; pp. 2504–2509. [Google Scholar] [CrossRef]
- Zhao, P.; Yao, W.; Wen, J.; Jiang, L.; Wang, S.; Cheng, S. Improved synergetic excitation control for transient stability enhancement and voltage regulation of power systems. Int. J. Electr. Power Energy Syst. 2015, 68, 44–51. [Google Scholar] [CrossRef]
- Fattollahi-Dehkordi, A.; Shahgholian, G.; Fani, B. Decentralized synergistic control of multi-machine power system using power system stabilizer. Signal Process. Renew. Energy 2020, 4, 1–21. [Google Scholar]
- Mir, A.S.; Singh, A.K.; Pal, B.C.; Senroy, N.; Tu, J. Adequacy of Lyapunov Control of Power Systems Considering Modelling Details and Control Indices. IEEE Trans. Power Syst. 2023, 38, 2275–2289. [Google Scholar] [CrossRef]
- Ospina, L.D.P.; Salazar, V.U.; Ospina, D.P. Dynamic Equivalents of Nonlinear Active Distribution Networks Based on Hammerstein-Wiener Models: An Application for Long-Term Power System Phenomena. IEEE Trans. Power Syst. 2022, 37, 4286–4296. [Google Scholar] [CrossRef]
- Zhao, J.; Zhang, Y.; Wang, X. Model-Free Predictive Current Control of PMSM Drives Based on Variable Sequence Space Vector Modulation Using an Ultra-Local Model. IEEE Trans. Transp. Electrif. 2024, 10, 3518–3528. [Google Scholar] [CrossRef]
- Fathollahi, A.; Gheisarnejad, M.; Andresen, B.; Farsizadeh, H.; Khooban, M.-H. Robust artificial intelligence controller for stabilization of full-bridge converters feeding constant power loads. IEEE Trans. Circuits Syst. II Express Briefs 2023, 70, 3504–3508. [Google Scholar] [CrossRef]
- Wang, B.; Fan, H.; Li, Z.; Feng, G.; Han, Y. An Ultra-Local Model-Based Control Method with the Bus Voltage Supervisor for Hybrid Energy Storage System in Electric Vehicles. IEEE J. Emerg. Sel. Top. Power Electron. 2024, 12, 461–471. [Google Scholar] [CrossRef]
- Hou, Z.; Lei, T. Constrained Model Free Adaptive Predictive Perimeter Control and Route Guidance for Multi-Region Urban Traffic Systems. IEEE Trans. Intell. Transp. Syst. 2022, 23, 912–924. [Google Scholar] [CrossRef]
- Ren, J.C.; Liu, D.; Wan, Y. Model-Free Adaptive Iterative Learning Control Method for the Czochralski Silicon Monocrystalline Batch Process. IEEE Trans. Semicond. Manuf. 2021, 34, 398–407. [Google Scholar] [CrossRef]
- Fliess, M.; Join, C. Intelligent PID controllers. In Proceedings of the 2008 16th Mediterranean Conference on Control and Automation, Ajaccio, France, 25–27 June 2008; pp. 326–331. [Google Scholar] [CrossRef]
- Wang, H.P.; Mustafa, G.I.Y.; Tian, Y. Model-free fractional-order sliding mode control for an active vehicle suspension system. Adv. Eng. Softw. 2018, 115, 452–461. [Google Scholar] [CrossRef]
- Younes, Y.A.; Drak, A.; Noura, H.; Rabhi, A.; Hajjaji, A.E. Model-free control of a quadrotor vehicle. In Proceedings of the 2014 International Conference on Unmanned Aircraft Systems (ICUAS), Orlando, FL, USA, 27–30 May 2014; pp. 1126–1131. [Google Scholar] [CrossRef]
- Huang, S.; Xiong, L.; Wang, J.; Li, P.; Wang, Z.; Ma, M. Fixed-Time Fractional-Order Sliding Mode Controller for Multimachine Power Systems. IEEE Trans. Power Syst. 2021, 36, 2866–2876. [Google Scholar] [CrossRef]
- Kundur, P. Power System Stability and Control; McGraw-Hill: New York, NY, USA, 2007. [Google Scholar]
- Fathollahi, A.; Kargar, A.; Derakhshandeh, S.Y. Enhancement of power system transient stability and voltage regulation performance with decentralized synergetic TCSC controller. Int. J. Electr. Power Energy Syst. 2022, 135, 107533. [Google Scholar] [CrossRef]
- Long, B.; Zhang, J.; Shen, D.; Rodríguez, J.; Guerrero, J.M.; Chong, K.T. Ultralocal Model-Free Predictive Control of T-Type Grid-Connected Converters Based on Extended Sliding-Mode Disturbance Observer. IEEE Trans. Power Electron. 2023, 38, 15494–15508. [Google Scholar] [CrossRef]
- Fliess, M. Model-free control and intelligent PID controllers: Towards a possible trivialization of nonlinear control? IFAC Proc. 2009, 42, 1531–1550. [Google Scholar] [CrossRef]
- Mosayebi, M.; Fthollahi, A.; Gheisarnejad, M.; Farsizadeh, H.; Khooban, M.H. Smart Emergency EV-to-EV Portable Battery Charger. Inventions 2022, 7, 45. [Google Scholar] [CrossRef]
- Fliess, M.; Join, C. Stability margins and model-free control: A first look. In Proceedings of the 2014 European Control Conference (ECC), Strasbourg, France, 24–27 June 2014; pp. 454–459. [Google Scholar]
- Coskun, M.Y.; İtik, M. Intelligent PID control of an industrial electro-hydraulic system. ISA Trans. 2023, 139, 484–498. [Google Scholar] [CrossRef]
- Wang, Q.-G.; Liu, T.; Nie, Z.-Y.; Hao, S.; Ren, X.; Zhang, D.; Wang, L. A generalized control scheme for system uncertainty estimation and cancellation. Trans. Inst. Meas. Control 2021, 43, 2921–2933. [Google Scholar] [CrossRef]
- Jeong, Y.W.; Park, J.B.; Jang, S.H.; Lee, K.Y. A New Quantum-Inspired Binary PSO: Application to Unit Commitment Problems for Power Systems. IEEE Trans. Power Syst. 2010, 43, 1486–1495. [Google Scholar] [CrossRef]
- Hong, Y.Y.; Hsiao, C.Y. Under-Frequency Load Shedding in a Standalone Power System with Wind-Turbine Generators Using Fuzzy PSO. IEEE Trans. Power Deliv. 2022, 37, 1140–1150. [Google Scholar] [CrossRef]
- Ferreira, N.M.F.; Machado, J.A.T. Mathematical Methods in Engineering; Springer: Dordrecht, The Netherlands, 2014. [Google Scholar]
- Fathollahi, A.; Andresen, B. Multi-Machine Power System Transient Stability Enhancement Utilizing a Fractional Order-Based Nonlinear Stabilizer. Fractal Fract. 2023, 7, 808. [Google Scholar] [CrossRef]
- Keumarsi, V.; Simab, M.; Shahgholian, G. An integrated approach for optimal placement and tuning of power system stabilizer in multi-machine systems. Int. J. Electr. Power Energy Syst. 2014, 63, 132–139. [Google Scholar] [CrossRef]


| 10.81 | 0.913 | 0.038 | 0.723 | 0.213 | |
| 20.22 | 0.310 | 0.066 | 0.878 | 0.019 | |
| 7.025 | 0.516 | 0.112 | 1.400 | 0.015 | |
| 9.442 | 1.422 | 0.045 | 0.456 | 0.050 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fathollahi, A.; Andresen, B. Enhancing Transient Stability in Multi-Machine Power Systems through a Model-Free Fractional-Order Excitation Stabilizer. Fractal Fract. 2024, 8, 419. https://doi.org/10.3390/fractalfract8070419
Fathollahi A, Andresen B. Enhancing Transient Stability in Multi-Machine Power Systems through a Model-Free Fractional-Order Excitation Stabilizer. Fractal and Fractional. 2024; 8(7):419. https://doi.org/10.3390/fractalfract8070419
Chicago/Turabian StyleFathollahi, Arman, and Björn Andresen. 2024. "Enhancing Transient Stability in Multi-Machine Power Systems through a Model-Free Fractional-Order Excitation Stabilizer" Fractal and Fractional 8, no. 7: 419. https://doi.org/10.3390/fractalfract8070419
APA StyleFathollahi, A., & Andresen, B. (2024). Enhancing Transient Stability in Multi-Machine Power Systems through a Model-Free Fractional-Order Excitation Stabilizer. Fractal and Fractional, 8(7), 419. https://doi.org/10.3390/fractalfract8070419







