Mittag-Leffler Synchronization in Finite Time for Uncertain Fractional-Order Multi-Delayed Memristive Neural Networks with Time-Varying Perturbations via Information Feedback
Abstract
:1. Introduction
2. Theoretical Basis and Model Construction
3. Finite-Time Synchronization Results
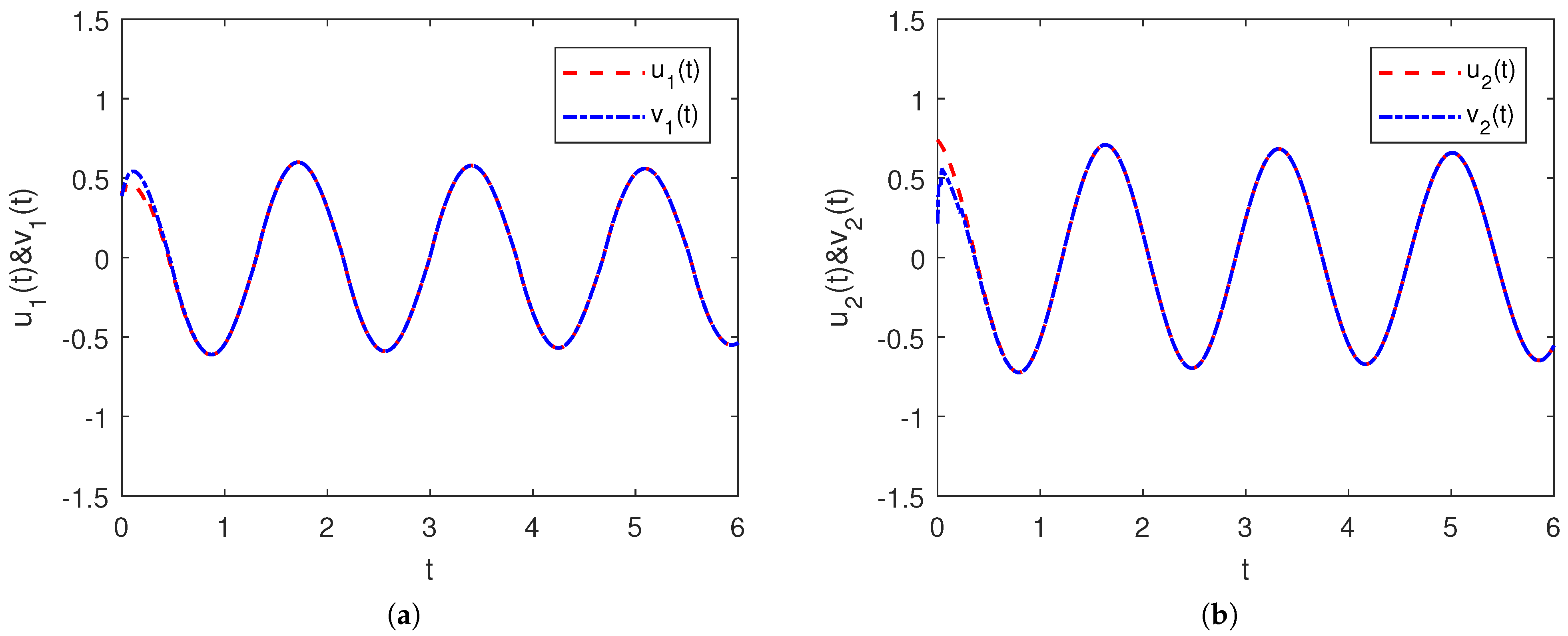
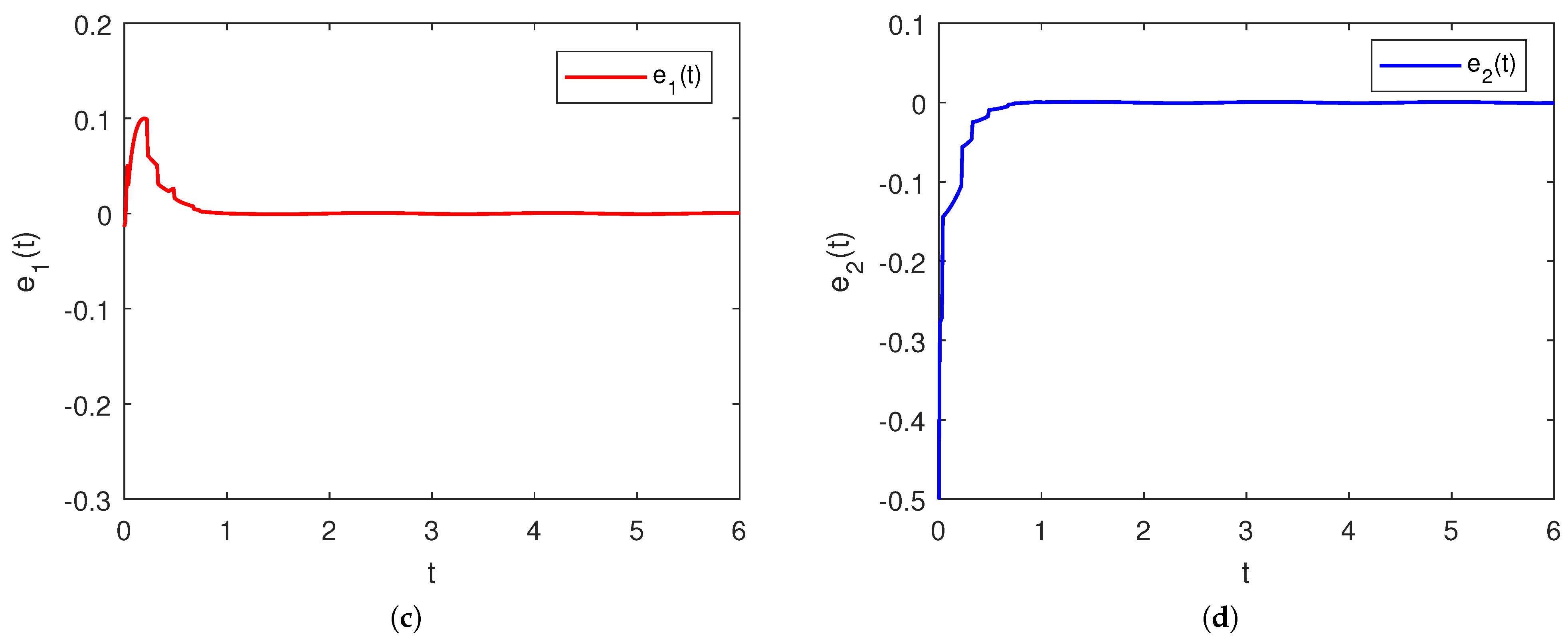
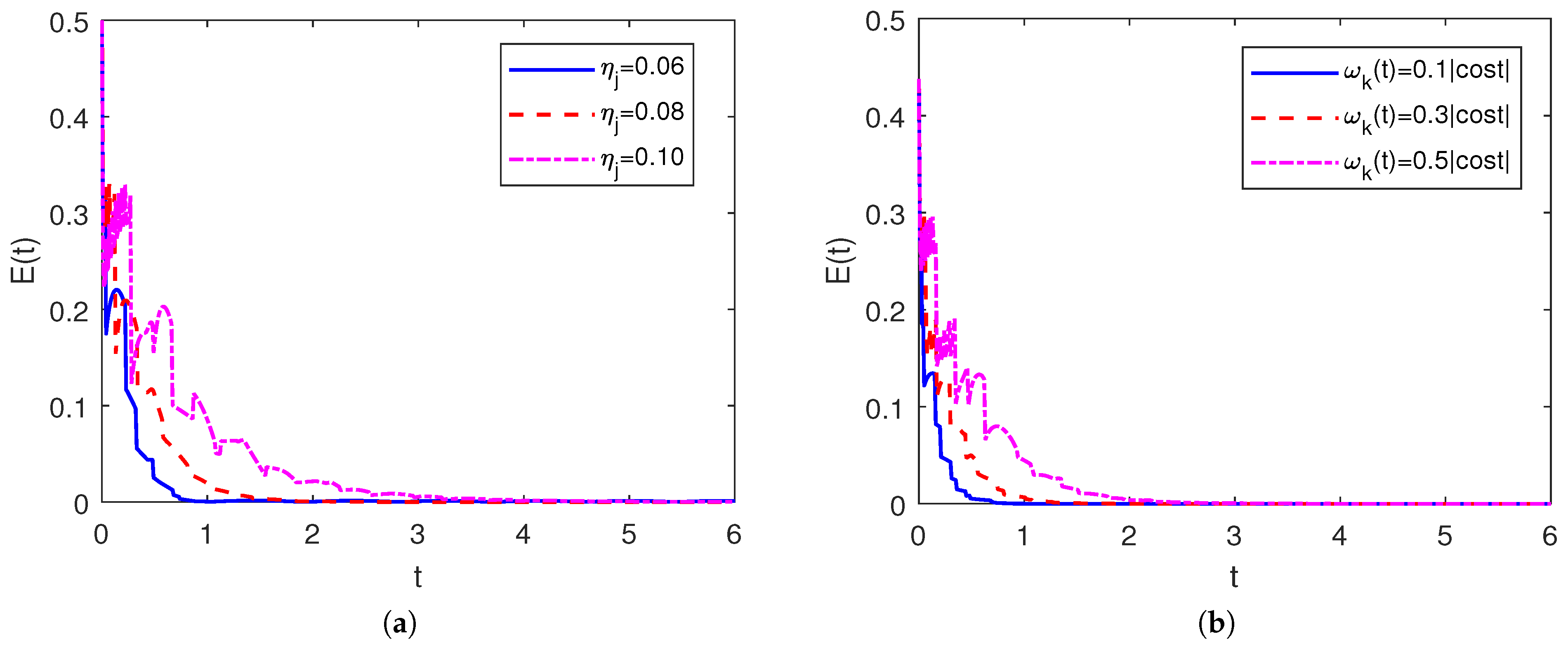
4. Illustrative Experiments
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tang, Z.; Xuan, D.L.; Park, J.H.; Wang, Y.; Feng, J.W. Impulsive effects based distributed synchronization of heterogeneous coupled neural networks. IEEE Trans. Netw. Sci. Eng. 2021, 8, 498–510. [Google Scholar] [CrossRef]
- Fan, H.G.; Chen, X.J.; Shi, K.B.; Wen, H. Distributed delayed impulsive control for μ-synchronization of multi-link structure networks with bounded uncertainties and time-varying delays of unmeasured bounds: A novel Halanay impulsive inequality approach. Chaos Solitons Fractals 2024, 186, 115226. [Google Scholar] [CrossRef]
- Zhong, Q.S.; Han, S.; Shi, K.B.; Zhong, S.M.; Kwon, O.-M. Co-design of adaptive memory event-triggered mechanism and aperiodic intermittent controller for nonlinear networked control systems. IEEE Trans. Circuits Syst.-Express Briefs 2022, 69, 4979–4983. [Google Scholar] [CrossRef]
- Cai, J.Y.; Yi, C.B.; Wu, Y.; Liu, D.Q.; Zhong, D.G. Leader-following consensus of nonlinear singular switched multi-agent systems via sliding mode control. Asian J. Control 2024, 26, 1–14. [Google Scholar] [CrossRef]
- Zhou, C.; Wang, C.H.; Yao, W.; Lin, H.R. Observer-based synchronization of memristive neural networks under dos attacks and actuator saturation and its application to image encryption. Appl. Math. Comput. 2022, 425, 127080. [Google Scholar] [CrossRef]
- Cheng, J.; Lin, A.; Cao, J.D.; Qiu, J.L.; Qi, W.H. Protocol-based fault detection for discrete-time memristive neural networks with effect. Inf. Sci. 2022, 615, 118–135. [Google Scholar] [CrossRef]
- Tang, C.; Li, X.Q.; Wang, Q. Mean-field stochastic linear quadratic optimal control for jump-diffusion systems with hybrid disturbances. Symmetry 2024, 16, 642. [Google Scholar] [CrossRef]
- Fan, H.G.; Rao, Y.; Shi, K.B.; Wen, H. Time-varying function matrix projection synchronization of Caputo fractional-order uncertain memristive neural networks with multiple delays via mixed open loop feedback control and impulsive control. Fractal Fract. 2024, 8, 301. [Google Scholar] [CrossRef]
- Shi, K.B.; Cai, X.; She, K.; Wen, S.P.; Zhong, S.M.; Park, P.; Kwon, O.-M. Stability analysis and security-based event-triggered mechanism design for T-S fuzzy NCS with traffic congestion via DoS attack and its application. IEEE Trans. Fuzzy Syst. 2023, 31, 3639–3651. [Google Scholar] [CrossRef]
- Kong, F.C.; Zhu, Q.X.; Huang, T.W. New fixed-time stability lemmas and applications to the discontinuous fuzzy inertial neural networks. IEEE Trans. Fuzzy Syst. 2021, 29, 3711–3722. [Google Scholar] [CrossRef]
- Ding, K.; Zhu, Q.X. A note on sampled-data synchronization of memristor networks subject to actuator failures and two different activations. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 2097–2101. [Google Scholar] [CrossRef]
- Adhikari, S.P.; Yang, C.; Kim, H.; Chua, L.O. Memristor bridge synapse-based neural network and its learning. IEEE Trans. Neural Netw. Learn. Syst. 2012, 23, 1426–1435. [Google Scholar] [CrossRef]
- Dou, H.; Shen, F.; Zhao, J.; Mu, X.Y. Understanding neural network through neuron level visualization. Neural Netw. 2023, 168, 484–495. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Park, J.H.; Zhong, S.M.; Yang, H.L. A switched operation approach to sampled-data control stabilization of fuzzy memristive neural networks with time-varying delay. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 891–900. [Google Scholar] [CrossRef] [PubMed]
- Alsaedi, A.; Cao, J.D.; Ahmad, B.; Alshehri, A.; Tan, X.G. Synchronization of master-slave memristive neural networks via fuzzy output-based adaptive strategy. Chaos Solitons Fractals 2022, 158, 112095. [Google Scholar] [CrossRef]
- Hua, W.T.; Wang, Y.T.; Liu, C.Y. New method for global exponential synchronization of multi-link memristive neural networks with three kinds of time-varying delays. Appl. Math. Comput. 2024, 471, 128593. [Google Scholar] [CrossRef]
- Bao, H.B.; Park, J.H.; Cao, J.D. Exponential synchronization of coupled stochastic memristor-based neural networks with time-varying probabilistic delay coupling and impulsive delay. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 190–201. [Google Scholar] [CrossRef]
- Li, X.F.; Zhang, W.B.; Fang, J.A.; Li, H.Y. Finite-time synchronization of memristive neural networks with discontinuous activation functions and mixed time-varying delays. Neurocomputing 2019, 340, 99–109. [Google Scholar] [CrossRef]
- Yu, T.H.; Cao, J.D.; Rutkowski, L.; Luo, Y.P. Finite-time synchronization of complex-valued memristive-based neural networks via hybrid controls. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 3938–3947. [Google Scholar] [CrossRef]
- Fu, Q.H.; Zhong, S.M.; Jiang, W.B.; Xie, W.Q. Projective synchronization of fuzzy memristive neural networks with pinning impulsive control. J. Frankl. Inst. 2020, 357, 10387–10409. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Chen, L.P.; Cao, J.D.; Wu, R.C.; Machado, J.A.T.; Lopes, A.M.; Yang, H.J. Stability and synchronization of fractional-order memristive neural networks with multiple delays. Neural Netw. 2017, 94, 76–85. [Google Scholar] [CrossRef]
- Gu, Y.J.; Wang, H.; Yu, Y.G. Synchronization for commensurate Riemann-Liouville fractional-order memristor-based neural networks with unknown parameters. J. Frankl. Inst. 2020, 357, 8870–8898. [Google Scholar] [CrossRef]
- Chen, J.J.; Zeng, Z.G.; Jiang, P. Global Mittag-Leffler stability and synchronization of memristor-based fractional-order neural networks. Neural Netw. 2014, 51, 1–8. [Google Scholar] [CrossRef]
- Bao, H.B.; Cao, J.D. Projective synchronization of fractional-order memristor-based neural networks. Neural Netw. 2015, 63, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.Z.; Yang, Y.Q.; Wang, F. Projective synchronization of fractional-order memristor-based neural networks with switching jumps mismatch. Phys. A 2017, 471, 402–415. [Google Scholar] [CrossRef]
- Velmurugan, G.; Rakkiyappan, R. Hybrid projective synchronization of fractional-order memristor-based neural networks with time delays. Nonlinear Dyn. 2016, 83, 419–432. [Google Scholar] [CrossRef]
- Li, X.M.; Liu, X.G.; Wang, F.X. Anti-synchronization of fractional-order complex-valued neural networks with a leakage delay and time-varying delays. Chaos Solitons Fractals 2023, 174, 113754. [Google Scholar] [CrossRef]
- Peng, L.B.; Li, X.F.; Bi, D.J.; Xie, X.; Xie, Y.L. Pinning multisynchronization of delayed fractional-order memristor-based neural networks with nonlinear coupling and almost-periodic perturbations. Neural Netw. 2021, 144, 372–383. [Google Scholar] [CrossRef]
- Gu, Y.J.; Yu, Y.G.; Wang, H. Projective synchronization for fractional-order memristor-based neural networks with time delays. Neural Comput. Appl. 2019, 31, 6039–6054. [Google Scholar] [CrossRef]
- Song, S.; Song, X.N.; Balsera, I.T. Mixed H∞ and passive projective synchronization for fractional-order memristor-based neural networks with time delays via adaptive sliding mode control. Neural Process. Lett. 2018, 47, 443–462. [Google Scholar] [CrossRef]
- Mao, X.Y.; Wang, X.M.; Lu, Y.X.; Qin, H.Y. Synchronizations control of fractional-order multidimension-valued memristive neural networks with delays. Neurocomputing 2024, 563, 126942. [Google Scholar] [CrossRef]
- Si, X.; Wang, Z.; Fan, Y. Quantized control for finite-time synchronization of delayed fractional-order memristive neural networks: The Gronwall inequality approach. Expert Syst. Appl. 2023, 215, 119310. [Google Scholar] [CrossRef]
- Peng, X.; Wu, H.Q.; Song, K.; Shi, J.X. Global synchronization in finite time for fractional-order neural networks with discontinuous activations and time delays. Neural Netw. 2017, 94, 46–54. [Google Scholar] [CrossRef] [PubMed]
- Mao, K.; Liu, X.Y.; Cao, J.D.; Hu, Y.F. Finite-time bipartite synchronization of coupled neural networks with uncertain parameters. Phys. A 2022, 585, 126431. [Google Scholar] [CrossRef]
- Yang, X.J.; Li, C.D.; Huang, T.W.; Song, Q.K.; Huang, J.J. Synchronization of fractional-order memristor-based complex-valued neural networks with uncertain parameters and time delays. Chaos Solitons Fractals 2018, 110, 105–123. [Google Scholar] [CrossRef]
- Yu, Y.G.; Zhang, S. Robust synchronization of memristor-based fractional-order Hopfield neural networks with parameter uncertainties. Neural Comput. Appl. 2019, 31, 3533–3542. [Google Scholar]
- Yao, W.; Wang, C.H.; Sun, Y.C.; Gong, S.Q.; Lin, H.R. Event-triggered control for robust exponential synchronization of inertial memristive neural networks under parameter disturbance. Neural Netw. 2023, 164, 67–80. [Google Scholar] [CrossRef] [PubMed]
- Yan, H.Y.; Qiao, Y.H.; Ren, Z.H.; Duan, L.J.; Miao, J. Master-slave synchronization of fractional-order memristive MAM neural networks with parameter disturbances and mixed delays. Commun. Nonlinear Sci. Numer. Simul. 2023, 120, 107152. [Google Scholar] [CrossRef]
- Liu, P.; Zeng, Z.; Wang, J. Asymptotic and finite-time cluster synchronization of coupled fractional-order neural networks with time delay. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 4956–4967. [Google Scholar] [CrossRef]
- Abdeljawad, T.; SThabet, T.; Kedim, I.; Ayari, M.I.; Khan, A. A higher-order extension of Atangana–Baleanu fractional operators with respect to another function and a Gronwall-type inequality. Bound. Value Probl. 2023, 2023, 49. [Google Scholar] [CrossRef]
- Alzahrani, A.B.; Saadeh, R.; Abdoon, M.A.; Elbadri, M.; Berir, M.; Qazza, A. Effective methods for numerical analysis of the simplest chaotic circuit model with Atangana–Baleanu Caputo fractional derivative. J. Eng. Math. 2024, 144, 9. [Google Scholar] [CrossRef]
- Yasmin, H. Application of aboodh homotopy perturbation transform method for fractional-order convection–reaction-diffusion equation within Caputo and Atangana–Baleanu operators. Symmetry 2023, 15, 453. [Google Scholar] [CrossRef]
- Zhang, S.; Yu, Y.G.; Wang, H. Mittag-Leffler stability of fractional-order Hopfield neural networks. Nonlinear Anal. Hybrid Syst. 2015, 16, 104–121. [Google Scholar] [CrossRef]
- Li, H.L.; Jiang, Y.L.; Wang, Z.L.; Zhang, L.; Teng, Z.D. Global Mittag-Leffler stability of coupled system of fractional-order differential equations on network. Appl. Math. Comput. 2015, 270, 269–277. [Google Scholar] [CrossRef]
- Arslan, E.; Narayanan, G.; Syed Ali, M.; Arik, S.; Saroha, S. Controller design for finite-time and fixed-time stabilization of fractional-order memristive complex-valued BAM neural networks with uncertain parameters and time-varying delays. Neural Netw. 2020, 130, 60–74. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, H.; Chen, X.; Shi, K.; Liang, Y.; Wang, Y.; Wen, H. Mittag-Leffler Synchronization in Finite Time for Uncertain Fractional-Order Multi-Delayed Memristive Neural Networks with Time-Varying Perturbations via Information Feedback. Fractal Fract. 2024, 8, 422. https://doi.org/10.3390/fractalfract8070422
Fan H, Chen X, Shi K, Liang Y, Wang Y, Wen H. Mittag-Leffler Synchronization in Finite Time for Uncertain Fractional-Order Multi-Delayed Memristive Neural Networks with Time-Varying Perturbations via Information Feedback. Fractal and Fractional. 2024; 8(7):422. https://doi.org/10.3390/fractalfract8070422
Chicago/Turabian StyleFan, Hongguang, Xijie Chen, Kaibo Shi, Yaohua Liang, Yang Wang, and Hui Wen. 2024. "Mittag-Leffler Synchronization in Finite Time for Uncertain Fractional-Order Multi-Delayed Memristive Neural Networks with Time-Varying Perturbations via Information Feedback" Fractal and Fractional 8, no. 7: 422. https://doi.org/10.3390/fractalfract8070422
APA StyleFan, H., Chen, X., Shi, K., Liang, Y., Wang, Y., & Wen, H. (2024). Mittag-Leffler Synchronization in Finite Time for Uncertain Fractional-Order Multi-Delayed Memristive Neural Networks with Time-Varying Perturbations via Information Feedback. Fractal and Fractional, 8(7), 422. https://doi.org/10.3390/fractalfract8070422








