FLRNN-FGA: Fractional-Order Lipschitz Recurrent Neural Network with Frequency-Domain Gated Attention Mechanism for Time Series Forecasting
Abstract
:1. Introduction
- A new Fractional-order Lipschitz Recurrent Neural Network with a Frequency-domain Gated Attention mechanism is proposed for time series prediction. Extensive experimental results on five datasets demonstrate the effectiveness of this method.
- This paper introduces fractional calculus to describe the system dynamics of recurrent neural networks, effectively improving the model’s prediction accuracy.
- In this paper, piecewise recurrent units are introduced to reduce the number of iterations of recurrent units. By reconstructing the weight matrix of the recurrent layer to control the system’s dynamic changes, the gradient problem in recurrent neural networks is effectively alleviated.
- This paper combines gated techniques with an attention mechanism to regulate attention information, which can reduce the number of model parameters and effectively improve the model’s efficiency and accuracy.
2. Related Work
A Time Series Forecasting Model Based on RNNs
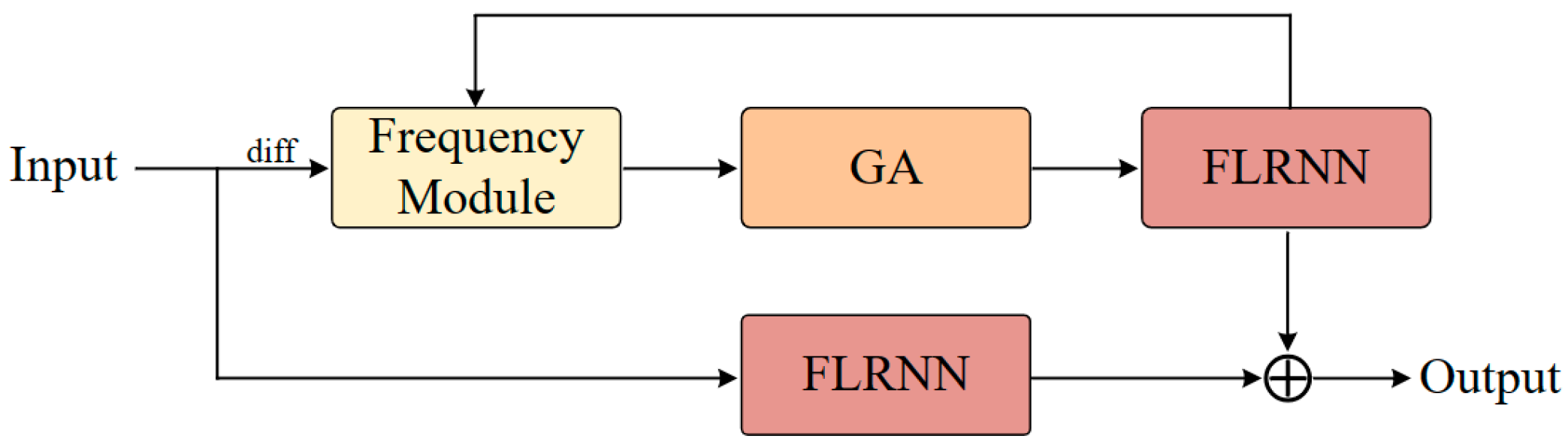
3. Methods
3.1. FLRNN
3.2. Frequency Module
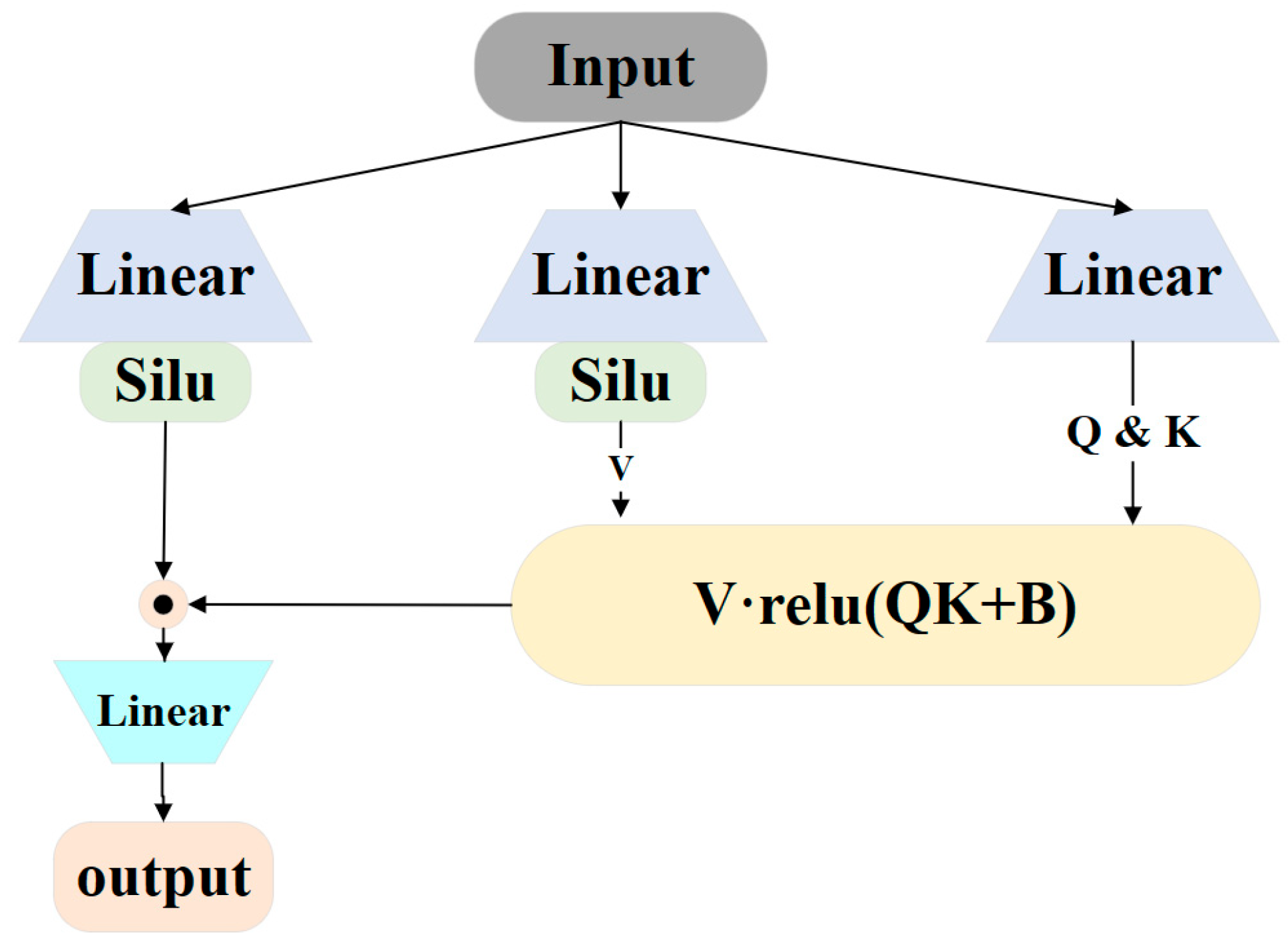
3.3. Gated Attention Mechanism
3.4. Gated Attention Mechanism
| Algorithm 1 FLRNN-FGA | |
| Input: Multivariate time series data | |
| Section 3.1: FLRNN module | |
| Step 1 Data input instantiation of the RNN model, Equation (1) | |
| Step 2 Integrating all hidden layers using fractional calculus, Equations (2)~(6) | |
| Step 3 Output of the FLRNN module | |
| Section 3.2: Frequency Module | |
| Step 4 Fourier transform converts the time domain into the frequency domain, Equation (7) | |
| Step 5 Select the low-frequency components to reduce noise. | |
| Section 3.3: Gated Attention mechanism | |
| Step 6 Capture the correlations between features using the attention mechanism. | |
| Step 7 Calculate the final output through the gated attention layer using Equation (8). | |
| Output: The output of the prediction results | |
4. Experiments
4.1. Datasets
- (a)
- Electricity dataset: the hourly electricity consumption records of 321 users from 2012 to 2014;
- (b)
- ETT dataset: Transformer data from July 2016 to July 2018;
- (c)
- Weather dataset: 21 meteorological indicator records from every 10 min throughout 2020;
- (d)
- Exchange dataset: the daily exchange rate records of eight countries from 1990 to 2016;
- (e)
- Traffic dataset: the hourly road occupancy rates records measured by different sensors on highways in the San Francisco Bay Area.
4.2. Baselines and Evaluation Metrics
- ⮚
- CN: Temporal Convolutional Network, a deep learning method that utilizes one-dimensional dilated convolutions and causal convolutions to process sequential data.
- ⮚
- LSTM: Long Short-Term Memory Network, a deep learning method that uses gated structures to retain long-term information to learn long-term dependencies.
- ⮚
- LSTNet: A method that combines Convolutional Neural Networks and Long Short-Term Memory Networks.
- ⮚
- Informer [37]: A Transformer variant that utilizes sparse self-attention.
- ⮚
- Autoformer [43]: A Transformer variant that employs inter-series attention.
- ⮚
- FEDformer [38]: A Transformer variant that uses the frequency domain to analyze time series data.
4.3. Experimental Settings
4.4. Main Results
4.5. Ablation Study
- w/o fractional calculus.
- w/o frequency module and gated structure, respectively.
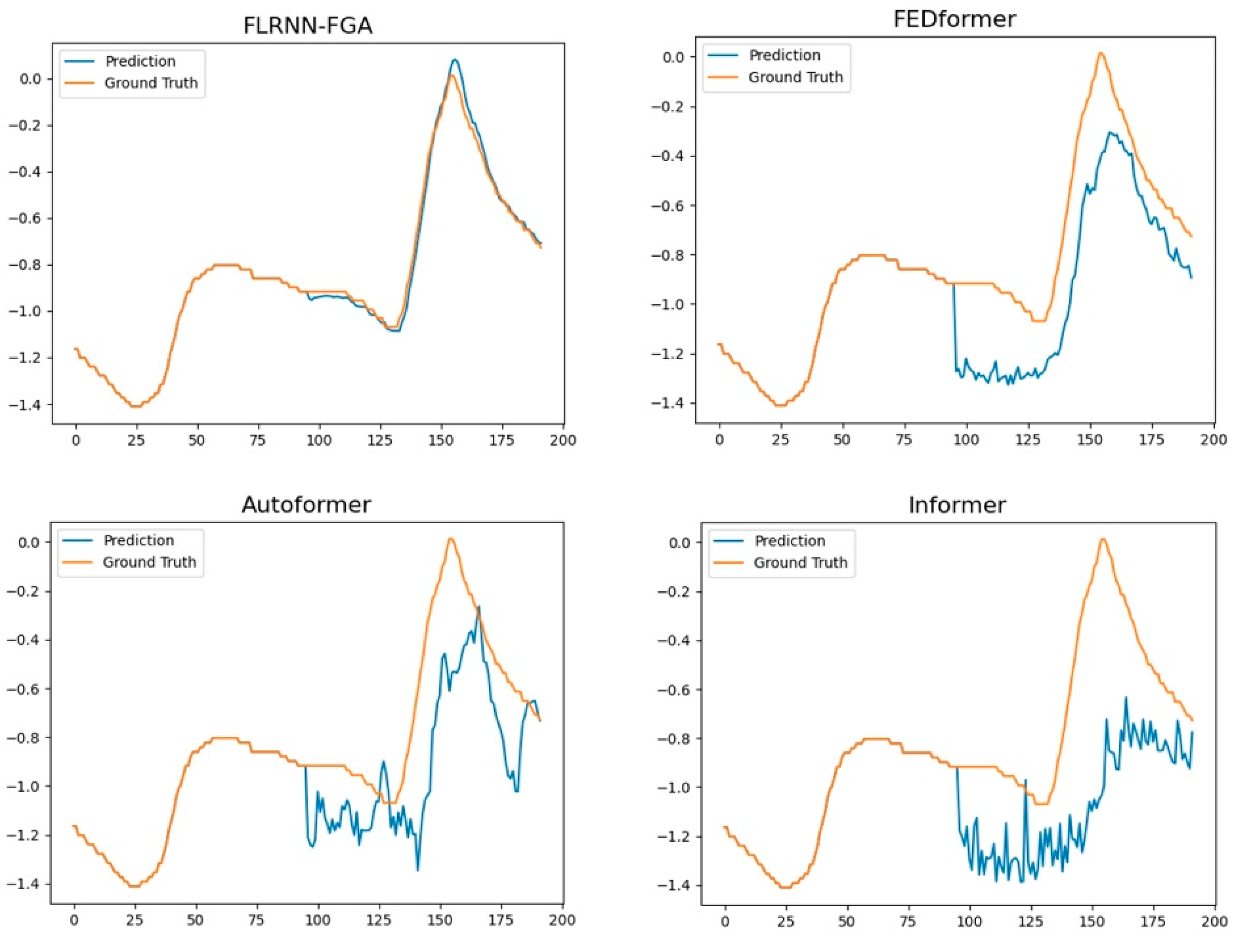
4.6. Visualization
4.7. Computational Efficiency Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, Z.L.; Zhang, G.W.; Yu, J.; Xu, L.Y. Dynamic graph structure learning for multivariate time series forecasting. Pattern Recognit. 2023, 138, 109423. [Google Scholar] [CrossRef]
- Klein, N.; Smith, M.S.; Nott, D.J. Deep distributional time series models and the probabilistic forecasting of intraday electricity prices. J. Appl. Econom. 2023, 38, 493–511. [Google Scholar] [CrossRef]
- Khashei, M.; Bijari, M. A novel hybridization of artificial neural networks and ARIMA models for time series forecasting. Appl. Soft Comput. 2011, 11, 2664–2675. [Google Scholar] [CrossRef]
- Masini, R.P.; Medeiros, M.C.; Mendes, E.F. Machine learning advances for time series forecasting. J. Econ. Surv. 2023, 37, 76–111. [Google Scholar] [CrossRef]
- Selvin, S.; Vinayakumar, R.; Gopalakrishnan, E.A.; Menon, V.K.; Soman, K.P. Stock price prediction using LSTM, RNN and CNN-sliding window model. In Proceedings of the 2017 International Conference on Advances in Computing, Communications and Informatics (icacci), Udupi, India, 13–16 September 2017. [Google Scholar]
- Vlahogianni, E.I.; Karlaftis, M.G.; Golias, J.C. Optimized and meta-optimized neural networks for short-term traffic flow prediction: A genetic approach. Transp. Res. Part C Emerg. Technol. 2005, 13, 211–234. [Google Scholar] [CrossRef]
- Kumar, B.; Yadav, N. A novel hybrid model combining βsarma and lstm for time series forecasting. Appl. Soft Comput. 2023, 134, 110019. [Google Scholar] [CrossRef]
- Pedregal, D.J.; Young, P.C. Statistical approaches to modelling and forecasting time series. In Companion to Economic Forecasting; Wiley: Hoboken, NJ, USA, 2002; pp. 69–104. [Google Scholar]
- Li, X.; Li, N.; Ding, S.; Cao, Y.; Li, Y. A novel data-driven seasonal multivariable grey model for seasonal time series forecasting. Inf. Sci. 2023, 642, 119165. [Google Scholar] [CrossRef]
- Garcia, R.; Contreras, J.; Van Akkeren, M.; Garcia, J. A GARCH forecasting model to predict day-ahead electricity prices. IEEE Trans. Power Syst. 2005, 20, 867–874. [Google Scholar] [CrossRef]
- Yi, K.; Zhang, Q.; Fan, W.; He, H.; Hu, L.; Wang, P.; An, N.; Cao, L.; Niu, Z. FourierGNN: Rethinking multivariate time series forecasting from a pure graph perspective. Adv. Neural Inf. Process. Syst. 2024, 36. [Google Scholar]
- Pan, Z.; Jiang, Y.; Garg, S.; Schneider, A.; Nevmyvaka, Y.; Song, D. S2 IP-LLM: Semantic Space Informed Prompt Learning with LLM for Time Series Forecasting. In Proceedings of the Forty-First International Conference on Machine Learning, Vienna, Austria, 21–27 July 2024. [Google Scholar]
- Liang, J.; Cao, J.; Fan, Y.; Zhang, K.; Ranjan, R.; Li, Y.; Timofte, R.; Van Gool, L. Conv2former: A simple transformer-style convnet for visual recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2024. early access. [Google Scholar]
- Liang, J.; Cao, J.; Fan, Y.; Zhang, K.; Ranjan, R.; Li, Y.; Timofte, R.; Van Gool, L. Vrt: A video restoration transformer. IEEE Trans. Image Process. 2024, 33, 2171–2182. [Google Scholar] [CrossRef]
- Polson, N.G.; Sokolov, V.O. Deep learning for short-term traffic flow prediction. Transp. Res. Part C Emerg. Technol. 2017, 79, 1–17. [Google Scholar] [CrossRef]
- Zeng, A.; Chen, M.; Zhang, L.; Xu, Q. Are transformers effective for time series forecasting? In Proceedings of the AAAI Conference on Artificial Intelligence, Washington, DC, USA, 7–14 February 2023; Volume 37, pp. 11121–11128. [Google Scholar] [CrossRef]
- Siami-Namini, S.; Tavakoli, N.; Namin, A.S. A comparison of ARIMA and LSTM in forecasting time series. In Proceedings of the 2018 17th IEEE International Conference on Machine Learning and Applications (ICMLA), Orlando, FL, USA, 17–20 December 2018. [Google Scholar]
- Hinton, G.E. Learning distributed representations of concepts. In Proceedings of the Eighth Annual Conference of the Cognitive Science Society, Amherst, MA, USA, 1–4 August 1986. [Google Scholar]
- Xiaotong, H.; Chen, C. Time Series Prediction Based on Multi-dimensional Cross-scale LSTM Model. Comput. Eng. Des. 2023, 44, 440–446. [Google Scholar]
- Bengio, Y.; Simard, P.; Frasconi, P. Learning long-term dependencies with gradient descent is difficult. IEEE Trans. Neural Netw. 1994, 5, 157–166. [Google Scholar] [CrossRef] [PubMed]
- Pascanu, R.; Mikolov, T.; Bengio, Y. On the difficulty of training recurrent neural networks. In Proceedings of the International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Funahashi, K.-I.; Nakamura, Y. Approximation of dynamical systems by continuous time recurrent neural networks. Neural Netw. 1993, 6, 801–806. [Google Scholar] [CrossRef]
- Li, X.-D.; Ho, J.K.; Chow, T.W. Approximation of dynamical time-variant systems by continuous-time recurrent neural networks. IEEE Trans. Circuits Syst. II Express Briefs 2005, 52, 656–660. [Google Scholar]
- Trischler, A.P.; D’Eleuterio, G.M. Synthesis of recurrent neural networks for dynamical system simulation. Neural Netw. 2016, 80, 67–78. [Google Scholar] [CrossRef]
- Lechner, M.; Hasani, R. Learning long-term dependencies in irregularly-sampled time series. arXiv 2020, arXiv:200604418. [Google Scholar]
- Rubanova, Y.; Chen, R.T.; Duvenaud, D.K. Latent ordinary differential equations for irregularly-sampled time series. Adv. Neural Inf. Process. Syst. 2019, 32. [Google Scholar]
- Ding, H.; Li, W.; Qiao, J. A self-organizing recurrent fuzzy neural network based on multivariate time series analysis. Neural Comput. Appl. 2021, 33, 5089–5109. [Google Scholar] [CrossRef]
- Park, H.; Lee, G.; Lee, K. Dual recurrent neural networks using partial linear dependence for multivariate time series. Expert Syst. Appl. 2022, 208, 118205. [Google Scholar] [CrossRef]
- Erichson, B.; Azencot, O.; Queiruga, A.; Hodgkinson, L.; Mahoney, M. Lipschitz Recurrent Neural Networks. In Proceedings of the International Conference on Learning Representations (ICLR), Vienna, Austria, 4 May 2021. [Google Scholar]
- Zhao, C.; Dai, L.; Huang, Y. Fractional Order Sequential Minimal Optimization Classification Method. Fractal Fract. 2023, 7, 637. [Google Scholar] [CrossRef]
- Xia, L.; Ren, Y.; Wang, Y. Forecasting China’s total renewable energy capacity using a novel dynamic fractional order discrete grey model. Expert Syst. Appl. 2024, 239, 122019. [Google Scholar] [CrossRef]
- Lai, G.; Chang, W.C.; Yang, Y.; Liu, H. Modeling long-and short-term temporal patterns with deep neural networks. In Proceedings of the 41st International ACM SIGIR Conference on Research & Development in Information Retrieval, Ann Arbor, MI, USA, 8–12 July 2018; pp. 95–104. [Google Scholar]
- Wen, R.; Torkkola, K.; Narayanaswamy, B.; Madeka, D. A multi-horizon quantile recurrent forecaster. arXiv 2017, arXiv:1711.11053. [Google Scholar]
- Tan, Y.; Xie, L.; Cheng, X. Neural Differential Recurrent Neural Network with Adaptive Time Steps. arXiv 2023. [Google Scholar]
- Bergsma, S.; Zeyl, T.; Rahimipour Anaraki, J.; Guo, L. C2FAR: Coarse-to-fine autoregressive networks for precise probabilistic forecasting. Adv. Neural Inf. Process. Syst. 2022, 35, 21900–21915. [Google Scholar]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond efficient transformer for long sequence time-series forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual Event, 2–9 February 2021; Volume 35, pp. 11106–11115. [Google Scholar]
- Zhou, T.; Ma, Z.; Wen, Q.; Wang, X.; Sun, L.; Jin, R. Fedformer: Frequency enhanced decomposed transformer for long-term series forecasting. In Proceedings of the International Conference on Machine Learning, Baltimore, MD, USA, 17–23 July 2022. [Google Scholar]
- Sun, Y.; Dong, L.; Huang, S.; Ma, S.; Xia, Y.; Xue, J.; Wang, J.; Wei, F. Retentive Network: A Successor to Transformer for Large Language Models. arXiv 2023, arXiv:2307.08621. [Google Scholar]
- Gu, A.; Dao, T. Mamba: Linear-Time Sequence Modeling with Selective State Spaces. arXiv 2023, arXiv:2312.00752. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 5998–6008. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Wu, H.; Xu, J.; Wang, J.; Long, M. Autoformer: Decomposition transformers with auto-correlation for long-term series forecasting. Adv. Neural Inf. Process. Syst. 2021, 34, 22419–22430. [Google Scholar]



| Models | FLRNN-FGA (Ours) | FEDformer | Autoformer | Informer | LSTNet | LSTM | TCN | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Metric | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | |
| Electricity | 96 | 0.130 | 0.228 | 0.183 | 0.297 | 0.201 | 0.317 | 0.274 | 0.368 | 0.680 | 0.645 | 0.375 | 0.437 | 0.985 | 0.813 |
| 192 | 0.151 | 0.251 | 0.195 | 0.308 | 0.222 | 0.334 | 0.296 | 0.386 | 0.725 | 0.676 | 0.442 | 0.473 | 0.996 | 0.821 | |
| 336 | 0.167 | 0.269 | 0.212 | 0.313 | 0.231 | 0.338 | 0.300 | 0.394 | 0.828 | 0.727 | 0.439 | 0.473 | 1.000 | 0.824 | |
| 720 | 0.192 | 0.296 | 0.231 | 0.343 | 0.254 | 0.361 | 0.373 | 0.439 | 0.957 | 0.811 | 0.980 | 0.814 | 1.438 | 0.784 | |
| Ettm2 | 96 | 0.124 | 0.240 | 0.203 | 0.287 | 0.255 | 0.339 | 0.365 | 0.453 | 3.142 | 1.365 | 2.041 | 1.073 | 3.041 | 1.330 |
| 192 | 0.154 | 0.271 | 0.269 | 0.328 | 0.281 | 0.340 | 0.533 | 0.563 | 3.154 | 1.369 | 2.249 | 1.112 | 3.072 | 1.339 | |
| 336 | 0.194 | 0.302 | 0.325 | 0.366 | 0.339 | 0.372 | 1.363 | 0.887 | 3.160 | 1.369 | 2.568 | 1.238 | 3.105 | 1.348 | |
| 720 | 0.236 | 0.344 | 0.421 | 0.415 | 0.422 | 0.419 | 3.379 | 1.338 | 3.171 | 1.368 | 2.720 | 1.287 | 3.135 | 1.354 | |
| Exchange | 96 | 0.118 | 0.255 | 0.139 | 0.276 | 0.197 | 0.323 | 0.847 | 0.752 | 1.551 | 1.058 | 1.453 | 1.049 | 3.004 | 1.432 |
| 192 | 0.207 | 0.341 | 0.256 | 0.369 | 0.300 | 0.369 | 1.204 | 0.895 | 1.477 | 1.028 | 1.846 | 1.179 | 3.048 | 1.444 | |
| 336 | 0.353 | 0.464 | 0.426 | 0.464 | 0.509 | 0.524 | 1.672 | 1.036 | 1.507 | 1.031 | 2.136 | 1.231 | 3.113 | 1.459 | |
| 720 | 1.284 | 0.823 | 1.090 | 0.800 | 1.447 | 0.941 | 2.478 | 1.310 | 2.285 | 1.243 | 2.984 | 1.427 | 3.150 | 1.458 | |
| Traffic | 96 | 0.410 | 0.265 | 0.562 | 0.349 | 0.613 | 0.388 | 0.719 | 0.391 | 1.107 | 0.685 | 0.843 | 0.453 | 1.438 | 0.784 |
| 192 | 0.433 | 0.277 | 0.562 | 0.346 | 0.616 | 0.382 | 0.696 | 0.379 | 1.157 | 0.706 | 0.847 | 0.453 | 1.463 | 0.794 | |
| 336 | 0.451 | 0.288 | 0.570 | 0.323 | 0.622 | 0.337 | 0.777 | 0.420 | 1.216 | 0.730 | 0.853 | 0.455 | 1.476 | 0.799 | |
| 720 | 0.502 | 0.306 | 0.596 | 0.368 | 0.660 | 0.408 | 0.864 | 0.472 | 1.481 | 0.805 | 1.500 | 0.805 | 1.499 | 0.804 | |
| Weather | 96 | 0.151 | 0.213 | 0.217 | 0.286 | 0.266 | 0.336 | 0.300 | 0.384 | 0.594 | 0.587 | 0.369 | 0.406 | 0.615 | 0.589 |
| 192 | 0.206 | 0.268 | 0.276 | 0.336 | 0.307 | 0.367 | 0.598 | 0.544 | 0.560 | 0.565 | 0.416 | 0.435 | 0.629 | 0.600 | |
| 336 | 0.268 | 0.320 | 0.339 | 0.380 | 0.359 | 0.395 | 0.578 | 0.523 | 0.597 | 0.587 | 0.455 | 0.454 | 0.639 | 0.608 | |
| 720 | 0.402 | 0.407 | 0.403 | 0.428 | 0.419 | 0.428 | 1.059 | 0.741 | 0.618 | 0.599 | 0.535 | 0.520 | 0.639 | 0.610 | |
| 1st Count | 37 | 3 | 0 | 0 | 0 | 0 | 0 | ||||||||
| Improvement | - | 18.15% | 31.52% | 149.36% | 281.52% | 232.80% | 357.32% | ||||||||
| Models | FLRNN-FGA | LRNN-FGA | RNN-FGA | ||||
|---|---|---|---|---|---|---|---|
| Metric | MSE | MAE | MSE | MAE | MSE | MAE | |
| Electricity | 96 | 0.130 | 0.228 | 0.183 | 0.273 | 0.179 | 0.277 |
| 192 | 0.151 | 0.251 | 0.188 | 0.281 | 0.190 | 0.288 | |
| 336 | 0.167 | 0.269 | 0.202 | 0.295 | 0.205 | 0.302 | |
| 720 | 0.192 | 0.296 | 0.241 | 0.328 | 0.242 | 0.336 | |
| Traffic | 96 | 0.410 | 0.265 | 0.588 | 0.343 | 0.633 | 0.364 |
| 192 | 0.433 | 0.277 | 0.585 | 0.339 | 0.629 | 0.366 | |
| 336 | 0.451 | 0.288 | 0.609 | 0.340 | 0.635 | 0.365 | |
| 720 | 0.502 | 0.306 | 0.636 | 0.357 | 0.676 | 0.377 | |
| Models | FLRNN-FGA (Ours) | w/o Gated Structure | w/o Frequency Module | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Metric | MSE | MAE | Paras/k | MSE | MAE | Paras/k | MSE | MAE | Paras/k | |
| ETTh2 | 96 | 0.188 | 0.305 | 355.76 | 0.335 | 0.395 | 381.46 | 0.312 | 0.374 | 752.24 |
| 192 | 0.236 | 0.340 | 380.52 | 0.434 | 0.457 | 406.23 | 0.406 | 0.432 | 777.01 | |
| 336 | 0.266 | 0.363 | 417.68 | 0.428 | 0.447 | 443.38 | 0.684 | 0.580 | 814.16 | |
| 720 | 0.337 | 0.421 | 516.75 | 2.019 | 0.976 | 542.46 | 1.225 | 0.751 | 913.23 | |
| Ettm2 | 96 | 0.124 | 0.250 | 355.76 | 0.190 | 0.278 | 381.46 | 0.201 | 0.284 | 752.24 |
| 192 | 0.154 | 0.271 | 380.52 | 0.256 | 0.332 | 406.23 | 0.260 | 0.328 | 777.01 | |
| 336 | 0.194 | 0.302 | 417.68 | 0.335 | 0.382 | 443.38 | 0.318 | 0.368 | 814.16 | |
| 720 | 0.236 | 0.344 | 516.75 | 0.443 | 0.441 | 542.46 | 0.489 | 0.471 | 913.23 | |
| #Para (M) | Memory (G) | Time (S) | MSE | |
|---|---|---|---|---|
| Informer | 62.80 | 1.54 | 52 | 0.365 |
| FEDformer | 83.70 | 2.44 | 174 | 0.203 |
| Autoformer | 59.70 | 1.97 | 38 | 0.255 |
| FLRNN-FGA | 1.60 | 0.49 | 45 | 0.124 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, C.; Ye, J.; Zhu, Z.; Huang, Y. FLRNN-FGA: Fractional-Order Lipschitz Recurrent Neural Network with Frequency-Domain Gated Attention Mechanism for Time Series Forecasting. Fractal Fract. 2024, 8, 433. https://doi.org/10.3390/fractalfract8070433
Zhao C, Ye J, Zhu Z, Huang Y. FLRNN-FGA: Fractional-Order Lipschitz Recurrent Neural Network with Frequency-Domain Gated Attention Mechanism for Time Series Forecasting. Fractal and Fractional. 2024; 8(7):433. https://doi.org/10.3390/fractalfract8070433
Chicago/Turabian StyleZhao, Chunna, Junjie Ye, Zelong Zhu, and Yaqun Huang. 2024. "FLRNN-FGA: Fractional-Order Lipschitz Recurrent Neural Network with Frequency-Domain Gated Attention Mechanism for Time Series Forecasting" Fractal and Fractional 8, no. 7: 433. https://doi.org/10.3390/fractalfract8070433
APA StyleZhao, C., Ye, J., Zhu, Z., & Huang, Y. (2024). FLRNN-FGA: Fractional-Order Lipschitz Recurrent Neural Network with Frequency-Domain Gated Attention Mechanism for Time Series Forecasting. Fractal and Fractional, 8(7), 433. https://doi.org/10.3390/fractalfract8070433







