Effects of In-Situ Stress on Damage and Fractal during Cutting Blasting Excavation

Abstract

Blasting excavation of rock masses under high in-situ stress often encounters difficulties in rock fragmentation and a high boulder rate. To gain a deeper understanding of this issue, the stress distribution of rock masses under dynamic and static loads was first studied through theoretical analysis. Then, the ANSYS/LS-DYNA software was employed to simulate the blasting crack propagation in rock masses under various in-situ stress conditions. The fractal dimension was introduced to quantitatively analyze the influence of in-situ stress on the distribution of blasting cracks. The results indicate that in-situ stress primarily affects crack propagation in the later stages of the explosion, while crack initiation and propagation in the early stages are mainly driven by the explosion load. In-situ stress significantly influences the damage area and fractal dimension of cut blasting. Under hydrostatic in-situ stress, as the in-situ stress increases, the damage area and fractal dimension of blasting cracks gradually decrease. Under non-hydrostatic in-situ stress, when the principal stress difference is small, in-situ stress promotes the damage area and fractal dimension of the surrounding rock, enhancing rock fragmentation. However, when the principal stress difference is large, in-situ stress inhibits the damage area and fractal dimension of the surrounding rock, hindering effective rock breaking.

1. Introduction

In recent years, China’s transportation industry has developed rapidly, with significant investment shifting from the eastern coast to the western mountainous regions [1,2,3]. Major projects, such as railway and highway tunnels, are extending to greater depths. For instance, the Sichuan–Tibet Railway Tunnel has a maximum buried depth of 2600 m, while the Ehan Expressway Tunnel reaches 1944 m. Currently, tunnel excavation primarily utilizes the drilling and blasting methods [4]. The excavation of deep rock masses results from the combined action of explosive loads and in-situ stress. In-situ stress is mainly composed of tectonic and self-weight stress of overlying strata. Compared to shallow rock masses, deep rock masses exhibit unique mechanical behaviors under high in-situ stress, which is becoming one of the main challenges in deep tunnel blasting excavation [5].

Numerous researchers have examined the damage evolution mechanism of rock under blasting loads [6,7,8]. Hoek et al. [9] discovered through field tests that in-situ stress influenced the propagation of blast-induced cracks, with cracks densely distributed parallel to the maximum principal stress. Bai et al. [10] numerically simulated the crack propagation of dual-hole blasting under different stress conditions, and proposed that in designing blasting schemes, the borehole spacing could be appropriately increased along the direction of maximum principal stress, and the explosive charge could be appropriately reduced. Ding et al. [11] conducted blasting experiments with similar materials and observed that increasing the maximum principal stress deflected the blasting crack toward the maximum principal stress direction but slowed down its propagation speed. Based on laboratory tests and numerical simulations, Ma et al. [12] concluded that in-situ stress guided the propagation direction of blasting cracks in deep rock masses, causing radial cracks to tend toward the direction of maximum principal stress. Zhang et al. [13] investigated the impact of confining pressure on the volume of the blasting fracture zone through model experiments and found that the fracture zone first increased and then decreased with rising confining pressure. Yi et al. [14] studied the influence mechanism of in-situ stress at different stages of blasting using numerical simulations, pointing out that in-situ stress primarily affected crack propagation in the later stage of an explosion, while crack initiation and early-stage propagation were mainly driven by explosion loads. Luo et al. [15] analyzed rock excavation damage under the combined action of in-situ stress and blasting load through theoretical analysis and numerical simulations, finding that as stress levels increased, the degree of damage first decreased and then increased.

The research indicates that the efficiency of blasting construction largely depends on cutting, and numerous scholars have investigated the damage evolution mechanism of cutting blasting under in-situ stress [16,17]. Using a two-dimensional plane strain model, Ding et al. [18] discovered that as in-situ stress increased, the fractal dimension and fractal damage of explosion cracks generally decreased. Xie et al. [19] employed the RHT model to study the damage mechanism of cutting blasting under varying hydrostatic pressures and lateral pressure coefficients. Yang et al. [20] used numerical simulations to examine the rock-breaking mechanism of cutting blasting in high in-situ stress rock masses, finding that the crack propagation length between holes decreased with increasing in-situ stress levels. Huang et al. [21] numerically simulated the rock-breaking process of four-hole cut blasting under different in-situ stress conditions, revealing that in-situ stress inhibited the propagation of cut blasting damage cracks and that the cut damage area decreased as in-situ stress increased. Xie et al. [22] studied the influence of in-situ stress on cut blasting and found that in-situ stress resists radial pressure and damage extension around the cut hole.

The present study primarily focuses on investigating the dynamic mechanical response of rock mass blasting under initial stress conditions. However, there is a lack of comprehensive quantitative analysis and research regarding the relationship between crack propagation behavior and damage characteristics in rock blasting under initial stress. Therefore, gaining a thorough understanding of how initial stress impacts the fracture mechanism of rock mass blasting is essential. Building upon existing research findings, this paper employs the dynamic finite element method to simulate the cracking process of rock mass blasting under varied in-situ stress conditions. Prior studies have demonstrated that rocks’ crack propagation under blasting loads displays significant fractal characteristics [23,24]. Hence, this paper utilizes fractal dimension analysis to quantitatively assess the influence of in-situ stress on the distribution of blasting cracks, thereby elucidating the mechanism through which in-situ stress affects the effectiveness of rock breaking in blasting operations. This research offers valuable insights for advancing the theory of cutting and blasting under in-situ stress conditions and provides practical guidance for engineering applications.

2. Theoretical Basis

In the blasting excavation of shallow rock mass, the primary concern is the influence of blasting load [25,26]. In contrast, during the excavation of deep rock masses, the load acting on the rock mass comprises the superposition of static load from in-situ conditions (including horizontal load $Px$ and vertical load $Py$) and dynamic stress $P(t)$ from blasting load. Therefore, both factors must be simultaneously considered in this study of deep rock blasting. Using single-hole blasting as an example, the stress state (${\sigma }_{rr}^s$, ${\sigma }_{\theta \theta }^s$ and ${\tau }_{r\theta }^s$ represent the radial stress, circumferential stress, and shear stress of a point, respectively) of the surrounding rock is illustrated in Figure 1.

2.1. Static Stress Field

In deep rock masses, the axial stress is typically much smaller than the in-situ stress in the two orthogonal directions. The static stress field induced by the in-situ stress can be simplified as a plane strain problem. Under the influence of in-situ stress, the static stress tensor around a circular hole in the elastic medium can be expressed as follows [27]:

$$\left\{\begin{array}{l}{\sigma }_{rr}^s={\displaystyle \frac{P_x+P_y}{2}}\left(1-{\displaystyle \frac{a^2}{r^2}}\right)+\left(1-{\displaystyle \frac{a^2}{r^2}}\right)\left(1-{\displaystyle \frac{3a^2}{r^2}}\right)\left({\displaystyle \frac{P_x-P_y}{2}}\cos 2\theta \right)\\ {\sigma }_{\theta \theta }^s={\displaystyle \frac{P_x+P_y}{2}}\left(1+{\displaystyle \frac{a^2}{r^2}}\right)-\left(1+3{\displaystyle \frac{a^4}{r^4}}\right)\left({\displaystyle \frac{P_x-P_y}{2}}\cos 2\theta \right)\\ {\tau }_{r\theta }^s=\left(1-{\displaystyle \frac{a^2}{r^2}}\right)\left(1+{\displaystyle \frac{3a^2}{r^2}}\right)\left({\displaystyle \frac{P_y-P_x}{2}}\sin 2\theta \right)\end{array}\right.$$

(1)

where ${\sigma }_{rr}^s$, ${\sigma }_{\theta \theta }^s$, and ${\tau }_{r\theta }^s$ are the radial stress, hoop stress, and shear stress, MPa, respectively; $a$ is the radius of the blasthole, m; $r$ represents the distance from the blasthole, m; $P_x$ and $P_y$ are the horizontal load and vertical loads in the static state, MPa, respectively.

2.2. Stress Field under Blasting Load

The stress redistribution caused by the dynamic load from blasting in the surrounding rock can be analyzed using the thick-walled cylinder model. It is assumed that the borehole exists within a uniform, elastic, and isotropic rock medium. In this homogeneous elastic medium, the dynamic load from blasting acts on the borehole wall, satisfying the continuity equation, the motion equation, and the constitutive equation of the material. This solution process is considered a plane strain problem, and the governing equation for the stress wave in the rock mass in polar coordinates can be expressed as follows [28]:

$$\left\{\begin{array}{l}{\displaystyle \frac{{\partial }^2\Phi (r,t)}{\partial r^2}}+{\displaystyle \frac{\partial \Phi (r,t)}{r\partial r}}-{\displaystyle \frac{{\partial }^2\Phi (r,t)}{C_p^2\partial t^2}}=0(\mathrm{r}>\mathrm{a},\mathrm{t}>0)\\ {\left.\Phi (r,t)\right|}_{r=0}={\left.{\displaystyle \frac{\partial \Phi (r,t)}{\partial t}}\right|}_{t=0}=0(\mathrm{r}⩾\mathrm{a})\\ \underset{r\to \infty }{\lim }\Phi (r,t)=0(\mathrm{t}>0)\\ {\sigma }_r(a,t)=p(t)\end{array}\right.$$

(2)

where $\Phi$ is the displacement potential function. By the Laplace transform, the potential function $\Phi$, radial stress ${\overline{\sigma }}_r$, and displacement function $u$ can be expressed as

$$\left\{\begin{array}{l}\overline{\Phi }(r,s)={\displaystyle \frac{\overline{p}(s)K_0\left(k_{d}r\right)}{(\lambda +2\mu )F^{*}(s)}}\\ {\overline{\sigma }}_r(r,s)={\displaystyle \frac{\frac{2K_1\left(k_{d}r\right)}{D^{2}r}+k_d{K}_0\left(k_{d}r\right)}{F^{*}(s)}}\\ {\overline{u}}_{(r,s)}{\displaystyle \frac{\partial \overline{\Phi }}{{\partial }_r}}=-{\displaystyle \frac{\overline{p}(s)K_1\left(k_{d}r\right)k_d}{(\lambda +2\mu )F^{*}(s)}}n\end{array}\right.$$

(3)

where $F^{*}(s)=\left[2k_d{K}_1\left(k_{d}a\right)\right]/(D^{2}a)+k_d^2{K}_0\left(k_{d}a\right)$, $k_d=s/C_d$, $C_d$ is the wave velocity under one-dimensional strain, $C_d^2=(\lambda +2\mu )/{\rho }_0$, $D^2=(\lambda +2\mu )/\mu$; $K_0$ and $K_1$ are the modified zero-order and first-order Bessel functions of the second kind, respectively.

When the load $p（t）$ is given, the radial stress ${\sigma }_{rr}^d$ and the tangential stress ${\sigma }_{\theta \theta }^d$ of any point in the plane can be obtained by solving the inverse Laplace transform:

$$\left\{\begin{array}{l}{\sigma }_{rr}^d=\lambda {\nabla }^2\Phi +2\mu {\displaystyle \frac{{\partial }^2\Phi }{\partial r^2}}\\ {\sigma }_{\theta \theta }^d=\lambda {\nabla }^2\Phi +{\displaystyle \frac{2\mu }{r}}{\displaystyle \frac{\partial \Phi }{\partial r}}\end{array}\right.$$

(4)

2.3. Superimposed Stress Field of Blasting Load and In-Situ Stress

Under the combined influence of in-situ stress and explosive load, the coupling stress generated by the unit dynamic load and static load is

$$\left\{\begin{array}{l}{\sigma }_r={\sigma }_{rr}^s+{\sigma }_{rr}^d\\ {\sigma }_{\theta }={\sigma }_{\theta \theta }^s+{\sigma }_{\theta \theta }^d\end{array}\right.$$

(5)

The combined interaction of blasting load and in-situ stress in rock mass results in the formation of a composite stress field. Throughout the blasting process, in-situ stress influences both radial and circumferential stress distribution, thereby inducing non-uniform stress field distribution [29]. Consequently, the comprehensive impact of blasting load and in-situ stress must be thoroughly accounted for in rock mass stress analysis. In-situ stress exerts varying effects on the dynamic load generated by blasting at different locations, potentially resulting in stress attenuation or amplification.

3. Numerical Simulation

Although theoretical analysis provides a general understanding of stress distribution in rock masses, the mechanical behavior of rock mass blasting is complex and nonlinear [30]. When elastic theory is applied to calculate the nonlinear large deformations caused by deep rock mass blasting, significant discrepancies arise between theoretical predictions and actual conditions. In recent years, numerical simulation methods have become widely adopted, offering a convenient alternative for analyzing these problems. Relevant research shows that the success of numerical simulations largely depends on the selection of an appropriate material model [31].

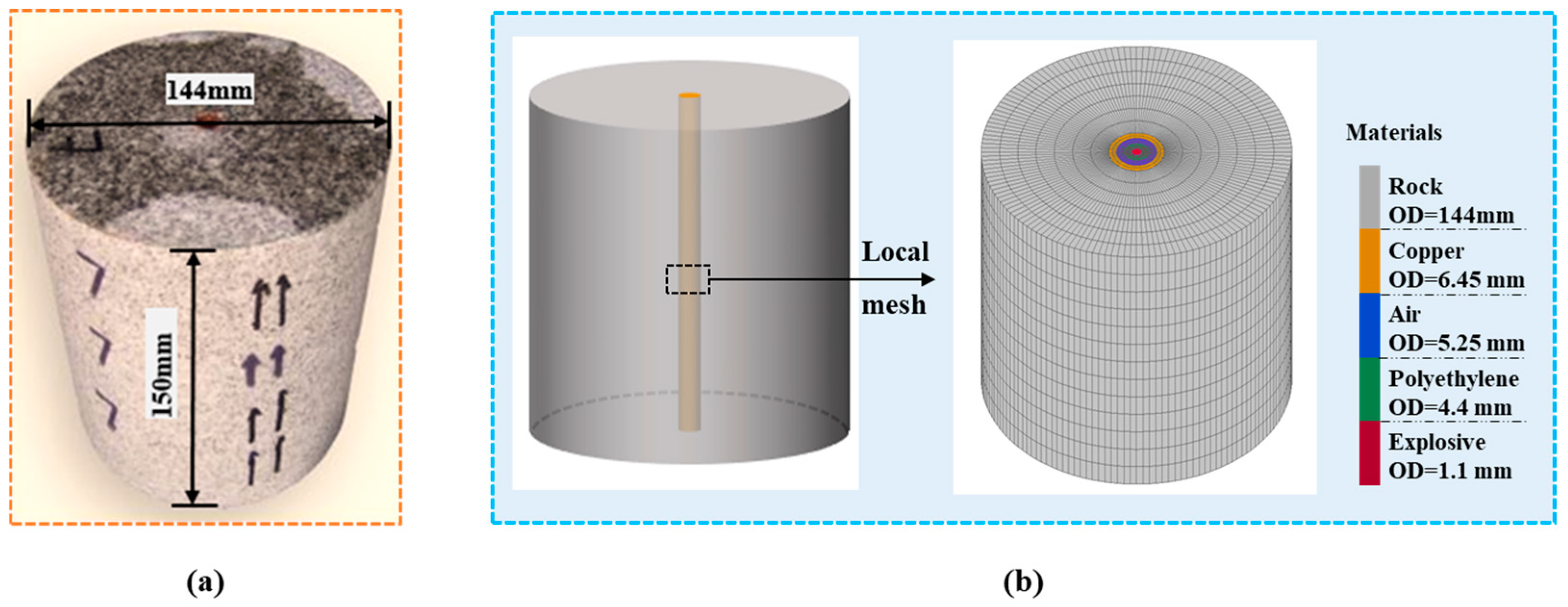
3.1. Material Parameters

The reliability of numerical simulation results largely depends on the material constitutive equation [32]. The Riedel–Hiermaier–Thoma (RHT), Holmquist–Johnson– Cook (HJC) and Concrete Continuous Cap Model (CSCM) are the models commonly used to simulate rock materials in ANSYS/LS-DYNA software. Numerical calculations have shown that the RHT model effectively describes strain hardening, strain rate sensitivity, compression damage softening, and other characteristics of rock-like materials during impact and explosion [33].

The RHT constitutive model considers the impact of strain rate on the constitutive relationship of rock-like materials. It also accounts for the varying effects of strain rate under compression and tension. The calculation formula is as follows:

$$F_{\mathrm{rate}}\left({\dot{\epsilon }}_{\mathrm{p}}\right)=\left\{\begin{array}{ll}{\left({\dot{\epsilon }}_{\mathrm{p}}/{\dot{\epsilon }}_0^{\mathrm{c}}\right)}^{{\beta }_{\mathrm{c}}}\hfill & 3p⩾f_{\mathrm{c}}\hfill \\ {\displaystyle \frac{p+f_{\mathrm{t}}/3}{f_{\mathrm{c}}/3+f_{\mathrm{t}}/3}}{\left({\dot{\epsilon }}_{\mathrm{p}}/{\dot{\epsilon }}_0^t\right)}^{{\beta }_{\mathrm{c}}}-{\displaystyle \frac{p-f_{\mathrm{t}}/3}{f_{\mathrm{c}}/3+f_{\mathrm{t}}/3}}{\left({\dot{\epsilon }}_{\mathrm{p}}/{\dot{\epsilon }}_0^c\right)}^{{\beta }_{\mathrm{i}}}\hfill & -f_{\mathrm{t}}<3p<f_{\mathrm{c}}\hfill \\ {\left({\dot{\epsilon }}_{\mathrm{p}}/{\dot{\epsilon }}_0^{\mathrm{c}}\right)}^{{\beta }_{\mathrm{c}}}\hfill & 3p⩽-f_{\mathrm{t}}\hfill \end{array}\right.$$

(6)

where $p$ is material pressure; $f_{\mathrm{c}}$ and $f_{\mathrm{t}}$ are uniaxial compressive strength and tensile strength, respectively; ${\dot{\epsilon }}_0^{\mathrm{c}}$ and ${\dot{\epsilon }}_0^{\mathrm{t}}$ are the reference strain rates under compressive and tensile loads, ${\dot{\epsilon }}_0^{\mathrm{c}}=3.0\times {10}^{-5}{\mathrm{s}}^{-1},$ ${\dot{\epsilon }}_0^{\mathrm{c}}=3.0\times {10}^{-5}{\mathrm{s}}^{-1},$ ${\dot{\epsilon }}_0^{\mathrm{t}}=3.0\times {10}^{-6}{\mathrm{s}}^{-1}$, respectively; ${\beta }_{\mathrm{c}}$ and ${\beta }_{\mathrm{t}}$ represent the compression and tensile strain rate indexes, respectively.

The RHT constitutive equation defines the damage variable (D) as the ratio of the cumulative equivalent plastic strain increment to the final failure equivalent plastic strain. The formula is

$$0\le D={\displaystyle \sum \frac{\Delta {\epsilon }_{\mathrm{p}}}{{\epsilon }_{\mathrm{p}}^{\mathrm{faiure}}}}\le 1$$

(7)

$${\epsilon }_{\mathrm{p}}^{\mathrm{faire}}=D_1{\left(p^{*}-HT{L}^{*}\right)}^{D_2}>{\epsilon }_{\mathrm{p}}^{\mathrm{m}}$$

(8)

where $\Delta {\epsilon }_{\mathrm{p}}$ is the equivalent plastic strain increment; ${\epsilon }_{\mathrm{p}}^{\mathrm{failure}}$ is the final failure equivalent plastic strain; $D_1$, $D_2$ are damage parameters, and $D_2=1$; $p^{*}$ is the normalized pressure $\left(p^{*}=p/f_{\mathrm{c}}\right)$; ${\epsilon }_{\mathrm{p}}^{\mathrm{m}}$ is the minimum equivalent plastic strain at material failure. When $D=0$, it means that the material has entered the damage softening stage, and the material has not accumulated damage. When $D=1$, it means that the material is completely damaged. $HT{L}^{*}$ is the normalized ultimate tensile strength.

To obtain the model parameters, tests such as rock density, porosity, uniaxial compression, Brazilian splitting, and quasi-static conventional triaxial tests were conducted. The measured mechanical parameters of granite are shown in

Table 1. Mechanical parameters of granite.

Parameter	Value	Parameter	Value	Parameter	Value	Parameter	Value
Density	2.62 kg·m−3	Elastic modulus	21.8 GPa	Shear strength	13.4 MPa	Tensile strength	12.3 MPa
Uniaxial Compressive Strength	112 MPa	Poisson ratio	0.26	Initial porosity	1.10%	Longitudinal wave velocity	4600 m·s−1

.

Based on the basic physical parameters of granite, most RHT model parameters can be determined using empirical formulas. However, some parameters, such as yield surface parameters $g_c^{*}$ and $g_t^{*}$, residual surface parameters ($A$) and ($N$), etc., are difficult to determine and sensitive to numerical calculation results. These parameters can be modified and optimized using the recommended values from the original RHT model literature [34] and the data from the split Hopkinson pressure bar (SHPB) dynamic mechanical test [35].

The Split Hopkinson Pressure Bar (SHPB) device primarily consists of four components: the loading drive system; the pressure bar test system; the data acquisition system; and the data processing system. The incident bar, transmitted bar, and specimen are modeled using the Solid164 three-dimensional solid element. A single-point integration algorithm and hourglass control are utilized in the model calculations. To improve computational efficiency, the modeling of the bullet is omitted, and the bullet’s incident wave is directly converted into a time-history stress applied to the end face of the incident rod to simulate loading. Automatic surface contact is used for the interaction between the specimen and the pressure bar [36,37]. In the SHPB system, the incident bar and transmitted bar lengths are 2000 mm and 1500 mm, respectively. The Brazilian disc rock sample has a diameter of 50 mm and a thickness of 25 mm. Both the incident and transmitted bars use a linear elastic material model with a density of 7850 kg/m³, an elastic modulus of 210 GPa, and a Poisson’s ratio of 0.25. The parameters in the RHT model are continuously adjusted using a trial-and-error method until the numerical simulation results match the experimental results. The comparison results are shown in Figure 2.

Figure 2a illustrates the stress wave propagation process, with the wave reaching the sample at approximately 1.0 ms. The majority of the stress wave’s energy reflects back to the incident bar, while only a small portion enters the transmission bar via the stress wave. The confirmation of the experiment’s dynamic stress balance is presented in Figure 2b. The superimposed wave of the incident and reflected waves closely align with the transmitted wave, suggesting that the sample has essentially reached a stress equilibrium state, thereby affirming the reliability of the experimental outcomes. In Figure 2c, the failure of the rock sample is compared to the simulation, revealing that the crack initiates at the contact end between the specimen and the bar, propagates along the weak plane, and eventually coalesces at both ends, resulting in macroscopic cracks penetrating the rock sample. A significant crushing zone forms on the contact surface, leading to tensile splitting failure of the specimen. The comparison between simulation and experimental failure modes exhibits striking similarities. The stress–strain curve obtained through the three-wave method is depicted in Figure 2d, showing a consistent trend with the experimental results and sharing the same peak strength [38]. Overall, the numerical simulation aligns well with the experimental data, effectively delineating the mechanical response of rock samples under high strain rates. Specific model parameters are outlined in

Table 2. RHT model parameters of rock.

Parameter	Value	Parameter	Value	Parameter	Value	Parameter	Value
${\rho }_0$	2620 kg·m−3	$G$	8.65 GPa	$A$	1.60	$B_0$	1.22
$B_1$	1.22	$D_1$	0.04	$N$	0.61	$f_c$	0.112 GPa
$f_s^{*}$	0.11	$f_t^{*}$	0.12	${\dot{\epsilon }}^c$	3 × 1025 s−1	${\beta }_c$	0.20
$\alpha$	0.5	$D_2$	1.0	${\dot{\epsilon }}^t$	3 × 1025 s−1	${\beta }_t$	0.10
$T_1$	55.44 GPa	$P_{co}$	6.0 GPa	$P_{el}$	0.07 GPa	$A_2$	67.64 GPa
$G_t^{*}$	0.68	$G_c^{*}$	0.53	$A_1$	55.44 GPa	$A_3$	32.44 GPa
$T_2$	0 GPa	${\dot{\epsilon }}_0^t$	3 × 10−5 s−1	${\dot{\epsilon }}_0^c$	3 × 10−6 s−1

.

The explosive material model is proposed to adopt the *MAT-HIGH-EXPLOSIVE-BURN model, which, combined with the JWL state equation, describes the relationship between volume, pressure, and energy of explosion products during the explosion process. Its equation of state can be expressed as [39]:

$$P_e=A\left(1-{\displaystyle \frac{{\omega }_{\mathrm{e}}}{R_1{V}_{\mathrm{e}}}}\right){\mathrm{e}}^{-R_1{V}_{\mathrm{e}}}+B\left(1-{\displaystyle \frac{{\omega }_{\mathrm{e}}}{R_2{V}_{\mathrm{e}}}}\right){\mathrm{e}}^{-R_2{V}_{\mathrm{e}}}+{\displaystyle \frac{{\omega }_{\mathrm{e}}{E}_0}{V_{\mathrm{e}}}}$$

(9)

where $P_0$ represents the detonation pressure; $A$, $B$, $R_1$, $R_2$ and ${\omega }_{\mathrm{e}}$ are independent constants describing the equation; $V_e$ denotes relative volume; $E_0$ represents initial specific internal energy. For numerical simulation, 2# emulsion explosive is utilized, with the parameters shown in

Table 3. Explosives and parameters of JWL equation of state.

Parameter	Value	Parameter	Value	Parameter	Value	Parameter	Value
${\rho }_e$/kg·m−3	1000	A/GPa	220	B/GPa	0.2	${\omega }_{\mathrm{e}}$	0.35
R1	4.5	R2	1.1	E0/GPa	8.56	D/s−1	4000

.

The air model adopts the null material model, namely, the *MAT_NULL material model, utilizing the *EOS_LINEAR_POLYNOMIAL linear polynomial state equation to describe its mechanical behavior. The formula for calculating pressure is as follows [40]:

$$P=C_0+C_1\mu +C_2{\mu }^2+C_3{\mu }^3+\left(C_4+C_5\mu +C_6{\mu }^2\right)E_0$$

(10)

where $C_0~C_6$ is a constant; $C_0$ = $C_2$ = $C_3$ = 0, $C_4$ = $C_5$ = 0.4; $\mu =1/(V-1)$; $V$ represents relative volume with a value of 1.0; $E_0$ denotes the unit initial specific internal energy, which is valued at 250 kJ·m⁻³.

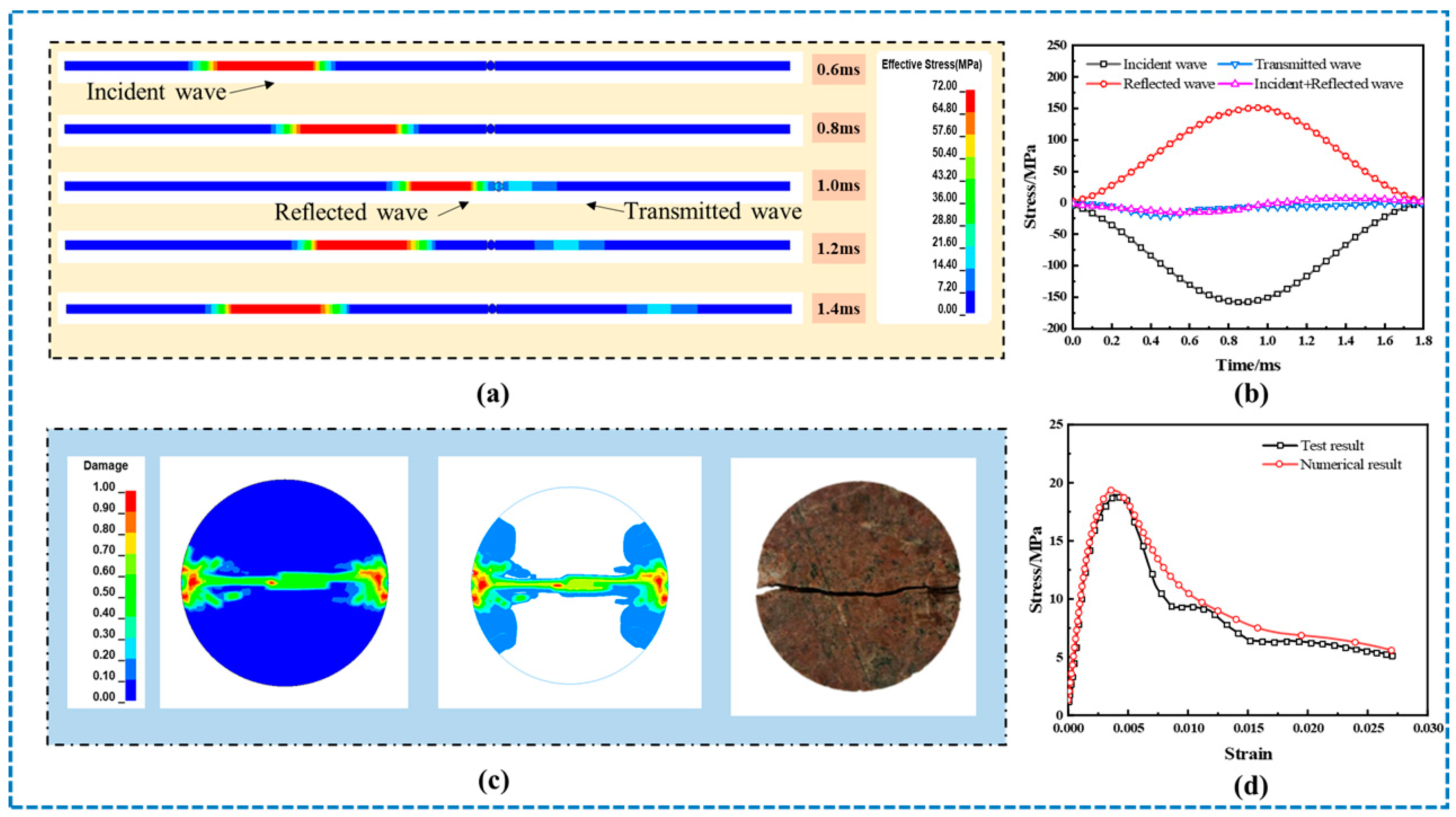
3.2. Material Parameter Verification

After determining the parameters of the numerical model, the rationality of the chosen rock, explosive, and air materials can be validated through relevant experiments [41]. The cylindrical rock samples utilized in the experiments conducted by Banadaki had dimensions of 150 mm in height and 144 mm in diameter. The blast hole and cartridge diameters were 6.45 mm and 1.1 mm, respectively. The cartridge was wrapped in polyethylene, with copper tubes nested on its outer side, as depicted in Figure 3a. This setup ensured that the fragments would not scatter post-explosion and aided in the subsequent scanning of the crack morphology of the complete section. A geometric model of identical dimensions was created and meshed using ANSYS/LS-DYNA software, as illustrated in Figure 3b.

After the stress wave generated by the explosion penetrates the rock sample, it induces various forms of damage within the specimen. Numerical simulations enable the observation of the complete fracture propagation process driven by the compressive stress wave and the free surface reflection wave. In the vicinity of the borehole, a shear failure zone emerges due to the explosion load exceeding the dynamic compressive strength of the rock. As the compressive stress wave reflects off the free surface, transforming into a tensile stress wave that rebounds into the sample, small cracks develop at the sample’s periphery once the tensile stress within the sample surpasses the dynamic compressive strength. Figure 4a,b compares the results of a numerical simulation and model test. It can be seen that the dense crack area, radial crack, and flake crack around the blast hole are in good agreement with the experimental results at a very macro level.

3.3. Computation Module

Due to the utilization of a cylindrical charge in the practical blasting operation, the hole diameter is significantly smaller than its length, allowing for the simplification of the model to a plane finite element problem [42]. The ANSYS/LS-DYNA software was employed to simulate the cutting blasting process of rock mass under in-situ stress, utilizing the Solid164 solid element. The model’s length and width were set to 500 cm, with a thickness of 1 cm. Non-reflective boundaries were applied to the model’s boundaries to mitigate the impact of boundary conditions. Displacement constraints were enforced in the normal z direction of the rock mass. The arrangement included four cutting holes and a hollow hole, with the empty hole having a diameter of 10 cm and the cutting holes 4.2 cm in diameter. A coupling charge was employed, with the specific spatial relationship depicted in Figure 5. In this paper, the Arbitrary Lagrangian–Eulerian (ALE) method is used to simulate rock cutting blasting under in-situ stress. Specifically, the Lagrange algorithm is used for the rock element, and the Euler algorithm is used for the explosive and air element. The coupling between solid and fluid is realized using the keyword * CONSTRAINED_LAGRANGE_IN_SOLID. Fluid materials and solid materials are modeled by separate nodes. In particular, fluid materials (air and explosives) are modeled by common nodes. The total number of solid grids is 250,000, and the total number of fluid grids is 30,000. The model is calculated by single point integration, and hourglass control is introduced to avoid hourglass in this model. The hourglass coefficient used in this simulation is 0.04. Confining pressure was applied around this model to simulate the in-situ stress, with non-reflective boundary conditions set to mimic an infinite rock mass. The model was discretized using a mapping grid, and the initiation mode was set to simultaneous initiation.

The numerical simulation of rock mass blasting under initial stress is conducted in two steps. First, initial stress is applied to the boundary, followed by the blasting calculation once the stress initialization stabilizes. Horizontal and vertical stresses are applied to the model to simulate the in-situ stress experienced by the rock mass. This paper examines two conditions: hydrostatic and non-hydrostatic stress fields. For the hydrostatic stress condition, stress levels of 0 MPa, 5 MPa, 10 MPa, 15 MPa, 20 MPa, and 30 MPa are used to analyze the influence of in-situ stress on rock mass blasting cracks. Under non-hydrostatic stress conditions, the vertical in-situ stress is maintained at 10 MPa, while lateral pressure coefficients of 0.5, 0.75, 1.0, 1.5, 2.0, and 2.5 are applied. The impact of these lateral pressure coefficients on rock mass blasting cracks is analyzed.

4. Analyzed and Discussed

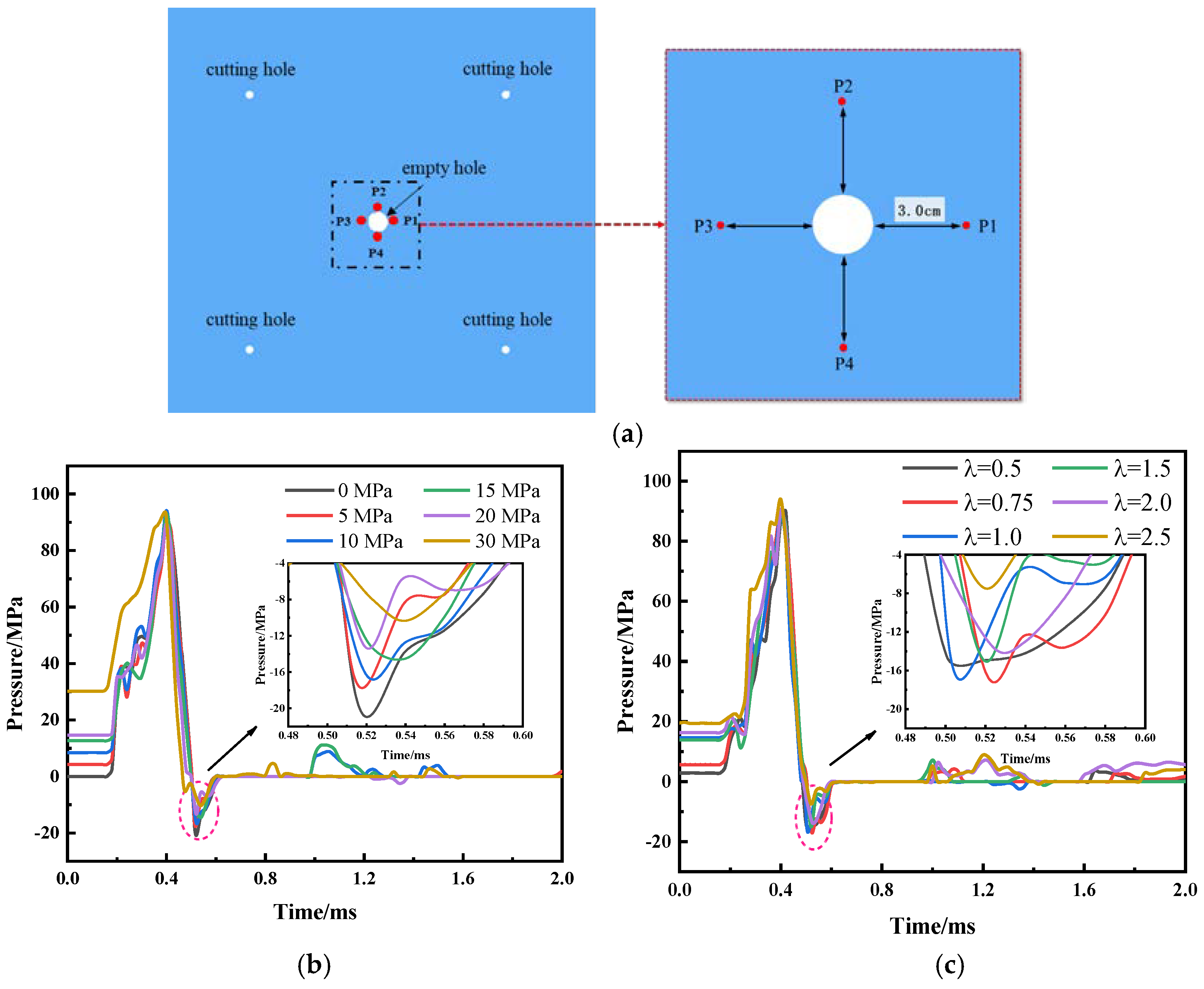
4.1. The Influence of In-Situ Stress on the Stress Field around the Empty Hole

In order to elucidate the rock fracturing impact of cut blasting amidst ground stress conditions, it is imperative to examine the alterations in the stress field surrounding the borehole across varying ground stress scenarios. The stress wave propagation within the vicinity of the void borehole constitutes the primary focus of this analysis, with the monitoring point configuration depicted in Figure 6a. Due to the model’s symmetry, analysis is solely conducted on measurement point P1 for objectivity. Figure 6b–c illustrates the pressure-time history curves generated by explosion stress waves under different in-situ stress conditions (hydrostatic pressure and non-hydrostatic pressure). As depicted in Figure 6b, the blasting shock wave reaches the empty hole around 0.37 ms and rapidly rises to 80 MPa. At this point, the compressive stress value of the shock wave is insufficient to exceed the compressive strength of the rock, thus incapable of crushing it. The damage near the hole primarily arises from the reflected tensile stress wave. With increasing levels of in-situ stress, the tensile stress value within the rock mass gradually diminishes, indicating that initial in-situ stress impedes the propagation of the explosion stress wave. Figure 6c portrays the stress–time history curve of the characteristic unit under the influence of non-hydrostatic in-situ stress. As the lateral pressure coefficient rises from 0.5 to 2.5, the tensile stress value initially increases and then decreases. At a lateral pressure coefficient of 0.75, the tensile stress value peaks, signifying optimal rock mass fragmentation by blasting at this juncture. A smaller difference between the two principal stresses enhances the effectiveness of rock mass crushing during blasting; conversely, a larger difference hampers the process.

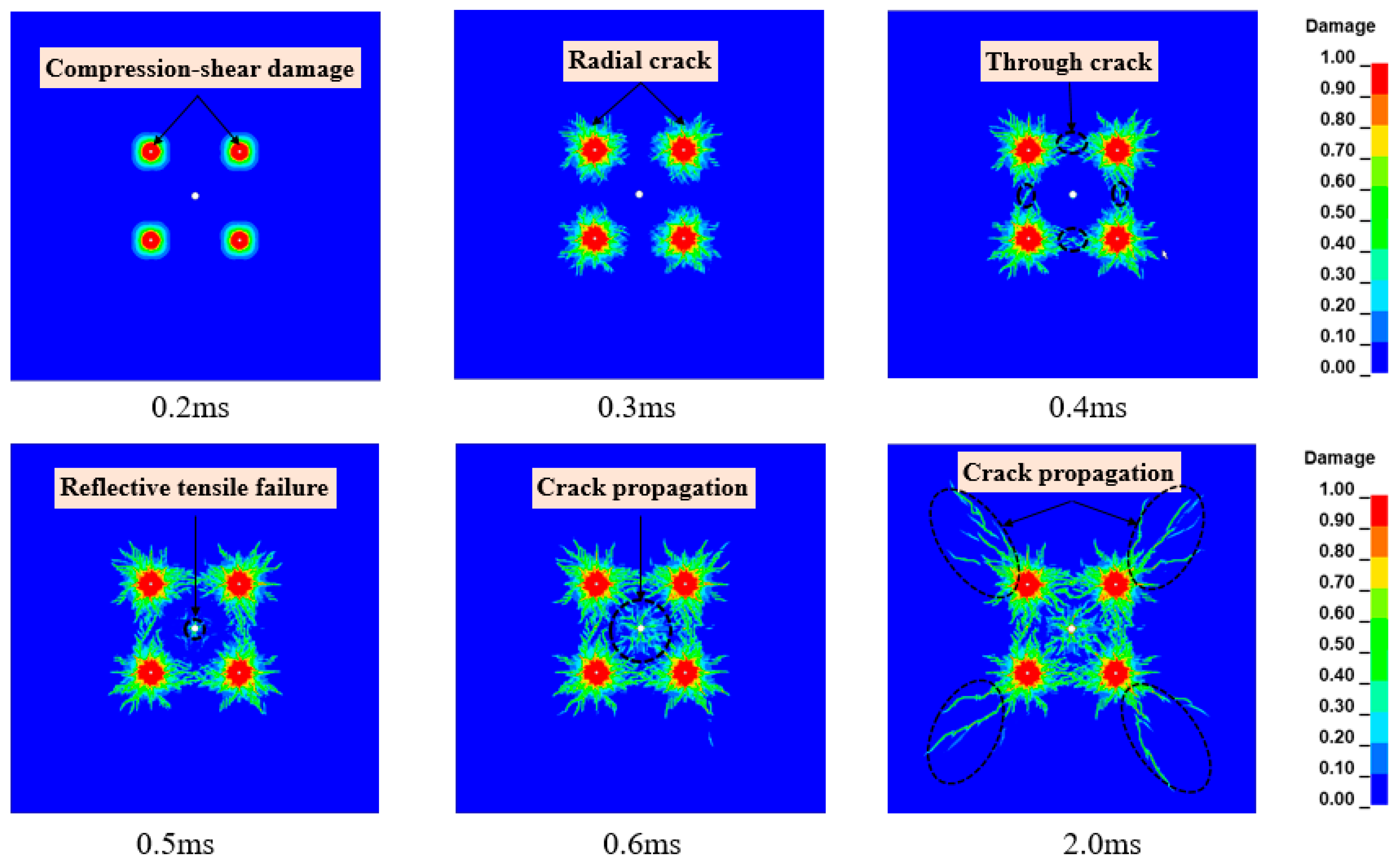
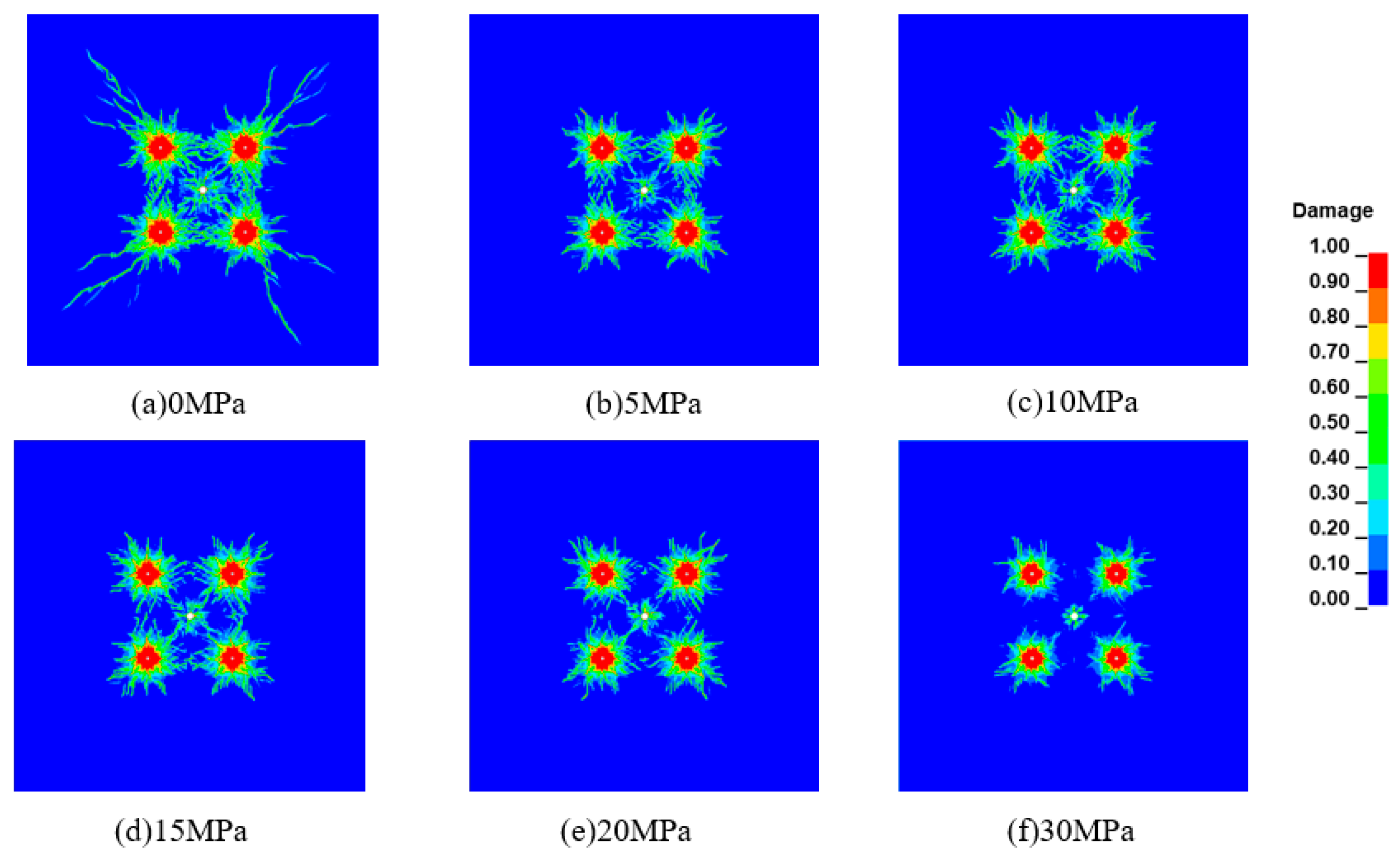
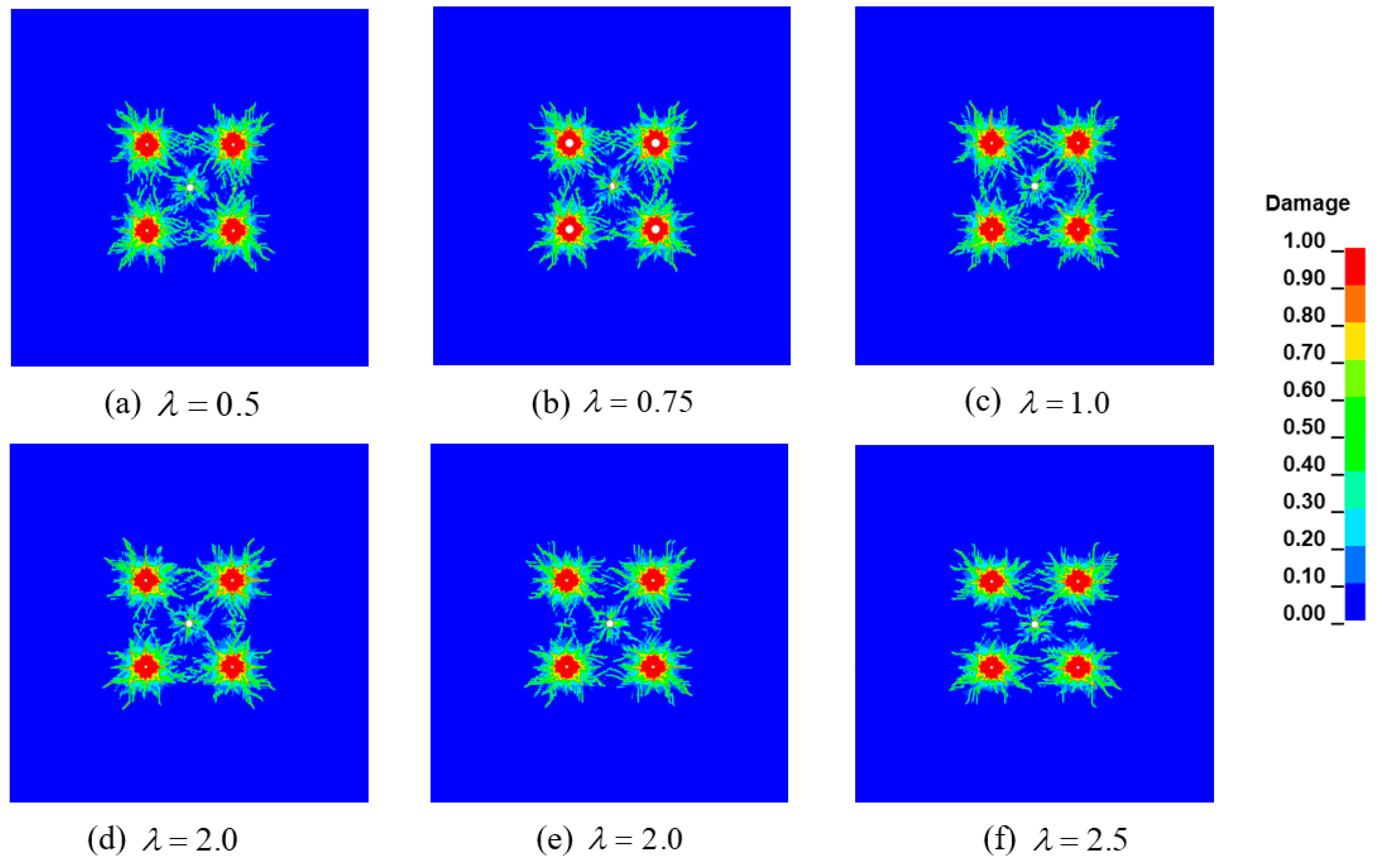
4.2. Damage Characteristics of Rock Mass under Different In-Situ Stress Conditions

Figure 7 illustrates the entire process of damage evolution in cut blasting under conditions of no in-situ stress. In LS-PrePost post-processing, rock mass damage is depicted by a damage cloud map, ranging from 0 to 1. Here, undamaged rock (D = 0) is shown in blue, while completely damaged rock (D = 1) is shown in red. The legend values range from 0 to 1, indicating varying damage levels caused by blasting.

During the blasting process, the rock mass is subjected to a variety of complex stress waves, including shock waves, tensile waves, and reflected waves. These stress waves cause damage to the rock mass at different time scales. At 0.2 ms, the cut hole is first subjected to the shock wave generated by the blasting load and the rock mass of the hole wall, forming a compression–shear damage zone. As the blasting shock wave propagates through the rock mass, its energy decays with increasing distance. At 0.3 ms, at this stage, the rock mass damage transitions from local compression-shear damage to a broader range of tensile damage. At 0.4 ms, the tensile stress damage zone around the cutting hole expands; some cracks connect, and the damage to the rock mass increases further. The expansion and connection of cracks lead to a decrease in rock mass strength. At 0.6 ms, the reflected tensile wave generated around the empty hole causes tensile stress damage. The tensile damage caused by the superposition of the reflected tensile wave causes the damage cracks to expand from the cut hole to the empty hole, further increasing the damage to the rock mass around the cut hole. By 2.0 ms, with the end of the blasting process, a large number of radial and secondary cracks have formed around the cutting hole, causing severe damage to the integrity of the rock mass.

Under different hydrostatic stress conditions, the cloud diagram of rock mass blasting damage is shown in Figure 8. It can be seen that the in-situ stress has a great influence on the damage distribution of rock mass, and the existence of in-situ stress will inhibit the crack propagation inside the rock mass. Specifically, when the local stress is less than 20 MPa, the damage between the cut holes is in a connected state. With the increase in in-situ stress level, the damage connectivity between boreholes decreases, and the damage degree near empty boreholes gradually decreases. Especially after the local stress reaches 20 MPa, the damage cracks between the cut holes are difficult to connect, and there are only sparse cracks in the central area. The rock mass here is not fully broken, and the blasting effect is poor, which will produce large blocks in practical engineering applications. When the local stress reaches 30 MPa, there are only a few cracks near the cutting hole and the empty hole, and the cracks between the holes cannot be smoothly penetrated, and the cutting effect cannot be formed. This shows that with the increase in the in-situ stress level, the propagation and expansion of the damage cracks are inhibited, which, in turn, affects the blasting crushing effect of the rock mass. Therefore, in practical engineering applications, it is necessary to take corresponding blasting technical measures for different in-situ stress conditions to improve the blasting effect and ensure the safety of the project.

Under non-hydrostatic pressure conditions, when the vertical in-situ stress is maintained at 10 MPa, and the lateral pressure coefficient increases from 0.5 to 2.5, the crack distribution resulting from rock blasting is illustrated in Figure 9. Generally, as the lateral pressure coefficient increases, the inhibitory effect on rock mass blasting damage becomes more significant. The number of burst cracks decreases, and their length shortens. When the lateral pressure coefficient is less than 1, the vertical in-situ stress predominates, and the horizontal in-situ stress is minimal. As the horizontal in-situ stress increases, the distribution of blasting cracks remains relatively unchanged. However, when the lateral pressure coefficient exceeds 1, the horizontal in-situ stress becomes dominant. At this stage, as the horizontal in-situ stress continues to increase, the length of the vertically propagating cracks is significantly reduced due to the inhibitory effect of the in-situ stress.

When the lateral pressure coefficient reaches 2.5, even the cracks between the upper and lower blast holes fail to connect, resulting in poor blasting fragmentation of the rock mass. These findings indicate that under high in-situ stress conditions, blasting damage in rock masses primarily develops along the direction of maximum in-situ stress.

Figure 10 illustrates the temporal variation in the damage area ($D\ge 0.2$) of the surrounding rock under in-situ stress. The curve indicates that the damage area initially increases before stabilizing. From Figure 10a, without in-situ stress, the damage area is 4.36 m². When the in-situ stress is 5, 10, 15, 20, and 30 MPa, the damage areas are 4.187, 3.394, 3.243, 3.019, and 2.640 m², respectively. This corresponds to reductions of 4.17%, 22.16%, 25.61%, 30.75%, and 39.45%. Hence, the damage area decreases with increasing in-situ stress, demonstrating a more pronounced inhibitory effect at higher stress values. Figure 10b presents the damage area variation under non-hydrostatic in-situ stress. When the lateral pressure coefficient is 0.75, the damage area reaches a maximum of 4.244 m². Conversely, at a lateral pressure coefficient of 2.5, the damage area is minimized at 3.193 m². A small difference between the two principal stresses results in a larger damage area, indicating that certain ranges of lateral pressure coefficients can exacerbate rock damage. Conversely, a larger difference between the principal stresses reduces the damage area, suggesting that higher lateral pressure coefficients more effectively inhibit rock damage.

Figure 11 illustrates the change in the surrounding rock damage over time under in-situ stress. The damage variation indicates the average propagation speed of cracks. The curve under in-situ stress exhibits a certain similarity in its variation law. Initially, the damage area remains relatively constant, representing the formation stage of the cutting hole fracture zone where in-situ stress has minimal effect. The second stage involves crack propagation in the cutting area, significantly influenced by in-situ stress. Figure 11a presents the damage velocity change curve under hydrostatic pressure. The peak damage velocity is 12.292 m/ms without in-situ stress. When the in-situ stress is 5 MPa, the peak damage velocity increases to 15.121 m/ms, a 23% increase. For local stresses of 10, 15, 20, and 30 MPa, the peak damage velocities are 15.121, 11.263, 10.743, and 8.360 m/ms, respectively, indicating reductions of 7.67%, 8.37%, 12.60%, and 30.75%. This shows that in-situ stress promotes crack propagation when it is below 5 MPa but inhibits it when above 5 MPa. Figure 11b displays the damage velocity change curve under non-hydrostatic in-situ stress. The peak damage velocity is highest at 14.340 m/ms when the lateral pressure coefficient is 0.75 and lowest at 10.881 m/ms when the coefficient is 2.5. This demonstrates that smaller differences between the two principal stresses enhance damage propagation, whereas larger differences inhibit it.

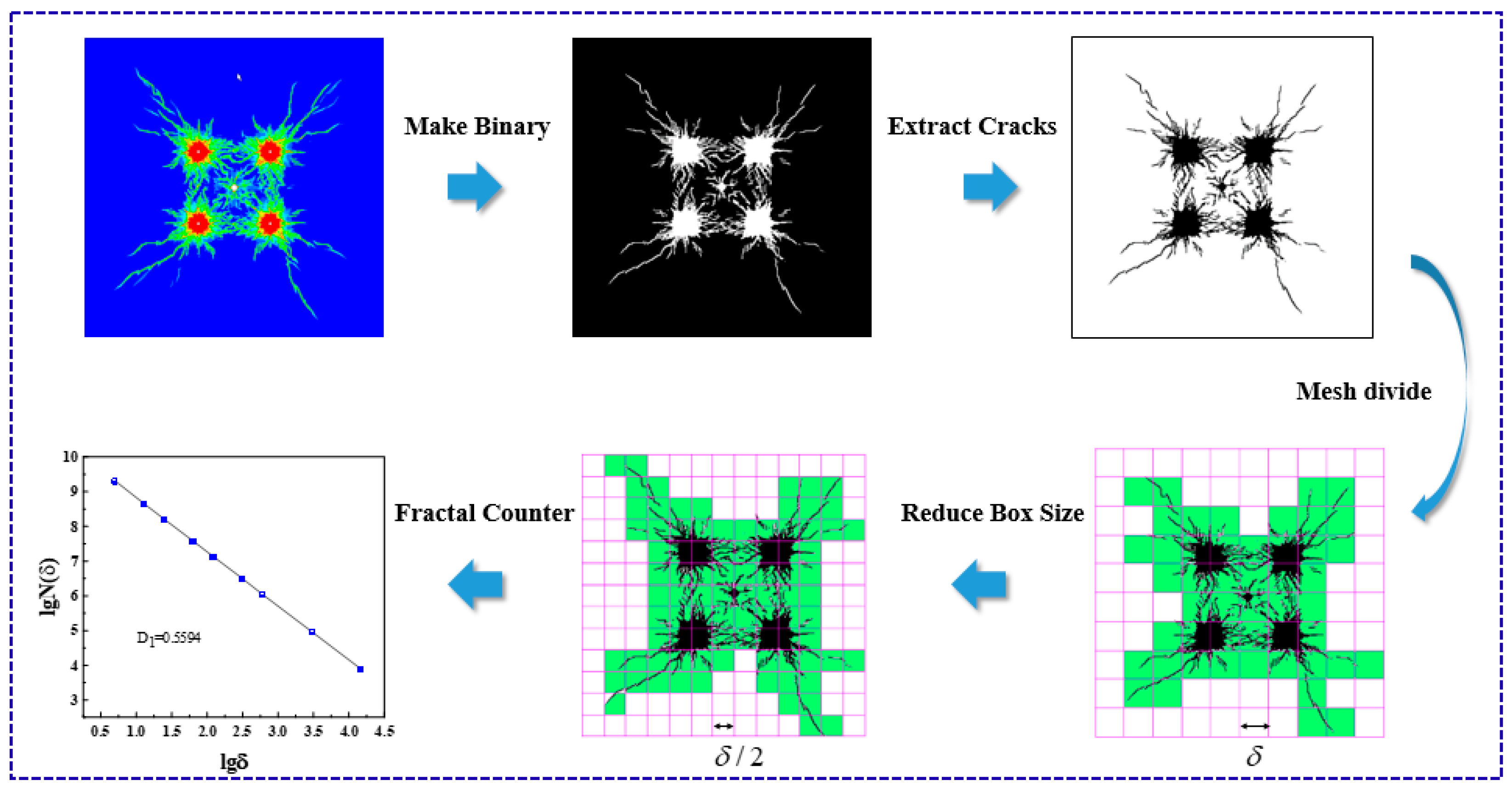
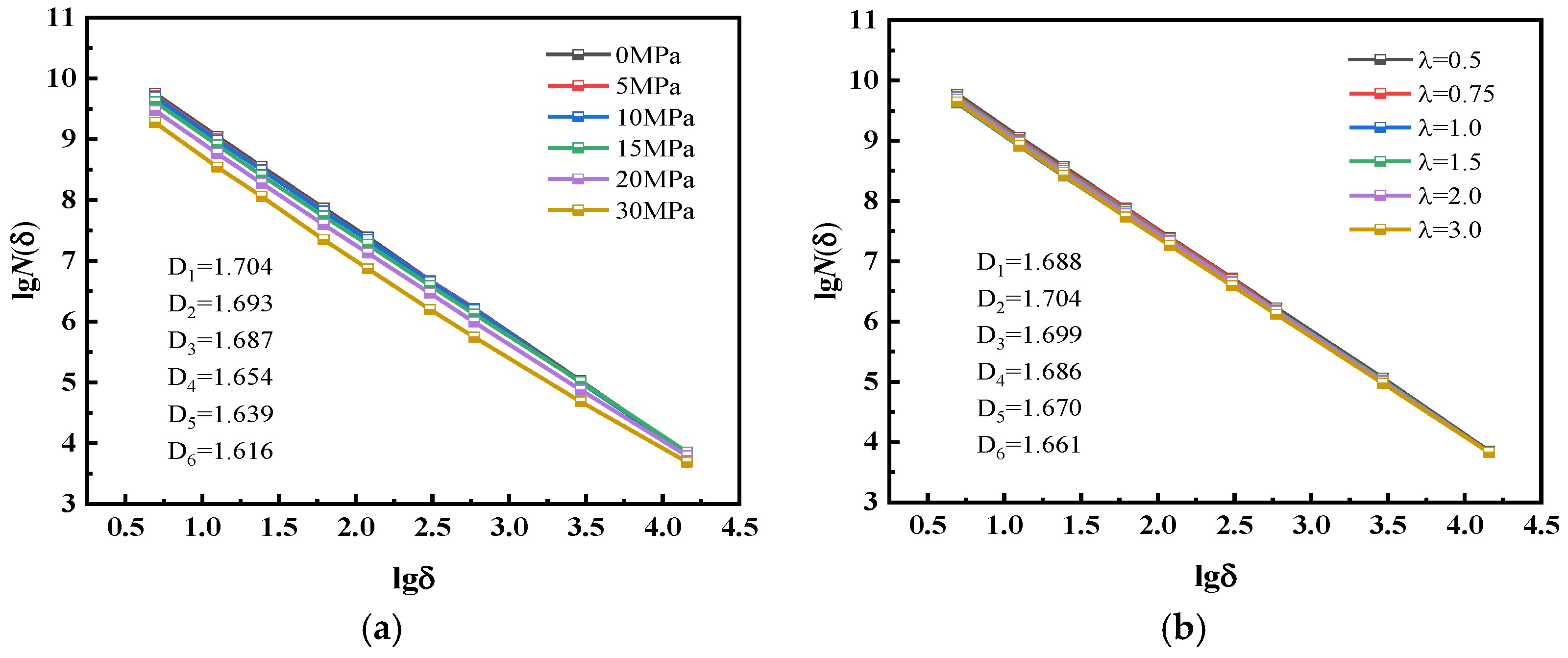
5. Damage Analysis of Rock Mass Based on Fractal Dimension

In recent years, some scholars have linked rock damage with fractal dimension and studied the distribution of cracks and holes in rock using fractal analysis to establish the relationship between fractal dimension and damage [43,44]. The fractal dimension serves as a characteristic parameter to quantify the degree of rock damage. It allows for the quantitative analysis of the evolution of the rock’s fracture field under blasting conditions, and it unifies the evolution of microcracks in the material with macroscopic failure characteristics.

$$\omega ={\displaystyle \frac{\Delta D_f}{D_0}}={\displaystyle \frac{D_f-D_0}{D_0}}$$

(11)

In this formula, $\omega$ is the fractal dimension of the damage area after blasting; $D_0$ is the fractal dimension of the original damage area; $D_f$ is the fractal dimension of the damage area increased by crack propagation after the explosion.

It can be observed that the greater the fractal dimension, the higher the degree of material damage. Under the influence of blasting loads, the damage is linearly related to the fractal dimension, indicating that the variation in rock damage can be quantitatively characterized by the fractal dimension. The expression of fractal dimension mainly includes the Hausdorff dimension, box-counting dimension, and filling dimension [45]. Among these, the box-counting dimension has been widely used in fractal research because it intuitively reflects the extent of the target within the study area, and its calculation method is relatively straightforward and simple.

The fractal dimension involves using a square lattice ($\delta \times \delta$) to cover a fractal curve, with the lattice size ($\delta$) changing systematically. By determining the size of the lattice boxes, the total number of boxes ($N$) needed to cover the fractal curve can be calculated [46]. Assuming that step ($i$) 1 covers the use of a (${\delta }_i\times {\delta }_i$) grid, and the number of boxes required is $N_i\left({\delta }_i\right)$, and that in step $i+1$ the grid to be covered is ${\delta }_{i+1}\times {\delta }_{i+1}$ and the number of boxes required is $N_{i+1}\left({\delta }_{i+1}\right)$, the following relationship can be found between the ratio of the number of boxes required and the ratio of the yardstick at any two scales:

$$N_{i+1}/N_i={\left(\delta /{\delta }_i\right)}^D$$

(12)

The fractal dimension $D_f$ can be expressed as

$$D_{\mathrm{f}}=\lg (N_{i+1}/N_i)/\left({\delta }_{i+1}/{\delta }_i\right)$$

(13)

Knowing the size of any two-step box and the corresponding number, we can directly calculate the fractal dimension [47]:

$$\lg N(\delta )=-D_{\mathrm{f}}\lg \delta +b$$

(14)

In the process of covering, a set of ($\delta ,N$) data is obtained, which is drawn into a double logarithmic coordinate map, and its slope is equal to the fractal dimension of the set. The calculation process of fractal dimension is shown in Figure 12.

The fractal dimension fitting lines of rock blasting cracks under different initial stresses are shown in Figure 13. The figure indicates that the damage cracks in the surrounding rock exhibit strong fractal characteristics, with a correlation coefficient (R²) of the fitting results greater than 0.96. Under hydrostatic stress, the fractal dimension decreases progressively as the stress increases. When the local stresses are 0, 5, 15, 20, and 30 MPa, the fractal dimensions of blasting cracks are 1.704, 1.693, 1.687, 1.654, and 1.616, respectively. These values represent reductions of 0.6%, 1.0%, 2.9%, 3.8%, and 5.2%, respectively. The in-situ stress progressively enhances the inhibitory effect on the expansion of blasting damage.

Under non-hydrostatic in-situ stress, when the lateral pressure coefficients ($\lambda$) are 0.5, 0.75, 1.0, 1.5, 2.0, and 3.0, the corresponding fractal dimensions of blasting cracks are 1.688, 1.704, 1.699, 1.686, 1.670, and 1.661, respectively. As the lateral pressure coefficient increases, the fractal dimension initially increases and then decreases. When the lateral pressure coefficient is 0.75, the fractal dimension is the largest, indicating that a smaller difference between the two principal stresses results in a relatively effective blasting effect on the rock mass. Conversely, a larger difference between the two principal stresses inhibits blasting damage propagation, with greater lateral pressure coefficients resulting in stronger inhibition.

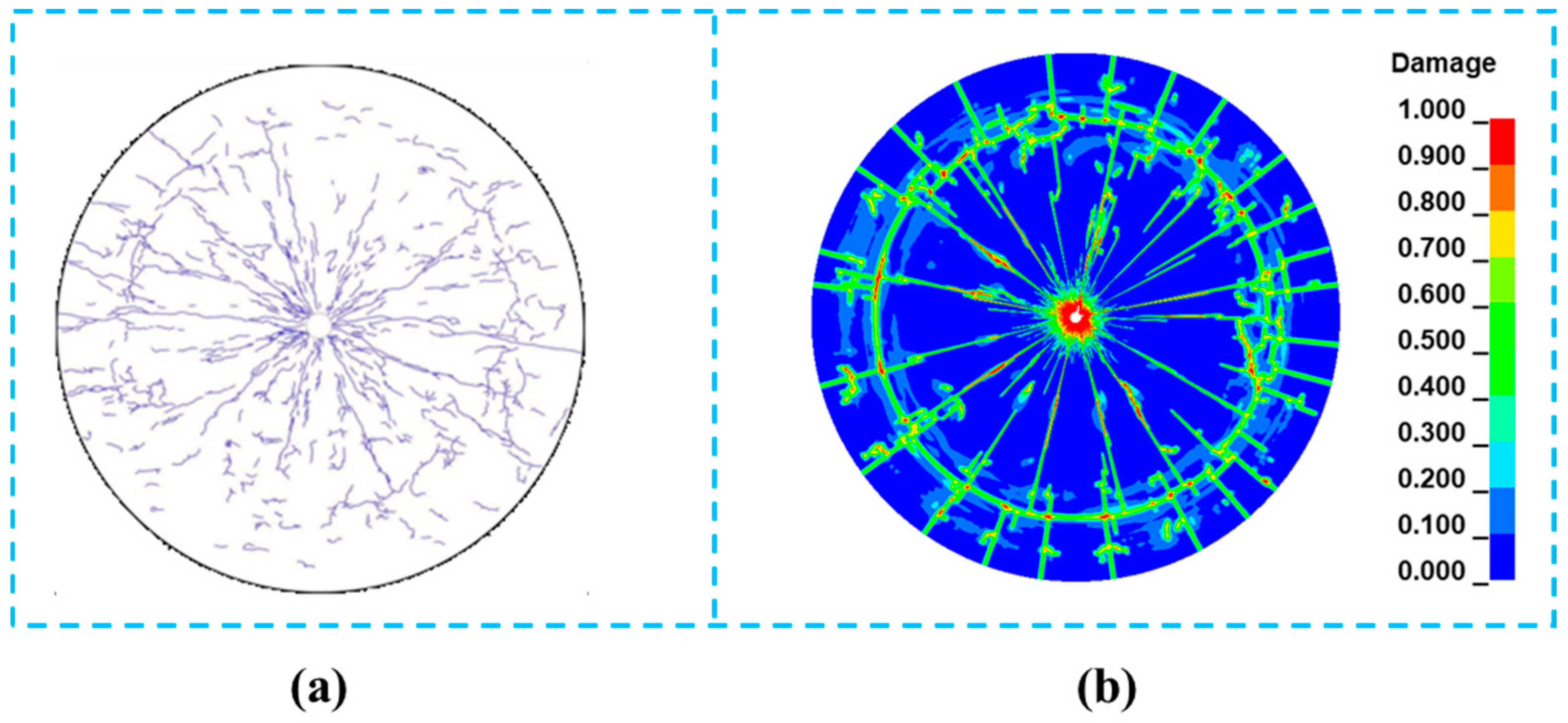
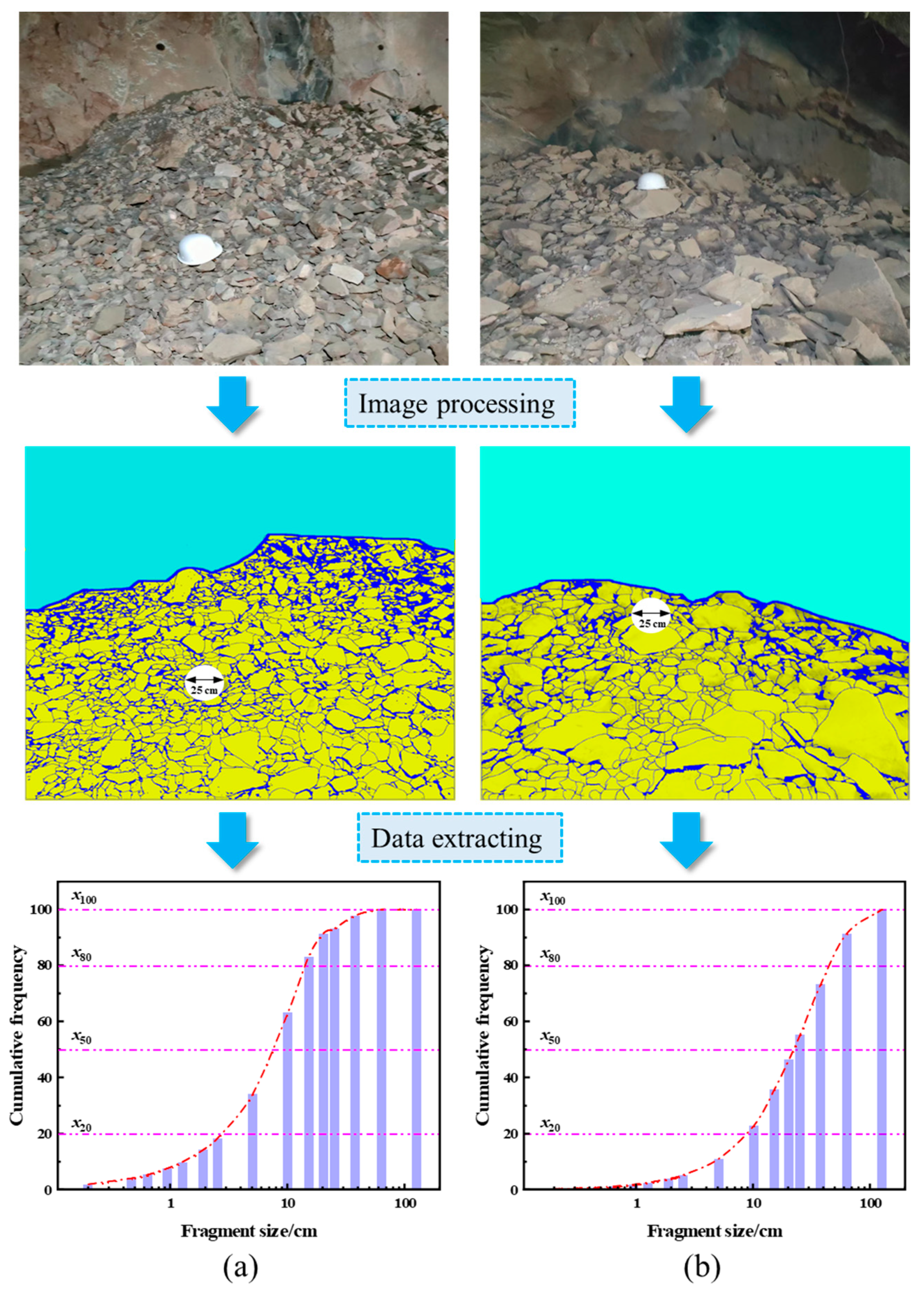
6. Engineering Case Analysis

6.1. Engineering Situations

The tunnel extends from DK131 346 to DK132 275, with a total length of 929 m. The landscape features prominent mountain peaks and valleys, resulting in undulating terrain, with the highest peak reaching approximately 800 m. The lithology predominantly consists of angular rock and granite, characterized by its hardness, completeness, and stable surrounding rock. Field stress tests indicate that at a depth of 100~200 m, the maximum horizontal principal stress is approximately 5 MPa, with an average lateral pressure coefficient of 0.95. At a depth of 500~600 m, the maximum horizontal principal stress increases to about 20 MPa, with an average lateral pressure coefficient of 0.97. The overall in-situ stress in the project area closely resembles a hydrostatic stress field.

Tunnel construction employed the step method, with the upper and lower step heights measuring 7 m and 4.31 m, respectively. The upper step section contained 100 holes with a diameter of 42 mm, a depth of 3.5 m, and a spacing of 0.8 to 1.2 m. Emulsion explosives (2# rock) were used, with each roll having a diameter of 32 mm. The total explosive dosage was 185 kg, with a maximum of 26 kg per shot. The explosive unit consumption was designed to be 0.85 kg/m³.

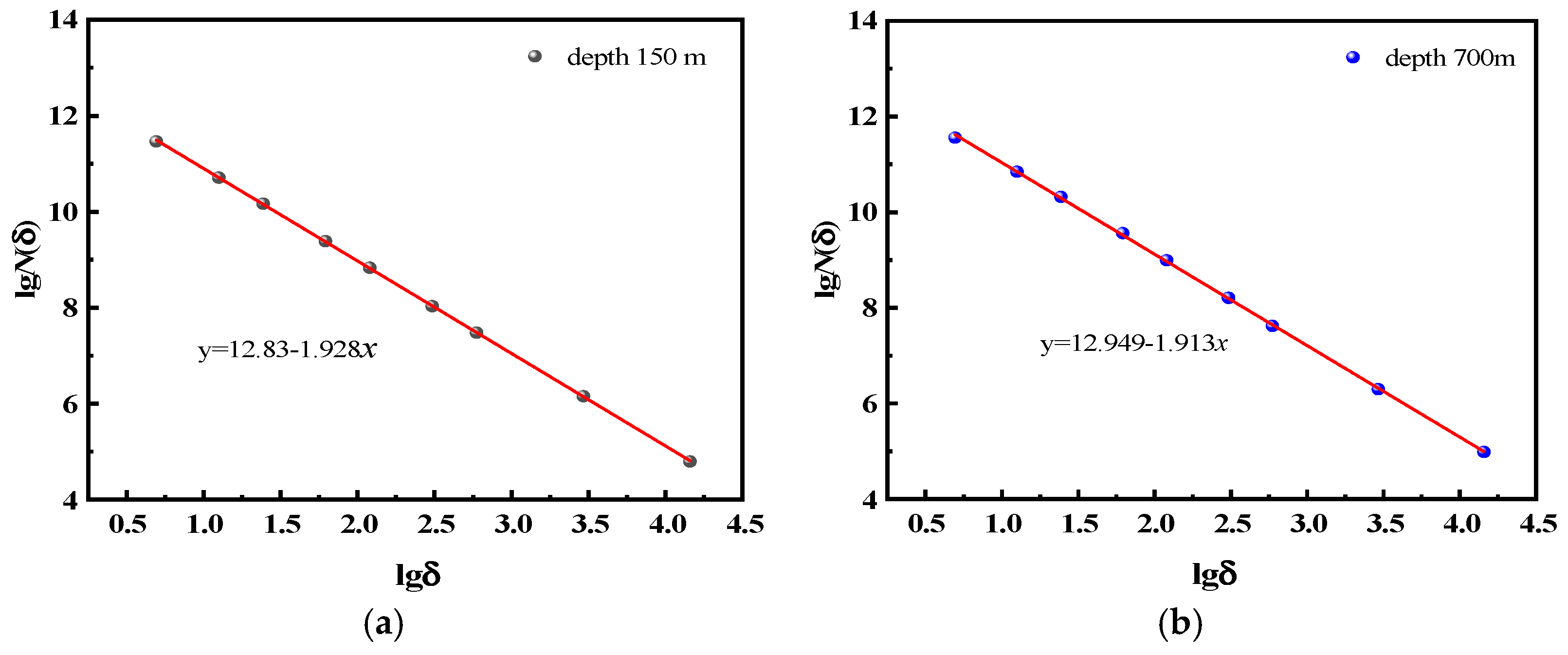
6.2. Comparative Analysis of Blast Blocks for Different Depths of Buried Rock

Two tunnel piles, DK131 578 (buried depth of approximately 150 m) and DK132 062 (buried depth of approximately 700 m), were selected for comparative analysis. Both blasts have similar lithology, excavation section size, and blasting parameters. The primary difference lies in the in-situ stress levels: at 150 m depth, the in-situ stress is about 5 MPa, while at 700 m depth, it is about 20 MPa. Therefore, comparing the bulkiness characteristics of rock blasting at different burial depths can illustrate the influence of in-situ stress on the bulkiness distribution of the blasted rock.

Figure 14 presents the distribution curves of rock blasting fragmentation at different depths. Generally, the rock mass at a burial depth of 700 m exhibits larger blasting block sizes. To investigate the effect of in-situ stress on the distribution characteristics of rock mass blasting block sizes, different characteristic sizes (small, average, large, and maximum block sizes) were selected for analysis. Figure 15 displays the characteristic dimensions of the blasting block sizes at various burial depths. For the shallow rock mass at a depth of 150 m, the characteristic dimensions are 2.8 cm, 7.78 cm, 14.24 cm, and 30.70 cm, respectively. For the deep rock mass at a burial depth of 700 m, the characteristic dimensions are 8.99 cm, 22.34 cm, 43.91 cm, and 87.35 cm. Figure 15 illustrates the characteristic sizes of small, average, large, and maximum block sizes for rock masses at different depths. At the two burial depths, the small, average, large, and maximum block sizes increased by factors of 2.21, 1.87, 2.08, and 1.84, respectively. The in-situ stress predominantly caused significant increases in small and large block sizes.

Figure 16a,b illustrates fractal curves depicting the fragmentation of rock mass due to blasting at various burial depths. The fractal dimensions for blasting at two distinct depths are 1.928 and 1.913, respectively. The fractal dimension decreases gradually with increasing in-situ stress, suggesting that blasting results in larger blocks, thereby reducing the degree of rock mass fragmentation. This finding aligns with the conclusions drawn from the aforementioned numerical simulation study, indicating that in-situ stress impedes crack propagation.

7. Conclusions

In this paper, the rock-breaking process of cut blasting under different in-situ stress conditions is numerically simulated. The fractal dimension is introduced to quantitatively analyze the influence of in-situ stress on the distribution of blasting cracks and further reveal the influence mechanism of in-situ stress on blasting rock-breaking effect.

(1)

In the initial stage, the damage area is basically the same. This stage is the formation stage of the cutting hole fracture zone, and the in-situ stress has little effect. The second stage is the propagation of cracks in the cutting area, which is greatly affected by the in-situ stress at this stage;

(2)

Damage to the rock mass is primarily influenced by the magnitude of tensile stress, which serves as an indicator of damage in the hollowing zone. As in-situ stress or the lateral pressure coefficient increases, the inter-hole tensile stress weakens more significantly, leading to greater inhibition of damage in the hollowing zone. Excessive in-situ stress or lateral pressure coefficient will prevent cracks between cavities from penetrating;

(3)

Under hydrostatic in-situ stress, with the increase in in-situ stress, the damage area and fractal dimension of blasting cracks gradually decrease. Under non-hydrostatic in-situ stress, when the principal stress difference is small, the in-situ stress has a promoting effect on the damage area and fractal dimension of surrounding rock, and the rock mass crushing effect is better. When the principal stress difference is large, the in-situ stress has an inhibitory effect on the damage area and fractal dimension of surrounding rock, which is not conducive to blasting rock breaking;

(4)

Both numerical simulations and field experiments indicate that in-situ stress impedes crack propagation. As in-situ stress rises, the fractal dimension progressively diminishes, suggesting that blasting results in the formation of larger blocks, consequently decreasing the extent of rock fragmentation.