A Fractional-Order Creep-Damage Model for Carbonaceous Shale Describing Coupled Damage Caused by Rainfall and Blasting
Abstract
1. Introduction
2. Specimen Preparation and Experimental Procedures
2.1. Specimen Material and Test Equipment
2.2. Test Design
3. Test Results and Analysis
4. Fractional-Order Creep-Damage Model and Parameter Identification
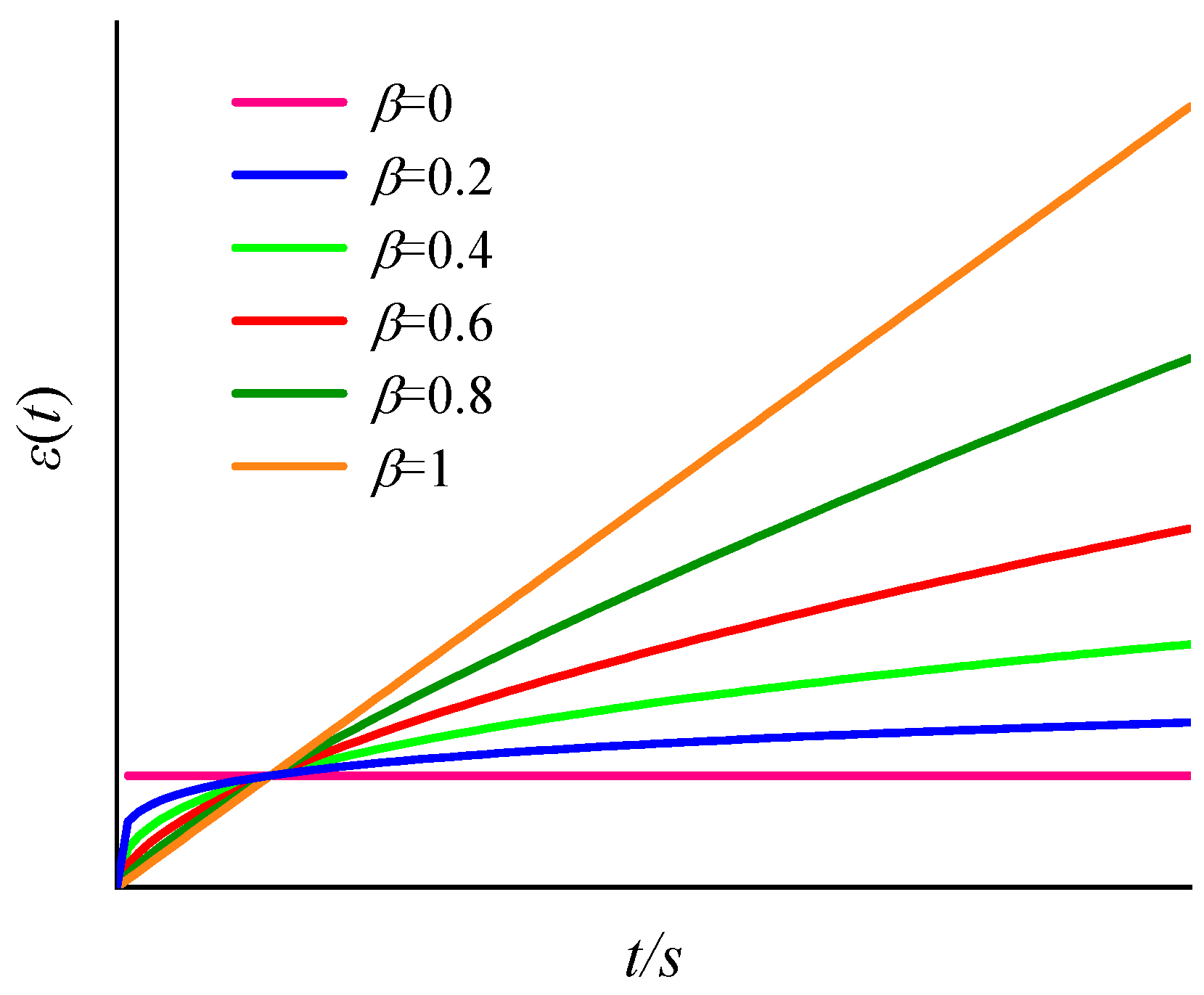
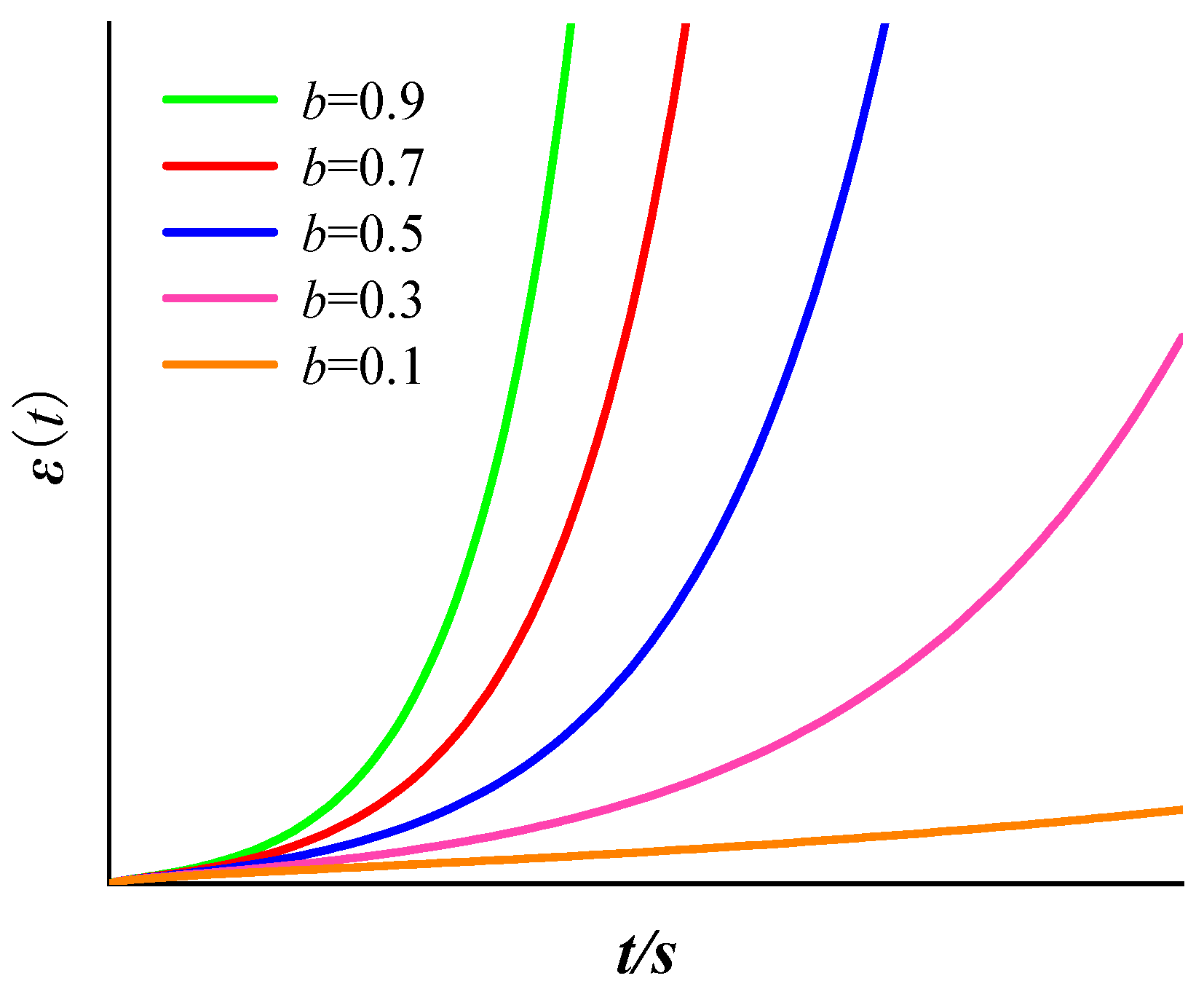
4.1. Fractional-Order Abel Dashpot
4.2. Fractional-Order Creep Constitutive Model
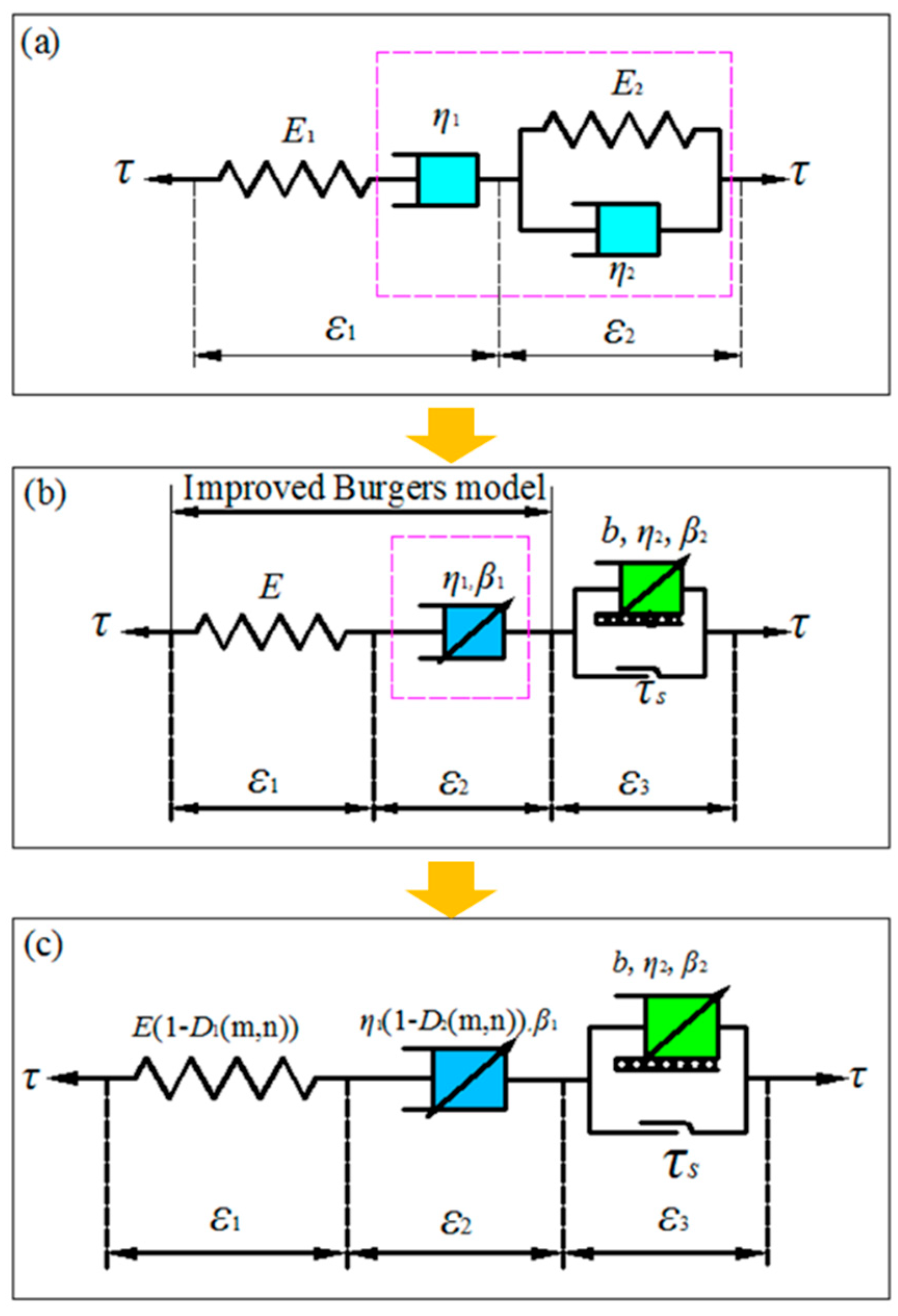
4.3. Fractional-Order Creep-Damage Constitutive Model
4.3.1. Definition of Damage Variables
- Definition of damage rate for instantaneous elastic modulus.
- 2.
- Definition of damage rate for viscosity coefficient.
- 3.
- Definition of damage rate under the combined action of dry–wet cycle and blasting vibration.
4.3.2. Damage Rate of Rainfall Dry–Wet Cycle and Blasting Vibration
- Damage rate caused by the rainfall dry–wet cycle.
- 2.
- Damage rate caused by blasting vibration.
- 3.
- Damage rate caused by the rainfall dry–wet cycle and blasting vibration.
4.3.3. Creep-Damage Constitutive Model
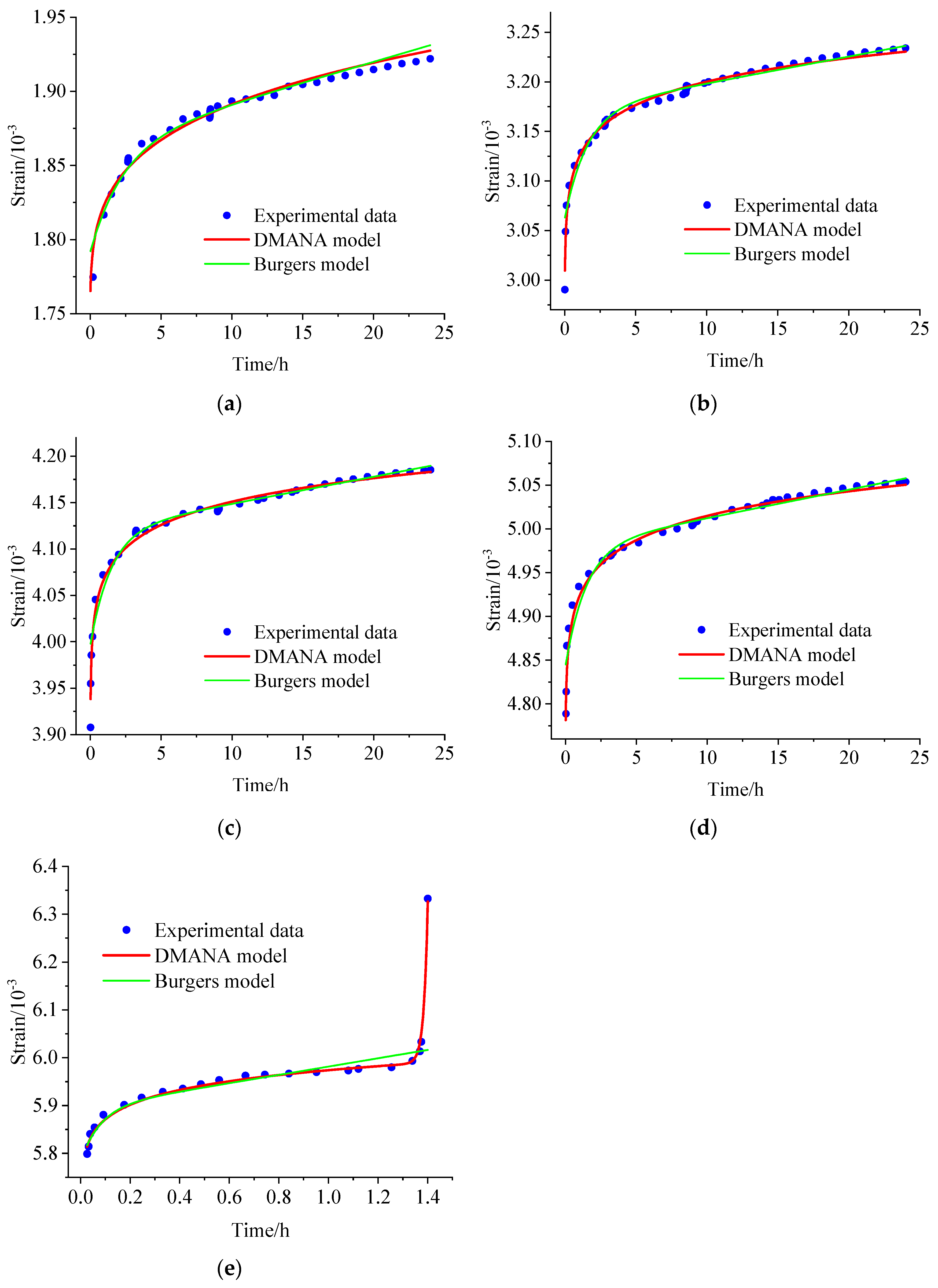
4.4. Parameter Identification
5. Discussion
6. Conclusions
- Carbonaceous shale has obvious creep characteristics, and especially under the influence of dry–wet cycles and vibration, the nonlinear characteristics of its creep curve are more obvious. As the number of dry–wet cycles and vibrations increases, the deceleration creep time increases, the steady-state creep rate increases, the long-term strength decreases, and the degree of damage intensifies. The damage of the specimen under the coupling effect of dry–wet cycle and vibration is much greater than that caused by a single factor.
- Based on the generalized strain equivalence principle, the coupled damage rate of the rainfall dry–wet cycle and blasting vibration for carbonaceous shale was defined. Based on the creep test results, the expression for the coupled damage of the rainfall dry–wet cycle and blasting vibration is determined.
- Based on the fractional calculus theory and the introduction of the Abel dashpot, a nonlinear fractional shear-creep constitutive model (DNFVP model) was established to characterize the coupled damage caused by rainfall dry–wet cycles and blasting vibration. The three-dimensional creep equation of the model was derived to describe the three-stage nonlinear creep characteristics of carbonaceous shale under the influence of rainfall dry–wet cycles and blasting vibration.
- The DNFVP model was used to fit the creep curve of carbonaceous shale, and the creep parameters of the creep model were determined. The fitting effect of the model was good, and the effectiveness of the model was verified.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| m | Number of dry–wet cycles |
| n | Number of vibrations |
| τ∞ | Long-term strength (MPa) |
| Dr | Damage rate of long-term strength with rainfall dry–wet cycles (%) |
| Db | Damage rate of long-term strength with blasting vibration (%) |
| τ | Shear stress (MPa) |
| ε | Strain |
| E | Elastic modulus (GPa) |
| η1 | Generalized viscosity coefficient of Abel dashpot (GPa·hβ) |
| β1 | Derivative order of Abel dashpot |
| η2 | Generalized viscosity coefficient of unsteady Abel dashpot (GPa·hβ) |
| β2 | Derivative order of unsteady Abel dashpot |
| b | Coefficient related to the material |
| η0 | Initial value of the generalized viscosity coefficient (GPa·hβ) |
| τs | Yield stress of the material (MPa) |
| t | Creep time (h) |
| Dr1(m) | Instantaneous elastic-modulus damage rate for m dry–wet cycles (%) |
| Er(0) | Instantaneous elastic modulus for 0 dry–wet cycle (GPa) |
| Er(m) | Instantaneous elastic modulus for m dry–wet cycle (GPa) |
| Db1(n) | Instantaneous elastic-modulus damage rate of n vibrations (%) |
| Eb(0) | Instantaneous elastic modulus for 0 vibration (GPa) |
| Eb(n) | Instantaneous elastic modulus for n vibrations (GPa) |
| Dr2(m) | Viscosity-coefficient damage rate for m dry–wet cycles (%) |
| ηr(0) | Viscosity coefficients for 0 dry–wet cycle (GPa·h) |
| ηr(m) | Viscosity coefficients for m dry–wet cycle (GPa·h) |
| Db2(n) | Viscosity-coefficient damage rate of n vibrations (%) |
| ηb(0) | Viscosity coefficients of 0 vibration (GPa·h) |
| ηb(n) | Viscosity coefficients of 0 and n vibrations (GPa·h) |
| D1(m,n) | Damage rate of the instantaneous elastic modulus under the combined action of dry–wet cycle and blasting vibration (%) |
| D2(m,n) | Damage rate of the viscosity coefficient under the combined action of dry–wet cycle and blasting vibration (%) |
References
- Tian, X.S.; Shi, Z.J.; Yin, G.; Wang, Y.; Tan, Q. Carbonate diagenetic products and processes from various diagenetic environments in Permian paleokarst reservoirs: A case study of the limestone strata of Maokou formation in Sichuan Basin, South China. Carbonate. Evaporite. 2017, 32, 431–433. [Google Scholar] [CrossRef]
- Pang, Q.; Hu, G.; Zhang, X.H.; Chen, C.; Gao, Z.L.; Shan, S.J. Organic geochemistry, sedimentary environment, and organic matter enrichment of limestone-marlstone rhythms in the middle Permian northern Sichuan Basin, China. Mar. Petrol. Geol. 2021, 134, 105306. [Google Scholar] [CrossRef]
- Li, J.; Hu, B.; Sheng, J.L.; Zhang, Z. Failure mechanism and treatment of mine Landslide with gently-inclined weak interlayer: A case study of Laoyingzui landslide in Emei, Sichuan, China. Geomech. Geophys. Geo. 2024, 10, 61. [Google Scholar] [CrossRef]
- Jing, H.W.; Yin, Q.; Yang, S.Q.; Chen, W.Q. Micro-Mesoscopic Creep Damage Evolution and Failure Mechanism of Sandy Mudstone. Int. J. Geomech. 2021, 21, 04021010. [Google Scholar] [CrossRef]
- Lyu, C.; Liu, J.F.; Ren, Y.; Liang, C.; Zhang, Q.X. Study on long-term uniaxial compression creep mechanical behavior of rocksalt-mudstone combined body. Int. J. Damage Mech. 2022, 31, 275–293. [Google Scholar] [CrossRef]
- Wang, Q.; Hu, X.; Xu, C.; Zhou, C.; He, C.C.; Ying, C.Y. Time-dependent behavior of saturated silty mudstone under different confining pressures. Bull. Eng. Geol. Environ. 2020, 79, 2621–2634. [Google Scholar] [CrossRef]
- Gao, R.B.; Wu, F.; Chen, J.; Zhu, C.; Ji, C.X. Study on creep characteristics and constitutive model of typical argillaceous salt rock in energy storage caverns in China. J. Energy Storage 2022, 50, 104248. [Google Scholar] [CrossRef]
- Dong, Z.K.; Li, Y.P.; Li, H.R.; Wang, Z.H.; Shi, X.L.; Chen, X.S.; Lu, Q.F. Experimental Study on the Influence of Temperature on Rock Salt Creep. Rock Mech. Rock Eng. 2023, 56, 3499–3518. [Google Scholar] [CrossRef]
- Liu, Z.B.; Shao, J.F.; Xie, S.Y.; Conil, N.; Zha, W.H. Effects of relative humidity and mineral compositions on creep deformation and failure of a claystone under compression. Int. J. Rock Mech. Min. 2018, 103, 68–76. [Google Scholar] [CrossRef]
- Mánica, M.; Gens, A.; Vaunat, J.; Ruiz, D.F. A time-dependent anisotropic model for argillaceous rocks. Application to an underground excavation in Callovo-Oxfordian claystone. Comput. Geotech. 2017, 85, 341–350. [Google Scholar] [CrossRef]
- Wang, Y.C.; Wang, Y.Y.; Su, C.Q.; Li, J.G. Study of Influence of Environmental Factors on Deep Shale Creep Properties. Shock. Vib. 2018, 2018, 9165238. [Google Scholar] [CrossRef]
- Zhang, B.; Peng, C.; Chen, S.; Hu, Y.; Li, X.; Zhao, J. The mechanical creep property of shale for different loads and temperatures. Int. J. Rock. Mech. Min. 2023, 163, 105327. [Google Scholar] [CrossRef]
- Gupta, N.; Mishra, B. Influence of stress-induced microcracks on viscoplastic creep deformation in Marcellus shale. Acta Geotech. 2021, 16, 1575–1595. [Google Scholar] [CrossRef]
- Jiang, H.P.; Jiang, A.N.; Zhang, F.R.; Feng, Y.P. Study on creep characteristics and fractional creep damage constitutive model of limestone under thermal-mechanical action. Int. J. Damage Mech. 2023, 32, 262–288. [Google Scholar] [CrossRef]
- Wang, B.X.; Li, T.C.; Li, C.T.; Du, Y.T.; An, X.G.; Li, Y. Study on the creep properties and fracture behavior of three different rock types with a single preexisting fissure. B Eng. Geol. Environ. 2023, 82, 255. [Google Scholar] [CrossRef]
- Sabitova, A.; Yarushina, V.M.; Stanchits, S.; Stukachev, V.; Khakimova, L.; Myasnikov, A. Experimental Compaction and Dilation of Porous Rocks During Triaxial Creep and Stress Relaxation. Rock. Mech. Rock. Eng. 2021, 54, 5781–5805. [Google Scholar] [CrossRef]
- Chu, Z.F.; Wu, Z.J.; Wang, Z.Y.; Weng, L.; Liu, Q.S.; Fan, L.F. Micro-mechanism of brittle creep in saturated sandstone and its mechanical behavior after creep damage. Int. J. Rock Mech. Min. 2022, 149, 104994. [Google Scholar] [CrossRef]
- Fu, F.T.; Xu, T.; Meredith, P.G.; Mitchell, T.M.; Heap, M.J.; Nara, Y. A meso-mechanical approach to time-dependent deformation and fracturing of partially saturated sandstone. Int. J. Rock Mech. Min. 2021, 145, 104840. [Google Scholar] [CrossRef]
- Wang, S.; Wang, J.E.; Wu, W.; Cui, D.S.; Su, A.J.; Xiang, W. Creep properties of clastic soil in a reactivated slow-moving landslide in the Three Gorges Reservoir Region, China. Eng. Geol. 2020, 267, 105493. [Google Scholar] [CrossRef]
- Ye, C.F.; Xie, H.P.; Wu, F.; Li, C.B. Study on the nonlinear time-dependent deformation characteristics and viscoelastic-plastic model of shale under direct shear loading path. B Eng. Geol. Environ. 2023, 82, 189. [Google Scholar] [CrossRef]
- Zhu, S.N.; Yin, Y.P.; Li, B.; Wei, Y.J. Shear creep characteristics of weak carbonaceous shale in thick layered Permian limestone, southwestern China. J. Earth Syst. Sci. 2019, 128, 28. [Google Scholar] [CrossRef]
- Wang, L.Q.; Huang, B.L.; Zhang, Z.H.; Dai, Z.W.; Zhao, P.; Hu, M.J. The analysis of slippage failure of the HuangNanBei slope under dry-wet cycles in the three gorges reservoir region, China. Geomat. Nat. Hazards Risk. 2020, 11, 1233–1249. [Google Scholar] [CrossRef]
- Chen, Y.L.; Hao, X.J.; Teng, J.Y.; Wen, Z.J. Creep behavior of water-containing bedded shale. J. Cent. South Univ. 2023, 30, 975–991. [Google Scholar] [CrossRef]
- Ma, L.; Hu, B.; Cui, K.; Wei, E.; Zhang, Z.; Wang, Z. A direct shear apparatus for intact rock under dynamic moisture content. PLoS ONE 2022, 17, e0272004. [Google Scholar] [CrossRef] [PubMed]
- Wei, E.J.; Hu, B.; Li, J.; Zhang, Z.; Ma, L.Y.; Wang, Z.Q. Study on creep mechanical properties of carbonaceous shale under dry-wet cycle. Phys. Scr. 2023, 98, 095022. [Google Scholar] [CrossRef]
- Babaeian, M.; Ataei, M.; Sereshki, F.; Sotoudeh, F.; Mohammadi, S. A new framework for evaluation of rock fragmentation in open pit mines. J. Rock Mech. Geotech. 2019, 11, 325–336. [Google Scholar] [CrossRef]
- Chu, F.J.; Liu, D.W.; Zhang, X.J.; Yu, H.; Zhu, G.L. Dynamic Response and Damage Regularity of Sandstone with Different Moisture States under Cyclic Loading. Fractal Fract. 2022, 6, 226. [Google Scholar] [CrossRef]
- Choi, Y.H.; Lee, S.S. Predictive Modelling for Blasting-Induced Vibrations from Open-Pit Excavations. Appl. Sci. 2021, 11, 7487. [Google Scholar] [CrossRef]
- Yuan, W.; Li, J.C.; Zou, C.J.; Zhao, J. A New Apparatus for Testing Shear-Slip Properties of Rock Joint Subjected to Dynamic Disturbance. Exp. Mech. 2024, 64, 745–759. [Google Scholar] [CrossRef]
- Zhou, S.; Jiang, H.; Fu, L.; Shan, Y.; Ye, W.; Guo, P. Experimental study on deformation and strength characteristics of granular soil-structure interface under coupled monotonic shear and vibration using a modified direct shear apparatus. Acta Geotech. 2023, 18, 2899–2913. [Google Scholar] [CrossRef]
- Zhu, W.C.; Li, S.H.; Li, S.; Niu, L.L. Influence of dynamic disturbance on the creep of sandstone: An experimental study. Rock Mech. Rock Eng. 2019, 52, 1023–1039. [Google Scholar] [CrossRef]
- Qiao, P.J.; Gong, Z.Q.; Liu, W.Q.; Zhang, Y.W.; Feng, G.L. Asymmetrical synchronization of extreme rainfall events in southwest China. Int. J. Climatol. 2022, 42, 5935–5948. [Google Scholar] [CrossRef]
- Tao, T.W.; Shi, W.B.; Liang, F.; Wang, X.M. Failure mechanism and evolution of the Jinhaihu landslide in Bijie City, China, on January 3, 2022. Landslides 2022, 19, 2727–2736. [Google Scholar] [CrossRef]
- Tang, H.M.; Zou, Z.X.; Xiong, C.R.; Wu, Y.P.; Hu, X.L.; Wang, L.Q.; Lu, S.; Criss, R.E.; Li, C.D. An evolution model of large consequent bedding rockslides, with particular reference to the Jiweishan rockslide in Southwest China. Eng. Geol. 2015, 186, 17–27. [Google Scholar] [CrossRef]
- Xu, Q.; Fan, X.M.; Huang, R.Q.; Yin, Y.P.; Hou, S.S.; Dong, X.J.; Tang, M.G. A catastrophic rockslide-debris flow in Wulong, Chongqing, China in 2009: Background, characterization, and causes. Landslides 2010, 7, 75–87. [Google Scholar] [CrossRef]
- Lin, H.; Zhang, X.; Cao, R.; Wen, Z. Improved nonlinear Burgers shear creep model based on the time-dependent shear strength for rock. Environ. Earth Sci. 2020, 79, 149. [Google Scholar] [CrossRef]
- Zheng, Z.; Yang, Y.; Pan, C. Determination of the parameters of rock viscoelastic creep model and analysis of parameter degradation. Sci. Rep. 2023, 13, 5739. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Wang, Y.; Wang, D.; Wang, L.; Zhang, S.; Li, C.; Teng, R. The creep behavior of rock shear seepage under different seepage-water pressures. Mech. Time-Depend. Mater. 2023, 27, 351–365. [Google Scholar] [CrossRef]
- Zhong, Z.X.; Sheng, J.L.; Hu, B.; Li, J.; Wang, Z.Q. Investigation of shear creep experiments and modelling of mudshale under dry-wet cycles of rainfall. Phys. Scr. 2024, 99, 025010. [Google Scholar] [CrossRef]
- Yao, W.; Hu, B.; Zhan, H.; Ma, C.; Zhao, N. A Novel Unsteady Fractal Derivative Creep Model for Soft Interlayers with Varying Water Contents. KSCE J. Civ. Eng. 2019, 23, 5064–5075. [Google Scholar] [CrossRef]
- Hu, B.; Wang, Z.; Li, J.; Wei, E.; Ma, L.; Liu, J.; Yu, X.B. A new shear creep damage model for rock masses after considering initial damage. PLoS ONE 2023, 18, e0280793. [Google Scholar] [CrossRef]
- Lai, Q.; Zhao, J.; Shi, B.; Liu, H.; Ji, L.; Li, Q.; Huang, R. Deformation evolution of landslides induced by coal mining in mountainous areas: Case study of the Madaling landslide, Guizhou, China. Landslides 2023, 20, 2003–2016. [Google Scholar] [CrossRef]
- Li, Z.; Li, W.; Xu, Q.; Lu, H.; Fu, P.; Guo, P.; Zhao, J.; Yu, C. Preliminary analysis of the catastrophic February 22nd 2023 Xinjing open-pit mine landslide, Inner Mongolia, China. Landslides 2024, 21, 1053–1067. [Google Scholar] [CrossRef]
- Dong, Q.; Sun, X.; Lei, N.Z.; Liu, B. Effect of Dry-Wet Cycling on the Degradation Characteristics and Mechanisms of Red Sandstone. Geofluids 2023, 2023, 9950331. [Google Scholar] [CrossRef]
- Tan, H.; Li, J.T.; Shi, Z.M.; Wang, M.X.; Wang, J.; Li, J. Damage evolution and failure characteristics of red sandstone with prefabricated crack under coupled dry-wet cycle-fatigue loading. Int. J. Fatigue 2023, 175, 107751. [Google Scholar] [CrossRef]
- Liu, X.; Li, Y.; Wang, W. Study on mechanical properties and energy characteristics of carbonaceous shale with different fissure angles under dry–wet cycles. Bull. Eng. Geol. Environ. 2022, 81, 319. [Google Scholar] [CrossRef]
- Liu, H.L.; Feng, X.H.; Liu, L.Y.; Li, T.J.; Tang, C.A. Mechanical properties and failure characteristics of anisotropic shale with circular hole under combined dynamic and static loading. Int. J. Rock. Mech. Min. 2023, 170, 105524. [Google Scholar] [CrossRef]
- Huang, J.; Chen, S.H.; Liu, M.L.; Li, K.P. Physical model test and numerical simulation study of cumulative damage to deep tunnel surrounding rock under cyclic blasting load. Int. J. Damage Mech. 2023, 32, 161–184. [Google Scholar] [CrossRef]
- Diethelm, K. The Analysis of Fractional Differential Equations—An Application-Oriented Exposition Using Differential Operators of Caputo Type; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Zhu, Q.Z. Multiscale Rock Damage Mechanics; Science Press: Beijing, China, 2019; ISBN 9787030606891. [Google Scholar]
- Lemaitre, J. How to use damage mechanics. Nucl. Eng. Des. 1984, 80, 233–245. [Google Scholar] [CrossRef]
- Zhang, Q.S.; Yang, G.S.; Ren, J.X. New study of damage variable and constitutive equation of rock. Chin. J. Rock Mech. Eng. 2003, 22, 30–34. [Google Scholar] [CrossRef]


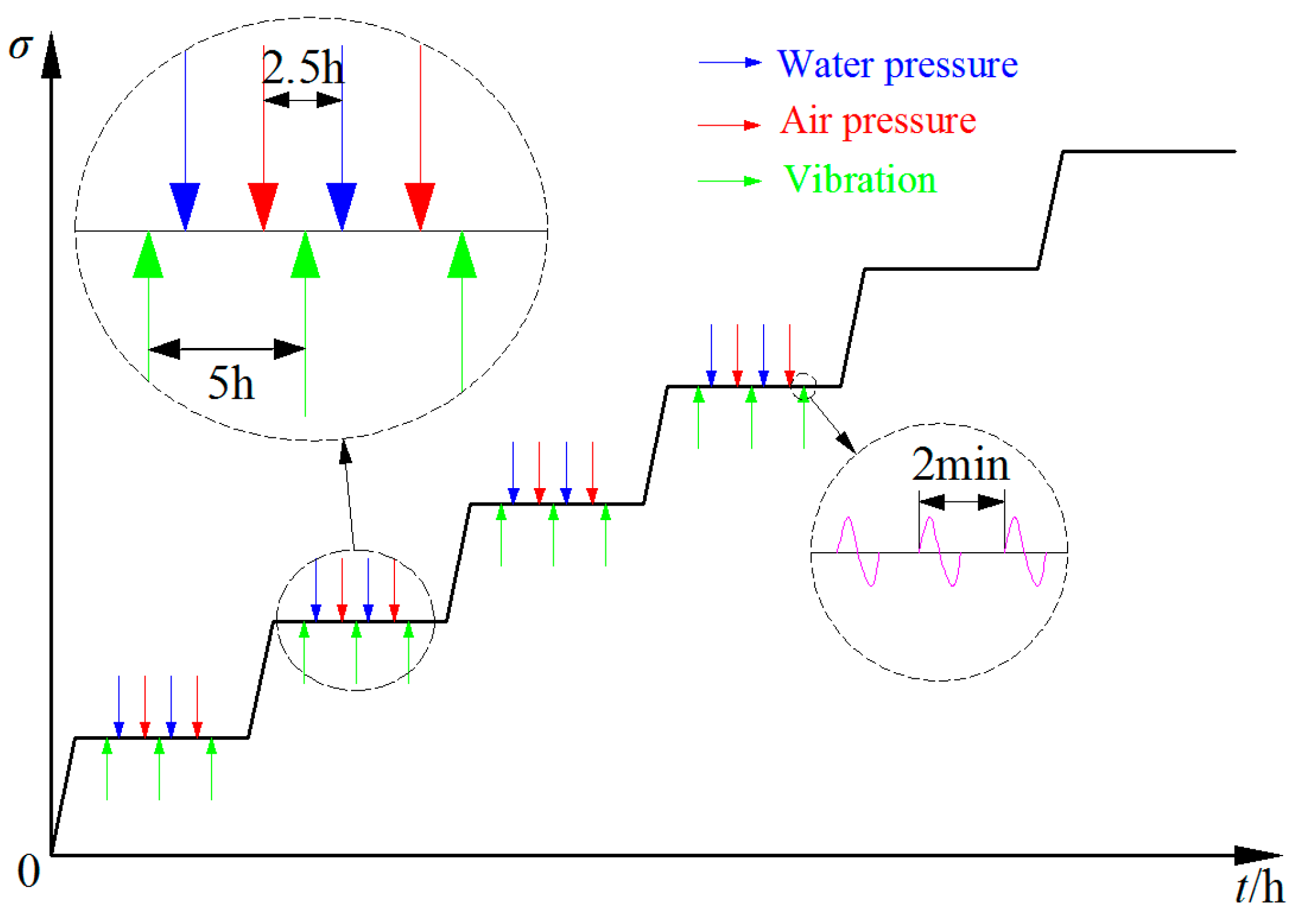
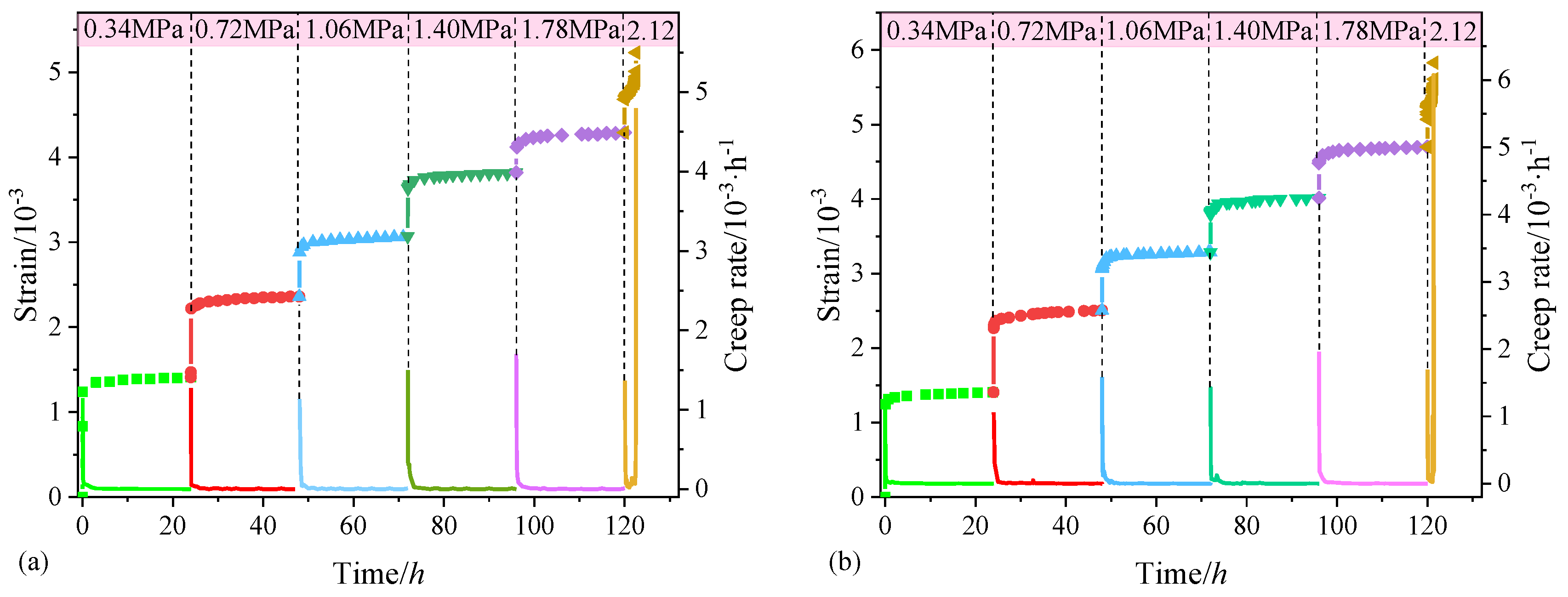


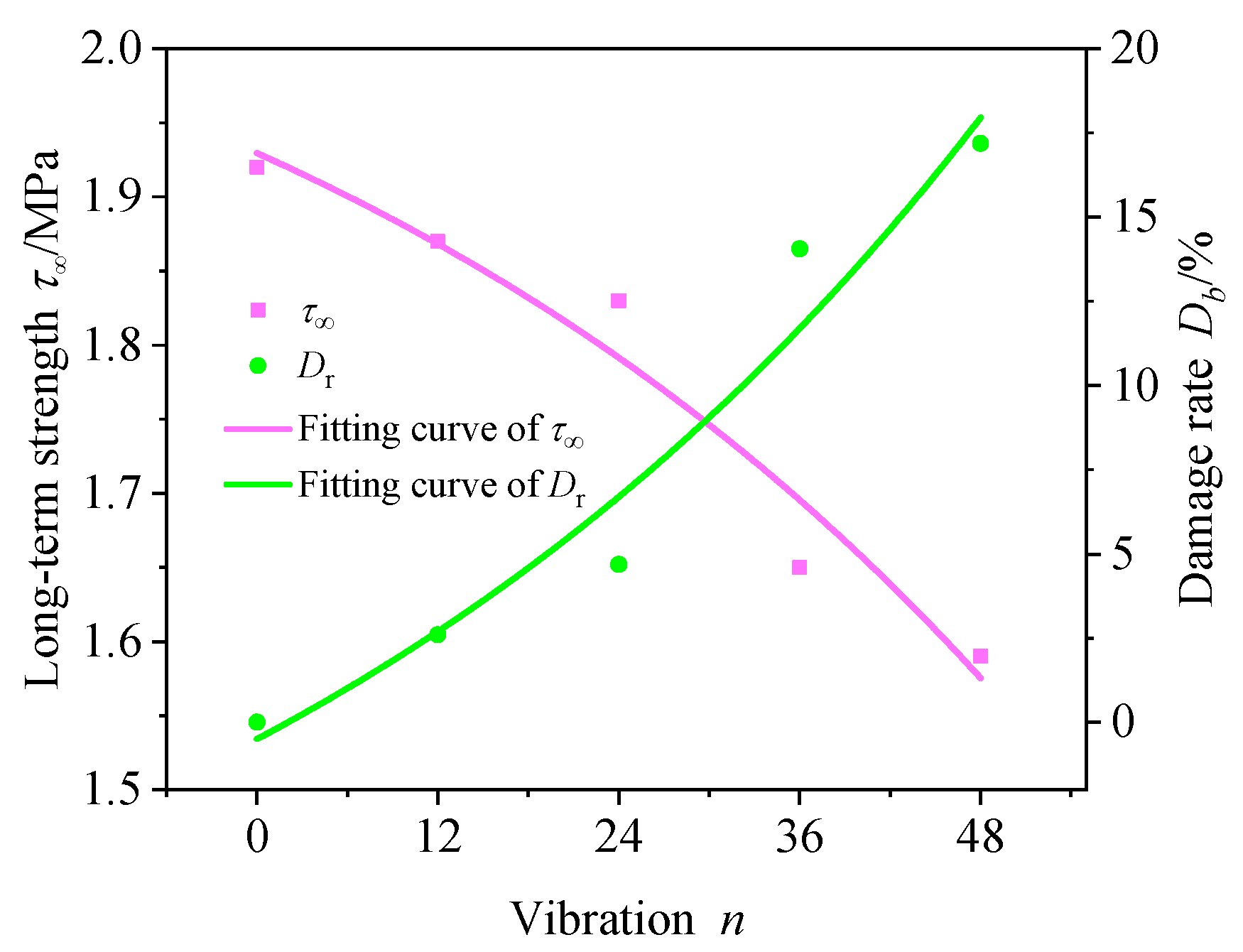
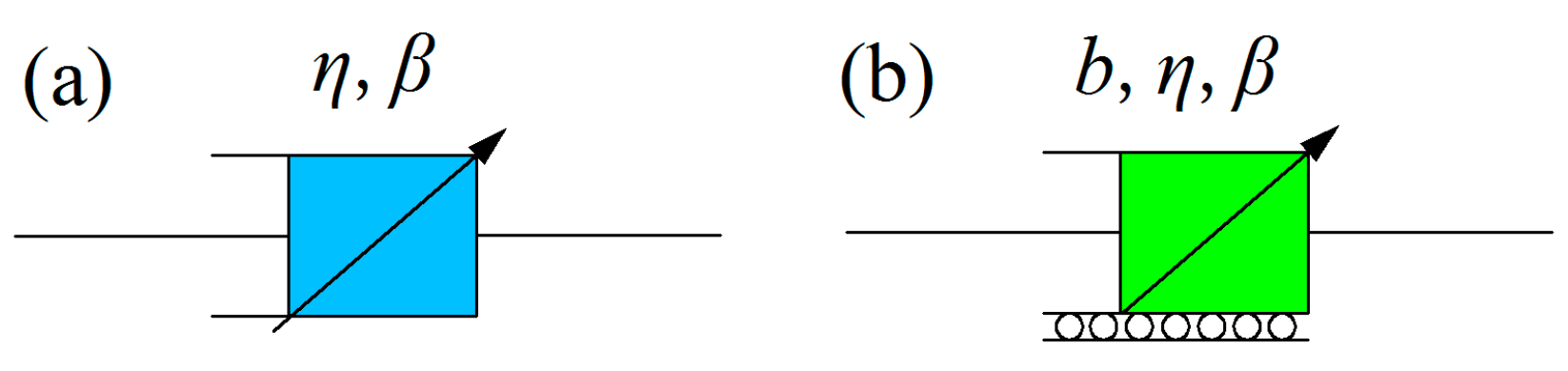
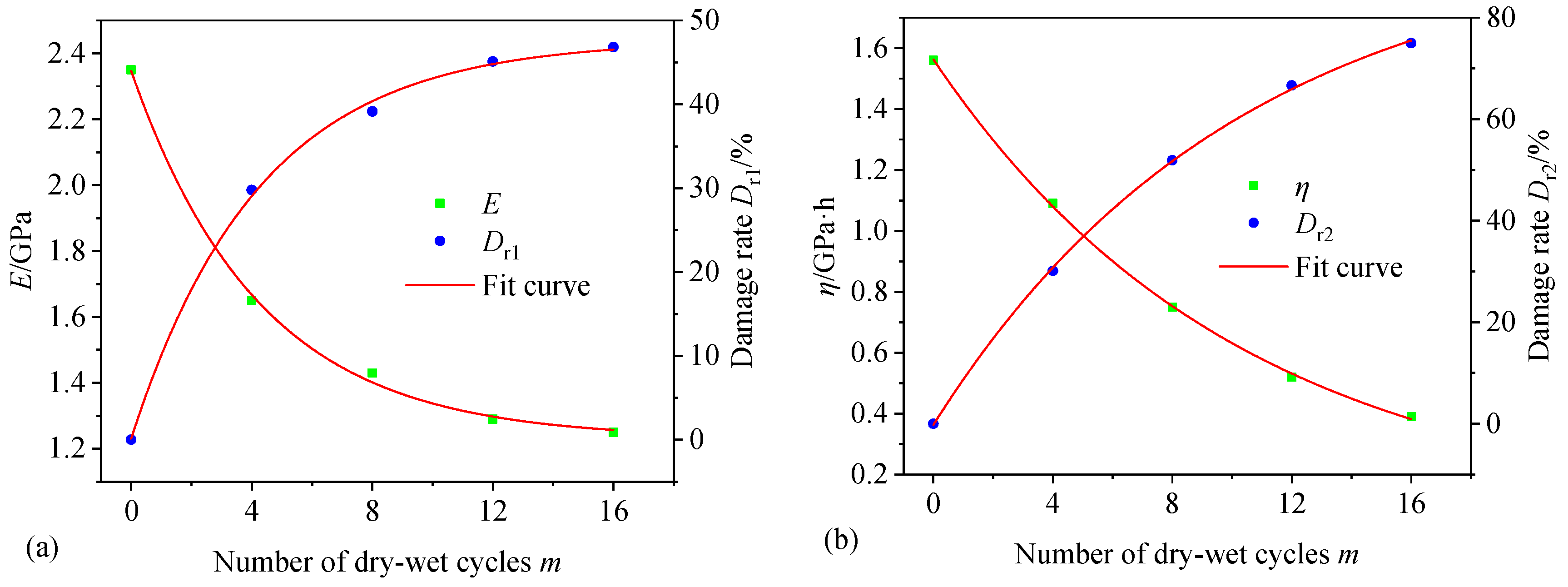

| Number of Dry–Wet Cycles m | E/GPa | η1/GPa·hβ |
|---|---|---|
| 0 | 2.35 | 1.56 |
| 4 | 1.65 | 1.09 |
| 8 | 1.43 | 0.75 |
| 12 | 1.29 | 0.52 |
| 16 | 1.25 | 0.39 |
| Number of Vibration n | E/GPa | η1/GPa·hβ |
|---|---|---|
| 0 | 2.35 | 1.56 |
| 12 | 1.55 | 1.18 |
| 24 | 1.36 | 0.94 |
| 36 | 1.07 | 0.81 |
| 48 | 1.01 | 0.76 |
| Number of Dry–Wet Cycles m | Number of Vibration n | E/GPa | η1/GPa·hβ |
|---|---|---|---|
| 0 | 0 | 2.35 | 1.56 |
| 8 | 0 | 1.43 | 0.75 |
| 0 | 24 | 1.36 | 0.94 |
| 8 | 24 | 0.84 | 0.45 |
| Shear Stress/MPa | E/GPa | η1/GPa·hβ | β1 | η2/GPa·hβ | b | β2 | R2 |
|---|---|---|---|---|---|---|---|
| 0.34 MPa | 0.36 | 0.611 | 0.222 | 0.936 | |||
| 0.72 MPa | 0.59 | 0.442 | 0.023 | 0.990 | |||
| 1.06 MPa | 0.94 | 0.264 | 0.015 | 0.986 | |||
| 1.40 MPa | 1.12 | 0.193 | 0.012 | 0.984 | |||
| 1.78 MPa | 0.84 | 0.452 | 0.020 | 5.32E6 | 7.13 | 0.5 | 0.993 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Hu, B.; Sheng, J.; Huang, L. A Fractional-Order Creep-Damage Model for Carbonaceous Shale Describing Coupled Damage Caused by Rainfall and Blasting. Fractal Fract. 2024, 8, 459. https://doi.org/10.3390/fractalfract8080459
Li J, Hu B, Sheng J, Huang L. A Fractional-Order Creep-Damage Model for Carbonaceous Shale Describing Coupled Damage Caused by Rainfall and Blasting. Fractal and Fractional. 2024; 8(8):459. https://doi.org/10.3390/fractalfract8080459
Chicago/Turabian StyleLi, Jing, Bin Hu, Jianlong Sheng, and Lei Huang. 2024. "A Fractional-Order Creep-Damage Model for Carbonaceous Shale Describing Coupled Damage Caused by Rainfall and Blasting" Fractal and Fractional 8, no. 8: 459. https://doi.org/10.3390/fractalfract8080459
APA StyleLi, J., Hu, B., Sheng, J., & Huang, L. (2024). A Fractional-Order Creep-Damage Model for Carbonaceous Shale Describing Coupled Damage Caused by Rainfall and Blasting. Fractal and Fractional, 8(8), 459. https://doi.org/10.3390/fractalfract8080459






