Voltage Controller Design for Offshore Wind Turbines: A Machine Learning-Based Fractional-Order Model Predictive Method
Abstract
:1. Introduction
- A hybrid PI-FOMPC random forest AC bus voltage controller for OWT.
- Focus on addressing OWT challenges, ensuring smooth voltage tracking and state estimation.
- Comparative analyses regarding other intelligent models.
- Superior performance demonstrated across key metrics: mean absolute error (MAE), mean absolute percentage error (MAPE), root mean squared error (RMSE), root mean squared percentage error (RMSPE), and R2.
- The integration of FO modeling, predictive control, and random forest algorithms for precise voltage control.
2. Relevant Principles
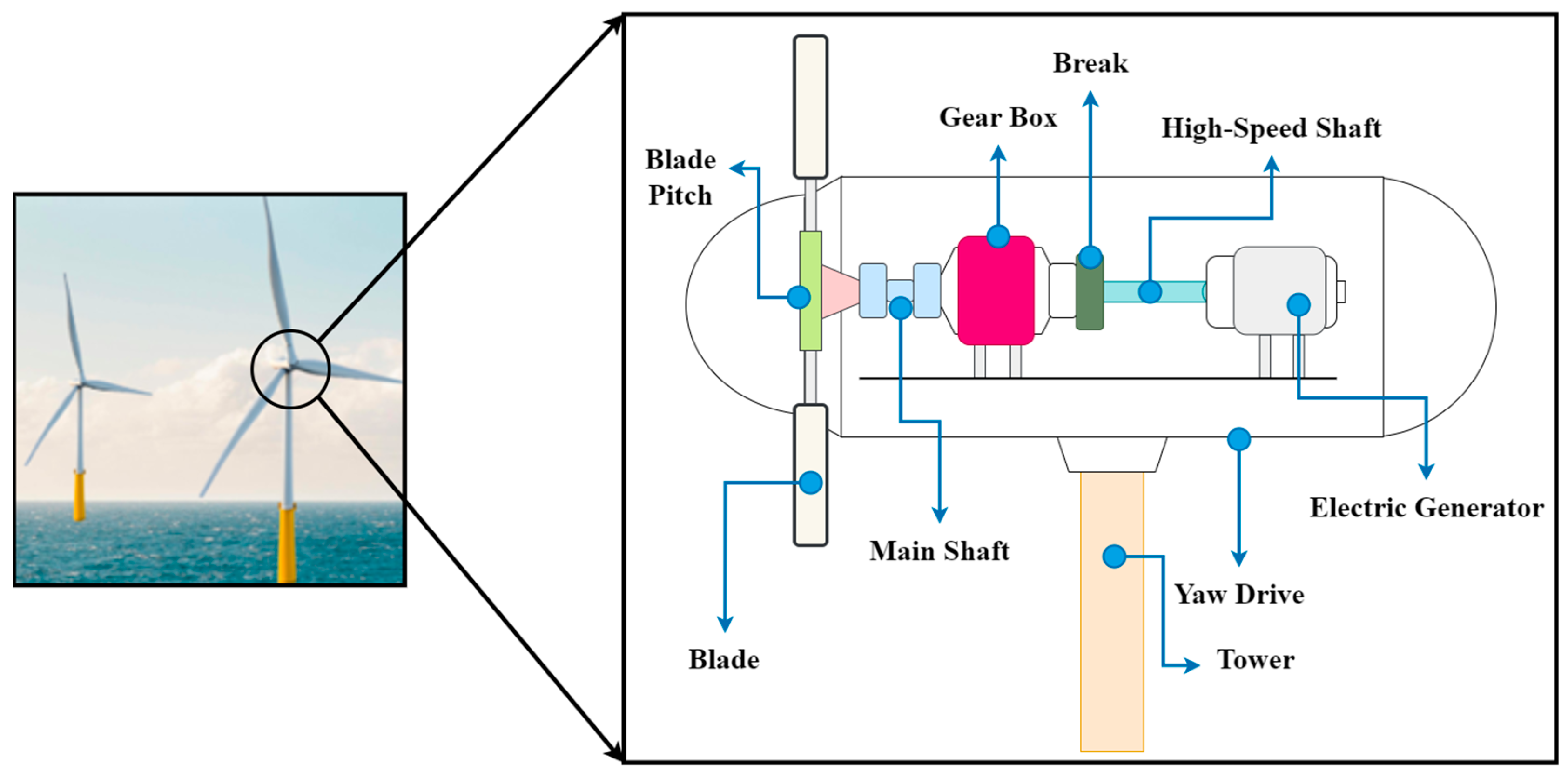
2.1. Offshore Wind Turbines
2.2. Modular Multilevel Converter (MMC)
3. Applied Control Concepts and Strategies
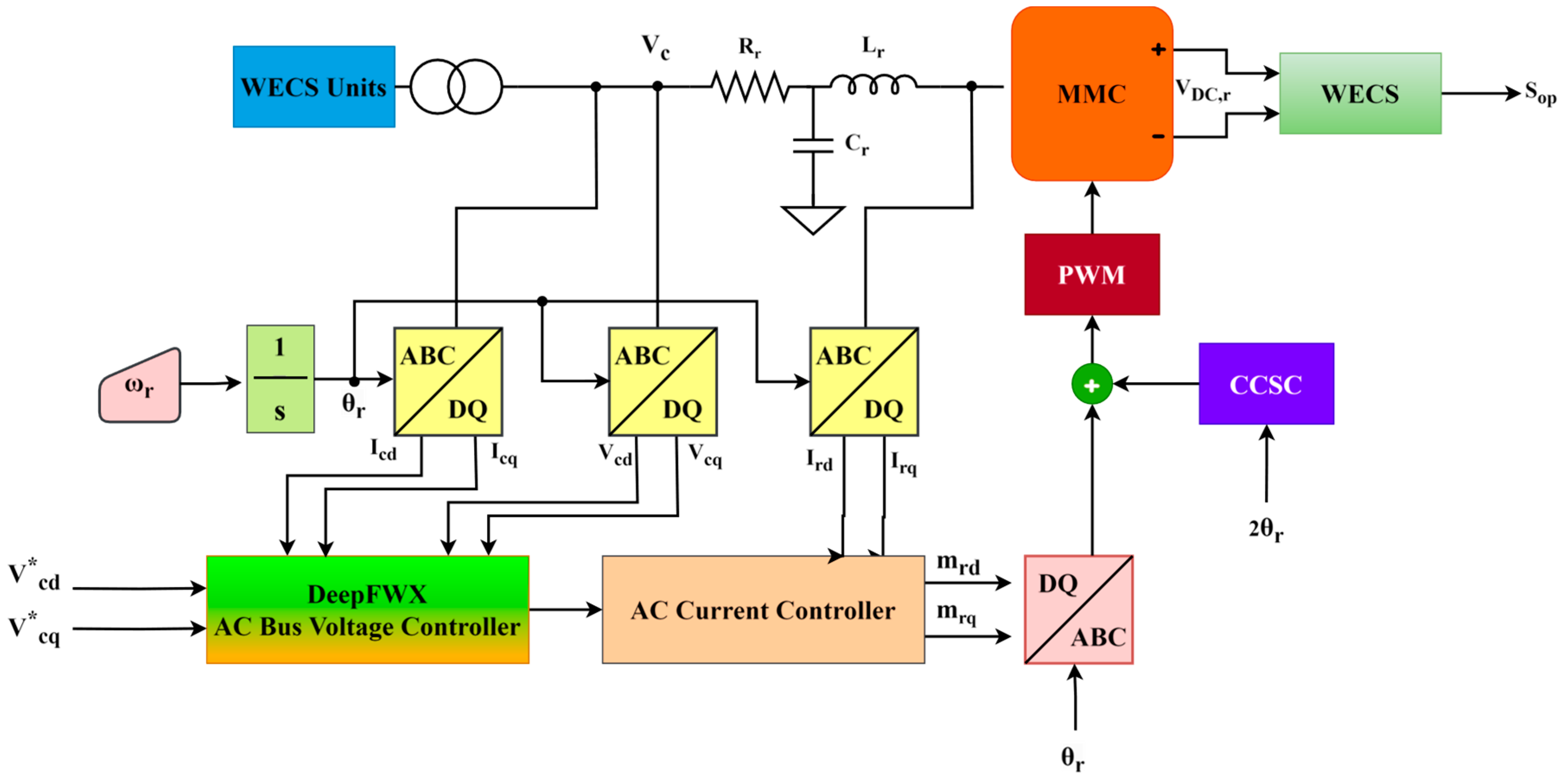
Overall Control Scheme
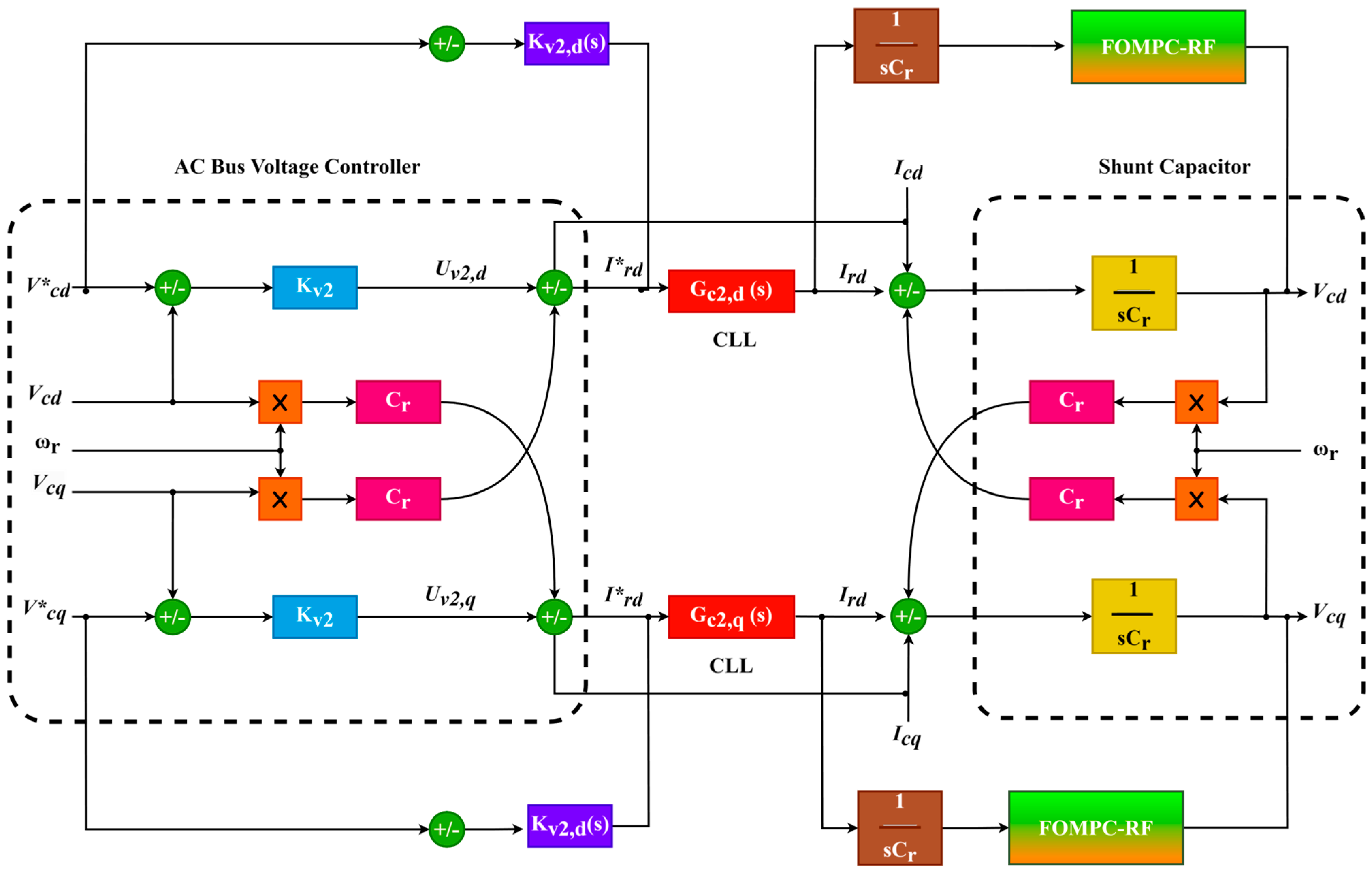
4. DeepFWX: FO Model Predictive Random Forest Controller
- The implementation of a model predictive controller;
- Tuning the MPC with fractional-order concepts;
- Applying FOMPC on the system for controlling purposes;
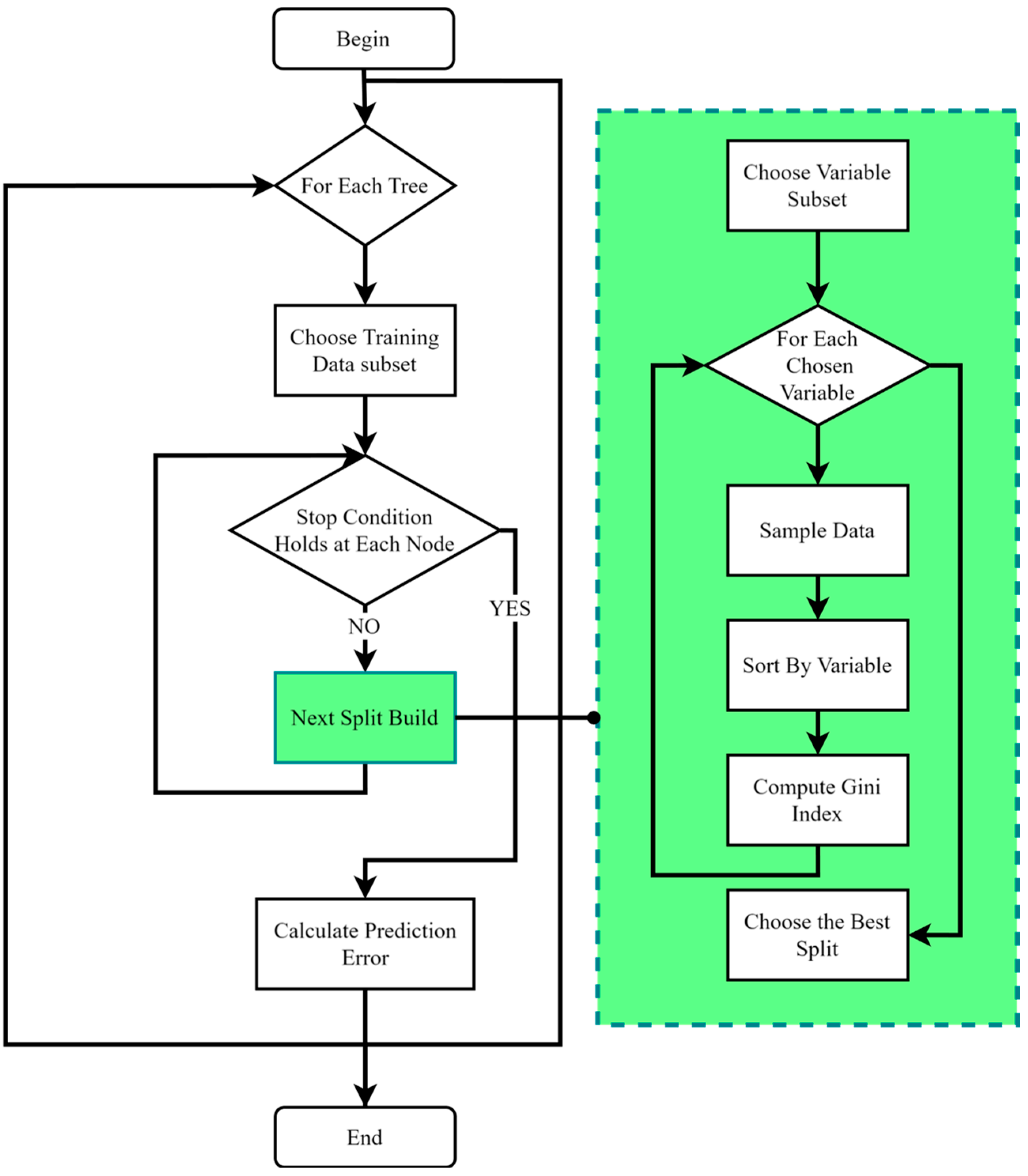
- Estimating FOMPC-applied system’s states using the machine learning algorithm of random forest.
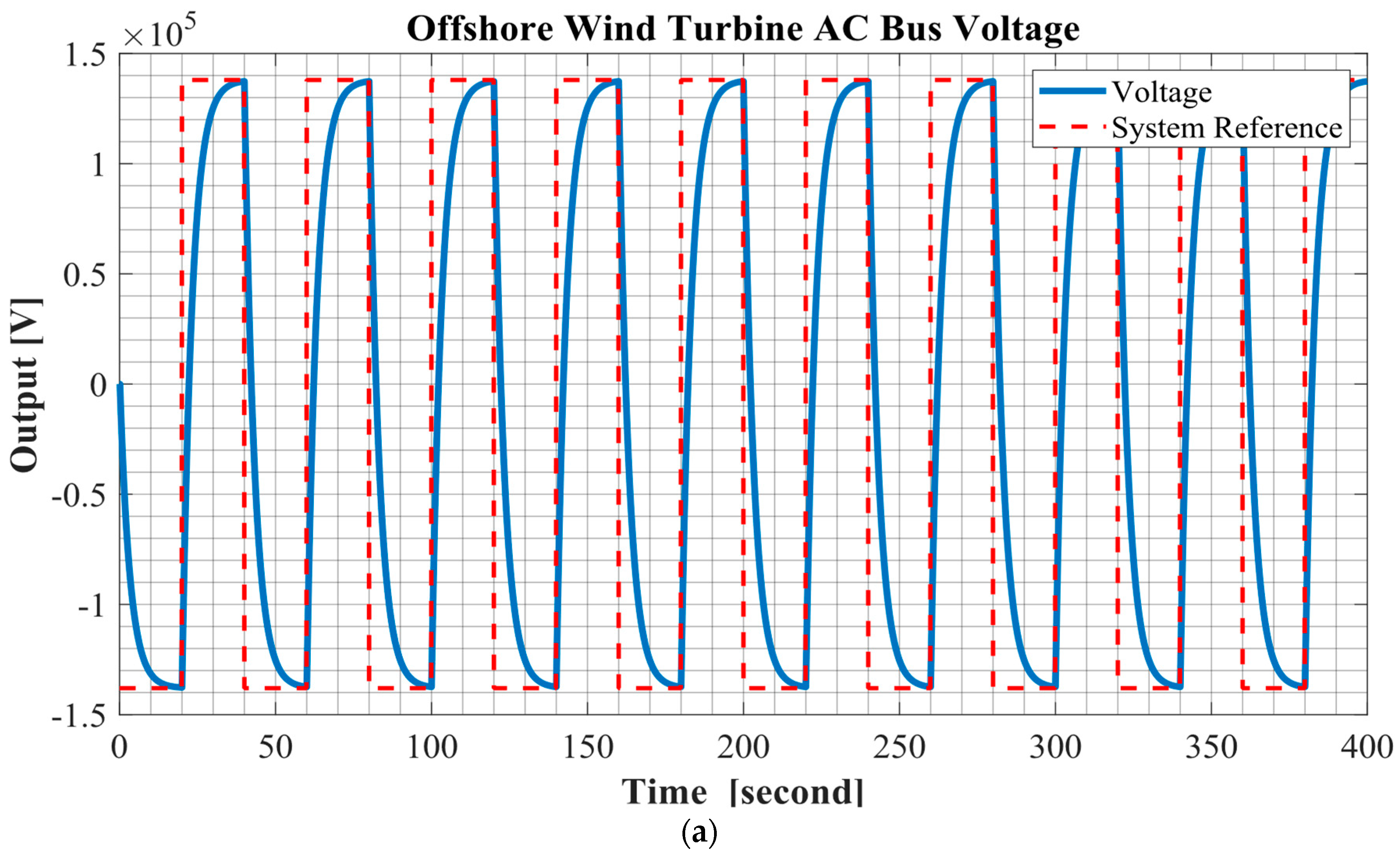
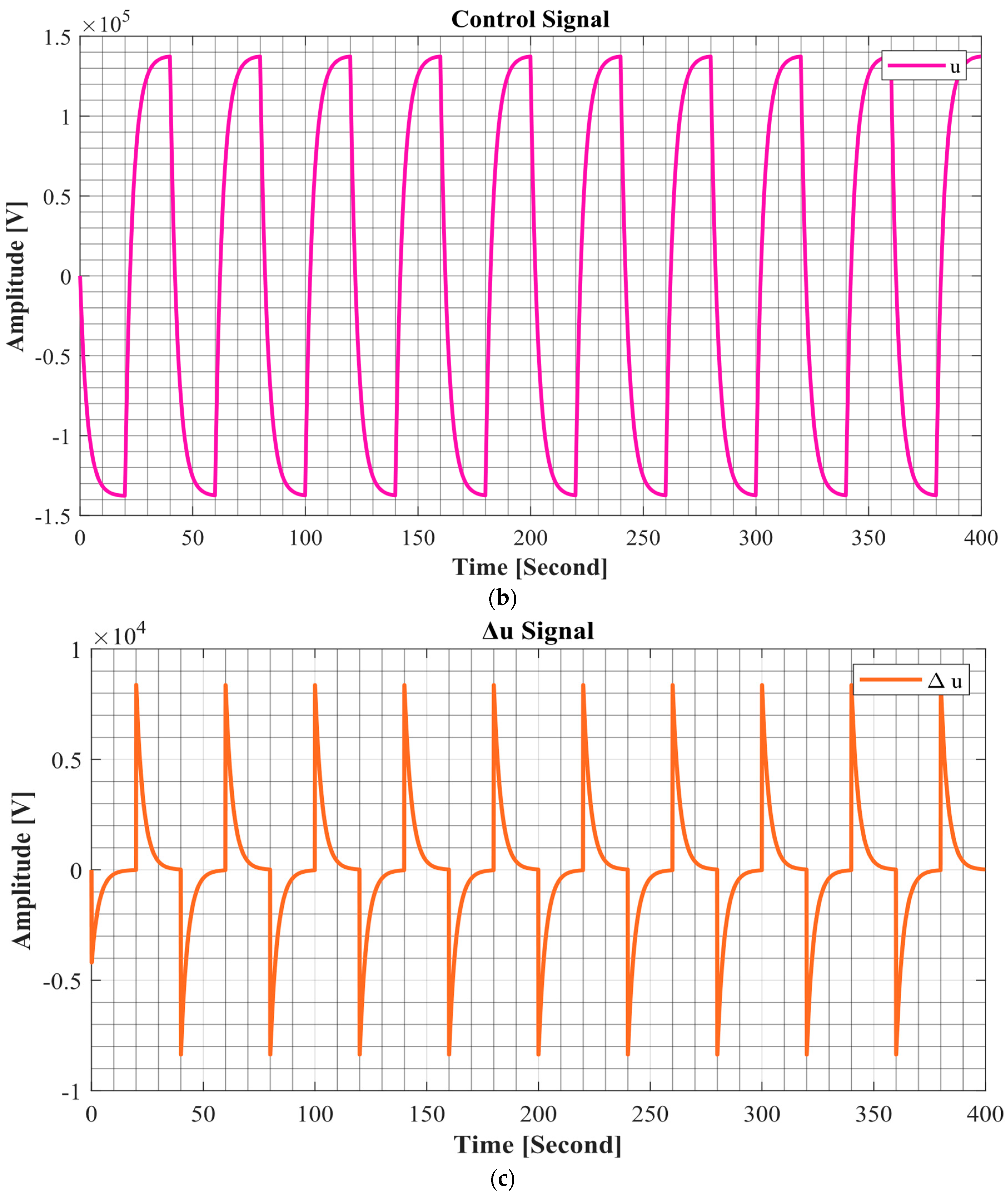
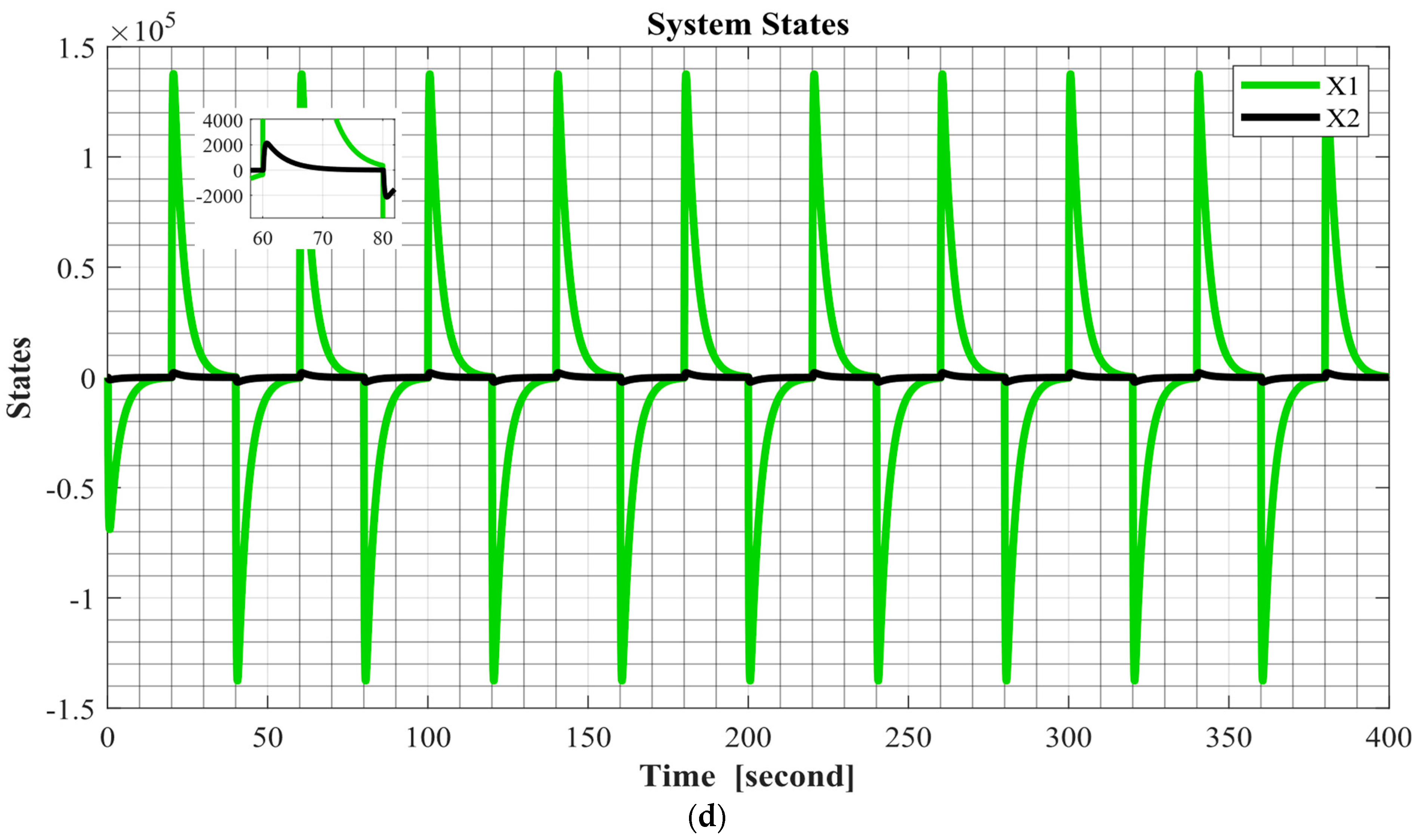
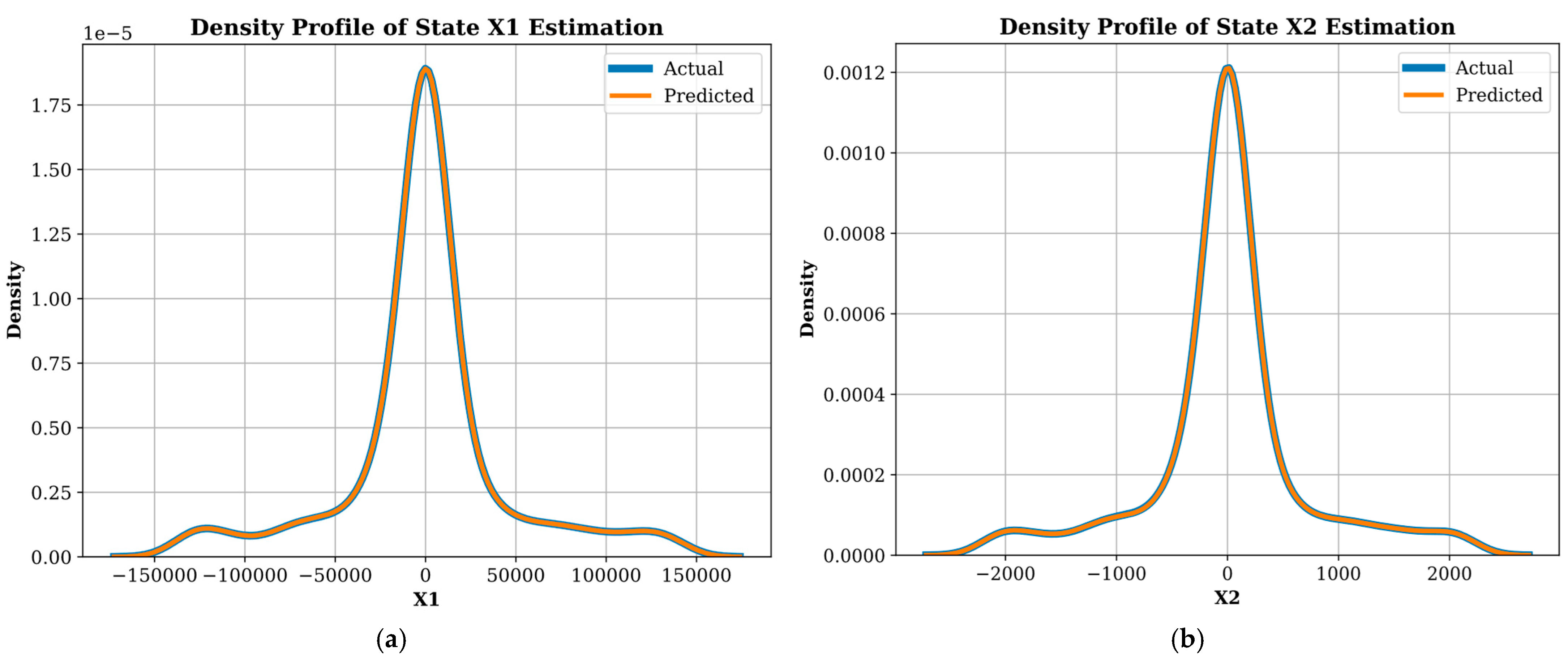
5. Simulations and Results
6. Challenges and Future Perspectives
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
References
- Alilou, M.; Azami, H.; Oshnoei, A.; Mohammadi-Ivatloo, B.; Teodorescu, R. Fractional-Order Control Techniques for Renewable Energy and Energy-Storage-Integrated Power Systems: A Review. Fractal Fract. 2023, 7, 391. [Google Scholar] [CrossRef]
- Zaid, S.A.; Bakeer, A.; Magdy, G.; Albalawi, H.; Kassem, A.M.; El-Shimy, M.E.; AbdelMeguid, H.; Manqarah, B. A New Intelligent Fractional-Order Load Frequency Control for Interconnected Modern Power Systems with Virtual Inertia Control. Fractal Fract. 2023, 7, 62. [Google Scholar] [CrossRef]
- Gulzar, M.M.; Gardezi, S.; Sibtain, D.; Khalid, M. Discrete-Time Modeling and Control for LFC Based on Fuzzy Tuned Fractional-Order PDμ Controller in a Sustainable Hybrid Power System. IEEE Access 2023, 11, 63271–63287. [Google Scholar] [CrossRef]
- El-Sousy, F.F.M.; Alqahtani, M.H.; Aljumah, A.S.; Aly, M.; Almutairi, S.Z.; Mohamed, E.A. Design Optimization of Improved Fractional-Order Cascaded Frequency Controllers for Electric Vehicles and Electrical Power Grids Utilizing Renewable Energy Sources. Fractal Fract. 2023, 7, 603. [Google Scholar] [CrossRef]
- Perumal, V.; Kannan, S.K.; Balamurugan, C.R. Grid Mode Selection Scheme based on a Novel Fractional Order Proportional Resonant Controller for Hybrid Renewable Energy Resources. Electr. Power Compon. Syst. 2023, 51, 1710–1729. [Google Scholar] [CrossRef]
- Singh, K.; Saroha, S.; Verma, A.; Prabhakar, P.; Kumar, K.; Madan, C. An Optimal Parameterized Fractional-Order PID Controller for the Single Phase Grid Integrated with Solar and Wind System. Cybern. Syst. 2023, 54, 1086–1110. [Google Scholar] [CrossRef]
- Guha, D.; Roy, P.K.; Banerjee, S. Adaptive fractional-order sliding-mode disturbance observer-based robust theoretical frequency controller applied to hybrid wind–diesel power system. ISA Trans. 2023, 133, 160–183. [Google Scholar] [CrossRef] [PubMed]
- Benbouhenni, H.; Hamza, G.; Oproescu, M.; Bizon, N.; Thounthong, P.; Colak, I. Application of fractional-order synergetic-proportional integral controller based on PSO algorithm to improve the output power of the wind turbine power system. Sci. Rep. 2024, 14, 609. [Google Scholar] [CrossRef]
- Mseddi, A.; Wali, K.; Abid, A.; Naifar, O.; Rhaima, M.; Mchiri, L. Advanced modeling and control of wind conversion systems based on hybrid generators using fractional order controllers. Asian J. Control 2024, 26, 1103–1119. [Google Scholar] [CrossRef]
- Benbouhenni, H.; Mosaad, M.I.; Colak, I.; Bizon, N.; Gasmi, H.; Aljohani, M.; Abdelkarim, E. Fractional-Order Synergetic Control of the Asynchronous Generator-Based Variable-Speed Multi-Rotor Wind Power Systems. IEEE Access 2023, 11, 133490–133508. [Google Scholar] [CrossRef]
- Benbouhenni, H.; Bizon, N.; Mosaad, M.I.; Colak, I.; Djilali, A.B.; Gasmi, H. Enhancement of the power quality of DFIG-based dual-rotor wind turbine systems using fractional order fuzzy controller. Expert Syst. Appl. 2024, 238, 121695. [Google Scholar] [CrossRef]
- Narayanan, G.; Ali, M.S.; Joo, Y.H.; Perumal, R.; Ahmad, B.; Alsulami, H. Robust Adaptive Fractional Sliding-Mode Controller Design for Mittag-Leffler Synchronization of Fractional-Order PMSG-Based Wind Turbine System. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 7646–7655. [Google Scholar] [CrossRef]
- Benbouhenni, H.; Colak, I.; Bizon, N.; Abdelkarim, E. Fractional-order neural control of a DFIG supplied by a two-level PWM inverter for dual-rotor wind turbine system. Meas. Control 2023, 57, 301–318. [Google Scholar] [CrossRef]
- Dong, Y.; Wang, J.; Ding, S.; Li, W. Adaptive fractional-order fault-tolerant sliding mode control scheme of DFIG wind energy conversion system. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2022, 237, 15–25. [Google Scholar] [CrossRef]
- Amiri, F.; Eskandari, M.; Moradi, M.H. Improved Load Frequency Control in Power Systems Hosting Wind Turbines by an Augmented Fractional Order PID Controller Optimized by the Powerful Owl Search Algorithm. Algorithms 2023, 16, 539. [Google Scholar] [CrossRef]
- Mohamed, N.A.; Hasanien, H.M.; Alkuhayli, A.; Akmaral, T.; Jurado, F.; Badr, A.O. Hybrid Particle Swarm and Gravitational Search Algorithm-Based Optimal Fractional Order PID Control Scheme for Performance Enhancement of Offshore Wind Farms. Sustainability 2023, 15, 11912. [Google Scholar] [CrossRef]
- Gasmi, H.; Benbouhenni, H.; Mendaci, S.; Colak, I. A new scheme of the fractional-order super twisting algorithm for asynchronous generator-based wind turbine. Energy Rep. 2023, 9, 6311–6327. [Google Scholar] [CrossRef]
- Labed, N.; Attoui, I.; Makhloufi, S.; Bouraiou, A.; Bouakkaz, M.S. PSO Based Fractional Order PI Controller and ANFIS Algorithm for Wind Turbine System Control and Diagnosis. J. Electr. Eng. Technol. 2023, 18, 2457–2468. [Google Scholar] [CrossRef]
- Delavari, H.; Sharifi, A. Adaptive reinforcement learning interval type II fuzzy fractional nonlinear observer and controller for a fuzzy model of a wind turbine. Eng. Appl. Artif. Intell. 2023, 123, 106356. [Google Scholar] [CrossRef]
- Kasbi, A.; Rahali, A. MPPT Performance and Power Quality Improvement by Using Fractional-Order Adaptive Backstepping Control of a DFIG-Based Wind Turbine with Disturbance and Uncertain Parameters. Arab. J. Sci. Eng. 2023, 48, 6595–6614. [Google Scholar] [CrossRef]
- Wang, Z.; Yin, W.; Liu, L.; Wang, Y.; Zhang, C.; Rui, X. Fractional-order Sliding Mode Control of Hybrid Drive Wind Turbine for Improving Low-voltage Ride-through Capacity. J. Mod. Power Syst. Clean Energy 2023, 11, 1427–1436. [Google Scholar] [CrossRef]
- Garkki, B.; Revathi, S. Direct speed fractional order controller for maximum power tracking on DFIG-based wind turbines during symmetrical voltage dips. Int. J. Dyn. Control 2023, 12, 211–226. [Google Scholar] [CrossRef]
- Zhang, Z.; Kou, P.; Zhang, Y.; Liang, D. Distributed model predictive control of all-dc offshore wind farm for short-term frequency support. IET Renew. Power Gener. 2023, 17, 458–479. [Google Scholar] [CrossRef]
- Jiang, P.; Zhang, T.; Geng, J.; Wang, P.; Fu, L. An MPPT Strategy for Wind Turbines Combining Feedback Linearization and Model Predictive Control. Energies 2023, 16, 4244. [Google Scholar] [CrossRef]
- Tang, M.; Wang, W.; Yan, Y.; Zhang, Y.; An, B. Robust model predictive control of wind turbines based on Bayesian parameter self-optimization. Front. Energy Res. 2023, 11, 1306167. [Google Scholar] [CrossRef]
- Jard, T.; Snaiki, R. Real-Time Repositioning of Floating Wind Turbines Using Model Predictive Control for Position and Power Regulation. Wind 2023, 3, 131–150. [Google Scholar] [CrossRef]
- Tian, D.; Tang, S.; Tao, L.; Li, B.; Wu, X. Peak shaving strategy for load reduction of wind turbines based on model predictive control. Energy Rep. 2023, 9, 338–349. [Google Scholar] [CrossRef]
- Ma, X.; Yu, J.; Yang, P.; Wang, P.; Zhang, P. An MPC based active and reactive power coordinated control strategy of PMSG wind turbines to enhance the support capability. Front. Energy Res. 2023, 11, 1159946. [Google Scholar] [CrossRef]
- Hu, Z.; Su, R.; Ling, K.-V.; Guo, Y.; Ma, R. Resilient Event-Triggered MPC for Load Frequency Regulation with Wind Turbines Under False Data Injection Attacks. IEEE Trans. Autom. Sci. Eng. 2023, 1–11. [Google Scholar] [CrossRef]
- Achar, A.; Djeriri, Y.; Benbouhenni, H.; Colak, I.; Oproescu, M.; Bizon, N. Self-filtering based on the fault ride-through technique using a robust model predictive control for wind turbine rotor current. Sci. Rep. 2024, 14, 1905. [Google Scholar] [CrossRef]
- Paulo, M.S.; Almeida, A.d.O.; de Almeida, P.M.; Barbosa, P.G. Control of an Offshore Wind Farm Considering Grid-Connected and Stand-Alone Operation of a High-Voltage Direct Current Transmission System Based on Multilevel Modular Converters. Energies 2023, 16, 5891. [Google Scholar] [CrossRef]
- Yaghini, H.H.; Kharrati, H.; Rahimi, A. Linear time-varying fractional-order model predictive attitude control for satellite using two reaction wheels. Aerosp. Sci. Technol. 2024, 145, 108901. [Google Scholar] [CrossRef]
- Oldham, K.; Spanier, J. The Fractional Calculus Theory and Applications of Differentiation and Integration to Arbitrary Order; Elsevier: Amsterdam, The Netherlands, 1974. [Google Scholar]
- Safari, A.; Sorouri, H.; Oshnoei, A. The Regulation of Superconducting Magnetic Energy Storages with a Neural-Tuned Fractional Order PID Controller Based on Brain Emotional Learning. Fractal Fract. 2024, 8, 365. [Google Scholar] [CrossRef]
- Safari, A.; Gharehbagh, H.K.; Nazari-Heris, M.; Oshnoei, A. DeepResTrade: A peer-to-peer LSTM-decision tree-based price prediction and blockchain-enhanced trading system for renewable energy decentralized markets. Front. Energy Res. 2023, 11, 1275686. [Google Scholar] [CrossRef]
- Safari, A.; Kharrati, H.; Rahimi, A. Multi-Term Electrical Load Forecasting of Smart Cities Using a New Hybrid Highly Accurate Neural Network-Based Predictive Model. Smart Grids Sustain. Energy 2023, 9, 8. [Google Scholar] [CrossRef]
- Safari, A.; Gharehbagh, H.K.; Heris, M.N. DeepVELOX: INVELOX Wind Turbine Intelligent Power Forecasting Using Hybrid GWO–GBR Algorithm. Energies 2023, 16, 6889. [Google Scholar] [CrossRef]
- Sadeghian, O.; Safari, A. Net saving improvement of capacitor banks in power distribution systems by increasing daily size switching number: A comparative result analysis by artificial intelligence. J. Eng. 2024, 2024, e12357. [Google Scholar] [CrossRef]
- Safari, A.; Ghavifekr, A.A. Use case of artificial intelligence and neural networks in energy consumption markets and industrial demand response. In Industrial Demand Response: Methods, Best Practices, Case Studies, and Applications; IET Digital Library: Stevenage, UK, 2022; Volume 4, p. 379. [Google Scholar]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T. Lightgbm: A highly efficient gradient boosting decision tree. In Advances in Neural Information Processing Systems; NIPS: Denver, CO, USA, 2017; Volume 30. [Google Scholar]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar]
- Mcculloch, W.S.; Pitts, W.H. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Hopfield, J.J. Neural networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci. USA 1982, 79, 2554–2558. [Google Scholar] [CrossRef] [PubMed]
- Fahim, P.; Vaezi, N.; Shahraki, A.; Khoshnevisan, M. An Integration of Genetic Feature Selector, Histogram-Based Outlier Score, and Deep Learning for Wind Turbine Power Prediction. Energy Sources Part A Recover. Util. Environ. Eff. 2022, 44, 9342–9365. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, B.; Xu, W. Multi-factor offshore short-term wind power prediction based on XGBoost. In Proceedings of the 2023 35th Chinese Control and Decision Conference (CCDC), Yichang, China, 20–22 May 2023. [Google Scholar]
- Quevedo-Reina, R.; Álamo, G.M.; Padrón, L.A.; Aznárez, J.J. Surrogate model based on ANN for the evaluation of the fundamental frequency of offshore wind turbines supported on jackets. Comput. Struct. 2023, 274, 106917. [Google Scholar] [CrossRef]
- Wei, C.-C.; Chiang, C.-S. Assessment of Offshore Wind Power Potential and Wind Energy Prediction Using Recurrent Neural Networks. J. Mar. Sci. Eng. 2024, 12, 283. [Google Scholar] [CrossRef]


| Control Methodology | Plants | Advantages | Disadvantages | Ref. |
|---|---|---|---|---|
| FO-IC | Power systems with RES | Improved precision and resilience in energy systems; handle dynamics effectively. | May be complex to implement and tune. | [2] |
| FO-PD | Hybrid system load frequency including RES | Enhanced load frequency control; can handle hybrid energy sources effectively. | Complexity in controller design and tuning. | [3] |
| FO | Electrical power infrastructures with RES | Designed specifically for RES; improves stability and performance. | Requires careful parameter tuning. | [4] |
| FO-PRC | Grid connection supply in hybrid RES | Improves stabilization speed and performance even with fluctuating power supply. | May not be suitable for all types of power fluctuations. | [5] |
| FO-PID | RES | Continuous power supply regulation; adaptable to different renewable sources. | Complexity in parameterization and maintenance. | [6] |
| AFO-SMC | Wind/diesel power systems | Enhanced disturbance rejection and robustness. | May be complex and computationally intensive. | [7] |
| FO-PID-PSO | Wind turbine power control | Optimizes control performance with particle swarm optimization (PSO); effective for wind turbine systems. | PSO might be computationally demanding. | [8] |
| FO | Wind conversion systems | Effective in regulating hybrid generator systems. | Integration complexity with hybrid generators. | [9] |
| FO | Multi-rotor wind power systems | Eliminates chattering problems in asynchronous generator-based variable speed systems. | Complexity in combining FO and traditional control theories. | [10] |
| FO-Fuzzy | Multi-rotor wind energy systems | Enhances control precision and robustness through fuzzy logic. | May be complex to design and tune fuzzy rules. | [11] |
| FO-Fractional SMC | Wind turbine systems with PMSG | Superior tracking precision, rapid response speed, and robustness. | Potential complexity in adaptive control design. | [12] |
| NN-FO | Dual-rotor wind turbine systems with varying speeds | Enhances the optimization of reactive/active power; integrates neural networks for improved control. | May require significant computational resources for neural network training. | [13] |
| Adaptive FO-SMC | Wind energy conversion system with induction generators | Achieves maximum power point tracking; fault-tolerant management. | Complex fault-tolerant design and integration. | [14] |
| FO-PID | Power networks with wind turbines | Effective for load frequency regulation; hybrid PSO and gravitational search methods enhance optimization. | Complexity in combining multiple optimization techniques. | [15] |
| FO-PID-PSO | Voltage source converters for OWTs | Optimizes operation and enhances the performance of converters. | Requires complex algorithm integration and parameter tuning. | [16] |
| FO-SMC-STA | Wind power system with an asynchronous generator | Improves performance and effectiveness in controlling wind power systems. | Complexity in integrating FO control with STA. | [17] |
| FO-PI-PSO | Wind turbine systems | Enhances stability even under faulty conditions through PSO integration. | Implementation complexity with fault tolerance. | [18] |
| Adaptive RL-FO | Wind turbines with DFIG | Accurate fault and disturbance estimation; handle uncertainty with adaptive observers. | Complexity in reinforcement learning and adaptive observer design. | [19] |
| FO Adaptive Back-Stepping Control | Generator-based wind turbines | Enhances maximum power point tracking performance by adjusting for disturbances. | Potential complexity in back-stepping design. | [20] |
| FO-SMC | Hybrid drive wind turbines | Improves performance during transient operations. | Implementation complexity and need for precise tuning. | [21] |
| FO-PI | WECS | Maintains low-voltage ride-through capabilities; enhances the efficiency of power extraction. | Potential complexity in maintaining ride-through capabilities. | [22] |
| MPC | DC-operated OWFs | Analyze frequency response; improve system performance. | Distributed control might be complex to implement and coordinate. | [23] |
| Feedback Linearization MPC | Generator-based WECS | Achieves maximum power point tracking by minimizing non-linearity. | May increase the computational load and complexity of the system. | [24] |
| Parameter-Adaptive | Wind power generation systems | Use Bayesian optimization for the self-optimization of controller parameters; handle wind speed variations. | Complexity in parameter adaptation and robustness. | [25] |
| MPC | Floating offshore wind turbines | Manag power, reposition floating turbines, and preserve structural stability. | Complexity in floating system control and stability management. | [26] |
| MPC | Wind turbine peak shaving | Enhances the regulation of peak power generation. | May require advanced MPC techniques and tuning. | [27] |
| MPC | Wind turbines with PMSG | Enhances grid reliability; manages active/reactive power effectively. | Coordination among multiple turbines and PMSGs can be complex. | [28] |
| Protector | Power systems with wind turbines | Increases RES generation and addresses issues related to fake data injection attacks. | Integration complexity and potential cybersecurity concerns. | [29] |
| Finite Space MPC | Interaction between wind farms and electric grid | Improves output from DFIG and considers fault ride-through technique. | Finite space MPC implementation can be complex and computationally demanding. | [30] |
| u [kV] | Δu | X1 [kV] | X2 [kV] | |
|---|---|---|---|---|
| Mean | −1.0631 | 343.55 | −1.0937 | 662.6547 |
| Variance | 12,964.39 | 5.6252 | 1300 | 1990 |
| Total Count | 4000 | |||
| Metric | X1 | X2 |
|---|---|---|
| MAE | 15.03 | 0.5797 |
| MAPE | 0.09% | 0.001374 |
| RMSE | 70.39 | 5.6371 |
| RMSPE | 0.34% | 0.008548 |
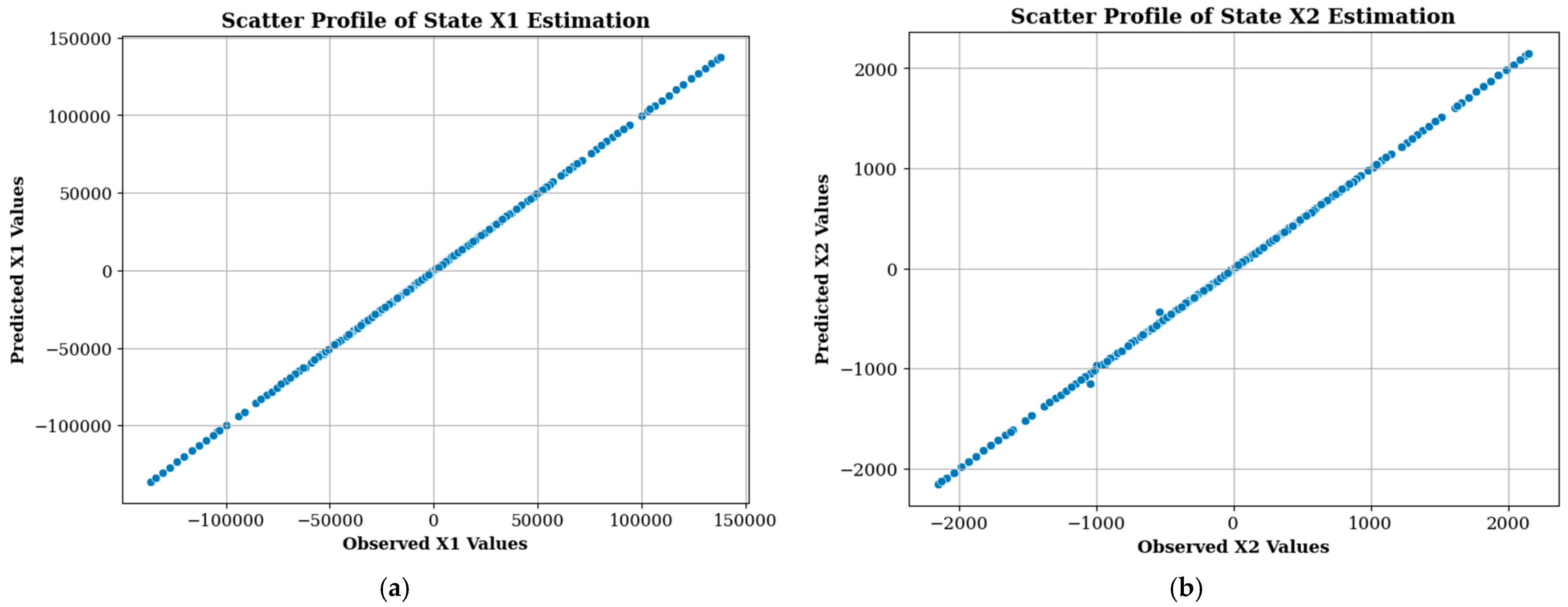
| R2 | 0.999998 | 0.999938 |
| X1 | |||||
| Metrics | DeepFWX | LGBM [44] | XGBoost [45] | ANN [46] | RNN [47] |
| MAE | 15.03 | 389.74 | 75.27 | 2508.2 | 4634.95 |
| MAPE | 0.09 | 33.19 | 0.95 | 170.04 | 244.81 |
| RMSPE | 0.34 | 236.85 | 1.82 | 2149.06 | 2296.38 |
| RMSE | 70.39 | 1493.54 | 195.03 | 9792.44 | 10,999.68 |
| R2 | 0.999998 | 0.998949 | 0.999982 | 0.954806 | 0.942976 |
| X2 | |||||
| Metrics | DeepFWX | LGBM [44] | XGBoost [45] | ANN [46] | RNN [47] |
| MAE | 0.58 | 6.96 | 1.58 | 40.46 | 97.46 |
| MAPE | 0.14 | 22.86 | 1.05 | 188.22 | 350.79 |
| RMSPE | 0.85 | 165.78 | 1.7 | 1651.23 | 2184.5 |
| RMSE | 5.64 | 18.49 | 5.05 | 122.66 | 188.64 |
| R2 | 0.999938 | 0.999332 | 0.99995 | 0.970622 | 0.930517 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Safari, A.; Hassanzadeh Yaghini, H.; Kharrati, H.; Rahimi, A.; Oshnoei, A. Voltage Controller Design for Offshore Wind Turbines: A Machine Learning-Based Fractional-Order Model Predictive Method. Fractal Fract. 2024, 8, 463. https://doi.org/10.3390/fractalfract8080463
Safari A, Hassanzadeh Yaghini H, Kharrati H, Rahimi A, Oshnoei A. Voltage Controller Design for Offshore Wind Turbines: A Machine Learning-Based Fractional-Order Model Predictive Method. Fractal and Fractional. 2024; 8(8):463. https://doi.org/10.3390/fractalfract8080463
Chicago/Turabian StyleSafari, Ashkan, Hossein Hassanzadeh Yaghini, Hamed Kharrati, Afshin Rahimi, and Arman Oshnoei. 2024. "Voltage Controller Design for Offshore Wind Turbines: A Machine Learning-Based Fractional-Order Model Predictive Method" Fractal and Fractional 8, no. 8: 463. https://doi.org/10.3390/fractalfract8080463
APA StyleSafari, A., Hassanzadeh Yaghini, H., Kharrati, H., Rahimi, A., & Oshnoei, A. (2024). Voltage Controller Design for Offshore Wind Turbines: A Machine Learning-Based Fractional-Order Model Predictive Method. Fractal and Fractional, 8(8), 463. https://doi.org/10.3390/fractalfract8080463








