Wind Turbine Blade Fault Diagnosis: Approximate Entropy as a Tool to Detect Erosion and Mass Imbalance
Abstract
1. Introduction
2. Materials and Methods
2.1. Fractal Estimation Based on Correlation Dimension
2.2. Approximate Entropy
2.3. Lyapunov Exponent
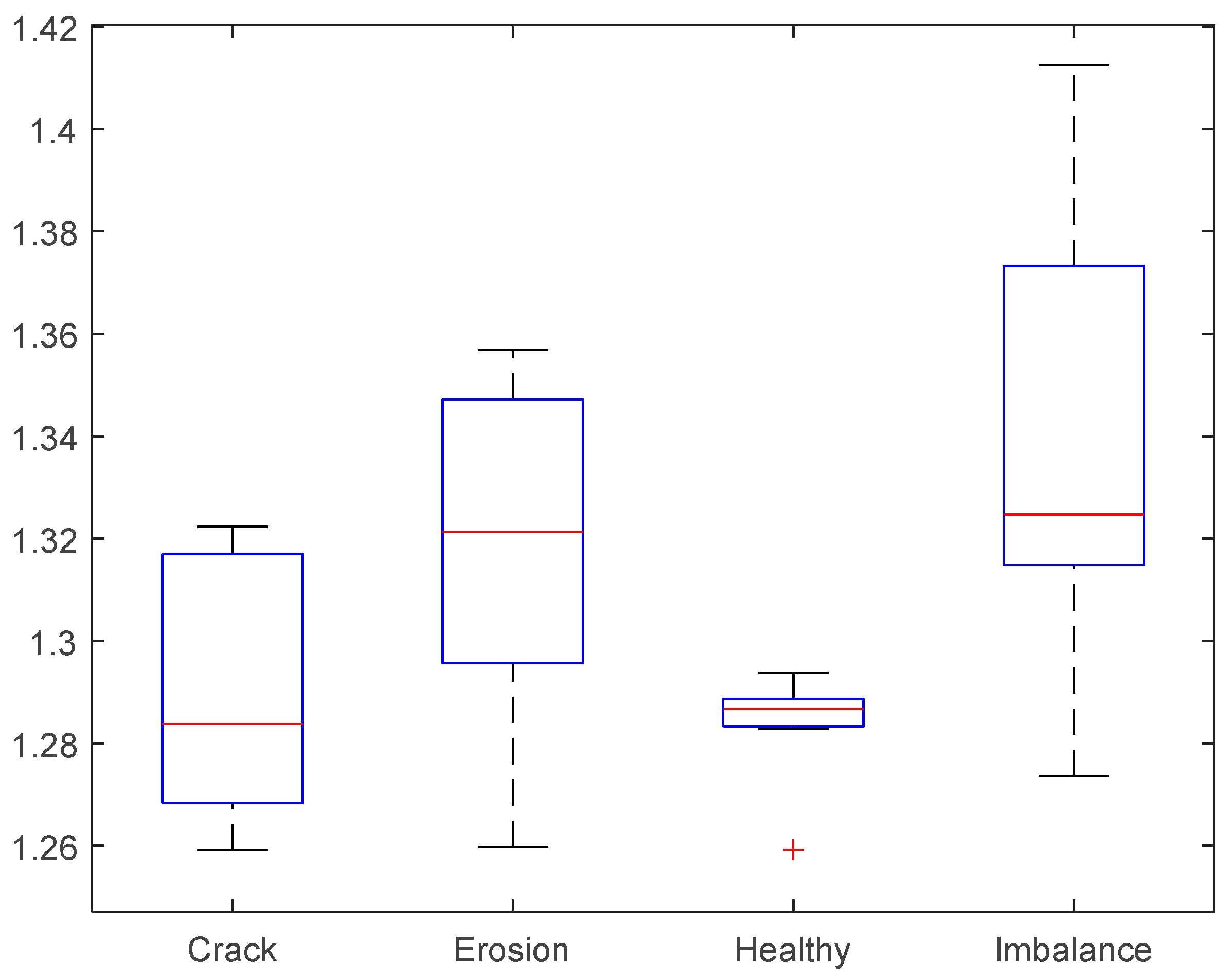
3. Results
4. Discussion and Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Santos, P.; Villa, L.; Reñones, A.; Bustillo, A.; Maudes, J. An SVM-based solution for fault detection in wind turbines. Sensors 2015, 15, 5627–5648. [Google Scholar] [CrossRef]
- Wang, Z.; Li, G.; Yao, L.; Cai, Y.; Lin, T.; Zhang, J.; Dong, H. Intelligent fault detection scheme for constant-speed wind turbines based on improved multiscale fuzzy entropy and adaptive chaotic Aquila optimization-based support vector machine. ISA Trans. 2023, 138, 582–602. [Google Scholar] [CrossRef] [PubMed]
- Qian, X.; Sun, T.; Zhang, Y.; Wang, B.; Gendeel, M.A.A. Wind turbine fault detection based on spatial-temporal feature and neighbor operation state. Renew. Energy 2023, 219, 119419. [Google Scholar] [CrossRef]
- Ohunakin, O.S.; Henry, E.U.; Matthew, O.J.; Ezekiel, V.U.; Adelekan, D.S.; Oyeniran, A.T. Conditional monitoring and fault detection of wind turbines based on Kolmogorov-Smirnov non-parametric test. Energy Rep. 2024, 11, 2577–2591. [Google Scholar] [CrossRef]
- Pérez-Pérez, E.-J.; Puig, V.; López-Estrada, F.-R.; Valencia-Palomo, G.; Santos-Ruiz, I.; Samada, S.E. Fault detection and isolation in wind turbines based on neuro-fuzzy qLPV zonotopic observers. Mech. Syst. Signal Process. 2023, 191, 110183. [Google Scholar] [CrossRef]
- Pérez-Pérez, E.-J.; López-Estrada, F.-R.; Puig, V.; Valencia-Palomo, G.; Santos-Ruiz, I. Fault diagnosis in wind turbines based on ANFIS and Takagi-Sugeno interval observers. Expert Syst. Appl. 2022, 206, 117698. [Google Scholar] [CrossRef]
- Tong, R.; Li, P.; Lang, X.; Liang, J.; Cao, M. A novel adaptive weighted kernel extreme learning machine algorithm and its application in wind turbine blade icing fault detection. Measurement 2021, 185, 110009. [Google Scholar] [CrossRef]
- Jordi, Z.J.; Erasmo, C.; Rafael, C.-A. Multi-criteria optimal design of small wind turbine blades based on deep learning methods. Energy 2024, 293, 130625. [Google Scholar] [CrossRef]
- Chen, W.; Qiu, Y.; Feng, Y.; Li, Y.; Kusiak, A. Diagnosis of wind turbine faults with transfer learning algorithms. Renewable Energy 2021, 163, 2053–2067. [Google Scholar] [CrossRef]
- Jaramillo, F.; Gutiérrez, J.M.; Orchard, M.; Guarini, M.; Astroza, R. A Bayesian approach for fatigue damage diagnosis and prognosis of wind turbine blades. Mech. Syst. Signal Process. 2022, 174, 109067. [Google Scholar] [CrossRef]
- Khan, P.W.; Yeun, C.Y.; Byun, Y.C. Fault detection of wind turbines using SCADA data and genetic algorithm-based ensemble learning. Eng. Fail. Anal. 2023, 148, 107209. [Google Scholar] [CrossRef]
- Ling, X.; Xin, Y.; Aijun, H.; Hao, S.; Penghe, W. Condition monitoring and anomaly detection of wind turbine based on cascaded and bidirectional deep learning networks. Appl. Energy 2022, 305, 117925. [Google Scholar]
- Reihane, R.; Zhiwei, G.; Nanlin, J.; Aihua, Z. Convolutional neural network fault classification based on time-series analysis for benchmark wind turbine machine. Renew. Energy 2022, 185, 916–931. [Google Scholar]
- Dibaj, A.; Gao, Z.; Nejad, A.R. Fault detection of offshore wind turbine drivetrains in different environmental conditions through optimal selection of vibration measurements. Renew. Energy 2023, 203, 161–176. [Google Scholar] [CrossRef]
- Qiao, L.; Zhang, Y.; Wang, Q. Fault detection in wind turbine generators using a meta-learning-based convolutional neural network. Mech. Syst. Signal Process. 2023, 200, 110528. [Google Scholar] [CrossRef]
- Tao, C.; Tao, T.; He, S.; Bai, X.; Liu, Y. Wind turbine blade icing diagnosis using B-SMOTE-Bi-GRU and RFE combined with icing mechanism. Renew. Energy 2024, 221, 119741. [Google Scholar] [CrossRef]
- Liu, W.-X.; Yin, R.-P.; Zhu, P.-Y. Deep learning approach for sensor data prediction and sensor fault diagnosis in wind turbine blade. IEEE Access 2022, 10, 117225–117234. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, X.; Xiong, Y.; dai, f.; Zhang, Y. Intelligent fault diagnosis of turbine blade cracks via multiscale sparse filtering and multi-kernel support vector machine for information fusion. Adv. Eng. Inform. 2023, 56, 101979. [Google Scholar] [CrossRef]
- Yao, Y.; Wang, N. Fault diagnosis model of adaptive miniature circuit breaker based on fractal theory and probabilistic neural network. Mech. Syst. Signal Process. 2020, 142, 106772. [Google Scholar] [CrossRef]
- Dao, P.B.; Staszewski, W.J. Lamb wave based structural damage detection using cointegration and fractal signal processing. Mech. Syst. Signal Process. 2014, 49, 285–301. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, Y.; Zhu, Y. Intelligent fault diagnosis of rolling element bearing based on SVMs and fractal dimension. Mech. Syst. Signal Process. 2007, 21, 2012–2024. [Google Scholar] [CrossRef]
- Liu, H.; Song, W.; Niu, Y.; Zio, E. A generalized cauchy method for remaining useful life prediction of wind turbine gearboxes. Mech. Syst. Signal Process. 2021, 153, 107471. [Google Scholar] [CrossRef]
- Hao, Q.; Shen, Y.; Wang, Y.; Liu, J. An adaptive extraction method for rail crack acoustic emission signal under strong wheel-rail rolling noise of high-speed railway. Mech. Syst. Signal Process. 2021, 154, 107546. [Google Scholar] [CrossRef]
- Zhang, Y.; Ren, G.; Wu, D.; Wang, H. Rolling bearing fault diagnosis utilizing variational mode decomposition based fractal dimension estimation method. Measurement 2021, 181, 109614. [Google Scholar] [CrossRef]
- Wang, B.; Li, H.; Hu, X.; Wang, C.; Sun, D. Rolling bearing fault diagnosis based on fine-grained multi-scale Kolmogorov entropy and WOA-MSVM. Heliyon 2024, 10, e27986. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Li, Y.; Noman, K.; Wang, D.; Feng, K.; Liu, Z.; Deng, Z. Cumulative spectrum distribution entropy for rotating machinery fault diagnosis. Mech. Syst. Signal Process. 2024, 206, 110905. [Google Scholar] [CrossRef]
- Zhou, J.; Chen, C.; Guo, J.; Wang, L.; Liu, Z.; Feng, C. A novel rolling bearing fault diagnosis method based on continuous hierarchical fractional range entropy. Measurement 2023, 220, 113395. [Google Scholar] [CrossRef]
- Ye, Y.; Wei, L.; Li, F.; Zeng, J.; Hecht, M. Multislice Time-Frequency image Entropy as a feature for railway wheel fault diagnosis. Measurement 2023, 216, 112862. [Google Scholar] [CrossRef]
- Jin, Z.; Xiao, Y.; He, D.; Wei, Z.; Sun, Y.; Yang, W. Fault diagnosis of bearing based on refined piecewise composite multivariate multiscale fuzzy entropy. Digit. Signal Process. 2023, 133, 103884. [Google Scholar] [CrossRef]
- Ma, C.; Li, Y.; Wang, X.; ZCai, Z. Early fault diagnosis of rotating machinery based on composite zoom permutation entropy. Reliab. Eng. Syst. Saf. 2023, 230, 108967. [Google Scholar] [CrossRef]
- Tan, H.; Xie, S.; Zhou, H.; Ma, W.; Yang, C.; Zhang, J. Sensible multiscale symbol dynamic entropy for fault diagnosis of bearing. Int. J. Mech. Sci. 2023, 256, 108509. [Google Scholar] [CrossRef]
- Zhou, C.; Jia, Y.; Zhao, S.; Yang, Q.; Liu, Y.; Zhang, Z.; Wang, T. A mechanical part fault diagnosis method based on improved multiscale weighted permutation entropy and multiclass LSTSVM. Measurement 2023, 214, 112671. [Google Scholar] [CrossRef]
- Zhao, D.; Liu, S.; Du, H.; Wang, L.; Miao, Z. Deep branch attention network and extreme multi-scale entropy based single vibration signal-driven variable speed fault diagnosis scheme for rolling bearing. Adv. Eng. Inform. 2023, 55, 101844. [Google Scholar] [CrossRef]
- Huang, P.; Chen, X.; Chai, Y.; Ma, L. A unified framework of fault detection and diagnosis based on fractional-order chaos system. Aerosp. Sci. Technol. 2022, 130, 107871. [Google Scholar] [CrossRef]
- Zhao, Z.; Jia, M.; Wang, F.; Wang, S. Intermittent chaos and sliding window symbol sequence statistics-based early fault diagnosis for hydraulic pump on hydraulic tube tester. Mech. Syst. Signal Process. 2009, 23, 1573–1585. [Google Scholar] [CrossRef]
- Hsieh, C.-H.; Yau, H.-T.; Lin, H.-C. Study on real-time extension fault detection for a XXY stage by using chaos synchronization. J. Appl. Res. Technol. 2015, 13, 305–312. [Google Scholar] [CrossRef]
- Li, Z.; Peng, Z. A new nonlinear blind source separation method with chaos indicators for decoupling diagnosis of hybrid failures: A marine propulsion gearbox case with a large speed variation. Chaos Solitons Fractals 2016, 89, 27–39. [Google Scholar] [CrossRef]
- Lucena-Junior, J.A.; de Vasconcelos Lima, T.L.; Pereira Bruno, G.; Brito, A.V.; de Souza Ramos, J.G.G.; Belo, F.A.; Cavalcante Lima-Filho, A. Chaos theory using density of maxima applied to the diagnosis of three-phase induction motor bearings failure by sound analysis. Comput. Ind. 2020, 123, 103304. [Google Scholar] [CrossRef]
- Przystałka, P.; Moczulski, W. Methodology of neural modelling in fault detection with the use of chaos engineering. Eng. Appl. Artif. Intell. 2015, 41, 25–40. [Google Scholar] [CrossRef]
- Grassberger, P.; Procaccia, I. Measuring the strangeness of strange attractors. Phys. D 1983, 9, 189–208. [Google Scholar] [CrossRef]
- Grassberger, P.; Procaccia, I. Characterization of strange attractors. Phys. Rev. Lett. 1983, 50, 346–349. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef] [PubMed]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Phys. D 1985, 16, 285–317. [Google Scholar] [CrossRef]
- Rosenstein, M.T.; Collins, J.J.; De Luca, C.J. A practical method for calculating largest Lyapunov exponents from small data sets. Phys. D 1993, 65, 117–134. [Google Scholar] [CrossRef]
- Phillips, J.D. Sources of nonlinearity and complexity in geomorphic systems. Prog. Phys. Geogr. 2003, 27, 1–23. [Google Scholar] [CrossRef]
- Shu, Z.R.; Chan, P.W.; Li, Q.S.; He, X.H.; Cai, C.Z. Characterising the variability in ocean data using fractal and correlation dimension analysis. Appl. Ocean Res. 2023, 138, 103590. [Google Scholar] [CrossRef]
- Camastra, F.; Capone, V.; Ciaramella, A.; Riccio, A.; Staiano, A. Prediction of environmental missing data time series by support vector machine regression and correlation dimension estimation. Environ. Model. Softw. 2022, 150, 105343. [Google Scholar] [CrossRef]
- Zheng, Y.; Wen, Y.; Pan, T.; Liu, Y.; Zhou, Y.; Li, R.; Zhou, Y. Fractal characteristics and damage evaluation of corroded beams under four-point bending tests based on acoustic emission techniques. Measurement 2022, 202, 111792. [Google Scholar] [CrossRef]
- Ocak, H. Automatic detection of epileptic seizures in EEG using discrete wavelet transform and approximate entropy. Expert Syst. Appl. 2009, 36, 2027–2036. [Google Scholar] [CrossRef]
- Jones, K.A.; Paterson, C.A.; Hamilton, D.J.; Small, A.D.; Martin, W.; Robinson, J.; Goodfield, N.E.R. Optimising approximate entropy for assessing cardiac dyssynchrony with radionuclide ventriculography. Biomed. Signal Process. Control 2021, 68, 102703. [Google Scholar] [CrossRef]
- Cao, Y.; He, Y.; Yang, J.; Gan, C. A method for weak impact signal discrimination based on para-approximate entropy. Prog. Nucl. Energy 2012, 60, 53–60. [Google Scholar] [CrossRef]
- Lahmiri, S.; Bekiros, S. Complexity measures of high oscillations in phonocardiogram as biomarkers to distinguish between normal heart sound and pathological murmur. Chaos Solitons Fractals 2022, 154, 111610. [Google Scholar] [CrossRef]
- Lahmiri, S.; Bekiros, S.; Bezzina, F. Complexity analysis and forecasting of variations in cryptocurrency trading volume with support vector regression tuned by Bayesian optimization under different kernels: An empirical comparison from a large dataset. Expert Syst. Appl. 2022, 209, 118349. [Google Scholar] [CrossRef]
- Lahmiri, S.; Tadj, C.; Gargour, C.; Bekiros, S. Characterization of infant healthy and pathological cry signals in cepstrum domain based on approximate entropy and correlation dimension. Chaos Solitons Fractals 2021, 143, 110639. [Google Scholar] [CrossRef]
- Fei, K.; Wang, W.; Yang, Q.; Tang, S. Chaos feature study in fractional Fourier domain for preictal prediction of epileptic seizure. Neurocomputing 2017, 249, 290–298. [Google Scholar] [CrossRef]
- Eskandari, A.H.; Ghezelbash, F.; Shirazi-Adl, A.; Larivière, C. Comparative evaluation of different spinal stability metrics. J. Biomech. 2024, 162, 111901. [Google Scholar] [CrossRef] [PubMed]
- Chakraborty, S.; Nandy, A.; Yamaguchi, T.; Bonnet, V.; Venture, G. Accuracy of image data stream of a markerless motion capture system in determining the local dynamic stability and joint kinematics of human gait. J. Biomech. 2020, 104, 109718. [Google Scholar] [CrossRef] [PubMed]
- Ogaili, A.A.F.; Jaber, A.A.; Hamzah, M.N. Wind turbine blades fault diagnosis based on vibration dataset analysis. Data Brief 2023, 49, 109414. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, Z.; Wang, Z.; Wang, Y.; Yang, R.; Zhu, T.; Luo, F.; Liu, K. Using Fractal Theory to Study the Influence of Movable Oil on the Pore Structure of Different Types of Shale: A Case Study of the Fengcheng Formation Shale in Well X of Mahu Sag, Junggar Basin, China. Fractal Fract. 2024, 8, 242. [Google Scholar] [CrossRef]
- Hu, F.; Zhang, K.; Zhu, K.; Li, B.; Zhang, Z.; He, Y. Fractal analysis on the crushing characteristics of soil-soft rock mixtures under compaction. Fractal Fract. 2024, 8, 90. [Google Scholar] [CrossRef]
- Zhang, J.; Ni, X.; Liu, X.; Su, E. Influences of different acid solutions on pore structures and fractal features of coal. Fractal Fract. 2024, 8, 82. [Google Scholar] [CrossRef]
- Guo, S.; Zhang, L.; Pu, H.; Zheng, Y.; Li, B.; Wu, P.; Qiu, P.; Ma, C.; Feng, Y. Dynamic compressive mechanical property characteristics and fractal dimension applications of coal-bearing mudstone at real-time temperatures. Fractal Fract. 2023, 7, 695. [Google Scholar] [CrossRef]
- Ozturk, N.; Begovic, H.; Demir, P.; Can, F.; Yagcioglu, S. Effects of transverse friction massage on the electromechanical delay components and fractal dimension of surface electromyography in quadriceps muscles. Fractal Fract. 2023, 7, 620. [Google Scholar] [CrossRef]
- Zhang, Q.; Pei, Y.; Shen, Y.; Wang, X.; Lai, J.; Wang, M. A New Perspective on Predicting Roughness of Discontinuity from Fractal Dimension D of Outcrops. Fractal Fract. 2023, 7, 496. [Google Scholar] [CrossRef]
- Machorro-Lopez, J.M.; Yanez-Borjas, J.J.; Valtierra-Rodriguez, M.; Amezquita-Sanchez, J.P. Entropy wavelet-based method to increase efficiency in highway bridge damage identification. Appl. Sci. 2024, 14, 3298. [Google Scholar] [CrossRef]
- Yao, B.; Wu, C.; Zhang, X.; Yao, J.; Xue, J.; Zhao, Y.; Li, T.; Pu, J. The EEG-based fusion entropy-featured identification of isometric contraction forces under the same action. Sensors 2024, 24, 2323. [Google Scholar] [CrossRef] [PubMed]
- Rojas, A.J. Differential entropy-based fault-detection mechanism for power-constrained networked control systems. Entropy 2024, 26, 259. [Google Scholar] [CrossRef] [PubMed]
- Cui, Z.; Zhou, Y.; Li, R. Complex dynamics analysis and chaos control of a fractional-order three-population food chain model. Fractal Fract. 2023, 7, 548. [Google Scholar] [CrossRef]
- Ren, L.; Muhsen, S.; Shateyi, S.; Saberi-Nik, H. Dynamical behaviour, control, and boundedness of a fractional-order chaotic system. Fractal Fract. 2023, 7, 492. [Google Scholar] [CrossRef]
- Vonesch, A.; Duhot, C.; Lelard, T.; Léonard, G.; Błażkiewicz, M.; Mouras, H. Non-linear measures of postural control in response to painful and non-painful visual stimuli. Entropy 2023, 25, 1561. [Google Scholar] [CrossRef] [PubMed]



| Two-Sample t-Test | Two-Sample F-Test | |
|---|---|---|
| Healthy versus crack | 0.139 | 0.1928 |
| Healthy versus erosion | 0.4214 | 0.8129 |
| Healthy versus imbalance | 0.2371 | 0.0117 |
| Crack versus erosion | 0.5247 | 0.2805 |
| Crack versus imbalance | 0.4375 | 0.1669 |
| Two-Sample t-Test | Two-Sample F-Test | |
|---|---|---|
| Healthy versus crack | 0.5536 | 0.0585 |
| Healthy versus erosion | 0.0291 | 0.0152 |
| Healthy versus imbalance | 0.0093 | 0.0031 |
| Crack versus erosion | 0.1202 | 0.5211 |
| Crack versus imbalance | 0.0309 | 0.1895 |
| Two-Sample t-Test | Two-Sample F-Test | |
|---|---|---|
| Healthy versus crack | 0.7431 | 0.6897 |
| Healthy versus erosion | 0.832 | 0.9333 |
| Healthy versus imbalance | 0.5419 | 0.0762 |
| Crack versus erosion | 0.9163 | 0.752 |
| Crack versus imbalance | 0.7981 | 0.1577 |
| t-Test | F-Test | |
|---|---|---|
| Correlation dimension | ||
| Healthy < crack | 0.0695 | 0.9036 |
| Healthy > crack | 0.9305 | 0.0964 |
| Healthy < erosion | 0.2107 | 0.5936 |
| Healthy > erosion | 0.7893 | 0.4064 |
| Healthy < imbalance | 0.1185 | 0.9941 |
| Healthy > imbalance | 0.8815 | 0.0059 |
| Approximate entropy | ||
| Healthy < crack | 0.2768 | 0.0292 |
| Healthy > crack | 0.7232 | 0.9708 |
| Healthy < erosion | 0.0146 | 0.0076 |
| Healthy > erosion | 0.9854 | 0.9924 |
| Healthy < imbalance | 0.0047 | 0.0016 |
| Healthy > imbalance | 0.9953 | 0.9984 |
| Lyapunov exponent | ||
| Healthy < crack | 0.6285 | 0.6551 |
| Healthy > crack | 0.3715 | 0.3449 |
| Healthy < erosion | 0.5840 | 0.5334 |
| Healthy > erosion | 0.4160 | 0.4666 |
| Healthy < imbalance | 0.7290 | 0.9619 |
| Healthy > imbalance | 0.2710 | 0.0381 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lahmiri, S. Wind Turbine Blade Fault Diagnosis: Approximate Entropy as a Tool to Detect Erosion and Mass Imbalance. Fractal Fract. 2024, 8, 484. https://doi.org/10.3390/fractalfract8080484
Lahmiri S. Wind Turbine Blade Fault Diagnosis: Approximate Entropy as a Tool to Detect Erosion and Mass Imbalance. Fractal and Fractional. 2024; 8(8):484. https://doi.org/10.3390/fractalfract8080484
Chicago/Turabian StyleLahmiri, Salim. 2024. "Wind Turbine Blade Fault Diagnosis: Approximate Entropy as a Tool to Detect Erosion and Mass Imbalance" Fractal and Fractional 8, no. 8: 484. https://doi.org/10.3390/fractalfract8080484
APA StyleLahmiri, S. (2024). Wind Turbine Blade Fault Diagnosis: Approximate Entropy as a Tool to Detect Erosion and Mass Imbalance. Fractal and Fractional, 8(8), 484. https://doi.org/10.3390/fractalfract8080484







