Dynamics of the Traveling Wave Solutions of Fractional Date–Jimbo–Kashiwara–Miwa Equation via Riccati–Bernoulli Sub-ODE Method through Bäcklund Transformation
Abstract
1. Introduction
2. Algorithm
3. Problem Execution
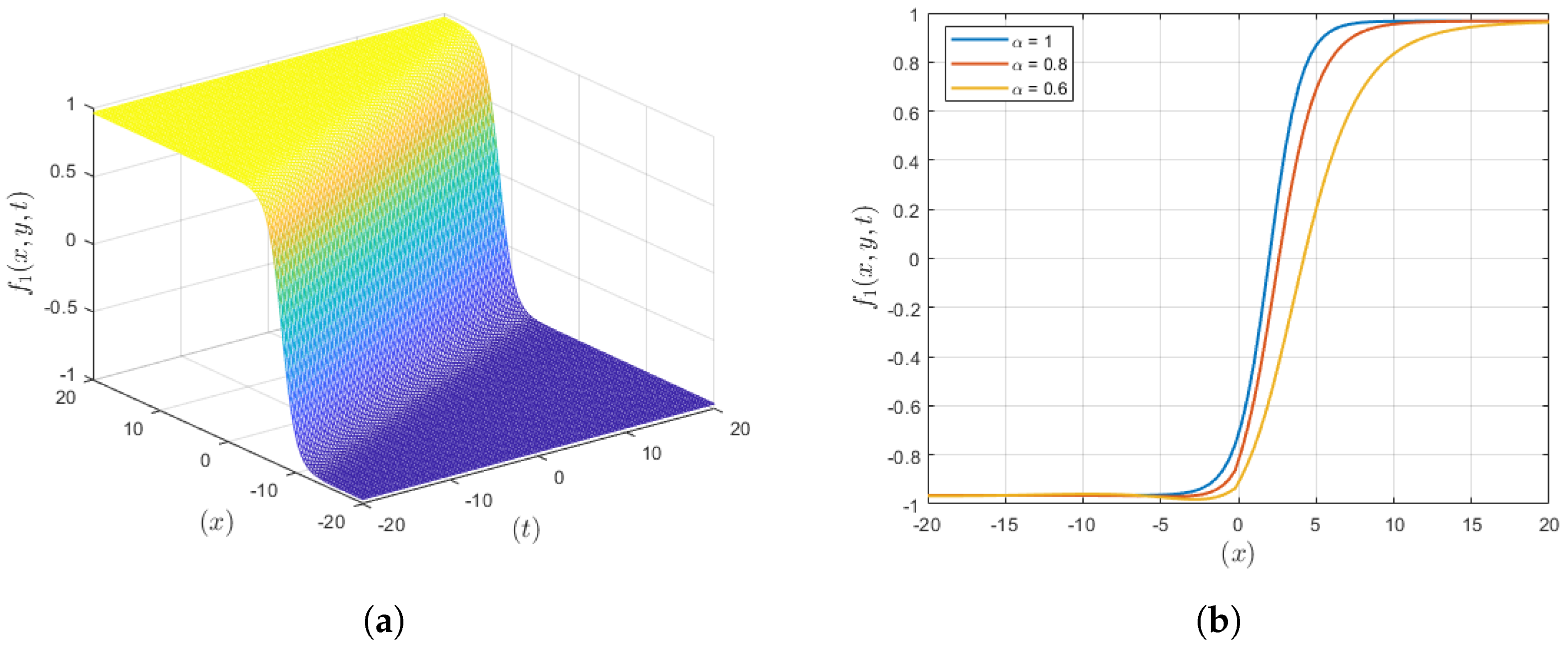
3.1. Solution Set 1
3.2. Solution Set 2
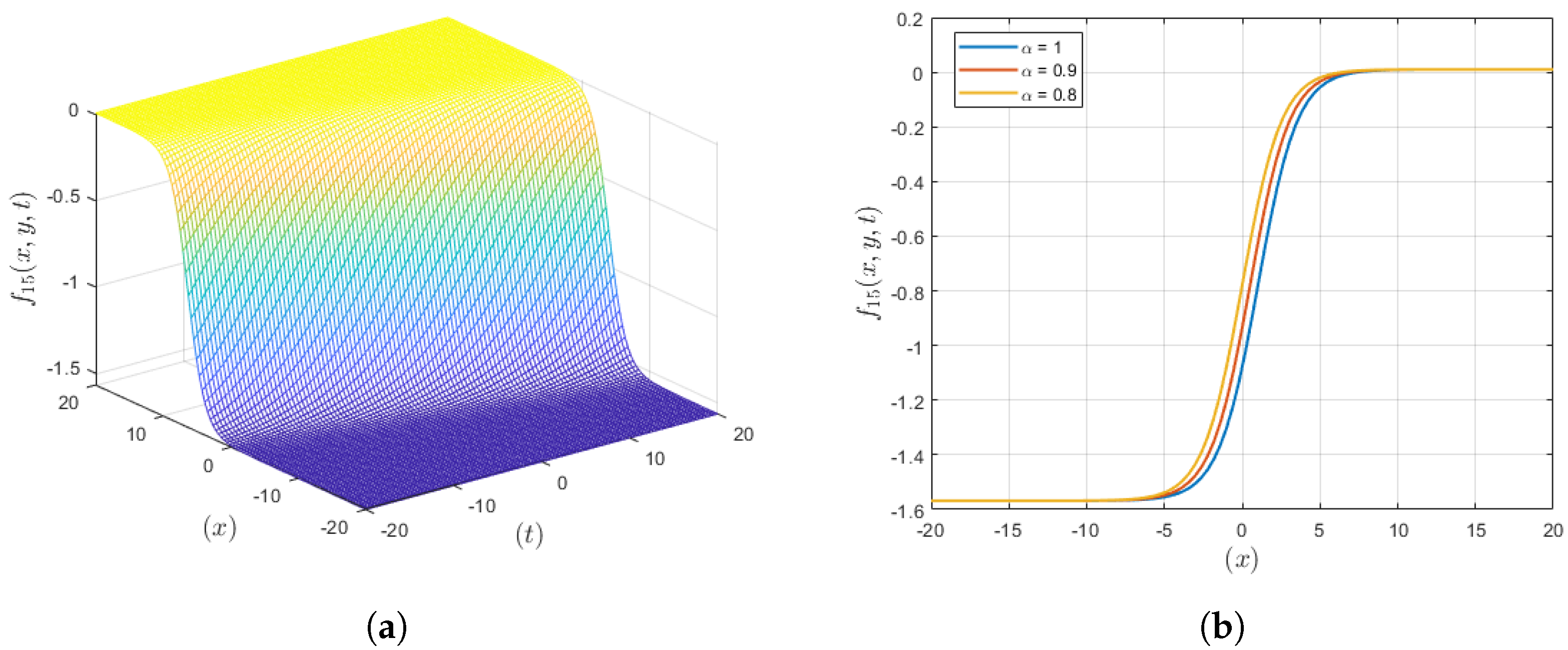
3.3. Solution Set 3
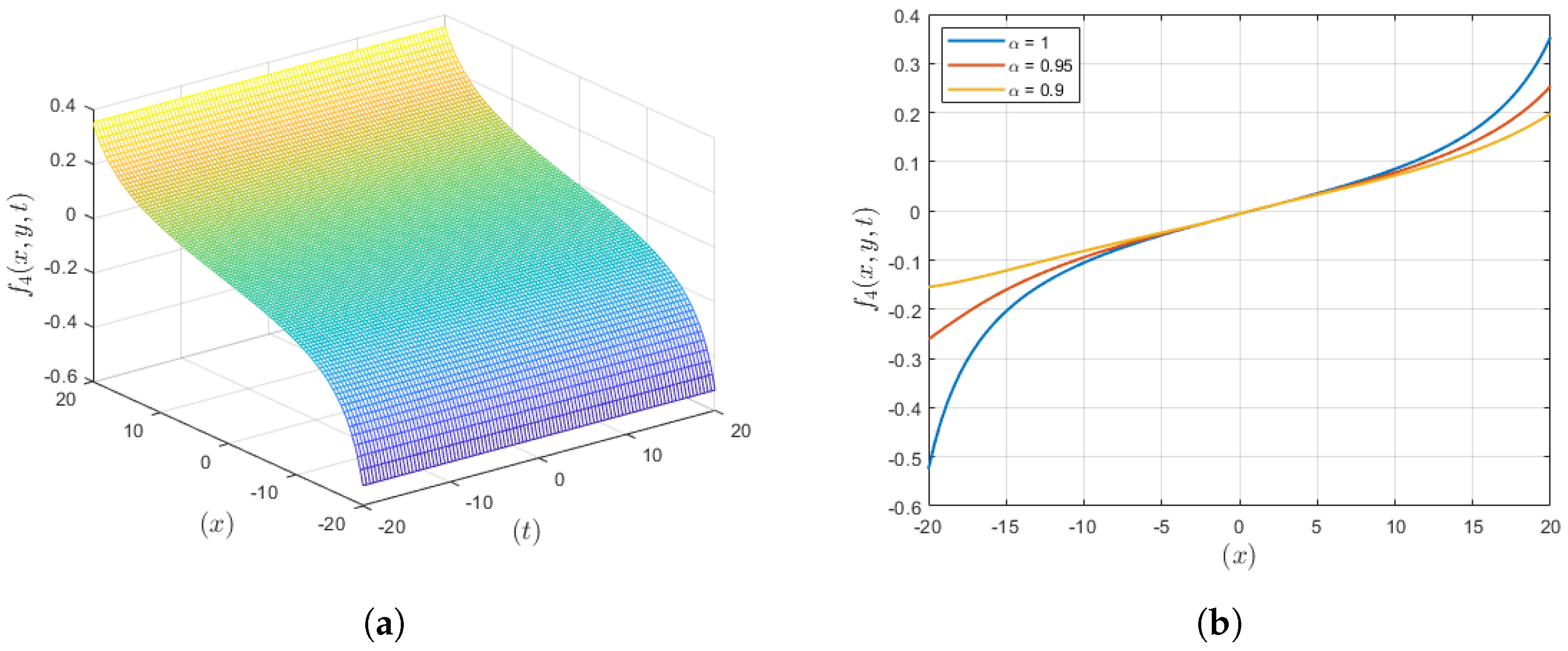
3.4. Solution Set 4
3.5. Solution Set 5
3.6. Solution Set 6
3.7. Solution Set 7
3.8. Solution Set 8
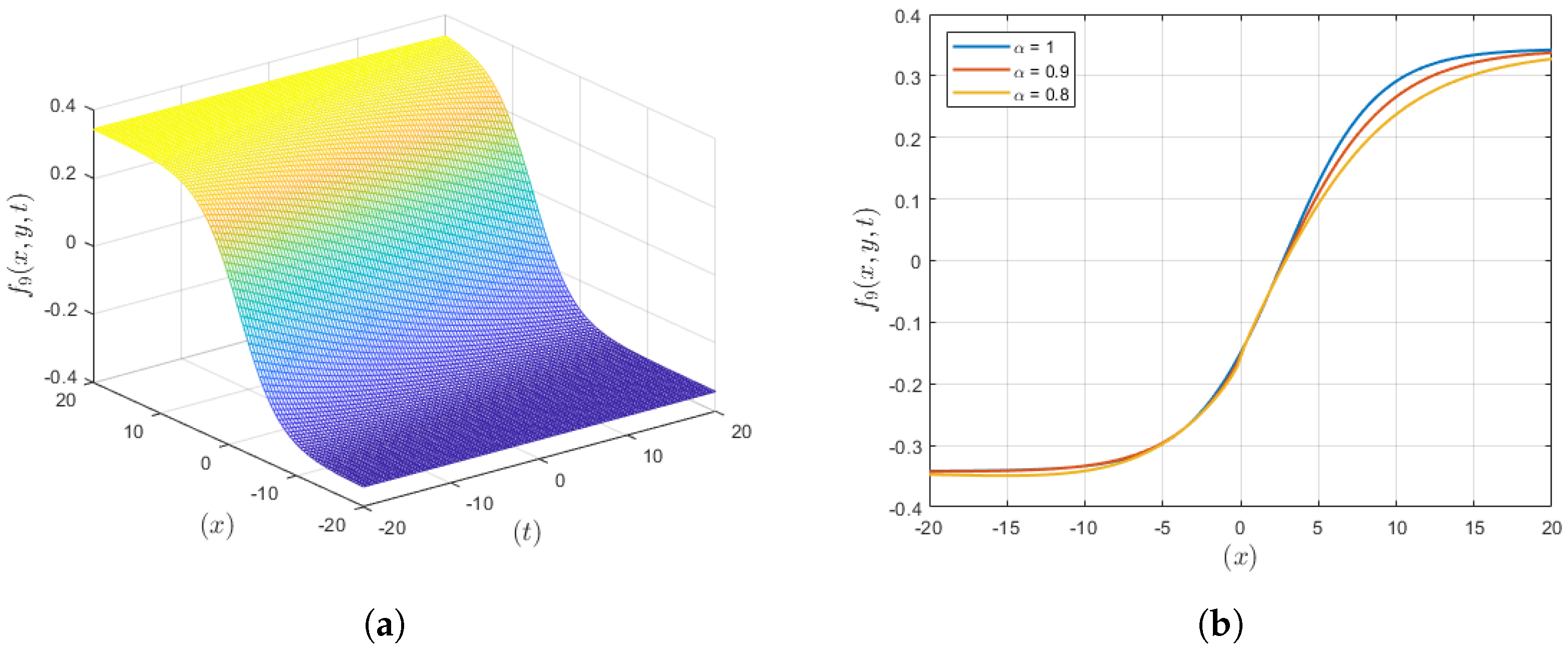
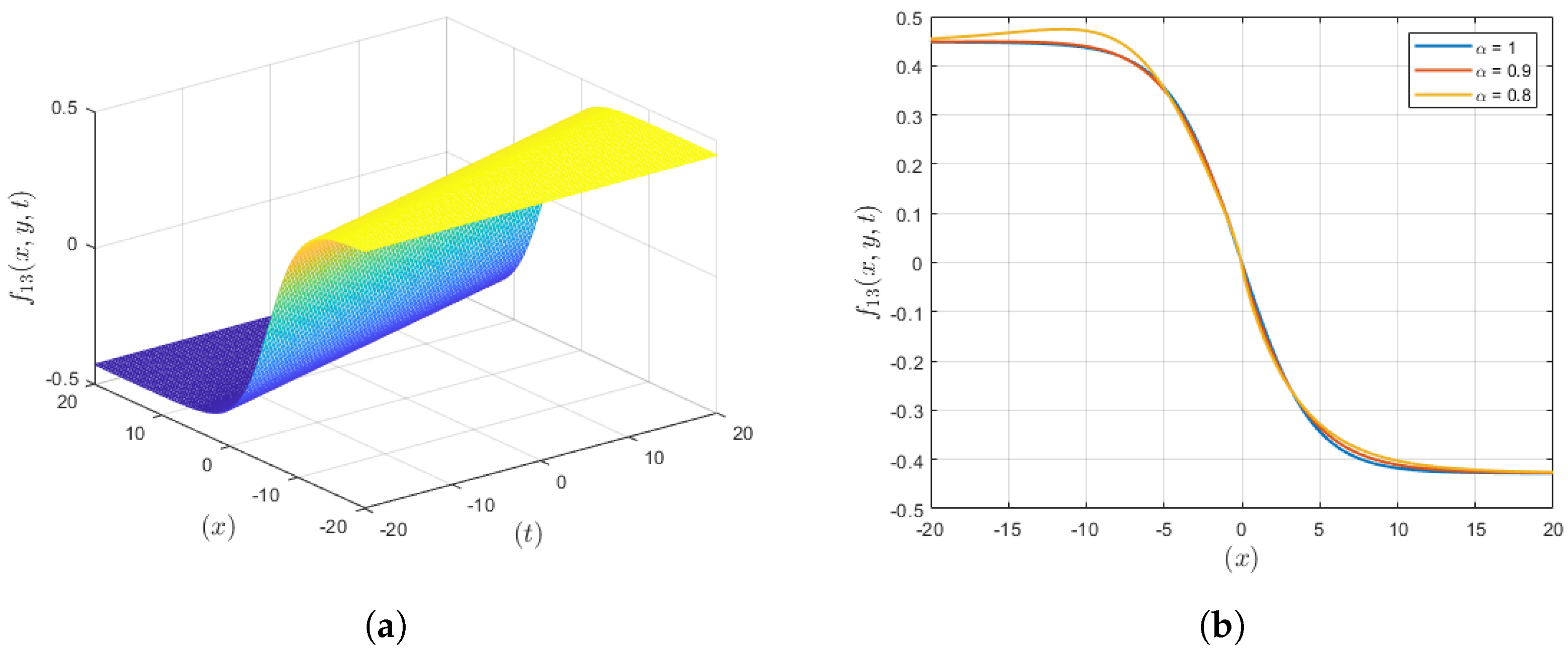
3.9. Solution Set 9
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, M.L.; Zhou, Y.B.; Li, Z.B. Application of a homogeneous balance method to exact solutions of nonlinear equations in mathematical physics. Phys. Lett. A 1996, 216, 67–75. [Google Scholar] [CrossRef]
- Fan, E.; Zhang, H. A note on the homogeneous balance method. Phys. Lett. A 1998, 246, 403–406. [Google Scholar] [CrossRef]
- Mahak, N.; Akram, G. Exact solitary wave solutions of the (1+1)-dimensional Fokas-Lenells equation. Optik 2020, 208, 1–9. [Google Scholar] [CrossRef]
- Rezazadeh, H.; Manafian, J.; Khodadad, F.S.; Nazari, F. Traveling wave solutions for density dependent conformable fractional diffusion-reaction equation by the first integral method and the improved tan (ϕ(x)/2)-expansion method. Opt. Quantum Electron. 2018, 50, 1–15. [Google Scholar] [CrossRef]
- Lu, D. Jacobi elliptic function solutions for two variant Boussinesq equations. Chaos Soliton Fractals 2005, 24, 1373–1385. [Google Scholar] [CrossRef]
- Jafari, H.; Kadkhoda, N.; Baleanu, D. Fractional Lie group method of the time-fractional Boussinesq equation. Nonlinear Dyn. 2015, 81, 1569–1574. [Google Scholar] [CrossRef]
- Raza, N.; Aslam, M.R.; Rezazadeh, H. Analytical study of resonant optical solitons with variable coefficients in Kerr and non-Kerrlaw media. Opt. Quantum Electron. 2019, 51, 59. [Google Scholar] [CrossRef]
- Gao, W.; Rezazadeh, H.; Pinar, Z.; Baskonus, H.M.; Sarwar, S.; Yel, G. Novel explicit solutions for the nonlinear Zoomeron equation by using newly extended direct algebraic technique. Opt. Quantum Electron. 2020, 52, 1–13. [Google Scholar] [CrossRef]
- Abdel-Gawad, H.I.; Osman, M.S. On the Variational Approach for Analyzing the Stability of Solutions of Evolution Equations. Kyungpook Math. J. 2013, 53, 661–680. [Google Scholar] [CrossRef]
- Abdel-Gawad, H.I.; Osman, M. On shallow water waves in a medium with time-dependent dispersion and nonlinearity coefficients. J. Adv. Res. 2014, 6, 593–599. [Google Scholar] [CrossRef]
- Ali, M.N.; Osman, M.S.; Husnine, S.M. On the analytical solutions of conformable time-fractional extended Zakharov-Kuznetsov equation through (G′/G2)-expansion method and the modified Kudryashov method. SeMA J. 2019, 76, 15–25. [Google Scholar] [CrossRef]
- Ali, K.K.; Osman, M.; Abdel-Aty, M. New optical solitary wave solutions of Fokas-Lenells equation in optical fiber via Sine-Gordon expansion method. Alex. Eng. J. 2020, 59, 1191–1196. [Google Scholar] [CrossRef]
- Kumar, A.; Pankaj, R.D. Tanh–coth scheme for traveling wave solutions for Nonlinear Wave Interaction model. J. Egypt. Math. Soc. 2015, 23, 282–285. [Google Scholar] [CrossRef]
- Domairry, G.; Mohsenzadeh, A.; Famouri, M. The application of homotopy analysis method to solve nonlinear differential equation governing Jeffery–Hamel flow. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 85–95. [Google Scholar] [CrossRef]
- Zhang, Z.Y. Exact traveling wave solutions of the perturbed Klein-Gordon equation with quadratic nonlinearity in (1+1)-dimension. Part I: Without local inductance and dissipation effect. Turk. J. Phys. 2013, 37, 259–267. [Google Scholar] [CrossRef]
- Fan, E. Extended tanh-function method and its applications to nonlinear equations. Phys. Lett. A 2000, 277, 212–218. [Google Scholar] [CrossRef]
- Sarikaya, M.Z.; Budak, H.; Usta, H. On generalized the conformable fractional calculus. TWMS J. Appl. Eng. Math. 2019, 9, 792–799. [Google Scholar]
- Akbar, M.A.; Ali, N.H.M.; Islam, M.T. Multiple closed form solutions to some fractional order nonlinear evolution equations in physics and plasma physics. AIMS Math. 2019, 4, 397–411. [Google Scholar] [CrossRef]
- Liu, T. Exact solutions to time-fractional fifth order KdV equation by trial equation method based on symmetry. Symmetry 2019, 11, 742. [Google Scholar] [CrossRef]
- Alshammari, S.; Al-Sawalha, M.M.; Shah, R. Approximate analytical methods for a fractional-order nonlinear system of Jaulent–Miodek equation with energy-dependent Schrodinger potential. Fractal Fract. 2023, 7, 140. [Google Scholar] [CrossRef]
- Alderremy, A.A.; Shah, R.; Iqbal, N.; Aly, S.; Nonlaopon, K. Fractional series solution construction for nonlinear fractional reaction-diffusion Brusselator model utilizing Laplace residual power series. Symmetry 2022, 14, 1944. [Google Scholar] [CrossRef]
- Yasmin, H.; Alshehry, A.S.; Ganie, A.H.; Mahnashi, A.M. Perturbed Gerdjikov–Ivanov equation: Soliton solutions via Backlund transformation. Optik 2024, 298, 171576. [Google Scholar] [CrossRef]
- Elsayed, E.M.; Nonlaopon, K. The Analysis of the Fractional-Order Navier-Stokes Equations by a Novel Approach. J. Funct. Spaces 2022, 2022, 8979447. [Google Scholar] [CrossRef]
- Alqhtani, M.; Saad, K.M.; Weera, W.; Hamanah, W.M. Analysis of the fractional-order local Poisson equation in fractal porous media. Symmetry 2022, 14, 1323. [Google Scholar] [CrossRef]
- Hajar, F.I.; Hasan, B.; Choonkil, P.; Osman, M.S. M-lump, N-soliton solutions, and the collision phenomena for the (2+1)- dimensional Date–Jimbo–Kashiwara-Miwa equation. Results Phys. 2020, 19, 103329. [Google Scholar]
- Wazwaz, A.M. A (2+1)–dimensional time–dependent Date–Jimbo–Kashiwara–Miwa equation: Painleve integrability and multiple soliton solutions. Comput. Math. Appl. 2020, 79, 1145–1149. [Google Scholar] [CrossRef]
- Adem, A.R.; Yildirim, Y.; Yasar, E. Complexiton solutions and soliton solutions: (2+1)–dimensional Date–Jimbo–Kashiwara–Miwa equation. Pramana 2019, 92, 1–12. [Google Scholar] [CrossRef]
- Yuan, Y.Q.; Tian, B.; Sun, W.R.; Chai, J.; Liu, L. Wronskian and Grammian solutions for a (2+1)-dimensional Date–Jimbo–Kashiwara–Miwa equation. Comp. Math. Appl. Int. J. 2017, 74, 873–879. [Google Scholar] [CrossRef]
- Abdelrahman, M.A.E.; Sohaly, M.A. Solitary waves for the modified Korteweg-de Vries equation in deterministic case and random case. J. Phys. Math. 2017, 8, 214. [Google Scholar] [CrossRef]
- Abdelrahman, M.A.E.; Sohaly, M.A. Solitary waves for the nonlinear Schrödinger problem with the probability distribution function in the stochastic input case. Eur. Phys. J. Plus 2017, 132, 339. [Google Scholar] [CrossRef]
- Yang, X.F.; Deng, Z.C.; Wei, Y. A Riccati-Bernoulli sub-ODE method for nonlinear partial differential equations and its application. Adv. Differ. Equ. 2015, 1, 117–133. [Google Scholar] [CrossRef]
- Lu, D.; Shi, Q. New Jacobi elliptic functions solutions for the combined KdV-mKdV equation. Int. J. Nonlinear Sci. 2010, 10, 320–325. [Google Scholar]
- Zhang, Y. Solving STO and KD equations with modified Riemann-Liouville derivative using improved (G/G′)-expansion function method. Int. J. Appl. Math. 2015, 45, 16–22. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Sawalha, M.M.; Noor, S.; Alqudah, M.; Aldhabani, M.S.; Ullah, R. Dynamics of the Traveling Wave Solutions of Fractional Date–Jimbo–Kashiwara–Miwa Equation via Riccati–Bernoulli Sub-ODE Method through Bäcklund Transformation. Fractal Fract. 2024, 8, 497. https://doi.org/10.3390/fractalfract8090497
Al-Sawalha MM, Noor S, Alqudah M, Aldhabani MS, Ullah R. Dynamics of the Traveling Wave Solutions of Fractional Date–Jimbo–Kashiwara–Miwa Equation via Riccati–Bernoulli Sub-ODE Method through Bäcklund Transformation. Fractal and Fractional. 2024; 8(9):497. https://doi.org/10.3390/fractalfract8090497
Chicago/Turabian StyleAl-Sawalha, M. Mossa, Saima Noor, Mohammad Alqudah, Musaad S. Aldhabani, and Roman Ullah. 2024. "Dynamics of the Traveling Wave Solutions of Fractional Date–Jimbo–Kashiwara–Miwa Equation via Riccati–Bernoulli Sub-ODE Method through Bäcklund Transformation" Fractal and Fractional 8, no. 9: 497. https://doi.org/10.3390/fractalfract8090497
APA StyleAl-Sawalha, M. M., Noor, S., Alqudah, M., Aldhabani, M. S., & Ullah, R. (2024). Dynamics of the Traveling Wave Solutions of Fractional Date–Jimbo–Kashiwara–Miwa Equation via Riccati–Bernoulli Sub-ODE Method through Bäcklund Transformation. Fractal and Fractional, 8(9), 497. https://doi.org/10.3390/fractalfract8090497








