Applications of Mittag–Leffler Functions on a Subclass of Meromorphic Functions Influenced by the Definition of a Non-Newtonian Derivative
Abstract
1. Introduction and Definition
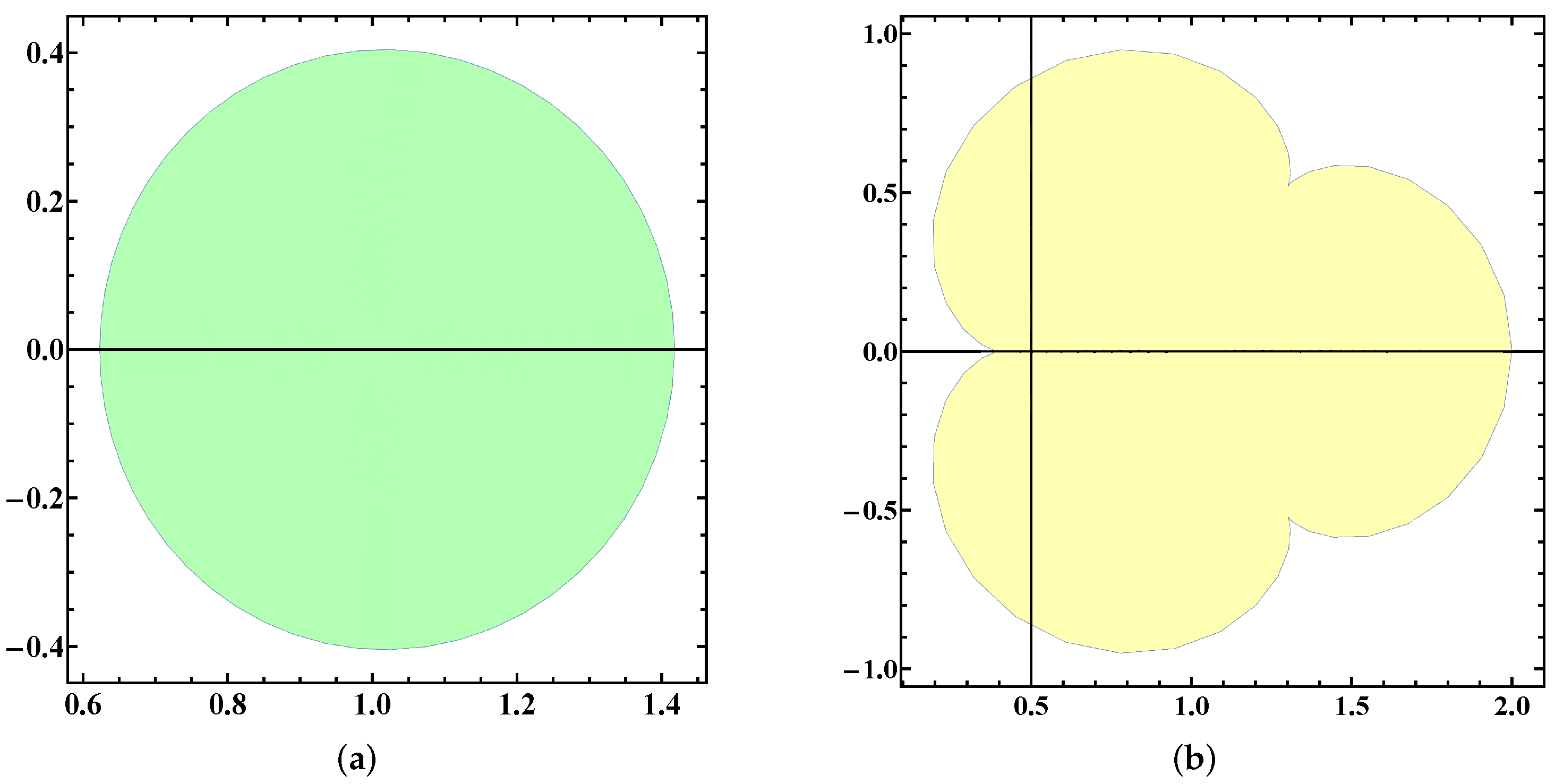
2. Main Results
3. Analytic Functions with Respect to Symmetric Points
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Srivastava, H.M.; Bansal, M.; Harjule, P. A study of fractional integral operators involving a certain generalized multi-index Mittag–Leffler function. Math. Methods Appl. Sci. 2018, 41, 6108–6121. [Google Scholar] [CrossRef]
- Aouf, M.K.; El-Emam, F.Z. Fekete–Szegö problems for certain classes of meromorphic functions involving q-Al-Oboudi differential operator. J. Math. 2022, 2022, 4731417. [Google Scholar] [CrossRef]
- Horrigue, S.; Madian, S.M. Some inclusion relationships of meromorphic functions associated to new generalization of Mittag–Leffler function. Filomat 2020, 34, 1545–1556. [Google Scholar] [CrossRef]
- Umadevi, E.; Karthikeyan, K.R. A subclass of close-to-convex function involving Srivastava-Tomovski operator. In Recent Developments in Algebra and Analysis. ICRDM 2022. Trends in Mathematics; Leung, H.H., Sivaraj, R., Kamalov, F., Eds.; Birkhäuser: Cham, Switzerland, 2024. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Tomovski, Ž. Fractional calculus with an integral operator containing a generalized Mittag–Leffler function in the kernel. Appl. Math. Comput. 2009, 211, 198–210. [Google Scholar] [CrossRef]
- Tomovski, Ž.; Pogány, T.K.; Srivastava, H.M. Laplace type integral expressions for a certain three-parameter family of generalized Mittag–Leffler functions with applications involving complete monotonicity. J. Frankl. Inst. 2014, 351, 5437–5454. [Google Scholar] [CrossRef]
- Tomovski, Ž.; Hilfer, R.; Srivastava, H.M. Fractional and operational calculus with generalized fractional derivative operators and Mittag–Leffler type functions. Integral Transform. Spec. Funct. 2010, 21, 797–814. [Google Scholar] [CrossRef]
- Aouf, M.K.; Shamandy, A.; Mostafa, A.O.; Madian, S.M. Properties of some families of meromorphic p-valent functions involving certain differential operator. Acta Univ. Apulensis 2009, 20, 7–16. [Google Scholar]
- El-Ashwah, R.M.; Aouf, M.K. Differential subordination and superordination on p-valent meromorphic function defined by extended multiplier transformations. Europ. J. Pure Appl. Math. 2010, 3, 1070–1085. [Google Scholar]
- Karthikeyan, K.R.; Murugusundaramoorthy, G. Properties of a Class of Analytic Functions Influenced by Multiplicative Calculus. Fractal Fract. 2024, 8, 131. [Google Scholar] [CrossRef]
- Bashirov, A.E.; Kurpinar, E.M.; Özyapıcı, A. Multiplicative calculus and its applications. J. Math. Anal. Appl. 2008, 337, 36–48. [Google Scholar] [CrossRef]
- Bashirov, A.E.; Mısırlı, E.; Tandoğdu, Y.; Özyapıcı, A. On modeling with multiplicative differential equations. Appl. Math. J. Chin. Univ. 2011, 26, 425–438. [Google Scholar] [CrossRef]
- Ma, W.C.; Minda, D. A unified treatment of some special classes of univalent functions. In Proceedings of the Conference on Complex Analysis, Tianjin, China, 19–23 June 1992; International Press: Boston, MA, USA, 1992; pp. 157–169. [Google Scholar]
- Karthikeyan, K.R.; Murugusundaramoorthy, G.; Bulboacă, T. Properties of λ-pseudo-starlike functions of complex order defined by subordination. Axioms 2021, 10, 86. [Google Scholar] [CrossRef]
- Gandhi, S.; Gupta, P.; Nagpal, S.; Ravichandran, V. Starlike functions associated with an Epicycloid. Hacet. J. Math. Stat. 2022, 51, 1637–1660. [Google Scholar] [CrossRef]
- Ahmad, A.; Gong, J.; Al-Shbeil, I.; Rasheed, A.; Ali, A.; Hussain, S. Analytic Functions Related to a Balloon-Shaped Domain. Fractal Fract. 2023, 7, 865. [Google Scholar] [CrossRef]
- Sakaguchi, K. On a certain univalent mapping. J. Math. Soc. Japan 1959, 11, 72–75. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Breaz, D.; Karthikeyan, K.R.; Murugusundaramoorthy, G. Applications of Mittag–Leffler Functions on a Subclass of Meromorphic Functions Influenced by the Definition of a Non-Newtonian Derivative. Fractal Fract. 2024, 8, 509. https://doi.org/10.3390/fractalfract8090509
Breaz D, Karthikeyan KR, Murugusundaramoorthy G. Applications of Mittag–Leffler Functions on a Subclass of Meromorphic Functions Influenced by the Definition of a Non-Newtonian Derivative. Fractal and Fractional. 2024; 8(9):509. https://doi.org/10.3390/fractalfract8090509
Chicago/Turabian StyleBreaz, Daniel, Kadhavoor R. Karthikeyan, and Gangadharan Murugusundaramoorthy. 2024. "Applications of Mittag–Leffler Functions on a Subclass of Meromorphic Functions Influenced by the Definition of a Non-Newtonian Derivative" Fractal and Fractional 8, no. 9: 509. https://doi.org/10.3390/fractalfract8090509
APA StyleBreaz, D., Karthikeyan, K. R., & Murugusundaramoorthy, G. (2024). Applications of Mittag–Leffler Functions on a Subclass of Meromorphic Functions Influenced by the Definition of a Non-Newtonian Derivative. Fractal and Fractional, 8(9), 509. https://doi.org/10.3390/fractalfract8090509







