Stability Analysis Study of Time-Fractional Nonlinear Modified Kawahara Equation Based on the Homotopy Perturbation Sadik Transform
Abstract
1. Introduction
2. Important Preliminaries
3. The Projected Scheme
4. Existence and Uniqueness of Solutions with Caputo–Prabhakar Derivative
Stability Analysis
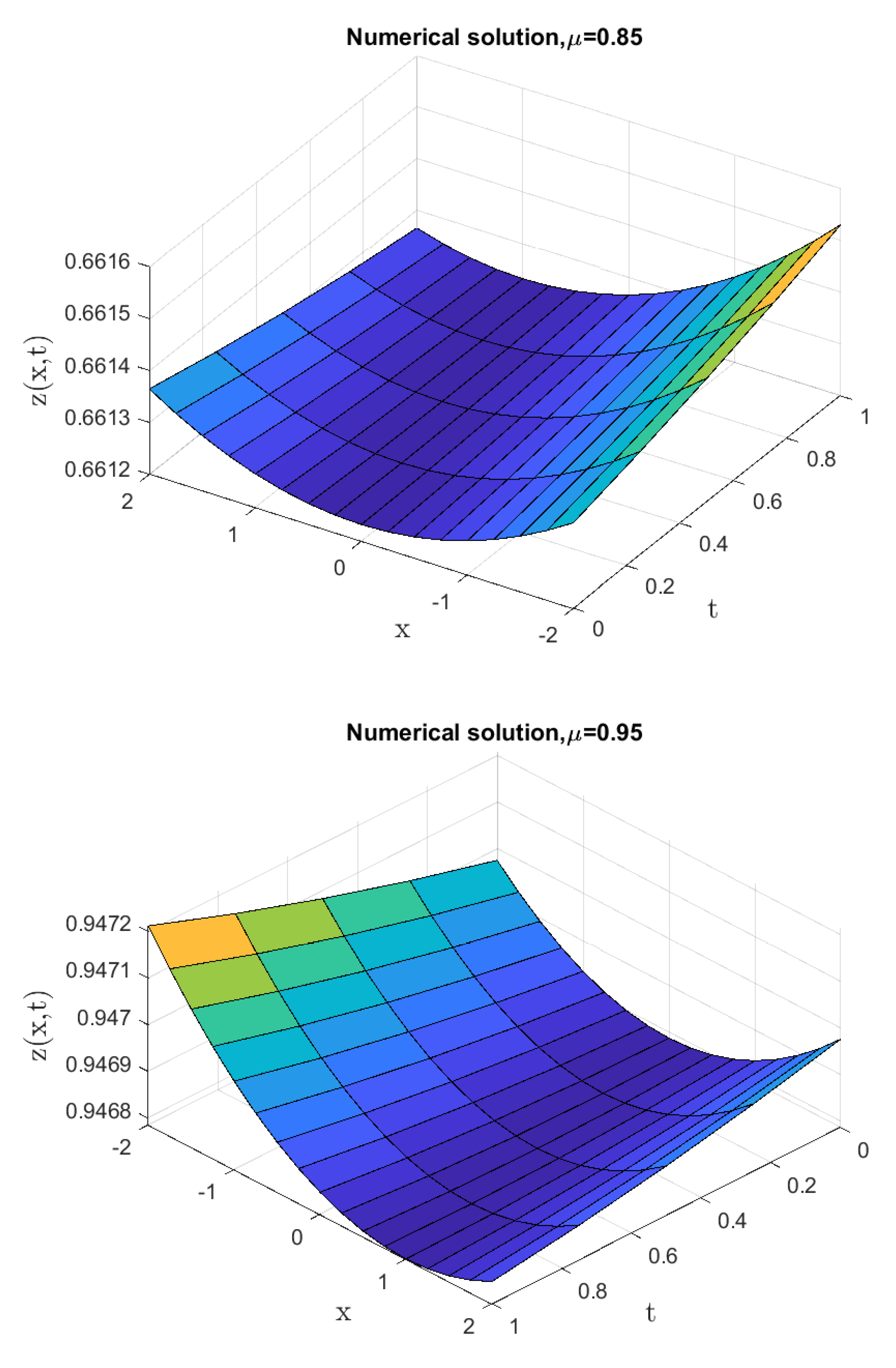
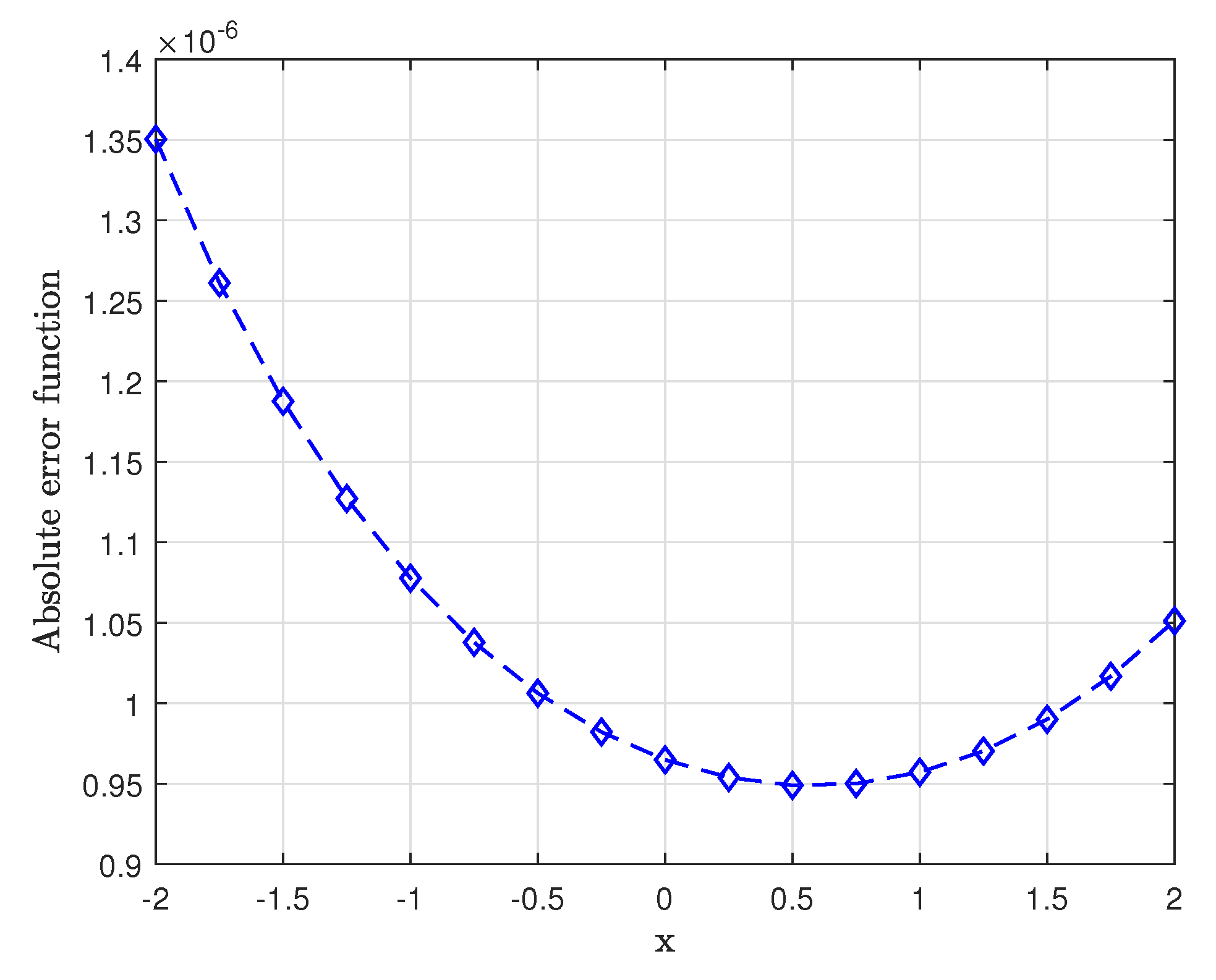
5. Computational Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Amiataei, A.; Derakhshan, M. Stability analysis and numerical simulation of non-steady partial differential model in the human pulmonary capillaries using finite differences technique. Hacet. J. Math. Stat. 2023, 52, 1658–1676. [Google Scholar] [CrossRef]
- Diethelm, K.; Baleanu, D.; Scalas, E. Fractional Calculus: Models and Numerical Methods; World Scientific: Singapore, 2012. [Google Scholar]
- Goswami, A.; Singh, J.; Kumar, D. An efficient analytical approach for fractional equal width equations describing hydro-magnetic waves in cold plasma. Phys. A Stat. Mech. Appl. 2019, 524, 563–575. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Saigo, M.; Saxena, R.K. Generalized Mittag-Leffler function and generalized fractional calculus operators. Integral Transform. Spec. Funct. 2004, 15, 31–49. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Academic Press: Cambridge, MA, USA; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Farid, G.; Pecaric, J.; Tomovski, Z. Opial-type inequalities for fractional integral operator involving Mittag-Leffler function. Fract. Differ. Calc. 2015, 5, 93–106. [Google Scholar] [CrossRef]
- Kako, M. Nonlinear wave modulation in cold magnetized plasmas. J. Phys. Soc. Jpn. 1972, 33, 1678–1687. [Google Scholar] [CrossRef]
- Xiong, T.; Lv, Y.; Yi, W. Nonlinear Vibration and Control of Underwater Supercavitating Vehicles. IEEE Access 2018, 6, 62503–62513. [Google Scholar] [CrossRef]
- Yépez-Martínez, H.; Gómez-Aguilar, J.F. A new modified definition of Caputo-Fabrizio fractional-order derivative and their applications to the Multi Step Homotopy Analysis Method (MHAM). J. Comput. Appl. Math. 2019, 346, 247–260. [Google Scholar] [CrossRef]
- Kosari, S.; Xu, P.; Shafi, J.; Derakhshan, M.H. An efficient hybrid numerical approach for solving two-dimensional fractional cable model involving time-fractional operator of distributed order with error analysis. Numer. Algorithms 2024, 1–20. [Google Scholar] [CrossRef]
- Lu, D.; Seadawy, A.R.; Arshad, M. Bright-dark solitary wave and elliptic function solutions of unstable nonlinear Schrödinger equation and their applications. Opt. Quantum Electron. 2018, 50, 23. [Google Scholar] [CrossRef]
- Singh, J.; Kumar, D.; Qurashi, M.A.; Baleanu, D. Analysis of a new fractional model for damped Bergers’ equation. Open Phys. 2017, 5, 35–41. [Google Scholar] [CrossRef]
- Shchepetil’inikov, V.A.; Starodubtsev, P.A.; Traskovskii, V.I.; Senchenko, A.G.; Alifanov, R.N. Method of the finding the nonlinear phenomenas in ocean from moving undersea object and their theoretical explanation. J. Sib. Fed. Univ. Math. Phys. 2010, 3, 267–275. [Google Scholar]
- Derakhshan, M.H.; Kumar, P.; Salahshour, S. A high-order space-time spectral method for the distributed-order time-fractional telegraph equation. Int. J. Dyn. Control 2024, 12, 2778–2794. [Google Scholar] [CrossRef]
- Garra, R.; Garrappa, R. The Prabhakar or three parameter Mittag-Leffler function: Theory and application. Commun. Nonlinear Sci. Numer. Simul. 2018, 56, 314–329. [Google Scholar] [CrossRef]
- Garra, R.; Gorenflo, R.; Polito, F.; Tomovski, Ž. Hilfer-Prabhakar derivatives and some applications. Appl. Math. Comput. 2014, 242, 576–589. [Google Scholar] [CrossRef]
- Kawahara, T. Oscillatory solitary waves in dispersive media. J. Phys. Soc. Jpn. 1972, 33, 260–264. [Google Scholar] [CrossRef]
- Amick, C.J.; McLeod, J.B. A singular perturbation problem in water waves. Stab. Appl. Anal. Cont. Media 1992, 1, 127–148. [Google Scholar]
- Amick, C.J.; Kirchgässner, K.A. Theory of solitary water-waves in the presence of surface tension. Arch. Ration. Mech. Anal. 1989, 105, 1–49. [Google Scholar] [CrossRef]
- Kurulay, M. Approximate analytic solutions of the modified Kawahara equation with homotopy analysis method. Adv. Differ. Equ. 2012, 2012, 178. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, J.; Baleanu, D. Modified Kawahara equation within a fractional derivative with non-singular kernel. Therm. Sci. 2018, 22, 789–796. [Google Scholar] [CrossRef]
- Arora, R.; Siddiqui, M.J.; Singh, V.P. Solution of modified equal width wave equation, its variant and non-homogeneous Burgers’ equation by RDT method. Am. J. Comput. Appl. Math. 2011, 1, 53–56. [Google Scholar] [CrossRef]
- Gardner, L.R.; Gardner, G.A. Solitary waves of the equal width wave equation. J. Comput. Phys. 1992, 101, 218–223. [Google Scholar] [CrossRef]
- Raslan, K.R. Collocation method using quartic B-spline for the equal width (EW) equation. Appl. Math. Comput. 2005, 168, 795–805. [Google Scholar] [CrossRef]
- Prabhakar, T.R. A singular integral equation with a generalized Mittag Leffler function in the kernel. Yokohama Math. J. 1971, 19, 7–15. [Google Scholar]
- Gorenflo, R.; Kilbas, A.A.; Mainardi, F.; Rogosin, S.V. Mittag-Leffler Functions, Related Topics and Applications; Springer: Berlin, Germany, 2014. [Google Scholar]
- Miskinis, P. The Havriliak-Negami susceptibility as a nonlinear and nonlocal process. Phys. Scr. 2009, 2009, 014019. [Google Scholar] [CrossRef]
- Garrappa, R.; Mainardi, F.; Guido, M. Models of dielectric relaxation based on completely monotone functions. Fract. Calc. Appl. Anal. 2016, 19, 1105–1160. [Google Scholar] [CrossRef]
- Stanislavsky, A.; Weron, K. Atypical case of the dielectric relaxation responses and its fractional kinetic equation. Fract. Calc. Appl. Anal. 2016, 19, 212–228. [Google Scholar] [CrossRef]
- Giusti, A.; Colombaro, I. Prabhakar-like fractional viscoelasticity. Commun. Nonlinear Sci. Numer. Simul. 2018, 6, 38–143. [Google Scholar] [CrossRef]
- D’Ovidio, M.; Polito, F. Fractional Diffusion-Telegraph Equations and Their Associated Stochastic Solutions. Theory Probab. Appl. 2018, 62, 552–574. [Google Scholar] [CrossRef]
- An, J.; Hese, E.V.; Baes, M. Phase-space consistency of stellar dynamical models determined by separable augmented densities. Mon. Not. R. Astron. Soc. 2012, 422, 652–664. [Google Scholar] [CrossRef][Green Version]
- Beghin, L.; Orsingher, E. Fractional Poisson processes and related planar random motions. Electron. J. Probab. 2009, 14, 1790–1826. [Google Scholar] [CrossRef]
- Górska, K.; Horzela, A.; Bratek, L.; Penson, K.A.; Dattoli, G. The probability density function for the Havriliak-Negami relaxation. arXiv 2016, arXiv:1611.06433. [Google Scholar]
- Shaikh, S.L. Introducing a new integral transform Sadik transform. Am. Int. J. Res. Sci. Technol. Eng. Math. 2018, 22, 100–102. [Google Scholar]
- Shaikh, S.L. Some applications of the new integral transform for Partial differential Equations. Math. J. Interdiscip. Sci. 2018, 7, 45–49. [Google Scholar] [CrossRef]
- Shaikh, S.L. Sadik transform in control theory. Int. J. Innov. Sci. Res. Technol. 2018, 3, 1–3. [Google Scholar]
- Jumarie, G. Laplace’s transform of fractional order via the Mittag-Leffler function and modified Riemann-Liouville derivative. Appl. Math. Lett. 2009, 22, 1659–1664. [Google Scholar] [CrossRef]
- Kexue, L.; Jigen, P. Laplace transform and fractional differential equations. Appl. Math. Lett. 2011, 24, 2019–2023. [Google Scholar] [CrossRef]
- Abhale, N.S.; Pawar, S.S. Fundamental properties of Sadik transform and it’s applications. J. Appl. Math. Comput. 2019, 6, 995–999. [Google Scholar]
- Lu, T.T.; Zheng, W.Q. Adomian decomposition method for first order PDEs with unprescribed data. Alex. Eng. J. 2020, 60, 2563–2572. [Google Scholar] [CrossRef]
- Li, W.; Pang, Y. Application of Adomian decomposition method to nonlinear systems. Adv. Differ. Equ. 2020, 2020, 67. [Google Scholar] [CrossRef]
- Zeidan, D.; Chau, C.K.; Lu, T.T.; Zheng, W.Q. Mathematical studies of the solution of Burgers’ equations by Adomian decomposition method. Math. Methods Appl. Sci. 2020, 43, 2171–2188. [Google Scholar] [CrossRef]
- Pasha, S.A.; Nawaz, Y.; Arif, M.S. The modified homotopy perturbation method with an auxiliary term for the nonlinear oscillator with discontinuity. J. Low Freq. Noise Vib. Act. Control 2019, 38, 1363–1373. [Google Scholar] [CrossRef]
- Veeresha, P.; Prakasha, D.G.; Kumar, D. An efficient technique for nonlinear time-fractional Klein-Fock-Gordon equation. Appl. Math. Comput. 2020, 364, 124637. [Google Scholar] [CrossRef]
- Yu, D.N.; He, J.H.; Garcıa, A.G. Homotopy perturbation method with an auxiliary parameter for nonlinear oscillators. J. Low Freq. Noise Vib. Act. Control 2019, 38, 1540–1554. [Google Scholar] [CrossRef]
- Khalid, M.; Khan, F.S.; Sultana, M. A highly accurate numerical method for solving nonlinear time-fractional differential difference equation. Math. Methods Appl. Sci. 2019, 44, 8243–8253. [Google Scholar] [CrossRef]
- Bhowmik, S.K.; Karakoc, S.B. Numerical solutions of the generalized equal width wave equation using the Petrov-Galerkin method. Appl. Anal. 2019, 21, 714–734. [Google Scholar] [CrossRef]
- GaziKarakoc, S.B.; Ali, K.K. Analytical and computational approaches on solitary wave solutions of the generalized equal width equation. Appl. Math. Comput. 2020, 71, 124933. [Google Scholar] [CrossRef]
- Anjum, N.; He, J.H. Laplace transform: Making the variational iteration method easier. Appl. Math. Lett. 2019, 1, 134–138. [Google Scholar] [CrossRef]
- Alomari, A.K.; Syam, M.I.; Anakira, N.R.; Jameel, A.F. Homotopy Sumudu transform method for solving applications in physics. Results Phys. 2020, 18, 103265. [Google Scholar] [CrossRef]
- Eshaghi, J.; Kazem, S.; Adibi, H. The local discontinuous Galerkin method for 2D nonlinear time-fractional advection-diffusion equations. Eng. Comput. 2019, 35, 1317–1332. [Google Scholar] [CrossRef]
- Goyal, M.; Prakash, A.; Gupta, S. An Efficient Perturbation Sumudu Transform Technique for the Time-Fractional Vibration Equation with a Memory Dependent Fractional Derivative in Liouville–Caputo Sense. Int. J. Appl. Comput. Math. 2021, 7, 156. [Google Scholar] [CrossRef]
- Prakash, A.; Goyal, M.; Gupta, S. Fractional variational iteration method for solving time-fractional Newell-Whitehead-Segel equation. Nonlinear Eng. 2019, 8, 164–171. [Google Scholar] [CrossRef]
- Prakash, A.; Kaur, H. A New Numerical Method for a Fractional Model of Non-Linear Zakharov–Kuznetsov Equations via Sumudu Transform. In Methods of Mathematical Modelling: Fractional Differential Equations; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Redhwan, S.S.; Shaikh, S.L.; Abdo, M.S. Some properties of Sadik transform and its applications of fractional-order dynamical systems in control theory. Adv. Theory Nonlinear Anal. Its Appl. 2019, 4, 51–66. [Google Scholar] [CrossRef]
- Ghorbani, A. Beyond Adomian polynomials: He polynomials. Chaos Solitons Fractals 2009, 39, 1486–1492. [Google Scholar] [CrossRef]
- Bhatter, S.; Mathur, A.; Kumar, D.; Nisar, K.S.; Singh, J. Fractional modified Kawahara equation with Mittag-Leffler law. Chaos Solitons Fractals 2020, 131, 109508. [Google Scholar] [CrossRef]
- Jin, L. Application of variational iteration method and homotopy perturbation method to the modified Kawahara equation. Math. Comput. Model. 2009, 49, 573–578. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Kosari, S.; Shafi, J.; Derakhshan, M.H. Stability Analysis Study of Time-Fractional Nonlinear Modified Kawahara Equation Based on the Homotopy Perturbation Sadik Transform. Fractal Fract. 2024, 8, 512. https://doi.org/10.3390/fractalfract8090512
Chen Z, Kosari S, Shafi J, Derakhshan MH. Stability Analysis Study of Time-Fractional Nonlinear Modified Kawahara Equation Based on the Homotopy Perturbation Sadik Transform. Fractal and Fractional. 2024; 8(9):512. https://doi.org/10.3390/fractalfract8090512
Chicago/Turabian StyleChen, Zhihua, Saeed Kosari, Jana Shafi, and Mohammad Hossein Derakhshan. 2024. "Stability Analysis Study of Time-Fractional Nonlinear Modified Kawahara Equation Based on the Homotopy Perturbation Sadik Transform" Fractal and Fractional 8, no. 9: 512. https://doi.org/10.3390/fractalfract8090512
APA StyleChen, Z., Kosari, S., Shafi, J., & Derakhshan, M. H. (2024). Stability Analysis Study of Time-Fractional Nonlinear Modified Kawahara Equation Based on the Homotopy Perturbation Sadik Transform. Fractal and Fractional, 8(9), 512. https://doi.org/10.3390/fractalfract8090512







