Shallow-Water Wave Dynamics: Butterfly Waves, X-Waves, Multiple-Lump Waves, Rogue Waves, Stripe Soliton Interactions, Generalized Breathers, and Kuznetsov–Ma Breathers
Abstract
1. Introduction
2. Bright and Dark Lump Waves
3. Bright–Dark Lump with Periodic Waves (BLPs)
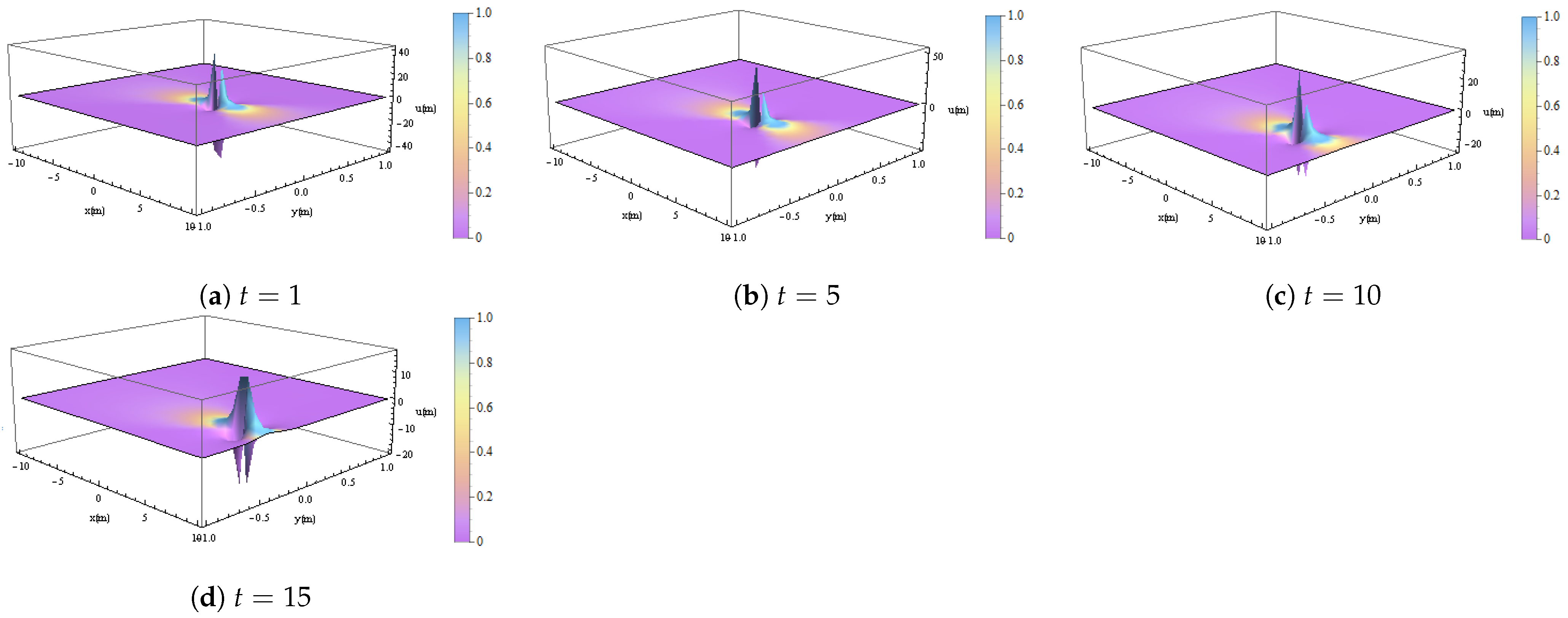
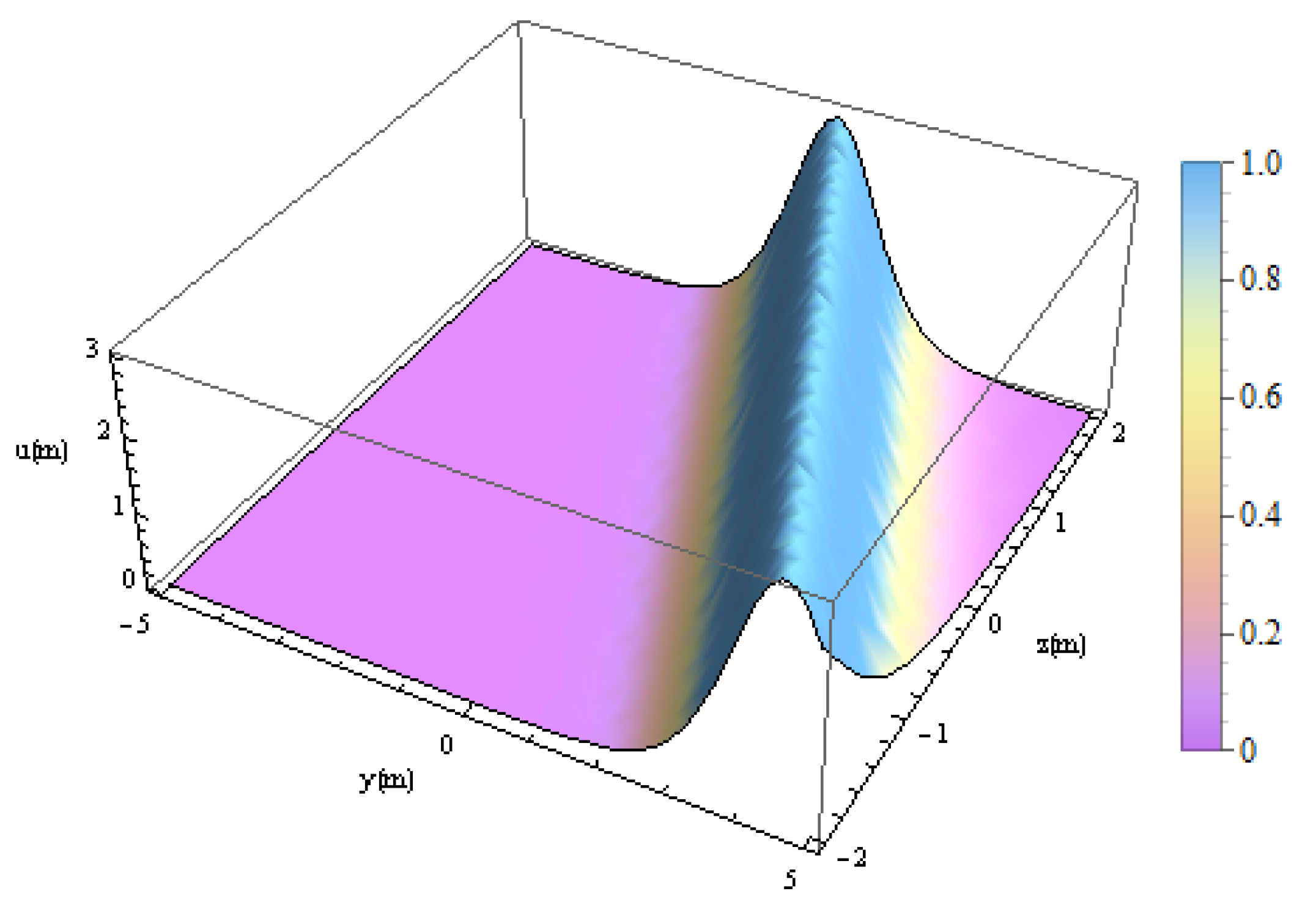
4. Rogue Wave (RW)
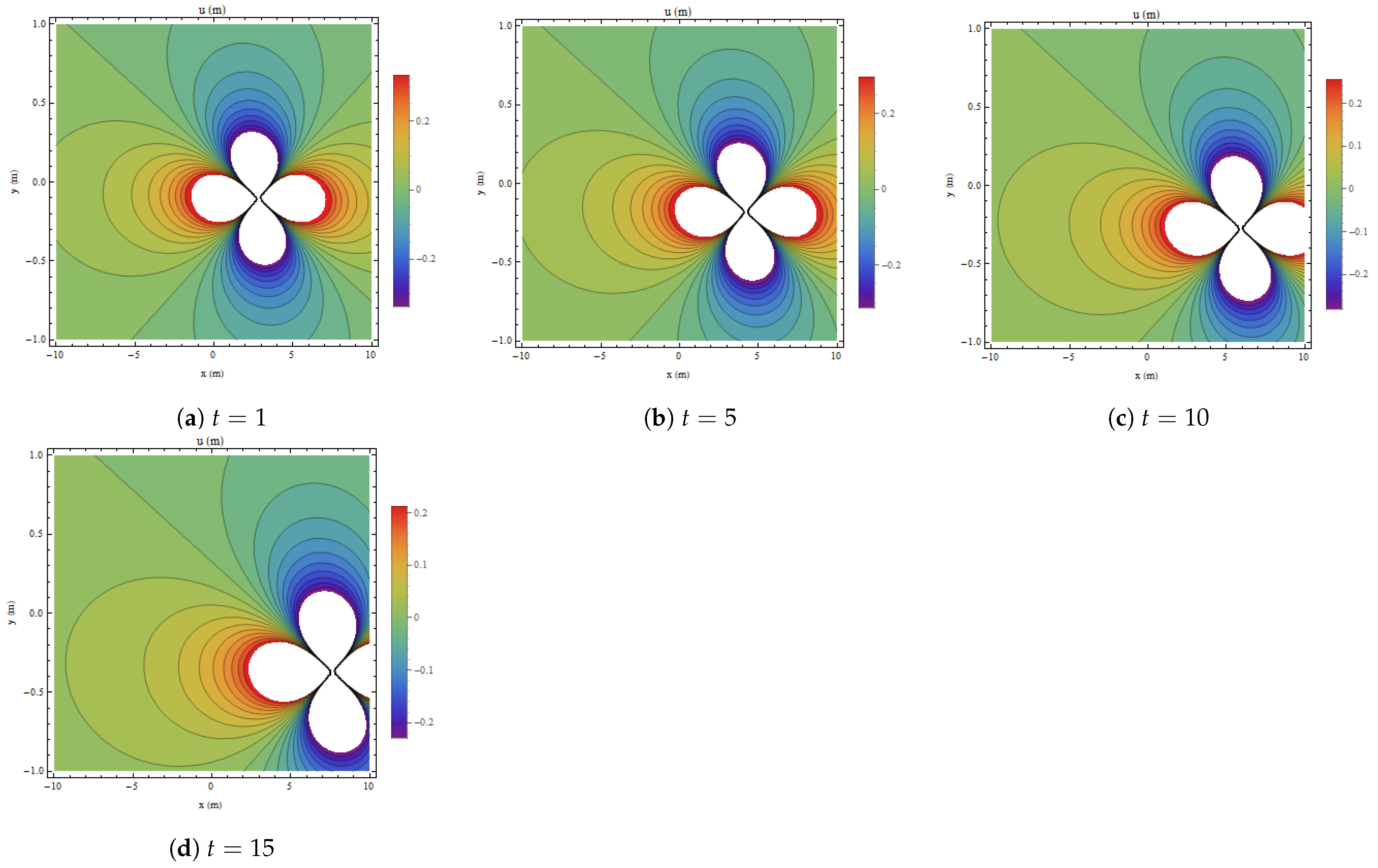
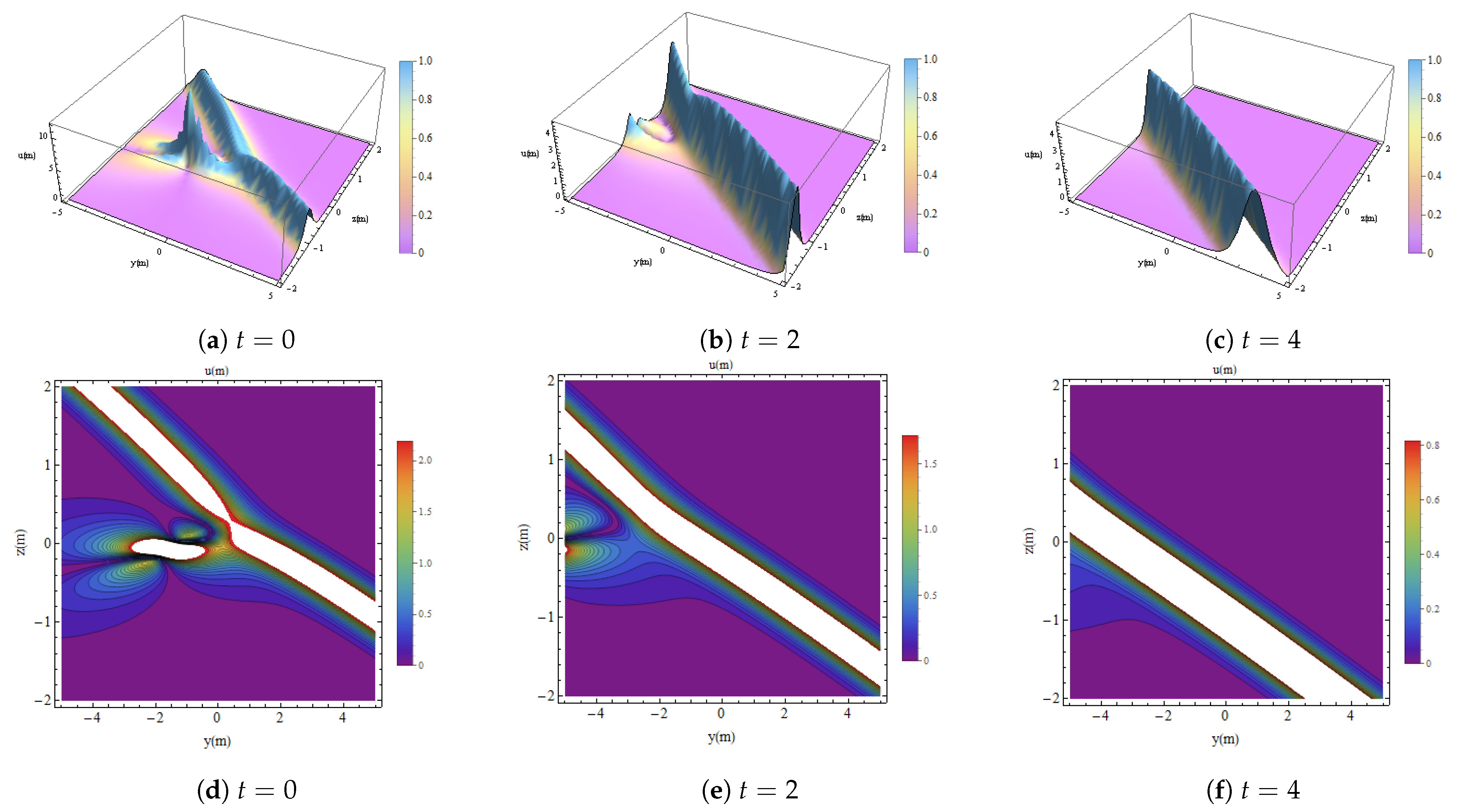
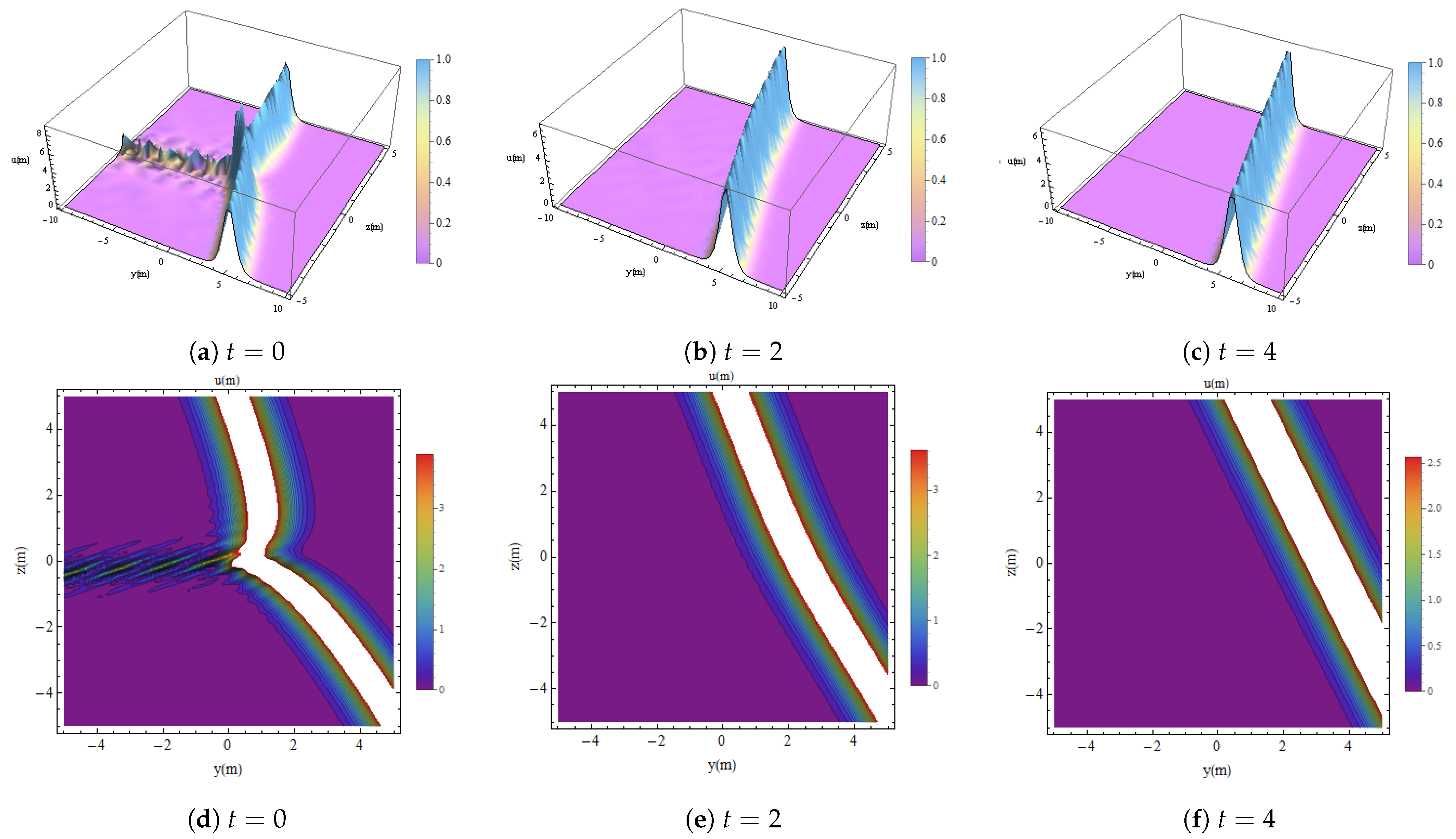
5. Lump One-Strip Soliton Interaction (L1SI)
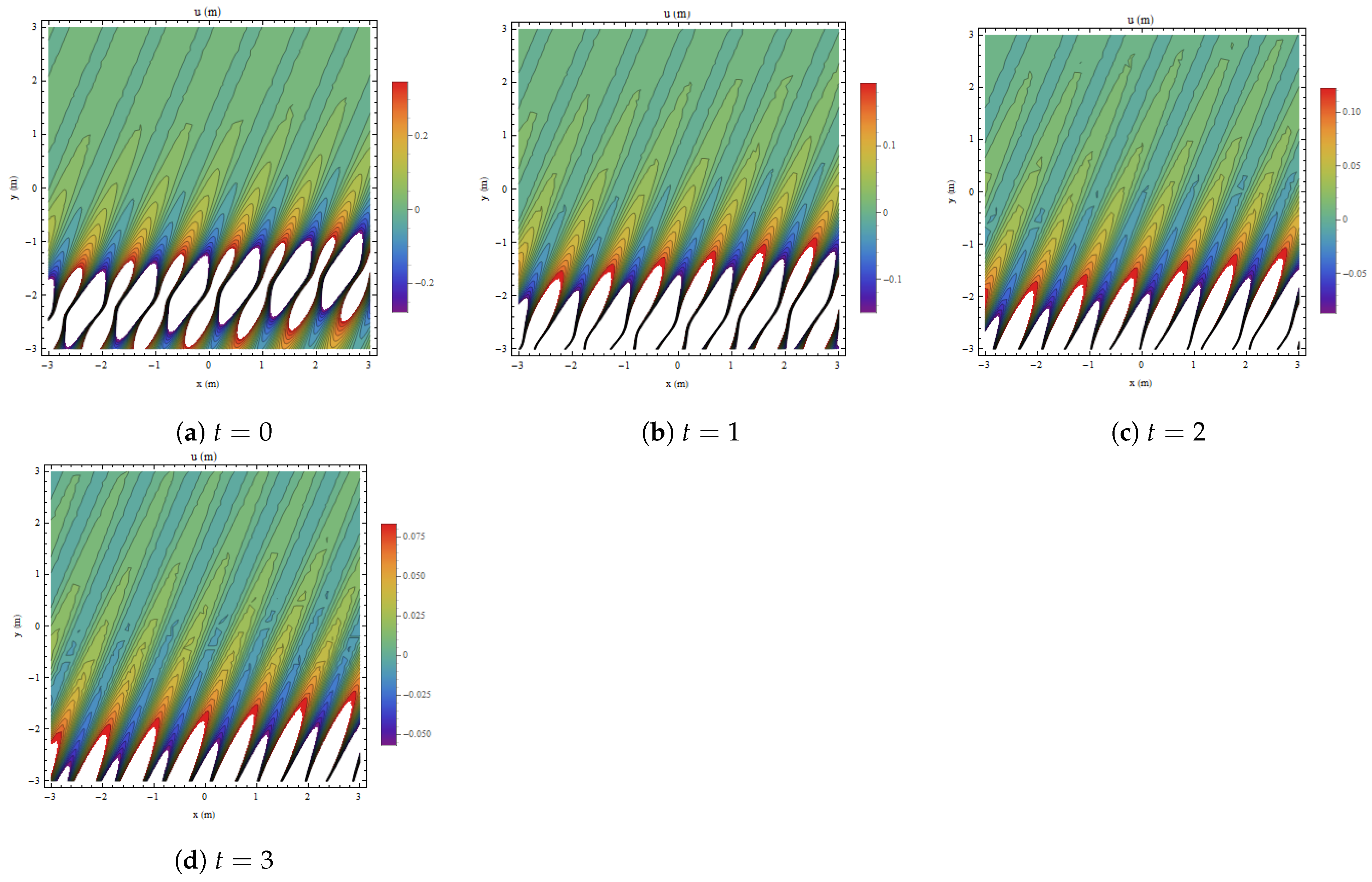
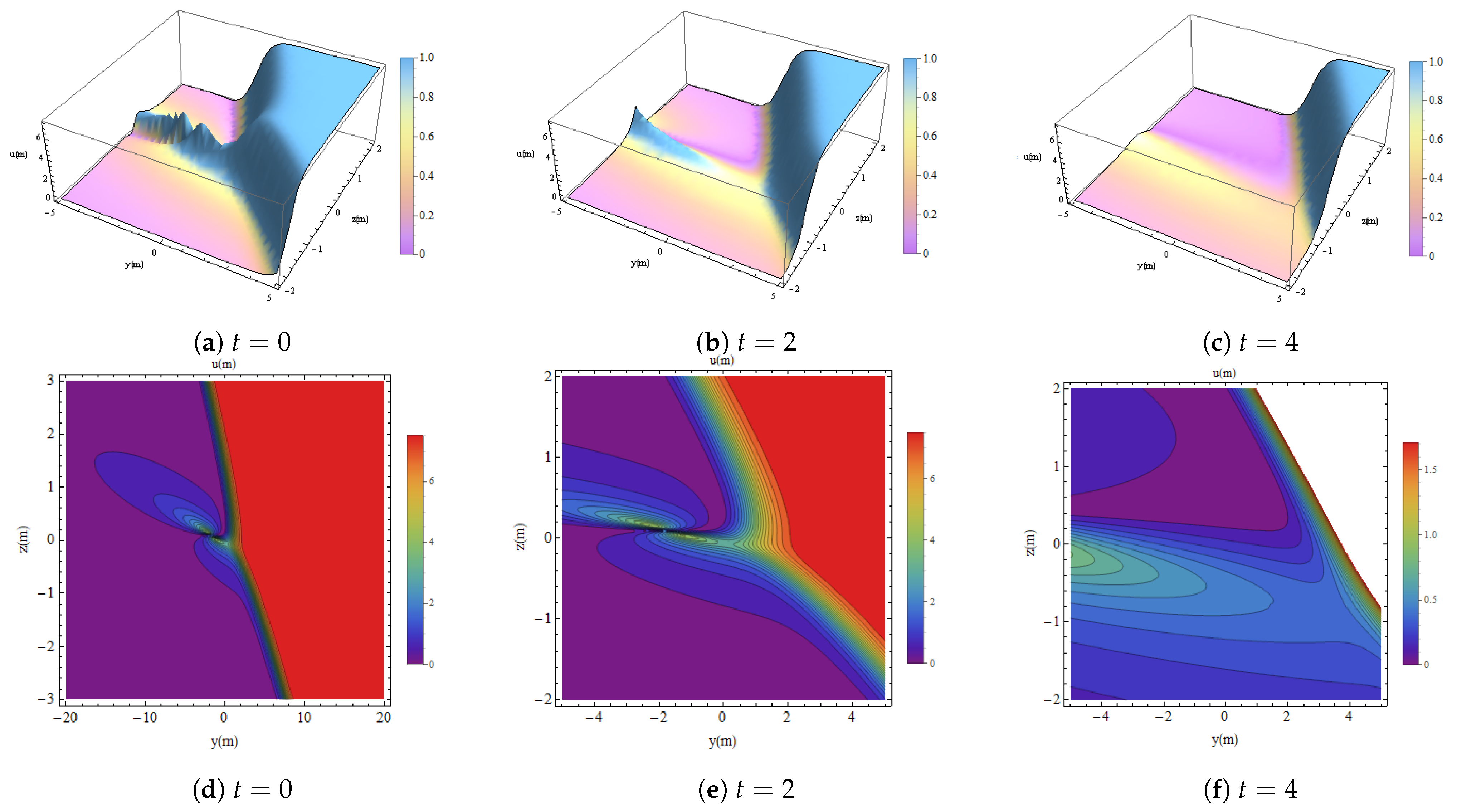
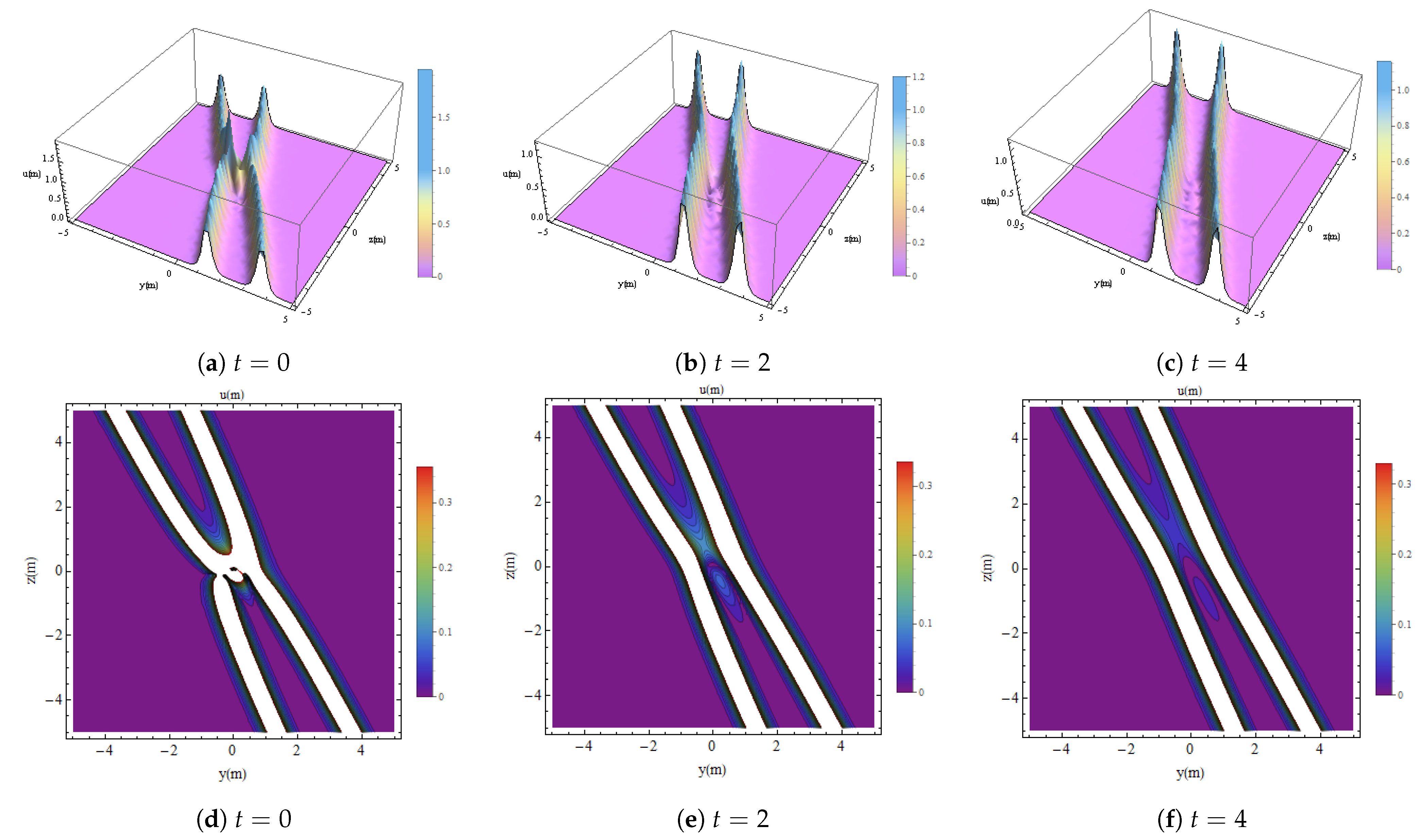
6. Lump Two-Strip Soliton Interaction (L2SI)
7. Interaction Between Lump, Periodic, and Strip Waves
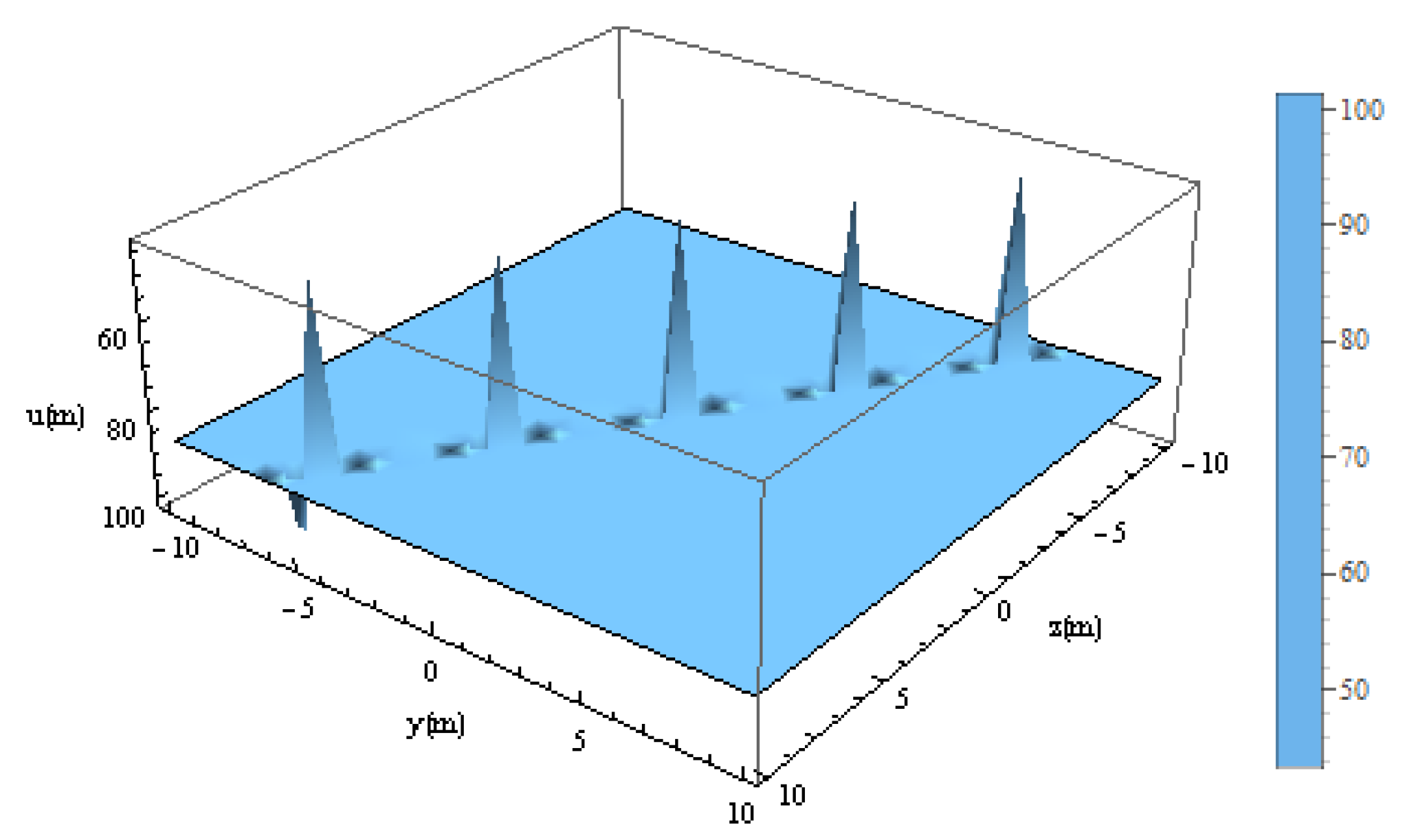
8. Interaction Between Lump, RWs, and Strip Waves
9. Ma Breather (MB) and the Associated RW
10. Kuznetsov–Ma Breather (KMB) and the Associated RW
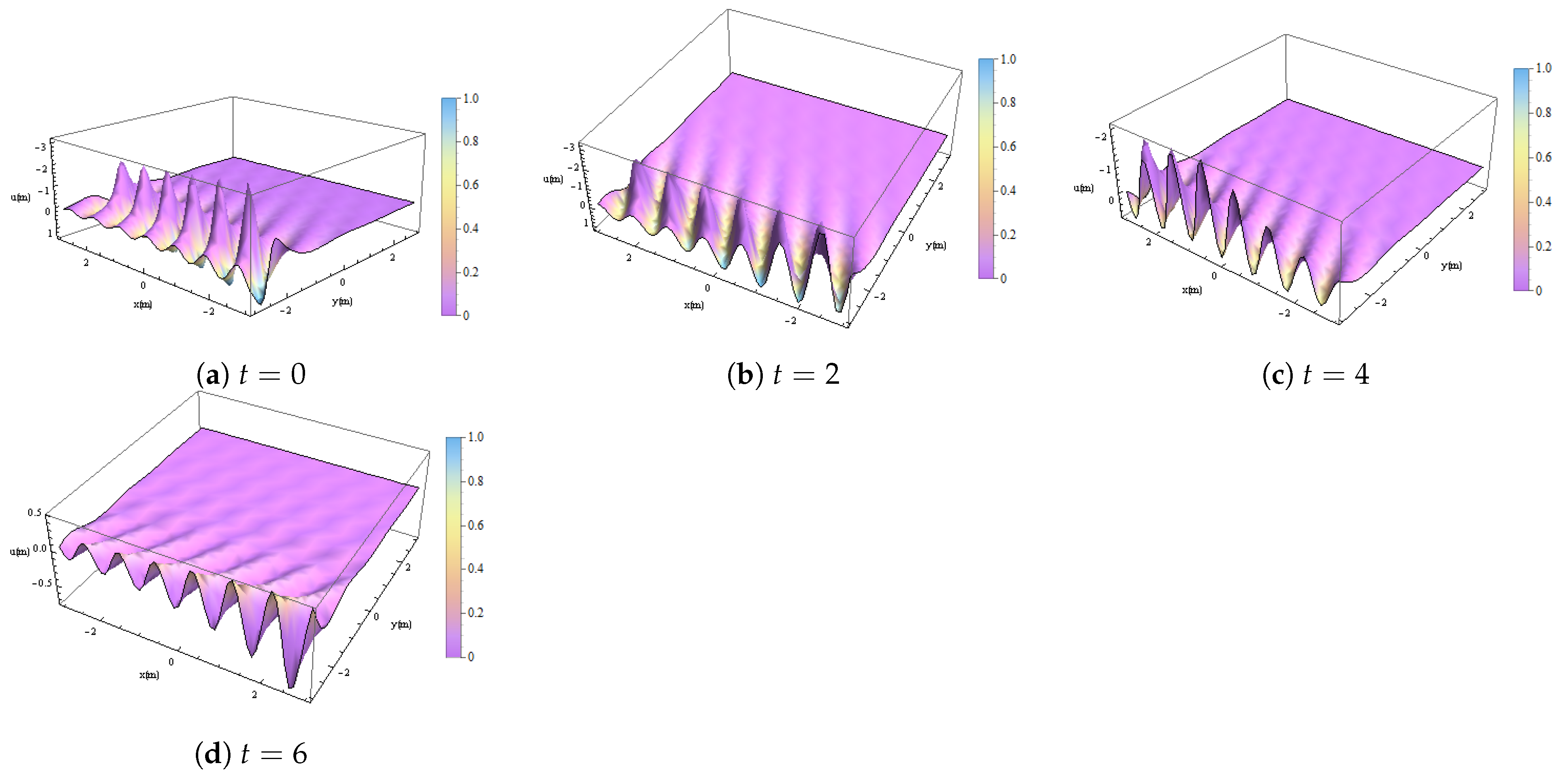
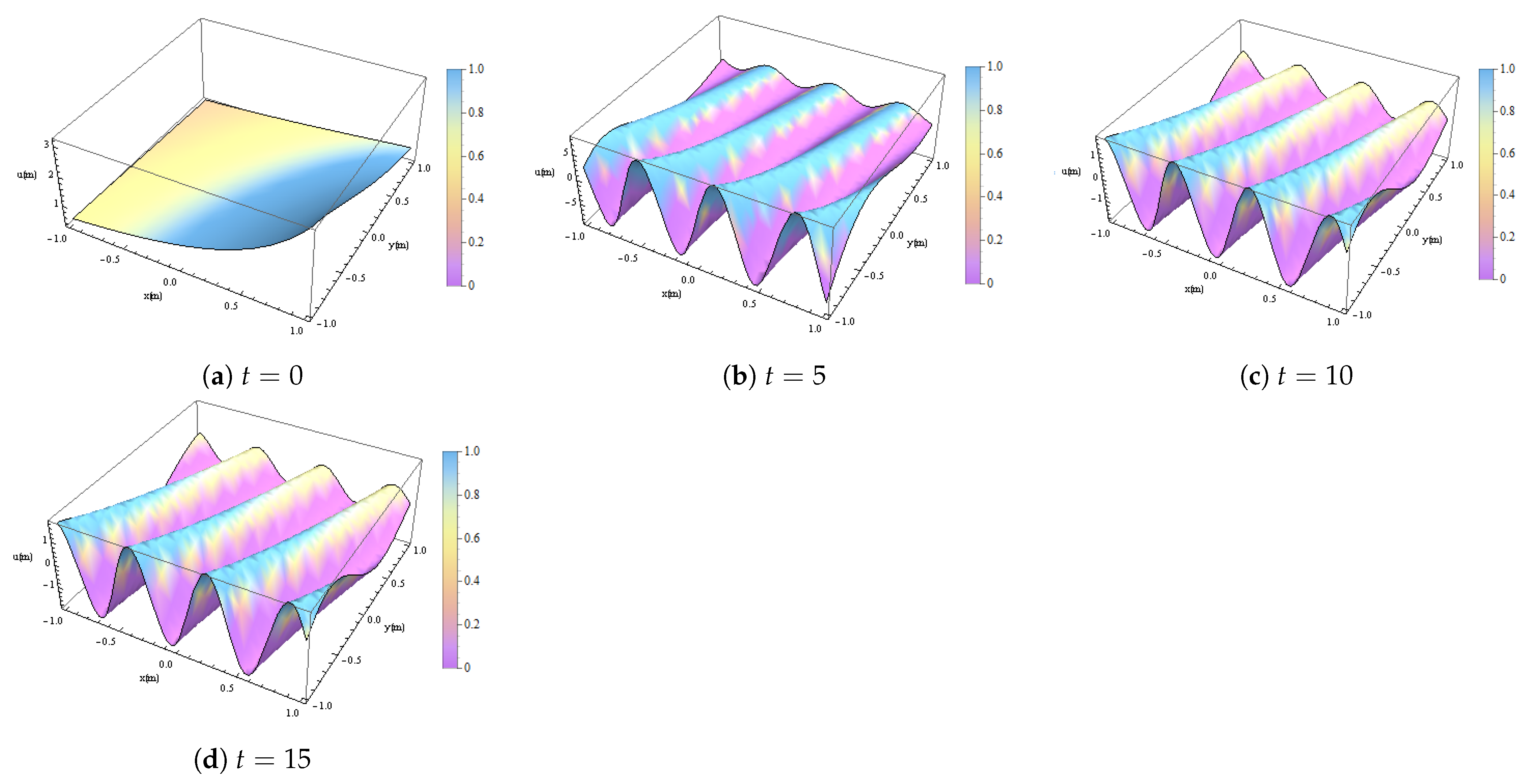
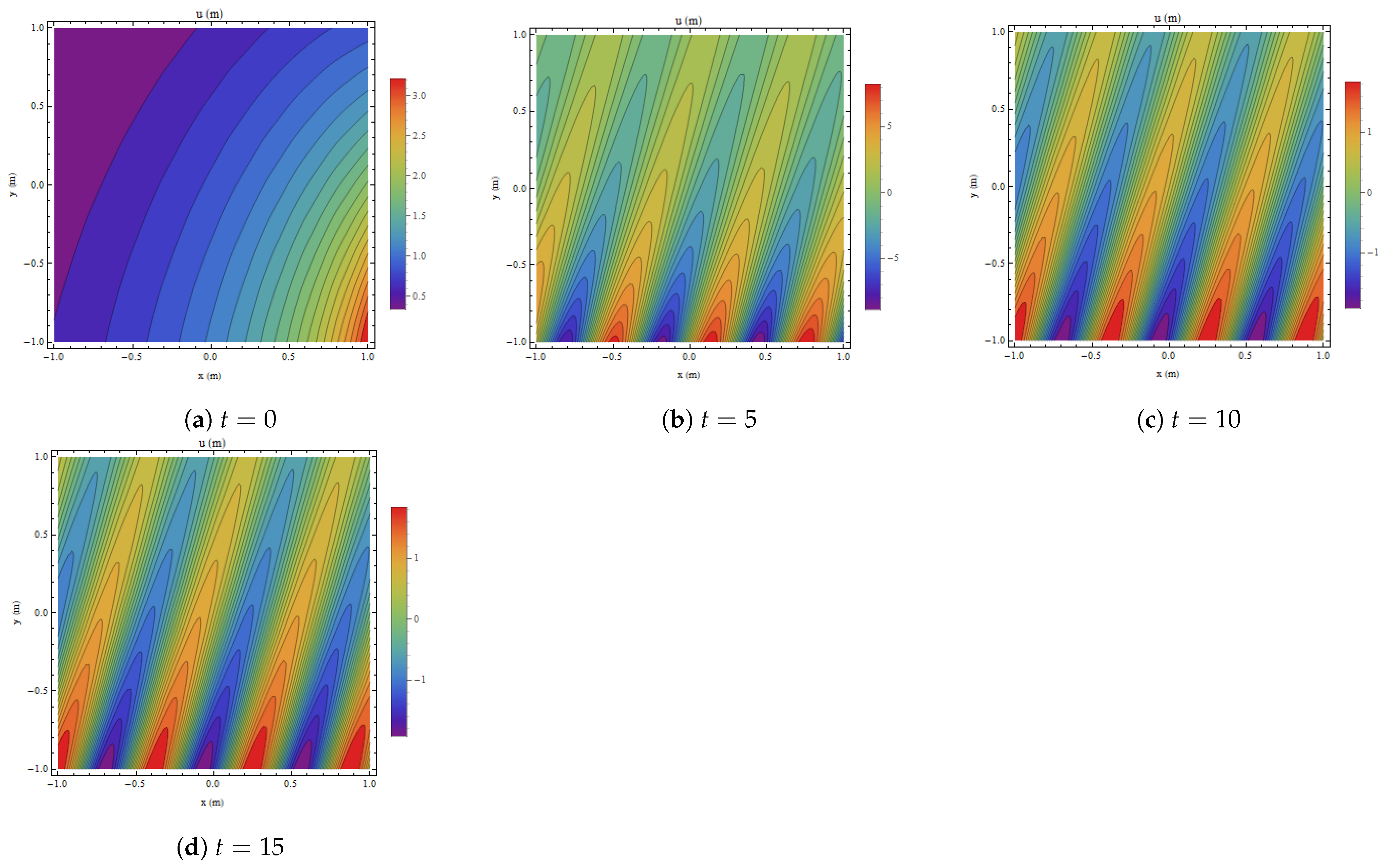
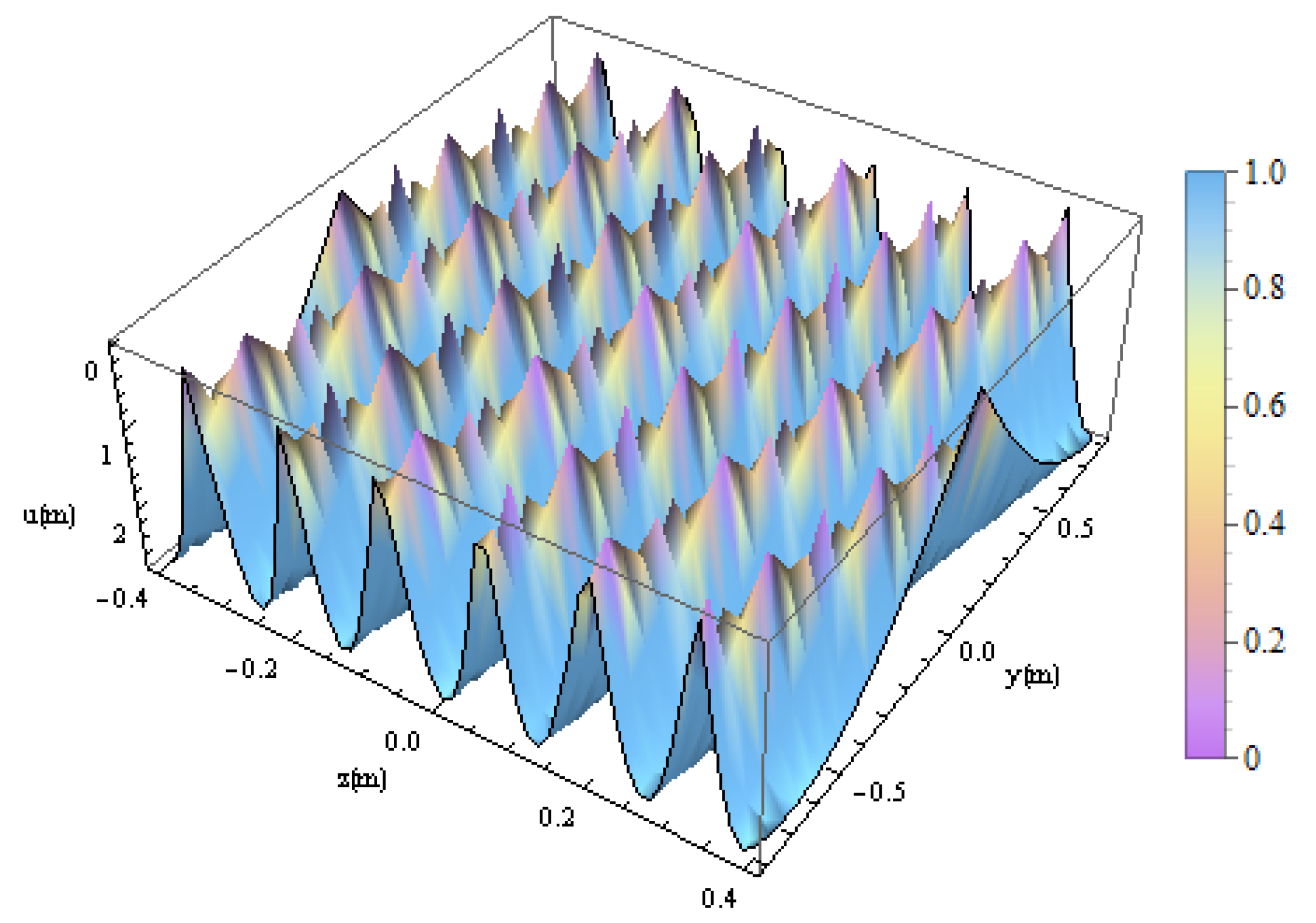
11. GBs
12. Symbolic Computation with Ansatz Function Technique
13. Solitary Waves (SWs)
14. Energy of the Wave
Energy of the Rogue Wave
15. Discussions
16. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bertoldi, K.; Vitelli, V.; Christensen, J.; Van Hecke, M. Flexible mechanical metamaterials. Nat. Rev. Mater. 2017, 11, 1–11. [Google Scholar] [CrossRef]
- Holmes, D.P. Elasticity and stability of shape-shifting structures. Curr. Opin. Colloid Interface Sci. 2019, 40, 118–137. [Google Scholar] [CrossRef]
- Deng, B.; Raney, J.R.; Tournat, V.; Bertoldi, K. Elastic vector solitons in soft architected materials. Phys. Rev. Lett. 2017, 18, 204102. [Google Scholar] [CrossRef] [PubMed]
- Deng, B.; Wang, P.; He, Q.; Tournat, V.; Bertoldi, K. Metamaterials with amplitude gaps for elastic solitons. Nat. Commun. 2018, 9, 3410. [Google Scholar] [CrossRef]
- Raney, J.R.; Nadkarni, N.; Daraio, C.; Kochmann, D.M.; Lewis, J.A.; Bertoldi, K. Stable propagation of mechanical signals in soft media using stored elastic energy. Proc. Natl. Acad. Sci. USA 2016, 113, 9722–9727. [Google Scholar] [CrossRef]
- Edelman, M. Comments on A note on stability of fractional logistic maps. Appl. Math. Lett. 2022, 125, 107787. [Google Scholar]
- Shen, S.; Yang, Z.J.; Pang, Z.G.; Ge, Y.R. The complex-valued astigmatic cosine-Gaussian soliton solution of the nonlocal nonlinear Schrödinger equation and its transmission characteristics. Appl. Math. Lett. 2022, 125, 107755. [Google Scholar] [CrossRef]
- Song, L.M.; Yang, Z.J.; Li, X.L.; Zhang, S.M. Coherent superposition propagation of Laguerre–Gaussian and Hermite–Gaussian solitons. Appl. Math. Lett. 2020, 102, 106114. [Google Scholar] [CrossRef]
- Shen, S.; Yang, Z.; Li, X.; Zhang, S. Periodic propagation of complex-valued hyperbolic-cosine-Gaussian solitons and breathers with complicated light field structure in strongly nonlocal nonlinear media. Commun. Nonlinear Sci. Numer. Simul. 2021, 103, 106005. [Google Scholar] [CrossRef]
- Yi, H.; Yao, Y.; Zhang, X.; Ma, G. High-order effect on the transmission of two optical solitons. Chin. Phys. B 2023, 32, 100509. [Google Scholar] [CrossRef]
- Li, X.L.; Guo, R. Interactions of Localized Wave Structures on Periodic Backgrounds for the Coupled Lakshmanan–Porsezian–Daniel Equations in Birefringent Optical Fibers. Ann. Phys. 2023, 535, 2200472. [Google Scholar] [CrossRef]
- Ahmed, S.; Seadawy, A.R.; Rizvi, S.T. Study of breathers, rogue waves and lump solutions for the nonlinear chains of atoms. Opt. Quantum Electron. 2022, 4, 1–28. [Google Scholar] [CrossRef]
- Seadawy, A.R.; Rizvi, S.T.; Ahmed, S. Weierstrass and Jacobi elliptic, bell and kink type, lumps, Ma and Kuznetsov breathers with rogue wave solutions to the dissipative nonlinear Schrödinger equation. Chaos Solitons Fractals 2022, 160, 112258. [Google Scholar] [CrossRef]
- Seadawy, A.R.; Rizvi, S.T.; Ahmed, S. Multiple lump, generalized breathers, Akhmediev breather, manifold periodic and rogue wave solutions for generalized Fitzhugh-Nagumo equation: Applications in nuclear reactor theory. Chaos Solitons Fractals 2022, 161, 112326. [Google Scholar] [CrossRef]
- Ma, Y.L. N-solitons, breathers and rogue waves for a generalized Boussinesq equation. Int. J. Comput. Math. 2020, 97, 1648–1661. [Google Scholar] [CrossRef]
- Seadawy, A.R.; Rizvi, S.T.; Ahmed, S.; Bashir, A. Lump solutions, Kuznetsov–Ma breathers, rogue waves and interaction solutions for magneto electro-elastic circular rod. Chaos Solitons Fractals 2022, 163, 112563. [Google Scholar] [CrossRef]
- Hietarinta, J. Introduction to the Hirota bilinear method. In Integrability of Nonlinear Systems; Springer: Berlin/Heidelberg, Germany, 1997; Volume 1, pp. 95–103. [Google Scholar]
- Zuo, J.M.; Zhang, Y.M. The Hirota bilinear method for the coupled Burgers equation and the high-order Boussinesq—Burgers equation. Chin. Phys. B 2011, 20, 010205. [Google Scholar] [CrossRef]
- Liu, Y.; Wen, X.Y.; Wang, D.S. The N-soliton solution and localized wave interaction solutions of the (2+1)-dimensional generalized Hirota-Satsuma equation. Comput. Math. Appl. 2019, 77, 947–966. [Google Scholar] [CrossRef]
- Li, B.Q.; Ma, Y.L. Hybrid soliton and breather waves, solution molecules and breather molecules of a (3 + 1)-dimensional Geng equation in shallow water waves. Phys. Lett. A 2023, 52, 106822. [Google Scholar] [CrossRef]
- Ahmed, S.; Seadawy, A.R.; Rizvi, S.T.; Mubaraki, A.M. Homoclinic breathers and soliton propagations for the nonlinear (3 + 1)-dimensional Geng dynamical equation. Results Phys. 2023, 20, 106822. [Google Scholar] [CrossRef]
- Geng, X. Algebraic-geometrical solutions of some multidimensional nonlinear evolution equations. J. Phys. A Math. Gen. 2003, 36, 2289. [Google Scholar] [CrossRef]
- Yin, Y.H.; Lü, X.; Ma, W.X. Bäcklund transformation, exact solutions and diverse interaction phenomena to a (3 + 1)-dimensional nonlinear evolution equation. Nonlinear Dyn. 2022, 108, 4181. [Google Scholar] [CrossRef]
- Bai, C.L.; Zhao, H. Generalized method to construct the solitonic solutions to (3 + 1)-dimensional nonlinear equation. Phys. Lett. A 2006, 354, 428. [Google Scholar] [CrossRef]
- Ahmed, I.; Seadawy, A.R.; Lu, D. Kinky breathers, W-shaped and multi-peak solitons interaction in (2+1)-dimensional nonlinear Schrödinger equation with Kerr law of nonlinearity. Eur. Phys. J. Plus 2019, 134, 1. [Google Scholar] [CrossRef]
- Johnson, R.S. A Modern Introduction to the Mathematical Theory of Water Waves; Cambridge University Press: Cambridge, UK, 1997; Volume 1, p. 19. [Google Scholar]
- Dodd, R.K.; Eilbeck, J.C.; Gibbon, J.D.; Morris, H.C. Solitons and Nonlinear Wave Equations. J. Appl. Math. Mech. 1985, 65, 354. [Google Scholar] [CrossRef]
- Benjamin, T.B. The stability of solitary waves. Proc. R. Soc. Lond. Math. Phys. Sci. 1972, 328, 153. [Google Scholar]
- Huang, X.; Chen, Z.; Zhao, W.; Zhang, Z.; Zhou, C.; Yang, Q.; Tian, J. An extreme internal solitary wave event observed in the northern South China Sea. Sci. Rep. 2016, 6, 30041. [Google Scholar] [CrossRef]
- Beer, F.P.; Johnston, E.R.; DeWolf, J.T.; Mazurek, D.F.; Sanghi, S. Mechanics of Materials; Mcgraw-Hill: New York, NY, USA, 1992. [Google Scholar]
- American Society of Civil Engineers. Minimum Design Loads and Associated Criteria for Buildings and Other Structures; American Society of Civil Engineers: Reston, VA, USA, 2020. [Google Scholar]
- Gulvanessian, H.; Calgaro, J.A.; Holický, M. Designers Guide to Eurocode: Basis of Structural Design: EN 1990; ICE Publishing: Washington, DA, USA, 2012. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, S.; Rehman, U.; Fei, J.; Khalid, M.I.; Chen, X. Shallow-Water Wave Dynamics: Butterfly Waves, X-Waves, Multiple-Lump Waves, Rogue Waves, Stripe Soliton Interactions, Generalized Breathers, and Kuznetsov–Ma Breathers. Fractal Fract. 2025, 9, 31. https://doi.org/10.3390/fractalfract9010031
Ahmed S, Rehman U, Fei J, Khalid MI, Chen X. Shallow-Water Wave Dynamics: Butterfly Waves, X-Waves, Multiple-Lump Waves, Rogue Waves, Stripe Soliton Interactions, Generalized Breathers, and Kuznetsov–Ma Breathers. Fractal and Fractional. 2025; 9(1):31. https://doi.org/10.3390/fractalfract9010031
Chicago/Turabian StyleAhmed, Sarfaraz, Ujala Rehman, Jianbo Fei, Muhammad Irslan Khalid, and Xiangsheng Chen. 2025. "Shallow-Water Wave Dynamics: Butterfly Waves, X-Waves, Multiple-Lump Waves, Rogue Waves, Stripe Soliton Interactions, Generalized Breathers, and Kuznetsov–Ma Breathers" Fractal and Fractional 9, no. 1: 31. https://doi.org/10.3390/fractalfract9010031
APA StyleAhmed, S., Rehman, U., Fei, J., Khalid, M. I., & Chen, X. (2025). Shallow-Water Wave Dynamics: Butterfly Waves, X-Waves, Multiple-Lump Waves, Rogue Waves, Stripe Soliton Interactions, Generalized Breathers, and Kuznetsov–Ma Breathers. Fractal and Fractional, 9(1), 31. https://doi.org/10.3390/fractalfract9010031





