The Relationship Between the Fractal Dimension and the Evolution of Rock-Forming Minerals Crystallization on the Example of the Northwestern Part of the Lovozero Intrusion
Abstract
1. Introduction
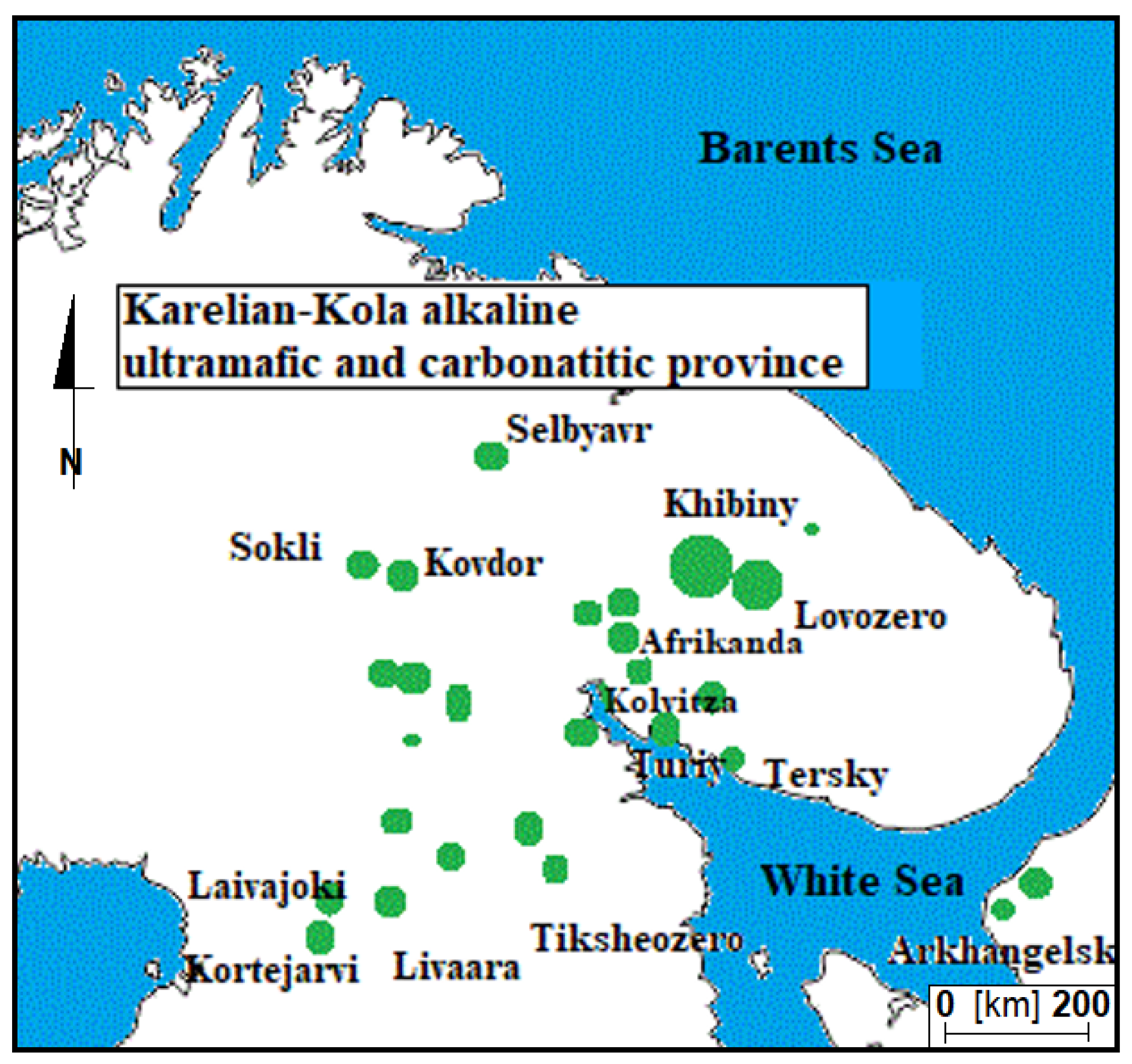
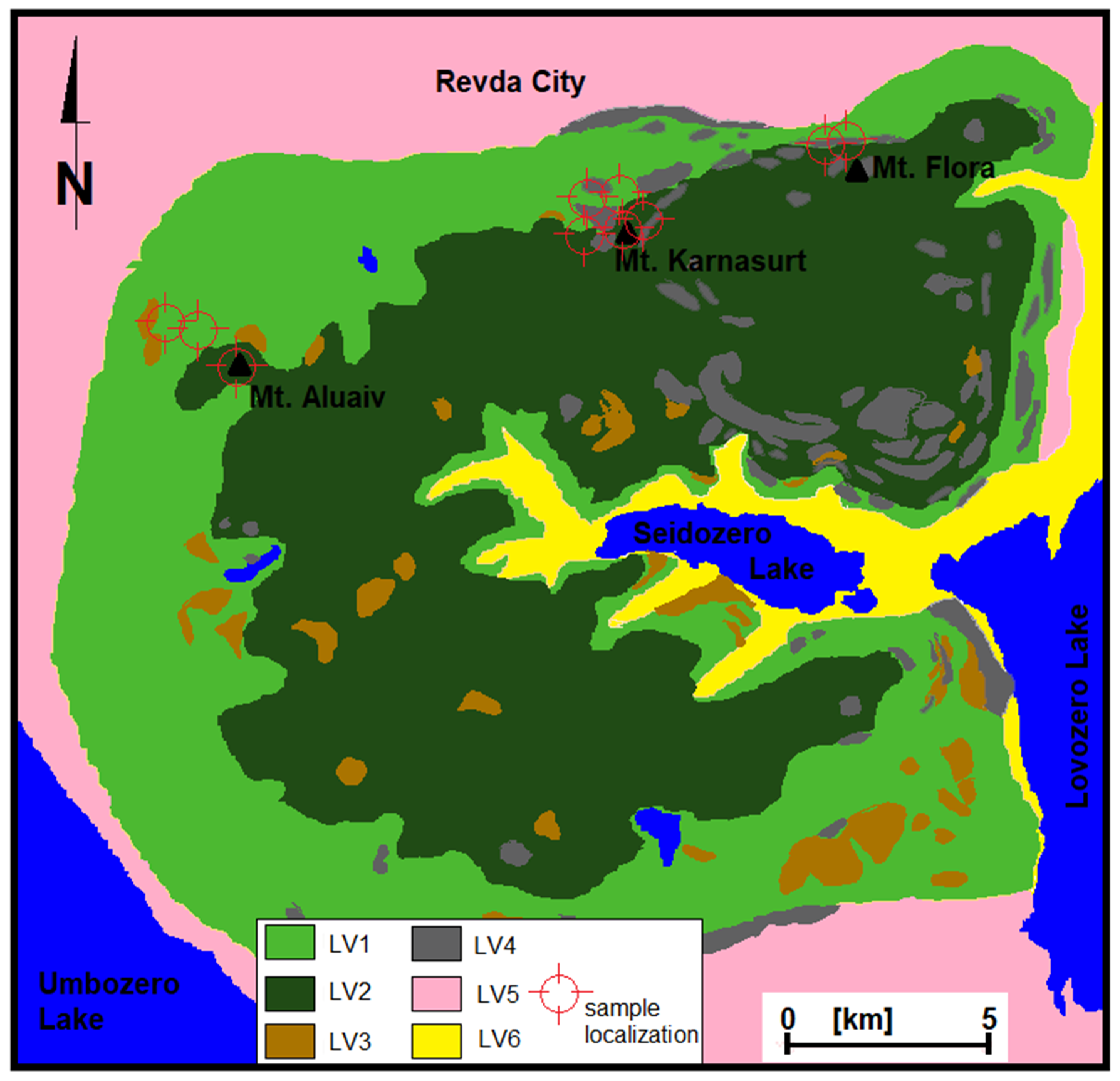
2. Geology of the Lovozero Massif
3. Type of Analyzed Rocks
3.1. Massive Syenites
3.2. Nepheline-Aegirine Foyaites
3.3. Aegirine Nepheline Lujavrites
3.4. Aegirine Eudialyte Lujavrites
3.5. Aegirine Eudialyte Foyaites
3.6. Jovites
3.7. Augitic Porphyrites
3.8. Vein Rocks
4. Materials and Methods
- 1.
- Sampling and field observation.
- 2.
- Making thin section plates of rocks.
- 3.
- Selecting minerals for testing and taking micrographs.
- 4.
- Petrographic analyses and selection of minerals.
- 5.
- Assessment of the size of minerals for fractal analysis (if the minerals are too small, a micrograph can be taken at point 3 with a different magnification).
- 6.
- Performing fractal analysis.
- 7.
- Further interpretation in combination with petrographic knowledge obtained from observations.
5. Results
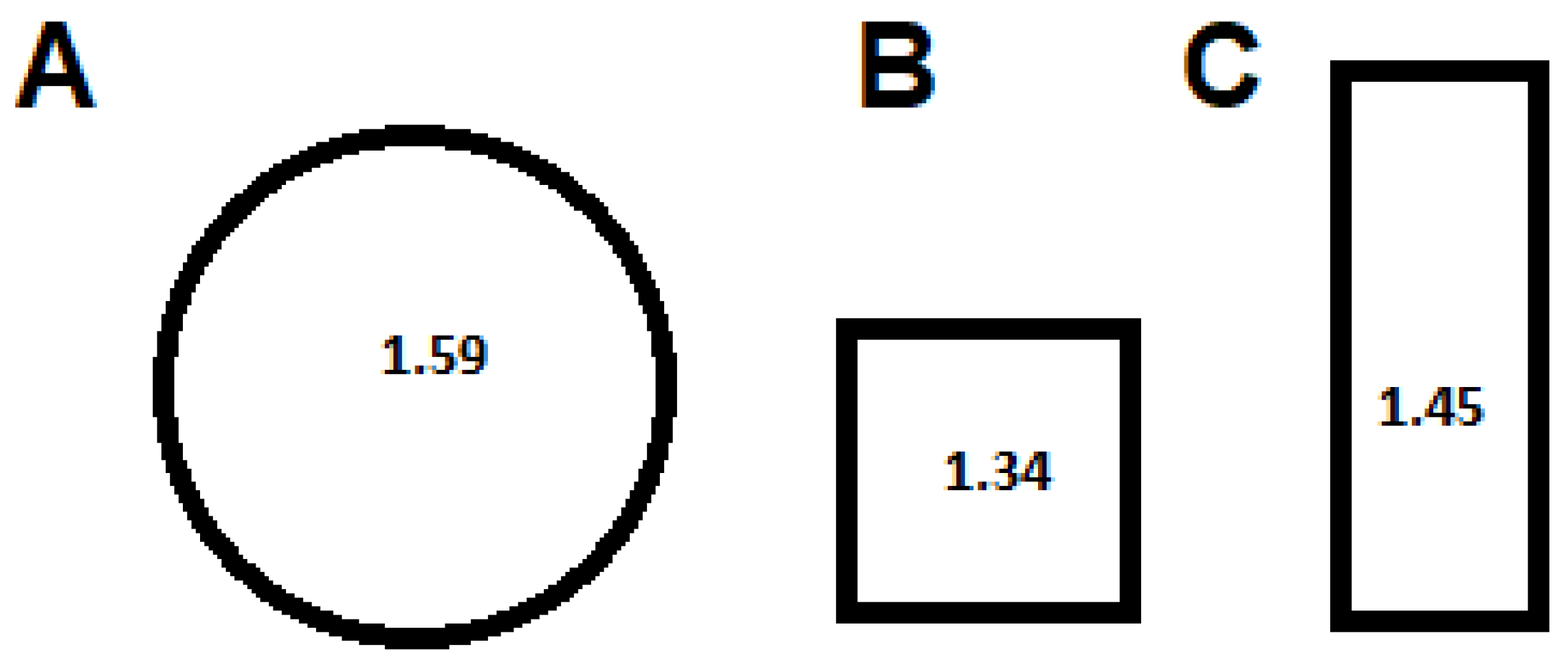
5.1. Identification of the Shape of the Rock-Forming Minerals in the Studied Rocks
5.2. Calculated Fractal Dimension Results for Syenite Rock-Forming Minerals
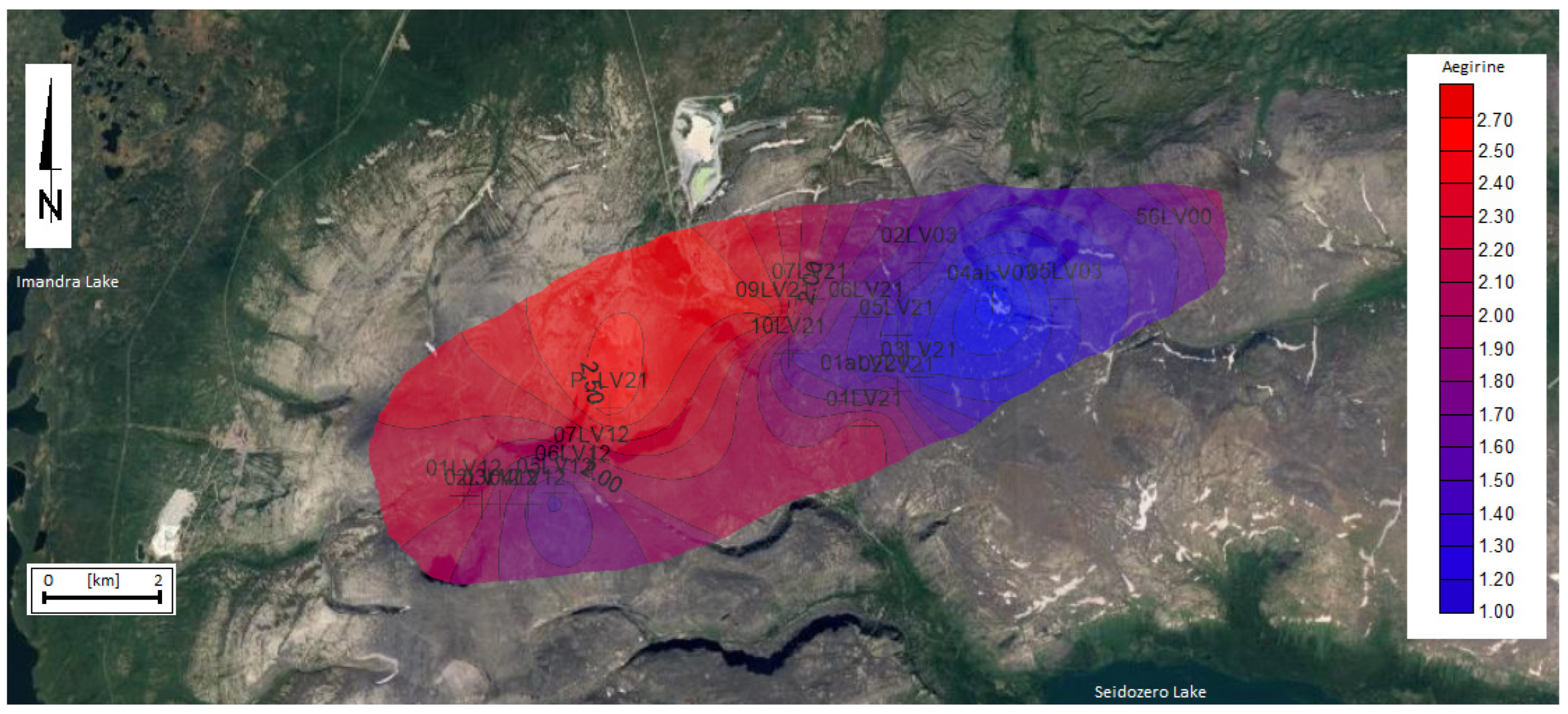
5.3. Distribution of Fractal Dimension Maps of the Crystals and the Interpretation of These Data
5.4. Interpretation of Fractal Distribution of Crystals in a Discussion of Intrusion Evolution
6. Discussion
7. Conclusions
- The authors demonstrated the possibility of displaying the shape of the studied rock-forming minerals in the form of a digital indicator, which is measured in a repeatable and precise manner, regardless of the human factor.
- Changes in the fractal dimension coefficient were documented, which can be correlated with a specific type of rock (significant differences for the layered zone and porphyrites).
- Visualization of these results showed the diversity of the fractal dimension coefficient within individual rock types. This allowed the interpretation of areas with different intensity of post-magmatic and metasomatic processes. The correlation of these areas coincides with prospective places of REE mineralization, which was performed in a conventional way.
- Correlation of changes in the fractal dimension coefficient with the results of classical petrographic descriptions allows for the determination of zones characterized by different textural properties of rocks, which can be the basis for further interpretation and application of these data.
- This method is complementary to the classical petrographic description, supplementing it with precise spatial data.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Vladykin, N. Alkaline Rocks, Kimberlites and Carbonatites: Geochemistry and Genesis; Springer Nature: Cham, Switzerland, 2022; p. 262. [Google Scholar]
- Kukharenko, A.A. The Caledonian Complex of Ultrabasic and Alkaline Rocks and Carbonatites of the Kola Peninsula and Northern Karelia; Nedra: Moskov, Russia, 1965; p. 215. (In Russian) [Google Scholar]
- Kogarko, L.N. Alkaline Rocks of the Eastern of Baltic Shield (Kola Peninsula); Special Publications; Geological Society: London, UK, 1987; Volume 30, pp. 531–544. [Google Scholar]
- Kogarko, L.N.; Kononova, V.A.; Orlova, M.P.; Woolley, A.R. Alkaline Rocks and Carbonatites of the World: Former USSR; Chapman & Hall: London, UK, 1995; p. 22. [Google Scholar]
- Rebetsky, Y.L.; Sim, L.A.; Kozyrev, A.A. Possible mechanism of horizontal overpressure generation of the Khibiny, Lovozero, and Kovdor ore clusters on the Kola Peninsula. Geol. Ore Depos. 2017, 59, 265–280. [Google Scholar] [CrossRef]
- Chen, T.L.; Shi, Z.L.; Wen, A.; Yan, D.; Gou, J.; Chen, J.; Liu, Y.; Chen, R. Multifractal characteristics, and spatial variability of soil particle-size distribution in different l, and use patterns in a small catchment of the Three Gorges Reservoir Region. China J. Mt. Sci. 2021, 18, 111–125. [Google Scholar] [CrossRef]
- Lehmann, P.; Stahla, M.; Papritz, A.; Gygi, A.; Fluher, H. A Fractal Approach to Model Soil Structure, and to Calculate Thermal Conductivity of Soils. Transp. Porous Media 2003, 52, 313–332. [Google Scholar] [CrossRef]
- Martin, M.A.; Reyes, M. A Fractal Interaction Model for Winding Paths through Complex Distributions: Application to Soil Drainage Networks. Pure Appl. Geophys. 2008, 165, 1153–1165. [Google Scholar] [CrossRef][Green Version]
- Kincal, C.; Koca, M.Y.; Ozden, G.; Demirbasa, N. Fractal parameter approach on weathering grade determination of Cesme (Izmir, Turkey) tuffs. Bull. Eng. Geol. Environ. 2010, 69, 617–629. [Google Scholar] [CrossRef]
- Zheru, Z.; Huahi, M.; Cheng, Q. Fractal Geometry of Element Distribution on Mineral Surfaces. Math. Geol. 2001, 33, 2. [Google Scholar] [CrossRef]
- Mohammadi, A.; Khakzad, A.; Omran, N.R.; Mahvi, M.R.; Moarefvand, P.; Afzal, P. Application of number–size (N-S) fractal model for separation of mineralized zones in Dareh-Ashki gold deposit, Muteh Complex, Central Iran. Arab. J. Geosci. 2013, 6, 4387–4398. [Google Scholar] [CrossRef]
- Zhengli, M.; Jian Qing, L.; Yang, B. The geochemical multi-fractal characteristics, and mineralization of the Dehelongwa copper-gold deposit. Chin. J. Geochem. 2014, 33, 280–288. [Google Scholar] [CrossRef]
- Fowler, A.D. Self-organized mineral textures of igneous rocks: The fractal approach. Earth-Sci. Rev. 1990, 29, 47–55. [Google Scholar] [CrossRef]
- Fowler, A.D. Mineral Crystallinity in Igneous Rocks: Fractal Method. Fractals in the Earth Sciences; Springer: Boston, MA, USA, 1995; pp. 237–249. [Google Scholar]
- Turcotte, D.L. Fractals in petrology. Lithos 2002, 65, 261–271. [Google Scholar] [CrossRef]
- Kruhl, J.K. Fractal-geometry techniques in the quantification of complex rock structures: A special view on scaling regimes, inhomogeneity and anisotropy. J. Struct. Geol. 2013, 46, 2–21. [Google Scholar] [CrossRef]
- Słaby, E.; Domonik, A.; Śmigielski, M.; Majzner, K.; Motuza, G.; Goetze, J.; Simon, K.; Moszumańska, I.; Kruszewski, Ł.; Rydelek, P. Protomylonite evolution potentially revealed by the 3D depiction, and fractal analysis of chemical data from a feldspar. Contrib. Miner. Petrol. 2014, 167, 995. [Google Scholar] [CrossRef]
- Voitsekhovsky, Y.L.; Shpachenko, A.K.; Skiba, V.I. Cell-zonal textures of tinguaites from the Kola Peninsula. Geol. Rundsch. 1997, 86, 531–538. [Google Scholar] [CrossRef]
- Huber, M.; Stępniewska, K. Application of the Fractal Dimension Calculation Technique to Determine the Shape of Selected Monchepluton Intrusion Crystals (NE Fennoscandia). Minerals 2021, 11, 1140. [Google Scholar] [CrossRef]
- Gulbin, Y.L.; Evangulova, E.B. Morphometry of Quartz Aggregates in Granites: Fractal Images Referring to Nucleation and Growth Processes. Math. Geol. 2003, 35, 819–833. [Google Scholar] [CrossRef]
- Golsanami, N.; Fernando, S.G.; Jayasuriya, M.N.; Yan, W.; Dong, H.; Cui, L.; Dong, X.; Barzgar, E. Fractal Properties of Various Clay Minerals Obtained from SEM Images. Hindawi Geofluids 2021, 5516444. [Google Scholar] [CrossRef]
- Van Damme, H.; Levitz, P.; Fripiat, J.J.; Alcover, J.F.; Gatineau, L.; Bergaya, F. Clay minerals: A molecular approach to their (fractal) microstructure. In Physics of Finely Divided Matter: Proceedings of the Winter School, Les Houches, France, 25 March–5 April 1985; Springer: Berlin/Heidelberg, Germany, 1985. [Google Scholar] [CrossRef]
- Malekani, K.; Rice, J.A.; Lin, J.S. Comparison of techniques for determining the fractal dimensions of clay minerals. Clays Clay Miner. 1996, 44, 677–685. [Google Scholar] [CrossRef]
- Cells, R.; Cornejo, J.; Hermosin, M.C. Surface fractal dimensions of synthetic clay-hydrous iron oxide associations from nitrogen adsorption isotherms and mercury porosimetry. Clay Miner. 1996, 31, 355–363. [Google Scholar] [CrossRef]
- Yongfu, X. Surface fractal dimension of swelling clay minerals. Fractals 2003, 11, 353–362. [Google Scholar] [CrossRef]
- Pernyeszi, T.; Dékány, I. Surface fractal and structural properties of layered clay minerals monitored by small-angle X-ray scattering and low-temperature nitrogen adsorption experiments. Colloid Polym. Sci. 2003, 281, 73–78. [Google Scholar] [CrossRef]
- Potter, N.J.; Ferguson, M.R.M.; Kamenetsky, V.S.; Chakhmouradian, A.R.; Sharygin, V.V.; Thompson, J.M.; Goemann, K. Textural evolution of perovskite in the Afrikanda alkaline–ultramafic complex, Kola Peninsula, Russia. Contrib. Mineral. Petrol. 2018, 173, 100. [Google Scholar] [CrossRef]
- Petigen, H.O.; Jürgens, H.; Saupe, D. Fractals for the Classroom; Springer: New York, NY, USA, 1992; p. 546. [Google Scholar]
- Feniak, M.W. Grain sizes and shapes of various minerals in igneous rocks. Am. Mineral. J. Earth Planet. Mater. 1944, 29, 415–421. [Google Scholar]
- Kogarko, L.N.; Williams, C.T.; Woolley, A.R. Compositional evolution and cryptic variation in pyroxenes of the peralkaline Lovozero intrusion, Kola Peninsula, Russia. Mineral. Mag. 2006, 70, 347–359. [Google Scholar] [CrossRef]
- Atamanov, A.V.; Lugov, S.F.; Feygin, Y.M. New results on the geology of the Lovozero massif. Int. Geol. Rev. 1962, 4, 570–577. [Google Scholar] [CrossRef]
- Mokrushina, O.D.; Mikhailova, J.A.; Pakhomovsky, Y.A. Fenitization at the Lovozero Alkaline Massif, NW Russia: Composition and Evolution of Fluids. Geosciences 2023, 13, 305. [Google Scholar] [CrossRef]
- Atsushi, T. A numerical experiment of crystallization for a binary eutectic system with application to igneous textures. J. Geophys. Res. Solid Earth 2001, 106, 4037–4060. [Google Scholar] [CrossRef]
- Burke, K.; Roberts, D.; Ashwal, L.D. Alkaline rocks and carbonatites of northwestern Russia and northern Norway: Linked Wilson cycle records extending over two billion years. Tectonics 2007, 26, 1–10. [Google Scholar] [CrossRef]
- Kargin, A.V.; Nosova, A.A.; Sazonova, L.V.; Tretyachenko, V.V.; Larionova, Y.O.; Kovalchuk, E.V. Ultramafic Alkaline Rocks of Kepino Cluster, Arkhangelsk, Russia: Different Evolution of Kimberlite Melts in Sills and Pipes. Minerals 2021, 11, 540. [Google Scholar] [CrossRef]
- Moriyama, T.; Ishihara, S. Alkaline rocks and related REE resources of the Kola Alkaline Carbonatite Province, NW Russia. Shigen-Chishitsu 2006, 56, 205–211. [Google Scholar]
- Dougal, J.; Petford, N. The Field Description of Igneous Rocks; John Wiley & Sons: London, UK, 2011; p. 256. [Google Scholar]
- Cross, W.; Iddings, J.P.; Pirsson, L.V.; Washington, V.S. The texture of igneous rocks. J. Geol. 1906, 14, 692–707. [Google Scholar] [CrossRef][Green Version]
- Chakhmouradian, A.R.; Mitchell, R.H. New data on pyrochlore- and perovskite-group minerals from the Lovozero alkaline complex, Russia. Eur. J. Mineral. 2002, 42, 821–836. [Google Scholar] [CrossRef]
- Huber, M. Mineralogical-Petrographic Characteristic of the Selected Alkaline Massifs of the Kola Peninsula; TMKarpinski Publisher: Suchy Las, Poland, 2015; p. 187. (In Polish) [Google Scholar]
- Fanasev, B.V. Mineral Resources of the Alkaline—Ultrabasic Massifs of the Kola Peninsula; Roza Vetrov: Apatity, Russia, 2011; p. 151. (In Russian) [Google Scholar]
- Akimenko, M.I.; Kogarko, L.N.; Sorokhtina, N.V.; Kononkova, N.N.; Mamontov, V.P. A New Occurrence of Alkaline Magmatism on the Kola Peninsula: An Agpaitic Dyke in the Kandalaksha Region. Dokl. Earth Sci. 2014, 458, 1125–1128. [Google Scholar] [CrossRef]
- Nivin, V.A. Variations in the Composition and Origin of Hydrocarbon Gases from Inclusions in Minerals of the Khibiny and Lovozero Plutons, Kola Peninsula, Russia. Geol. Ore Depos. 2011, 53, 699–707. [Google Scholar] [CrossRef]
- Potter, N.J.; Kamenetsky, V.S.; Chakhmouradian, A.R.; Kamenetsky, M.B.; Goemann, K.; Rodemann, T. Polymineralic inclusions in oxide minerals of the Afrikanda alkaline-ultramafic complex: Implications for the evolution of perovskite mineralization. Contrib. Mineral. Petrol. 2020, 175, 18. [Google Scholar] [CrossRef]
- Nivin, V.A.; Treloar, P.J.; Konopleva, N.G.; Ikorskya, S.V. A review of the occurrence, form and origin of C-bearing species in the Khibiny Alkaline Igneous Complex, Kola Peninsula, NW Russia. Lithos 2005, 85, 93–112. [Google Scholar] [CrossRef]
- Lapin, A.V.; Lyagushkin, A.P. The Kovdor Apatite–Francolite Deposit as a Prospective Source of Phosphate Ore. Geol. Ore Depos. 2014, 56, 61–80. [Google Scholar] [CrossRef]
- Rass, I.T.; Petrenko, D.B.; Koval’chuk, E.V.; Yakushev, A.I. Phoscorites and Carbonatites: Relations, Possible Petrogenetic Processes, and Parental Magma, with Reference to the Kovdor Massif, Kola Peninsula. Geochem. Int. 2020, 58, 753–778. [Google Scholar] [CrossRef]
- Kogarko, L.N. Chemical Composition and Petrogenetic Implications of Apatite in the Khibiny Apatite-Nepheline Deposits (Kola Peninsula). Minerals 2018, 8, 532. [Google Scholar] [CrossRef]
- Kogarko, L.N. Conditions of Accumulation of Radioactive Metals in the Process of Differentiation of Ultrabasic Alkaline-Carbonatite Rock Associations. Geol. Ore Depos. 2014, 56, 230–238. [Google Scholar] [CrossRef]
- Adushkin, V.V.; Goev, A.G. Traces of Plume Processes in the Present-Day Velocity Structure of the Lithosphere of the Khibiny–Lovozero Tectonic Cluster. Dokl. Earth Sci. 2023, 9, 1–5. [Google Scholar] [CrossRef]
- Zartman, R.E.; Kogarko, L.N. Lead isotopic evidence for interaction between plume and lower crust during emplacement of peralkaline Lovozero rocks and related rare-metal deposits, East Fennoscandia, Kola Peninsula, Russia. Contrib. Mineral. Petrol. 2017, 172, 32. [Google Scholar] [CrossRef]
- Arzamastsev, A.A.; Glaznev, V.N. Plume-Lithosphere Interaction in the Presence of an Ancient Sublithospheric Mantle Keel: An Example from the Kola Alkaline Province. Dokl. Earth Sci. 2008, 419, 384–387. [Google Scholar] [CrossRef]
- Arzamastsev, A.A.; Arzamastseva, L.V. Geochemical Indicators of the Evolution of the Ultrabasic—Alkaline Series of Paleozoic Massifs of the Fennoscandian Shield. Petrology 2013, 21, 249–279. [Google Scholar] [CrossRef]
- Kramm, U.; Kogarko, L.N.; Kononova, V.A.; Vartiainen, H. The Kola alkaline province of the CIS and Finland: Precise Rb–Sr ages define 380–360 Ma age range for all magmatism. Lithos 1993, 30, 33–44. [Google Scholar] [CrossRef]
- Zaitsev, A.; Bell, K. Sr and Nd isotope data of apatite, calcite, and dolomite as indicators of source, and the relationships of phoscorites and carbonatites from the Kovdor massif, Kola peninsula, Russia. Contrib. Miner. Pet. 1995, 121, 324–335. [Google Scholar] [CrossRef]
- Kogarko, L.N. Zirconium and Hafnium Fractionation in Differentiation of Alkali Carbonatite Magmatic Systems. Geol. Ore Depos. 2016, 58, 173–181. [Google Scholar] [CrossRef]
- Arzamastsev, A.A.; Mitrofanov, F.P. Paleozoic Plume-Lithospheric Processes in Northeastern Fennoscandia: Evaluation of the Composition of the Parental Mantle Melts and Magma Generation Conditions. Petrology 2009, 17, 300–313. [Google Scholar] [CrossRef]
- Sorokhtin, N.V.; Zaitsev, V.A.; Petrov, S.V.; Kononkovaa, N.N. Estimation of Formation Temperature of the Noble Metal Mineralization of the Kovdor Alkaline-Ultrabasic Massif (Kola Peninsula). Geochem. Int. 2021, 59, 474–490. [Google Scholar] [CrossRef]
- Huber, M.; Iakovleva, O.; Zhigunova, G.; Menshakova, M.Y. Special Interest Tourism (SIT) in Murmansk (Arctic NE Scandinavia): Touristic Route around the City to Explore the Oldest Rocks in Europe. Heritage 2023, 6, 2664–2687. [Google Scholar] [CrossRef]
- Bayanova, T.B. Age of Benchmark Geological Complexes of the Kola Region, and Magmatism Processes Action; Nauka: St. Petersburg, Russia, 2004; p. 174. [Google Scholar]
- Pozhylienko, V.I.; Gavrilienko, B.V.; Zhirov, D.V.; Zhabin, S.V. Geology of the Ore Regions in Murmansk District; Kola Scientific Center, Russian Academy of Sciences: Apatity, Russia, 2002; p. 360. [Google Scholar]
- Bayanova, T.B.; Pozhylienko, V.I.; Smolkin, V.F.; Kudryshov, N.M.; Kaulina, T.V.; Vetrin, V.R. Katalogue of the Geochronology Data of N-E Part of the Baltic Shield; Kola Science Center of the Russian Academy of Sciences Publisher: Apatity, Russia, 2002; p. 53. (In Russian) [Google Scholar]
- Mitrofanov, A.F. Geological Characteristics of Kola Peninsula; Russian Academy of Science Publ.: Apatity, Russia, 2000; p. 166. [Google Scholar]
- Sindern, S.; Zaitsev, A.N.; Demény, A.; Bell, K.; Chakmouradian, A.R.; Kramm, U.; Moutte, J.; Rukhlov, A.S. Mineralogy and geochemistry of silicate dyke rocks associated with carbonatites from the Khibiny complex (Kola, Russia)—Isotope constraints on the genesis and small-scale mantle sources. Mineral. Petrol. 2004, 80, 215–239. [Google Scholar] [CrossRef]
- Kogarko, L.N. Geochemistry of Fractionation of Coherent Elements (Zr and Hf) during the Profound Differentiation of Peralkaline Magmatic Systems: A Case Study of the Lovozero Complex. Geochem. Int. 2016, 54, 1–6. [Google Scholar] [CrossRef]
- Arzamastsev, A.A.; Arzamastseva, L.V.; Zhirova, A.M.; Glaznev, V.N. Model of Formation of the Khibiny–Lovozero Ore-Bearing volcanic-Plutonic Complex. Geol. Ore Depos. 2013, 55, 341–356. [Google Scholar] [CrossRef]
- Kogarko, L.N.; Lahaye, Y.; Brey, G.P. Plume-related mantle source of super-large rare metal deposits from the Lovozero and Khibiny massifs on the Kola Peninsula, Eastern part of Baltic Shield: Sr, Nd and Hf isotope systematics. Miner. Petrol. 2010, 98, 197–208. [Google Scholar] [CrossRef]
- Hałas, S.; Huber, M.; Piestrzynski, A. Petrology of gabbroides and isotope signature of sulfide mineralization from Fedorov-Pansky layered mafic intrusion, Kola peninsula, Russia. Geochronometria 2009, 33, 19–22. [Google Scholar] [CrossRef]
- Evzerov, V.Y. Glacier Deposits As Unique Formations in the Loose Cover of the Baltic Shield. Lithol. Miner. Resour. 2001, 36, 109–115. [Google Scholar] [CrossRef]
- Korsakova, O.P. Pleistocene marine deposits in the coastal areas of Kola Peninsula (Russia). Quat. Int. 2009, 206, 3–15. [Google Scholar] [CrossRef]
- Arzamastsev, A.A. Unique Paleozoic Intrusions of the Kola Peninsula; Russian Academy of Science Publ.: Apatity, Russia, 1994; p. 79. [Google Scholar]
- Veselovskiy, R.V.; Arzamastsev, A.A.; Demina, L.I.; Travin, A.V.; Botsyun, S.B. Paleomagnetism, geochronology, and magnetic mineralogy of Devonian dikes from the Kola alkaline province (NE Fennoscandian Shield). Izv. Phys. Solid Earth 2013, 49, 526–547. [Google Scholar] [CrossRef]
- Arzamastsev, A.A.; Wu, F.Y. U-Pb Geochronology and Sr-Nd Isotopic Systematics of Minerals from the Ultrabasic–Alkaline Massifs of the Kola Province. Petrology 2014, 22, 462–479. [Google Scholar] [CrossRef]
- Arzamastsev, A.A.; Arzamastseva, L.V.; Bea, F.; Montero, P. Trace Elements in Minerals as Indicators of the Evolution of Alkaline Ultrabasic Dike Series: LA-ICP-MS Data for the Magmatic Provinces of Northeastern Fennoscandia and Germany. Petrology 2009, 17, 46–72. [Google Scholar] [CrossRef]
- Huber, M.; Rusek, A.; Menshakova, M.; Zhigunova, G.; Chmiel, S.; Iakovleva, O. Possibilities of Sustainable Development including Improvement in Air Quality for the City of Murmansk-Examples of Best Practice from Scandinavia. Climate 2022, 10, 15. [Google Scholar] [CrossRef]
- Gusev, A.S.; Baykin, Y.L.; Vashukevich, N.V.; Belichev, A.A. Zone of Technogenic Pollution of the Pervouralsk-Revda Industrial Hub: Soil Assessment and Land Use Issues. J. Environ. Manag. Tour. Craiova 2020, 11, 1054–1059. [Google Scholar] [CrossRef]
- Lalomov, A.V.; Grigorieva, A.V.; Zaitsev, V.A. The Mineral Composition of Rare-Metal Placers of the Lovozero Massif. Geol. Ore Depos. 2022, 64, 3–14. [Google Scholar] [CrossRef]
- Glebovitsky, V.A. Early Precambrian of the Baltic Shield; Nauka: St. Petersburg, Russia, 2005; p. 710. [Google Scholar]
- Boruckiy, B.E. Rock-Forming Minerals of the High-Alkaline Complexes; Nauka: Moscov, Russia, 1989; p. 214. (In Russian) [Google Scholar]
- Pozhilienko, V.I.; Gavrilenko, B.V.; Zhirov, C.V.; Zhabin, S.V. Geology of Mineral Areas of the Murmansk Region; Kola Scientific Center, Russian Academy of Sciences: Moscow, Russia, 2002; p. 360. (In Russian) [Google Scholar]
- Huber, M.; Kamiński, D.; Czernel, G.; Kozlov, E. Optical and Spectroscopic Properties of Lorenzenite, Loparite, Perovskite, Titanite, Apatite, Carbonates from the Khibiny, Lovozero, Kovdor, and Afrikanda Alkaline Intrusion of Kola Peninsula (NE Fennoscandia). Crystals 2022, 12, 224. [Google Scholar] [CrossRef]
- Arzamastsev, A.; Yakovenchuk, V.; Pakhomovsky, Y.; Ivanyuk, G. The Khibiny and Lovozero alkaline massifs: Geology and unique mineralization. In Proceedings of the 33rd International Geological Congress Excursion, Oslo, Norway, 22 July–2 August 2008. [Google Scholar]
- Ivanyuk, G.Y.; Pakhomovsky, Y.A.; Yakovenchuk, V.N. Eudialyte Group Minerals in Rocks of Lovozero Layered Complex at Mt. Karnasurt and Mt. Kedykvyrpakhk. Geol. Ore Depos. 2015, 57, 600–613. [Google Scholar] [CrossRef]
- Nivin, V.A. Helium and Argon Isotopes in Rocks and Minerals of the Lovozero Alkaline Massif. Geochem. Int. 2008, 46, 482–502. [Google Scholar] [CrossRef]
- Arzamastsev, A.A.; Arzamastseva, L.V.; Zaraiskii, G.P. Contact Interaction of Agpaitic Magmas with Basement Gneisses: An Example of the Khibiny and Lovozero Massifs. Petrology 2011, 19, 109–133. [Google Scholar] [CrossRef]
- Britvin, S.N.; Ivanov, G.Y.; Yakuvenchuk, V.N. Mineralogical Accessory on the Kola Peninsula; World of Stones: Moskov, Russia, 1995; pp. 5–6. (In Russian) [Google Scholar]
- Kogarko, L.N. Geochemistry of Rare Earth Metals in the Ore Eudialyte Complex of the Lovozero Rare Earth Deposit. Dokl. Earth Sci. 2020, 491, 231–234. [Google Scholar] [CrossRef]
- Huber, M.; Zhigunova, G.; Menshakova, M.; Iakovleva, O.; Karimova, M. Geoheritage of the Monchegorsk Igneous Layered Paleoproterozoic Intrusion (Kola Peninsula, Arctic Russia): Evaluation and Geotourism Opportunities. Heritage 2021, 4, 3583–3610. [Google Scholar] [CrossRef]
- Huber, M.; Iakovleva, O.; Zhigunova, G.; Menshakova, M.Y.; Gainanova, R.I.; Moroniak, M. Geoheritage of the Western Khibiny ingenious alkaline rocks intrusion (Kola Peninsula, Arctic Russia): Evaluation, and geotourism opportunities. Geoheritage 2021, 13, 72. [Google Scholar] [CrossRef]
- Mikhailova, J.A.; Ivanyuk, G.Y.; Kalashnikov, A.O.; Pakhomovsky, Y.A.; Bazai, A.V.; Yakovenchuk, V.N. Petrogenesis of the Eudialyte Complex of the Lovozero Alkaline Massif (Kola Peninsula, Russia). Minerals 2019, 9, 581. [Google Scholar] [CrossRef]
- Nivin, V.A. Occurrence Forms, Composition, Distribution, Origin and Potential Hazard of Natural Hydrogen–Hydrocarbon Gases in Ore Deposits of the Khibiny and Lovozero Massifs: A Review. Minerals 2019, 9, 535. [Google Scholar] [CrossRef]
- Kogarko, L.N.; Williams, C.T.; Wolley, A.R. Chemical evolution and petrogenetic implications of loparite in the layered, agpaitic Lovozero complex, Kola Peninsula, Russia. Mineral. Petrol. 2002, 74, 1–24. [Google Scholar]
- Chakhmouradian, A.R.; Reguir, E.P.; Mitchell, R.H. Strontium-apatite: New occurrences, and the extent of Sr-for-Ca substitution in apatite-group minerals. Can. Mineral. 2002, 40, 121–136. [Google Scholar] [CrossRef]
- Foroutan-pour, K.; Dutilleul, P.; Smith, D.L. Advances in the implementation of the box-counting method of fractal dimension estimation. Appl. Math. Comput. 1999, 105, 195–210. [Google Scholar] [CrossRef]
- Lim, M.; Kartiwa, A.; Napitupulu, H. Estimation of Citarum Watershed Boundary’s Length Based on Fractal’s Power Law by the Modified Box-Counting Dimension Algorithm. Mathematics 2023, 11, 384. [Google Scholar] [CrossRef]
- Robinsn, J.C.; Sharples, N. Strict inequality in the box-counting dimension product formulas. Real Anal. Exch. 2012, 38, 95–120. [Google Scholar] [CrossRef]
- Schleuter, E.M.; Zimmerman, R.W.; Withespoon, P.A.; Cook, N.G.W. The fractal dimenntion of pores in sedimentary rocks and its influence on preanbility. Engeeniering Geol. 1997, 48, 199–215. [Google Scholar] [CrossRef]
- Peng, R.; Yang, Y.; Ju, Y.; Mao, L.; Yang, Y. Computation of fractal dimension of rock pores based on gray CT images. Mech. Eng. 2011, 56, 3346–3357. [Google Scholar] [CrossRef]
- Zhao, F.; Sun, Q.; Zhang, W. Fractal analysis of pore structure of granite after variable thermal cycles. Environ. Earth Sci. 2019, 78, 677. [Google Scholar] [CrossRef]
- Lai, Y.; Zhao, K.; He, Z.; Yu, X.; Yan, Y.; Li, Q.; Shao, H.; Zhang, X.; Zhou, Y. Fractal characteristics of rocks and mesoscopic fractures at different loading rates. Geomech. Energy Environ. 2023, 33, 100431. [Google Scholar] [CrossRef]
- Kalashnikov, A.O.; Konopleva, N.G.; Pakhomovsky, Y.A.; Ivanyuk, G.Y. Rare Earth Deposits of the Murmansk Region, Russia—A Review. Econ. Geol. 2016, 111, 1529–1559. [Google Scholar] [CrossRef]
- Kogarko, L.N. A New Geochemical Criterion for Rare-Metal Mineralization of High-Alkalic Magmas (Lovozero Deposit, Kola Peninsula). Dokl. Earth Sci. 2019, 487, 922–924. [Google Scholar] [CrossRef]
- Shubin, I.I.; Filina, M.I.; Kogarko, L.N. Evolution of pyroxenes of the Lovozero rare metal deposit (Lower Zone). Geochem. Int. 2021, 59, 92–98. [Google Scholar] [CrossRef]
- Kogarko, L.N. Peculiarities of the Formation of Loparite Ores: The Lovozero Rare Metal Deposit, East Fennoscandia. Dokl. Earth Sci. 2022, 505, 524–526. [Google Scholar] [CrossRef]
- Churkin, M.; Soleimani, G.; Carter, C.; Robinson, R. Geology of the Soviet Arctic: Kola Peninsula to Lena River. In The Arctic Ocean; Nairn, A.E.M., Churkin, M., Stehli, F.G., Eds.; Springer: Boston, MA, USA, 1981; pp. 331–375. [Google Scholar] [CrossRef]




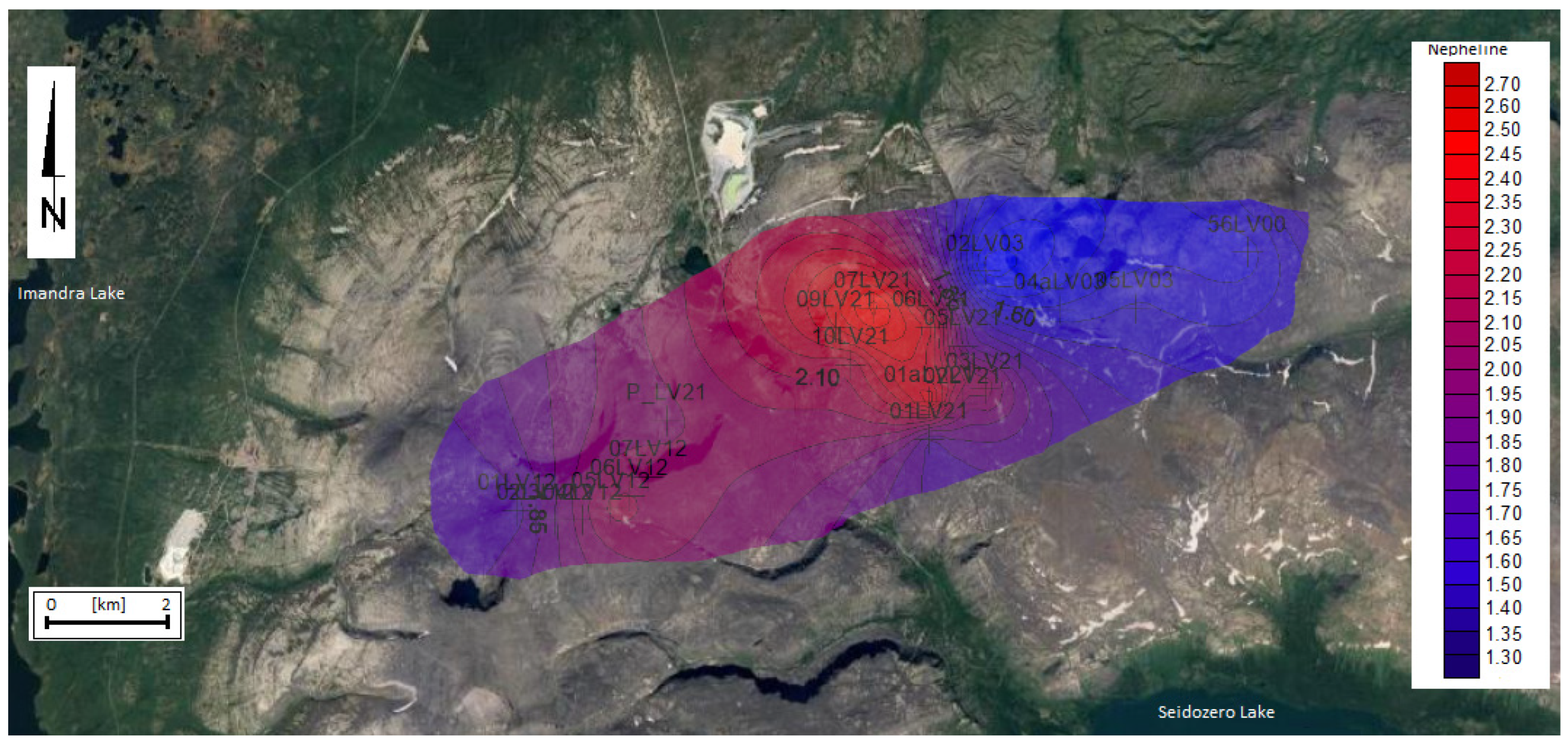

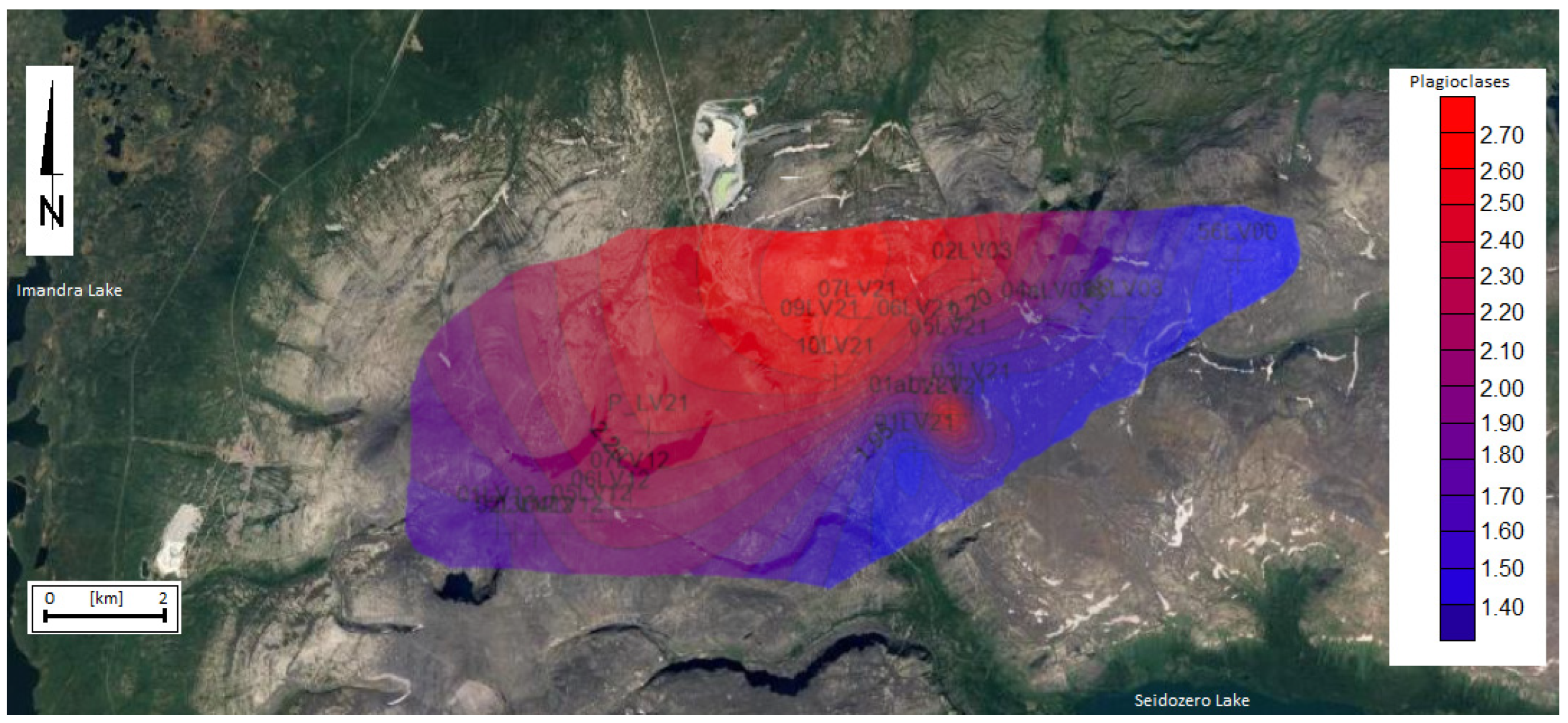
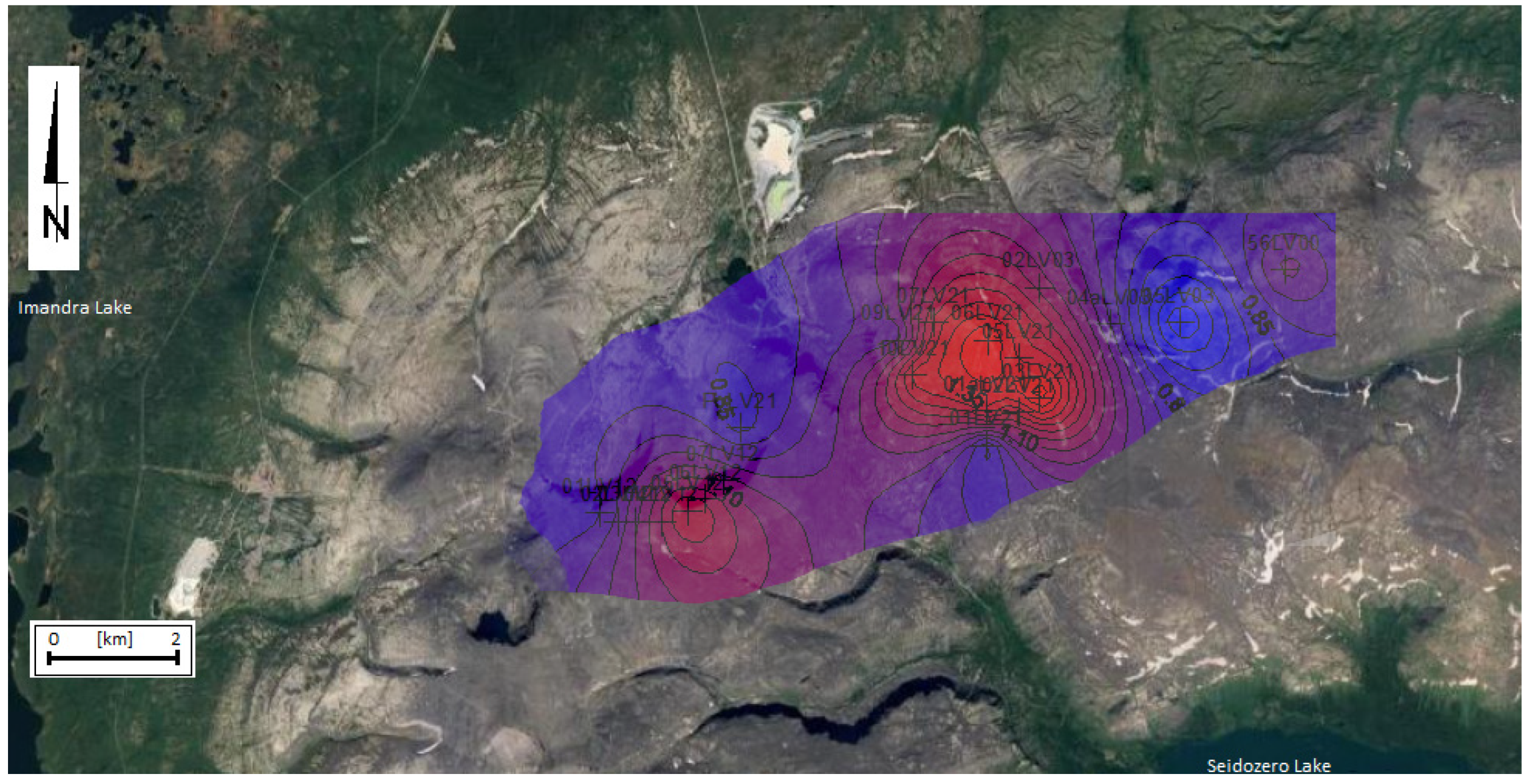
| Sample | EUD | AEG | NE | KFS | Sample | EUD | AEG | NE | KFS |
|---|---|---|---|---|---|---|---|---|---|
| 01aLV21_1 | 2.73 | 1.36 | 2.14 | 2.05 | 05LV12 | 2.65 | 1.65 | 2.07 | 2.13 |
| 01aLV21_2 | 2.27 | 1.60 | 2.03 | 2.34 | 05LV21_1 | 2.16 | 1.62 | 1.94 | 1.95 |
| 01aLV21_3 | 2.28 | 1.83 | 1.70 | 1.43 | 05LV21_2 | 2.15 | 1.69 | 1.76 | 2.43 |
| 01aLV21_4 | 2.03 | 2.09 | 2.63 | 2.35 | 05LV21_3 | 1.44 | 1.12 | 1.74 | 2.04 |
| 01aLV21_5 | 1.08 | 2.57 | 2.37 | 05LV21_4 | 1.83 | 1.36 | 2.00 | 1.52 | |
| 01aLV21_7 | 2.36 | 1.76 | 2.64 | 1.38 | 05LV21 | 1.90 | 1.45 | 1.86 | 1.98 |
| 01aLV21_6 | 2.61 | 06LV21_1 | 1.41 | 1.74 | 2.29 | ||||
| 01LV21 | 2.33 | 1.62 | 2.33 | 1.99 | 06LV21_2 | 2.65 | 1.68 | 2.25 | 1.90 |
| 01LV12_1 | 1.81 | 1.79 | 1.38 | 1.99 | 06LV21_3 | 1.62 | 2.10 | ||
| 01LV12_2 | 2.15 | 2.21 | 1.84 | 2.04 | 06LV21_4 | 2.27 | 1.15 | 2.74 | |
| 01LV12_3 | 1.94 | 2.37 | 2.10 | 1.92 | 06LV21 | 2.11 | 1.55 | 2.27 | 2.25 |
| 01LV12 | 1.97 | 2.13 | 1.77 | 1.98 | 07LV21_1 | 2.41 | 1.46 | 2.10 | 2.42 |
| 01LV21_1 | 1.97 | 2.17 | 2.08 | 1.53 | 07LV21_2 | 2.63 | 1.57 | 2.77 | |
| 01LV21_2 | 1.80 | 2.11 | 1.76 | 1.90 | 07LV21_3 | 2.39 | 2.71 | 2.58 | |
| 01LV21_3 | 1.87 | 1.52 | 1.99 | 1.80 | 07LV21_4 | 2.52 | 2.00 | 2.51 | 2.41 |
| 01LV21_4 | 1.82 | 2.58 | 1.34 | 07LV21 | 2.49 | 1.94 | 2.49 | 2.42 | |
| 01LV21 | 1.86 | 2.09 | 1.79 | 1.74 | 09LV21_1 | 2.29 | 2.66 | 2.37 | 2.41 |
| 02LV03_1 | 1.25 | 1.86 | 1.46 | 09LV21_3 | 1.65 | 2.46 | 2.27 | 2.38 | |
| 02LV03_2 | 2.26 | 1.28 | 2.09 | 09LV21_4 | 2.50 | 2.14 | 2.27 | 2.45 | |
| 02LV03_3 | 1.38 | 1.32 | 2.56 | 09LV21 | 2.15 | 2.42 | 2.30 | 2.41 | |
| 02LV03 | 1.55 | 1.62 | 1.35 | 2.32 | 10LV21_1 | 2.46 | 2.00 | 1.60 | |
| 02LV21_1 | 1.45 | 2.55 | 2.27 | 2.63 | 10LV21_2 | 1.73 | 1.41 | 2.37 | |
| 02LV21_2 | 2.28 | 1.38 | 1.72 | 2.48 | 10LV21_3 | 1.43 | 1.66 | 2.34 | 2.13 |
| 02LV21_3 | 2.06 | 1.40 | 1.86 | 2.33 | 10LV21_4 | 2.41 | 1.65 | 2.63 | |
| 02LV21 | 1.93 | 1.77 | 1.95 | 2.48 | 10LV21 | 2.01 | 1.68 | 2.10 | 2.38 |
| 03LV21_1 | 1.83 | 1.25 | 2.34 | 56LV00_1 | 2.43 | 1.38 | |||
| 03LV21_2 | 2.06 | 1.79 | 1.89 | 56LV00_2 | 2.01 | 1.70 | 1.83 | ||
| 03LV21_3 | 1.76 | 1.18 | 1.96 | 1.88 | 56LV00_3 | 2.49 | 1.66 | 1.52 | 1.64 |
| 03LV21 | 1.88 | 1.31 | 2.06 | 1.88 | 56LV00 | 2.31 | 1.58 | 1.52 | 1.74 |
| 04aLV03 | 2.40 | 1.00 | P_Lv21_1 * | 1.94 | 2.60 | 2.04 | 1.95 | ||
| 04aLV03 | 2.40 | 1.00 | P_Lv21_2 * | 1.85 | 2.53 | 1.93 | 2.55 | ||
| 05LV03_1 | 1.76 | 1.76 | 1.61 | P_LV21 * | 1.89 | 2.57 | 1.98 | 2.25 | |
| 05LV03_2 | 2.89 | 1.00 | MIN | 2.94 | 2.71 | 2.77 | 2.74 | ||
| 05LV03 | 2.33 | 1.38 | 1.61 | MAX | 0.85 | 0.95 | 1.28 | 1.38 | |
| 05LV12_1 | 2.77 | 2.05 | AVERAGE | 2.11 | 1.75 | 2.01 | 2.13 | ||
| 05LV12_2 | 2.23 | 2.49 | 2.13 | Standart deviation | 0.63 | 0.57 | 0.81 | 1.12 | |
| 05LV12_3 | 2.94 | 1.26 | 1.65 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huber, M.; Stępniewska, K.; Huber, M.W. The Relationship Between the Fractal Dimension and the Evolution of Rock-Forming Minerals Crystallization on the Example of the Northwestern Part of the Lovozero Intrusion. Fractal Fract. 2025, 9, 100. https://doi.org/10.3390/fractalfract9020100
Huber M, Stępniewska K, Huber MW. The Relationship Between the Fractal Dimension and the Evolution of Rock-Forming Minerals Crystallization on the Example of the Northwestern Part of the Lovozero Intrusion. Fractal and Fractional. 2025; 9(2):100. https://doi.org/10.3390/fractalfract9020100
Chicago/Turabian StyleHuber, Miłosz, Klaudia Stępniewska, and Mirosław Wiktor Huber. 2025. "The Relationship Between the Fractal Dimension and the Evolution of Rock-Forming Minerals Crystallization on the Example of the Northwestern Part of the Lovozero Intrusion" Fractal and Fractional 9, no. 2: 100. https://doi.org/10.3390/fractalfract9020100
APA StyleHuber, M., Stępniewska, K., & Huber, M. W. (2025). The Relationship Between the Fractal Dimension and the Evolution of Rock-Forming Minerals Crystallization on the Example of the Northwestern Part of the Lovozero Intrusion. Fractal and Fractional, 9(2), 100. https://doi.org/10.3390/fractalfract9020100







