Variable-Order Time-Fractional Kelvin Peridynamics for Rock Steady Creep
Abstract
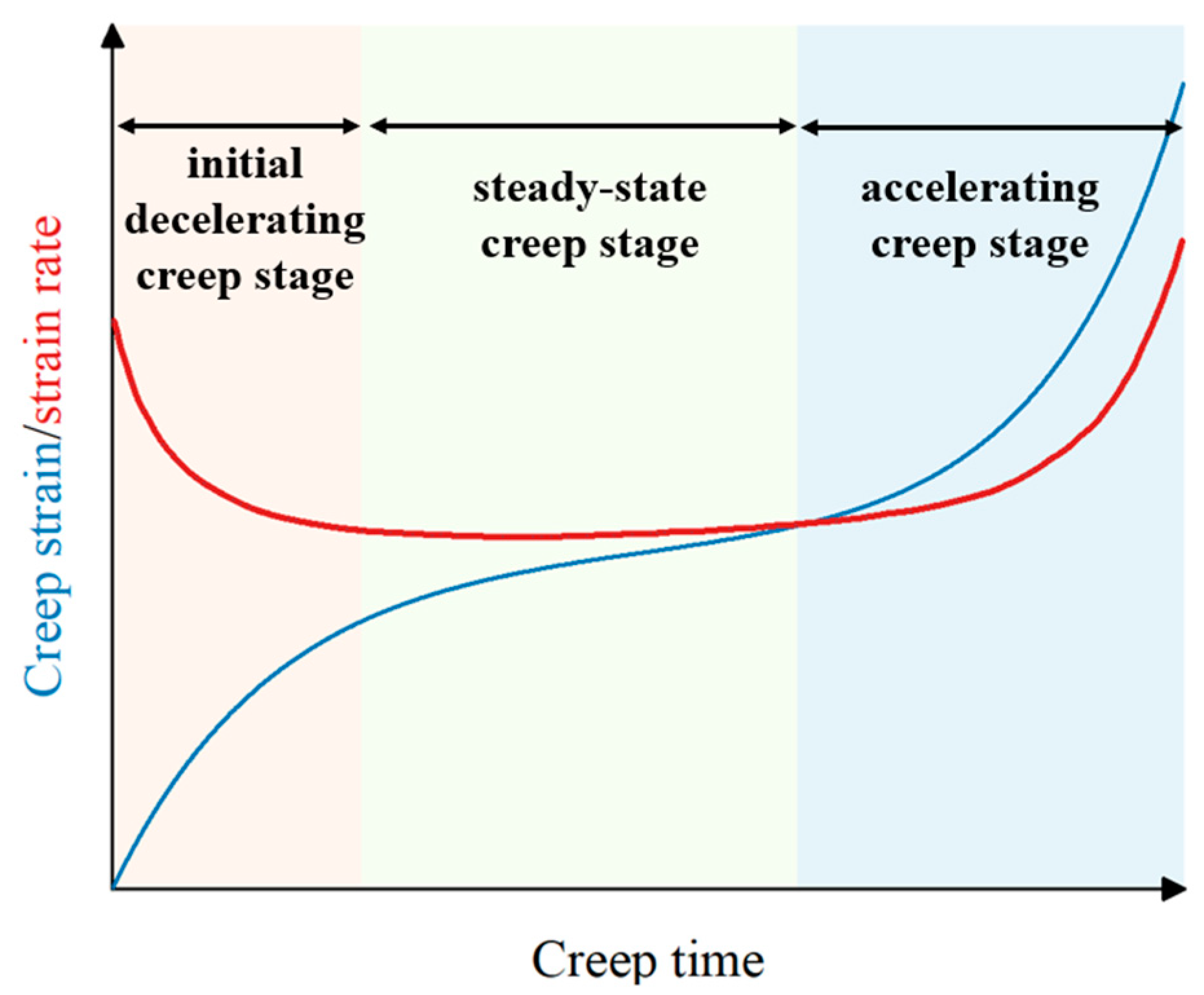
1. Introduction
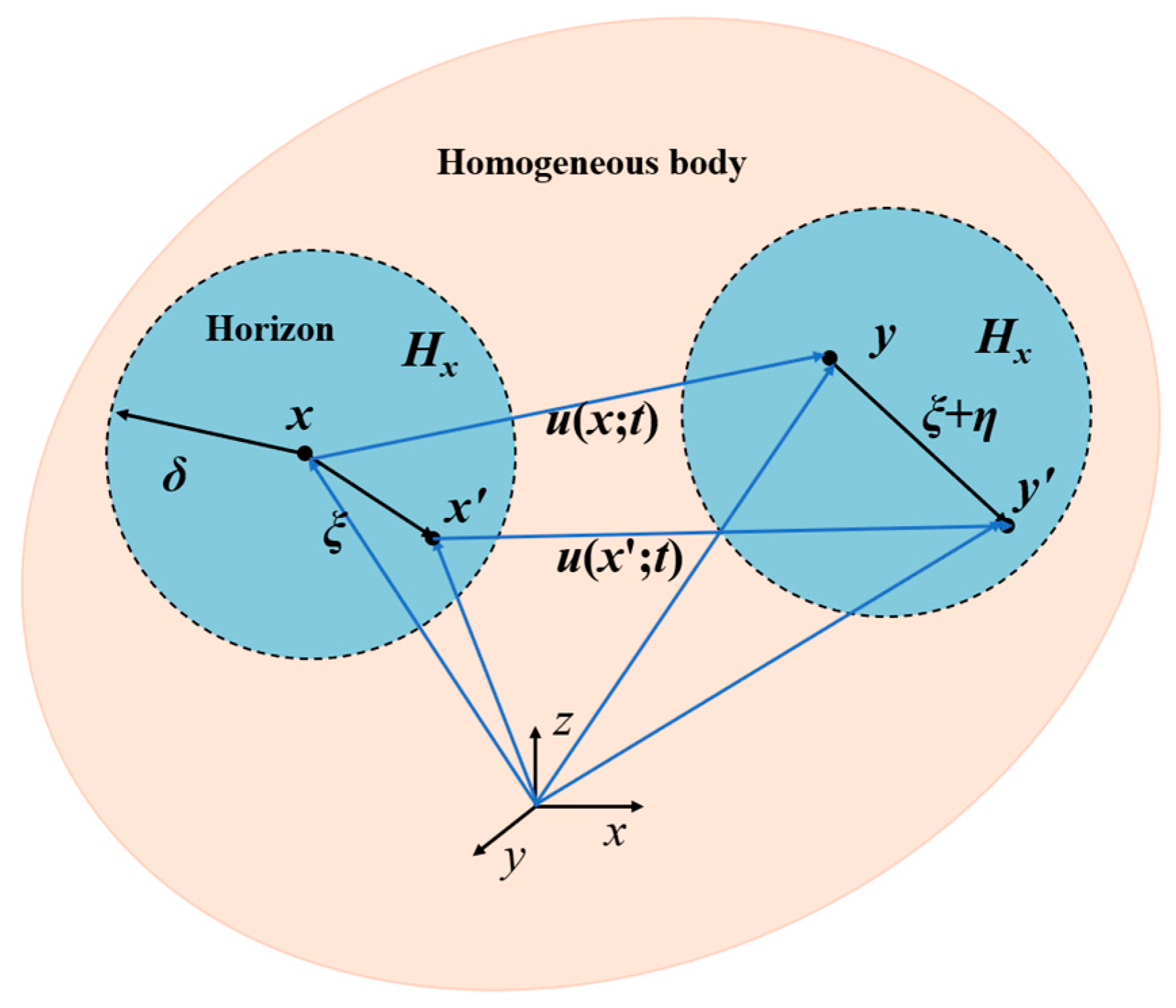
2. Numerical Model
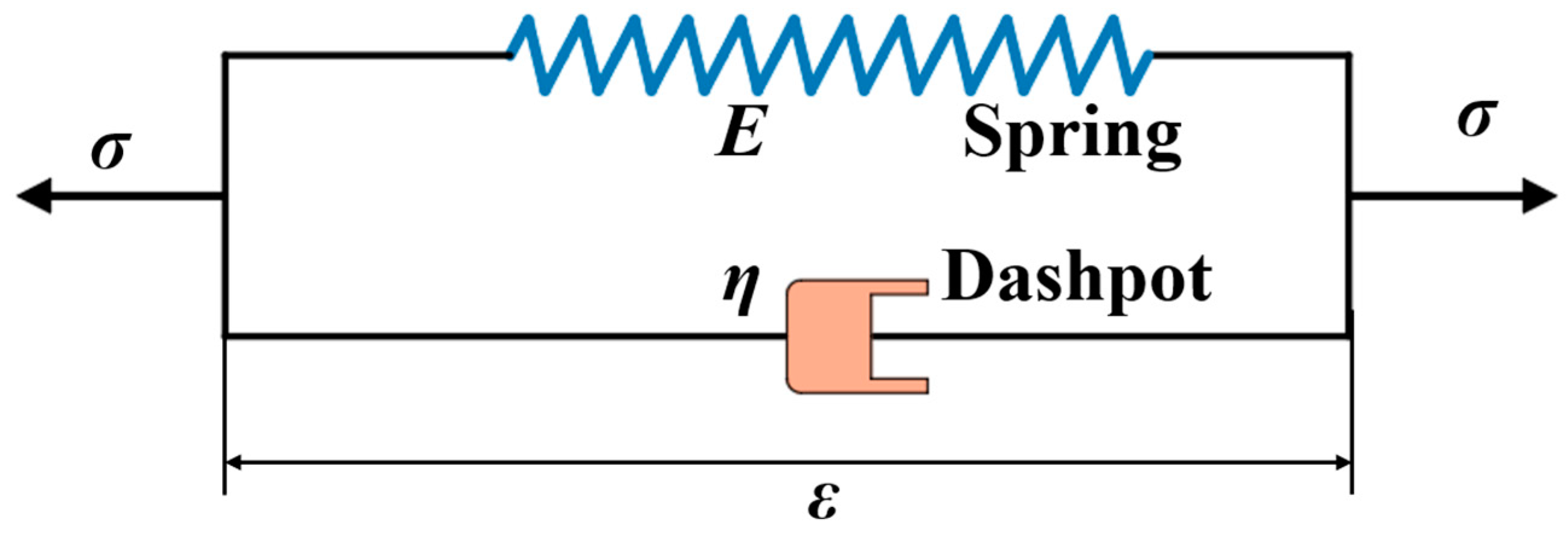
2.1. Kelvin Peridynamics
2.2. Constant-Order Time-Fractional Kelvin Peridynamics
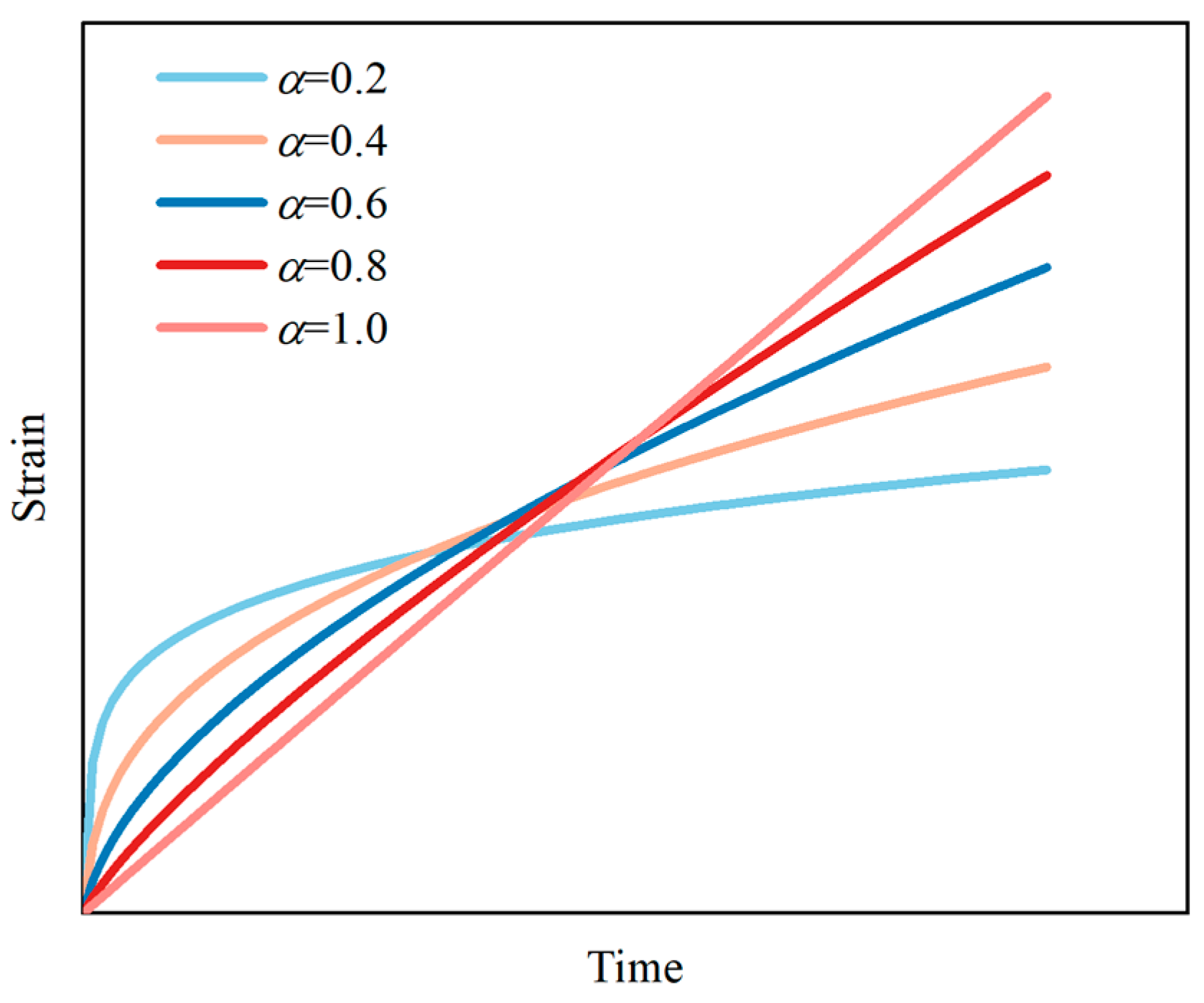
2.3. Variable-Order Time-Fractional Kelvin Peridynamics
3. Numerical Implementation
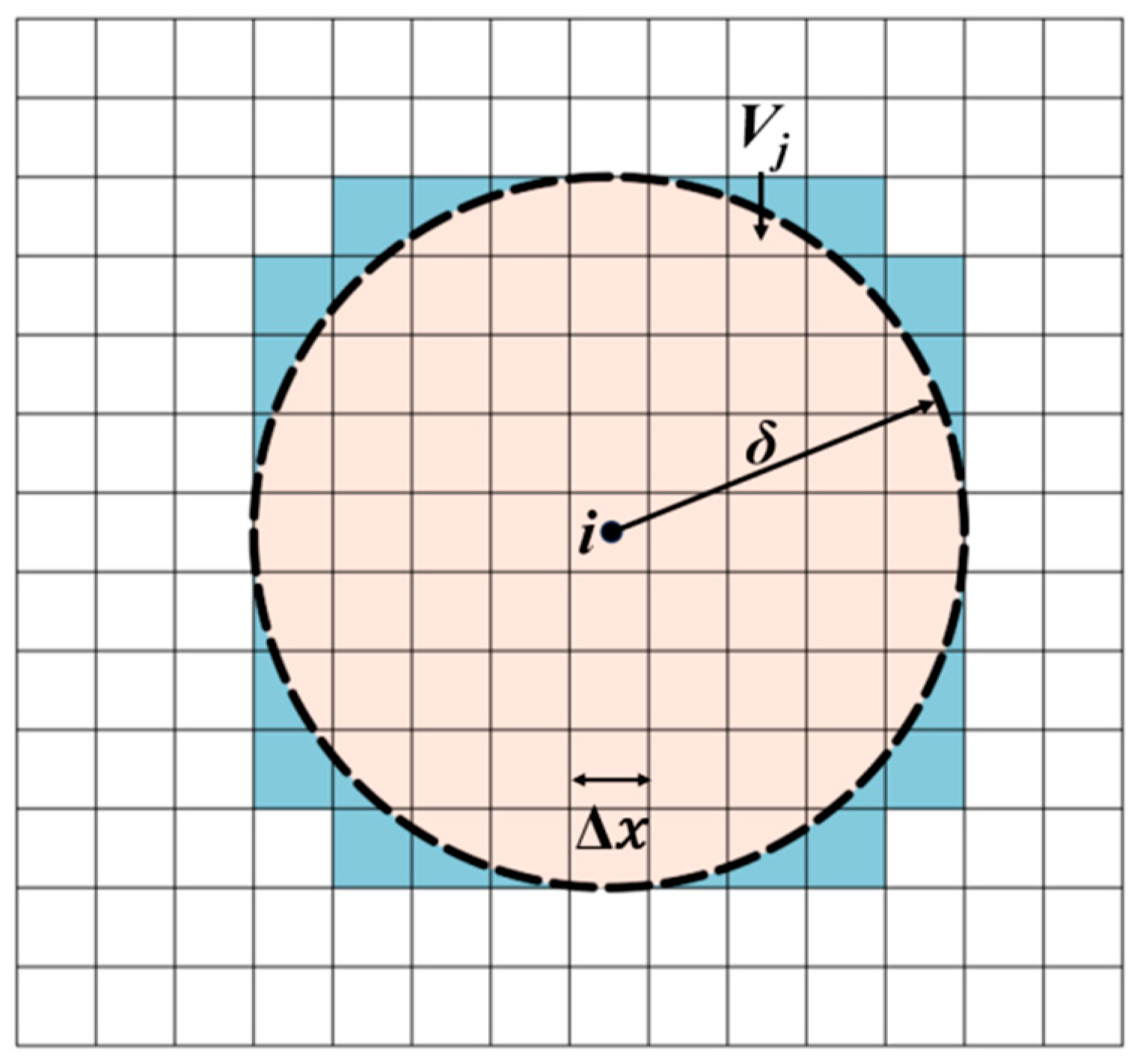
3.1. Numerical Discretization
3.2. The Evaluation Algorithm for the Model Parameters
4. Numerical Example
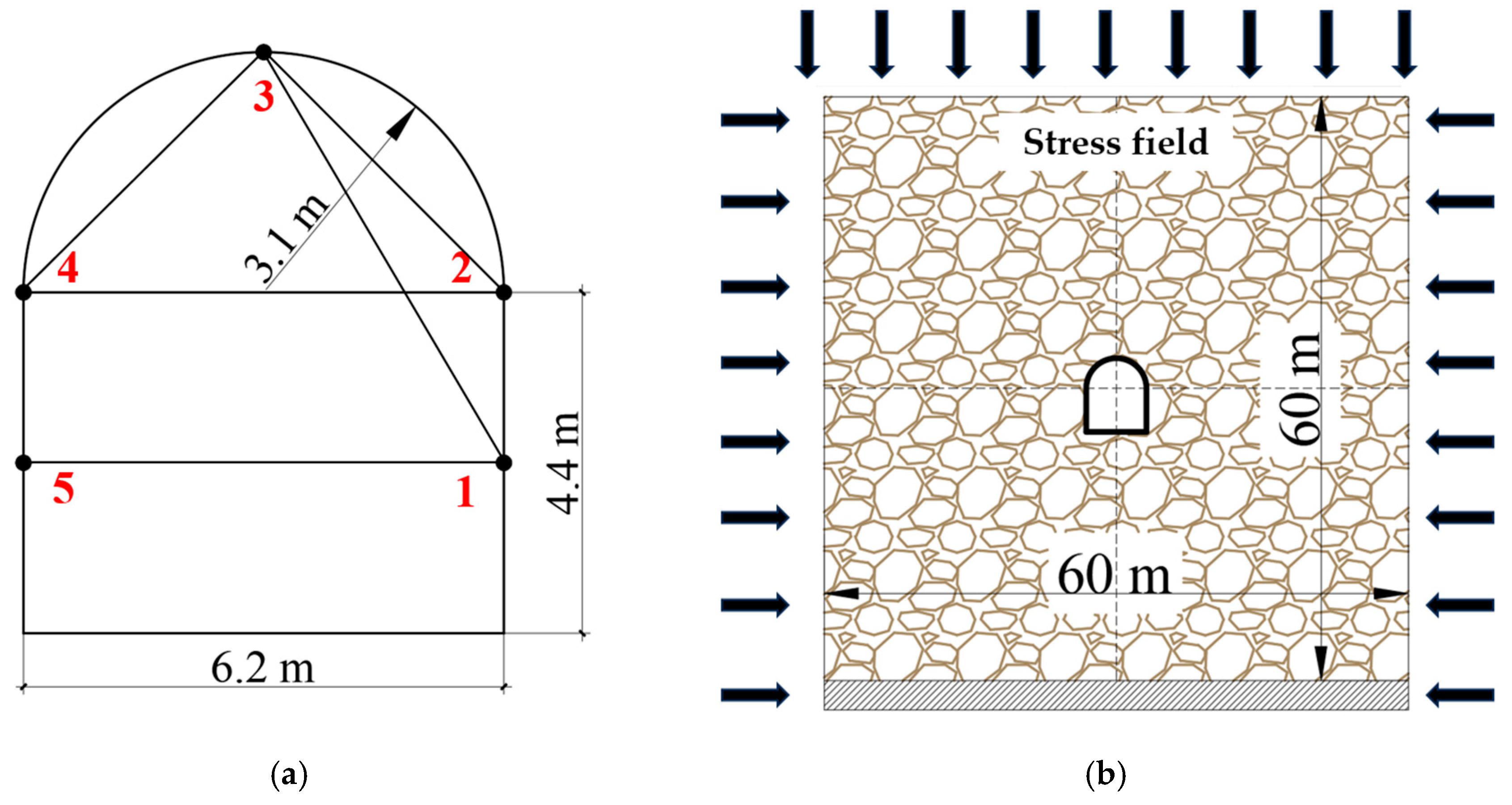
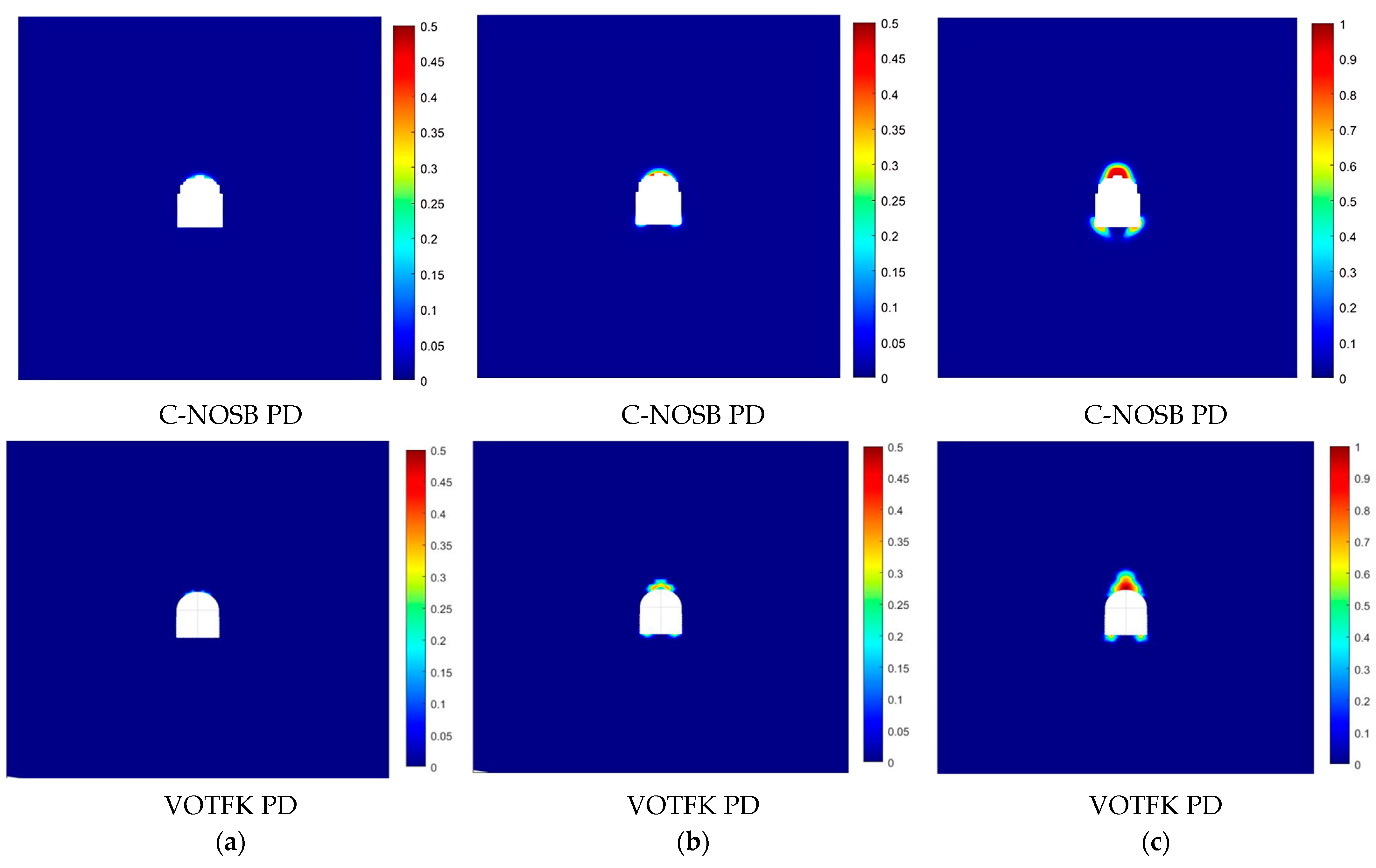
4.1. Simple Compression Creep Test of Sandstone
| Algorithm 1. A Particle Method Levenberg–Marquardt Algorithm. |
| With the given initial data, the boundary information and the observation data : Inputs:. Initialize the self-adaptive guess and a small enough. for Iterations do respectively to obtain . . Update the search direction by the Armijo rule: find the smallest possible such that . Otherwise update and continue looping. end |
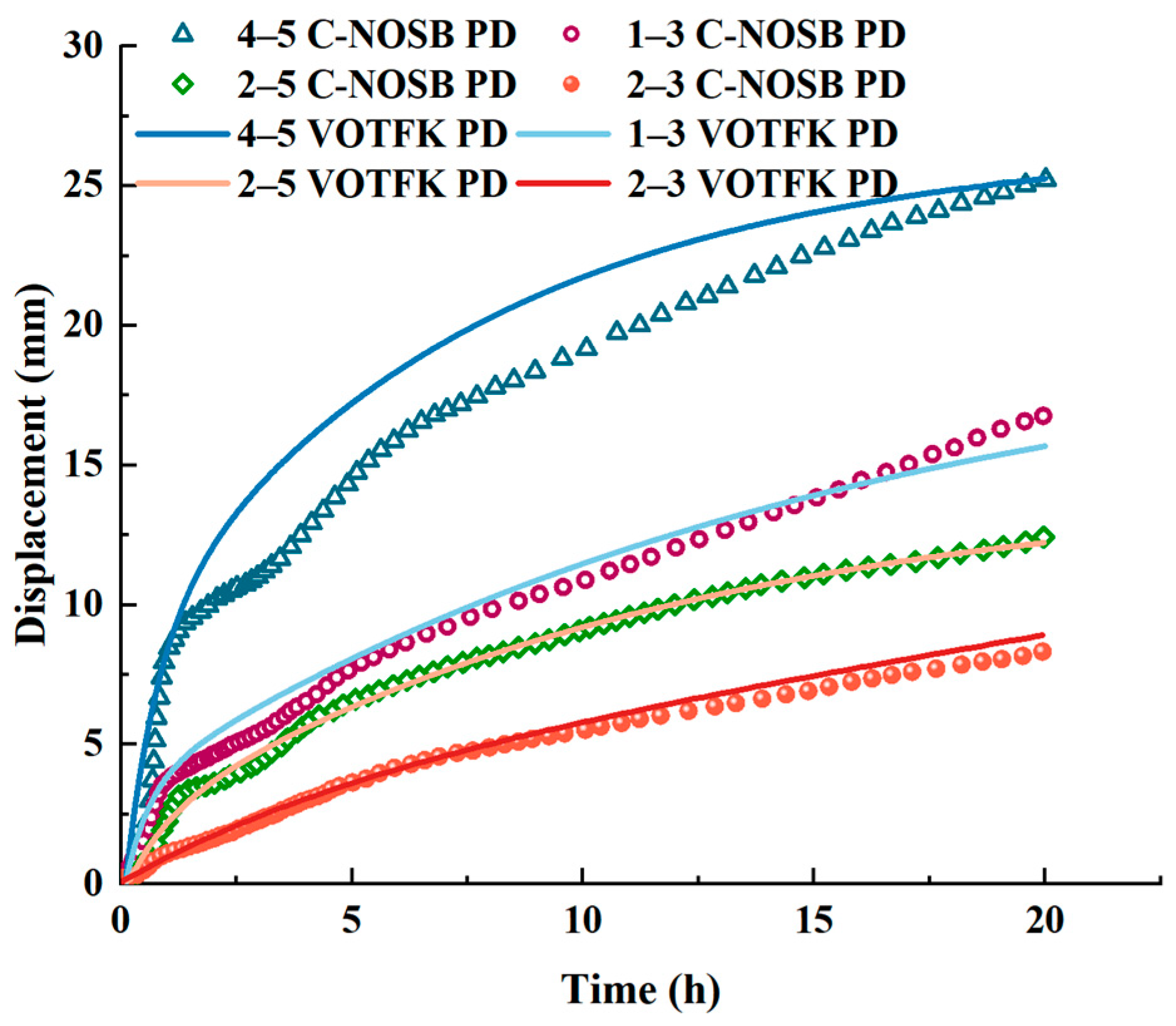
4.2. Numerical Test of Tunnel Rheology Behavior
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, Q.; Wang, Y.; Zan, Y.; Lu, W.; Bai, X.; Guo, J. Peridynamics simulation of the fragmentation of ice cover by blast loads of an underwater explosion. J. Mar. Sci. Technol. 2018, 23, 52–66. [Google Scholar] [CrossRef]
- Xu, T.; Xu, Q.; Deng, M.; Ma, T.; Yang, T.; Tang, C.-A. A numerical analysis of rock creep-induced slide: A case study from Jiweishan Mountain, China. Environ. Earth Sci. 2014, 72, 2111–2128. [Google Scholar] [CrossRef]
- Hou, Z.; Wundram, L.; Meyer, R.; Schmidt, M.; Schmitz, S.; Were, P. Development of a long-term wellbore sealing concept based on numerical simulations and in situ-testing in the Altmark natural gas field. Environ. Earth Sci. 2012, 67, 395–409. [Google Scholar] [CrossRef]
- Gao, Y.H.; Zhou, Z.; Zhang, H.; Jin, S.; Yang, W.; Meng, Q.H. Viscoelastoplastic displacement solution for deep buried circular tunnel based on a fractional derivative creep model. Adv. Civ. Eng. 2021, 2021, 3664578. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Y.; Li, Y.; Jiang, W.; Wang, Y. Experimental study on the failure mechanism of tunnel surrounding rock under different groundwater seepage paths. Geofluids 2021, 2021, 8856365. [Google Scholar] [CrossRef]
- Yu, J.; Liu, G.; Cai, Y.; Zhou, J.; Liu, S.; Tu, B. Time-dependent deformation mechanism for swelling soft-rock tunnels in coal mines and its mathematical deduction. Int. J. Geomech. 2020, 20, 04019186. [Google Scholar] [CrossRef]
- Koellerr, C. Applications of fractional calculus to the theory of viscoelasticity. J. Appl. Mech. 1984, 51, 299–307. [Google Scholar] [CrossRef]
- Tian, D.L.; Zhou, X.P. The kinematic-constraint-inspired non-ordinary state-based peridynamics with fractional viscoelas-tic-viscoplastic constitutive model to simulating time-dependent deformation and failure of rocks. Comput. Methods Appl. Mech. Eng. 2024, 424, 116873. [Google Scholar] [CrossRef]
- Yin, D.; Zhang, W.; Cheng, C.; Li, Y. Fractional time-dependent Bingham model for muddy clay. J. Non-Newton. Fluid. Mech. 2012, 187, 32–35. [Google Scholar] [CrossRef]
- Liu, X.; Li, D. Nonlinear damage creep model based on variable-order fractional theory for rock materials. SN Appl. Sci. 2020, 2, 2029. [Google Scholar] [CrossRef]
- Sun, H.G.; Chen, W.; Wei, H.; Chen, Y.Q. A comparative study of constant-order and variable-order fractional models in characterizing memory property of systems. Eur. Phys. J. Spec. Top. 2011, 193, 185–192. [Google Scholar] [CrossRef]
- Liu, X.; Li, D.; Han, C.; Shao, Y. A Caputo variable-order fractional damage creep model for sandstone considering effect of relaxation time. Acta Geotech. 2022, 17, 153–167. [Google Scholar] [CrossRef]
- Shin, J.H.; Potts, D.M.; Zdravkovic, L. The effect of pore-water pressure on NATM tunnel linings in decomposed granite soil. Can. Geotech. J. 2005, 42, 1585–1599. [Google Scholar] [CrossRef]
- Wu, H.N.; Shen, S.L.; Chen, R.P.; Zhou, A. Three-dimensional numerical modelling on localised leakage in segmental lining of shield tunnels. Comput. Geotech. 2020, 122, 103549. [Google Scholar] [CrossRef]
- Wang, Q.Y.; Zhu, W.C.; Xu, T.; Niu, L.L.; Wei, J. Numerical simulation of rock creep behavior with a damage-based constitutive law. Int. J. Geomech. 2017, 17, 04016044. [Google Scholar] [CrossRef]
- Li, B.; Yu, H.; Ji, D.; Wang, F.; Lei, Z.; Wu, H. Pore-scale imbibition patterns in layered porous media with fractures. Phys. Fluids 2024, 36, 012120. [Google Scholar] [CrossRef]
- Wang, C.; Liu, B.; Mohammadi, M.-R.; Fu, L.; Fattahi, E.; Motra, H.B.; Hazra, B.; Hemmati-Sarapardeh, A.; Ostadhassan, M. Integrating experimental study and intelligent modeling of pore evolution in the Bakken during simulated thermal progression for CO2 storage goals. Appl. Energy 2024, 359, 122693. [Google Scholar] [CrossRef]
- Reddy, J.N. An Introduction to Continuum Mechanics; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Silling, S.A. Reformulation of elasticity theory for discontinuities and long-range forces. J. Mech. Phys. Solids 2000, 48, 175–209. [Google Scholar] [CrossRef]
- Silling, S.A.; Askari, E. A meshfree method based on the peridynamic model of solid mechanics. Comput. Struct. 2005, 83, 1526–1535. [Google Scholar] [CrossRef]
- Kilic, B.; Madenci, E. Prediction of crack paths in a quenched glass plate by using peridynamic theory. Int. J. Fract. 2009, 156, 165–177. [Google Scholar] [CrossRef]
- Lai, X.; Ren, B.; Fan, H.; Li, S.; Wu, C.T.; Regueiro, R.A.; Liu, L. Peridynamics simulations of geomaterial fragmentation by impulse loads. Int. J. Numer. Anal. Methods Geomech. 2015, 39, 1304–1330. [Google Scholar]
- Oterkus, E.; Madenci, E.; Weckner, O.; Silling, S.; Bogert, P.; Tessler, A. Combined finite element and peridynamic analyses for predicting failure in a stiffened composite curved panel with a central slot. Compos. Struct. 2012, 94, 839–850. [Google Scholar]
- Weckner, O.; Mohamed, N.A.N. Viscoelastic material models in peridynamics. Appl. Math. Comput. 2013, 219, 6039–6043. [Google Scholar] [CrossRef]
- Ha, Y.D.; Lee, J.; Hong, J.W. Fracturing patterns of rock-like materials in compression captured with peridynamics. Eng. Fract. Mech. 2015, 144, 176–193. [Google Scholar]
- Zhou, X.P.; Shou, Y.D. Numerical simulation of failure of rock-like material subjected to compressive loads using improved peridynamic method. Int. J. Geomech. 2017, 17, 04016086. [Google Scholar] [CrossRef]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity: An Introduction to Mathematical Models; World Scientific: Singapore, 2022. [Google Scholar]
- Farno, E.; Baudez, J.-C.; Eshtiaghi, N. Comparison between classical Kelvin-Voigt and fractional derivative Kelvin-Voigt models in prediction of linear viscoelastic behaviour of waste activated sludge. Sci. Total Environ. 2018, 613, 1031–1036. [Google Scholar] [PubMed]
- Gao, C.; Zhou, Z.; Li, Z.; Li, L.; Cheng, S. Peridynamics simulation of surrounding rock damage characteristics during tunnel excavation. Tunn. Undergr. Space Technol. 2020, 97, 103289. [Google Scholar]
- Zaky, M.; Hendy, A.; Suragan, D. A note on a class of Caputo fractional differential equations with respect to another function. Math. Comput. Simul. 2022, 196, 289–295. [Google Scholar] [CrossRef]
- Suzuki, J.L.; Kharazmi, E.; Varghaei, P.; Naghibolhosseini, M.; Zayernouri, M. Anomalous nonlinear dynamics behavior of fractional viscoelastic beams. J. Comput. Nonlinear Dyn. 2021, 16, 111005. [Google Scholar]
- Zheng, X.; Wang, H. A hidden-memory variable-order time-fractional optimal control model: Analysis and approximation. SIAM J. Control Optim. 2021, 59, 1851–1880. [Google Scholar]
- Benson, D.A.; Schumer, R.; Meerschaert, M.M.; Wheatcraft, S.W. Fractional dispersion, Lévy motion, and the MADE tracer tests. Transp. Porous Media 2001, 42, 211–240. [Google Scholar]
- Pang, G.; Lu, L.; Karniadakis, G.E. fPINNs: Fractional physics-informed neural networks. SIAM J. Sci. Comput. 2019, 41, A2603–A2626. [Google Scholar]
- Zayernouri, M.; Karniadakis, G.E. Fractional spectral collocation methods for linear and nonlinear variable order FPDEs. J. Comput. Phys. 2015, 293, 312–338. [Google Scholar]
- Kilic, B.; Madenci, E. An adaptive dynamic relaxation method for quasi-static simulations using the peridynamic theory. Theor. Appl. Fract. Mech. 2010, 53, 194–204. [Google Scholar]
- Underwood, P. Dynamic Relaxation, in: Computational Method for Transient Analysis. Chapter 1983, 5, 245–256. [Google Scholar]
- Foster, J.T.; Silling, S.A.; Chen, W.W. Viscoplasticity using peridynamics. Int. J. Numer. Methods Eng. 2010, 81, 1242–1258. [Google Scholar]
- Parks, M.L.; Lehoucq, R.B.; Plimpton, S.J.; Silling, S.A. Implementing peridynamics within a molecular dynamics code. Comput. Phys. Commun. 2008, 179, 777–783. [Google Scholar]
- Tian, D.L.; Zhou, X.P. A novel kinematic-constraint-inspired non-ordinary state-based peridynamics. Appl. Math. Model. 2022, 109, 709–740. [Google Scholar]
- Javili, A.; Ekiz, E.; McBride, A.T.; Steinmann, P. Continuum-kinematics-inspired peridynamics: Thermo-mechanical problems. Contin. Mech. Thermodyn. 2021, 33, 2039–2063. [Google Scholar]
- Chen, B.R.; Feng, X. Universal viscoelastoplastic combination model and its engineering applications. Chin. J. Rock. Mech. Eng. 2008, 27, 1028–1035. [Google Scholar]


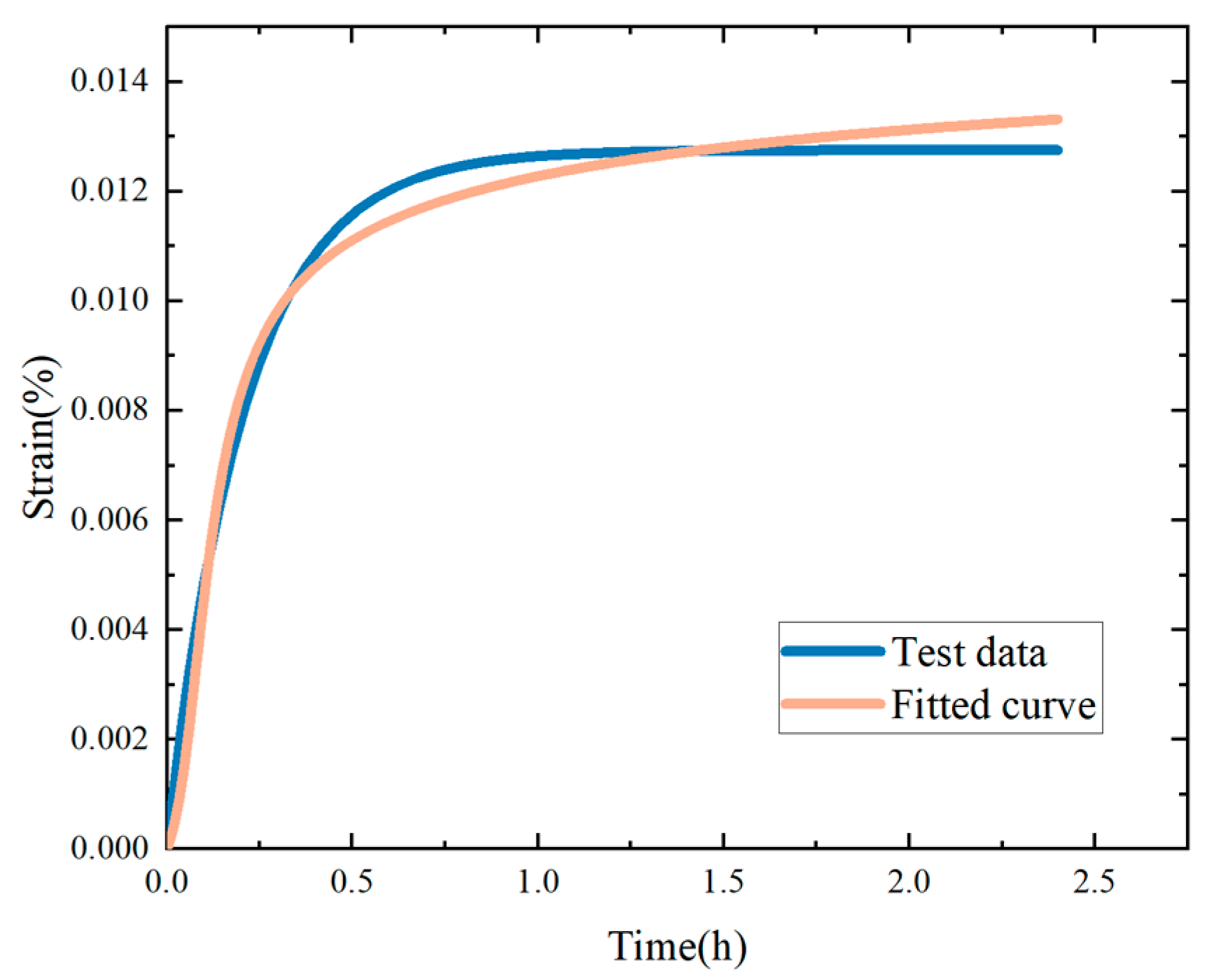

| Model | E (MPa) | μ (MPa·s) | α |
|---|---|---|---|
| COTFK PD | 68.1 | 9.6 | 0.12 |
| VOTFK PD | 72.3 | 9.3 | e−9.50t |
| E (MPa) | μ (MPa·h) | α |
|---|---|---|
| 609.2 | 2772.1 | e−15.1t |
| Time (h) | Test Result (mm) | VTOFK PD (mm) | Error (%) |
|---|---|---|---|
| 0.00 | 0.00 | 0.00 | 0.00 |
| 0.83 | 4.58 | 3.40 | 25.76 |
| 1.93 | 5.51 | 5.28 | 4.17 |
| 2.85 | 6.28 | 6.21 | 1.11 |
| 3.69 | 7.23 | 6.98 | 3.46 |
| 5.20 | 8.17 | 8.23 | 0.73 |
| 5.95 | 9.11 | 8.81 | 3.29 |
| 7.05 | 9.58 | 9.61 | 0.31 |
| 8.13 | 10.51 | 10.33 | 1.71 |
| 9.15 | 10.81 | 10.98 | 1.57 |
| 10.07 | 11.28 | 11.49 | 1.86 |
| 10.81 | 11.59 | 11.53 | 0.52 |
| 12.16 | 12.21 | 12.64 | 3.52 |
| 13.41 | 12.84 | 13.23 | 3.04 |
| 13.92 | 12.99 | 13.45 | 3.54 |
| 14.92 | 13.78 | 13.58 | 1.45 |
| 16.18 | 14.07 | 14.38 | 2.20 |
| 17.10 | 14.54 | 15.04 | 3.44 |
| 18.44 | 15.01 | 15.18 | 1.13 |
| 19.03 | 15.31 | 15.37 | 0.39 |
| 19.97 | 15.30 | 15.67 | 2.42 |
| Mean error | 3.13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, C.; Dong, T.; Qi, Y.; Guo, X. Variable-Order Time-Fractional Kelvin Peridynamics for Rock Steady Creep. Fractal Fract. 2025, 9, 197. https://doi.org/10.3390/fractalfract9040197
Liu C, Dong T, Qi Y, Guo X. Variable-Order Time-Fractional Kelvin Peridynamics for Rock Steady Creep. Fractal and Fractional. 2025; 9(4):197. https://doi.org/10.3390/fractalfract9040197
Chicago/Turabian StyleLiu, Chang, Tiantian Dong, Yuhang Qi, and Xu Guo. 2025. "Variable-Order Time-Fractional Kelvin Peridynamics for Rock Steady Creep" Fractal and Fractional 9, no. 4: 197. https://doi.org/10.3390/fractalfract9040197
APA StyleLiu, C., Dong, T., Qi, Y., & Guo, X. (2025). Variable-Order Time-Fractional Kelvin Peridynamics for Rock Steady Creep. Fractal and Fractional, 9(4), 197. https://doi.org/10.3390/fractalfract9040197





