New Perspectives of Hermite–Hadamard–Mercer-Type Inequalities Associated with ψk-Raina’s Fractional Integrals for Differentiable Convex Functions
Abstract
:1. Introduction
- If and , then the -RFIs reduce to the classical Riemann–Liouville (R-L) integrals.
- If and , then Definition 5 reduces to Definition 1.
- If and , then Definition 5 reduces to Definition 3.
- If and , then Definition 5 reduces to Definition 4.
2. Inequalities of the H-H-M-Type for -Raina’s Fractional Integrals
3. Related Results of the H-H-M-Type Inequalities for -Raina’s Fractional Integrals
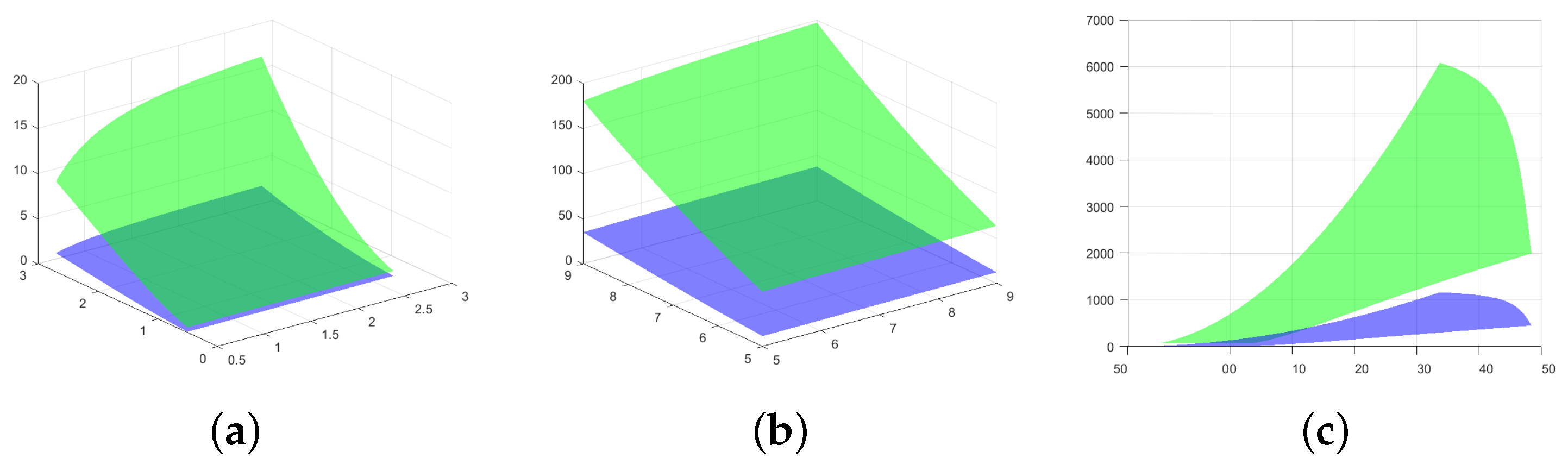
4. Visual Evaluation
5. Applications
5.1. Modified Bessel Function
5.2. q-Digamma Function
6. Discussions and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lakshmikantham, V. Differential and Integral Inequalities: Theory and Applications, Vol. I: Ordinary Differential Equations; Academic Press: Cambridge, MA, USA, 1969. [Google Scholar]
- Javed, M.Z.; Awan, M.U.; Bin-Mohsin, B.; Budak, H.; Dragomir, S.S. Some Classical Inequalities Associated with Generic Identity and Applications. Axioms 2024, 13, 533. [Google Scholar] [CrossRef]
- Walter, W. Differential and Integral Inequalities; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 55. [Google Scholar]
- Zhu, C.; Fečkan, M.; Wang, J. Fractional Integral Inequalities for Differentiable Convex Mappings and Applications to Special Means and a Midpoint Formula. J. Appl. Math. Stat. Inform. 2012, 8, 21–28. [Google Scholar] [CrossRef]
- Denton, Z.; Vatsala, A.S. Fractional Integral Inequalities and Applications. Comput. Math. Appl. 2010, 59, 1087–1094. [Google Scholar] [CrossRef]
- Ciurdariu, L.; Grecu, E. Hermite–Hadamard–Mercer-Type Inequalities for Three-Times Differentiable Functions. Axioms 2024, 13, 413. [Google Scholar] [CrossRef]
- Kermausuor, S.; Nwaeze, E.R. Mathematical Inequalities in Fractional Calculus and Applications. Fractal Fract. 2024, 8, 471. [Google Scholar] [CrossRef]
- Hussain, T.; Ciurdariu, L.; Grecu, E. A New Inclusion on Inequalities of the Hermite–Hadamard–Mercer Type for Three-Times Differentiable Functions. Mathematics 2024, 12, 3711. [Google Scholar] [CrossRef]
- Rashid, S.; Abdeljawad, T.; Jarad, F.; Noor, M.A. Some Estimates for Generalized Riemann-Liouville Fractional Integrals of Exponentially Convex Functions and Their Applications. Mathematics 2019, 7, 807. [Google Scholar] [CrossRef]
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific: Singapore, 2000. [Google Scholar]
- Baleanu, D.; Güvenç, Z.B.; Machado, J.T. New Trends in Nanotechnology and Fractional Calculus Applications; Springer: Berlin/Heidelberg, Germany, 2010; Volume 10. [Google Scholar]
- Atangana, A. Application of Fractional Calculus to Epidemiology; Fractional Dynamics; Walter de Gruyter: Warsaw, Poland, 2015; Volume 2015, pp. 174–190. [Google Scholar]
- Magin, R. Fractional Calculus in Bioengineering, part 1. Crit. Rev. Biomed. Eng. 2004, 32, 1. [Google Scholar]
- Monje, C.A.; Vinagre, B.M.; Feliu, V.; Chen, Y. Tuning and Auto-Tuning of Fractional Order Controllers for Industry Applications. Control Eng. Pract. 2008, 16, 798–812. [Google Scholar] [CrossRef]
- Dragomir, S.S. New Estimation of the Remainder in Taylor’s Formula using Grüss Type Inequalities and Applications. Math. Ineq. Appl. 1999, 2, 183–194. [Google Scholar] [CrossRef]
- Jensen, J.L.W.V. Sur les Fonctions Convexes et les Inégalités entre les Valeurs Moyennes. Acta Math. 1906, 30, 175–193. [Google Scholar]
- Hadamard, J. Étude sur les Propriétés des Fonctions entières et en particulier d’une Fonction considérée par Riemann. J. Math. Pures Appl. 1893, 171–216. [Google Scholar]
- Hermite, C. Sur deux Limites d’une Intégrale Définie. Mathesis 1883, 3, 1–82. [Google Scholar]
- Dragomir, S.S.; Agarwal, R.P. Two Inequalities for Differentiable Mappings and Applications to Special Means of Real Numbers and to Trapezoidal Formula. Appl. Math. Lett. 1998, 11, 91–95. [Google Scholar]
- Askey, R. The q-gamma and q-beta Functions. Appl. Anal. 1978, 8, 125–141. [Google Scholar]
- Mercer, A.M. A Variant of Jensen’s Inequality. J. Inequal. Pure Appl. Math. 2003, 4, 73. [Google Scholar]
- Podlubny, I. An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of their Solution and some of their Applications. Math. Sci. Eng. 1999, 198, 340. [Google Scholar]
- Abdeljawad, T.; Ali, M.A.; Mohammed, P.O.; Kashuri, A. On Inequalities of Hermite–Hadamard–Mercer Type Involving Riemann–Liouville Fractional Integrals. AIMS Math. 2020, 5, 7316–7331. [Google Scholar] [CrossRef]
- Mubeen, S.; Habibullah, G.M. k-Fractional Integrals and Applications. Int. J. Contemp. Math. 2012, 7, 89–94. [Google Scholar]
- Raina, R.K. On Generalized Wright’s Hypergeometric Functions and Fractional Calculus Operators. East Asian Math. J. 2005, 21, 191–203. [Google Scholar]
- Set, E.; Dragomir, S.S.; Gözpınar, A. Some Generalized Hermite-Hadamard Type Inequalities Involving Fractional Integral Operator Functions Whose Second Derivatives in Absolute Value Are s-Convex. RGMIA Res. Rep. Coll. 2017, 20, 14. [Google Scholar]
- Agarwal, R.P.; Luo, M.-J.; Raina, R.K. On Ostrowski Type Inequalities. Fasc. Math. 2016, 204, 5–27. [Google Scholar] [CrossRef]
- Tunc, T.; Budak, H.; Usta, F.; Sarikaya, M.Z. On New Generalized Fractional Integral Operators and Related Inequalities. Konuralp J. Math. 2017, 8, 268–278. [Google Scholar]
- Jhanthanam, S.; Tariboon, J.; Ntouyas, S.K.; Nonlaopon, K. On q-Hermite–Hadamard Inequalities for Differentiable Convex Functions. Mathematics 2019, 7, 632. [Google Scholar] [CrossRef]
- Butt, S.I.; Umar, M.; Khan, K.A.; Kashuri, A.; Emadifar, H. Fractional Hermite–Jensen–Mercer Integral Inequalities with Respect to Another Function and Application. Complexity 2021, 2021, 9260828. [Google Scholar] [CrossRef]
- Kang, Q.; Butt, S.I.; Nazeer, W.; Nadeem, M.; Nasir, J.; Yang, H. New Variant of Hermite–Jensen–Mercer Inequalities via Riemann–Liouville Fractional Integral Operators. J. Math. 2020, 2020, 4303727. [Google Scholar] [CrossRef]
- Kian, M.; Moslehian, M. Refinements of the Operator Jensen–Mercer Inequality. Electron. J. Linear Algebra 2013, 26, 742–753. [Google Scholar]
- Butt, S.I.; Kashuri, A.; Umar, M.; Aslam, A.; Gao, W. Hermite–Jensen–Mercer Type Inequalities via Ψ-Riemann–Liouville k-Fractional Integrals. AIMS Math. 2020, 5, 5193–5220. [Google Scholar] [CrossRef]
- Alomari, M.; Darus, M.; Kirmaci, U.S. Refinements of Hadamard-type Inequalities for Quasi-Convex Functions with Applications to Trapezoidal Formula and to Special Means. Comput. Math. Appl. 2010, 59, 225–232. [Google Scholar] [CrossRef]
- Mohammed, P.O.; Brevik, I. A new Version of the Hermite–Hadamard Inequality for Riemann–Liouville Fractional Integrals. Symmetry 2020, 12, 610. [Google Scholar] [CrossRef]
- Barani, A.; Barani, S.; Dragomir, S.S. Refinements of Hermite-Hadamard Type Inequality for Functions Whose Second Derivatives Absolute Values are Quasi Convex. RGMIA Res. Rep. Coll. 2011, 14, 1–9. [Google Scholar]
- Mohammed, P.O.; Abdeljawad, T. Modifications of certain fractional integral inequalities for convex function. Adv. Differ. Equ. 2020, 2020, 69. [Google Scholar]
- Milton, K.A.; Parashar, P.; Brevik, I.; Kennedy, G. Self-stress on a dielectric ball and Casimir-Polder forces. Ann. Phys. 2020, 412, 168008. [Google Scholar]
- Parashar, P.; Milton, K.A.; Shajesh, K.V.; Brevik, I. Electromagnetic delta-function sphere. Phys. Rev. D 2017, 96, 085010. [Google Scholar]
- Brevik, I.; Marachevsky, V.N. Casimir surface force on a dilute dielectric ball. Phys. Rev. D 1999, 60, 085006. [Google Scholar]
- Mohammed, P.O.; Abdeljawad, T.; Baleanu, D.; Kashuri, A.; Hamassalh, F.; Agarwal, P. New fractional inequalities of Hermite-Hadamard type involving the incomplete gamma functions. J. Inequalities Appl. 2020, 2020, 263. [Google Scholar]
- Mitrinovic, D.S.; Pecaric, J.; Fink, A.M. Classical and New Inequalities in Analysis; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 61. [Google Scholar]
- Kantala, J.; Wannalookkhee, F.; Nonlaopon, K.; Budak, H. Some quantum Integral Inequalities for (p, h)-Convex Functions. Mathematics 2023, 11, 1072. [Google Scholar] [CrossRef]
- Budak, H.; Bas, U.; Kara, H.; Samei, M.E. New refinements of the Hermite-Hadamard Inequalities based on ψ-Hilfer Fractional Integral. J. Korean Math. Soc. 2024, 31, 311–324. [Google Scholar]
- Budak, H.; Kosem, P.; Kara, H. On new Milne-Type Inequalities for Fractional Integrals. J. Inequalities Appl. 2023, 2023, 10. [Google Scholar]
- Hyder, A.A.; Budak, H.; Barakat, M.A. Milne-Type Inequalities via Expanded Fractional Operators: A Comparative Study with Different Types of Functions. AIMS Math. 2024, 5, 11228–11246. [Google Scholar]
- Vivas-Cortez, M.; Javed, M.Z.; Awan, M.U.; Dragomir, S.S.; Zidan, A.M. Properties and Applications of Symmetric Quantum Calculus. Fractal Fract. 2024, 8, 107. [Google Scholar] [CrossRef]
- Watson, G.N. A Treatise on the Theory of Bessel Functions; Cambridge University Press: Cambridge, UK, 1922; Volume 2. [Google Scholar]
- Luke, Y.L. Special Functions and Their Approximations; Academic Press: Cambridge, MA, USA, 1969; Volume 2. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hussain, T.; Ciurdariu, L.; Grecu, E. New Perspectives of Hermite–Hadamard–Mercer-Type Inequalities Associated with ψk-Raina’s Fractional Integrals for Differentiable Convex Functions. Fractal Fract. 2025, 9, 203. https://doi.org/10.3390/fractalfract9040203
Hussain T, Ciurdariu L, Grecu E. New Perspectives of Hermite–Hadamard–Mercer-Type Inequalities Associated with ψk-Raina’s Fractional Integrals for Differentiable Convex Functions. Fractal and Fractional. 2025; 9(4):203. https://doi.org/10.3390/fractalfract9040203
Chicago/Turabian StyleHussain, Talib, Loredana Ciurdariu, and Eugenia Grecu. 2025. "New Perspectives of Hermite–Hadamard–Mercer-Type Inequalities Associated with ψk-Raina’s Fractional Integrals for Differentiable Convex Functions" Fractal and Fractional 9, no. 4: 203. https://doi.org/10.3390/fractalfract9040203
APA StyleHussain, T., Ciurdariu, L., & Grecu, E. (2025). New Perspectives of Hermite–Hadamard–Mercer-Type Inequalities Associated with ψk-Raina’s Fractional Integrals for Differentiable Convex Functions. Fractal and Fractional, 9(4), 203. https://doi.org/10.3390/fractalfract9040203




