Mechanism Modeling and Analysis of Fractional-Order Synchronous Generator
Abstract
1. Introduction
- This paper first presents the fractional-order voltage equations of a synchronous generator in both the three-phase stationary coordinate system and the synchronous rotating coordinate system.
- This paper derives a second-order plus a non-integer synchronous generator model under simplified assumptions for the synchronous generator and names it the 2 + α order synchronous generator model.
- This paper establishes a single-machine infinite system that includes the 2 + α order synchronous generator model and PID+PSS excitation control. Based on this system, this paper investigates the dynamic operating characteristics of the 2 + α order synchronous generator model under three different disturbance conditions.
- The digital simulations presented in this study reveal that higher-order generator inductance is more effective in mitigating mechanical oscillations, whereas lower-order inductance facilitates terminal voltage recovery and suppresses oscillations in electromagnetic power output.
2. A Brief Introduction of Caputo Fractional Calculus and Fractional-Order Inductance
2.1. Definition of Fractional Calculus
2.2. Fractional-Order Inductance
3. Fractional-Order Synchronous Generator Voltage Equation
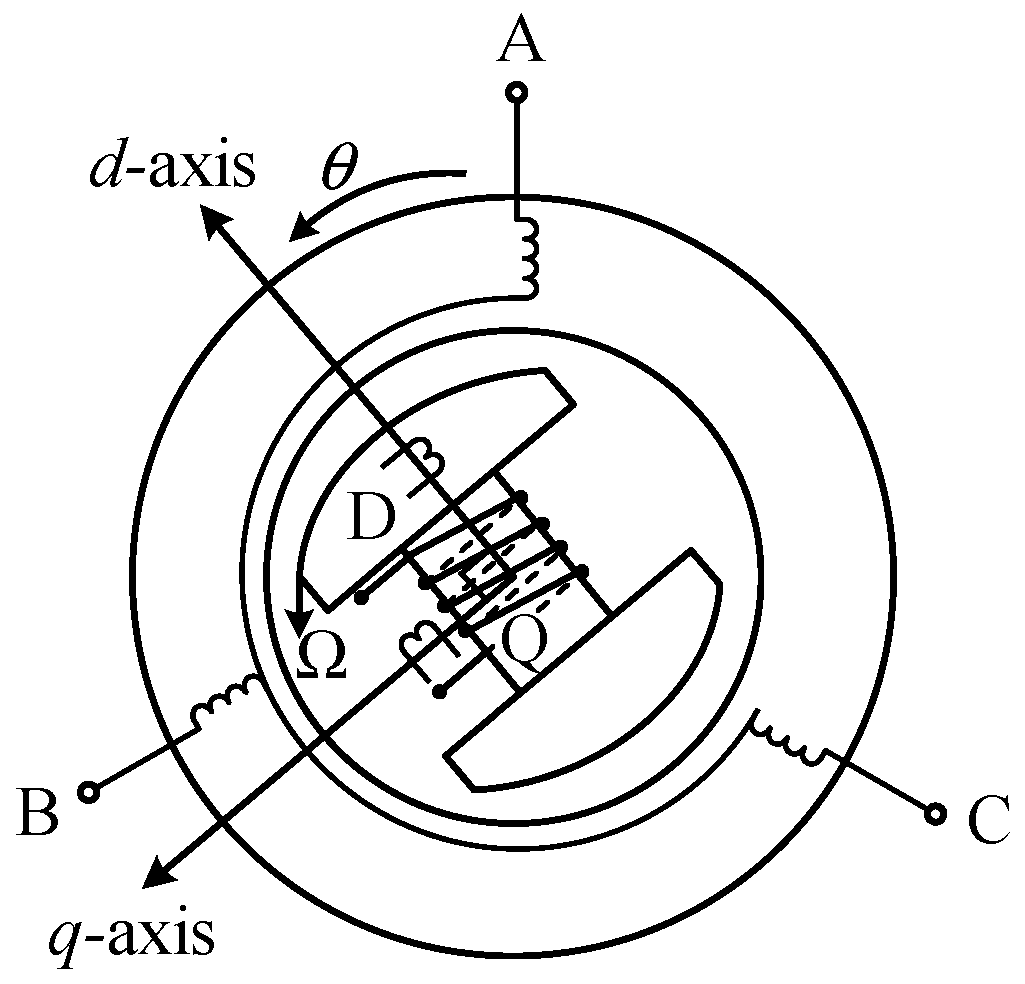
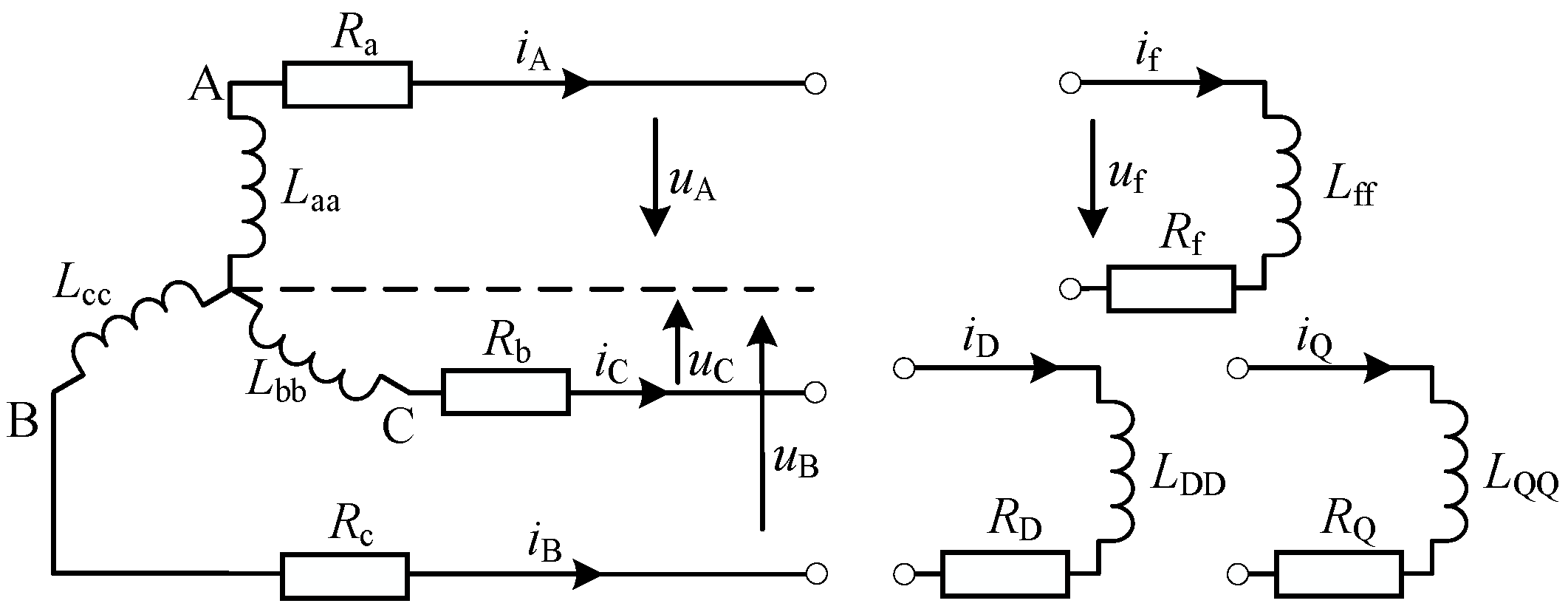
3.1. Establishing the Synchronous Generator Stator Voltage Equation in the Three-Phase Stationary Coordinate System (A-B-C)
3.2. Establishing the Fractional-Order Synchronous Generator Stator Voltage Equation in the Three-Phase Stationary Coordinate System (A-B-C)
3.3. Establishing the Fractional-Order Synchronous Generator Stator Voltage Equation in the Synchronous Rotating Coordinate System (d-q-0)
3.4. Establishing the Fractional-Order Synchronous Generator Rotor Voltage Equation in the Synchronous Rotating Coordinate System (d-q-0)
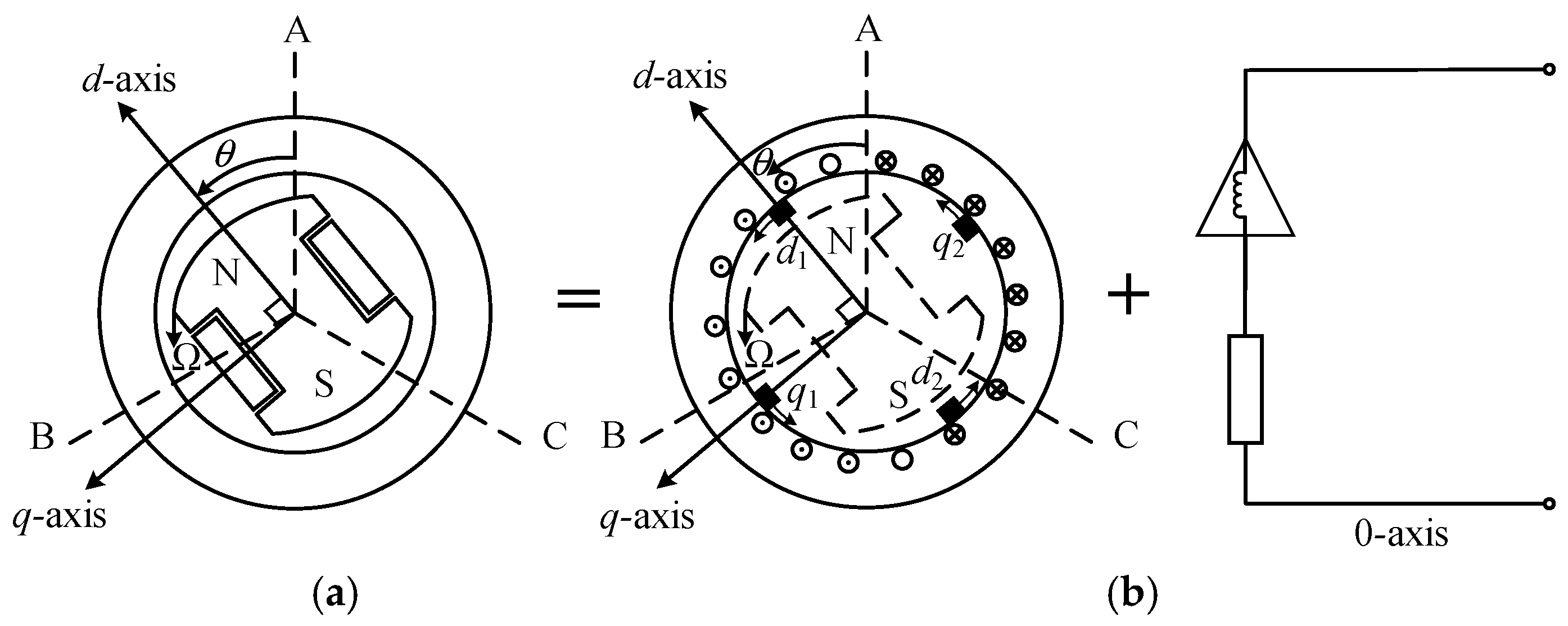
3.5. Fractional-Order Synchronous Generator 2 + α Order Model
- (1)
- Ignore the transients of the stator d and q windings and set in the stator voltage equation.
- (2)
- In the stator voltage equation, assuming , during transient processes where speed changes are small, the error caused by is negligible.
- (3)
- Ignore the D winding and Q winding, as their effects can be approximately considered by adding damping terms to the rotor motion equation.
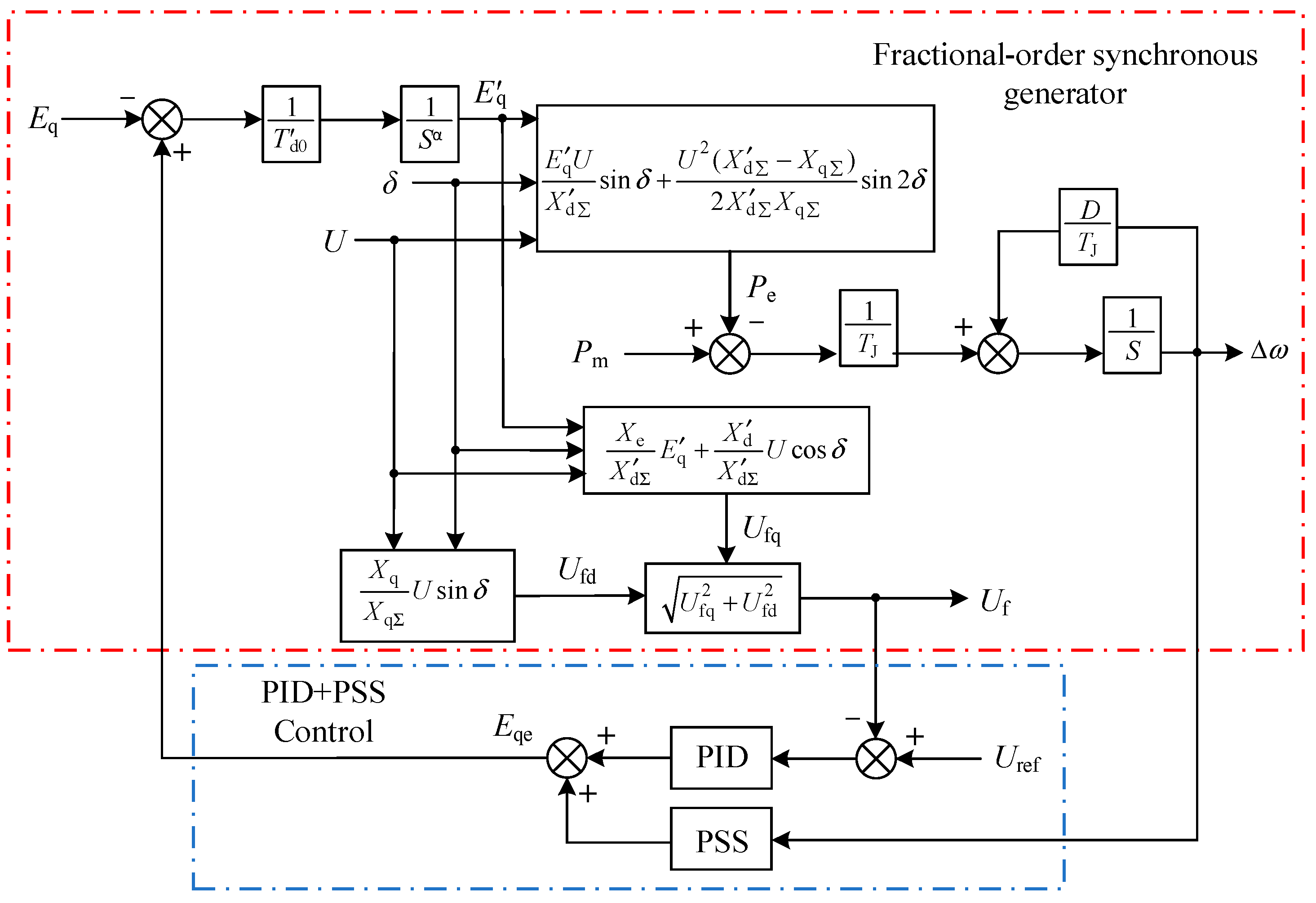
4. Mathematical Model of a Fractional-Order Excitation Control System for Synchronous Generators
4.1. Single-Machine Infinite Bus Power System Model
4.2. PID + PSS Excitation Control Design
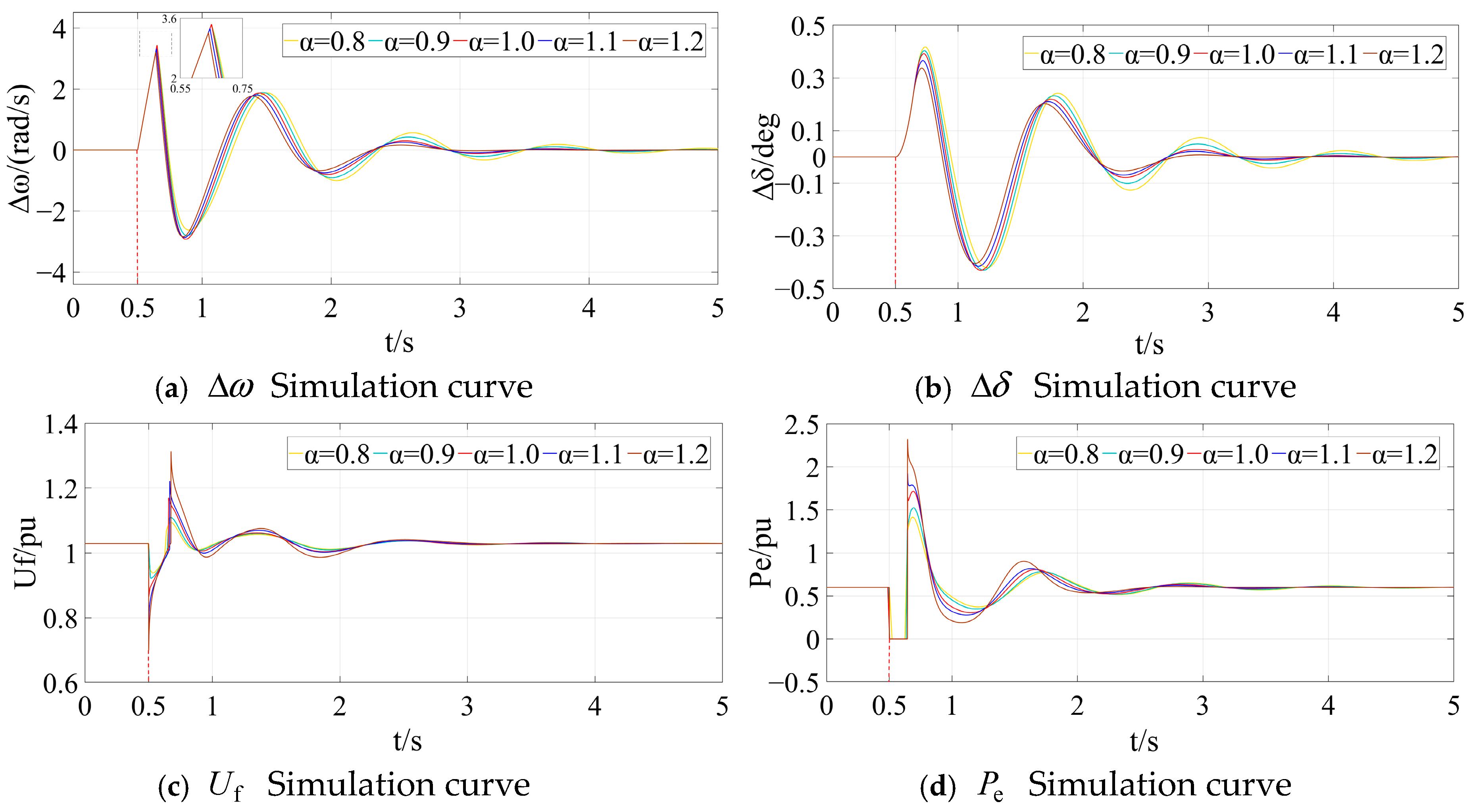
5. Digit Simulation and Analysis
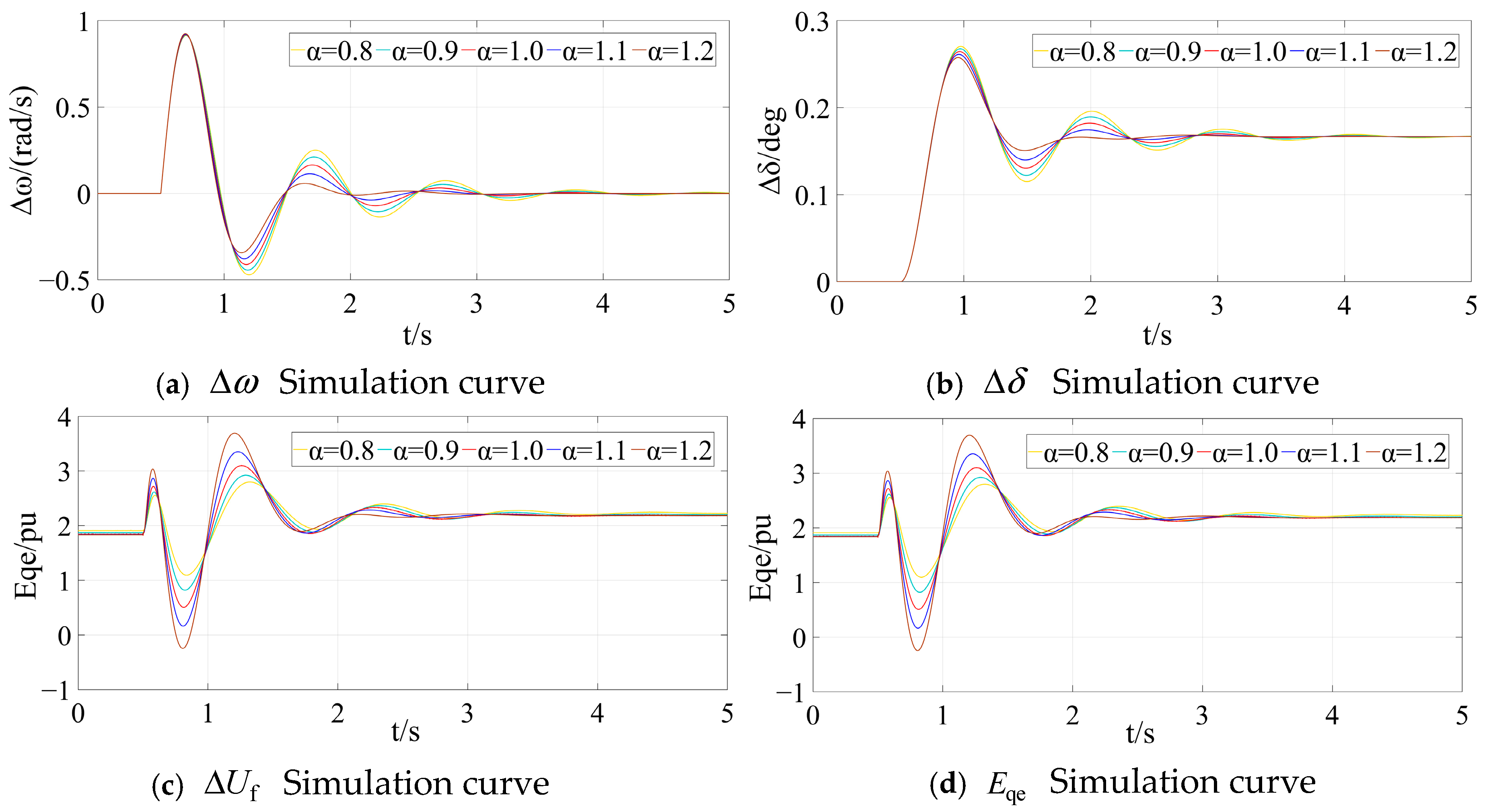
5.1. Simulation Scheme I
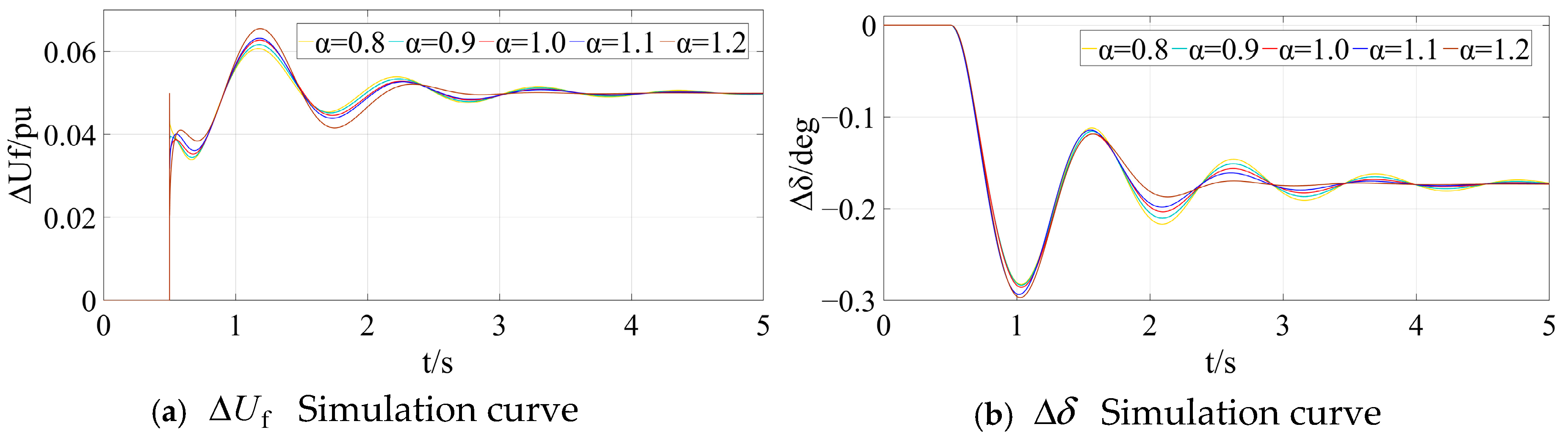
5.2. Simulation Scheme II
5.3. Simulation Scheme III
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Podlubny, I. Fractional-Order Systems and Fractional-Order Controllers; Academic: New York, NY, USA, 1994. [Google Scholar]
- Hilfer, R. Applications of fractional calculus in physics. In Applications of Fractional Calculus in Physics; World Scientific: Singapore, 2000; pp. 87–130. [Google Scholar]
- Djordjevic, V.D.; Atanackovic, T.M. On the application of fractional calculus in mechanics. In Proceedings of the 1st Serbian Congress on Theoretical and Applied Mechanics, Belgrade, Serbia, 10–13 April 2007; pp. 1–10. [Google Scholar]
- Kimeu, J.M. Fractional Calculus: Definitions and Applications. Master’s Thesis, Department of Mathematics, Western Kentucky University, Bowling Green, KY, USA, 2009. [Google Scholar]
- Baleanu, D.; Günvenc, Z.B.; Machado, J.A.T. New Trends in Nanotechnology and Fractional Calculus Applications; Springer: Berlin, Germany, 2010. [Google Scholar]
- Zahra, W.K.; Hikal, M.M.; Bahnasy, T.A. Solutions of fractional order electrical circuits via Laplace transform and nonstandard finite difference method. J. Egypt. Math. Soc. 2017, 25, 252–261. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic: New York, NY, USA, 1999. [Google Scholar]
- Zhou, Y.; Xu, G.; Huang, Y. Experiment analysis on motor-generator pair system for providing inertia of renewable energy. In Proceedings of the 21st International Conference on Electrical Machines and Systems (ICEMS), Jeju, Republic of Korea, 7–10 October 2018; pp. 1–6. [Google Scholar]
- Allagui, A.; Freeborn, T.J.; Elwakil, A.S.; Fouda, M.E.; Maundy, B.J.; Radwan, A.G.; Said, Z.; Abdelkareem, M.A. Review of fractional-order electrical characterization of supercapacitors. J. Power Sources 2018, 400, 457–467. [Google Scholar] [CrossRef]
- Chen, X.; Xi, L.; Zhang, Y.; Ma, H.; Huang, Y.; Chen, Y. Fractional techniques to characterize non-solid aluminum electrolytic capacitors for power electronic applications. Nonlinear Dyn. 2019, 98, 3125–3141. [Google Scholar] [CrossRef]
- Elwakil, A.S.; Allagui, A.; Freeborn, T.J.; Maundy, B.J. Further experimental evidence of the fractional-order energy equation in supercapacitors. AEU-Int. J. Electron. Commun. 2017, 78, 209–212. [Google Scholar] [CrossRef]
- Tessarolo, A. Accurate computation of multiphase synchronous machine inductances based on winding function theory. IEEE Trans. Energy Convers. 2012, 27, 895–904. [Google Scholar] [CrossRef]
- Niu, H.; Liu, L.; Jin, D.; Liu, S. High-tracking-precision sensorless control of PMSM system based on fractional order model reference adaptation. Fractal Fract. 2023, 7, 21. [Google Scholar] [CrossRef]
- Luo, S.; Song, Y.; Lewis, F.L.; Garrappa, R.; Li, S. Dynamic analysis and fuzzy fixed-time optimal synchronization control of unidirectionally coupled FO permanent magnet synchronous generator system. IEEE Trans. Fuzzy Syst. 2023, 31, 1742–1755. [Google Scholar] [CrossRef]
- Narayanan, G.; Ali, M.S.; Joo, Y.H.; Perumal, R.; Ahmad, B.; Alsulami, H. Robust adaptive fractional sliding-mode controller design for Mittag-Leffler synchronization of fractional-order PMSG-based wind turbine system. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 7646–7655. [Google Scholar] [CrossRef]
- Anbalagan, P.; Joo, Y.H. Stabilization analysis of fractional-order nonlinear permanent magnet synchronous motor model via interval type-2 fuzzy memory-based fault-tolerant control scheme. ISA Trans. 2023, 142, 310–324. [Google Scholar] [CrossRef] [PubMed]
- Luo, S.; Jian, Y.; Gao, Q. Synchronous generator modeling and semi-physical simulation. In Proceedings of the 22nd International Conference on Electrical Machines and Systems (ICEMS), Harbin, China, 11–14 August 2019; pp. 1–6. [Google Scholar]
- Retière, N.M.; Ivanes, M.S. An introduction to electric machine modeling by systems of noninteger order. Application to double-cage induction machine. IEEE Trans. Energy Convers. 1999, 14, 1026–1032. [Google Scholar] [CrossRef]
- Sambariya, D.K.; Prasad, R. Robust power system stabilizer design for single machine infinite bus system with different membership functions for fuzzy logic controller. In Proceedings of the 7th International Conference on Intelligent Systems and Control (ISCO), Coimbatore, India, 4–5 January 2013; pp. 1–6. [Google Scholar]
- Abubakr, H.; Vasquez, J.C.; Mahmoud, K.; Darwish, M.M.F.; Guerrero, J.M. Robust PID-PSS design for stability improvement of grid-tied hydroturbine generator. In Proceedings of the 22nd International Middle East Power Systems Conference (MEPCON), Assiut, Egypt, 14–16 December 2021; pp. 1–6. [Google Scholar]
- Xue, D.Y. Fractional Calculus and Fractional-Order Control; Science Press: Beijing, China, 2018. [Google Scholar]
- IEEE Standard 421.5-2016; IEEE Recommended Practice for Excitation System Models for Power System Stability Studies. IEEE: Piscataway, NJ, USA, 2016.
- Kundur, P.; Paserba, J.; Ajjarapu, V.; Andersson, G.; Bose, A.; Canizares, C.; Hatziargyriou, N.; Hill, D.; Stankovic, A.; Taylor, C.; et al. Definition and classification of power system stability. IEEE Trans. Power Syst. 2004, 19, 1387–1401. [Google Scholar]
- Sarkar, D.U.; Prakash, T.; Singh, S.N. Fractional order PID-PSS design using hybrid deep learning approach for damping power system oscillations. IEEE Trans. Power Syst. 2025, 40, 543–555. [Google Scholar] [CrossRef]
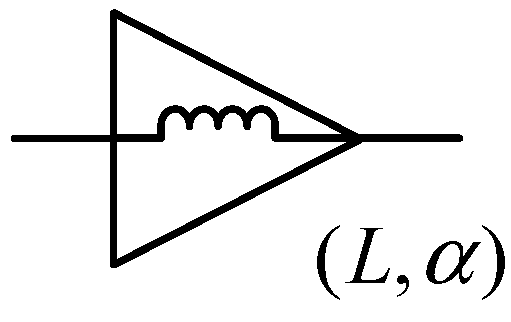

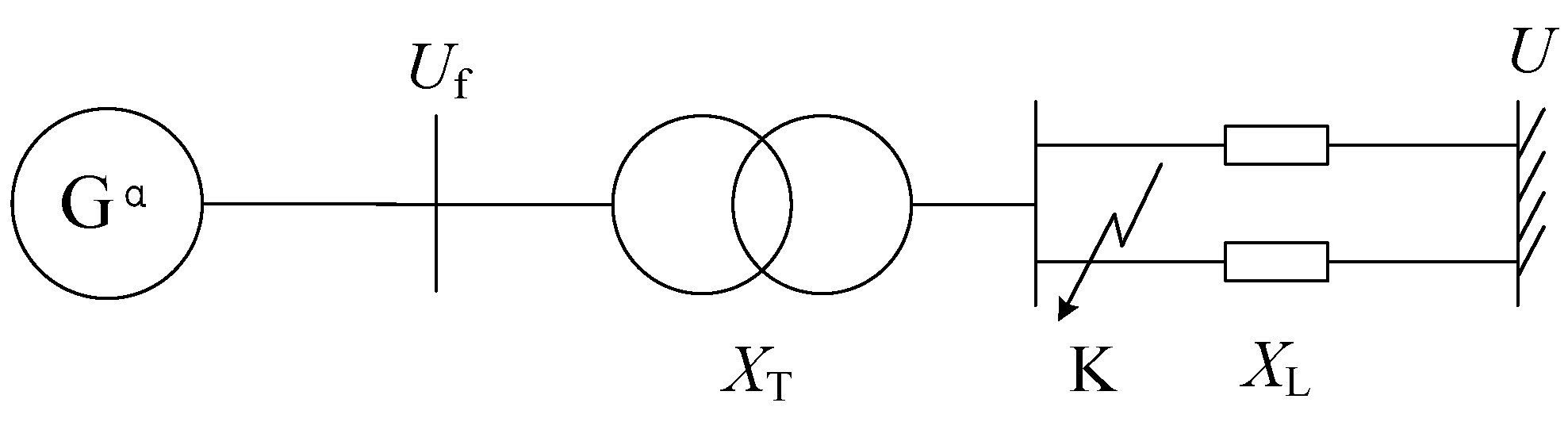

| Model Parameters | Value |
|---|---|
| d- | 2.12 p.u. |
| q- | 2.12 p.u. |
| d- | 0.26 p.u. |
| 0.24 p.u. | |
| Generator damping coefficient | 2 |
| 4.06 s | |
| 5.8 s |
| Order of Inductance () | Steady-State Error (p.u.) | Overshoot (%) | Response Time (s) |
|---|---|---|---|
| 0.8 | 0.330 | 0.249 | 0.825 |
| 0.9 | 0.333 | 0.317 | 0.983 |
| 1.0 | 0.339 | 0.418 | 1.025 |
| 1.1 | 0.345 | 0.534 | 1.143 |
| 1.2 | 0.352 | 0.689 | 1.362 |
| Order of Inductance () | Steady-State Error (p.u.) | Overshoot (%) | Response Time (s) | |||
|---|---|---|---|---|---|---|
| 0.8 | 0 | 0 | 0.063 | 1.362 | 1.000 | 4.532 |
| 0.9 | 0 | 0 | 0.078 | 1.543 | 1.021 | 4.074 |
| 1.0 | 0 | 0 | 0.137 | 1.862 | 1.124 | 3.485 |
| 1.1 | 0 | 0 | 0.187 | 2.205 | 1.342 | 2.997 |
| 1.2 | 0 | 0 | 0.276 | 2.872 | 1.580 | 2.455 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, J.; Gong, Z.; Li, X.; Tang, S.; Wang, C.; Lan, Y. Mechanism Modeling and Analysis of Fractional-Order Synchronous Generator. Fractal Fract. 2025, 9, 244. https://doi.org/10.3390/fractalfract9040244
Xu J, Gong Z, Li X, Tang S, Wang C, Lan Y. Mechanism Modeling and Analysis of Fractional-Order Synchronous Generator. Fractal and Fractional. 2025; 9(4):244. https://doi.org/10.3390/fractalfract9040244
Chicago/Turabian StyleXu, Junhua, Zheng Gong, Xiaocong Li, Songqin Tang, Chunwei Wang, and Yue Lan. 2025. "Mechanism Modeling and Analysis of Fractional-Order Synchronous Generator" Fractal and Fractional 9, no. 4: 244. https://doi.org/10.3390/fractalfract9040244
APA StyleXu, J., Gong, Z., Li, X., Tang, S., Wang, C., & Lan, Y. (2025). Mechanism Modeling and Analysis of Fractional-Order Synchronous Generator. Fractal and Fractional, 9(4), 244. https://doi.org/10.3390/fractalfract9040244






