Qualitative Analysis of a Three-Dimensional Dynamical System of Fractal-Fractional-Order Evolution Differential Equations with Terminal Boundary Conditions
Abstract
1. Introduction
2. Elementary Results
3. Existence of Solutions
- ()
- Assume that the nonlinear functions are continuous.
- ()
- Assume that is a matrix of continuous real functions such that for some and for all i = 1, 2, 3.
- ()
- Assume that for any and for all such that the following relations hold:
- ()
- For all we have
- It maps bounded sets of into bounded sets of ,
- It is equi-continuous.
- :
- is bounded.
- :
- is equi-continuous.
4. Stability Analysis
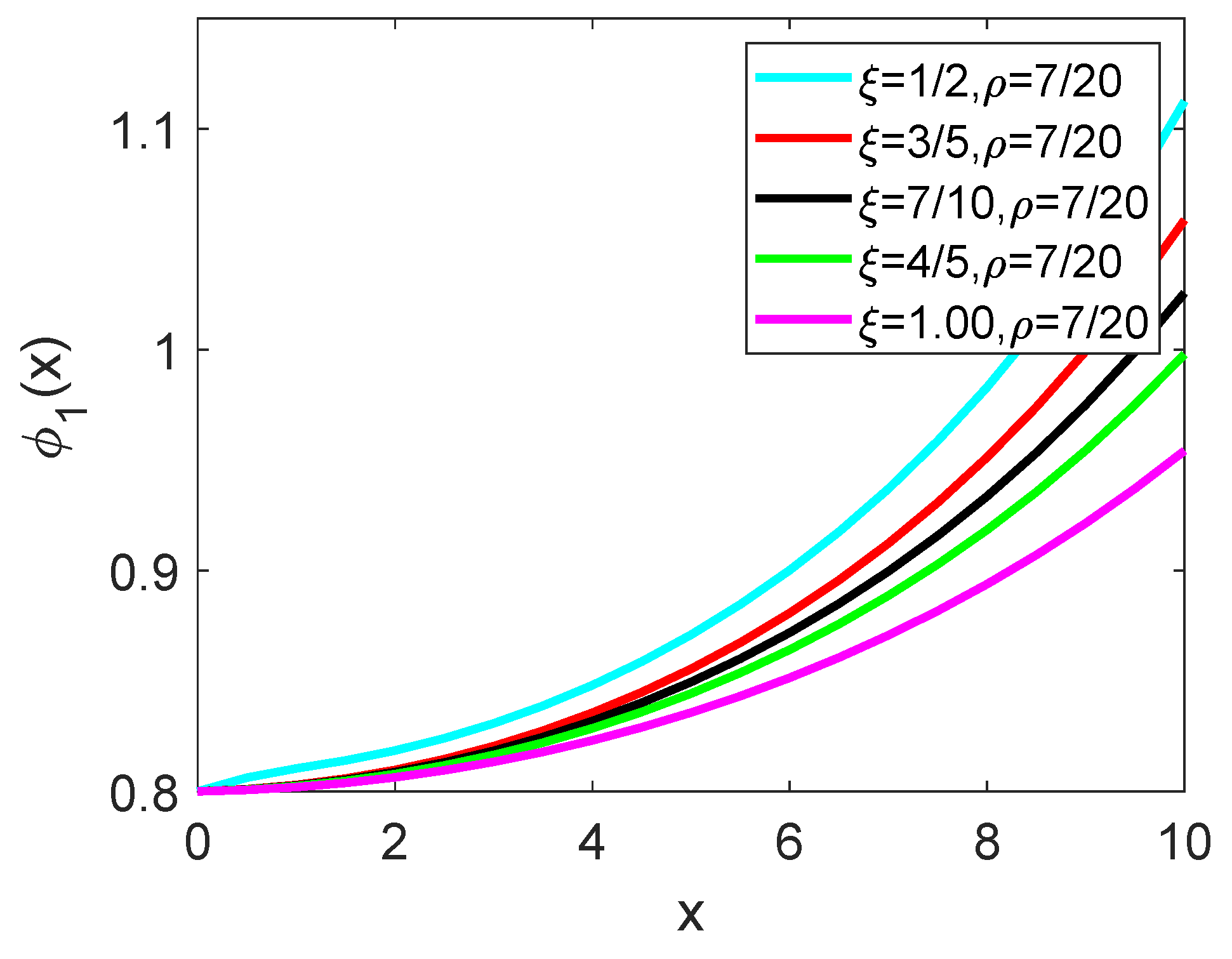
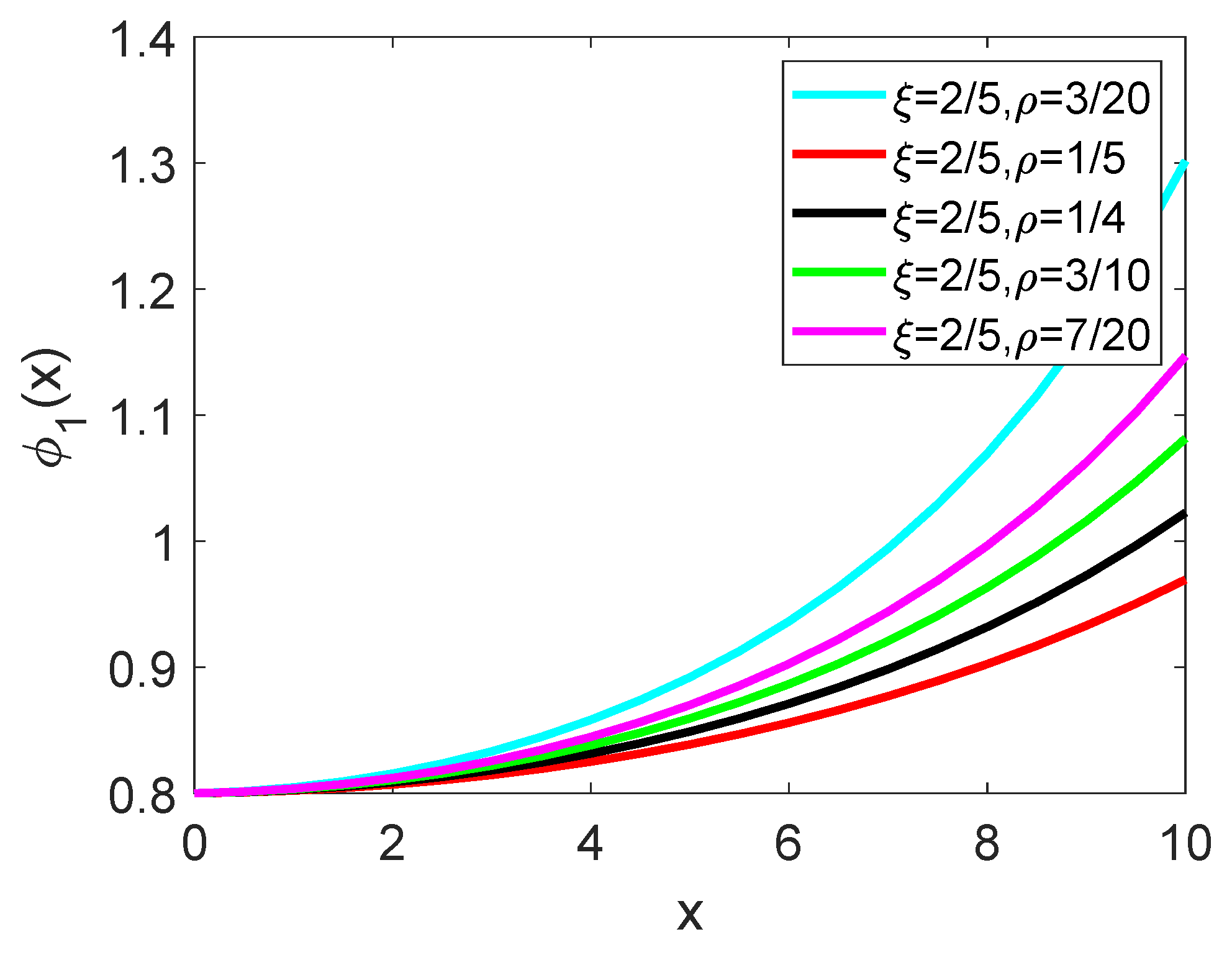
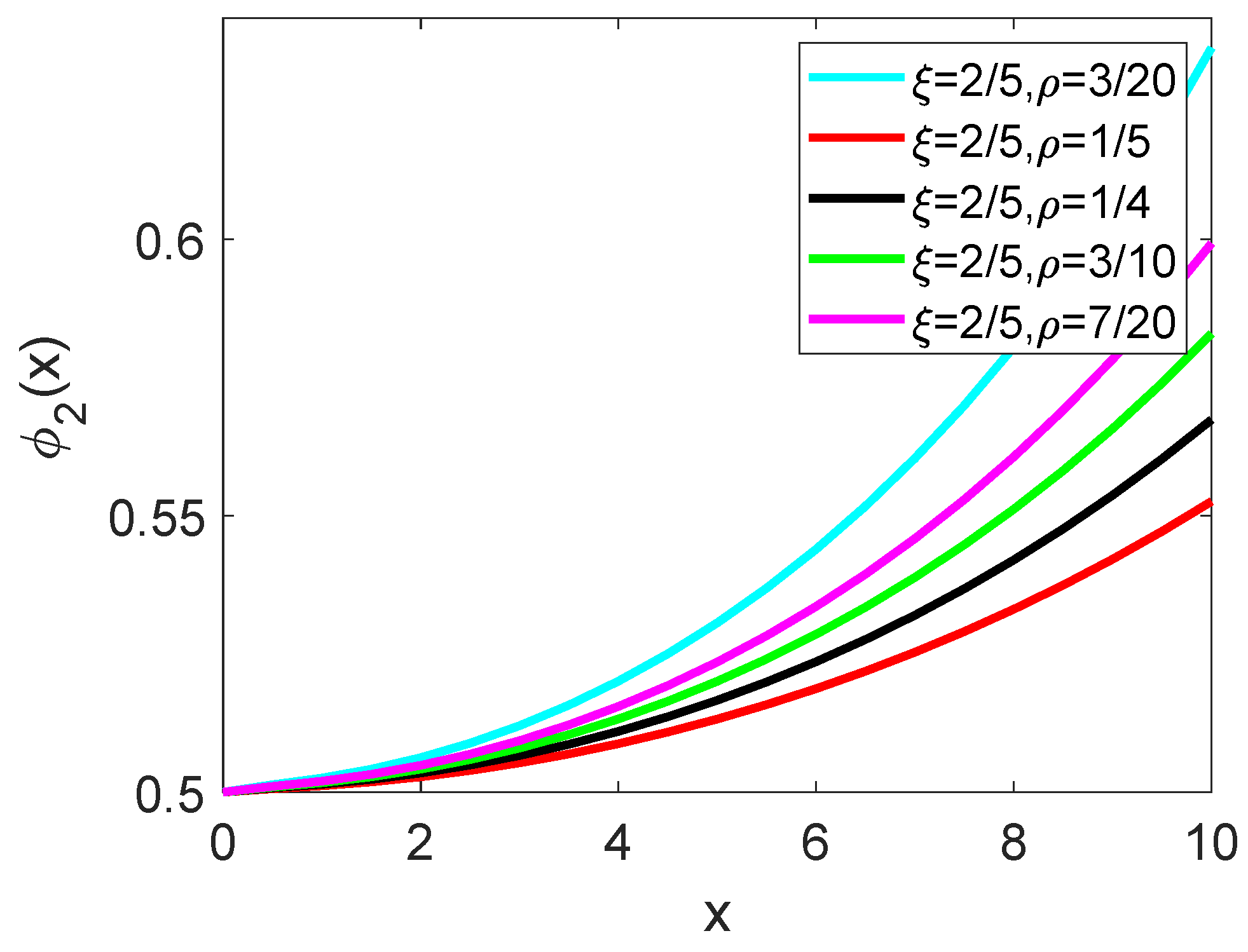
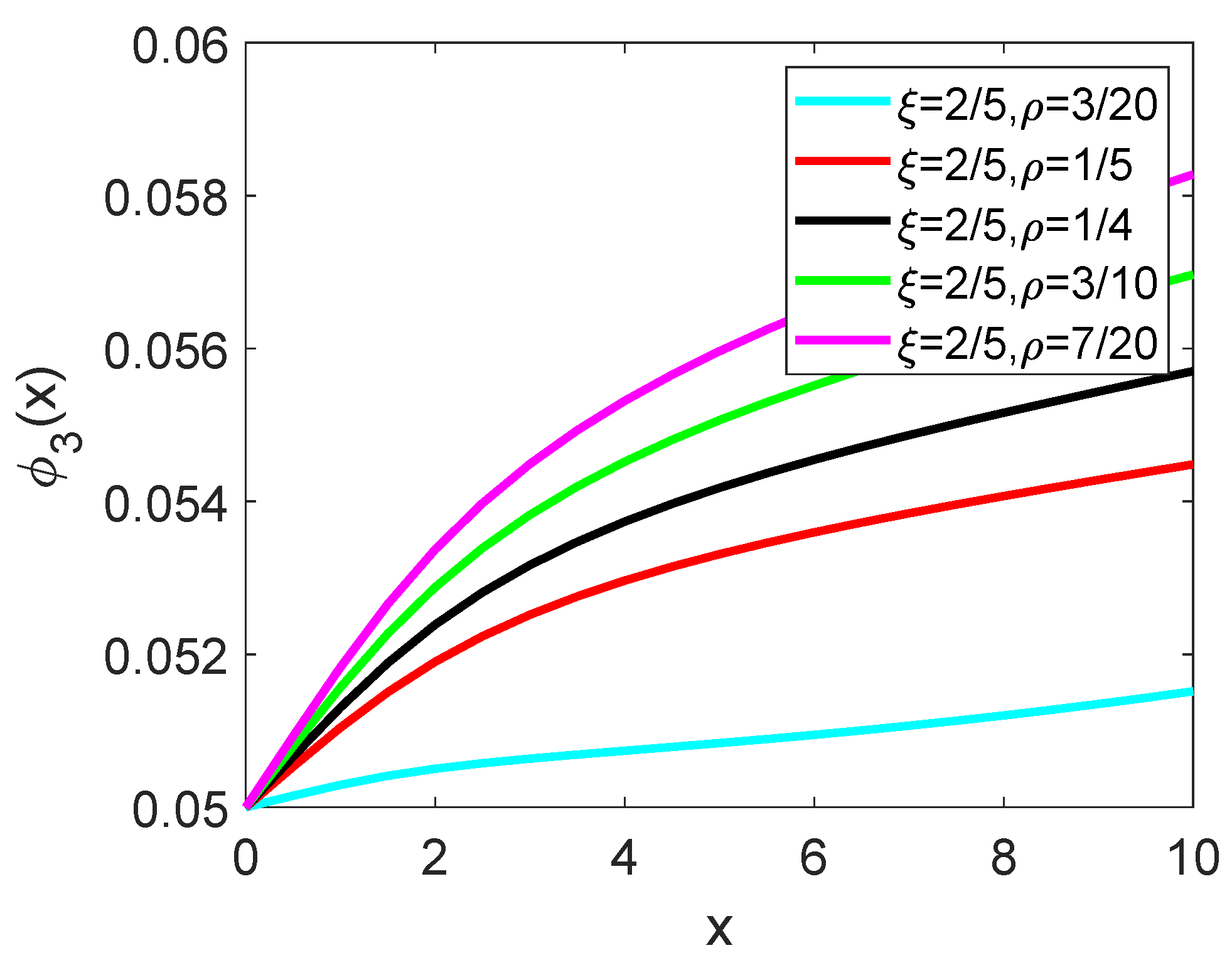
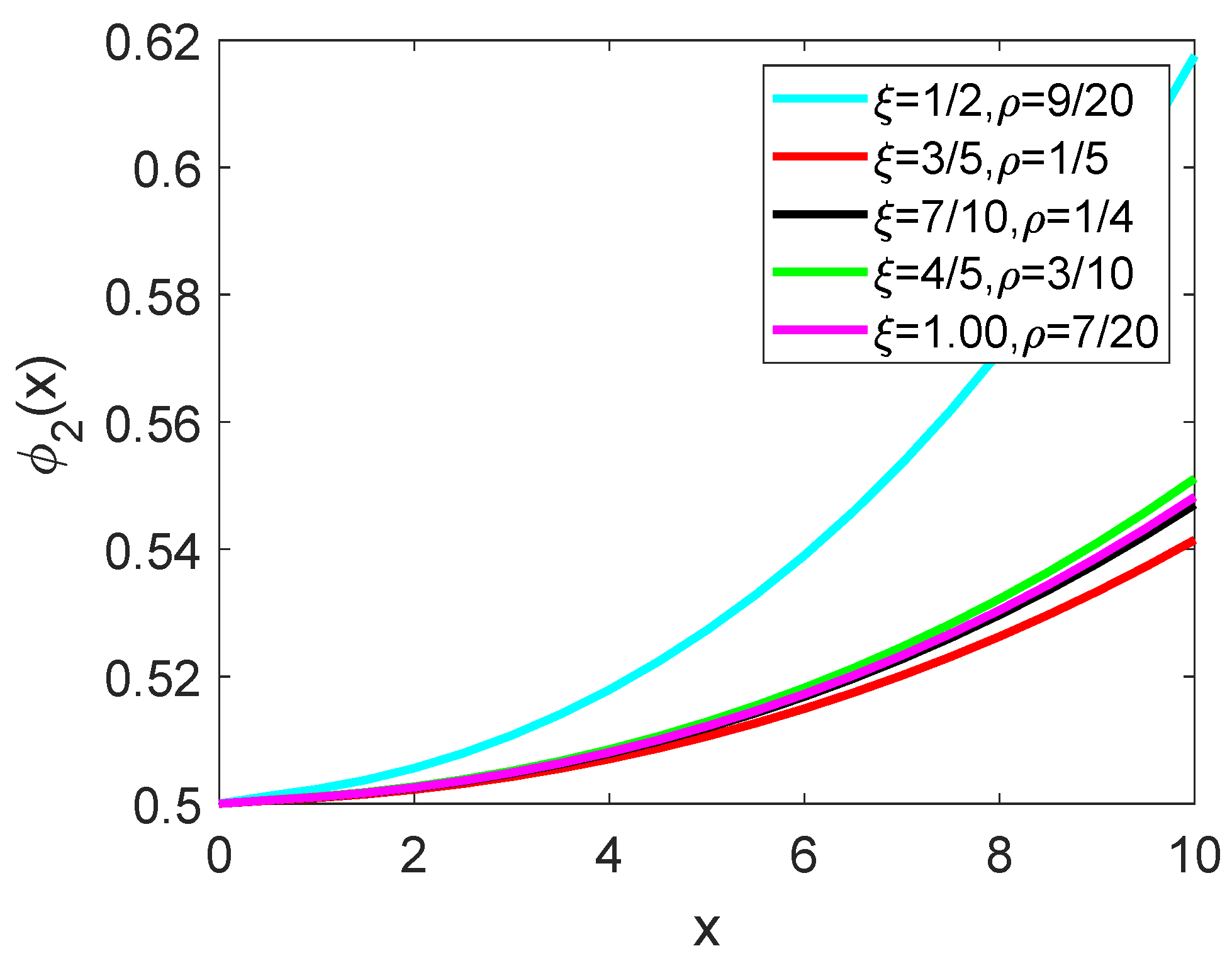
5. Illustrative Problem
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives: Theory and Applications; Gordon and Breach: North Holland, The Netherlands, 1993. [Google Scholar]
- Alazopoulos, K.A. Non-local continuum mechanics and fractional calculus. Mech. Res. Commun. 2006, 33, 753–757. [Google Scholar] [CrossRef]
- Carpinteri, A.; Cornetti, P.; Sapora, A. A fractional calculus approach to nonlocal elasticity. Eur. Phys. J. Spec. Top. 2011, 193, 193. [Google Scholar] [CrossRef]
- Baleanu, D.; Karaca, Y.; Vázquez, L.; Macías-Díaz, J.E. Advanced fractional calculus, differential equations and neural networks: Analysis, modeling and numerical computations. Phys. Scr. 2023, 98, 110201. [Google Scholar] [CrossRef]
- Rossikhin, Y.A.; Shitikova, M.V. Application of fractional calculus for dynamic problems of solid mechanics: Novel trends and recent results. Appl. Mech. Rev. 2010, 63, 010801. [Google Scholar] [CrossRef]
- Yang, X.J. Advanced Local Fractional Calculus and Its Applications; World Science: New York, NY, USA, 2012. [Google Scholar]
- Fan, J.; He, J. Fractal derivative model for air permeability in hierarchic porous media. Abstr. Appl. Anal. 2012, 2012, 354701. [Google Scholar] [CrossRef]
- Akgül, A. Analysis and new applications of fractal fractional differential equations with power law kernel. Discret. Contin. Dyn. Syst. S 2021, 14, 3401–3417. [Google Scholar] [CrossRef]
- Karaca, Y.; Baleanu, D. A novel R/S fractal analysis and wavelet entropy characterization approach for robust forecasting based on self-similar time series modeling. Fractals 2020, 28, 2040032. [Google Scholar] [CrossRef]
- Hamza, A.; Osman, O.; Ali, A.; Alsulami, A.; Aldwoah, K.; Mustafa, A.; Saber, H. Fractal-Fractional-Order Modeling of Liver Fibrosis Disease and Its Mathematical Results with Subinterval Transitions. Fractal Fract. 2024, 8, 638. [Google Scholar] [CrossRef]
- Karaca, Y.; Moonis, M.; Baleanu, D. Fractal and multifractional-based predictive optimization model for stroke subtypes’ classification. Chaos Solitons Fractals 2020, 136, 109820. [Google Scholar] [CrossRef]
- Alraqad, T.; Almalahi, M.A.; Mohammed, N.; Alahmade, A.; Aldwoah, K.A.; Saber, H. Modeling Ebola Dynamics with a Piecewise Hybrid Fractional Derivative Approach. Fractal Fract. 2024, 8, 596. [Google Scholar] [CrossRef]
- File, G.; Reddy, Y.N. Terminal boundary-value technique for solving singularly perturbed delay differential equations. J. Taibah Univ. Sci. 2014, 8, 289–300. [Google Scholar] [CrossRef]
- Palamides, A.P.; Yannopoulos, T.G. Terminal value problem for singular ordinary differential equations: Theoretical analysis and numerical simulations of ground states. Bound. Value Probl. 2006, 2006, 28719. [Google Scholar] [CrossRef]
- Shreve, W.E. Terminal value problems for second order nonlinear differential equations. SIAM J. Appl. Math. 1970, 18, 783–791. [Google Scholar] [CrossRef]
- Aftabizadeh, A.R.; Lakshmikantham, V. On the theory of terminal value problems for ordinary differential equations. Nonlinear Anal. Theory Methods Appl. 1981, 5, 1173–1180. [Google Scholar] [CrossRef]
- Diethelm, K. An extension of the well-posedness concept for fractional differential equations of Caputo’s type. Appl. Anal. 2014, 93, 2126–2135. [Google Scholar] [CrossRef]
- Shiri, B.; Wu, G.C.; Baleanu, D. Terminal value problems for nonlinear systems of fractional differential equations. Appl. Numer. Math. 2021, 170, 162–178. [Google Scholar] [CrossRef]
- Ford, N.J.; Morgado, M.L.; Rebelo, M. High order numerical methods for fractional terminal value problems. Comput. Methods Appl. Math. 2014, 14, 55–70. [Google Scholar] [CrossRef]
- Boichuk, O.; Feruk, V. Terminal value problem for the system of fractional differential equations with additional restrictions. Math. Model. Anal. 2025, 30, 120–141. [Google Scholar] [CrossRef]
- Bao, N.T.; Caraballo, T.; Tuan, N.H.; Zhou, Y. Existence and regularity results for terminal value problem for nonlinear fractional wave equations. Nonlinearity 2021, 34, 1448. [Google Scholar] [CrossRef]
- Assanova, A.T.; Uteshova, R.E. A singular boundary value problem for evolution equations of hyperbolic type. Chaos Solitons Fractals 2021, 143, 110517. [Google Scholar] [CrossRef]
- Racke, R. Lectures on Nonlinear Evolution Equations: Initial Value Problems; Birkhäuser: Basel, Switzerland, 2015. [Google Scholar]
- Atangana, A. Fractal-fractional differentiation and integration: Connecting fractal calculus and fractional calculus to predict complex systems. Chaos Solitons Fractals 2017, 102, 396–406. [Google Scholar] [CrossRef]
- Shah, K.; Abdeljawad, T. Study of radioactive decay process of uranium atoms via fractals-fractional analysis. S. Afr. J. Chem. Eng. 2024, 48, 63–70. [Google Scholar] [CrossRef]
- Khan, H.; Aslam, M.; Rajpar, A.H.; Chu, Y.M.; Etemad, S.; Rezapour, S.; Ahmad, H. A new fractal-fractional hybrid model for studying climate change on coastal ecosystems. Fractals 2024, 32, 2440015. [Google Scholar] [CrossRef]
- Khan, H.; Alzabut, J.; Shah, A.; He, Z.Y.; Etemad, S.; Rezapour, S.; Zada, A. On fractal-fractional waterborne disease model: A study on theoretical and numerical aspects via simulations. Fractals 2023, 31, 2340055. [Google Scholar] [CrossRef]
- Shah, A.; Khan, H.; De la Sen, M.; Alzabut, J.; Etemad, S.; Deressa, C.T.; Rezapour, S. On non-symmetric fractal-fractional modeling for ice smoking. Symmetry 2022, 15, 87. [Google Scholar] [CrossRef]
- Madani, Y.A.; Rabih, M.N.A.; Alqarni, F.A.; Ali, Z.; Aldwoah, K.A.; Hleili, M. Existence, Uniqueness, and Stability of a Nonlinear Tripled Fractional Order Differential System. Fractal Fract. 2024, 8, 416. [Google Scholar] [CrossRef]
- Algolam, M.S.; Osman, O.; Ali, A.; Mustafa, A.; Aldwoah, K.; Alsulami, A. Fixed Point and Stability Analysis of a Tripled System of Nonlinear Fractional Differential Equations with n-Nonlinear Terms. Fractal Fract. 2024, 8, 697. [Google Scholar] [CrossRef]
- Bainov, D.D.; Simenonv, P.S. Impulsive Differential Equations: Periodic Solutions and Applications; Longman: Harlow, UK, 1993. [Google Scholar]
- Ali, A.; Rabiei, F.; Shah, K. On Ulam’s Type Stability for a Class of Impulsive Fractional Differential Equations with Nonlinear Integral Boundary Conditions. J. Nonlinear Sci. Appl. 2017, 10, 4760–4775. [Google Scholar] [CrossRef]
- Pietsch, A. History of Banach Spaces and Linear Operators; Springer Science & Business Media: Cham, Switzerland, 2007. [Google Scholar]
- Granas, A.; Dugundji, J. Fixed Point Theory; Springer: New York, NY, USA, 2003. [Google Scholar]
- Schaefer, H. Über die Methode der a Priori-Schranken. Math. Ann. 1955, 129, 415–416. [Google Scholar] [CrossRef]
- Rus, I.A. Ulam Stabilities of Ordinary Differential Equations in a Banach Space. Carpath. J. Math. 2010, 26, 103–107. [Google Scholar]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gassem, F.; Ali, A.; Aldwoah, K.; Egami, R.H.; Osman, O.; Younis, B.; Touati, A. Qualitative Analysis of a Three-Dimensional Dynamical System of Fractal-Fractional-Order Evolution Differential Equations with Terminal Boundary Conditions. Fractal Fract. 2025, 9, 259. https://doi.org/10.3390/fractalfract9040259
Gassem F, Ali A, Aldwoah K, Egami RH, Osman O, Younis B, Touati A. Qualitative Analysis of a Three-Dimensional Dynamical System of Fractal-Fractional-Order Evolution Differential Equations with Terminal Boundary Conditions. Fractal and Fractional. 2025; 9(4):259. https://doi.org/10.3390/fractalfract9040259
Chicago/Turabian StyleGassem, F., Arshad Ali, Khaled Aldwoah, Ria H. Egami, Osman Osman, Bakri Younis, and Amel Touati. 2025. "Qualitative Analysis of a Three-Dimensional Dynamical System of Fractal-Fractional-Order Evolution Differential Equations with Terminal Boundary Conditions" Fractal and Fractional 9, no. 4: 259. https://doi.org/10.3390/fractalfract9040259
APA StyleGassem, F., Ali, A., Aldwoah, K., Egami, R. H., Osman, O., Younis, B., & Touati, A. (2025). Qualitative Analysis of a Three-Dimensional Dynamical System of Fractal-Fractional-Order Evolution Differential Equations with Terminal Boundary Conditions. Fractal and Fractional, 9(4), 259. https://doi.org/10.3390/fractalfract9040259








