Some Results Related to Booth Lemniscate and Integral Operators

Abstract

In this work, we explore the impact of integral operators such as the Libera and Alexander operators on specific families of analytic functions introduced in the literature and find some of their remarkable results. Using techniques from differential subordination and convolution theory, we establish results concerning the radius of convexity and convolution properties for these function classes. Additionally, we investigate how these integral operators influence the geometric properties of functions in $\mathcal{BS}\left(\mu \right)$ and $\mathcal{KS}\left(\mu \right)$, leading to new insights into their structural behavior.

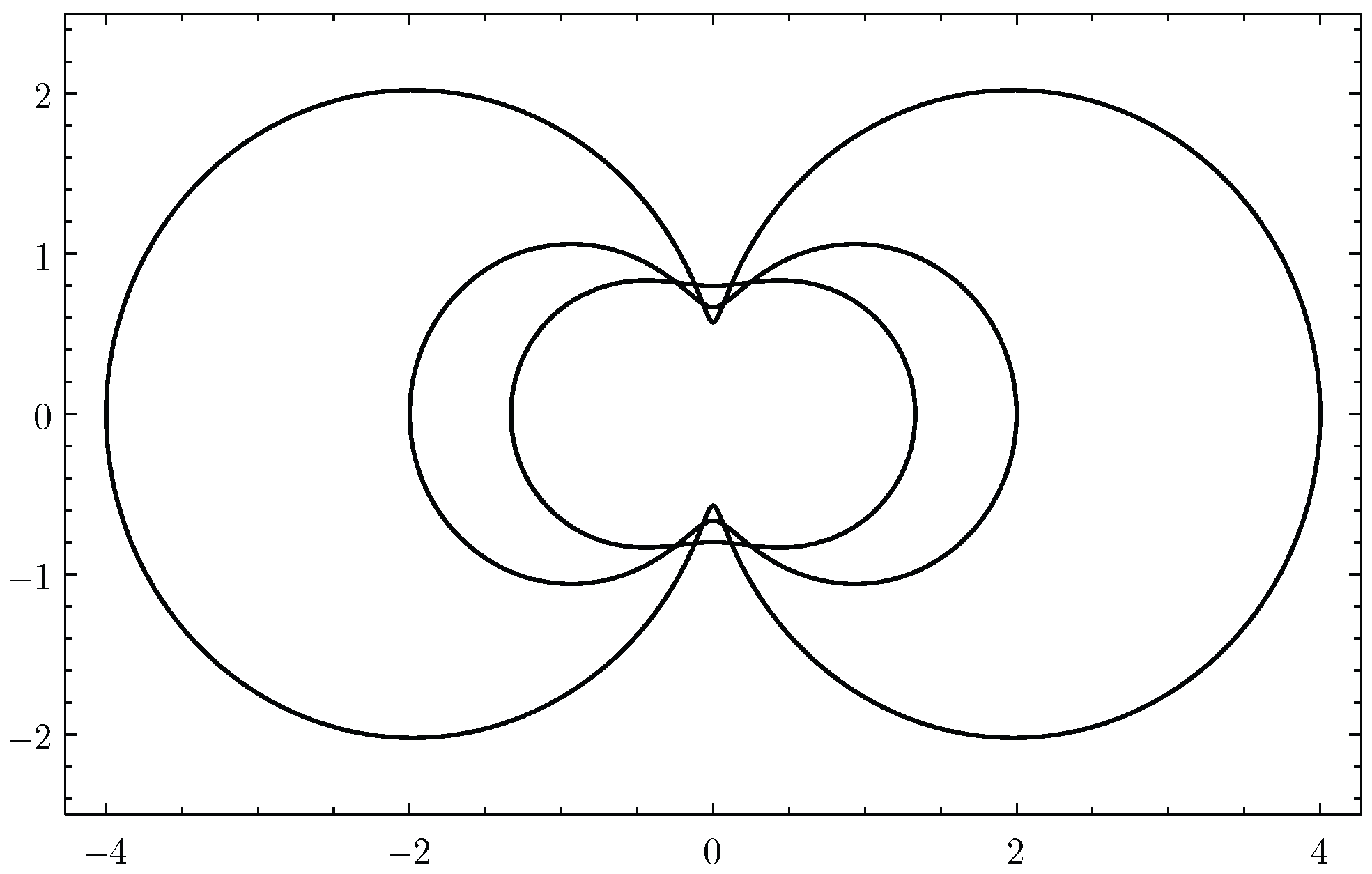
1. Introduction

Consider the class $\mathcal{A}$ consisting of functions q, analytic over $\mathcal{U}$, where

$$\mathcal{U}=\{z:z\in \mathbb{C};|z|<1\},$$

standardized via

$$q\left(z\right)=z+\sum _{r=2}^{\infty }{a}_r{z}^r\hspace{1em}(z\in \mathcal{U}).$$

(1)

Let $\mathcal{S}$ represent the set of functions within $\mathcal{A}$ that demonstrate univalence across $\mathcal{U}$. A function $q\in \mathcal{S}$ is classified as starlike (related to the origin) if $\lambda q\left(z\right)\in q\left(\mathcal{U}\right)$ for all $\lambda$ in the interval $[0,1]$. The collection of all starlike functions over $\mathcal{U}$ is symbolized by ${\mathcal{S}}^{\ast }$. Furthermore, a function $q\in \mathcal{A}$ is characterized as starlike of order $\delta$, $0⩽\delta ⩽1$, symbolized as $q\in {\mathcal{S}}^{\ast }\left(\delta \right)$, provided it adheres to:

$$\mathcal{R}\mathcal{e}{\displaystyle \frac{z{q}^{\prime }\left(z\right)}{q\left(z\right)}}>\delta ,(z\in \mathcal{U}).$$

In particular,

$${\mathcal{S}}^{\ast }\left(0\right)\equiv {\mathcal{S}}^{\ast }.$$

A function $q\in \mathcal{A}$ is defined as convex of order $\delta$, $0⩽\delta ⩽1$, symbolized as $q\in \mathcal{K}\left(\delta \right)$, provided it satisfies the subsequent criterion:

$$\mathcal{R}\mathcal{e}\{{\displaystyle \frac{z{q}^{″}\left(z\right)}{q^{\prime }\left(z\right)}}+1\}>\delta ,(z\in \mathcal{U}).$$

In particular, we put

$$\mathcal{K}\left(0\right)\equiv \mathcal{K},$$

which is known as the class of all convex functions in $\mathcal{U}$. A function $q\in \mathcal{A}$ is a member of the class $\mathcal{K}$ precisely when $z{q}^{\prime }\left(z\right)$ lies in the class ${\mathcal{S}}^{\ast }$.

The literature, as evidenced by [1,2,3], showcases a variety of published works examining the function classes in question. Alternative subdivisions of starlike and convex functions are explored in [4,5]. Nunokawa et al. [6] have examined sufficient conditions for starlikeness. Also, the subclasses of analytic functions that exhibit starlike properties relative to a boundary point are investigated in [7,8].

Given the analytic functions q and p within $\mathcal{U}$, we define q as subordinate to p, symbolized by $q\prec p$, assuming the demonstrability of an analytic function v on $\mathcal{U}$, satisfying

$$v\left(0\right)=0$$

and

$$\left|v\right(z\left)\right|⩽\left|z\right|<1$$

under the constraint that

$$q\left(z\right)=p\left(v\right(z\left)\right).$$

Furthermore, provided p is a univalent on $\mathcal{U}$, then $q\prec p$ holds if and only if

$$q\left(0\right)=0$$

and

$$q\left(\mathcal{U}\right)\subset p\left(\mathcal{U}\right).$$

Ma and Minda [9] presented a specific category of starlike functions as follows:

$$S^{\ast }\left(\psi \right):=\left\{q\in \mathcal{A},{\displaystyle \frac{z{q}^{\prime }\left(z\right)}{q\left(z\right)}}\prec \psi \left(z\right),z\in \mathcal{U}\right\},$$

(2)

where $\psi$ is a univalent function with $\mathcal{R}\mathcal{e}\psi \left(z\right)>0$, $\psi \left(\mathcal{U}\right)$ is starlike over $\psi \left(0\right)=1$ and possesses reflectional symmetry across the real axis, and ${\psi }^{\prime }\left(0\right)>0$.

The field of Ma–Minda starlike functions has been a subject of considerable scholarly interest throughout recent decades. Several scholars have recently developed subsets of analytic functions determined by the geometric configuration of their image domains, for example, the circular disk, right half-plane, conic domain, and generalized conic domains, by varying $\psi$ in (2). Further specialized instances within the Ma–Minda function class are detailed in publications [10,11,12].

As demonstrated by Piejko and Sokol [3], we consider a collection of univalent functions defined over $\mathcal{U}$, characterized by the following:

$$T_{\mu }\left(z\right)={\displaystyle \frac{z}{1-\mu z^2}}=z+\sum _{r=1}^{\infty }{\mu }^r{z}^{2r+1},(z\in \mathcal{U}),$$

(3)

where $\mu \in [0,1)$.

$$\mathcal{R}\mathcal{e}\left\{{\displaystyle \frac{z{T}_{\mu }^{\prime }\left(z\right)}{T_{\mu }\left(z\right)}}\right\}=\mathcal{R}\mathcal{e}\left\{{\displaystyle \frac{1+\mu z^2}{1-\mu z^2}}\right\}>0,(z\in \mathcal{U}),$$

then $T_{\mu }\left(z\right)$ is starlike in $\mathcal{U}$. Additionally,

$$T_{\mu }\left(\mathcal{U}\right)=D\left(\mu \right),$$

where

$$D\left(\mu \right)=\{a+ib\in \mathbb{C}\mid {(a^2+b^2)}^2-{\displaystyle \frac{a^2}{{(1-\mu )}^2}}-{\displaystyle \frac{b^2}{(1+{\mu }^2)}}<0\},$$

when $\mu \in [0,1)$ and

$$D\left(1\right)=\{a+ib\in \mathbb{C}\mid a+ib\ne i\lambda ,\forall \lambda \in (-\infty ,1/2]\cup [1/2,\infty \left)\right\}.$$

The curve

$${(a^2+b^2)}^2-{\displaystyle \frac{a^2}{{(1-\mu )}^2}}-{\displaystyle \frac{b^2}{(1+{\mu }^2)}}=0,\left((a,b)\ne 0\right),$$

is termed the Booth lemniscate of elliptic type (see Figure 1).

The lemniscate curve finds utility across a spectrum of mathematical disciplines, including number theory, mathematical physics, and differential equations. Also, the lemniscate can be used to define conformal mappings, which have applications in fields like fluid dynamics and electrostatics. For more explanations, see [13,14,15,16]. Also, references [17,18,19] delve into other properties of the lemniscates, such as the Hadamard product and radius estimates.

Building upon the foundational work outlined in these publications, the current study delves into the properties of the subclasses $\mathcal{BS}\left(\mu \right)$ and $\mathcal{KS}\left(\mu \right)$, as delineated below. We now refer to the definition presented by Kargar et al. 2019 [13].

Definition 1. 

Let $q\in \mathcal{A}$ and $\mu \in [0,1)$. We let $\mathcal{BS}\left(\mu \right)$ denote the set of functions q fulfilling the condition

$${\displaystyle \frac{z{q}^{\prime }\left(z\right)}{q\left(z\right)}}-1\prec T_{\mu }\left(z\right),$$

where $T_{\mu }\left(z\right)$ is given by (3).

Additionally, we utilize the subsequent result presented in [13].

Lemma 1. 

Let $T_{\mu }$ be given by (3). Then,

$${\displaystyle \frac{1}{\mu -1}}<\mathcal{R}\mathcal{e}{T}_{\mu }\left(z\right)\}<{\displaystyle \frac{1}{1-\mu }},(z\in \mathcal{U}),$$

where $\mu \in [0,1)$.

From Lemma 1, if $q\in \mathcal{BS}\left(\mu \right)$, then:

$${\displaystyle \frac{\mu }{\mu -1}}<\mathcal{R}\mathcal{e}\left\{{\displaystyle \frac{z{q}^{\prime }\left(z\right)}{q\left(z\right)}}\right\}<{\displaystyle \frac{2-\mu }{1-\mu }},(z\in \mathcal{U}).$$

(4)

In particular, $\mathcal{BS}\left(0\right)\subset {\mathcal{S}}^{\ast }$.

Definition 2. 

Let $q\in \mathcal{A}$ and $\mu \in [0,1)$. We let $\mathcal{KS}\left(\mu \right)$ denote the set of functions q fulfilling the condition

$${\displaystyle \frac{z{q}^{\prime \prime }\left(z\right)}{q^{\prime }\left(z\right)}}\prec T_{\mu }\left(z\right),$$

(5)

where $T_{\mu }\left(z\right)$ is represented by (3).

Remark 1. 

From Definitions 1 and 2, $q\in \mathcal{KS}\left(\mu \right)$ if and only if $z{q}^{\prime }\in \mathcal{BS}\left(\mu \right)$.

Also, by Lemma 1, if $q\in \mathcal{KS}\left(\mu \right)$, then

$${\displaystyle \frac{1}{\mu -1}}<\mathcal{R}\mathcal{e}\left\{{\displaystyle \frac{z{q}^{\prime \prime }\left(z\right)}{q^{\prime }\left(z\right)}}\right\}<{\displaystyle \frac{1}{1-\mu }},(z\in \mathcal{U}).$$

(6)

In particular, $\mathcal{KS}\left(0\right)\subset \mathcal{K}$.

The ensuing lemmas are crucial for the demonstration of our findings.

Lemma 2 

([20]). Let $\mathsf{\Omega }\subset \mathbb{C}$ and $g\left(z\right)=a+{\sum }_{i=r}^{\infty }{a}_i{z}^i$, ($z\in \mathcal{U}$), with

$$\mathcal{R}\mathcal{e}\alpha >0.$$

provided a function

$$\varphi :{\mathbb{C}}^3\times \mathcal{U}\to \mathbb{C}$$

conforms to the condition

$$\varphi \left(\rho i,\xi ,\gamma ,\nu ;z\right)\notin \mathsf{\Omega },(z\in \mathcal{U}),$$

for all ρ, ξ, γ, $\nu \in \mathbb{R}$,

$$\xi ⩽-{\displaystyle \frac{r}{2}}{\displaystyle \frac{{|a-i\rho |}^2}{\mathcal{R}\mathcal{e}\alpha }},\xi +\gamma ⩽0,$$

then

$$\varphi \left(g\left(z\right),z{g}^{\prime }\left(z\right),z^2{g}^{″}\left(z\right);z\right)\in \mathsf{\Omega }⟹\mathcal{R}\mathcal{e}g\left(z\right)>0.$$

Lemma 3 

([21]). Let $q\in \mathcal{KS}\left(\mu \right)$. If $0<\mu <1$, then

$$q^{\prime }\left(z\right)\prec f\left(z\right)={\left({\displaystyle \frac{1+\sqrt{\mu }z}{1-\sqrt{\mu }z}}\right)}^{{\displaystyle \frac{1}{2\sqrt{\mu }}}},$$

(7)

and f is the best dominant, and if $\mu =0$, then

$$q^{\prime }\left(z\right)\prec exp\left(z\right),$$

(8)

and $exp\left(z\right)$ is the best dominant. Additionally, for the $\mu \in (0,1)$,

$$|arg\left\{q^{\prime }\left(z\right)\right\}|<{\displaystyle \frac{1}{2\sqrt{\mu }}}arctan\left\{{\displaystyle \frac{2\sqrt{\mu }}{1-\mu }}\right\}.$$

(9)

Lemma 4 

(Libera ([22], Lemma 1)). Let h be a convex function in $\mathcal{U}$ and let N and M be analytic over $\mathcal{U}$ with

$$N\left(0\right)=M\left(0\right).$$

If

$$\mathcal{R}e\{{\displaystyle \frac{z{N}^{\prime }\left(z\right)}{N\left(z\right)}}\}>0,$$

then

$$\begin{array}{c}\hfill {\displaystyle \frac{M^{\prime }\left(z\right)}{N^{\prime }\left(z\right)}}\prec h\left(z\right)⟹{\displaystyle \frac{M\left(z\right)}{N\left(z\right)}}\prec h\left(z\right).\end{array}$$

Theorem 1 

(Orouji ([21], Theorem 2.2)). For $0⩽\mu <1$, $\mathcal{KS}\left(\mu \right)\subset \mathcal{S}$.

Theorem 2 

(Orouji ([21], Theorem 2.3)). Let

$$q\left(z\right)=z+{\sum }_{r=2}^{\infty }{a}_r{z}^r\in \mathcal{KS}\left(\mu \right),$$

then,

(a) 

If $\mu \in (0,{\displaystyle \frac{1}{4}}]$, then

$${\displaystyle \frac{q\left(z\right)}{z}}\prec f\left(z\right)={\displaystyle \frac{1}{z}}{\int }_0^z{\left({\displaystyle \frac{1+\sqrt{\mu }\lambda }{1-\sqrt{\mu }\lambda }}\right)}^{{\displaystyle \frac{1}{2\sqrt{\mu }}}}d\lambda ,$$

(10)

and $f\left(z\right)$ is the best -dominant and convex. Also if $\mu =0$, then

$${\displaystyle \frac{q\left(z\right)}{z}}\prec {\displaystyle \frac{1}{z}}(e^z-1),$$

(11)

and ${\displaystyle \frac{1}{z}}(e^z-1)$ is the best -dominant and convex.

(b) 

If $\mu \in [{\displaystyle \frac{1}{4}},1)$, then

$${\displaystyle \frac{q\left(z\right)}{z}}\prec {\left({\displaystyle \frac{1+z}{1-z}}\right)}^{{\displaystyle \frac{1}{2\sqrt{\mu }}}},$$

(12)

and so for $\mu \in [{\displaystyle \frac{1}{4}},1)$, we have

$$\mathcal{R}e\left\{{\displaystyle \frac{q\left(z\right)}{z}}\right\}>0.$$

(c) 

If $\mu \in [{\displaystyle \frac{1}{4}},1)$, then

$$\sqrt{{\displaystyle \frac{q\left(z\right)}{z}}}\prec \sqrt{{\displaystyle \frac{2}{z}}ln(1+z)-1}.$$

(13)

Therefore,

$$\mathcal{R}\mathcal{e}\left\{\sqrt{{\displaystyle \frac{q\left(z\right)}{z}}}\right\}>\sqrt{-1+2ln2}.$$

2. Main Results

The integral and differential operators play significant roles in the theory of differential subordination. They can be used to derive sharp inequalities for diverse families of analytic functions.

Motivated by the results of the existing literature, we study special integral operators in this research. Initially, we establish one of the main results within this section and then we obtain some results about integral operators on classes $\mathcal{BS}\left(\mu \right)$ and $\mathcal{KS}\left(\mu \right)$.

The following theorem references the integral operator $I_{\beta ,\delta }\left[q\right]$, as defined by Miller and Mocanu in [20]. Further characteristics pertaining to this operator are detailed in [20].

Theorem 3. 

Let $q\in \mathcal{BS}\left(\mu \right)$, with $\mu \in (0,1)$. If

$$0<\beta ⩽\delta ⩽{\displaystyle \frac{1-\mu }{2\mu }}$$

and $\mu (\beta +\delta )⩽\delta$, then $I_{\beta ,\delta }\left[q\right]\in {\mathcal{S}}^{\ast }$, where

$$I_{\beta ,\delta }\left[q\right]\left(z\right)={\left[{\displaystyle \frac{\beta +\delta }{z^{\delta }}}{\int }_0^z{q}^{\beta }\left(\lambda \right){\lambda }^{\delta -1}d\lambda \right]}^{{\displaystyle \frac{1}{\beta }}}.$$

(14)

For the case $\mu =0$, if $\beta ⩽\delta$, then $I_{\beta ,\delta }\left[q\right]\in {\mathcal{S}}^{\ast }$.

Proof. 

Let

$$T=I_{\beta ,\delta }\left[q\right],$$

and

$$g\left(z\right)={\displaystyle \frac{z{T}^{\prime }\left(z\right)}{T\left(z\right)}}.$$

According to the relation (4) and by the hypothesis, we have

$$\mathcal{R}\mathcal{e}\{\beta {\displaystyle \frac{z{q}^{\prime }\left(z\right)}{q\left(z\right)}}+\delta \}>{\displaystyle \frac{\beta \mu }{\mu -1}}+\delta ={\displaystyle \frac{\mu (\beta +\delta )-\delta }{\mu -1}}⩾0.$$

Thus, from ([20], Corollary 2.5c.2), $T\in \mathcal{A}$ and

$${\displaystyle \frac{T\left(z\right)}{z}}\ne 0,$$

then g is analytic in $\mathcal{U}$ and

$$g\left(0\right)=1.$$

By the relation (14),

$$T^{\beta }\left(z\right)z^{\delta }=(\beta +\delta ){\int }_0^z{q}^{\beta }\left(\lambda \right){\lambda }^{\delta -1}d\lambda ,$$

and so

$$\beta g\left(z\right)+\delta =\beta {\displaystyle \frac{z{T}^{\prime }\left(z\right)}{T\left(z\right)}}+\delta ={\displaystyle \frac{(\beta +\delta )q^{\beta }\left(z\right)}{T^{\beta }\left(z\right)}}.$$

(15)

By taking the logarithmic derivative of both sides of relation (15),

$$g\left(z\right)+{\displaystyle \frac{z{g}^{\prime }\left(z\right)}{\beta g\left(z\right)+\delta }}={\displaystyle \frac{z{q}^{\prime }\left(z\right)}{q\left(z\right)}}\prec T_{\mu }\left(z\right)+1.$$

Therefore,

$$\mathsf{\Psi }\left(g\left(z\right),z{g}^{\prime }\left(z\right)\right)\prec T_{\mu }\left(z\right)+{\displaystyle \frac{1}{1-\mu }},$$

where

$$\mathsf{\Psi }(r,s)=r+{\displaystyle \frac{s}{\beta r+\delta }}+{\displaystyle \frac{\mu }{1-\mu }}.$$

Since

$$\mathcal{R}\mathcal{e}\{T_{\mu }\left(z\right)\}>{\displaystyle \frac{1}{\mu -1}},$$

this implies that

$$\mathcal{R}\mathcal{e}\{\mathsf{\Psi }\left(g\left(z\right),z{g}^{\prime }\left(z\right)\right)\}>0$$

for all $z\in \mathcal{U}$. Thus,

$$\mathsf{\Psi }\left(g\left(z\right),z{g}^{\prime }\left(z\right)\right)\in \mathsf{\Omega },$$

where

$$\mathsf{\Omega }=\{w:\mathcal{R}\mathcal{e}w>0\}.$$

Furthermore,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathcal{R}\mathcal{e}\left\{\mathsf{\Psi }\right(\rho i,\xi \left)\right\}& =\xi \mathcal{R}\mathcal{e}\left\{{\displaystyle \frac{1}{\delta +\beta \rho i}}\right\}+{\displaystyle \frac{\mu }{1-\mu }}\hfill \\ \hfill & ={\displaystyle \frac{\delta \xi }{{\delta }^2+{\beta }^2{\rho }^2}}+{\displaystyle \frac{\mu }{1-\mu }}\hfill \\ \hfill & ⩽-{\displaystyle \frac{1}{2}}{\displaystyle \frac{\delta (1+{\rho }^2)}{{\delta }^2+{\beta }^2{\rho }^2}}+{\displaystyle \frac{\mu }{1-\mu }},\hfill \end{array}\end{array}$$

(16)

where $\rho \in \mathbb{R}$ and

$$\xi ⩽-{\displaystyle \frac{1+{\rho }^2}{2}}.$$

Now, assume

$$h\left(\lambda \right)=-{\displaystyle \frac{1}{2}}{\displaystyle \frac{\delta (1+\lambda )}{{\delta }^2+{\beta }^2\lambda }},$$

where

$$\lambda ={\rho }^2\in [0,\infty ).$$

Since

$$h^{\prime }\left(\lambda \right)={\displaystyle \frac{-\delta }{2}}{\displaystyle \frac{{\delta }^2-{\beta }^2}{{({\delta }^2+{\beta }^2\lambda )}^2}}⩽0,$$

the function h is decreasing, hence

$${\displaystyle \frac{-\delta }{2{\beta }^2}}<h\left(\lambda \right)⩽{\displaystyle \frac{-1}{2\delta }}.$$

(17)

Now, by the hypothesis and from (16) and (17), we have

$$\mathcal{R}e\{\mathsf{\Psi }(\rho i,\xi )\}⩽{\displaystyle \frac{-1}{2\delta }}+{\displaystyle \frac{\mu }{1-\mu }}⩽{\displaystyle \frac{\mu }{\mu -1}}+{\displaystyle \frac{\mu }{1-\mu }}=0,$$

and if $\mu =0$, then it is clear that

$$\mathcal{R}e\left\{\mathsf{\Psi }\right(\rho i,\xi \left)\right\}<0,$$

when $\rho \in \mathbb{R}$ and

$$\xi ⩽-{\displaystyle \frac{1+{\rho }^2}{2}}.$$

From Lemma 2, we infer that

$$\mathcal{R}e\left\{g\right(z\left)\right\}>0.$$

Then, $T\in {\mathcal{S}}^{\ast }$ and the proof is completed. □

Setting

$$\delta =\beta =1$$

in Theorem 3, we derive the ensuing corollary.

Corollary 1. 

Let $q\in \mathcal{BS}\left(\mu \right)$ with $\mu \in [0,{\displaystyle \frac{1}{3}}]$. Then, $L\left[q\right]\in {\mathcal{S}}^{\ast }$, where

$$L\left[q\right]\left(z\right)={\displaystyle \frac{2}{z}}{\int }_0^{z}q\left(\lambda \right)d\lambda ,(z\in \mathcal{U})$$

(18)

is the Libera operator, initially defined by Libera [22].

Corollary 2. 

Let $q\in \mathcal{BS}\left(\mu \right)$ with $\mu \in [0,3-2\sqrt{2}]$. If

$$T=L\left[q\right]$$

is given by (18), then

$${\displaystyle \frac{q\left(z\right)}{T\left(z\right)}}-1\prec {\displaystyle \frac{1}{2}}{T}_{\mu }\left(z\right),(z\in \mathcal{U}).$$

(19)

Proof. 

Suppose

$$M\left(z\right)=zq\left(z\right)$$

and

$$N\left(z\right)={\int }_0^{z}q\left(\lambda \right)d\lambda .$$

By Piejko and Sokół’s method ([23], Corollary 3.3), the function $T_{\mu }\left(z\right)$ is convex for $\mu \in [0,3-2\sqrt{2}]$.

Also,

$$1+{\displaystyle \frac{z{T}^{\prime }\left(z\right)}{T\left(z\right)}}=2{\displaystyle \frac{q\left(z\right)}{T\left(z\right)}},(z\in \mathcal{U}),$$

and by Corollary 1, for all $\mu \in [0,{\displaystyle \frac{1}{3}}]$,

$$\mathcal{R}\mathcal{e}\left\{{\displaystyle \frac{z{T}^{\prime }\left(z\right)}{T\left(z\right)}}\right\}=\mathcal{R}\mathcal{e}\{{\displaystyle \frac{2q\left(z\right)}{T\left(z\right)}}-1\}>0.$$

Therefore, $\mathcal{R}\mathcal{e}\left\{{\displaystyle \frac{q\left(z\right)}{T\left(z\right)}}\right\}>0$ and

$$\mathcal{R}\mathcal{e}\left\{{\displaystyle \frac{z{N}^{\prime }\left(z\right)}{N\left(z\right)}}\right\}=\mathcal{R}\mathcal{e}\left\{{\displaystyle \frac{zq\left(z\right)}{{\int }_0^{z}q\left(\lambda \right)d\lambda }}\right\}=2\mathcal{R}\mathcal{e}\left\{{\displaystyle \frac{q\left(z\right)}{T\left(z\right)}}\right\}>0,\hspace{1em}(z\in \mathcal{U}).$$

(20)

Since $q\in \mathcal{BS}\left(\mu \right)$,

$${\displaystyle \frac{M^{\prime }\left(z\right)}{N^{\prime }\left(z\right)}}={\displaystyle \frac{z{q}^{\prime }\left(z\right)+q\left(z\right)}{q\left(z\right)}}\prec T_{\mu }\left(z\right)+2,(z\in \mathcal{U}).$$

Thus, by using Lemma 4,

$${\displaystyle \frac{M\left(z\right)}{N\left(z\right)}}={\displaystyle \frac{2q\left(z\right)}{T\left(z\right)}}\prec T_{\mu }\left(z\right)+2,(z\in \mathcal{U})$$

or

$${\displaystyle \frac{q\left(z\right)}{T\left(z\right)}}\prec {\displaystyle \frac{1}{2}}{T}_{\mu }\left(z\right)+1,(z\in \mathcal{U}).$$

□

Theorem 4. 

Let $q\in \mathcal{KS}\left(\mu \right)$ with $\mu \in [0,{\displaystyle \frac{1}{3}}]$, then $L\left[q\right]\in \mathcal{K}$, where $L\left[q\right]$ is determined by (17).

Proof. 

Let $q\in \mathcal{KS}\left(\mu \right)$. From (6), we have

$$\mathcal{R}e\{{\displaystyle \frac{z{q}^{″}\left(z\right)}{q^{\prime }\left(z\right)}}+1\}>{\displaystyle \frac{\mu }{\mu -1}},(z\in \mathcal{U}).$$

(21)

Since $\mu \in [0,{\displaystyle \frac{1}{3}}]$,

$$\mathcal{R}e\{{\displaystyle \frac{z{q}^{″}\left(z\right)}{q^{\prime }\left(z\right)}}+1\}>-{\displaystyle \frac{1}{2}},(z\in \mathcal{U}),$$

(22)

and according to Miller and Mocanu ([20], Corollary 2.6g.2), we deduce that $L\left[q\right]\in \mathcal{K}$. □

Now, we recall the Alexander integral operator, denoted by $A\left[q\right]$, from J. W. Alexander [24]. This operator is a fundamental tool in complex analysis, particularly in the study of geometric function theory.

Theorem 5. 

Let $q\in \mathcal{BS}\left(\mu \right)$ with $\mu \in [0,1)$. If $A\left[q\right]$ is formulated as

$$A\left[q\right]\left(z\right)={\int }_0^z{\displaystyle \frac{q\left(\lambda \right)}{\lambda }}d\lambda ,(z\in \mathcal{U}),$$

(23)

then $A\left[q\right]\in \mathcal{KS}\left(\mu \right)$, where $A\left[q\right]$ is called the Alexander operator.

Proof. 

Set

$$A\left[q\right]=T.$$

It is clear that

$${\displaystyle \frac{z{T}^{\prime \prime }\left(z\right)}{T^{\prime }\left(z\right)}}={\displaystyle \frac{z^{\prime }q\left(z\right)}{q\left(z\right)}}-1,(z\in \mathcal{U}),$$

(24)

then from the hypothesis, we obtain $q\in \mathcal{KS}\left(\mu \right)$. □

Theorem 6. 

Let $q\in \mathcal{A}$ and β be a real number with $0<\beta <1$. Also, let $\mu \in [0,1)$ and $\mu ⩽1-\beta$. If

$${\displaystyle \frac{1}{\beta }}{\displaystyle \frac{z{q}^{\prime \prime }\left(z\right)}{q^{\prime }\left(z\right)}}\prec T_{\mu }\left(z\right),(z\in \mathcal{U}),$$

(25)

then $L\left[q\right]\in {\mathcal{S}}^{\ast }$ and so $q\in {\mathcal{S}}^{\ast }$, where $L\left[q\right]$ is represented by (17).

Proof. 

Let

$$g\left(z\right)={\displaystyle \frac{z{q}^{\prime }\left(z\right)}{q\left(z\right)}}.$$

Since $T_{\mu }$ is starlike and $0<\beta <1$, we have

$$\beta T_{\mu }\left(z\right)\prec T_{\mu }\left(z\right),$$

then the relation (25) implies that $q\in \mathcal{KS}\left(\mu \right)$. Therefore, by Theorem 1, q is univalent, and so g is analytic in $\mathcal{U}$. By a simple computation and the relation (25), we obtain

$${\displaystyle \frac{z{g}^{\prime }\left(z\right)}{g\left(z\right)}}+g\left(z\right)=\mathsf{\Psi }\left(g\left(z\right),z{g}^{\prime }\left(z\right)\right)=1+{\displaystyle \frac{z{q}^{\prime \prime }\left(z\right)}{q^{\prime }\left(z\right)}}\prec 1+\beta T_{\mu }\left(z\right),(z\in \mathcal{U}),$$

where

$$\mathsf{\Psi }(r,s)={\displaystyle \frac{s}{r}}+r.$$

Now, from Lemma 1,

$$\mathcal{R}\mathcal{e}\{1+\beta T_{\mu }\}>1+{\displaystyle \frac{\beta }{\mu -1}}={\displaystyle \frac{\mu +\beta -1}{\mu -1}}⩾0,$$

and so

$$\mathcal{R}\mathcal{e}\left\{\mathsf{\Psi }\left(g\left(z\right),z{g}^{\prime }\left(z\right)\right)\right\}>0$$

for all $z\in \mathcal{U}$. By utilizing Lemma 2, we should show that $\mathsf{\Psi }(\rho i,\xi )\notin \mathsf{\Omega }$, where

$$\mathsf{\Omega }=\{w:\mathcal{R}\mathcal{e}w>0\},\hspace{1em}\rho \in \mathbb{R}$$

and

$$\xi ⩽-{\displaystyle \frac{1+{\rho }^2}{2}}.$$

We have

$$\mathcal{R}\mathcal{e}\left\{\mathsf{\Psi }(\rho i,\xi )\right\}=\mathcal{R}\mathcal{e}\{{\displaystyle \frac{\xi }{\rho i}}+\rho i\}=0.$$

(26)

Thus,

$$\mathcal{R}e\left\{g\right(z\left)\right\}>0$$

and then $q\in {\mathcal{S}}^{\ast }$. Now, since $L\left[{\mathcal{S}}^{\ast }\right]\subset {\mathcal{S}}^{\ast }$, we have $L\left[q\right]\in {\mathcal{S}}^{\ast }$. □

Theorem 7. 

Let $q\in \mathcal{KS}\left(\mu \right)$ with $\mu \in [0,3-2\sqrt{2}]$. If $q\in {\mathcal{S}}^{\ast }$, then $q\in \mathcal{BS}\left(\mu \right)$.

Proof. 

Suppose

$$M\left(z\right)=z{q}^{\prime }\left(z\right)$$

and

$$N\left(z\right)=q\left(z\right).$$

According to the hypothesis,

$$\mathcal{R}e\{{\displaystyle \frac{z{N}^{\prime }\left(z\right)}{N\left(z\right)}}\}>0$$

in $\mathcal{U}$. Also by ([23], Corollary 3.3), the function $T_{\mu }\left(z\right)+1$ is convex for $\mu \in [0,3-2\sqrt{2}]$. On the other hand, by (5),

$${\displaystyle \frac{M^{\prime }\left(z\right)}{N^{\prime }\left(z\right)}}={\displaystyle \frac{z{q}^{″}\left(z\right)+q^{\prime }\left(z\right)}{q^{\prime }\left(z\right)}}\prec T_{\mu }\left(z\right)+1,(z\in \mathcal{U}).$$

Therefore, by Lemma 4,

$${\displaystyle \frac{M\left(z\right)}{N\left(z\right)}}={\displaystyle \frac{z{q}^{\prime }\left(z\right)}{q\left(z\right)}}\prec T_{\mu }\left(z\right)+1,(z\in \mathcal{U}),$$

and so $q\in \mathcal{BS}\left(\mu \right)$. □

Remark 2. 

For $q\in \mathcal{BS}\left(\mu \right)$, we have

$$\mathcal{R}e\left\{{\displaystyle \frac{z{q}^{\prime }\left(z\right)}{q\left(z\right)}}\right\}>{\displaystyle \frac{\mu }{\mu -1}}.$$

For the class $\mathcal{BS}\left(\mu \right)$, the problem of finding the radius of starlikeness of order δ ($0⩽\delta <1$) has been considered.

By [13], $q\in \mathcal{BS}\left(\mu \right)$ is starlike of order $\delta$ ($0⩽\delta <1$) in the disk

$$\left|z\right|<{\displaystyle \frac{\sqrt{1+4\mu (1-\delta )}-1}{2\mu (1-\delta )}}.$$

Motivated by this work, if $q\in \mathcal{KS}\left(\mu \right)$, from the relation (5), we have

$$\mathcal{R}e\{{\displaystyle \frac{z{q}^{″}\left(z\right)}{q^{\prime }\left(z\right)}}+1\}>{\displaystyle \frac{\mu }{\mu -1}},$$

so we can discuss the radius of convexity of order $\delta$ in the class $\mathcal{KS}\left(\mu \right)$.

Theorem 8. 

Let $q\in \mathcal{KS}\left(\mu \right)$ with $\mu \in (0,1)$. Then, q is convex of order δ in the disk

$$\left|z\right|<{\displaystyle \frac{\sqrt{1+4\mu (1-\delta )}-1}{2\mu (1-\delta )}},$$

where $\delta \in [0,1)$. This result is sharp.

Proof. 

This theorem and Theorem 2.1 in [13] are proved similarly. Note that for the function

$$q\left(z\right)={\int }_0^z{\left({\displaystyle \frac{1+\sqrt{\mu }\lambda }{1-\sqrt{\mu }\lambda }}\right)}^{{\displaystyle \frac{1}{2\sqrt{\mu }}}}d\lambda ,$$

the result is sharp. □

Setting $\delta =0$ in Theorem 8, we infer the corollary below.

Corollary 3. 

Let $q\in \mathcal{KS}\left(\mu \right)$ with $\mu \in (0,1)$. Then, q is convex in the disk

$$\left|z\right|<{\displaystyle \frac{\sqrt{1+4\mu }-1}{2\mu }}.$$

This result is sharp.

Let

$$B\left(z\right)=\sum _{r=0}^{\infty }{a}_r{z}^r$$

and

$$D\left(z\right)=\sum _{r=0}^{\infty }{b}_r{z}^r.$$

The Hadamard product, also referred to as convolution, for a pair of power series is defined in the following manner:

$$\begin{array}{c}\hfill (B\ast D)\left(z\right)=B\left(z\right)\ast D\left(z\right)=\sum _{r=0}^{\infty }{a}_r{b}_r{z}^r.\end{array}$$

If $\mu \in \mathbb{C}$ and

$$l\left(z\right)={\displaystyle \frac{z}{1-z}},$$

then

$$(B\ast \mu D)\left(z\right)=\mu (B\ast D)\left(z\right),B\left(z\right)\ast l\left(z\right)=B\left(z\right),z{B}^{\prime }\left(z\right)=B\left(z\right)\ast z{l}^{\prime }\left(z\right)$$

and

$$z{B}^{\prime }\left(z\right)\ast D\left(z\right)=B\left(z\right)\ast z{D}^{\prime }\left(z\right).$$

Convolution holds a pivotal position within the geometric function theory. It enables the analysis of complex functions, particularly in areas like Fourier analysis and differential equations. Also, convolution provides a powerful tool for understanding the interactions between different components of a complex system and is widely applied in fields such as physics, engineering, and computer science. In the next theorems, we investigate convolution properties in the subclasses $\mathcal{BS}\left(\mu \right)$ and $\mathcal{KS}\left(\mu \right)$.

Theorem 9. 

Let

$$q\left(z\right)=z+\sum _{r=2}^{\infty }{a}_r{z}^r$$

with $\mu \in [0,1)$. If $q\in \mathcal{BS}\left(\mu \right)$, then

$${\displaystyle \frac{q\left(z\right)}{z}}\ast h_{\mu }\left(z\right)\ne 0,(z\in \mathcal{U}),$$

(27)

where

$$h_{\mu }\left(z\right):=h(\mu ,x)\left(z\right)={\displaystyle \frac{z(-\frac{1}{x}+\mu x-1)+1}{{(1-z)}^2}},(z\in \mathcal{U},|x|=1).$$

(28)

Also the relation (27) holds if and only if

$$\sum _{r=1}^{\infty }{B}_r{z}^{r-1}\ne 0,(z\in \mathcal{U}),$$

(29)

where

$$B_r=((r-1)(\mu x-{\displaystyle \frac{1}{x}})+1)a_r,(r⩾1,|x|=1).$$

Proof. 

Let $q\in \mathcal{BS}\left(\mu \right)$. By Definition 1,

$${\displaystyle \frac{z{q}^{\prime }\left(z\right)}{q\left(z\right)}}-1\ne {\displaystyle \frac{x}{1-\mu x^2}},\left(\right|x|=1,z\in \mathcal{U})$$

or

$$(1-\mu x^2)z{q}^{\prime }\left(z\right)+(\mu x^2-x-1)q\left(z\right)\ne 0.$$

(30)

According to the properties of the Hadamard product, the relation (30) is identical to

$$q\left(z\right)\ast \left[(1-\mu x^2){\displaystyle \frac{z}{{(1-z)}^2}}+(\mu x^2-x-1){\displaystyle \frac{z}{1-z}}\right]\ne 0,$$

or

$${\displaystyle \frac{q\left(z\right)}{z}}\ast \left[{\displaystyle \frac{(1-\mu x^2)+(\mu x^2-x-1)(1-z)}{{(1-z)}^2}}\right]\ne 0,$$

or

$${\displaystyle \frac{q\left(z\right)}{z}}\ast (-x)\left[{\displaystyle \frac{z\left(\frac{1+x-\mu x^2}{-x}\right)+1}{{(1-z)}^2}}\right]\ne 0.$$

(31)

Since $\left|x\right|=1$, we have $x\ne 0$. Then the relation (31) holds if and only if

$${\displaystyle \frac{q\left(z\right)}{z}}\ast \left[{\displaystyle \frac{z(-\frac{1}{x}+\mu x-1)+1}{{(1-z)}^2}}\right]\ne 0.$$

(32)

Since

$${\displaystyle \frac{1}{{(1-z)}^2}}=\sum _{r=1}^{\infty }r{z}^{r-1},$$

the relation (32) is identical to

$$\sum _{r=1}^{\infty }{a}_r{z}^{r-1}\ast \left[(\mu x-{\displaystyle \frac{1}{x}}-1)\sum _{r=1}^{\infty }(r-1)z^{r-1}+\sum _{r=1}^{\infty }r{z}^{r-1}\right]\ne 0$$

or

$$\sum _{r=1}^{\infty }((r-1)(\mu x-{\displaystyle \frac{1}{x}})+1)a_r{z}^{r-1}\ne 0.$$

Therefore, the relation (32) holds if and only if

$$\sum _{r=1}^{\infty }{B}_r{z}^{r-1}\ne 0,(z\in \mathcal{U}),$$

where

$$B_r=((r-1)(\mu x-{\displaystyle \frac{1}{x}})+1)a_r,(r⩾1,|x|=1).$$

□

Theorem 10. 

Let

$$q\left(z\right)=z+\sum _{r=2}^{\infty }{a}_r{z}^r$$

with $\mu \in [0,1)$. If $q\in \mathcal{KS}\left(\mu \right)$, then

$${\displaystyle \frac{q\left(z\right)}{z}}\ast h_{\mu }\left(z\right)\ne 0,(z\in \mathcal{U}),$$

(33)

where

$$h_{\mu }\left(z\right):=h(\mu ,x)\left(z\right)={\displaystyle \frac{z(2\mu x-\frac{2}{x}-1)+1}{{(1-z)}^3}},(z\in \mathcal{U},|x|=1).$$

(34)

Also, the relation (33) holds if and only if

$$\sum _{r=1}^{\infty }{C}_r{z}^{r-1}\ne 0,(z\in \mathcal{U}),$$

(35)

where

$$C_r=r{a}_r[1+(\mu x-{\displaystyle \frac{1}{x}})(r-1)],(r⩾1,|x|=1).$$

Proof. 

Suppose $q\in \mathcal{KS}\left(\mu \right)$ and

$$p\left(z\right)=z{q}^{\prime }\left(z\right).$$

By the relation (5), $q\in \mathcal{KS}\left(\mu \right)$ precisely when

$${\displaystyle \frac{z{p}^{\prime }\left(z\right)}{p\left(z\right)}}-1={\displaystyle \frac{z{q}^{\prime \prime }\left(z\right)}{q^{\prime }\left(z\right)}}\prec {\displaystyle \frac{z}{1-\mu z^2}},(z\in \mathcal{U}).$$

Consequently,

$${\displaystyle \frac{z{p}^{\prime }\left(z\right)-p\left(z\right)}{p\left(z\right)}}\ne {\displaystyle \frac{x}{1-\mu x^2}},(z\in \mathcal{U},|x|=1)$$

or

$$(1-\mu x^2)z{p}^{\prime }\left(z\right)+(\mu x^2-x-1)p\left(z\right)\ne 0.$$

(36)

The relation (36) is equivalent to

$$p\left(z\right)\ast \left[(1-\mu x^2){\displaystyle \frac{z}{{(1-z)}^2}}+(\mu x^2-x-1){\displaystyle \frac{z}{1-z}}\right]\ne 0$$

or

$$q\left(z\right)\ast z{\left[(1-\mu x^2){\displaystyle \frac{z}{{(1-z)}^2}}+(\mu x^2-x-1){\displaystyle \frac{z}{1-z}}\right]}^{\prime }\ne 0.$$

(37)

The relation (37) holds if and only if

$${\displaystyle \frac{q\left(z\right)}{z}}\ast (-x)\left[{\displaystyle \frac{z(2\mu x-\frac{2}{x}-1)+1}{{(1-z)}^3}}\right]\ne 0,(x\ne 0,|x|=1)$$

or

$${\displaystyle \frac{q\left(z\right)}{z}}\ast \left[{\displaystyle \frac{z(2\mu x-\frac{2}{x}-1)+1}{{(1-z)}^3}}\right]\ne 0,(x\ne 0,|x|=1).$$

(38)

Since

$${\displaystyle \frac{1}{{(1-z)}^3}}=\sum _{r=2}^{\infty }{\displaystyle \frac{r(r-1)}{2}}{z}^{r-2},$$

the relation (38) is equivalent to

$$\sum _{r=1}^{\infty }{a}_r{z}^{r-1}\ast \left[\sum _{r=1}^{\infty }{\displaystyle \frac{r(r+1)}{2}}{z}^{r-1}+(2\mu x-{\displaystyle \frac{2}{x}}-1)\sum _{r=1}^{\infty }{\displaystyle \frac{r(r-1)}{2}}{z}^{r-1}\right]\ne 0$$

or

$$\sum _{r=1}^{\infty }r{a}_r(1+(\mu x-{\displaystyle \frac{1}{x}})(r-1))z^{r-1}\ne 0.$$

Therefore, the relation (38) holds if and only if

$$\sum _{r=1}^{\infty }{C}_r{z}^{r-1}\ne 0,(z\in \mathcal{U}),$$

where

$$C_r=r{a}_r[1+(\mu x-{\displaystyle \frac{1}{x}})(r-1)],(r⩾1,|x|=1).$$

□

3. Conclusions

This study explores a selection of geometric attributes pertaining to the subclasses $\mathcal{KS}\left(\mu \right)$ and $\mathcal{BS}\left(\mu \right)$ ($0⩽\mu <1$) of univalent functions, which are related to the Booth lemniscate within the open unit disk. We established some results on differential subordinations and integral operators such as $I_{\beta ,\delta }\left[q\right]$ given in (14) and the Libera and Alexander operators. Also, for the class $\mathcal{BS}\left(\mu \right)$ ($0⩽\mu <1$), finding the radius of starlikness of order $\delta$ ($0⩽\delta <1$) has been considered in [13], and in this paper, we obtained the radius of convexity of order $\delta$ in the class $\mathcal{KS}\left(\mu \right)$. For future works, we can discuss the relation between these classes and other famous and important integral operators. Also, by applying different subclasses of analytic functions, one can gain insights into their geometric properties, coefficient bounds, and other characteristics.

Recent scholarly investigations have increasingly focused on the application and analysis of q-fractional calculus operators. A comprehensive examination of various fractional calculus operators, encompassing both fractional integrals and derivatives, is evident in the existing literature (see [25,26,27]). The results presented in this paper prompt an inquiry into the potential for extending the established theorems to incorporate fractional integral operators. Such an extension represents a promising avenue for future research and discovery.